2. 浙江畅尔智能装备股份有限公司,浙江 缙云 321404
2. Zhejiang CHR Intelligent Equipment Limited Company, Jinyun 321404, China
机床关键结构件或部件在一定装配工艺及条件下的结构和性能优化,有助于实现机床整机动态特性的改善. 针对机床动态特性的基础性研究主要集中于以下几个方面:关键部件的动态特性分析;结构大件的有限元分析;结合面动态特性与动态参数获取等[1]. 其中,利用有限元方法和软件对机床关键部件的动态特性分析和优化设计成为重要手段,有大量的理论研究和应用成果报道[2-6]. 这些研究有效利用数值理论和有限元方法,开展机床结构轻量化设计和性能优化,弥补了传统机床设计方法难以确定结构与机床动态特性影响关系的不足,缺陷是缺乏实验佐证,特别是在一定的装配工艺及条件下,有限元模型的准确性难以保证. Altintas等[7]对目前机床设计中的有限元、刚柔耦合等分析技术进行讨论,认为机床结构、加工过程的集成仿真及耦合分析尚没有很好地应用于工程实际.
另一方面,Bin等[8-10]利用试验手段获取机床关键部件动态参数,提出改进方法. 采用试验方法可以获取准确的机床动态参数,但是试验成本较高,而且需要具备丰富的理论功底和实践经验. 此外,大型机床往往受到切削力谐波特性的干扰,很难准确地获得实际工况下的机床动态参数[11-13],即使获得机床准确的动态参数,也需要经过较长的周期才能对改进方案实施验证,目前在机械工程领域特别是机床工业中尚没有得到推广应用.
本文结合有限元方法和模态试验手段,对机床结构件的优化设计展开研究. 利用模态试验获得修正的有限元模型,采用拓扑优化方法和有限元软件,开展机床结构件动态性能优化设计.
1 拉床床台有限元基础仿真 1.1 拉床床台的结构特点拉床是一种高效率的金属切削机床,适宜大批量零件的加工. 由于拉床加工尺寸和形状位置精度高、操作维修方便、加工成本低且易实现自动化,其应用范围日益广泛,工艺范围由一般的内孔和平面拉削扩展到较复杂的型面加工. 如图1所示为LG5120SH-1600立式内拉床结构,包括底座、床身、床台(3大支撑件)、溜板、工作台等. 该型号拉床额定拉削力为20 kN,行程为1 600 mm. 其中床台作为3大支撑件之一,通过工作台与拉刀、工件、夹具等组成的拉削模块直接相连,静刚度和动态特性直接影响拉削质量. LG5120SH-1600的床台如图2所示,是钢板焊接的大型箱体类结构,由上端板、隔板、侧板、矩形筋板、内前板、外前板三角板、立板、背板、墙板、下端板、竖筋板、横筋板、前/后梯形板等组成,呈对称布置. 外观尺寸为930 mm × 570 mm × 2 005 mm,材料为Q235,质量为1.863 t,占拉床结构件总质量的27%. 作为拉床的3大支撑件之一,床台的性能要求是扭转刚度好,抗挠度强.

|
图 1 LG5120SH-1600立式内拉床结构 Fig. 1 Mechanical structure of vertical internal broaching machine LG5120SH-1600 |

|
图 2 LG5120SH-1600的床台结构 Fig. 2 Table base structure of LG5120SH-1600 |
为了提高有限元建模精度,有限元模型具有三维实体几何模型相同的尺寸. 对小尺寸的倒角、细孔几何特征等作了简化处理. 采用HyperWorks 11.0软件,开展几何前处理和网格划分. 为了减少计算量,提高计算精度,有限元模型全部采用六面体网格,如图3所示,包含359 186个节点和317 033个线性六面体单元. 用刚性连接模拟各筋板之间的焊接. 床台附加边界条件的设置从床台实际约束情况出发,尽可能地接近实际. 床台背面通过螺钉与床身连接,底部通过螺钉与底座连接,分别采用约束螺孔周围节点6个自由度的方法进行模拟.

|
图 3 床台有限元模型和边界条件 Fig. 3 Finite element model and boundary condition |
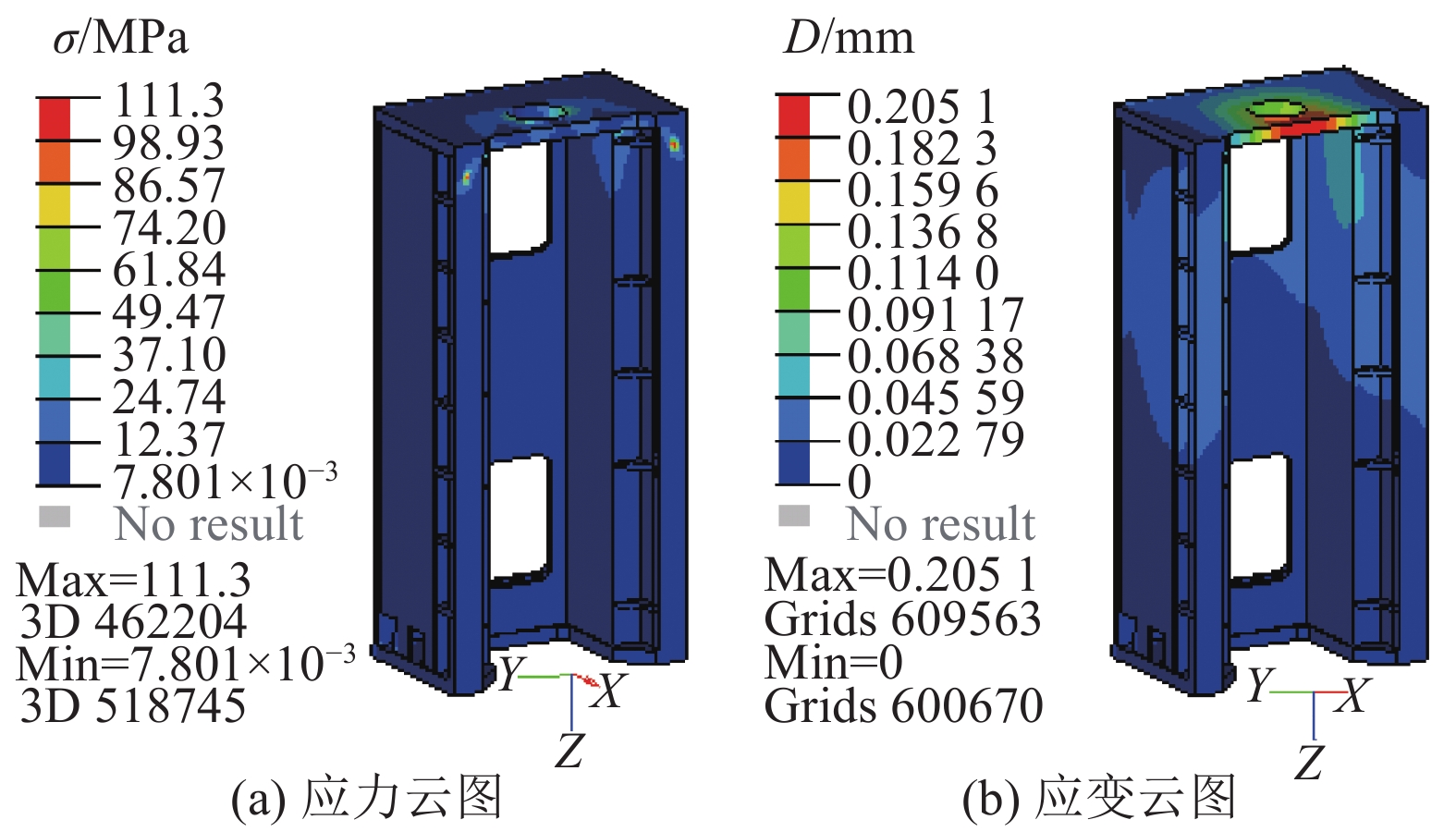
床台静力分析的主要目的是确定它的应力应变情况. 当施加载荷时,应尽可能接近实际工况. 由于床台受力主要集中在上端板(与工作台接触)圆孔中心竖直方向,在圆孔中心位置施加了一个–Z方向的集中力,大小为200 kN. 采用OptiStruct求解器求解得到应变应力云图,如图4所示. 图中,σ为应力,D为应变.
|
图 4 优化前床台静力学有限元分析结果 Fig. 4 Static results of original table base by finite element analysis |
根据仿真结果可知,床台变形的主要部位在床台顶部,最大变形为0.205 1 mm. 最大应力集中在床台顶部,最大应力为111.3 MPa. Q235的屈服强度
模态分析的必要前提是系统线性化[14],所以床台材料假设为线性弹性材料,且各向同性. 采用OptiStruct求解器求解,得到床台前8阶模态参数,图5给出其中前6阶固有频率及振型.

|
图 5 床台数值模态频率与振型 Fig. 5 First-six-step mode shapes and natural frequencies by finite element analysis |
在拉削过程中,拉刀对机床系统的激振频率为
| $f = \frac{v}{{0.06\,p}}.$ | (1) |
式中:v和p分别为拉削速度和拉刀齿距,本文所选的拉床型号分别取v和p为10 m/min和12 mm,可得f=13.38 Hz. 激励频率及倍频与床台第一阶频率相差较大,不会引起共振,满足拉削加工的需要.
2 床台的试验模态分析 2.1 振动测试系统试验所采用的振动测试系统主要包括:PC机、数字式采集系统、试验模态分析软件、加速度传感器和激振器. 实验时,加速度传感器采集各拾振点的加速度信号,经同轴电缆传递给LMS SCADAS Ⅲ前端,完成初步采样和处理;然后经过RJ45网线传输到PC,由PC上运行的实验模态分析软件Test.LAB软件进一步完成信号处理. 如表1所示为振动测试系统规格和性能参数.
| 表 1 振动测试系统规格和性能参数 Table 1 Specifications of vibration test system |
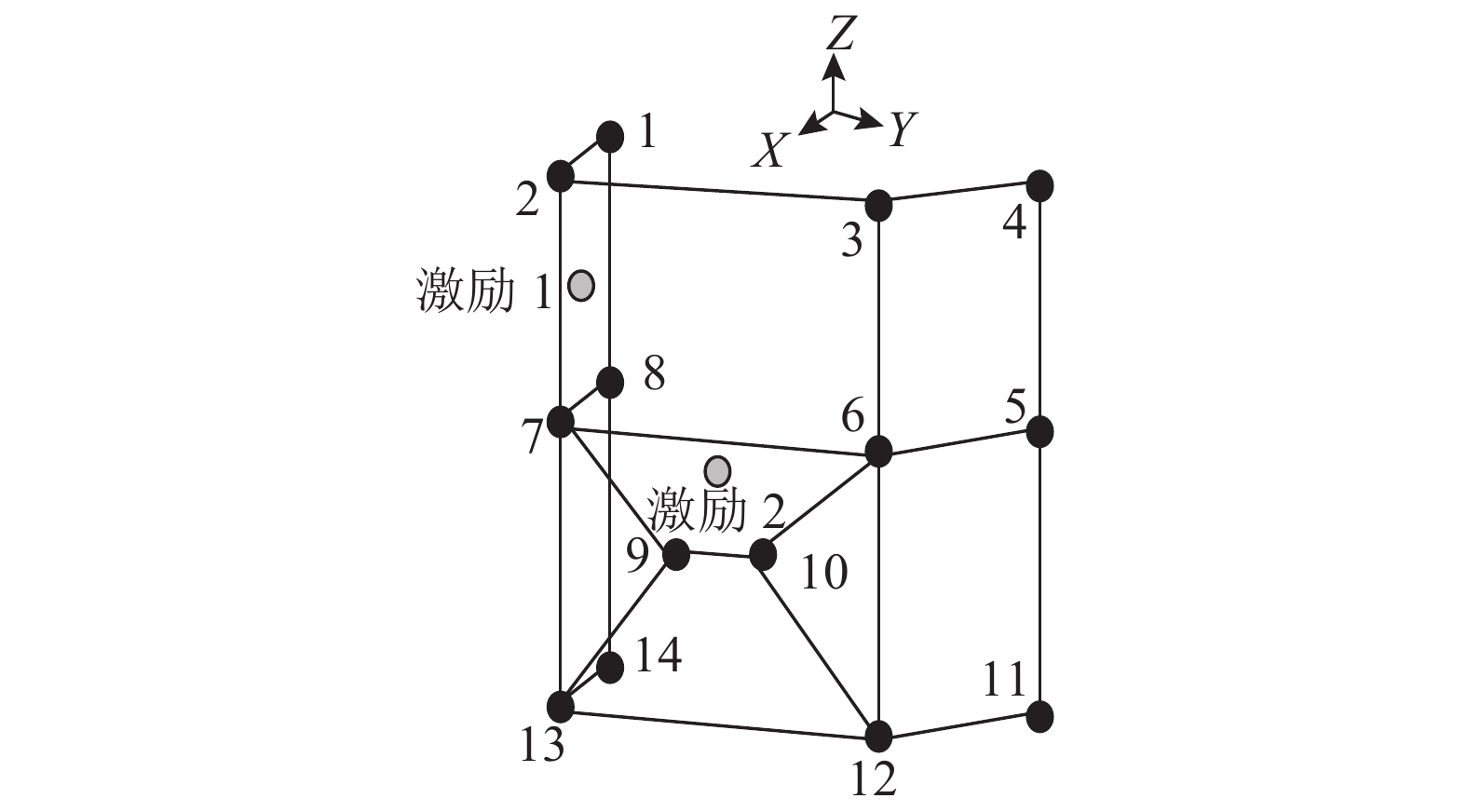
拾振点的布置非常重要,一般要求远离所关心的模态振型节点. 在床台模型上建立笛卡尔坐标系,原点位于背板上棱线中点位置,X轴为背板指向前板方向,Y轴为背板上棱线向右方向. 试验采用2台激振器分别从-X方向和+Y方向,同时对床台进行激振. 为了使感兴趣的模态全部激励起来,床台激励1点所设置的信号为Y方向上的扫频信号,床台激励2点所设置的信号为-X方向上的猝发随机信号. 如图6所示,在床台上共布置14个拾振点:前板上布置6个拾振点,左、右板上各布置3个拾振点,床台内部布置2个拾振点. 9点测试+Y方向响应,10点测试–Y方向响应. 如图7所示为实验现场拍摄的模态试验装置图.
|
图 6 拾振点分布 Fig. 6 Layout of response points |

|
图 7 模态试验现场照片 Fig. 7 Photograph of physical system for modal test |
为了获得实际工况条件下的模态参数,试验时床台底面和背面上的连接孔通过螺钉固定. 选取合适的激振持续时间和测试时间,若采集的响应信号时间历程过短,则难以估计模态参数. 激励和采集信号的时长为4 s,采样频率为2 048 Hz,一次历程中每个传感器采集到8 192个数据. 采用LMS Test.Lab软件进行信号处理. 表2给出采样频率、指数窗和谱线数等信号采集和处理的参数.
| 表 2 信号采集和处理参数设置 Table 2 Information on data acquisition and signal processing |
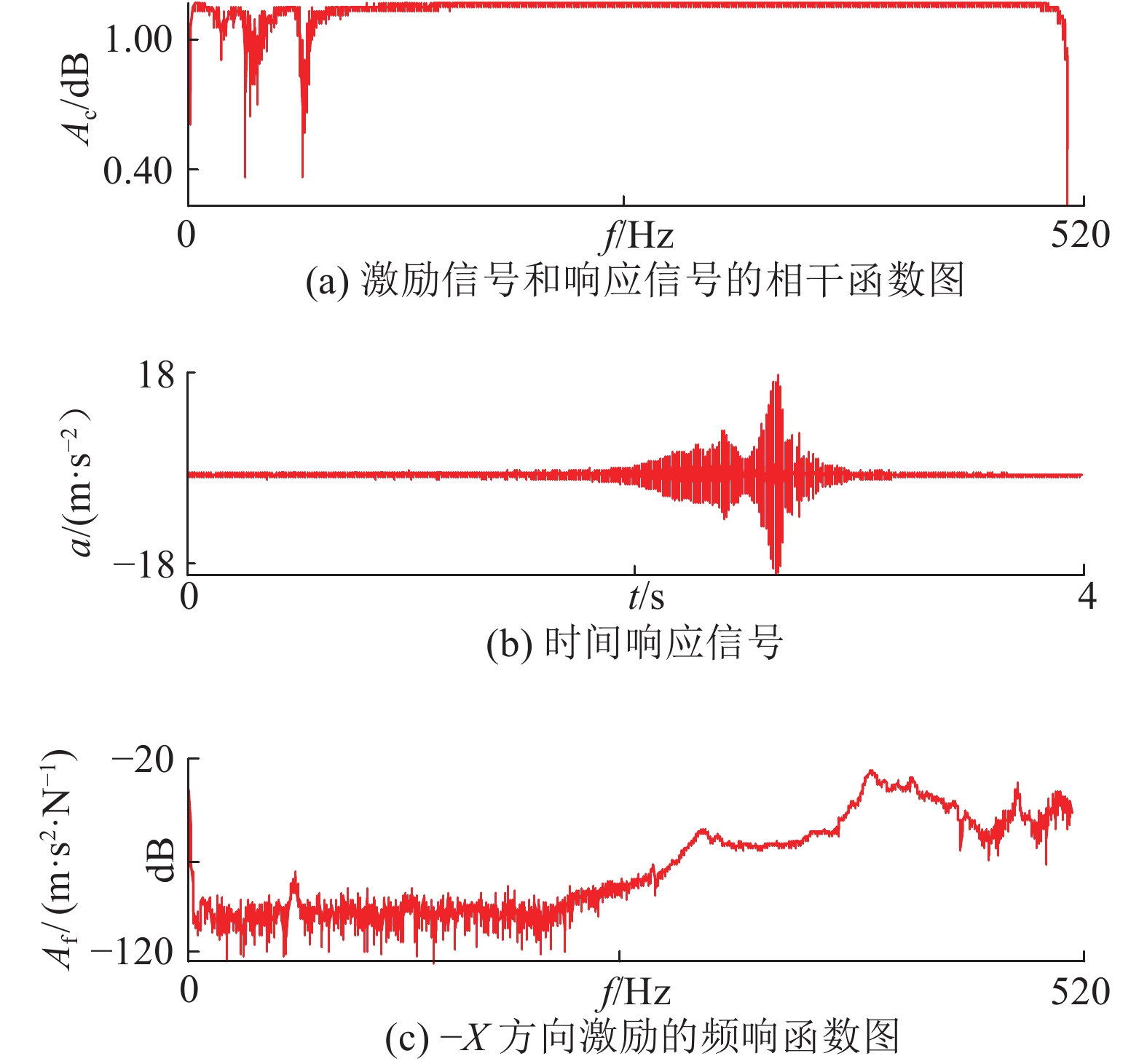
如图8(a)所示为拾振点7的激励信号和响应信号的相干函数图. 可见,在0~512 Hz下,激励信号和响应信号的相关系数大都为1,表明拾振点和激励点的分布是合理的. 为了消除结构动态的非线性,降低测量信号中的噪声影响,对每个拾振点重复10次进行平均处理,得到准确的FRF测量值. 如图8(b)、(c)所示分别为拾振点7的时间响应信号和–X方向激励的频响函数图. 图中,Ac、Af分别为相干函数幅值和频响函数幅值.
|
图 8 拾振点7的响应信号 Fig. 8 Signal profile of response point 7 |
采用PolyMAX法只需要极少量的运算和整理,并且产生的稳态图可以识别高度密集的模态,对每一个模态的频率、阻尼和振型都有极高的识别精度. 选择模态估计的频段为0~512 Hz,设定模态所用的最大模态阶数为32. 模态稳定的标准如下:频率标准、振型矢量和阻尼变化分别为1%、2%和5%,利用LMS. Test.lab软件和PolyMAX方法,生成模态稳态图,如图9所示. 图中,A为幅值. 从稳态图中选择稳定模态,得到床台的前6阶试验模态振型如图10所示,前8阶频率如表3所示. 表中,fn为固有频率,ζ为阻尼比.

|
图 9 模态稳态图(PolyMAX方法) Fig. 9 Mode stabilization diagram using PolyMAX method |

|
图 10 前6阶实验模态振型图 Fig. 10 First-six-step mode shapes from modal test |
| 表 3 床台试验模态参数 Table 3 Modal parameters from modal test |
试验模态分析结果要和理论模态分析结果进行对比,不仅可以验证拉床床台模型建立的准确性,而且可以为优化设计提供依据. 尽管由于某些不可避免的原因会产生误差,但在附加边界条件下的理论模态频率分析结果与试验模态频率分析结果基本一致. 对比如表4所示. 表中,fnT为试验固有频率,fnA为有限元固有频率,Δfn为误差.
| 表 4 有限元与试验分析固有频率的对比 Table 4 Comparison of natural frequencies from modal test and FE analysis |
由于床台本身的结构特点,自身的固有频率偏高,在拉床运动过程中,低阶的固有频率较整个机床的低阶模态频率较高,因此在计算出来的模态频率范围内,床台的低阶模态很容易越界. 由表4对比发现,床台前2阶实验模态与计算模态不一致,可以判断前2阶实验模态是整机模态,将前2阶试验模态从床台模态中剔除. 后6阶试验模态在理论模态中可以找到对应的模态频率,但是存在一定的差值. 从数据的可靠性上来看,有限元与试验分析得到的各阶固有频率相对差值小于5%,在可接受范围内.
如图11所示为剔除前2阶整机模态后床台的模态置信度(modal assurance criterion,MAC)矩阵. 主对角线MAC均为100%,非主对角线上各阶MAC都较小,证明实验与分析的振型向量具有一定的相关性,估计的模态参数比较可靠,同时证明建立的床台有限元模型是准确的.

|
图 11 实验与分析的MAC矩阵 Fig. 11 MAC between modes shapes from modal test and FE analysis |
拓扑优化的目的是寻求结构材料在设计空间最佳的分布形式,优化结构的某种性能或减轻结构的重量[15]. 变密度法SIMP(solid isotropic microstructures with penalization)作为众多拓扑优化方法中的一种,以其概念简单和易于实现等优点而得到了广泛的应用. 众多结构优化软件,如Optistruct、LS-Tasc 等,采用SIMP 法中的插值模型[16]. 在SIMP方法中,通过引入材料插值的方式引入连续变量,可以解决拓扑优化离散变量不连续的问题,SIMP方法的材料插值公式为
| $\begin{aligned}{E_i}{\rm{(}}{x_i}) = {E_{\min }} + x_i^{\rm p}({E_{\rm{0}}} - {E_{\min }}){\rm{ }};{{x_i} \in [0,1]}.\end{aligned}$ | (2) |
式中:i为单元号;
| $\left. \begin{array}{l} {\rm{min}}\,C(x) = \displaystyle\frac{{\rm{1}}}{{\rm{2}}}{{{U}}^{\rm T}}{{KU}} = \displaystyle\frac{1}{2}\displaystyle\sum\limits_{i = 1}^N {{E_i}({x_i}){ u}_i^{\rm T}{{{k}}_0}{{{u}}_i}}; \\{\rm{s}}{\rm{.t}}\,{\rm{. }}V(x) - {V^*} \leqslant {\rm{0}},{{KU}} = {{F}},\\0 \leqslant {x_{\min }} \leqslant {x_i}\leqslant{\rm{1}}.\end{array} \right\}$ | (3) |
式中:C为整体结构的平均柔顺度;K为总体刚度矩阵;U为结构的位移向量;N为整体单元的数量;
为了实现床台结构轻量化高刚度优化设计,采用基于变密度法的拓扑优化[17]. 为了获得床台清晰完整的应力传递路线,定义整个床台模型为设计空间. 床台在工作过程中承受单向拉削力作用力,在切削点处(上端板圆孔中心)的最大变形直接影响工件切削质量,是最重要的性能参数;此外,拉床的第1阶模态频率是反映拉床动态特性的重要参数. 开展床台优化时,必须满足切削点处最大变形和一阶模态频率性能的要求. 在优化设计中,要求切削点处的最大变形量不小于0.185 5 mm,第1阶模态频率不小于191 Hz.
以单元密度为设计变量,以体积最小化为目标函数,以床台切削点最大变形和床台一阶模态为约束条件,采用OptiStruct开展优化计算,经过19次迭代后收敛. 在后处理软件中,设置单元密度阈值为0.536,将不影响性能的材料自动去除后,如图12所示. 图中,Vf为密度比. 可见,内前板、竖筋板、侧板上端、前梯形板、下端板可减弱,上端板可增强.

|
图 12 床台结构拓扑优化结果 Fig. 12 Topology optimization results of table base structure |
根据图12和分析结果,对床台进行二次设计. 床台下部与底座连接,须起到支撑作用,所以不能去除优化,可以减薄下端板;内前板不与任何部件接触,可知该部分的刚度非常好,所以该部分可以进行去除优化;侧板减薄竖筋板、前梯形板根据材料分布重新布置,如图13所示.

|
图 13 二次设计后的拉床床台结构 Fig. 13 Redesigned table base structure of broaching machine |
对优化后的床台进行有限元静力学分析和模态分析. 图14给出优化后床台的应力应变云图. 对比分析图4可见,应力最大位置与应力集中区域在优化前、后未发生转移.

|
图 14 优化后床台静力学有限元分析结果 Fig. 14 Static results of redesigned table base by finite element analysis |
表5给出优化前、后的床台质量 M、切削点最大变形ε及第一阶固有频率 f1的对比情况. 可见,在减重5.7%的情况下,f1增大2.62%,ε增大2.70%,保持了良好的静态特性,提升了动态性能. 优化后床台的最大应力为112.0 MPa,安全系数为2.29.
| 表 5 优化前、后的床台性能对比 Table 5 Performance comparison of table base before and after optimization |
所选的拉床拉削速度和齿升量分别取v和p为10 m/min和12 mm. 根据1.4节的计算结果,可得拉削过程中拉刀对机床系统的激励频率f=13.38 Hz. 优化后的床台第1阶频率与激励频率及倍频相比存在较大差距,不会引起共振,满足拉削加工的需要.
4 结 语在获得拉床床台修正模型的基础上,利用拓扑优化方法开展床台结构的轻量化高刚度设计,在减重5.7%的情况下,切削点处变形增大2.7%,第1阶固有频率增加2.62%. 机床结构件获得了更好的动态性能,有助于提高机床整机刚度和切削质量.
与纯有限元仿真和优化相比,本文方法提供了实验验证,计算结果准确可靠;与机床动态测试和改进相比,本文利用拓扑优化理论和有限元方法的便利快捷,更具有可行性.
在试验模态分析中,为了激振1.863 t的床台,采样了2个大功率的LW-139-40激振器进行激振. 对于更大吨位的拉床整机及结构件,必须采用更多数量和更大功率的激振器进行激励,这不仅使得激励点的选择变得困难,而且会增加试验成本. 在后续的工作中,考虑利用工作模态分析来计算模态参数.
| [1] |
叶佩青, 王仁彻, 赵彤, 等. 机床整机动态特性研究进展[J]. 清华大学学报: 自然科学版, 2012, 52(12): 1758-1763. YE Pei-qing, WANG Ren-che, ZHAO Tong, et al. Recent research advances of whole machine tool dynamics[J]. Journal of Tsinghua University: Science and Technology, 2012, 52(12): 1758-1763. |
| [2] |
ZHAO L, MA J, CHEN W, et al. Lightweight design and verification of gantry machining center crossbeam based on structural bionic[J]. Journal of Bionic Engineering, 2011, 8(2): 201-206. |
| [3] |
KIM D, JUNG S, LEE J, et al. Parametric study on design of composite–foam–resin concrete sandwich structures for precision machine tool structures[J]. Composite Structures, 2006, 75(1-4): 408-414. DOI:10.1016/j.compstruct.2006.04.022 |
| [4] |
HULL P, CANFIELD S. Optimal synthesis of compliant mechanisms using subdivision and commercial FEA[J]. Journal of Mechanical Design, 2006, 128(2): 337-348. |
| [5] |
王磊, 刘海涛, 金涛, 等. 一种机床固定结合面形状的拓扑设计方法[J]. 振动工程学报, 2014, 27(4): 481-487. WANG Lei, LIU Hai-tao, JIN Tao, et al. A design method of fixed joint contact area topology-based equivalent model for machine tools[J]. Journal of Vibration Engineering, 2014, 27(4): 481-487. DOI:10.3969/j.issn.1004-4523.2014.04.002 |
| [6] |
戴磊, 关振群, 单菊林, 等. 机床结构三维参数化形状优化设计[J]. 机械工程学报, 2008, 44(5): 152-159. DAI Lei, GUAN Zhen-qun, SHAN Ju-lin, et al. 3D parameterized shape optimization design for machine tool mechanism[J]. Chinese Journal of Mechanical Engineering, 2008, 44(5): 152-159. DOI:10.3321/j.issn:0577-6686.2008.05.025 |
| [7] |
ALTINTAS Y, BRECHER C, WECK M, et al. Virtual machine tool[J]. CIRP Annals - Manufacturing Technology, 2005, 54(2): 115-138. DOI:10.1016/S0007-8506(07)60022-5 |
| [8] |
LI Bin, CAI Hui, MAO Xin-yong, et al. Estimation of CNC machine-tool dynamic parameters based on random cutting excitation through operational modal analysis[J]. International Journal of Machine Tools and Manufacture, 2013(71): 26-40. |
| [9] |
ELBESTAWI M A, VELDHUIS S C, DEIAB I M. Development of a novel modular and agile face machining technology[J]. Annals of the CIRP, 2002(49): 303-308. |
| [10] |
杨毅青, 刘强, 申江丽, 等. 基于动力学及切削特性耦合的数控机床结构设计[J]. 振动与冲击, 2013, 32(10): 198-202. YANG Yi-qing, LIU Qiang, SHEN Jiang-li, et al. Machine tool structure design based on the coupling analysis of dynamics and cutting performances[J]. Journal of Vibration and Shock, 2013, 32(10): 198-202. DOI:10.3969/j.issn.1000-3835.2013.10.036 |
| [11] |
GADE S, M LLER N, HERLUFSEN H, et al. Frequency domain techniques for operational modal analysis [C] // Proceedings of the 1st International Operational Modal Analysis Conference. Copenhagen, Denmark: Springer, 2005. https://link.springer.com/chapter/10.1007%2F978-3-319-15248-6_37
|
| [12] |
RAINIERI C, FABBROCINO G. Operational modal analysis of civil engineering structures: an introduction and guide for applications [M]. New York: Springer, 2014: 322.
|
| [13] |
JACOBSEN N J, ANDERSEN P, BRINCKER R. Using enhanced frequency domain decomposition as a robust technique to harmonic excitation in operational modal analysis [C] // Proceedings of International Conference on Noise and Vibration Engineering. Leuven, Belgium: Katholieke Universiteit Leuven Department of Mechanical Engineering, 2006.
|
| [14] |
BO Z, HAN D, XINJUN S. Modal analysis of board-level electronic package[J]. Microelectronic Engineering, 2008, 85(3): 610-620. |
| [15] |
罗震, 陈立平, 黄玉盈, 等. 连续体结构的拓扑优化设计[J]. 力学进展, 2004, 34(4): 463-476. LUO Zhen, CHEN Li-ping, HUANG Yu-ying, et al. Topological optimization design for continuum structures[J]. Advances in Mechanics, 2004, 34(4): 463-476. DOI:10.3321/j.issn:1000-0992.2004.04.005 |
| [16] |
匡兵, 刘娟, 段君伟, 等. 基于改进灵敏度过滤策略的SIMP方法[J]. 计算力学学报, 2017, 34(1): 81-87. KUANG Bing, LIU Juan, DUAN Jun-wei, et al. SIMP method based on modified sensitivity filtering strategy[J]. Chinese Journal of Computational Mechanics, 2017, 34(1): 81-87. |
| [17] |
XU Dong-kai, CHEN Jun, TANG Yu-cheng, et al. Topology optimization of die weight reduction for high-strength sheet[J]. International Journal of Mechanical Sciences, 2012(59): 73-82. |



