2. 高新船舶与深海开发装备协同创新中心(船海协创中心),上海 200240;
3. 上海交通大学 船舶海洋与建筑工程学院,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration (CISSE), Shanghai 200240, China;
3. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China
随着化石能源的日益枯竭和全球经济的持续发展,寻找可持续新能源成为世界关注的热点,风能作为一种清洁、廉价而丰富的新能源受到广泛关注. 到2015年年底,全球风电装机容量较上一年增加17%,达到433 GW[1]. 当前,国内外陆上风电的发展较成熟,但陆地空间有限,风力资源丰富的地区大多人口稀疏,远离耗电区域,陆上风电的开发潜力日渐降低. 海上风能资源丰富,世界上绝大部分海域风能密度大于200 W/m2[2],能够满足日益增长的能源需求,因此受到越来越多的关注. 考虑到经济性,在水深大于60 m的海域,固定式风电机组将不再适用,故深海海上风力发电多采用浮式平台基础[3]. 目前,研究较多的风力机浮式平台基础包括驳船型、半潜型、TLP型和Spar型等.
各国学者利用各种数值模拟手段对Jonkman等[4]提出的NREL 5 MW风机的各种浮式风力机概念进行广泛的研究和探讨. Jonkman等[5]应用FAST,对ITI驳船型、TLP型、OC3-Hywinds和坐底式风力机进行模拟计算,在模型开发和载荷分析方面进行比较研究. Zhang等[6]介绍海上风力机浮式基础设计的关键问题,如耦合动态分析模型和计算方法,建立有限元模型,利用SESAM软件计算不同工况下浮式风力机的总体运动响应和系泊力;结果表明,该半潜型浮式基础和系泊系统可以在有义波高小于4 m的海洋环境中安全运行. Cheng等[7]利用SIMO-RIFLEX-DMS程序,对Spar型、半潜式和TLP型3种垂直轴浮式风力发电机进行全耦合非线性时域仿真分析比较;结果表明,与TLP型浮式基础相比,Spar和半潜型浮式基础由于采用悬链系泊系统,可以减轻对结构负载和系泊张力的2P气动载荷影响,代价是具有更大的平台运动. Tran等[8]基于重叠网格,采用计算流体力学(CFD)方法对半潜式风力机进行耦合动态响应计算,采用VOF的耦合流体流动和多体动态分析方法,研究半潜式浮体的典型水动力响应. Zhao等[9]基于势流理论和BEM理论,对5 MW多柱张力腿式风力机进行动态耦合分析,比较与陆地式风力机的载荷影响差异,分析机舱加速度、塔底弯矩和平台纵荡运动响应;结果表明,该TLP式风力机具有良好的工作和生存能力. Goupee等[10]采用1/50的缩尺比,对TLP、半潜式和Spar型浮式风力机在不同的工况下进行实验比较;结果表明,不同的浮式基础各自具有优缺点,如TLP具有较小的机舱加速度和总体运动响应,但承受的系泊载荷远大于Spar和半潜式平台.
本文针对设计出的新型6 MW Spar型浮式风力机,考虑气动载荷和水动力载荷,利用气-液-固-弹性数值模拟软件FAST及Sesam软件,分析并验证该Spar型浮式基础在不同风浪组合下具有较好的总体运动性能,且首摇角在delta-line的控制下不会过大.
1 6 MW风力机设计参数目前,国内外浮式风力机实型机发展仍未成熟,针对100 m水深条件设计出新型Spar浮式风力机.
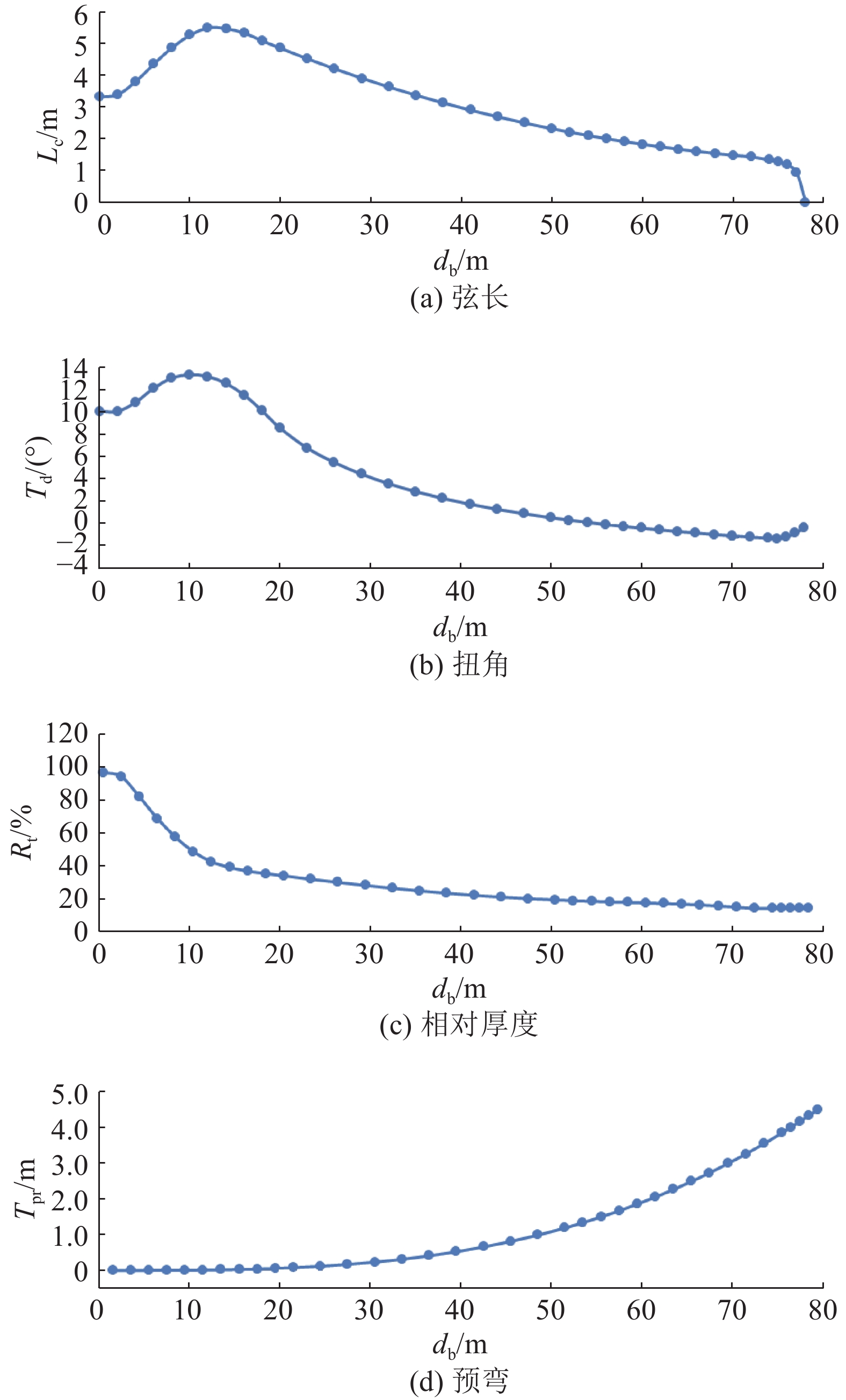
1.1 风机和塔架风机为传统的水平轴上风向三叶片中速永磁型风力发电机组,其中叶片采用NACA及DU系列改型的翼型. 塔架材料采用Q345钢,塔底位于静水面以上13 m处,塔身高度为83.806 m. 塔顶要承受机舱和风机的载荷,故塔顶厚度提高. 具体参数如表1所示,风机的弦长和扭角等外形数据如图1所示. 图中,Lc为弦长,Td为扭角,Rt为相对厚度,Tpr为预弯,db为叶片展向距离.
| 表 1 6 MW风机和塔架的总体参数 Table 1 Overall parameters of 6 MW wind turbine and tower |
|
图 1 叶片气动外形 Fig. 1 Aerodynamic profile of blade |
在额定推力下,塔架底部弯曲应力为
| $\begin{split} \sigma = &\frac{{Mh}}{W}= \displaystyle\frac{{891.7 \times 100}}{{\displaystyle\frac{\pi }{{32}} \times {8^3} \times \left[ {1 - {{\left( {\displaystyle\frac{{8 - 2 \times 0.04}}{8}} \right)}^4}} \right]}}=\\ &45.02\;{\rm MPa}. \end{split} $ |
该结果远远小于Q345钢的屈服强度,塔底外径与壁厚之比满足DNV规范[11]关于屈曲的要求.
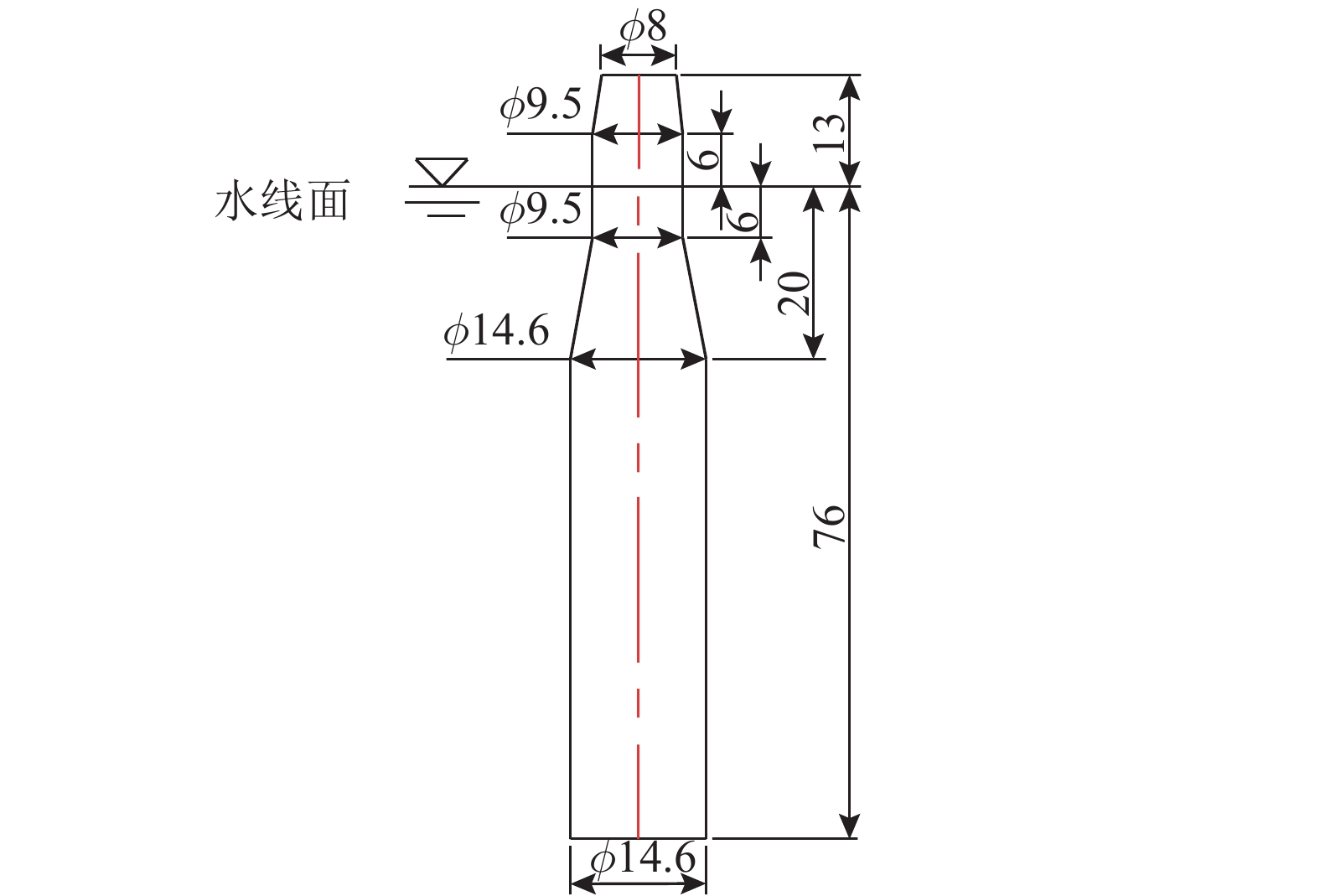
1.2 Spar型平台平台作为浮式风力机的重要支撑结构,平台性能对浮式风力机的总体运动响应起到重要影响. Spar型平台具有小水线面和大排水量的特点,能够提供浮式风力机所需的浮力和静水回复力. 平台顶部外径为8 m,底部外径为14.6 m. 表2给出平台的几何参数. 图2、3给出该风力机整体示意图和浮式基础的结构尺寸外形二维图,坐标系和平台自由度如图4所示.
| 表 2 浮式平台的几何参数 Table 2 Floating platform gross and geometry properties |

|
图 2 6 MW浮式风力机示意图 Fig. 2 Specifications of 6 MW floating wind turbine |
|
图 3 Spar平台二维图 Fig. 3 Two-dimensional figure of Spar platform |

|
图 4 坐标系和平台自由度 Fig. 4 Coordinate system and platform DOF |
设计出的该浮体的静倾角为4.3°,符合设计初稳性纵倾角不超过5°的设计原则[12]. 平台各自由度的固有周期都避开了波浪的能量集中范围. 通过进一步的计算表明,该平台的设计是可行的.
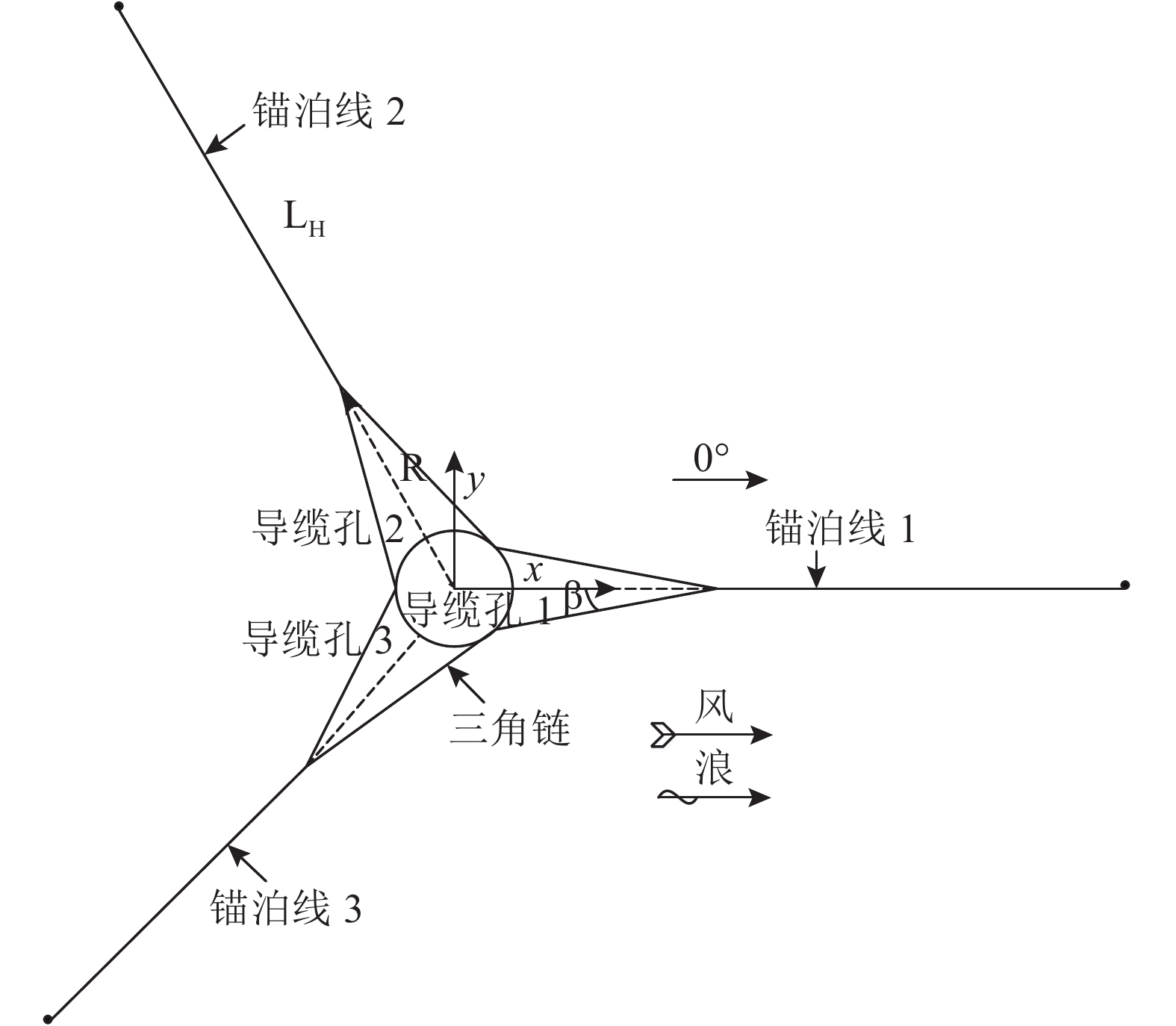
1.3 系泊系统平台的垂荡、横摇和纵摇运动由静水回复力、力矩来控制,由于外力作用而导致的偏移在外力消失后能够回到原有的平衡位置;纵荡、横荡的偏移须由锚链提供回复力. 该系泊系统包括3根互相成120°的悬链线,如图5所示,锚链的直径和单位长度质量及破断力根据API[13]的规范确定. 锚链设计的另一个重要方面在于控制平台的首摇运动,采用连接到导缆孔处的delta-line提供首摇回复力. 附加首摇刚度①为
① NIELSEN F G. Tuning the geometric and mass properties of hywind. Statoil (Internal document), 2009.
|
图 5 系泊系统分布 Fig. 5 Layout of mooring system |
| ${C_{66}} = \sum\limits_{i=1}^n {TR\cos \varphi \left( {1 + \frac{R}{{{L_{\rm H}}}}} \right)} .$ | (1) |
式中:
| 表 3 系泊系统性质 Table 3 Properties of mooring system |
耦合风机、塔架、平台和锚链运动的非线性时域运动方程为
| $\begin{split}&\displaystyle\sum\limits_{j = 1}^6 {\left\{ {\left( {{M_{ij}} + {m_{ij}}} \right){{\ddot x}_j}\left( t \right) + \int\limits_{ - \infty }^t {{{\dot x}_j}\left( \tau \right){K_{ij}}\left( {t - \tau } \right){\rm d}\tau + } } \right.} \\&\left. {{b_{vij}}{{\dot x}_j}\left( t \right) + {C_{ij}}{x_j}\left( t \right)} \right\}={F_i}^{{\rm Aero}}\left( t \right) + {F_i}^{{\rm Hyd}}\left( t \right) + {F_i}^{{\rm Moor}}\left( t \right) .\end{split}$ | (2) |
式中:
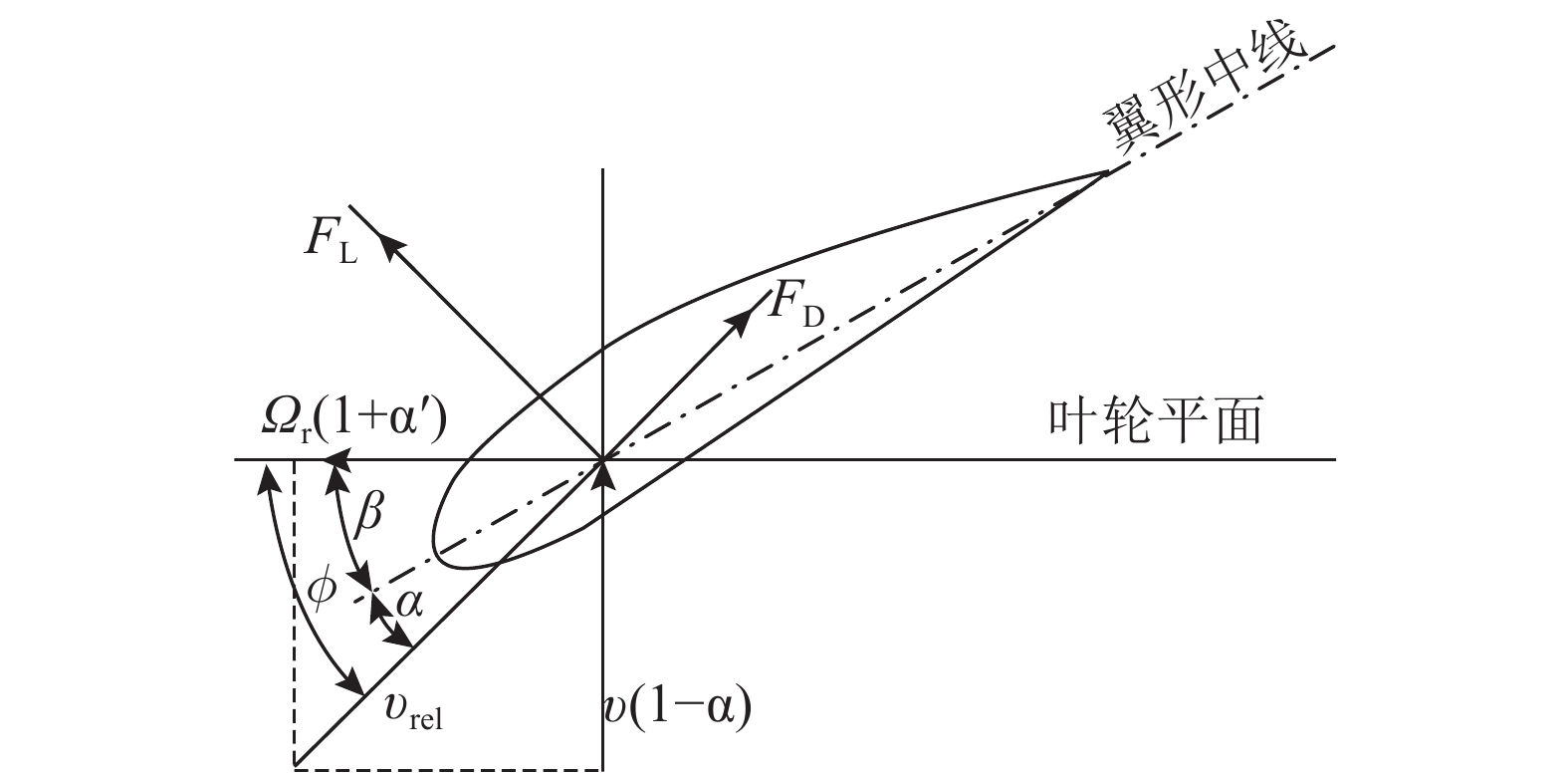
将基于叶素理论和动量理论的BEM理论应用于FAST程序中. 基本原理是将叶片沿展向离散成若干个独立的叶素,并在每个叶素中均定义一个叶切面;根据尾部气流状况,计算每个叶切面上的升阻力并投影到叶轮平面的法向和切向;然后将作用于所有叶切面上的力沿着叶片展向积分,可得作用于叶片的推力和扭矩,进而得到作用于整个风机的推力和输出功率. 作用于整个叶片的推力、扭矩和功率如下:
| $T = \frac{1}{2}\left( {{C_{\rm L}}\cos \phi + {C_{\rm D}}\sin \phi } \right)\rho {v^2}{(1 - a)^2}cB\frac{{\Delta r}}{{{{\sin }^2}\phi }},$ | (3) |
| $\begin{split}M =& \frac{1}{2}\left( {{C_{\rm L}}\sin \phi - {C_{\rm D}}\cos \phi } \right)\rho v\times\\ &(1 - a)\left(1 + a'\right) cB\frac{{\Delta r}}{{\sin \phi \cos \phi }}\varOmega r,\end{split}$ | (4) |
| $P = M\varOmega r.$ | (5) |
式中:
|
图 6 叶片截面的气动载荷 Fig. 6 Aerodynamic loads of blade section plane |
对于浮式风力机,受到的风载荷叶片气动载荷包括塔架受到的风载荷. 塔架受到的风载荷可以根据中国船级社(CCS)[15]规范计算得到:
| $F = 0.613\sum\limits_{i = 1}^n {\left( {{C_{{\rm h}i}}{C_{{\rm S}i}}{A_i}{V_{10}}^2} \right)} .$ | (6) |
式中:
与陆上风力机相比,海上浮式风力机还受到水动力载荷的作用. 频域内的波浪激励力计算公式为
| ${f_{{\rm w}j}} ={\rm i}\omega \rho \iint\limits_{{S_0}} {\left( {{\varphi _{\rm I}}\frac{{\partial {\varphi _j}}}{{\partial n}} - {\varphi _j}\frac{{\partial {\varphi _{\rm I}}}}{{\partial n}}} \right){\rm d}S}.$ |
式中:
入射势可以基于微幅波理论直接求解,辐射势通过求解具有自由面条件、物面条件、海底条件、无限远边界条件的拉普拉斯方程得到,进而求出附加质量、阻尼系数.
对于波浪力在时域内的计算,利用Cummins[16]提出的时域中波浪力与频域中波浪力传递函数之间的卷积关系,通过对脉冲响应函数和波面升高的卷积积分形式来表示波浪力的时程:
| ${F_i}^{{\rm Hyd}}\left( t \right) = \int\limits_0^t {{H_j}\left( {t - \tau } \right)\eta \left( \tau \right){\rm d}\tau } .$ | (7) |
式中:
对于本文的Spar浮式基础,通过势流理论计算得到的波浪力需要考虑由流体黏性引起的拖曳力进行修正. 根据Morison公式可知,由流体黏性在圆柱切片引起的水平拖曳力可以表示为
| ${\rm d}{F_i}^{{\rm viscous}}\left( {t,z} \right) = \frac{1}{2}{C_{\rm D}}{\rho _{\rm w}}\left( {D{\rm d}z} \right){u_i}\left( {t,z} \right)\left| {{u_i}\left( {t,z} \right)} \right|.$ | (8) |
式中:
锚链力计算采用考虑惯性力和阻力的有限元(FEAM)模型,将锚链视为弹性杆模型①. 建立流体中杆模型的控制方程如下:
① BAE Y H. Development of a dynamic mooring module FEAM for fast V8, 2014.
| $\rho \mathop r\limits^{..} + {C_{\rm{a}}}{\rho _{\rm{w}}}\mathop {{r^n}}\limits^{..} + \left(EIr''\right)'' - \left(\overline \lambda r'\right)' =m + {\overline F ^{\rm{d}}},$ | (9) |
| $\frac{1}{2}\left(r' \cdot r' - 1\right) = \frac{T}{{AE}} \approx \frac{\lambda}{{AE}}.\;$ | (10) |
式中:
采用2种数值模拟工具:挪威船级社(DNV)开发的Sesam软件和美国国家可再生能源实验室(NREL)开发的FAST软件.
通过Sesam软件中的Wadam模块进行频域水动力计算,得到关于Spar平台的水动力系数、静水回复力、单位波幅下的不同频率和方向的波浪激励力等一系列wamit文件. FAST基于BEM理论计算气动载荷,调用上述wamit文件计算水动力载荷,基于有限元法计算锚链力,从而实现针对该Spar浮式风力机的气-液-固-弹时域耦合数值模拟计算.
表4中,Dwind为风向,Dwave为浪向. 根据表4,定义4种类型工况(LC):LC1为衰减实验工况;LC2只有波浪载荷,波浪周期为4~125.66 s;为了验证环境载荷方向改变时,设计出的浮式风力机能够满足使用有效性,取北海工作海况[17]为LC3,其中包括只考虑风和风浪共存2种类型,考虑波浪作用时的波浪谱采用JONSWAP谱.
| 表 4 不同设计工况条件 Table 4 Summary of selected design load cases |
利用自由衰减法确定固有周期. 在测试中,风机处于停机状态且桨距角设置为90°,即风轮处于静止状态且风轮平面与总体坐标系的x轴平行. 表5给出该Spar浮式风力机各自由度的固有周期Tn.
| 表 5 6 MW Spar浮式风力机的固有周期 Table 5 Natural periods of 6 MW Spar-type FOWT |
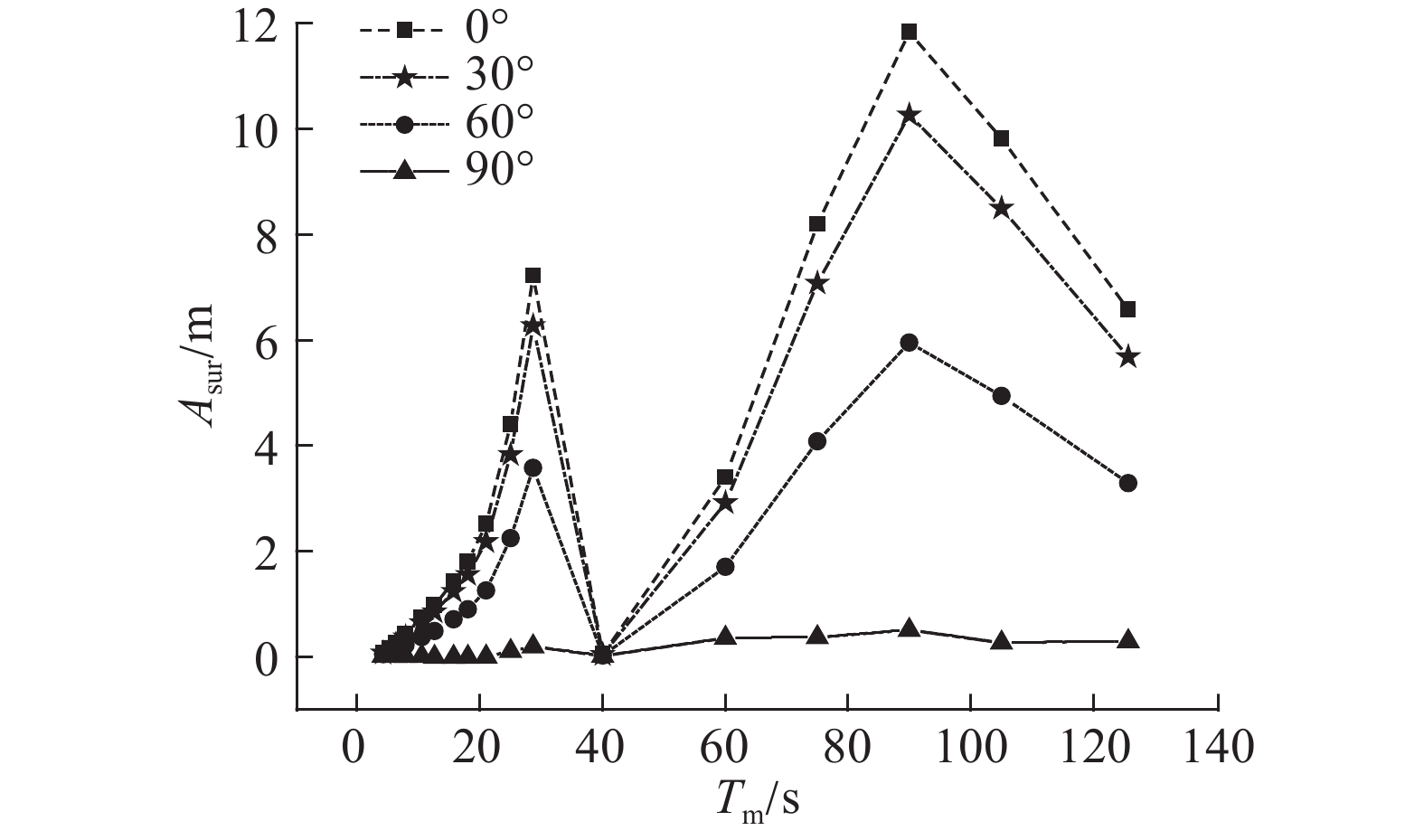
响应幅值算子表征浮式风力机系统的水动力性能. 环境条件LC2通过一系列规则波模拟,得到风力机总体运动响应的RAOs. 图7~10给出不同浪向下的各自由度RAOs仿真结果. 图中,Tm为周期,Asur为纵荡幅值,Ahea为垂荡幅值,Apit为纵摇幅值,AYaw为首摇幅值.
|
图 7 纵荡RAO Fig. 7 RAO for surge motion |

|
图 8 垂荡RAO Fig. 8 RAO for heave motion |
|
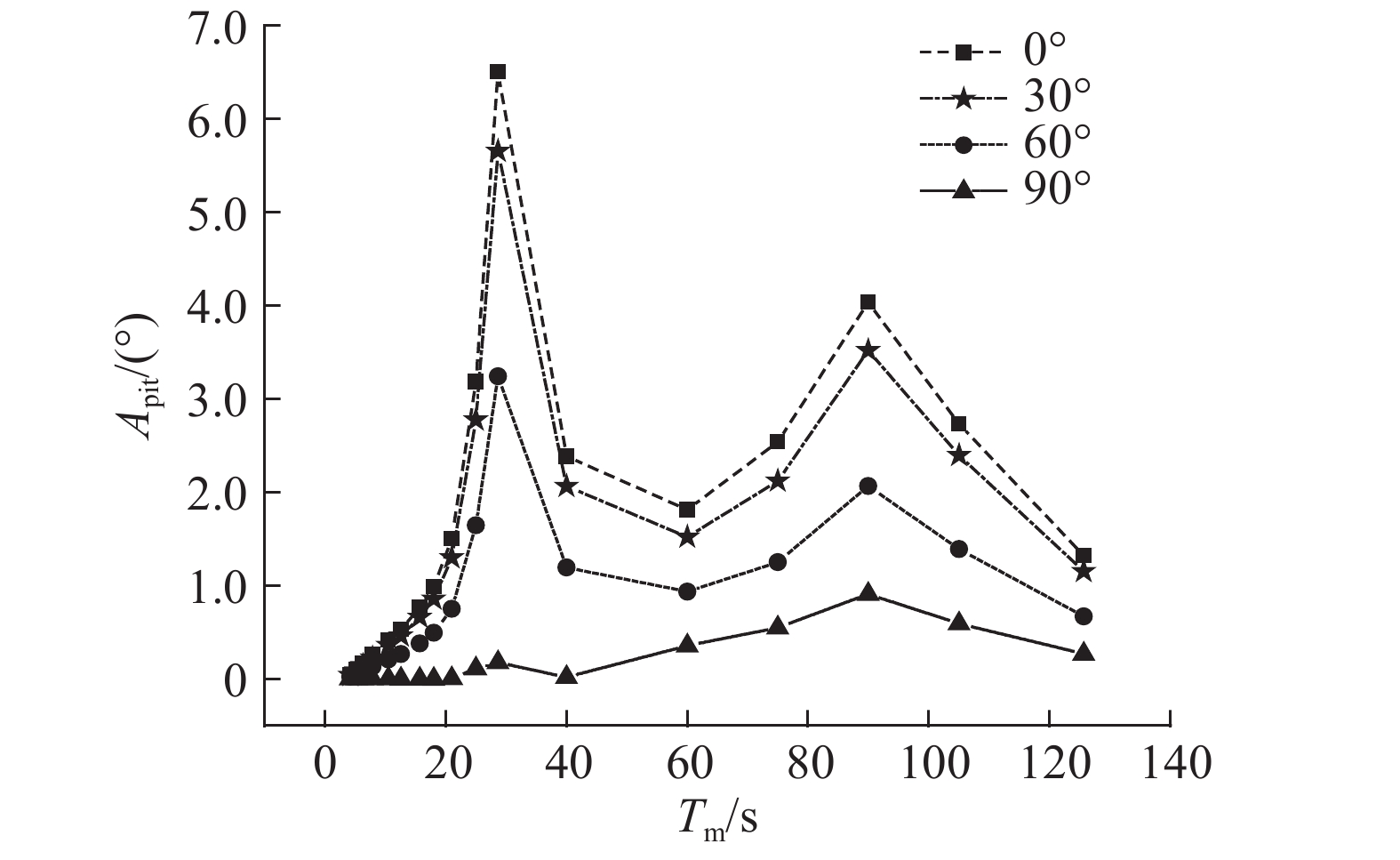
图 9 纵摇RAO Fig. 9 RAO for pitch motion |
|
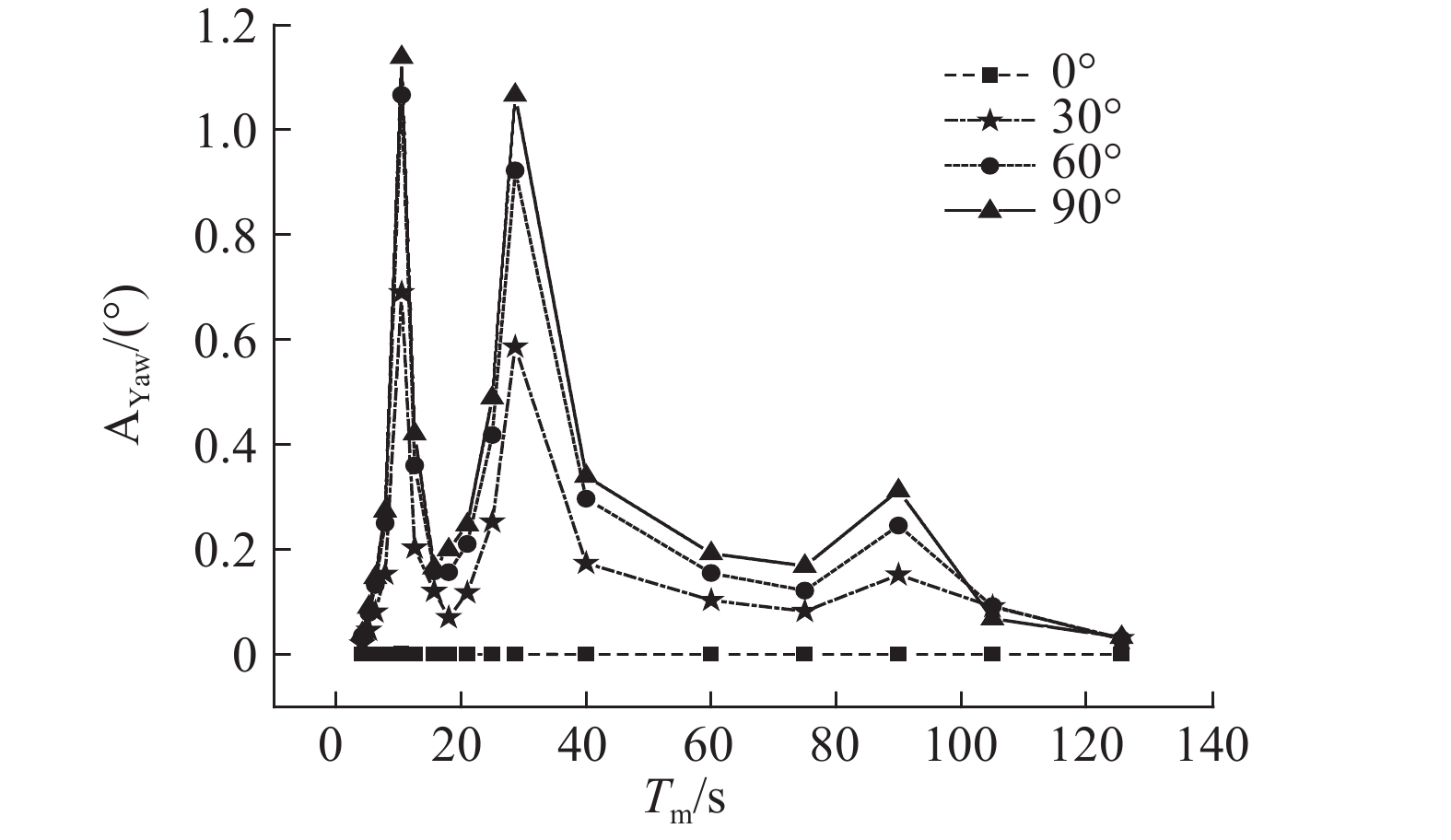
图 10 首摇RAO Fig. 10 RAO for yaw motion |
图7~10表明,在不同浪向情况下,同一自由度的RAOs具有相似的趋势,且各自由度RAOs的最大值均在该自由度对应的固有周期处. 对于纵荡、纵摇运动,各浪向均存在2个峰值,Tpit和Tsur分别为纵摇和纵荡的固有周期,表明纵荡和纵摇耦合作用较明显,且RAO随着浪向角的增大呈现下降趋势;对于垂荡运动,不同浪向对RAO的影响较小,在垂荡固有周期处存在明显的峰值,在纵荡固有周期处,运动幅值略微增大但不明显;对于首摇运动,当浪向为0°时,首摇运动几乎为0,其他各浪向均存在3个峰值,分别对应于首摇、纵摇和纵荡的固有周期,随着浪向角的增大,RAO在同一波浪周期处呈现上升趋势.
3.3 不同风浪向条件下平台运动响应研究6 MW风机的额定工作风速为10.5 m/s,此时桨距角为0.7°;当风速增大时,桨距角增大. 在额定风速下,该风力机所受到的推力最大,不同风速下的推力如表6所示. 表中,v为风速,n为风轮转速,θ为桨距角,FT为推力. 针对LC3工况中考虑波浪载荷时的计算结果表明,额定风速下平台的运动响应和锚链力最大,只给出10.5 m/s风速下的运动响应结果. 在工作海况下,风浪向的变化对平台运动响应产生较大的影响,共计算16个风浪共同作用的工作工况,如表7所示,并与4个只有风的工况进行比较.
| 表 6 不同风速下的推力 Table 6 Thrust at different wind speeds |
| 表 7 不同风向、浪向角下的额定工况 Table 7 Rated operating state with different wind and wave angles |
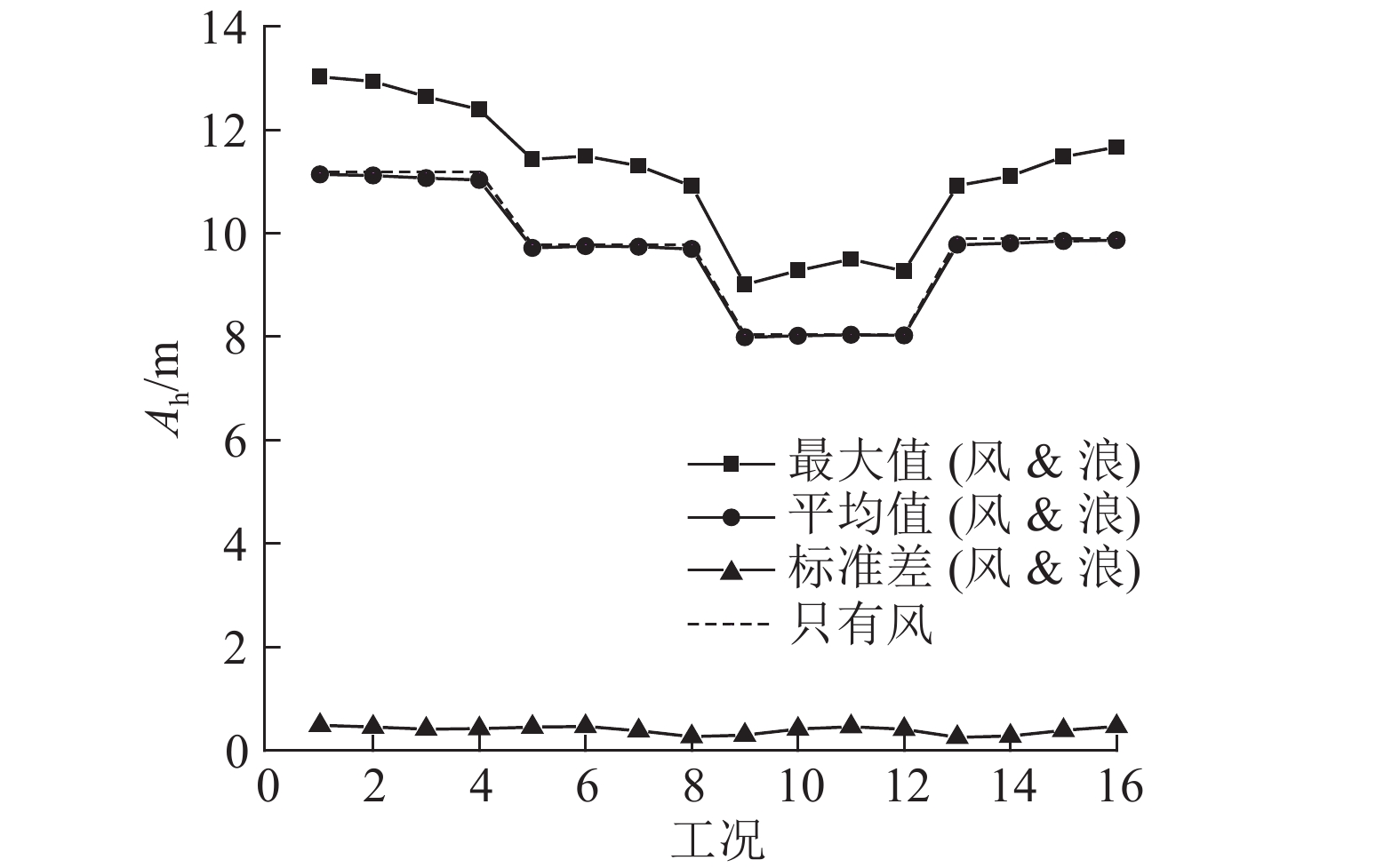
取不同风浪入射方向下Spar浮式风力机230~2 030 s时的运动结果进行统计分析,如图11~14所示. 如图11所示为x-y平面即水平面线运动响应统计值. 图中,Ah为水平运动幅值. 如图13所示为与z轴成一定夹角的角运动响应统计值. 图中,Aang为角运动幅值.
|
图 11 水平运动统计值 Fig. 11 Horizontal motion response statistics |
|
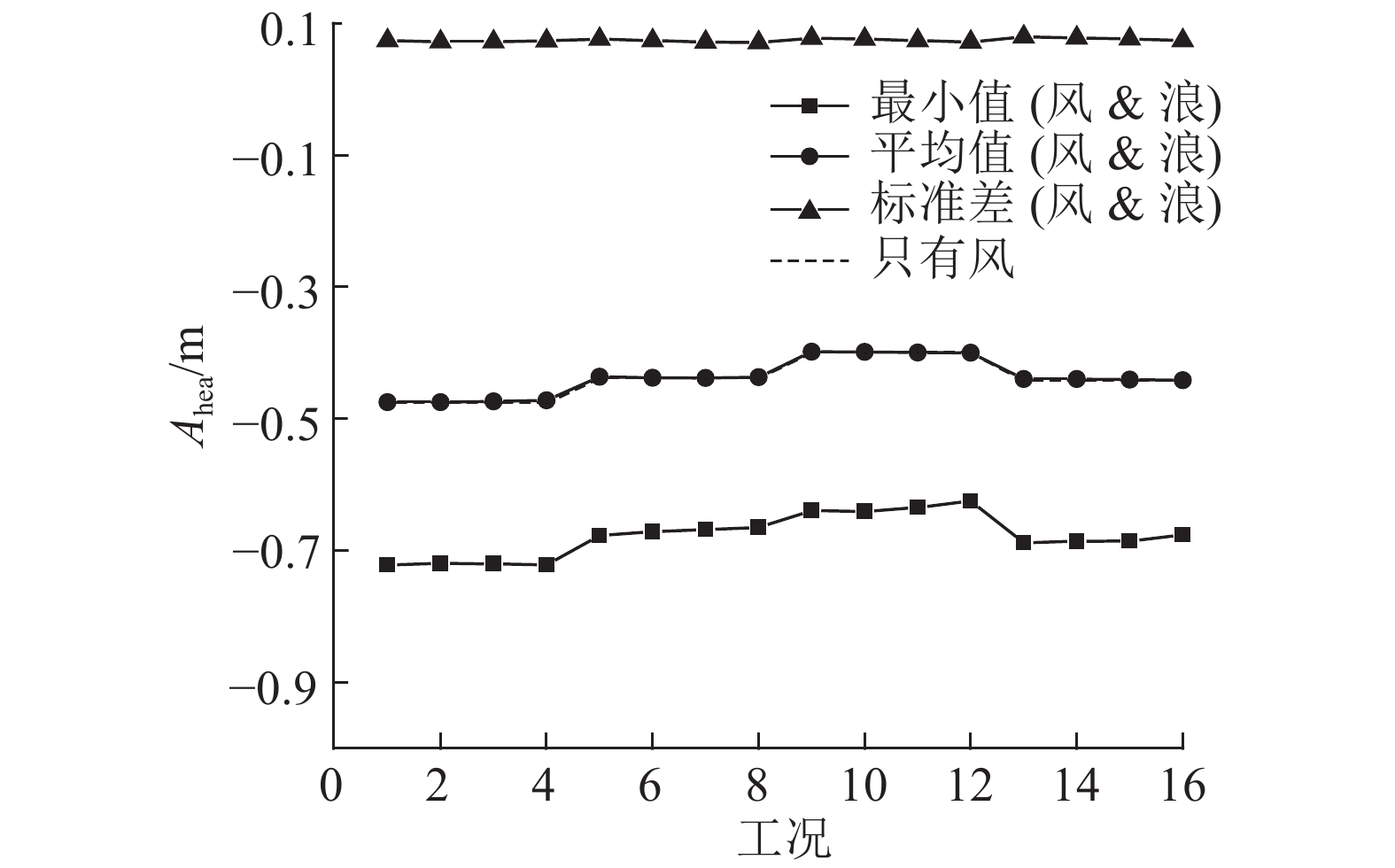
图 12 垂荡统计值 Fig. 12 Heave response statistics |
|
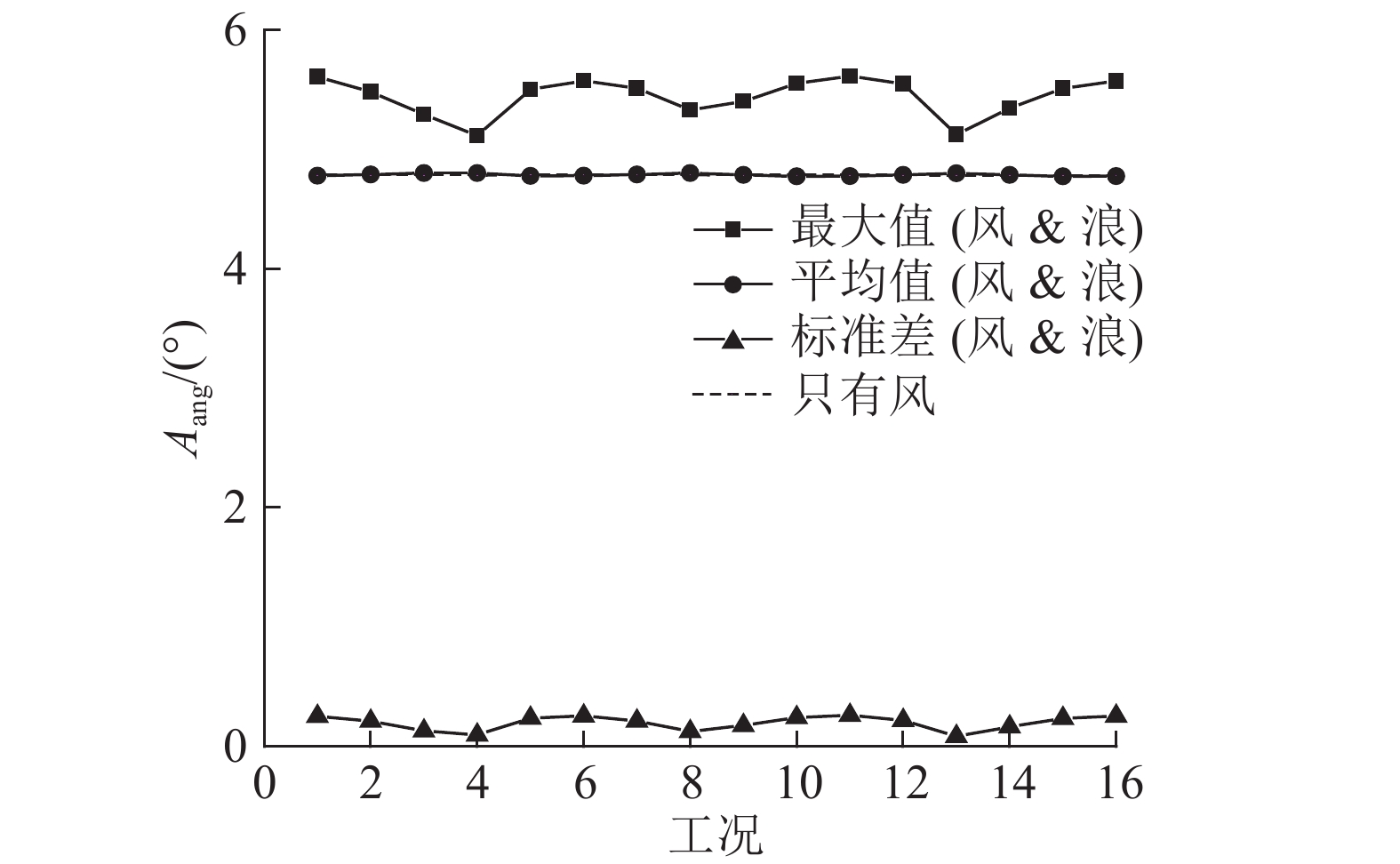
图 13 角运动统计值 Fig. 13 Angular motion response statistics |
|
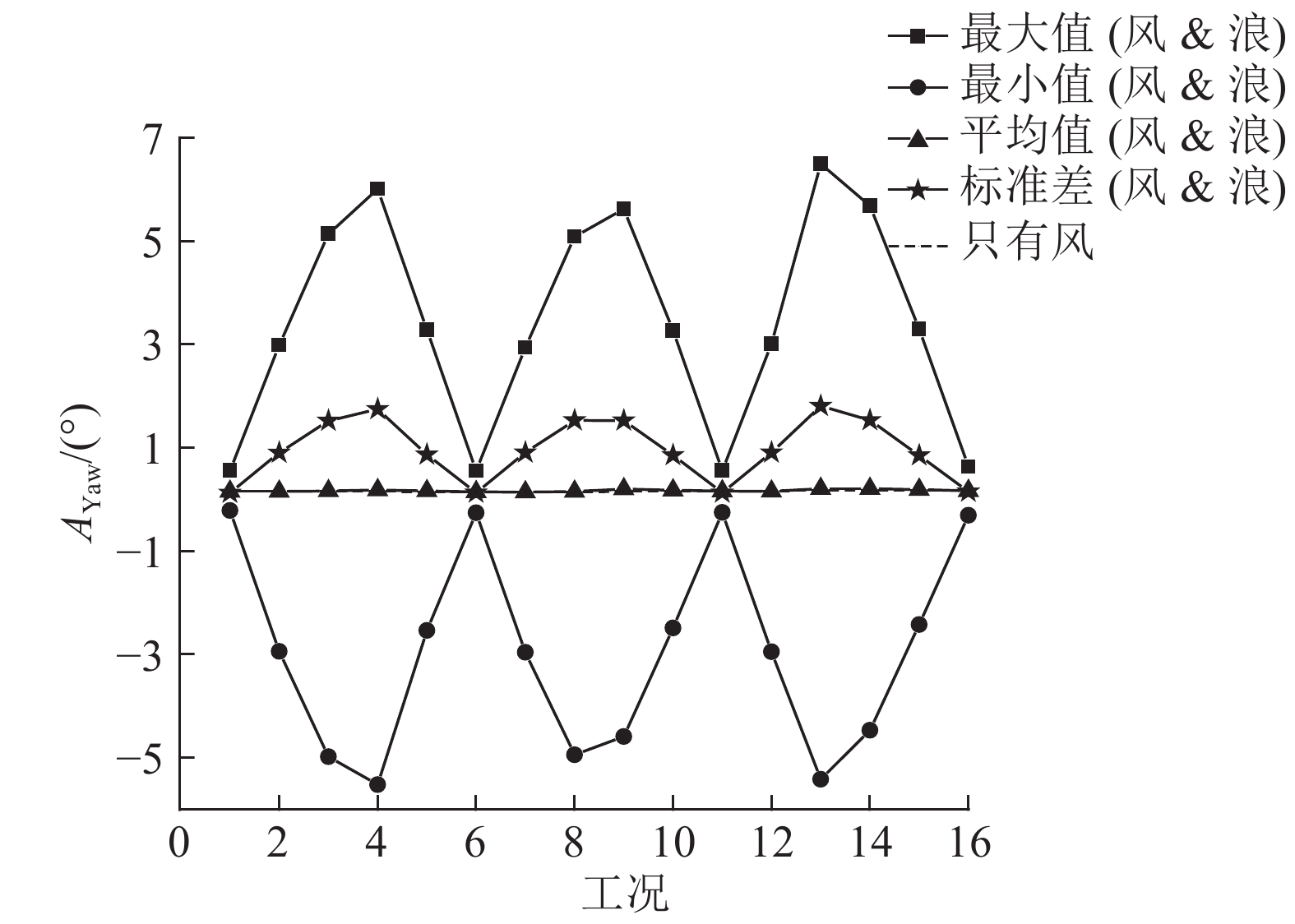
图 14 首摇统计值 Fig. 14 Yaw response statistics |
结果表明,风浪同向时,Spar平台的水平位移幅值和角运动幅值最大,风浪夹角越大,水平位移、角运动越小;风向60°下,水平位移幅值较小,且各工况的水平运动平均值和最大值趋势相同;风浪向的变化对垂荡运动的最大值、均值及标准差影响都不大,可见风浪向的改变不会影响垂荡的运动响应;对于首摇运动,当风浪同方向时,平台首摇角最大值、均值以及标准差最小,当风浪夹角增大时,首摇角最大值、均值以及标准差都增大,这表明由于Spar平台的对称性,风浪同向不会产生较大的首摇响应,较大的风浪夹角会导致较大的首摇运动响应. 最大首摇角只有6.496°,这表明具有delta-line的6 MW Spar型风力机具有良好的首摇运动响应,避免锚链缠绕现象的发生. 对于各自由度,各风浪共同作用下的运动响应均值与只有稳定风作用时的运动幅值基本保持一致;可见,在额定工作条件下,平台运动响应主要取决于风载荷,波浪载荷会改变平台在平衡位置附近的振荡运动,即风引起定常效应,波浪会引起周期效应.
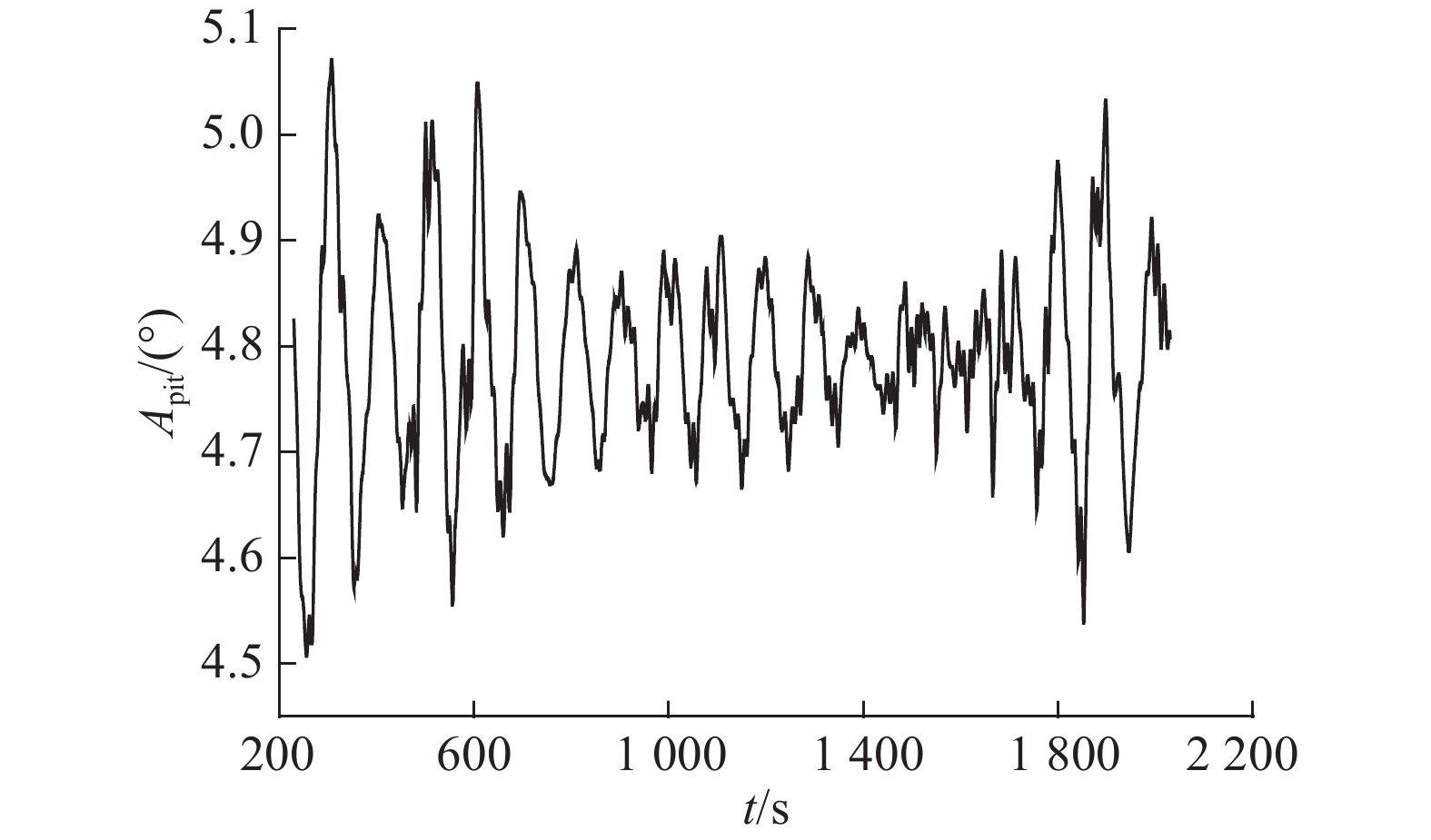
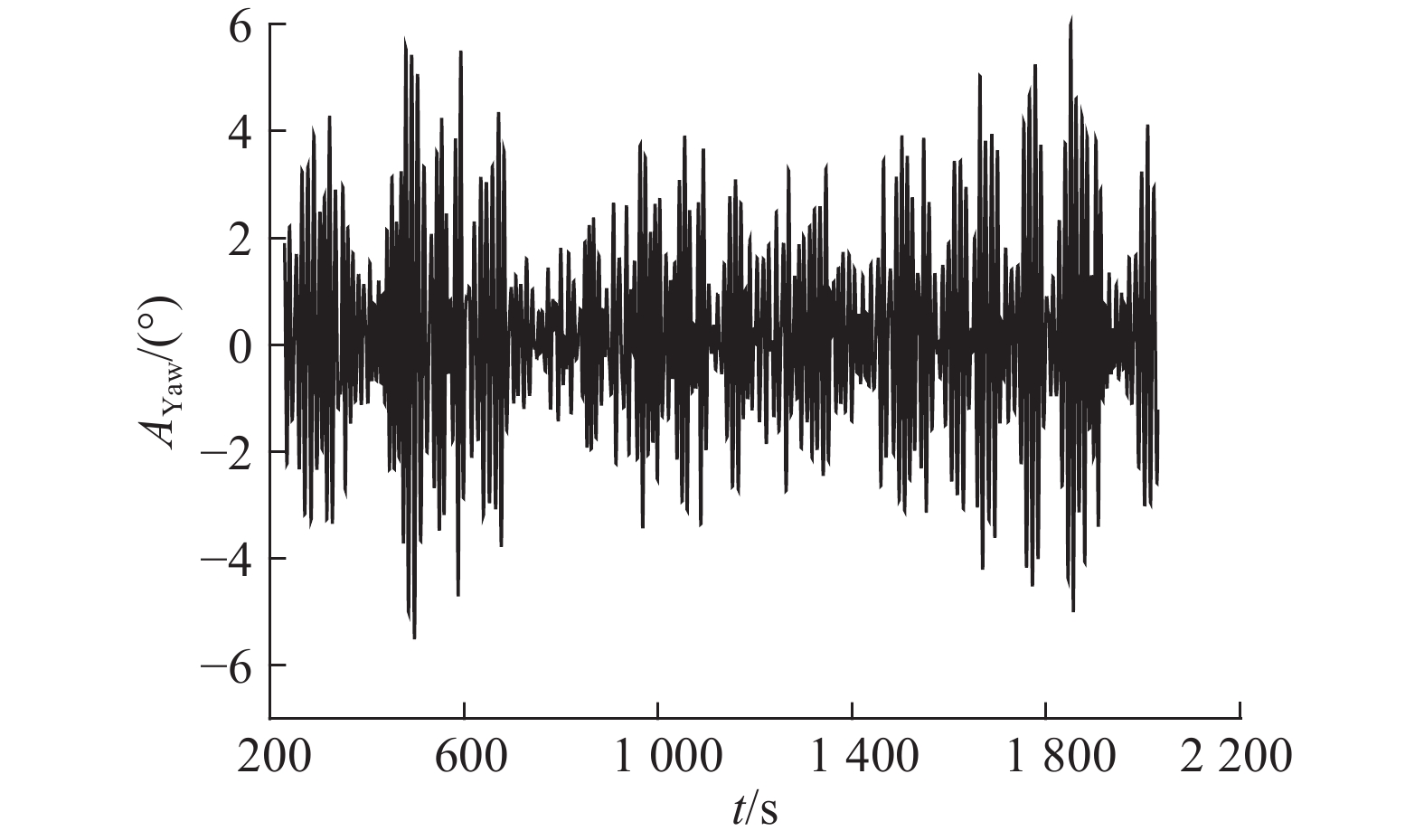
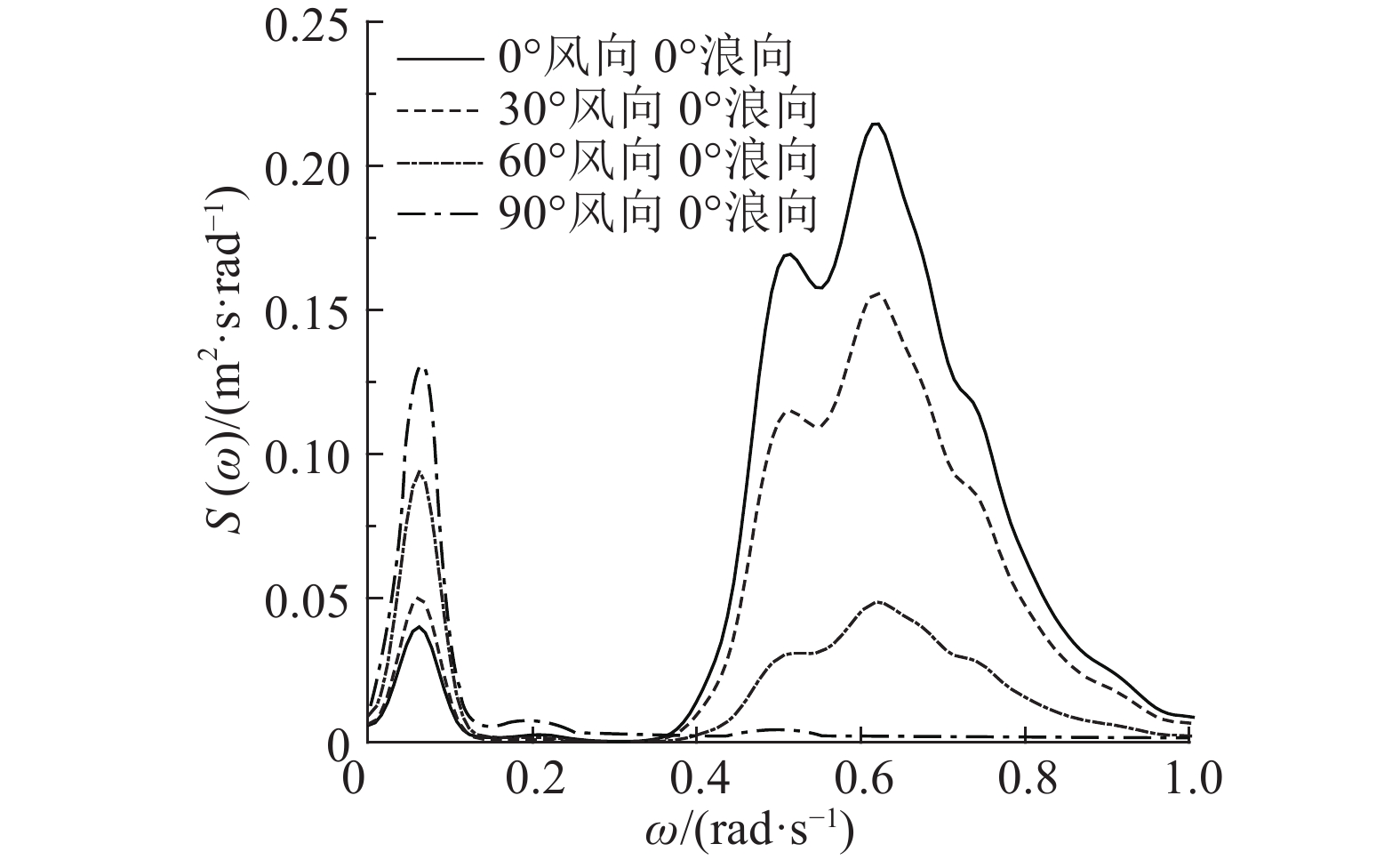
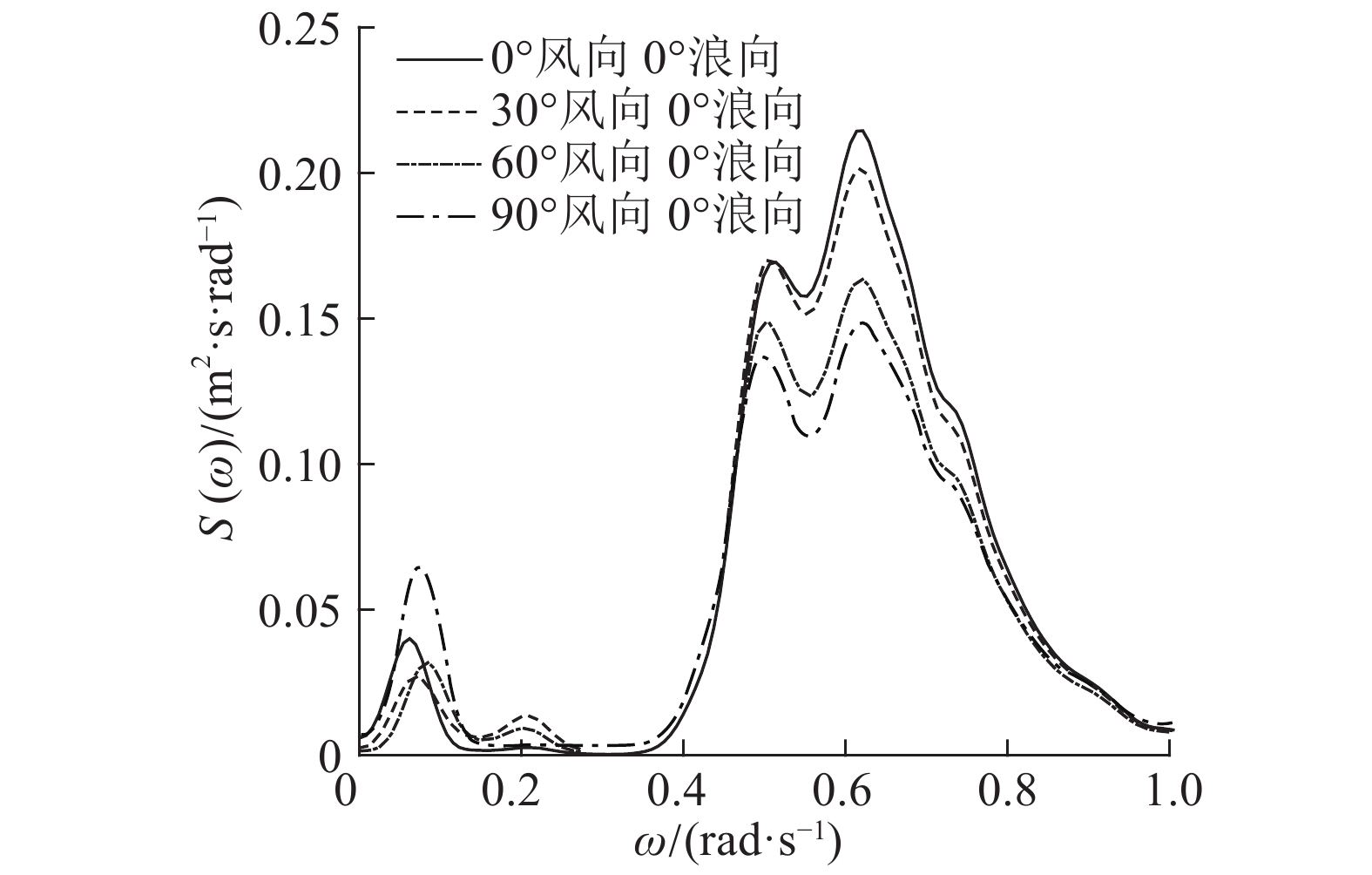
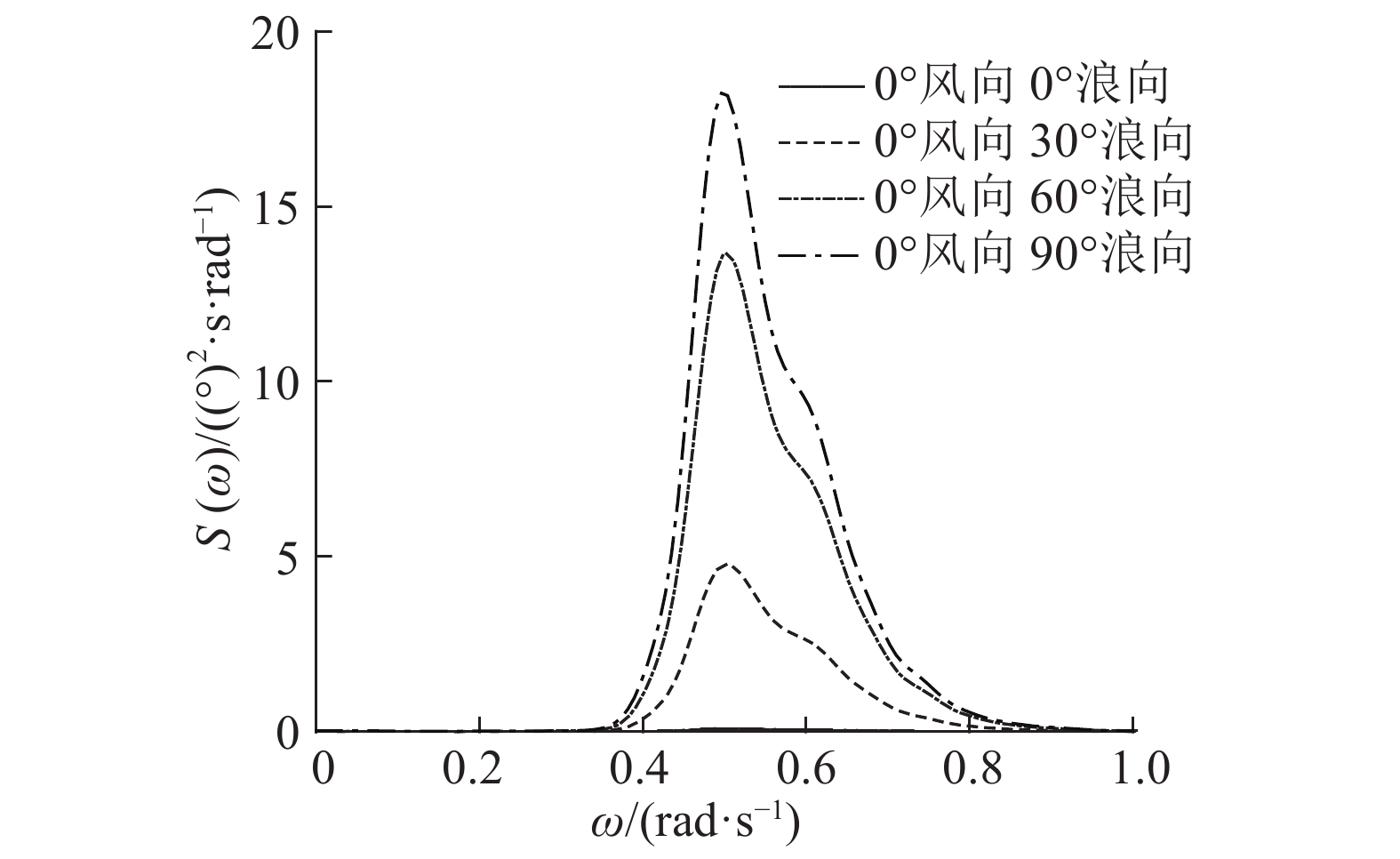
3.3.2 时域频域结果分析纵摇和首摇运动响应的好坏对Spar浮式风力机的生存情况起关键作用. 取风向为0°,浪向为90°,Spar平台纵摇和首摇的时域结果如图15、16所示. 如图17、18所示为经过傅里叶变换后,风向为0°、浪向变化的纵摇和首摇功率谱S(ω). 图中,ω为角频率. 如图19、20所示为浪向为0°、风向变化的纵摇和首摇功率谱.
|
图 15 纵摇时历曲线图 Fig. 15 Pitch time series |
|
图 16 首摇时历曲线图 Fig. 16 Yaw time series |
|
图 17 不同浪向的纵摇功率谱 Fig. 17 PSD of pitch with different wave direction |
|
图 18 不同风向的纵摇功率谱 Fig. 18 PSD of pitch with different wind direction |
|
图 19 不同浪向的首摇功率谱 Fig. 19 PSD of yaw with different wave direction |
|
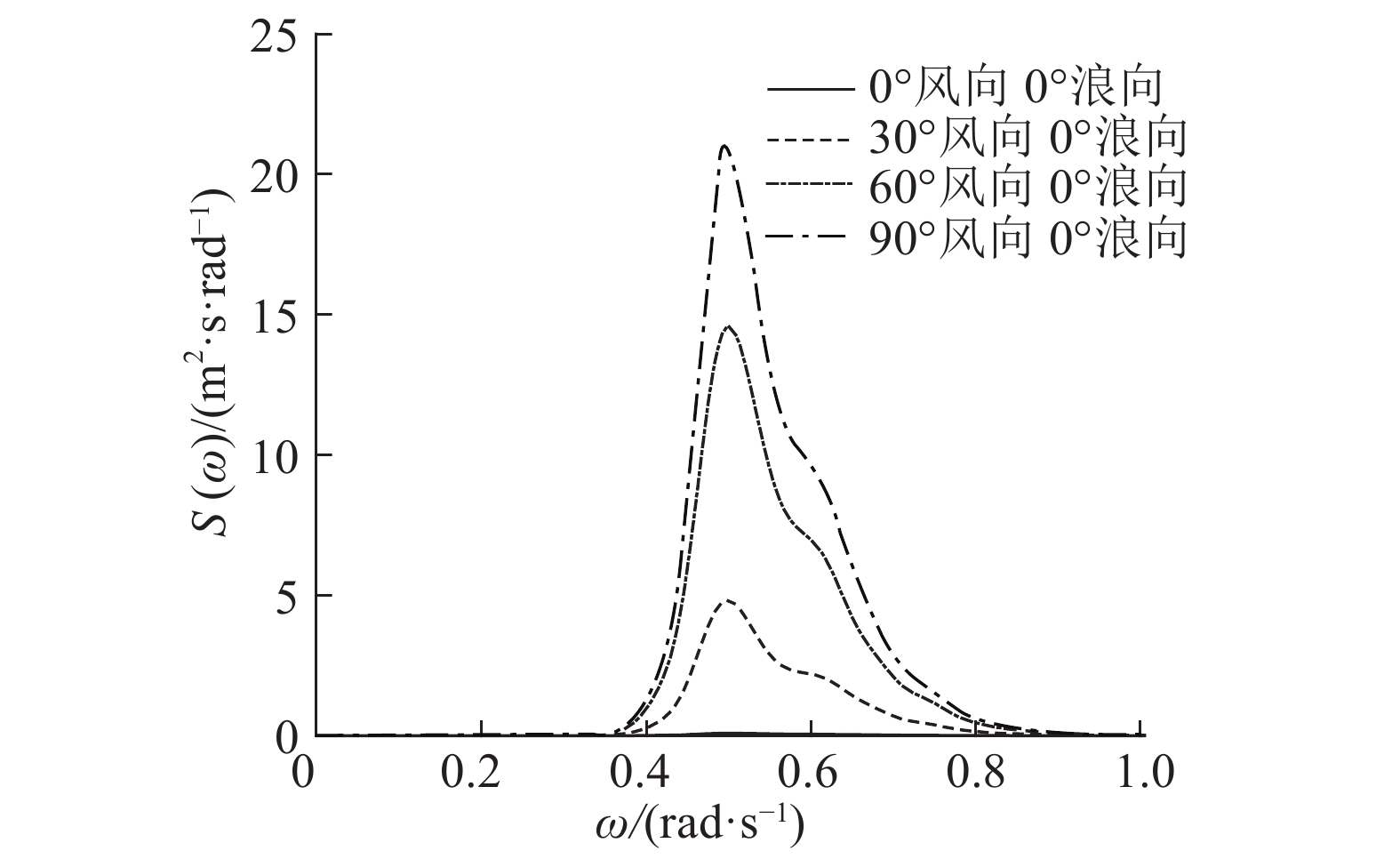
图 20 不同风向的首摇功率谱 Fig. 20 PSD of yaw with different wind direction |
图17、18表明,对于纵摇,存在3个峰值点,分别对应风力机的纵荡、纵摇固有周期及波浪周期. 在纵荡固有周期处,峰较明显,说明纵摇和纵荡耦合作用较明显. 当风向不变,波浪入射角增大时,纵摇在波浪周期处的功率谱幅值明显下降,说明波浪方向对纵摇动态响应的影响较大;浪向不变,风浪同向时纵摇的功率谱幅值最大,但变化较小,可见风浪同向会产生最大的纵摇响应,但风向变化对纵摇的动态响应影响较小.
图19、20表明,对于首摇,仅存在一个峰值点,说明在工作海况下,首摇与其他自由度的耦合作用很小. 当风浪同向时,首摇在波浪周期处的功率谱幅值最低;当风浪夹角增大时,首摇在波浪周期处的功率谱幅值明显增大. 可见,当风浪夹角较大时,会激发大幅首摇动态响应,与时域计算的结果一致.
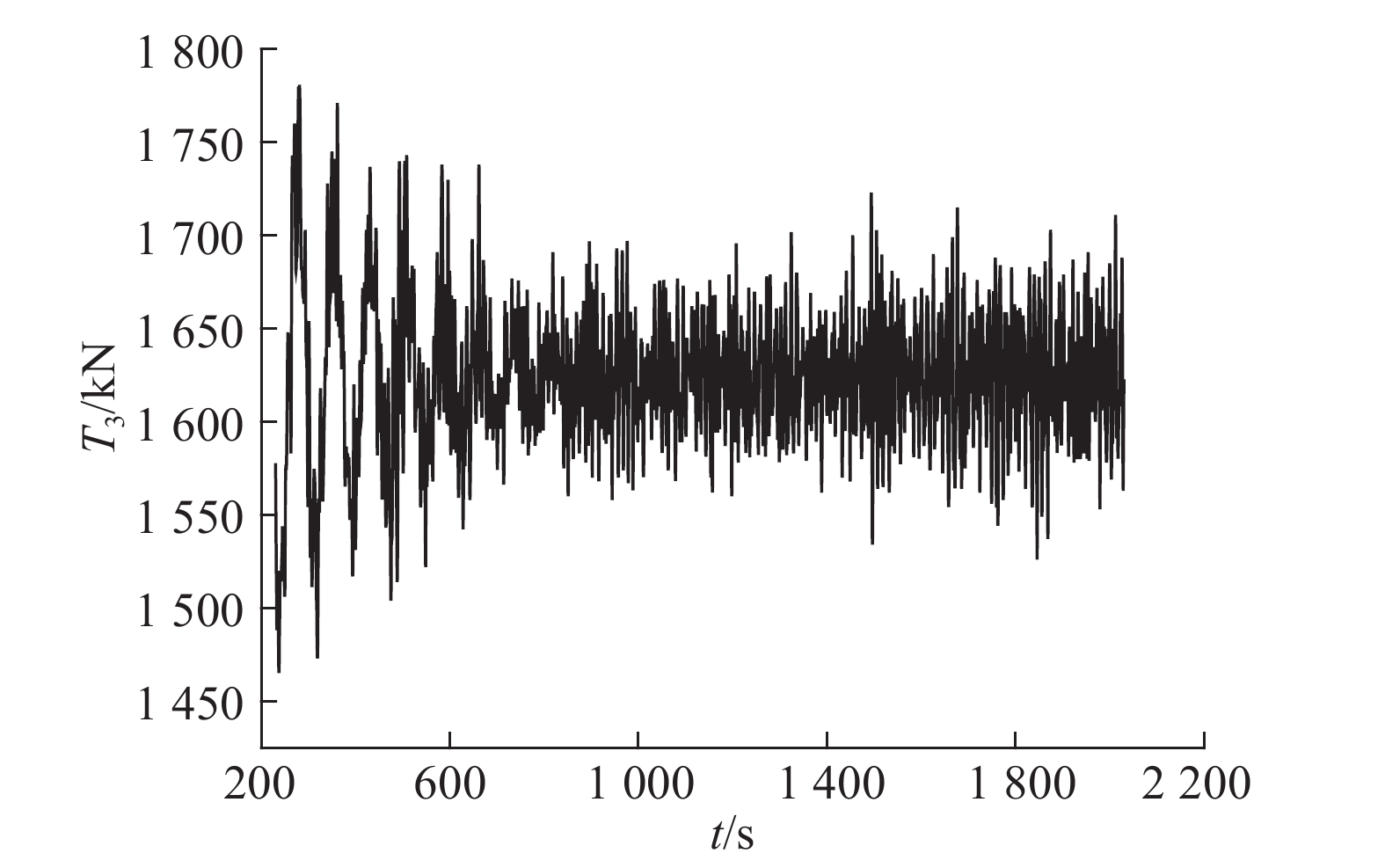
3.4 不同风浪向条件下系泊系统响应研究仅讨论会出现最大张力的系缆3,图21给出系缆3导缆孔处的张力T3在不同风浪方向条件下的统计结果,图22给出当风、浪入射角均为60°时的时历响应曲线,如图23、24所示为风向60°、浪向变化的张力频谱分析图和浪向60°、风向变化的张力频谱分析图.
|
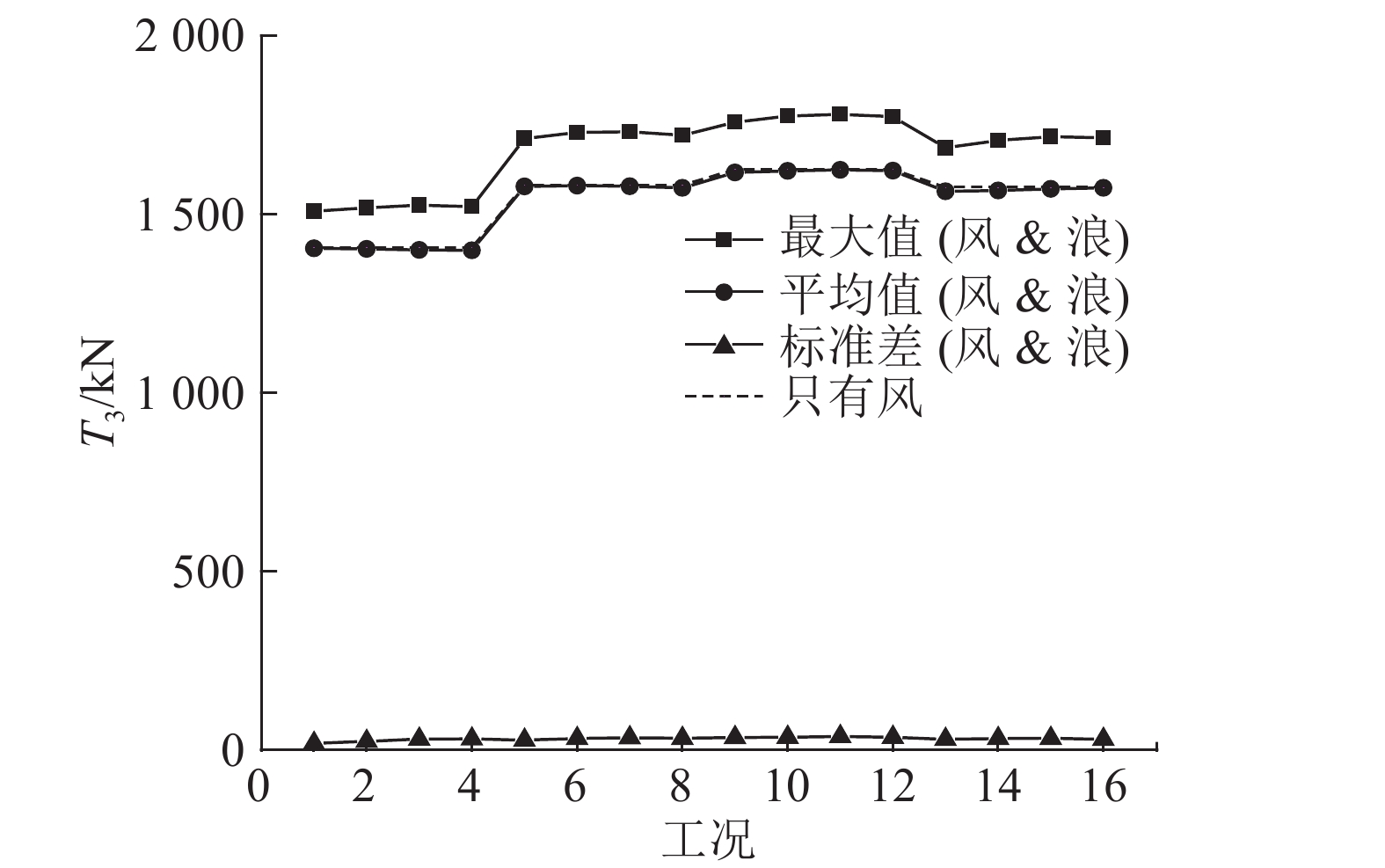
图 21 锚链3张力统计值 Fig. 21 Fair T3 response statistics |
|
图 22 锚链3张力时历曲线图 Fig. 22 Fair T3 time series |
|
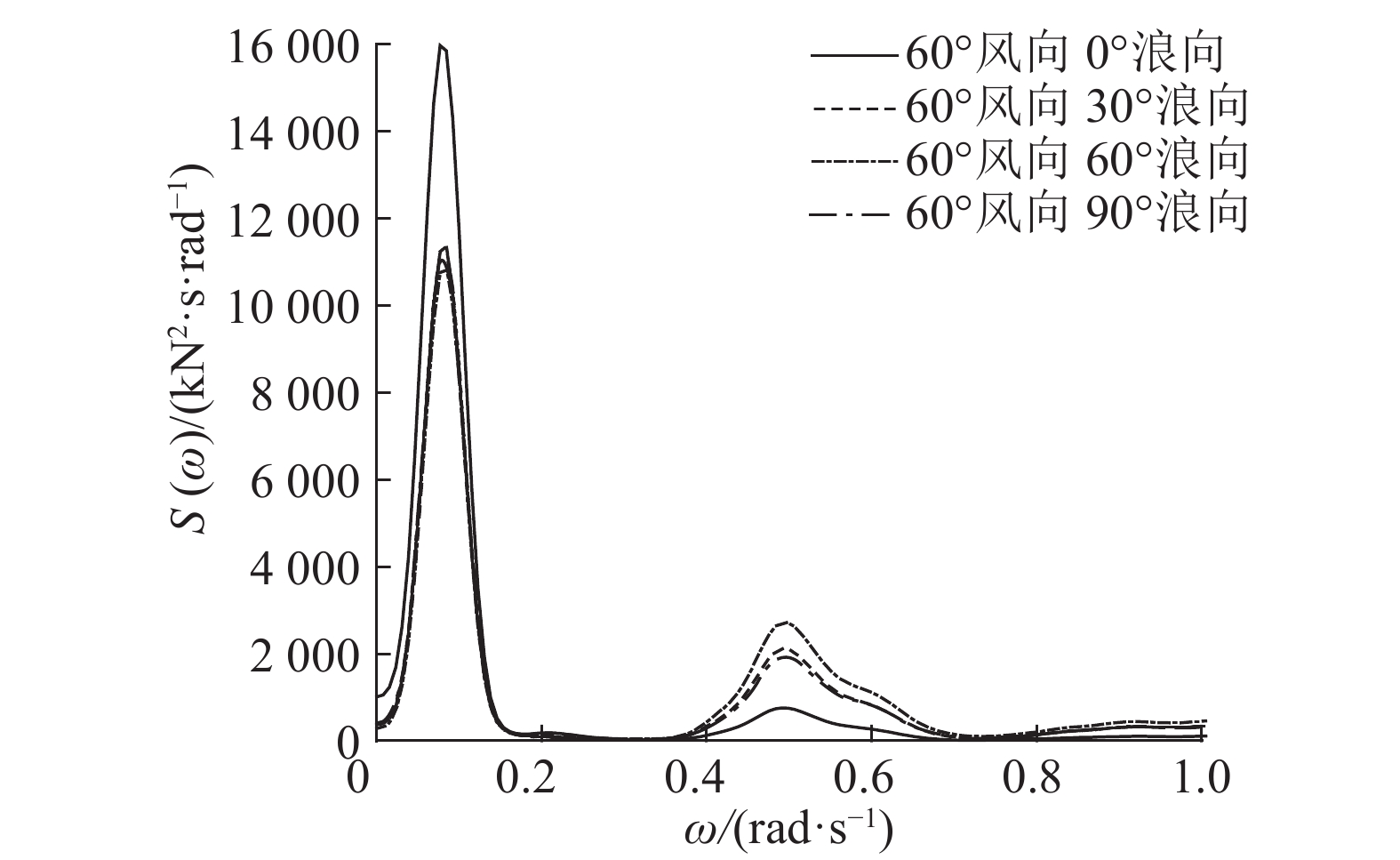
图 23 不同浪向的张力功率谱 Fig. 23 PSD of tension force with different wave direction |
|
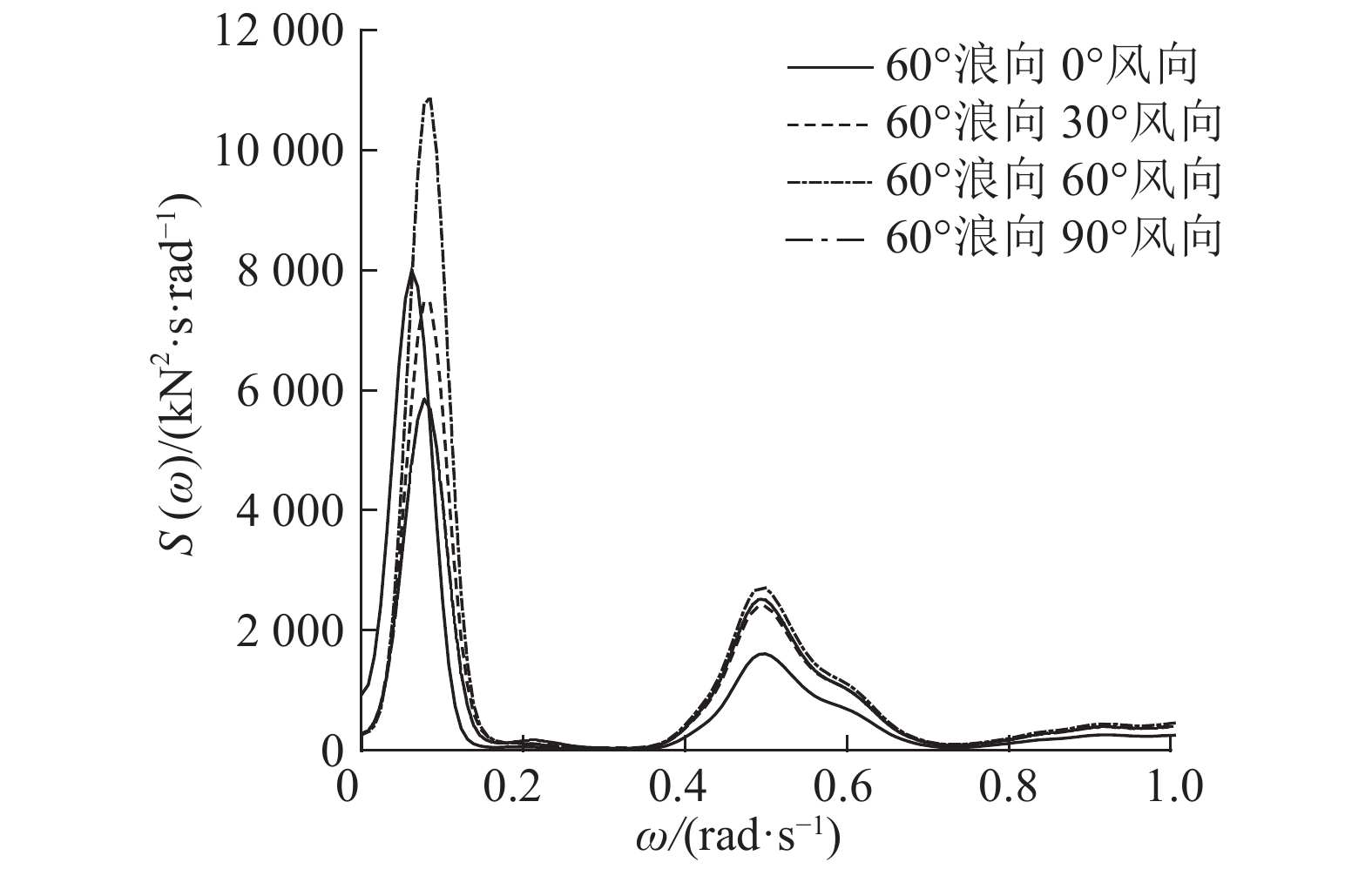
图 24 不同风向的张力功率谱 Fig. 24 PSD of tension force with different wind direction |
图21表明,系缆3的张力在额定工况条件下的均值与只有稳定风作用时的幅值基本保持一致. 在额定工作条件下,系缆张力主要取决于风载荷,波浪载荷会改变系缆张力的动态响应.
图23、24表明,系缆3的张力存在2个峰值点,分别对应风力机的纵荡和纵摇固有周期. 在纵荡固有周期处,峰较明显,说明能量主要集中在低频运动. 当风浪向夹角均为30°时,张力功率谱的幅值变化不大;当风浪同向时,在波浪谱峰周期处具有最大的张力功率谱幅值;在不同的风浪入射角下,系缆的最大张力不超过1 800 kN,证明采用该系泊系统能够保证系统安全运行.
4 结 论(1)Spar型浮式风力机纵荡和纵摇耦合作用较明显;当风浪同向时,会激发Spar型浮式风力机在该方向的大幅动态响应.
(2)风浪方向夹角越大,平台首摇运动响应越大;环境载荷方向对垂荡运动的影响不大.
(3)设计出的6 MW Spar浮式风力机在风浪的各种入射角下具有良好的运动响应,delta-line的存在能够避免首摇角过大而导致锚链互相缠绕的现象发生,系泊系统完全能够保证整个风力机的安全运行.
| [1] |
Global Wind Energy Council (GWEC) (2016). Global wind energy outlook 2016[R].[S. l.]: GWEC, 2016.
|
| [2] |
郑崇伟. 全球海域风能资源储量分析[J]. 中外能源, 2011, 16(7): 37-41. ZHENG Chong-wei. Analysis of wind energy reserves in global sea area[J]. Sino-Global Energy, 2011, 16(7): 37-41. |
| [3] |
黄维平, 刘建军, 赵战华. 海上风电基础结构研究现状及发展趋势[J]. 海洋工程, 2009, 27(2): 130-134. HUANG Wei-ping, LIU Jian-jun, ZHAO Zhan-hua. Research status and the development trend of offshore wind turbine structures[J]. The Ocean Engineering, 2009, 27(2): 130-134. DOI:10.3969/j.issn.1005-9865.2009.02.021 |
| [4] |
JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for offshore system development [R]. Colorado: National Renewable Energy Lab.(NREL), Golden, CO (United States), 2009.
|
| [5] |
JONKMAN J, MUSIAL W. Offshore code comparison collaboration (OC3) for IEA Wind Task 23 offshore wind technology and deployment [R]. Colorado: National Renewable Energy Lab.(NREL), Golden, CO (United States), 2010.
|
| [6] |
ZHANG R, TANG Y, HU J, et al. Dynamic response in frequency and time domains of a floating foundation for offshore wind turbines[J]. Ocean Engineering, 2013, 60(1): 115-123. |
| [7] |
CHENG Z, WANG K, GAO Z, et al. Dynamic response analysis of three floating wind turbine concepts with a two-bladed darrieus rotor[J]. Journal of Ocean and Wind Energy, 2015, 2(4): 213-222. |
| [8] |
TRAN T T, KIM D H. The coupled dynamic response computation for a semi-submersible platform of floating offshore wind turbine[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 147: 104-119. DOI:10.1016/j.jweia.2015.09.016 |
| [9] |
ZHAO Y, YANG J, HE Y, et al. Coupled dynamic response analysis of a multi-column tension-leg-type floating wind turbine[J]. China Ocean Engineering, 2016, 30(4): 505-520. |
| [10] |
GOUPEE A J, KOO B J, KIMBALL R W, et al. Experimental comparison of three floating wind turbine concepts[J]. Journal of Offshore Mechanics and Arctic Engineering, 2014, 136(2): 020906. |
| [11] |
DNV G L. Design of offshore wind turbine structures [S]. Oslo: [s.n.], 2016.
|
| [12] |
ZAMBRANO T, MACCREADY T, KICENIUK T, et al. Dynamic modeling of deepwater oore wind turbine structures in Gulf of Mexico storm conditions [C] // 25th International Conference on Offshore Mechanics and Arctic Engineering. St John's, Canada: ASME, 2006: 629–634.
|
| [13] |
API. API 2F specification for mooring chain [S]. Washington, DC: [s.n.], 1997.
|
| [14] |
BOSSANYI E A. Bladed for windows user manual [M]. Bristol: Garrad Hassan and Partners, 2000.
|
| [15] |
中国船级社. 海上移动平台入级与建造规范[S]. 北京: 人民交通出版社, 2005.
|
| [16] |
CUMMINS W E. The impulse response function and ship motions [R]. Washington DC : David Taylor Model Basin, 1962: 6–23.
|
| [17] |
KARIMIRAD M, MOAN T. Wave-and wind-induced dynamic response of a Spar-type offshore wind turbine[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2011, 138(1): 9-20. |



