为了满足客户多样化、个性化的需求,汽车制造商广泛地采用混流生产线进行装配作业. 以多品种、小批量为特色的混流生产模式使得装配线所需零部件的种类和数目显著增加,因而准时化物料供应调度逐步成为整车企业亟待解决的关键问题[1]. 据此可知,进行汽车装配线的物料供应调度研究对提高生产线的装配效率具有重要意义.
近年来,许多国内外学者对汽车装配线的物料供应问题进行了较深入的研究,研究内容主要集中在循环配送问题和单点配送问题两个方面[2]. 循环配送问题可以描述为配送设备依照固定的行车线路进行周期性的装配线物料供应活动,以设备装载能力为约束决策每次配送过程中各类物料的数目. 这一方面的研究相对较成熟,Emde等[3]提出多项式时间算法,用于求解以优化线边库存为目标的循环配送问题;Fathi等[4]构建循环配送问题的多目标模型,以优化线边库存和配送次数. 单点配送问题可以描述为配送设备以多批次、小批量的模式进行装配线物料供应活动,且每次配送活动仅涉及一个工位. 单点配送问题的研究相对较少,Boysen等[5]研究基于单个设备的汽车装配线单点配送问题,建立动态规划算法和启发式算法,以优化装配线的库存. Boysen等[6]系统地阐述了不同类型单点配送问题,给出各类问题的复杂度证明. 以上文献仅考虑单个设备的单点配送问题,实际的汽车装配线物料供应往往涉及到多个设备的联合配送调度. Luo等[7-8]研究多设备协作配送的调度问题,但优化指标为配送设备的最大完工时间、配置数目和等待时间等,未考虑生产线的库存状况.
汽车装配线的物料供应调度问题为复杂的组合优化问题,在大规模情形下,难以利用精确算法进行求解;因此,群智能算法成为解决这一难题的重要手段,目前应用于这一领域的算法包括蚁群算法、粒子群算法和遗传算法等. 教-学优化算法是Rao等[9]受教师与学生之间学习过程的启发而提出的一种新型的群智能算法. 与上述算法相比,教-学优化算法具有收敛速度快、控制参数少等优点,并且该算法在神经网络训练、资源项目调度等方面已经获得了成功应用. 标准TLBO算法采用实数编码方式,无法直接应用于离散问题的求解;此外,算法在迭代后期易陷入局部最优,全局搜索能力和深度寻优能力有待进一步的开发.
本文针对多个设备的联合配送问题进行建模,考虑各型号设备配送速度的差异性,构建以优化线边库存为目标的汽车装配线物料供应调度模型. 基于标准TLBO算法的框架和调度问题的性质,在编码与解码方法、强化算法的全局搜索能力和增强算法的深度寻优能力3个方面进行重新设计,构建混合教-学求解算法;利用仿真测试,验证了调度算法的有效性.
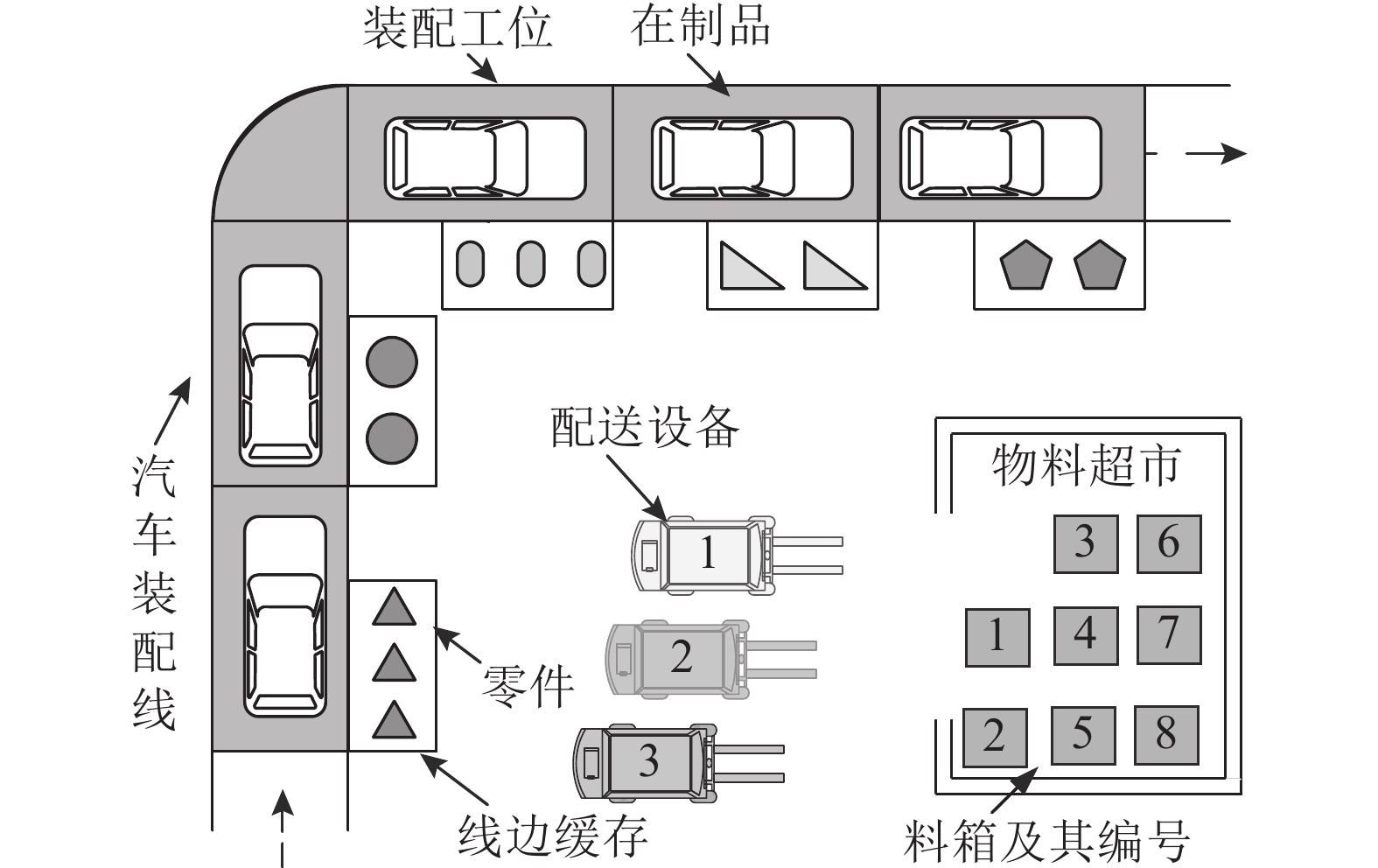
1 数学建模 1.1 问题描述在汽车装配车间,在制品依次流经各个工位进行装配作业,装配线所需零部件在物料超市进行分拣和装箱,各个料箱内装有一定数目的同类物料,并由多台不同型号的配送设备完成物料的上线作业,图 1给出汽车装配线物料供应的示意图.
|
图 1 装配线物料供应示意图 Fig. 1 Part-supply of mixed-model assembly lines |
为了清晰地描述汽车装配线的物料供应问题,给出如下基本假设. 1)作业车间采用装配线节拍时间,作为系统的基本时间单位;2)为了简化建模过程,假定每个工位负责装配一类物料,据此可以实现物料类型和工位的一一对应关系;3)各个料箱中的物料类型及数目已知;4)每次配送作业包含一个料箱,配送过程不可中断,各个设备在到达当前配送任务的目标工位后立刻返回物料超市,并开始后续的配送任务;5)各类型配送设备从超市到所有工位间的行驶时间为定值,由于装卸作业时间较短,忽略不计;6)各个工位在初始阶段的库存量已知;7)装配线的投产排序结果已知,因而各工位的需求为已知量;8)各工位不允许发生缺货.
为了有效地控制线边库存,实现装配线的准时化物料供应,构建的调度问题包含以下2个子问题:1)料箱分配问题,即确定各个设备所负责配送的料箱集合;2)料箱排序问题,即确定每个配送设备的料箱配送次序.
1.2 数学模型目标函数为最小化规划期内所有工位的最大加权库存,如下:
| ${\rm{min }}\,\,Z(\sigma ) = \mathop {\max }\limits_{s = 1, \cdots ,w;t = 1, \cdots ,T} \{ {\omega _s} {L_{s,t}}\}. $ | (1) |
式中:Z(σ) 为方案 σ 所产生的规划期内所有工位的最大加权库存,
约束条件如下.
1) 设备 k 第 p 次配送作业过程中料箱编号表示为
| $\left.\begin{array}{l}{r_{{l_k}(p)}} = \left\{ {\begin{array}{*{20}{l}}{{d_{{s_{{l_k}(p)}},k}}},&{p = 1};\\{{d_{{s_{{l_k}(p)}},k}} + \displaystyle\sum\limits_{q = 1}^{p - 1} {2 {d_{{s_{{l_k}(q)}},k}}} },&{p = 2, \cdots ,{n_k}};\end{array}} \right.\\\quad\quad\quad\quad k \in \{ 1,2, \cdots ,m\} ,\;\;\;p \in \{ 1,2, \cdots ,{n_k}\} .\end{array}\!\!\!\right\}\!\!\!\!$ | (2) |
式中: nk 为设备 k 的总配送次数,
2) t 时刻到达工位 s 处的料箱集合
| $\left.\begin{array}{l}{\varGamma _{s,t}} = \{ i \in \{ 1,2, \cdots ,n\} |{r_i} \leqslant t,{s_i} = s\} ;\\ s \in \{ 1,2, \cdots ,w\} ,\;\;t \in \{ 1,2, \cdots ,T\} .\end{array}\right\}$ | (3) |
式中:n 为料箱总数,ri 为料箱 i 到达目标工位的时间.
3) t 时刻工位 s 处库存 Ls, t 表示为
| $\left.\begin{array}{l}{L_{s,t}} = {\alpha _s} + \displaystyle\sum\limits_{i \in {\varGamma _{s,t}}} {{a_i}} - {D_{s,t}};\\ s \in \{ 1,2, \cdots ,w\} ,\;\;t \in \{ 1,2, \cdots ,T\} .\end{array}\right\}$ | (4) |
式中:αs 为工位 s 的初始库存量,ai为料箱 i 中的物料数目,Ds,t 为工位 s 在时刻 t 的累积物料需求量.
4) 装配线各工位在规划期内不允许缺货, 即
| ${L_{s,t}} \geqslant 0;\;\; s \in \{ 1,2, \cdots ,w\} ,\;\;t \in \{ 1,2, \cdots ,T\} .$ | (5) |
为了说明这一物料配送问题,给出如下算例. 2台配送设备负责2个工位的物料配送任务,各工位的初始库存量取值为
| 表 1 料箱信息 Table 1 Box information |
| 表 2 各工位需求信息 Table 2 Demand information at each station |
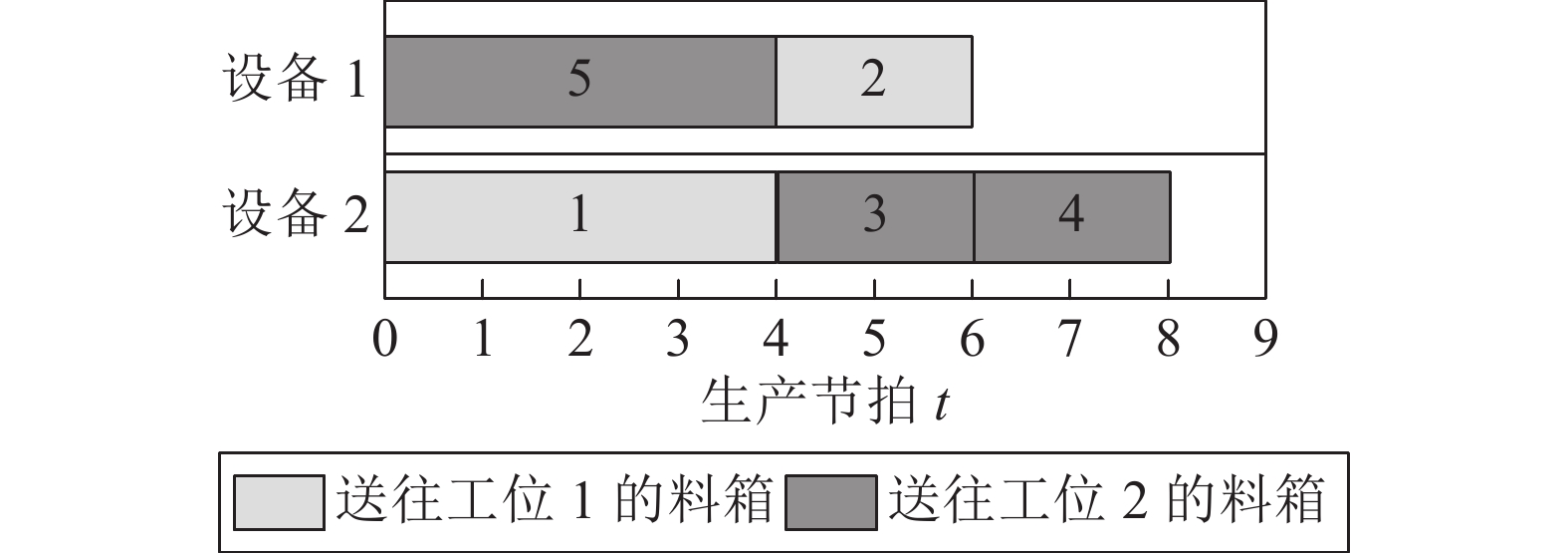
给定调度方案
|
图 2 甘特图 Fig. 2 Gantt chart |
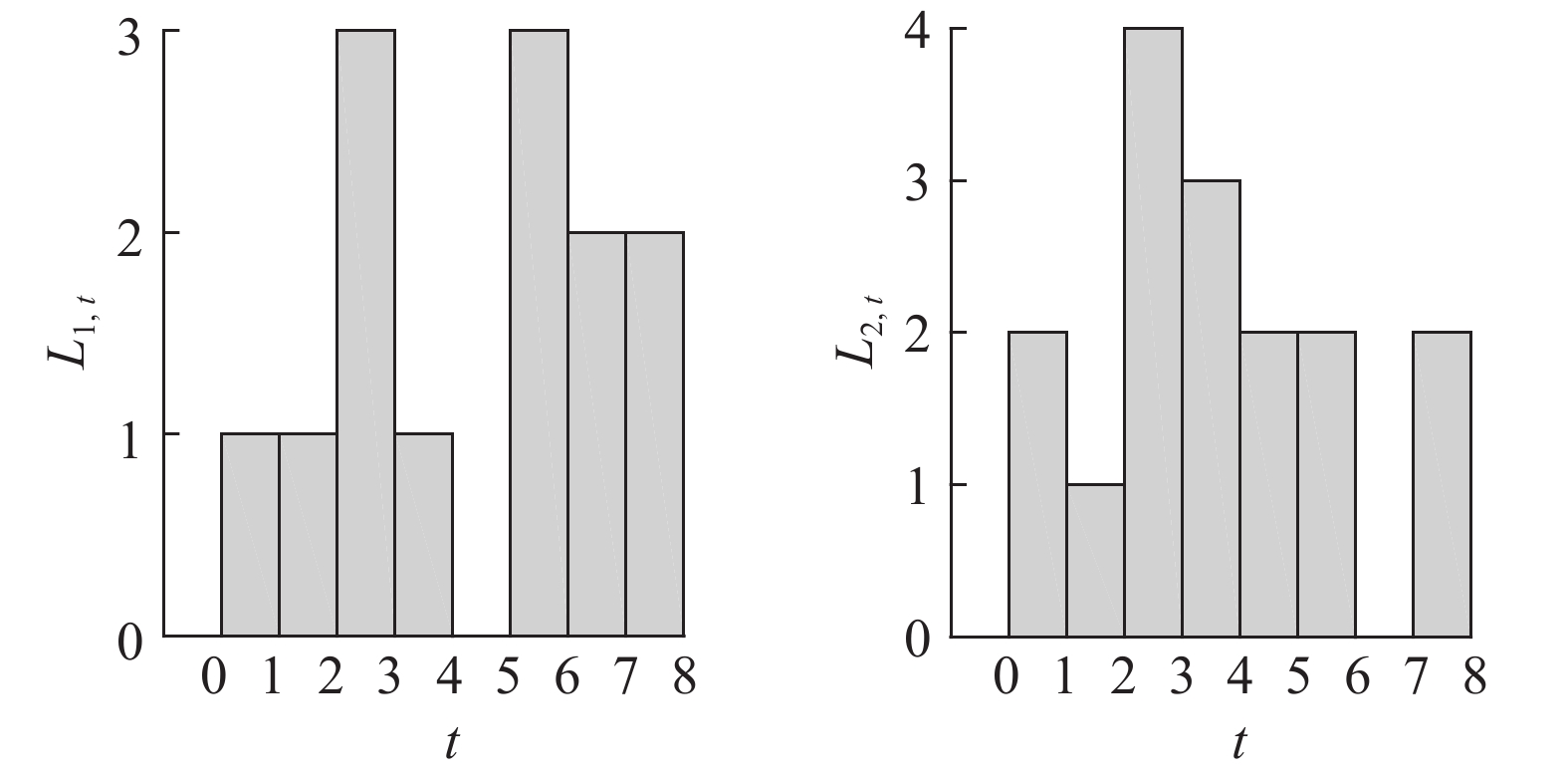
|
图 3 库存水平 Fig. 3 Inventory status |
依据假设可知,
性质1 已知调度方案 σ,对应的目标函数可以转化为
| $t_i^1 = \left\{ {\begin{array}{*{20}{l}} {\min \left\{ {{r_i},T} \right\}},&{\;{r_i} = \left\lceil {{r_i}} \right\rceil }; \\ {\min \left\{ {\left\lceil {{r_i}} \right\rceil ,T} \right\}},&{{\text{其他}}} .\end{array}} \right.$ |
性质2 已知方案 σ,构建集合
| $t_i^2 = \left\{ {\begin{array}{*{20}{l}} {\min \,\{ {r_i} - 1,T\} },&{\;{r_i} = \left\lfloor {{r_i}} \right\rfloor } ;\\ {\min\, \{ \left\lfloor {{r_i}} \right\rfloor ,T\} },&{{\text{其他}}} .\end{array}} \right.$ |
式中:
性质1可以用于简化目标函数的计算,性质2可以用于确定调度方案的可行性. 在后续求解算法的构造部分,将以上2条性质应用于适应度计算和剪枝算法设计,以增强算法的有效性.
2 标准TLBO算法TLBO算法隶属于群智能优化算法. 该算法以老师表示当前种群的最优解个体,以学生表示当前种群中的剩余个体,算法进化过程包括教学阶段和学习阶段2个方面. TLBO算法的流程归纳如下.
1)初始化算法和问题的相关参数,包括种群规模 P、变量的维度 D、变量各维度的取值
2)构建初始种群并计算适应度. 以rand(0,1)表示[0,1]之间的随机数,个体的初始化公式为
| ${x_d} = x_d^{\rm l} + {\rm rand}(0,1) \left(x_d^{\rm u} - x_d^{\rm l}\right).$ |
3)教学阶段. 求解当前群体每一维的平均值
| ${{ x}^{\rm{new}}} = {{ x}^{\rm{old}}} + {\rm{rand}}(0,1) \left({{ x}^{\rm b}} - \tau { {\bar x}}\right).$ |
式中:xb 为当前种群的最优解,教学因子
4)学习阶段. 针对当前种群中的每个个体 xold,随机选择另一个体 xr,利用学习公式进行种群的第2次更新. 以最小化问题为例,更新公式为
| ${{ x}^{\rm{new}}} = \left\{ {\begin{aligned}& {{{ x}^{\rm{old}}} + {\bf{rand}}{^{ D}} \left({{ x}^{\rm r}} - {{ x}^{\rm{old}}}\right)}, \quad\quad{\;f\left({{ x}^{\rm r}}\right)< f\left({{ x}^{\rm{old}}}\right)}; \\ & {{{ x}^{\rm{old}}} + {\bf{rand}}{^{D}} \left({{ x}^{\rm{old}}} - {{ x}^{\rm r}}\right)},\quad\quad{{\text{其他}}} .\end{aligned}} \right.$ |
式中:f 为目标函数值,randD 为 1×D 随机数矩阵,各维度取值为[0,1].
5)迭代终止条件判断. 若算法满足终止条件,则迭代结束;否则,循环运行3)、4).
3 HTLBO算法结合问题的性质构建HTLBO求解算法,算法的核心思想包括:1)构建特定的编码与解码方法,使得标准TLBO算法能够适用于求解离散问题;2)提出局部搜索流程,用于强化算法的全局开发能力;3)结合束搜索技术,构建融合问题特性的剪枝算法,以强化算法的深度寻优能力.
3.1 编码与解码、适应度计算编码过程:给定料箱数 n 和配送设备总数 m,HTLBO算法采用实数编码方式,对该物料配送问题进行编码. 编码长度为 n,每一位编码的取值为[1,m+1),编码的第 i 位对应于料箱 i.
解码过程:对编码进行取整操作,编码第 i 位的整数部分表示负责料箱 i 配送作业的设备标号,据此可以得到各配送设备的料箱集合. 针对同一配送设备上所有料箱对应的编码数值,按大小升序排列,据此可得各设备的料箱配送序列.
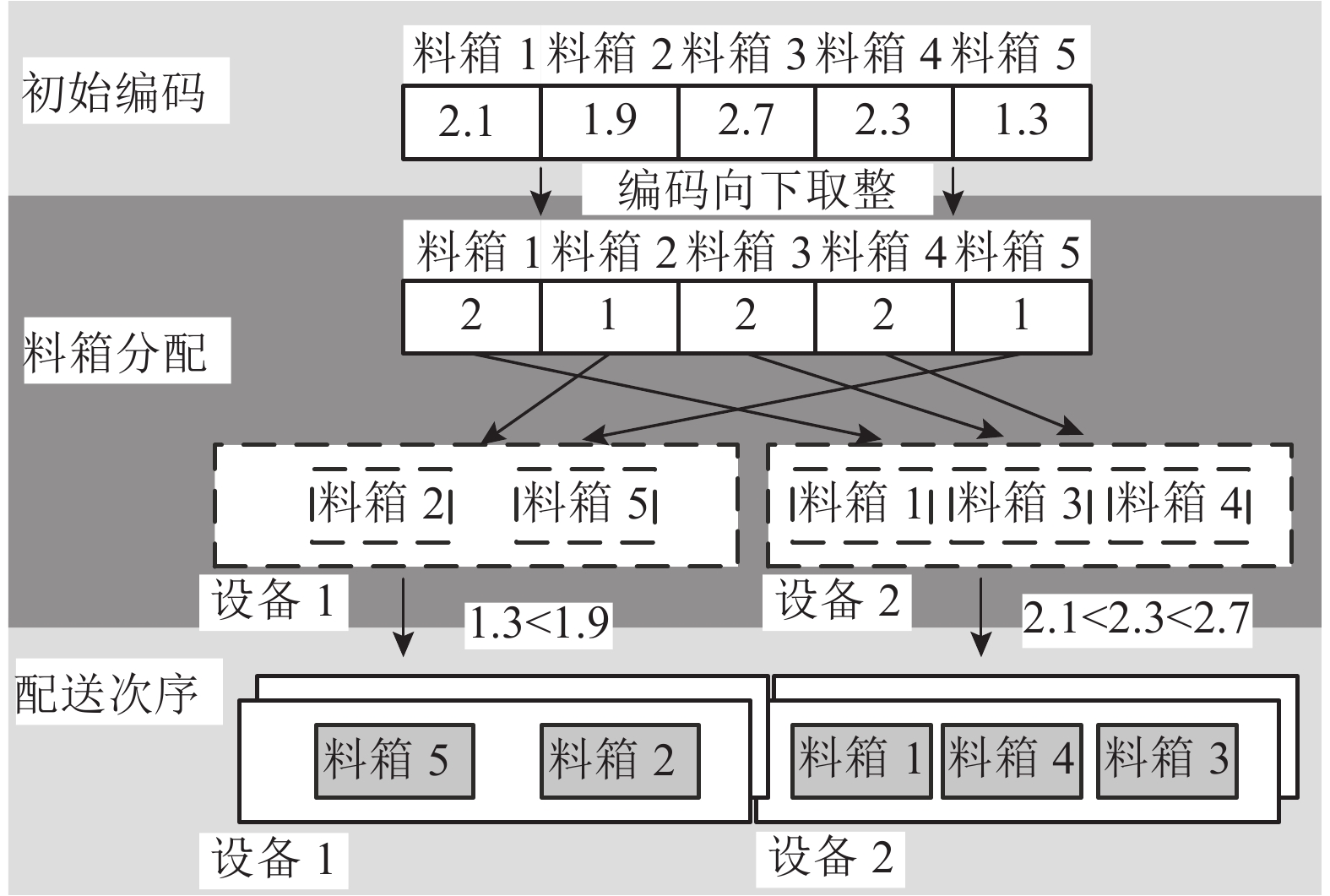
为了清晰地说明以上编码和解码过程,结合数学建模部分所给算例的参数设置,给出该算例一个编码 {2.1,1.9,2.7,2.3,1.3}. 对应的调度方案为
|
图 4 编码与解码示意图 Fig. 4 Encoding and decoding |
上述编码方式简洁有效,易于实现. 该编码方式未考虑装配线不缺货这一复杂约束. 此外,该约束无法通过简单的修复方法进行处理. 基于性质1和2,通过引入惩罚项来构造HTLBO算法的评价函数 f(σ),公式如下:
| $f(\sigma ) = \mathop {\max }\limits_{i \in \{ 1,2, \cdots ,n\} } \{ {\omega _{{s_i}}} {L_{{s_i},t_i^1}}\} + \beta \sum\limits_{i = 1}^n \;{\max \left\{ 0, - {L_{{s_i},t_i^2}}\right\} }. $ |
式中:β 为惩罚系数,取值为正.
3.2 局部搜索流程为了强化算法的全局开发能力,构建局部搜索流程,尽可能发掘问题的优质解[10]. 该局部搜索流程包含以下3种基本变异算子:交换、反转和插入. 3种算子的具体操作归纳如下.
1) 交换,随机选择当前解 σ 编码位置 p1和 p2处的编码数值并交换,生成新个体 σ'.
2) 反转,随机选择当前解 σ 编码位置 p1~p2处的编码数值并倒转,生成新个体 σ'.
3) 插入,随机选择当前解 σ 编码的2个位置 p1和 p2,将位置 p1上的编码数值插到 p2之前,生成新个体 σ'.
由该编码与解码方法可知,编码的第 i 位决定料箱 i 所对应配送设备的编号和料箱 i 在该设备上的配送次序. 上述3种变异算子能够使得变异部分编码所对应的料箱获得新的设备编号和配送次序. 构建的局部搜索流程融合以上3种基本算子,首先生成3种算子的随机排列
1)针对当前解 σ,基于算子O1生成新解 σ'. 若
2)针对当前解 σ, 基于算子O2生成新解 σ'. 若
3)针对当前解 σ,基于算子O3生成新解 σ'. 若
为了增强算法的局部挖掘能力,结合问题的性质和束搜索技术构建剪枝算法,力求提升当前种群中可行解的性能[11]. 给出当前可行解 σ 的瓶颈工位的定义. 结合瓶颈工位的概念,定义当前解 σ 的邻域结构. 给出剪枝算法的搜索流程.
给定可行解 σ,定义 Z(σ) 所在工位为 ŝ,ŝ 处的最大库存为 Lŝmax,变量 ŝ 和 Lŝmax 计算如下:
| $\hat s = \arg \mathop {\max }\limits_{s = 1,2, \cdots ,S} \{ {\omega _s} \cdot \max \{ {L_{s,t}}|t \in \{ 1,2, \cdots ,T\} \} \} ,$ |
| $L_{\hat s}^{\max } = \max\, \{ {L_{\hat s,t}}|t \in \{ {r_i}|i \in {B_{\hat s}}\} \}. $ |
据此可知,解 σ 中工位 ŝ 处的物料供应作业成为制约当前准时化物料供应调度的瓶颈. 定义工位 ŝ 为瓶颈工位,控制并改善瓶颈工位 ŝ 处的物料供应调度,有助于提高当前解 σ 的性能.
令 Bŝ 表示目标工位为 ŝ 的料箱所构成的集合,基于瓶颈工位的概念,定义当前可行解 σ 的邻域结构为:
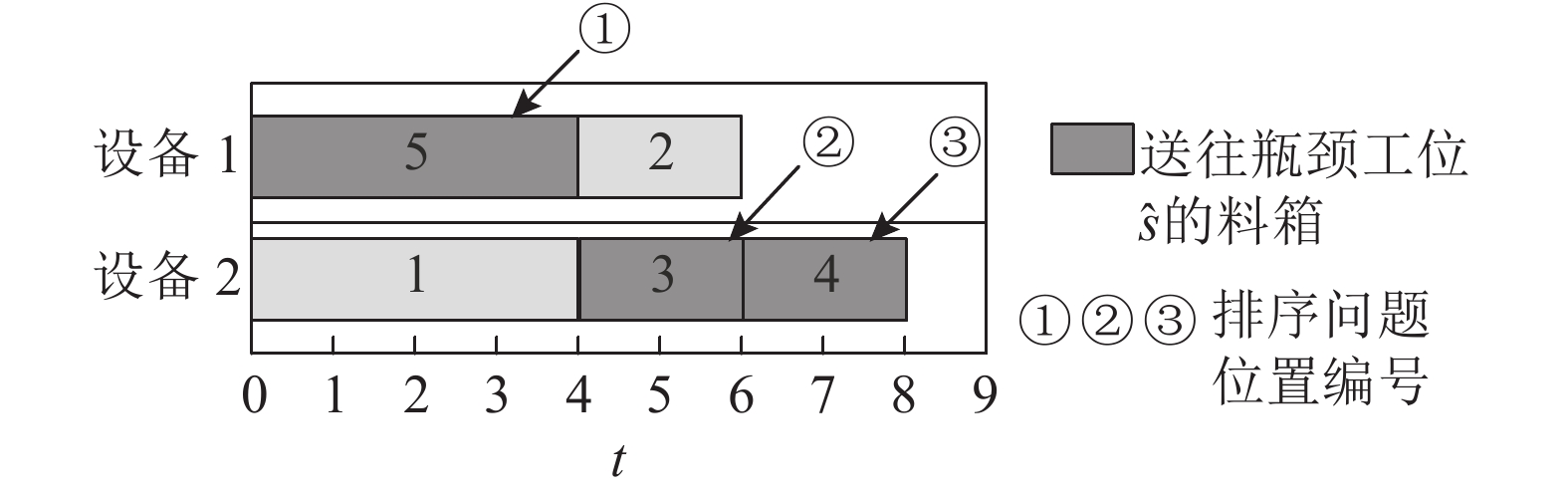
|
图 5 邻域结构示意图 Fig. 5 Diagram of neighbourhood |
根据问题假设可知,各类型设备的配送时间仅与料箱的目标工位相关. 新解 σ' 中工位 ŝ 接受物料更新的维持时间不变,但线边库存发生变化;其他工位料箱的到达时刻维持不变,库存随之维持与解 σ 相同的水平. 定义当前解 σ 在瓶颈工位 ŝ 处接受物料供应的时刻集合为
1)令
2)
3)
4)
5)更新Π, 即
搜索完毕后,选择Π中 Lmax 最小的子序列构建新解. 剪枝算法的优化过程包含2类剪枝操作,第1类剪枝为当前子序列在工位 ŝ 处的最大库存未优于解 s 的情况,即

|
图 6 剪枝算法优化示意图 Fig. 6 Diagram of pruning method |
如图 6所示,给出剪枝算法优化所给算例的示意图. 由搜索流程可得2个序列 {3,5,4} 和 {4,5,3},对应的 Lmax 分别为2和3,据此可得新的调度方案
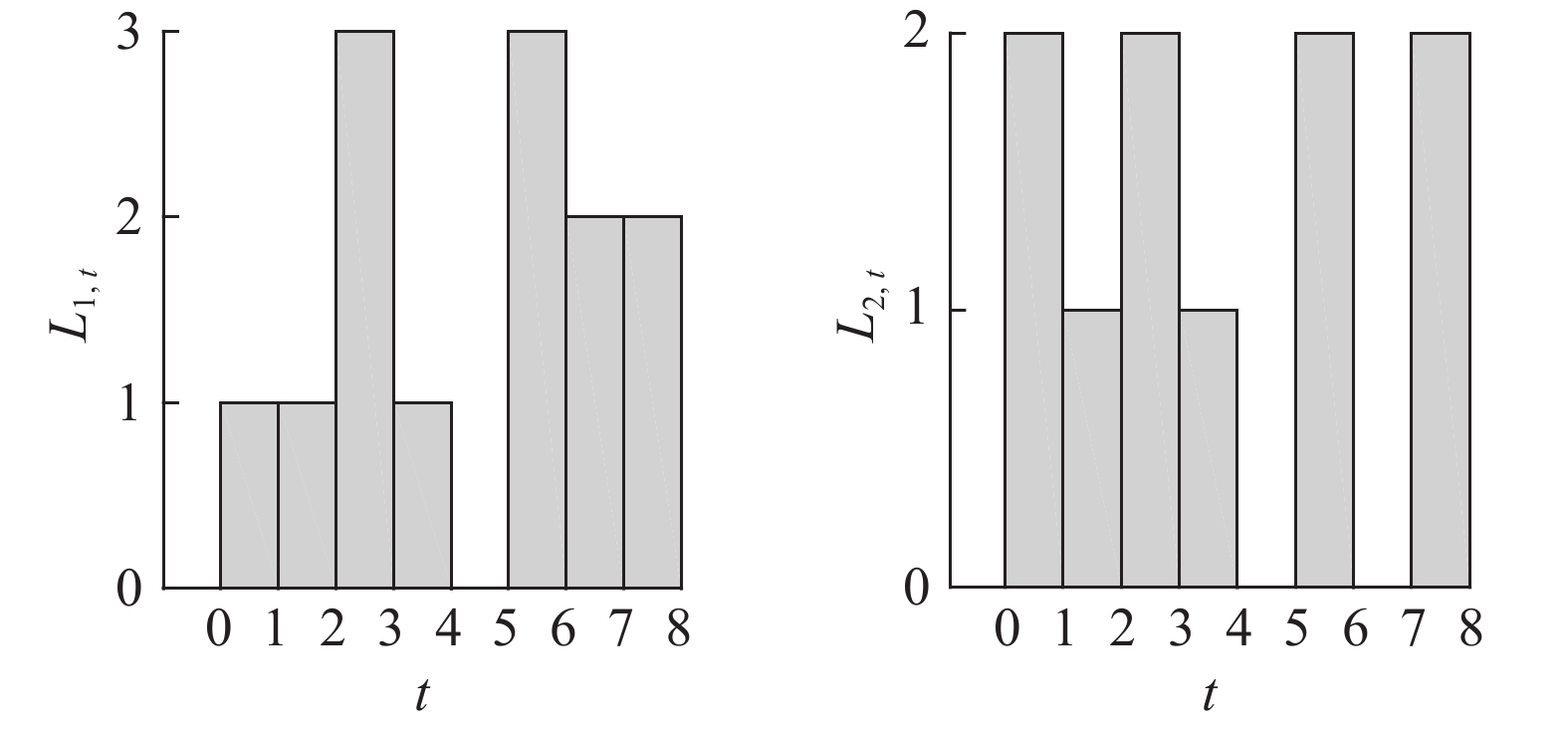
|
图 7 改进解的库存水平 Fig. 7 Inventory status of improved solution |
1)初始化算法参数和问题参数.
2)构建初始种群,计算适应度.
3)利用标准TLBO算法中教学阶段和学习阶段的邻域变换公式,更新当前种群.
4)针对当前种群中的每个解,利用局部搜索流程进行个体更新.
5)针对当前种群中的可行解,结合剪枝算法挖掘优秀解.
6)若算法满足终止条件,则终止优化流程并输出当前最优解;否则,转3).
3.5 时间复杂度分析分析HTLBO算法在迭代搜索过程中的相关操作的时间复杂度如下.
1)初始化每个个体的时间复杂度为 O(n).
2)对于每个个体进行解码涉及料箱分配和排序2个步骤,相应的时间复杂度分别为 O(n) 和
3)利用快速排序法对P个个体进行适应度排序,所需的时间复杂度为
4)教学和学习阶段的每个解更新均需耗时 O(n).
5)局部搜索中3种变异算子耗时均为 O(1).
6)剪枝算法采用广度优先的束搜索技术且搜索宽度设置为
据此可知, HTLBO算法所需的时间复杂度相对较低, 能够有效求解中大规模调度问题.
4 实验分析 4.1 算例构建考虑到构建的汽车装配线物料供应调度问题尚无标准测试集,为了验证算法的有效性,结合文献[5]的相关参数, 构建测试算例. 料箱数
针对测试算例 (n,m),各工位初始库存量、料箱中的物料量等相关参数设置如下.
1) 将 n 个料箱随机分配给 w 个装配工位,且保证每个工位至少分得一个料箱,据此可得各个料箱的目标工位
2)
3)
| ${D_{s,t}} = \left\{ {\begin{array}{*{20}{l}} {{D_{s,t}}},&{\;{\rm{rand(0,1)}} < 0.5}; \\ {{D_{s,t{\rm{ - }}1}}{\rm{ + }}1},&{{\text{其他}}} .\end{array}} \right.$ |
4) 工位 s 的物料需求总量为
选用Matlab2016b平台进行编程测试,在主频为2.4 GHz、内存为4 GB、Intel(R) Core(TM) i5-2430M CPU的便携式计算机上开展仿真实验, 将运行时间 τmax 设置为算法的终止条件.
4.2 HTLBO算法参数校验HTLBO算法包含3个重要参数:τmax 、剪枝算法控制参数
| 表 3 正交试验参数配置 Table 3 Parameter settings of orthogonal design |
| 表 4 正交试验测试结果 Table 4 Simulation results of orthogonal experiment |
采用直观分析法和方差分析法分析表 4的测试结果,表 5给出测试结果的极差分析,如表 6所示为测试结果的方差分析,其中显著性水平取值为0.05. 由表 5的极差分析可知,参数
| 表 5 测试结果极差分析 Table 5 Range analysis of simulation results |
| 表 6 测试结果方差分析 Table 6 Analysis of variance for simulation results |
为了验证HTLBO算法的优化性能,将其与标准教-学算法(TLBO)、模拟退火算法(simulated annealing, SA)[5]和离散粒子群算法(discrete particle swarm optimization,DPSO)[12]的测试结果进行对比,后两者为求解同类调度问题的有效算法. 针对每个算例,各个算法均独立运行15次并对测试结果进行统计. 在算法的参数设置方面,TLBO、SA和DPSO的求解时间设置为与HTLBO相同,TLBO和DPSO的种群规模设置为与HTLBO相同,3种对比算法的其余参数采用正交实验进行校验,以此保证对比实验的公平性.
为了直观、清晰地展示测试结果,依据文献[13]对仿真结果进行如下处理. 针对各算例,令 h 表示算法(
| 表 7 4种调度算法的测试结果 Table 7 Simultation results of four scheduling algorithoms |
由表 7可知,在与其他3种算法共计60组的对比测试中,53组算例的测试结果表明,HTLBO算法的优化结果显著优于对比算法;在剩余的7组对比测试中,HTLBO多次运行结果的均值优于对比算法. HTLBO算法相较于其他3种算法具有更强的寻优能力,能够有效地获得问题的满意解.
针对每个算例,定义变量

|
图 8 4种算法的稳定性对比 Fig. 8 Stability comparison of four scheduling algorithoms |
将HTLBO算法的求解结果与回溯算法[14]的优化结果进行对比. 回溯算法隶属于最优化搜索技术,能够有效地处理含复杂约束的组合优化问题,并取得问题的精确解,且已经被成功应用于求解同类型问题,但回溯法的计算耗时受问题规模的影响较大. 针对各个算例,设定回溯算法的计算时间为5 h,即18 000 s,仿真结果表明回溯算法能够在规定的时间内求得3个算例的精确解. 如表 8所示为对HTLBO算法和回溯算法的优化效果对比. 表中,ξ为偏差;top为运行时间;Z(B) 为利用回溯算法所得的最优解,其中GAPb 和 GAPa 为HTLBO算法在15次运行过程所得最优解和均值相对于 Z(B) 的百分比偏差,即
| $\begin{array}{l}{\rm{{GA{P_b}}}} = {\displaystyle\frac{{({Z_{\rm b}}({\rm{HTLBO}}) - Z(B))}}{{Z\left( B \right)}} \times 100{\text{%} } ,}\\{\rm{GA{P_a}}}={ \displaystyle\frac{{({Z_{\rm a}}({\rm{HTLBO}}) - Z(B))}}{{Z\left( B \right)}} \times 100{\text{%}} .}\end{array}$ |
由表 8的测试结果可知:在解的质量方面,HTLBO算法多次运行所得的最优解和均值与 Z(B) 较接近,算例(150,10)的 GAPb 和 GAPa 分别为0.184%和6.996%;在计算时间方面,HTLBO算法的用时远少于回溯算法,利用HTLBO算法和回溯算法求解算例(150,10)的用时分别为450和16 618 s.
| 表 8 HTLBO和回溯算法对比 Table 8 Comparison between HTLBO and backtracking |
以上对比测试验证了构建的HTLBO算法的有效性, 表明该算法能够获得大规模汽车装配线物料供应调度问题的满意解.
5 结 语本文以汽车装配线物料供应调度中的多设备联合配送问题为研究对象,构建以优化线边库存为目标的准时化配送模型,提出混合教-学求解算法. 构建特定的编码与解码方法,使得标准TLBO算法能够适用于当前离散调度问题的求解;结合多种变异算子构建局部搜索流程,有效增强了算法的全局开发能力;引入优化瓶颈工位物料供应的剪枝算法,使得混合算法的深度寻优能力得以强化. 利用仿真测试与分析验证了构建的调度算法的有效性.
后续研究可以探讨这一调度问题的近似算法和最优化算法的设计以及装配线物料供应过程中包含设备故障这一随机因素的动态调度问题.
| [1] |
周炳海, 彭涛. 混流装配生产线准时化物料补给调度方法[J]. 控制与决策, 2017, 32(6): 976-982. ZHOU Bing-hai, PENG Tao. Scheduling methods of just-in-time material replenishment in mixed-model assembly lines[J]. Control and Decision, 2017, 32(6): 976-982. |
| [2] |
BOYSEN N, EMDE S, HOECK M, et al. Part logistics in the automotive industry: decision problems, literature review and research agenda[J]. European Journal of Operational Research, 2015, 242(1): 107-120. DOI:10.1016/j.ejor.2014.09.065 |
| [3] |
EMDE S, FLIEDNER M, BOYSEN N. Optimally loading tow trains for just-in-time supply of mixed-model assembly lines[J]. IIE Transactions, 2012, 44(2): 121-135. DOI:10.1080/0740817X.2011.575442 |
| [4] |
FATHI M, RODRÍGUEZ V, ALVAREZ M J. A novel memetic ant colony optimization-based heuristic algorithm for solving the assembly line part feeding problem[J]. The International Journal of Advanced Manufacturing Technology, 2014, 75(1): 629-643. |
| [5] |
BOYSEN N, BOCK S. Scheduling just-in-time part supply for mixed-model assembly lines[J]. European Journal of Operational Research, 2011, 211(1): 15-25. DOI:10.1016/j.ejor.2010.10.029 |
| [6] |
BOYSEN N, BOCK S, FLIEDNER M. Scheduling of inventory releasing jobs to satisfy time-varying demand: an analysis of complexity[J]. Journal of Scheduling, 2013, 16(2): 185-198. DOI:10.1007/s10951-012-0266-0 |
| [7] |
LUO J, WU Y. Modelling of dual-cycle strategy for container storage and vehicle scheduling problems at automated container terminals[J]. Transportation Research Part E: Logistics and Transportation Review, 2015, 79: 49-64. DOI:10.1016/j.tre.2015.03.006 |
| [8] |
ZHENG K, TANG D, GU W, et al. Distributed control of multi-AGV system based on regional control model[J]. Production Engineering, 2013, 7(4): 433-441. DOI:10.1007/s11740-013-0456-4 |
| [9] |
RAO R V, PATEL V. An improved teaching-learning-based optimization algorithm for solving unconstrained optimization problems[J]. Scientia Iranica, 2013, 20(3): 710-720. |
| [10] |
SELS V, COELHO J, DIAS A M, et al. Hybrid tabu search and a truncated branch-and-bound for the unrelated parallel machine scheduling problem[J]. Computers and Operations Research, 2015, 53: 107-117. DOI:10.1016/j.cor.2014.08.002 |
| [11] |
PAREJO J A, RUIZ-CORTÉS A, LOZANO S, et al. Metaheuristic optimization frameworks: a survey and benchmarking[J]. Soft Computing, 2012, 16(3): 527-561. DOI:10.1007/s00500-011-0754-8 |
| [12] |
BEHNAMIAN J. Particle swarm optimization-based algorithm for fuzzy parallel machine scheduling[J]. International Journal of Advanced Manufacturing Technology, 2014, 75(5–8): 883-895. |
| [13] |
ZHANG R, SONG S, WU C. A hybrid artificial bee colony algorithm for the job shop scheduling problem[J]. International Journal of Production Economics, 2013, 141(1): 167-178. DOI:10.1016/j.ijpe.2012.03.035 |
| [14] |
RAO Y Q, WANG M C, WANG K P, et al. Scheduling a single vehicle in the just-in-time part supply for a mixed-model assembly line[J]. Computers and Operations Research, 2013, 40(11): 2599-2610. DOI:10.1016/j.cor.2013.05.007 |


