滚动轴承的状态监测与故障诊断一般以采集的振动信号作为分析对象,通过信号分析得到故障特征实现诊断. 由于轴承工况的不稳定和零部件的损伤等引起的非线性振动,采集到的信号大多表现出非线性、非平稳的特征,同时不可避免地受到各种噪声与信号调制干扰的影响[1]. 如何有效地抑制噪声等干扰,从成分复杂的振动信号中提取出故障特征成为故障检测的关键.
形态滤波(morphological filter,MF)是基于数学形态学变换的一种重要的非线性滤波方法[2]. 它利用结构元素与信号的形态特征进行匹配,可以有效地提取信号的边缘轮廓和形状特征,原理简明、运算简单高效,且具有明确的物理意义. 近年来,许多学者将形态滤波引入到旋转机械故障信号的冲击特征提取中,主要在形态学算子的构造和结构元素的选取方面进行拓展并取得一定的成果. 李豫川等[3]针对轴承复合故障源信号未知的问题,提出基于形态滤波和稀疏分量分析相结合的诊断方法,对观测信号进行形态滤波,可以提取重要调制特征并使信号满足稀疏性要求. Meng等[4]结合形态滤波和集合经验模态分解(ensemble empirical mode decomposition,EEMD),将开闭-闭开组合(combination morphological filter,CMF)及平移不变小波作为前置滤波单元抑制原始信号的窄带脉冲和随机噪声. Hu等[5]采用形态梯度算子(morphological gradient,MG)提取轴承信号的正负脉冲,将单个周期内的谐波波形作为基础构造新的结构元素(structuring element,SE). Dong 等[6]将闭开组合平均算子(average operator,AVG)引入到轴承振动信号的冲击成分提取过程中,利用信噪比来筛选降噪效果最佳的结构元素尺寸. 鄢小安等[7]构造出组合形态-hat变换形态算子,通过频响特性分析考察算子的滤波性质. 在上述方法中,有些形态算子的设计存在输出偏倚现象,结构元素的筛选方法计算复杂或缺乏普适性.
基于滚动轴承故障信号受谐波和随机噪声干扰严重的特点和形态学基本理论,本文根据腐蚀、膨胀、开、闭4大基本形态算子的性质,对冲击成分具有相同抑制作用、但作用方式不同的算子合并加强脉冲抑制效果合并对正冲击或者对负冲击具有抑制作用的算子,得到的2类算子组合作差反向提取出正负冲击,由此构造出新的组合差值形态算子(combination difference filter,CDIF). 选择其中两种组合差值形态算子的平均作为最终滤波输出,即平均组合差值形态滤波(average combination difference morphological filter,ACDIF). 结合峭度对冲击成分的敏感和Teager能量算子(Teager energy operator,TEO)对瞬态成分的敏感,引入Teager能量峭度[8](Teager energy kurtosis,TEK)确定最佳结构元素长度. 通过仿真信号和实际轴承振动数据的分析以及与现有滤波算子的实验对比,验证了该方法在故障诊断中的可行性和优越性.
1 数学形态学数学形态学是在积分几何和随机集论的基础上建立起来的一种数学分析方法. 为了实现滤波和特征提取,具有滤波窗作用的结构元素作为“探针”和待分析信号进行匹配;当信号局部形态特征和结构元素相匹配时,信息得以保留[9]. 膨胀(dilation)、腐蚀(erosion)、开运算(opening)和闭(closing)运算是数学形态学的4种基本算子.
设
| $(f\Theta g)(n) = \min \,[f(n + m) - g(m)],$ | (1) |
| $(f \oplus g)(n) = \max \,[f(n - m) + g(m)].$ | (2) |
| $(f \circ g)(n) = (f\Theta g \oplus g)(n),$ | (3) |
| $(f \bullet g)(n) = (f \oplus g\Theta g)(n).$ | (4) |
式中:
可以实现抑制噪声、提取信号特征目的的形态滤波器(又称形态算子)由膨胀、腐蚀、开运算和闭运算4种基本算子构成,主要有以下几种.
1)形态梯度算子MG.
| ${\text{MG}}(f(n)) = (f \oplus g)(n) - (f\Theta g)(n).$ | (5) |
2)形态差值算子(difference filter,DIF)
| $\begin{split} {\text{ DIF}}(f(n)) = (f \bullet g)(n) - (f \circ g)(n) = \hfill \\ {\text{ }}((f \bullet g)(n) - f(n)) + (f(n) - (f \circ g)(n)). \hfill \\ \end{split} $ | (6) |
式中:
3)闭开平均算子AVG.
| ${\text{AVG}}(f(n)) = [(f \bullet g)(n) + (f \circ g)(n)]/2.$ | (7) |
4)形态开-闭和闭-开算子.
| ${\text{FOC}}(f(n)) = (f \circ g \bullet g)(n),$ | (8) |
| ${\text{FCO}}(f(n)) = (f \bullet g \circ g)(n).$ | (9) |
为了克服开-闭和闭-开算子滤波结果的统计偏倚缺陷,采用开闭-闭开组合形态滤波算子,滤波输出为
| $y(n) = \frac{{{\text{FOC}}(f(n)) + {\text{FCO}}(f(n))}}{2}.$ | (10) |
形态梯度算子MG和形态差值算子DIF分别为膨胀与腐蚀、闭与开的差值运算,可以同时提取信号的正、负冲击,在故障信号特征提取中的应用较多. 由于基本算子的不可逆性质,它们对冲击的提取效果不同. 参照这两者滤波的基本思想:采用抑制负脉冲的算子减去抑制正脉冲的算子;将4种基本算子都融合到一起,提出平均组合差值形态滤波算法. 针对结构元素的自适应选择问题,引入Teager能量算子,快速响应不同信号不同形态运算方式对结构元素长度的筛选.
2.1 平均组合差值形态滤波腐蚀算子具有抑制正脉冲、平滑负脉冲的能力,减小信号峰值,加宽谷域;膨胀算子具有平滑正脉冲、抑制负脉冲的能力,增大信号谷值,扩展峰顶;开算子具有抑制正脉冲、保留负脉冲的能力,滤除信号上尖峰;闭算子具有保留正脉冲、抑制负脉冲的能力,滤除信号下尖峰[10]. 考虑到4种基本算子对脉冲的作用及不同的作用方式,将基本算子按脉冲抑制作用分为2类;对脉冲具有相同抑制作用但作用方式不同的算子集成加强抑制效果,最后两类算子组合作差反向提取出正负脉冲,由此得到的正负脉冲更加准确突出.
在ACDIF的形成过程中,将仿真信号
首先定义膨胀算子和闭算子的结合. 膨胀-闭(dilation-closing,DC)或闭-膨胀(closing-dilation,CD)滤波算子,定义如下:
| ${F_{{\text{DC}}}}(f(n)) = (f \oplus g \bullet g)(n),$ | (11) |
| ${F_{{\text{CD}}}}(f(n)) = (f \bullet g \oplus g)(n).$ | (12) |
再定义腐蚀算子和开算子的结合. 腐蚀-开(erosion-opening,EO)或开-腐蚀(opening-erosion,OE)滤波算子定义如下:
| ${F_{{\text{EO}}}}(f(n)) = (f\Theta g \circ g)(n),$ | (13) |
| ${F_{{\text{OE}}}}(f(n)) = (f \circ g\Theta g)(n).$ | (14) |
如图1所示,相对于基本滤波中的膨胀和闭对负脉冲的作用,腐蚀和开对正脉冲的作用,合并加强滤波中的DC、CD加强了对负脉冲的抑制效果,信号的正脉冲明显突出,负脉冲基本消失;EO、OE则相反,信号负脉冲明显突出,正脉冲基本消失.
为了同时提取正负脉冲,取
| ${F_{{\text{CD - OE}}}}(f(n)) = (f \bullet g \oplus g)(n) - (f \circ g\Theta g)(n),$ | (15) |
| ${F_{{\text{CD - EO}}}}(f(n)) = (f \bullet g \oplus g)(n) - (f\Theta g \circ g)(n),$ | (16) |
| ${F_{{\text{DC - OE}}}}(f(n)) = (f \oplus g \bullet g)(n) - (f \circ g\Theta g)(n),$ | (17) |
| ${F_{{\text{DC - EO}}}}(f(n)) = (f \oplus g \bullet g)(n) - (f\Theta g \circ g)(n).$ | (18) |
由文献[2,11]可知,当
如图1的差值提取部分,4种CDIF都同时将正负脉冲提取出来,通过实验分析可知,
| ${F_{{\text{ACDIF}}}} = \frac{{{F_{{\text{CD - EO}}}} + {F_{{\text{DC - EO}}}}}}{2}.$ | (19) |
最终ACDIF的输出信号整合了
结构元素和形态运算方式是影响形态滤波的2个最主要因素. 结构元素的特性与形状、高度和长度有关. 结构元素的形状对滤波效果的影响较小[12],最常用的是结构简单、计算效率高的直线型结构元素,其直线型结构元素的高度为零. 如何选择结构元素的最佳长度成为关键. 如果选择的元素过长可能导致冲击信号被当作噪声滤除;长度过短则会残留大量噪声,信号解调困难.

|
图 1 ACDIF滤波运算流程图 Fig. 1 Flowchart of ACDIF filter |
峭度是反映信号分布特性的无量纲统计参量,可以描述信号中冲击成分所占比重的大小,表达式为
| $K = \frac{{E{{(x - \mu )}^4}}}{{{\sigma ^{_4}}}}.$ | (20) |
式中:
Teager能量算子(Teager energy operator,TEO)是一种非线性算子,能够跟踪信号的瞬时能量. 对于连续时间信号
| $\varphi [x(t)] = {[\dot x(t)]^2} - x(t)\ddot x(t).$ | (21) |
式中:
对于离散时间信号
| $\varphi [x(n)] = {[x(n)]^2} - x(n + 1)x(n - 1).$ | (22) |
对于离散时间信号,Teager能量算子只需要3个样本数据计算任意时刻n处的信号源能量,对信号的瞬时变化具有良好的时间分辨率,能够检测信号中的瞬态成分[13]. Teager能量算子不仅考虑了信号幅值效应,而且考虑到信号瞬时频率的影响,可以提取频率较高的冲击信号.
Teager能量峭度(Teager energy kurtosis,TEK)是峭度和Teager 能量算子的融合,对于一维离散信号
| ${\text{TEK}} = \frac{{(N - 1)\displaystyle\sum\limits_{t = 1}^N \;{{{({\varphi _x}(t) - {{\bar \varphi }_x})}^4}} }}{{{{\left(\displaystyle\sum\limits_{t = 1}^N \;{{{({\varphi _x}(t) - {{\bar \varphi }_x})}^2}} \right)}^2}}}.$ | (23) |
式中:
为了验证所提平均组合差值形态滤波的有效性,采用仿真信号
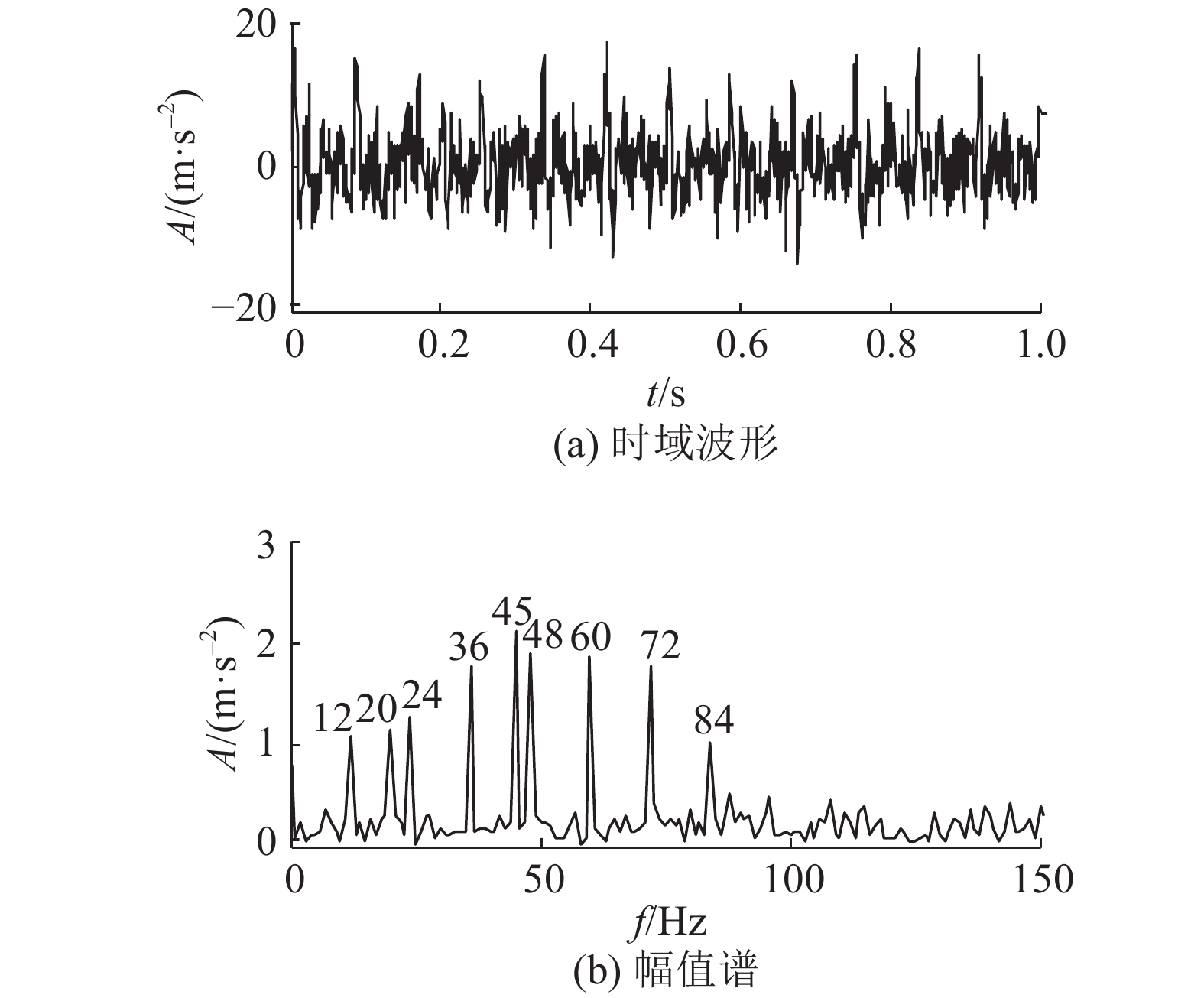
|
图 2 仿真信号时域波形及幅值谱 Fig. 2 Time-domain waveform and amplitude spectrum of simulated signal |
分别采用

|
图 3 4种组合差值滤波算子的输出结果 Fig. 3 Results of four CDIF filters |
| 表 1 组合差值滤波输出的各频率幅值 Table 1 Frequency amplitude of four CDIF filtering results |
采用ACDIF对仿真信号进行滤波处理,可以结合
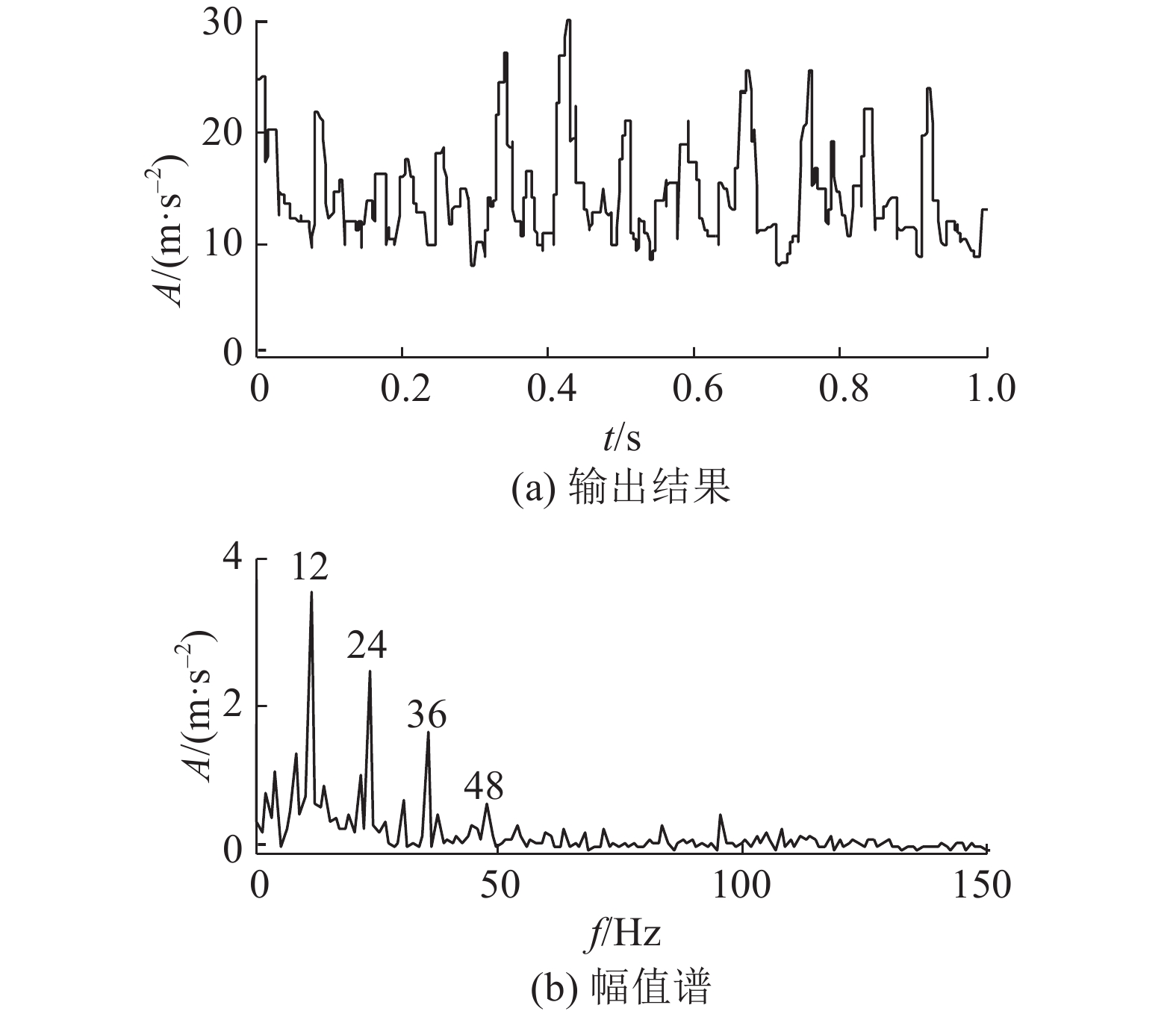
|
图 4 ACDIF滤波输出结果及幅值谱 Fig. 4 Filtering result and its amplitude spectrum of ACDIF |
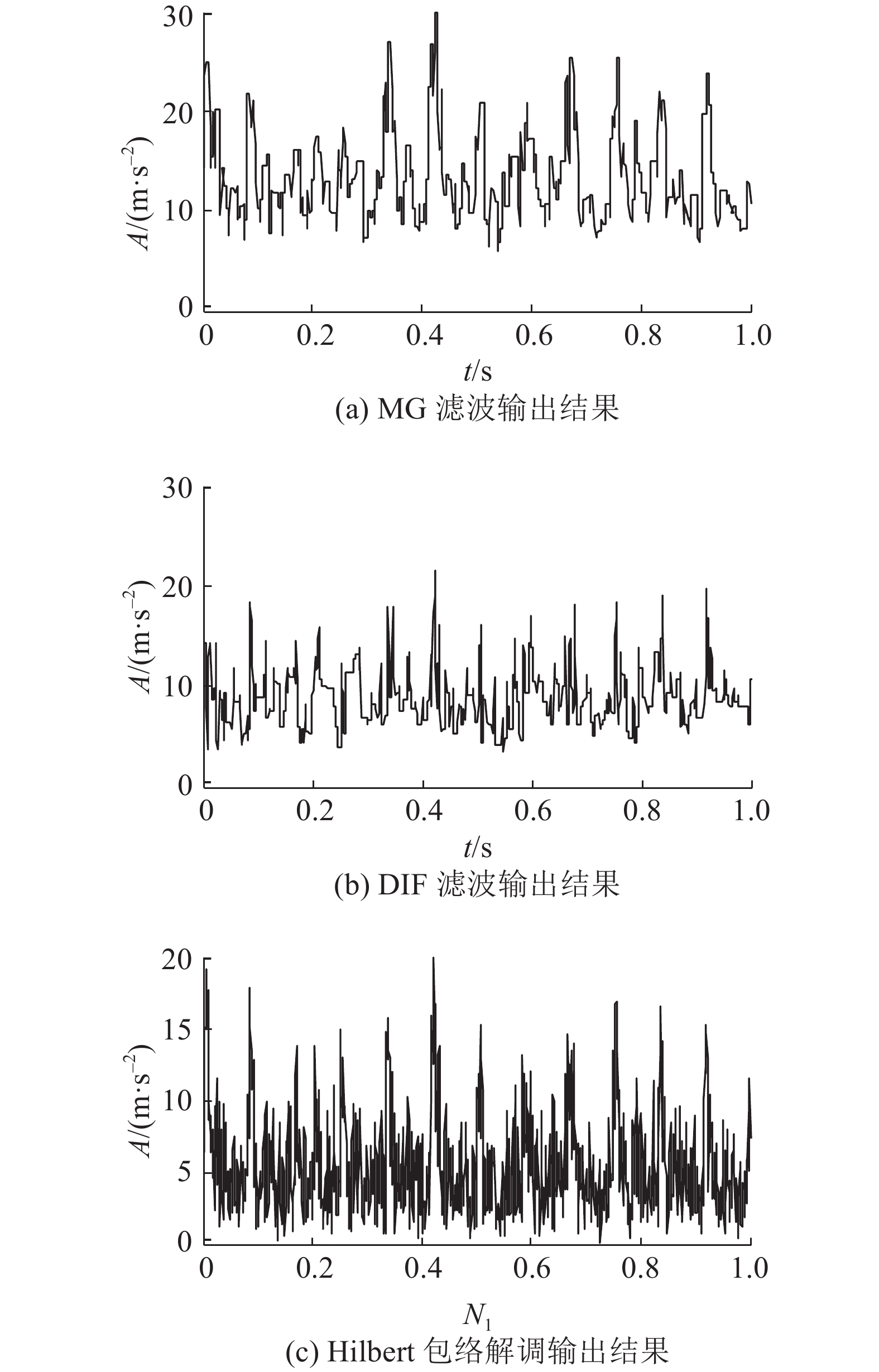
|
图 5 MG,DIF及Hilbert解调输出结果 Fig. 5 Filtering results of MG,DIF and Hilbert demodulation |
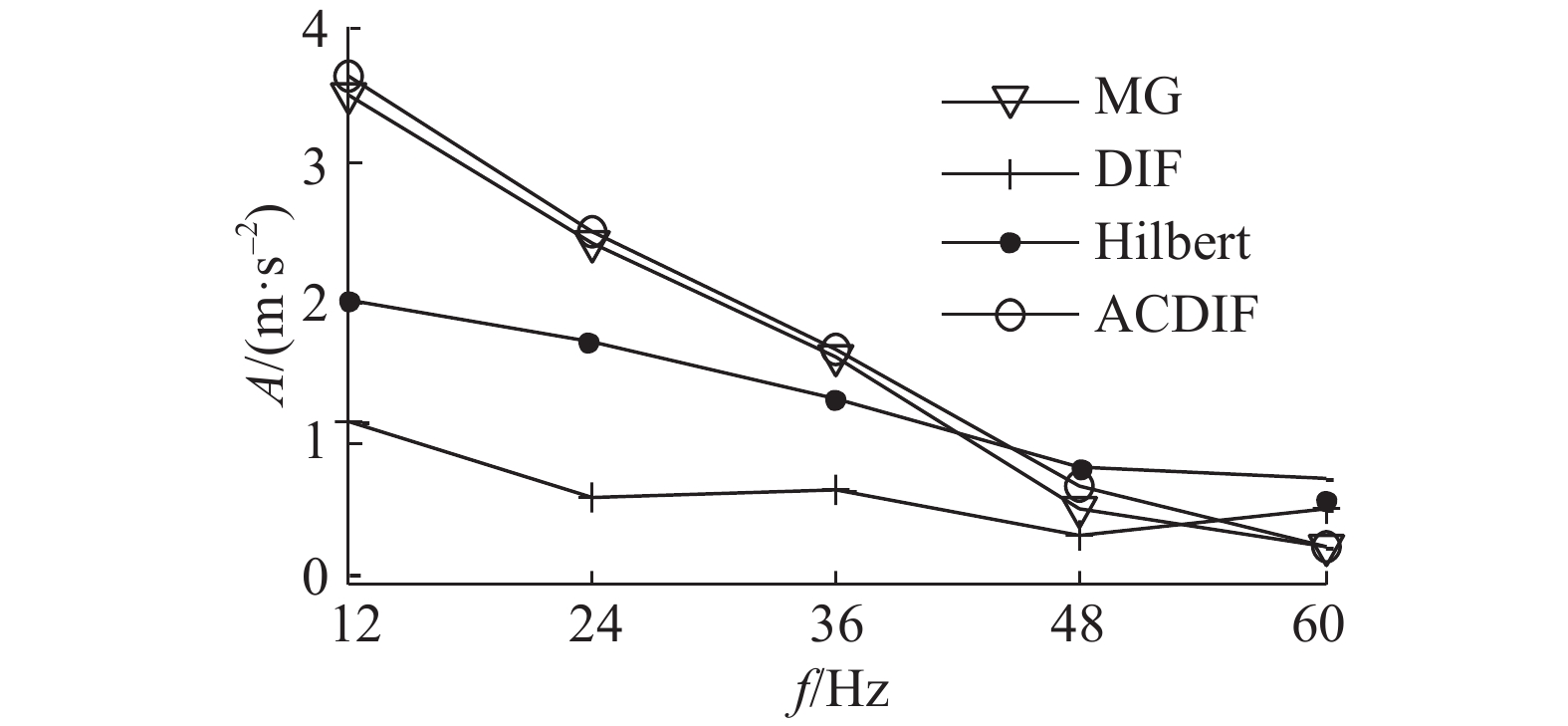
|
图 6 4种形态滤波效果的比较 Fig. 6 Comparison of MG,DIF,Hilbert demodulation and ACDIF |
为了验证所提方法在实际旋转机械故障诊断中抑制噪声和提取冲击特征的有效性,选用美国凯斯西储大学电气工程实验室的轴承内圈故障数据[15]进行分析. 试验台由功率为1.5 kW的电动机、扭矩传感器/译码器、测力计和电器控制装置等组成. 测试轴承为6205-2RS SKF深沟球轴承,参数如表2、3所示. 轴承主要的结构参数主要有轴承内径ri1、轴承外径ro1、厚度h1、节径D1、钢球直径d1、钢球数Z1、接触角α1. 轴承内圈故障数据主要有采样频率fis、N1、发动机转速n1、转轴基频fir、故障频率fi.
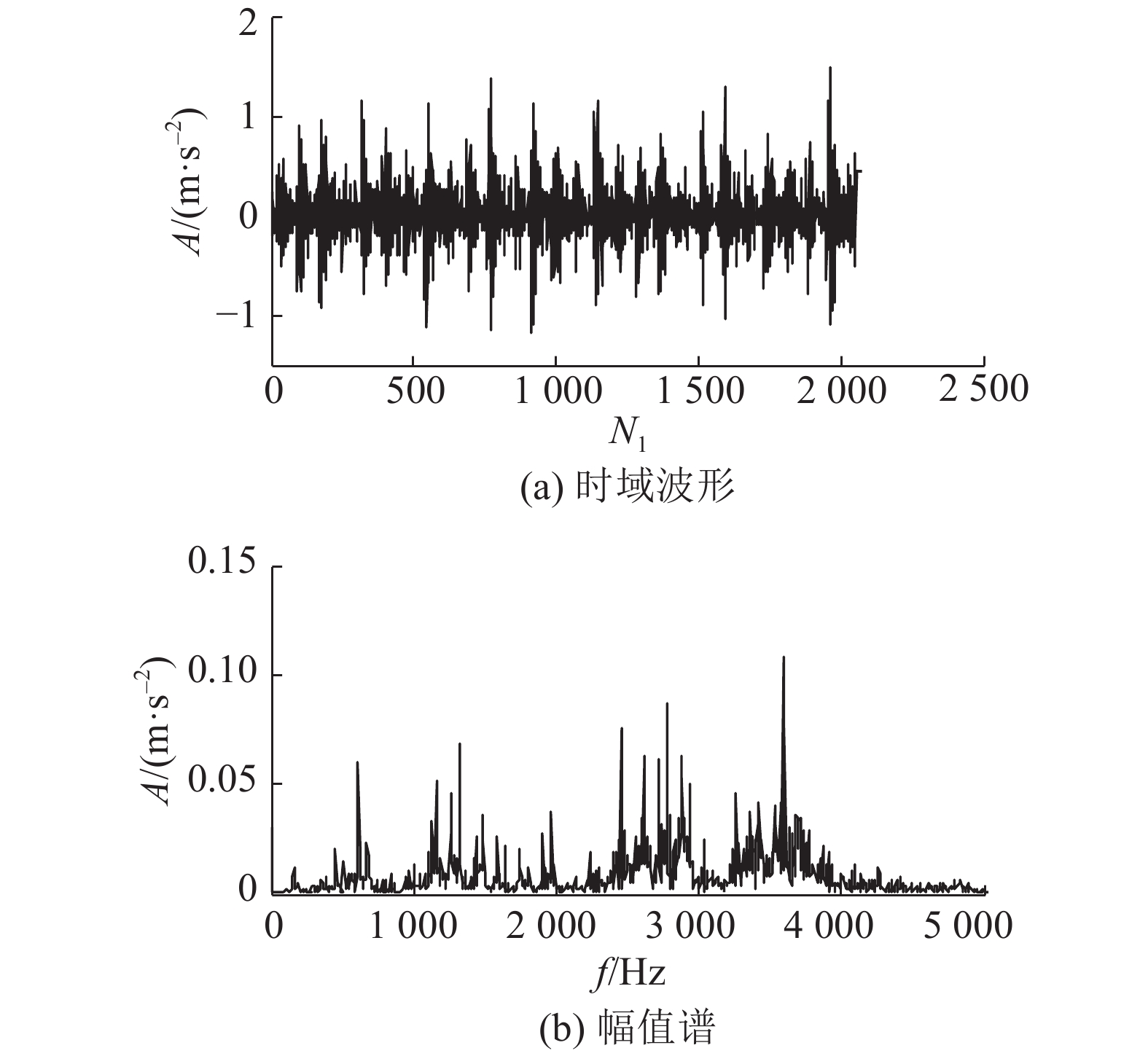
由图7的轴承内圈故障数据的时域波形和幅值谱可以看出,信号包含大量的脉冲和随机噪声,频谱成分复杂,难以直接判断内圈故障.
| 表 2 轴承结构参数 Table 2 Structure parameters of bearing |
| 表 3 轴承内圈故障数据 Table 3 Fault data of inner race |
|
图 7 内圈故障信号及幅值谱 Fig. 7 Time-domain waveform and amplitude spectrum of inner race fault signal |
对内圈故障信号进行ACDIF滤波,选择不同长度的直线型结构元素对信号进行分析,计算相应的TEK,TEK随SE长度LSE的变化曲线如图8所示. 在结构元素长度达到8以后,TEK变化缓慢,不再有显著的上升;随着SE的继续增大,有用信号通常会当作噪声去除,滤波输出的波形会膨胀,偏离原始信号,所以结构元素选择为8.

|
图 8 不同长度结构元素形态滤波的TEK Fig. 8 TEKs of filtering results under different lengths of SE |
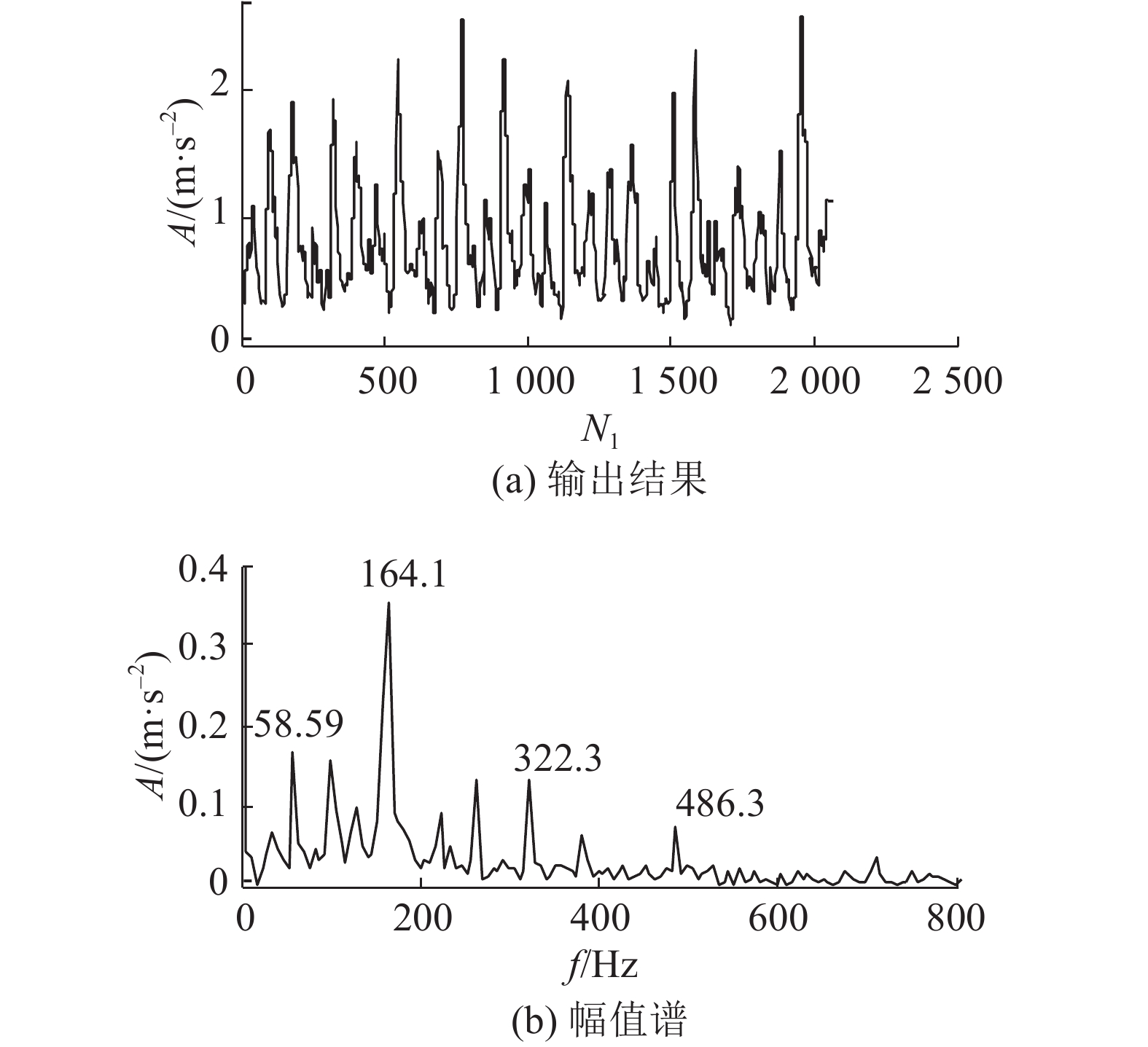
利用最佳结构元素长度对内圈信号进行ACDIF滤波,所得的时域波形和幅值谱如图9所示,经过滤波后的振动信号的噪声基本滤除,中高频成分得到了抑制,频率峰值集中在低频处. 图9(b)幅值谱中的58.59 Hz对应于2倍转频,164.1、322.3、486.3 Hz分别对应于外圈故障频率及两倍频和三倍频,故障频率及倍频的谱线清晰且突出,可以判断出轴承的内圈故障.
|
图 9 内圈信号ACDIF滤波输出波形及幅值谱 Fig. 9 Time-domain waveform and amplitude spectrum of ACDIF filtering result for inner race fault signal |
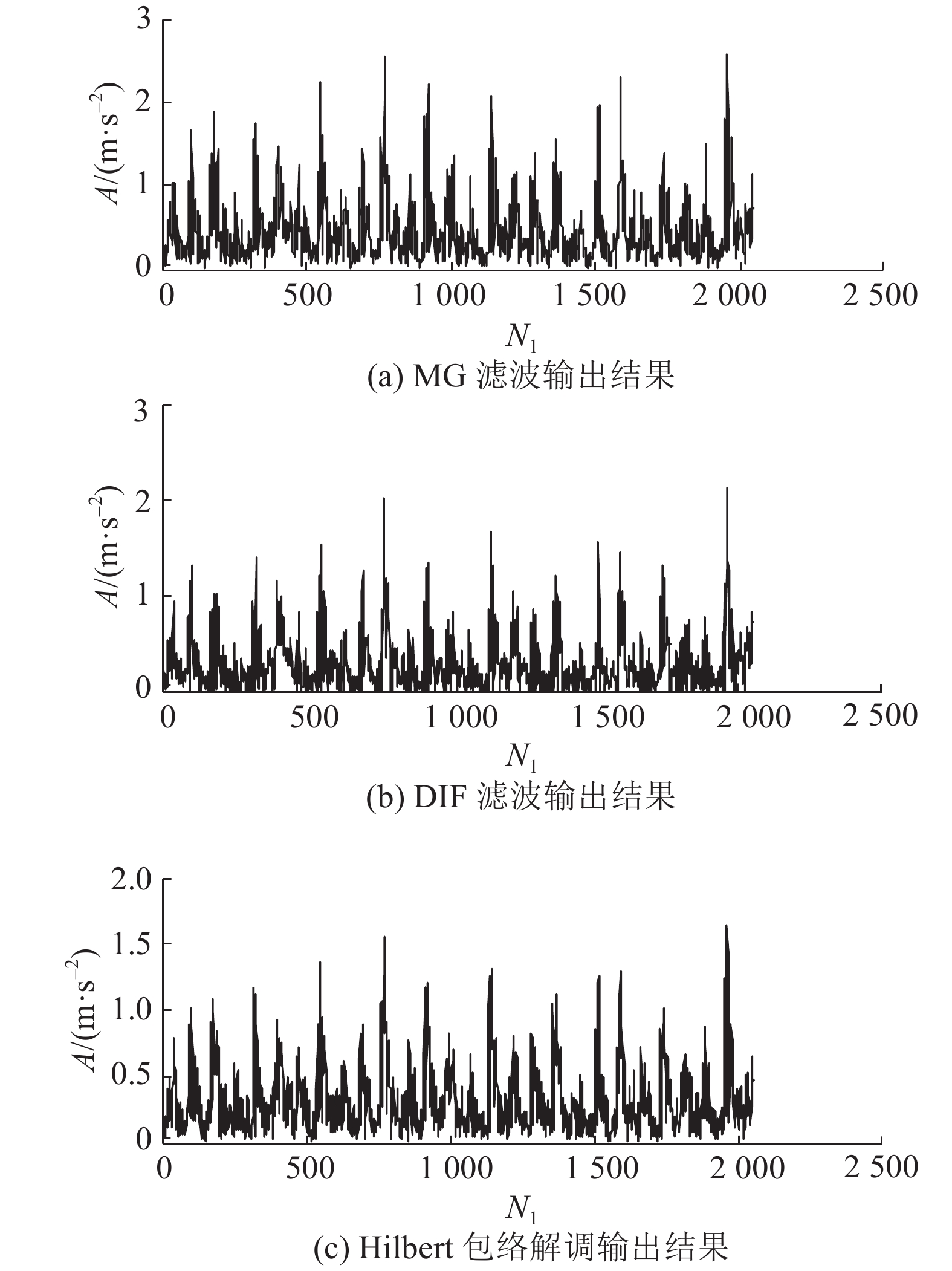
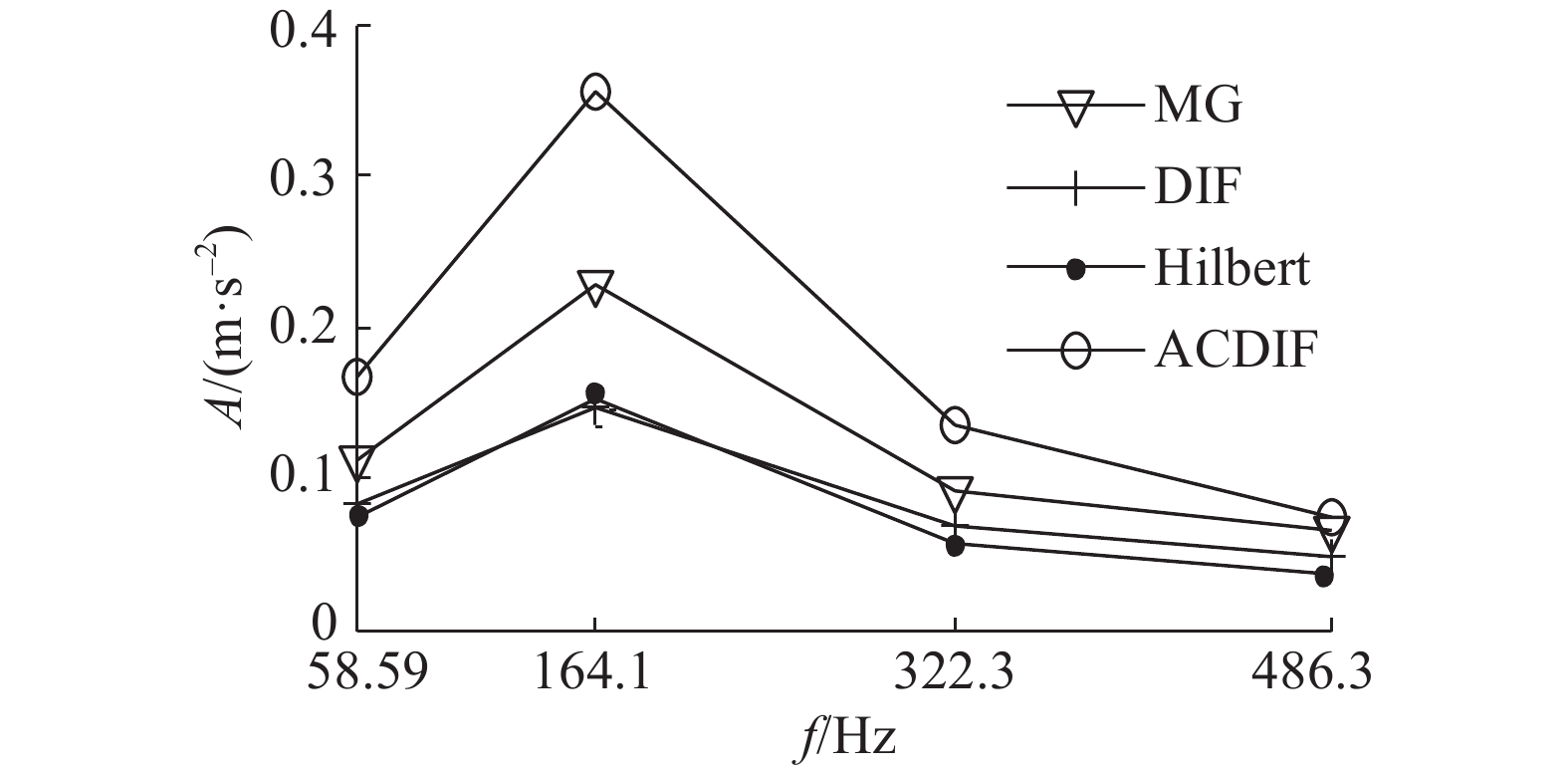
为了突出ACDIF的有效性,对内圈信号进行MG和DIF滤波,利用常用的峭度指标筛选SE长度以突出TEK的优点,MG和DIF的滤波结果如图10(a)、(b)所示,传统Hilbert包络解调结果如图10(c)所示,时域波形中含有大量噪声. 根据图11的比较分析可知,ACDIF的转频幅值和故障频率幅值最高,滤波效果优于对比方法,且ACDIF的输出波形更光滑,基本没有噪声的干扰.
|
图 10 内圈故障信号的MG、DIF及Hilbert解调输出结果 Fig. 10 Filtering result of MG,DIF and Hilbert demodulation for inner race fault signal |
|
图 11 4种方法的输出效果对比 Fig. 11 Comparison of MG,DIF,Hilbert demodulation and ACDIF |
为了进一步验证所提方法的优势,采用外圈故障失效模式下的样本进行分析研究. 加速轴承寿命试验机(ABLT-1A)由杭州轴承试验研究中心(HBRC)提供. 它由交流电机驱动,在同一根轴上同时开展4个轴承的寿命试验,试验台总体如图12所示,轴承各参数如表4、5所示. 轴承主要的结构参数主要有轴承型号B、负载L、节径D2、钢球直径d2、钢球数Z2、接触角α2. 轴承外圈故障数据主要有采样频率fos、采样点数N2、发动机转速n2、转轴基频for、故障频率fo.
轴承外圈故障信号主要表现为高频振动与故障特征信号的调制,幅值谱中应明显包含转频、故障频率及故障频率倍频[16]. 由于噪声污染严重,外圈故障信号的幅值谱(见图13(b))中信号频率集中在中、高频处,低频处的转频和故障频率难以识别.

|
图 12 加速轴承寿命试验机 Fig. 12 Bearing full-life test-bed |
| 表 4 轴承结构参数 Table 4 Structure parameters of bearing |
| 表 5 轴承外圈故障数据 Table 5 Fault data of outer race |

|
图 13 外圈故障信号及幅值谱 Fig. 13 Time-domain waveform and amplitude spectrum of outer race fault signal |
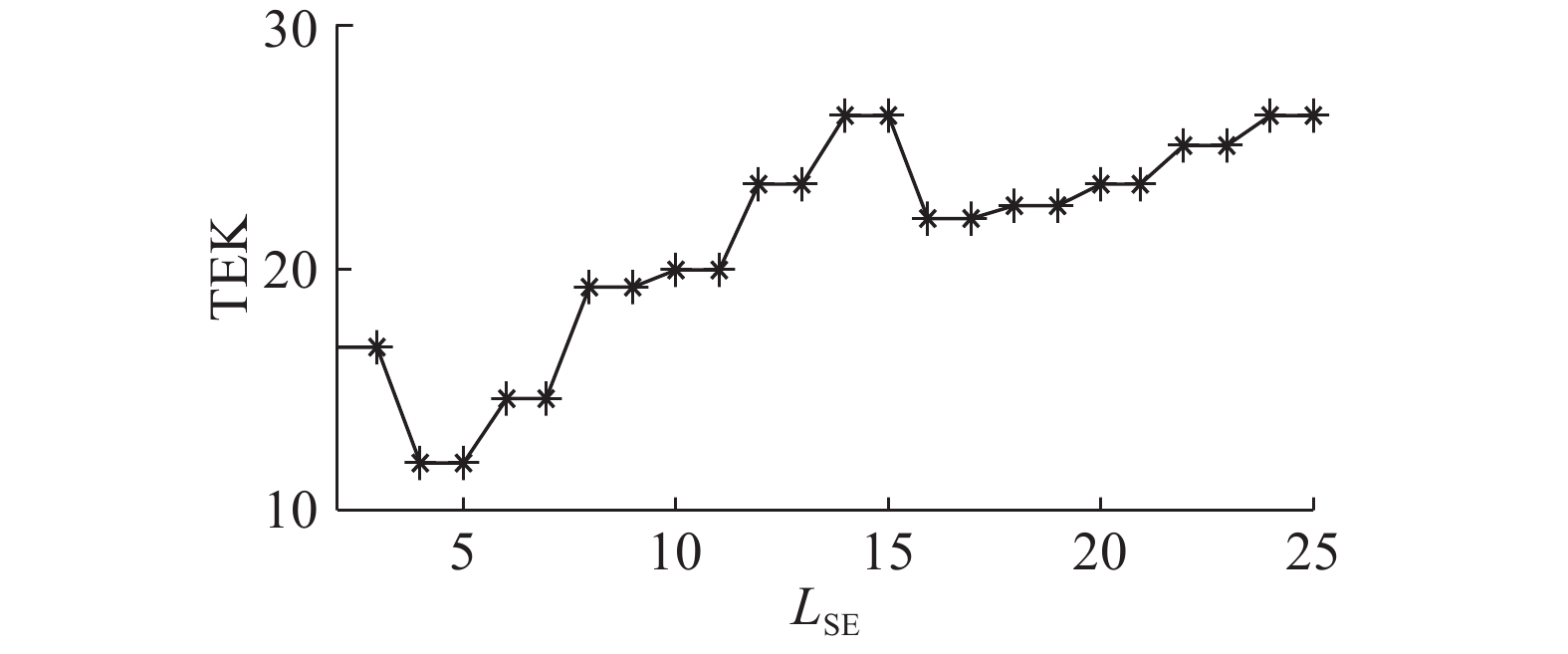
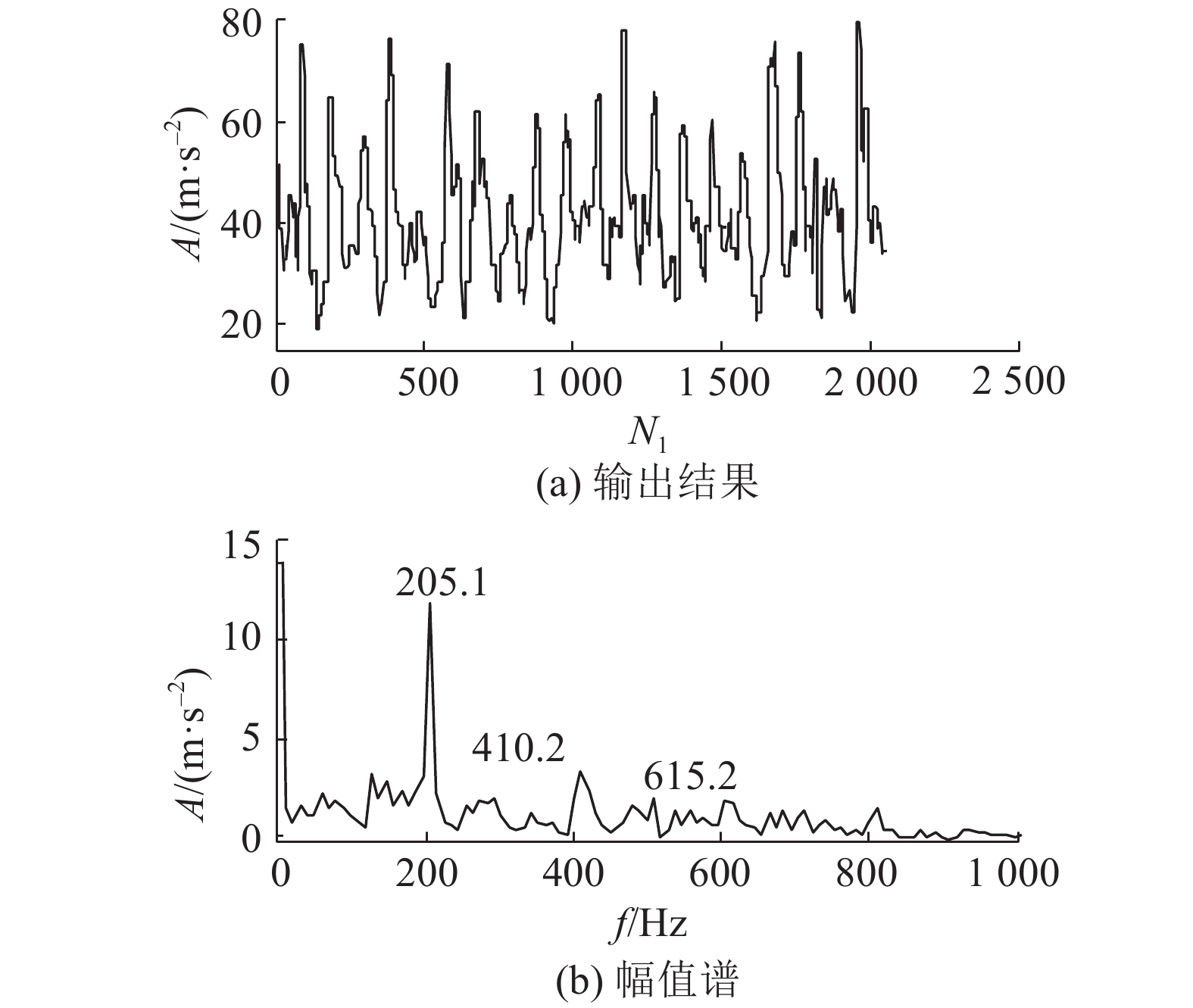
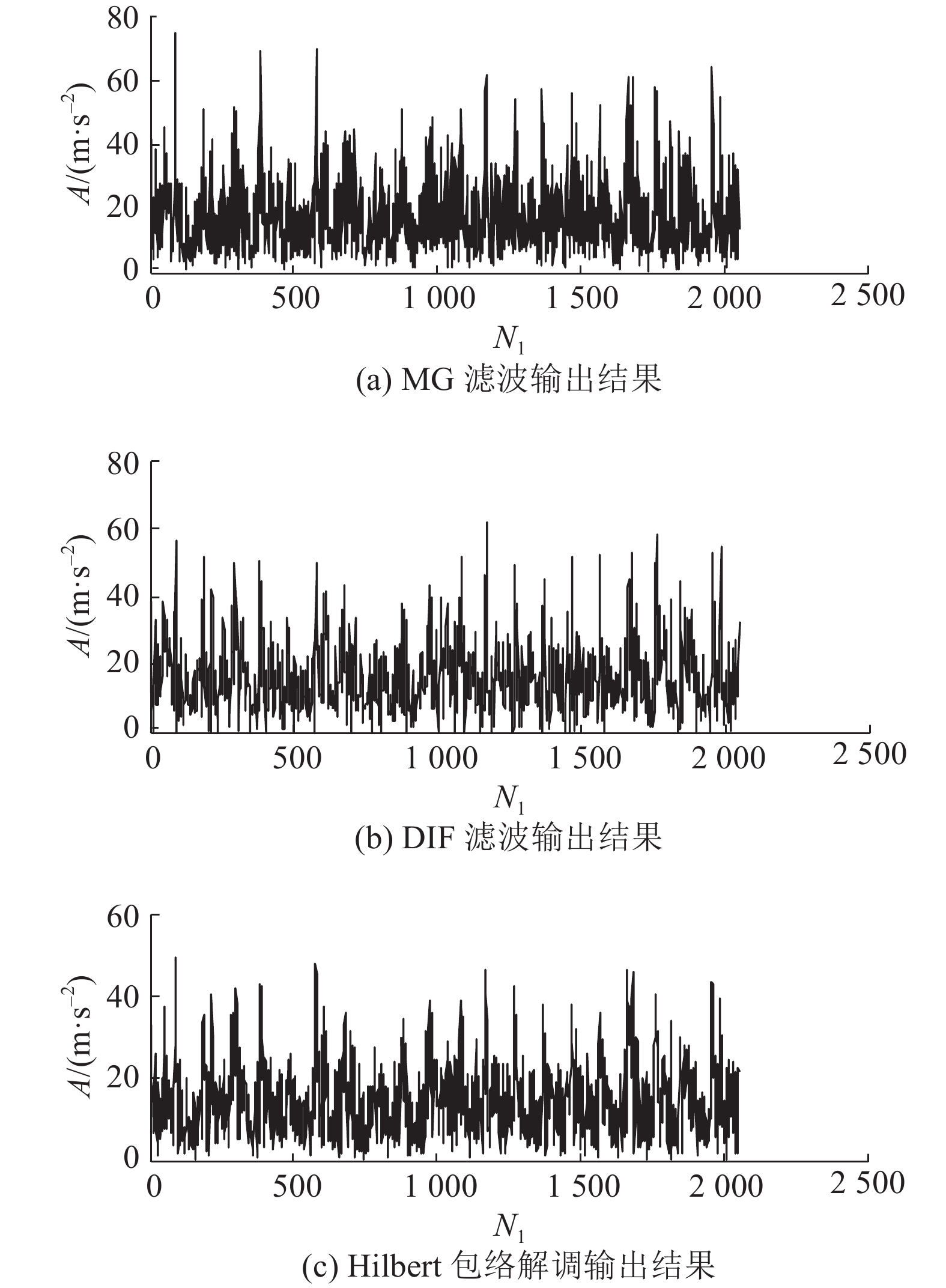
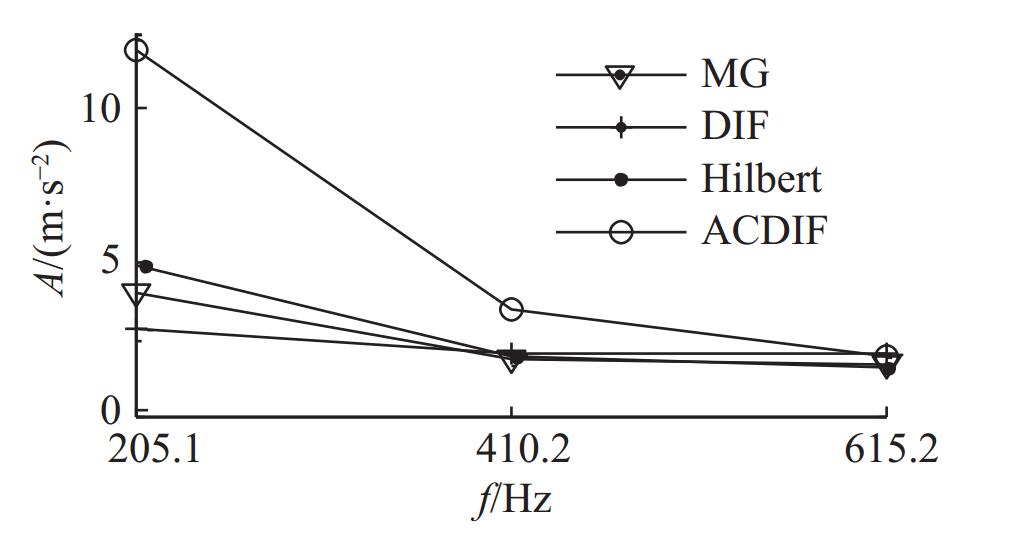
根据图14选择出SE的长度为14,对外圈故障信号进行ACDIF滤波,得到如图15所示的滤波结果,幅值谱中的故障频率及倍频的幅值较高突出. 其他3种对比方法的滤波结果(见图16)幅值谱中的故障频率幅值较低,难以识别. 由图17可以进一步判定MG和DIF的滤波效果劣于ACDIF.
|
图 14 不同长度结构元素形态滤波的TEK Fig. 14 TEKs of filtering results under different lengths of SE |
|
图 15 外圈信号ACDIF滤波输出波形及幅值谱 Fig. 15 Time-domain waveform and amplitude spectrum of ACDIF filtering result for outer race fault signal |
|
图 16 外圈信号的MG,DIF和Hilbert解调结果 Fig. 16 Filtering results of MG,DIF and Hilbert demodulation for outer race fault signal |
|
图 17 4种方法的故障特征频率幅值结果对比 Fig. 17 Fault feature frequency magnitude comparison of four methods |
根据形态滤波的基本原理,组合四大基本数学形态算子,构造出新的形态滤波器—平均组合差值形态滤波(ACDIF). 通过实验分析发现,该滤波器不仅结构设计简单,而且可以应用于振动信号的故障诊断. 通过该方法滤波之后的信号冲击特征被完整保留,干扰基本滤除,信号幅值谱中的故障频率及倍频谱线清晰显著.
利用滤波后信号的TEK筛选最佳结构元素长度,考虑了故障信号的冲击特性和瞬时能量的变化,提高了形态滤波处理的效率,使得滤波输出更加精确. 数值仿真和轴承外圈故障振动信号的试验结果表明,利用本文方法能够较好地将信号的冲击特征从成分复杂的背景噪声中提取出来. 与经典常用的形态滤波器比较可知,ACDIF滤出噪声干扰的效果更胜一筹.
本文存在以下不足:关于ACDIF增强信号冲击特征的背景知识有待进一步的说明,同时基于TEK的筛选最佳结构元素长度的自适应性值得进一步研究.
| [1] |
YU J. Local and nonlocal preserving projection for bearing defect classification and performance assessment[J]. IEEE Transactions on Industrial Electronics, 2012, 59(5): 2363-2376. DOI:10.1109/TIE.2011.2167893 |
| [2] |
MARAGOS P, SCHAFER R. Morphological filters-Part I: their set-theoretic analysis and relations to linear shift-invariant filters[J]. IEEE Transactions on Acoustics Speech and Signal Processing, 1987, 35(8): 1153-1169. DOI:10.1109/TASSP.1987.1165259 |
| [3] |
李豫川, 伍星, 迟毅林, 等. 基于形态滤波和稀疏分量分析的滚动轴承故障盲分离[J]. 振动与冲击, 2011, 30(12): 170-174. LI Yu-chuan, WU Xing, CHI Yi-lin, et al. Blind separation for bearing faults based on morphological filtering and sparse component analysis[J]. Journal of Vibration and Shock, 2011, 30(12): 170-174. DOI:10.3969/j.issn.1000-3835.2011.12.033 |
| [4] |
MENG L, XIANG J, WANG Y, et al. A hybrid fault diagnosis method using morphological filter-translation invariant wavelet and improved ensemble empirical mode decomposition[J]. Mechanical Systems and Signal Processing, 2015, 50: 101-115. |
| [5] |
HU Z, WANG C, ZHU J, et al. Bearing fault diagnosis based on improved morphological filter[J]. Measurement, 2016, 80: 163-178. DOI:10.1016/j.measurement.2015.11.028 |
| [6] |
DONG Y, LIAO M, ZHANG X, et al. Fault diagnosis of rolling element bearing based on modified morphological method[J]. Mechanical Systems and Signal Processing, 2011, 25: 1276-1286. DOI:10.1016/j.ymssp.2010.10.008 |
| [7] |
鄢小安, 贾民平. 参数优化的组合形态-hat变换及其在风力发电机组故障诊断中的应用[J]. 机械工程学报, 2016, 52(13): 103-110. YAN Xiao-an, JIA Min-ping. Parameter optimized morphological filter-hat transform and its application in fault diagnosis of wind turbine[J]. Journal of Mechanical Engineering, 2016, 52(13): 103-110. |
| [8] |
DENG L, ZHAO R. Fault feature extraction of a rotor system based on local mean decomposition and Teager energy kurtosis[J]. Journal of Mechanical Science and Technology, 2014, 28(4): 1161-1169. DOI:10.1007/s12206-013-1149-9 |
| [9] |
张文斌, 杨辰龙, 周晓军. 形态滤波方法在振动信号降噪中的应用[J]. 浙江大学学报: 工学版, 2009, 43(11): 2096-2099. ZHANG Wen-bin, YANG Chen-long, ZHOU Xiao-jun. Application of morphology filtering method in vibration signal de-noising[J]. Journal of Zhejiang University: Engineering Science, 2009, 43(11): 2096-2099. |
| [10] |
王书涛, 张金敏, 李圆圆, 等. 基于数学形态学和模糊聚类的旋转机械故障诊断[J]. 仪器仪表学报, 2012, 33(5): 1055-1061. WANG Shu-tao, ZHANG Jin-min, LI Yuan-yuan, et al. Rotating machinery fault diagnosis based on mathematical morphology and fuzzy clustering[J]. Chinese Journal of Scientific Instrument, 2012, 33(5): 1055-1061. DOI:10.3969/j.issn.0254-3087.2012.05.014 |
| [11] |
HARALICK R M, STERNBERG S R, ZHUANG X. Image analysis using mathematical morphology[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1987(4): 532-550. |
| [12] |
章立军, 杨德斌, 徐金梧, 等. 基于数学形态滤波的齿轮故障特征提取方法[J]. 机械工程学报, 2007, 43(2): 71-75. ZHANG Li-jun, YANG De-bin, XU Jin-wu, et al. Approach to extracting gear fault feature based on mathematical morphological filtering[J]. Journal of Mechanical Engineering, 2007, 43(2): 71-75. DOI:10.3321/j.issn:0577-6686.2007.02.011 |
| [13] |
王天金, 冯志鹏, 郝如江, 等. 基于Teager能量算子的滚动轴承故障诊断研究[J]. 振动与冲击, 2012, 31(2): 1-6. WANG Tian-jin, FENG Zhi-peng, HAO Ru-jiang, et al. Fault diagnosis of rolling element bearings based on Teager energy operator[J]. Journal of Vibration and Shock, 2012, 31(2): 1-6. DOI:10.3969/j.issn.1000-3835.2012.02.001 |
| [14] |
RAJ A S, MURALI N. Early classification of bearing faults using morphological operators and fuzzy inference[J]. IEEE Transactions on Industrial Electronics, 2013, 60(2): 567-574. DOI:10.1109/TIE.2012.2188259 |
| [15] |
Case western reserve university bearing data center website [EB/OL]. 2011–05–11. http//csegroups.case.edu/bearingdatacenter/pages/download-data-file.
|
| [16] |
张小龙, 张氢, 秦仙蓉, 等. 基于ITD-形态滤波和Teager能量谱的轴承故障诊断[J]. 仪器仪表学报, 2016, 37(4): 788-795. ZHANG Xiao-long, ZHANG Qing, QIN Xian-rong, et al. Fault diagnosis method for rolling bearing based on ITD-morphological filter and Teager energy spectrum[J]. Chinese Journal of Scientific Instrument, 2016, 37(4): 788-795. DOI:10.3969/j.issn.0254-3087.2016.04.010 |


