爬壁机器人属于特种机器人范畴,能够替代人工在高尺度结构物表面上执行探测、油漆喷涂、污垢清除、焊接等多项作业任务,在核电、船舶、海工、化工等行业都有广泛的应用前景,已受到国内外研究人员的密切关注[1-6].
爬壁机器人分类众多,按照吸附方式的不同,可以分为负压吸附、电磁吸附及永磁吸附;按照行走方式的不同,可以分为履带式、轮式及足式. 其中,永磁吸附轮式具有吸附可靠、相同质量下磁吸附力大、运动速度快、转向灵活等优点[7-12],本文所讨论的爬壁机器人即采用该种技术方案.
磁吸附组件是爬壁机器人的重要子系统,应产生足够的吸附力,以克服作业工具和机器人本体的重量,保证机器人在壁面上可靠工作. 生成较大的吸附力必然要求增加磁吸附组件的质量,这增大了驱动系统的负载,影响爬壁机器人在壁面上运动的灵活性[7]. 优化设计磁吸附组件,以兼顾爬壁机器人的可靠吸附与灵活运动,是爬壁机器人研制的关键技术之一,是本文讨论的重点.
针对上述问题,本文介绍爬壁机器人的机械结构;建立爬壁机器人的力学模型,获得磁吸附力的理论值;优化磁吸附组件结构,得到最优的结构参数;基于样机试验,验证磁吸附组件的性能.
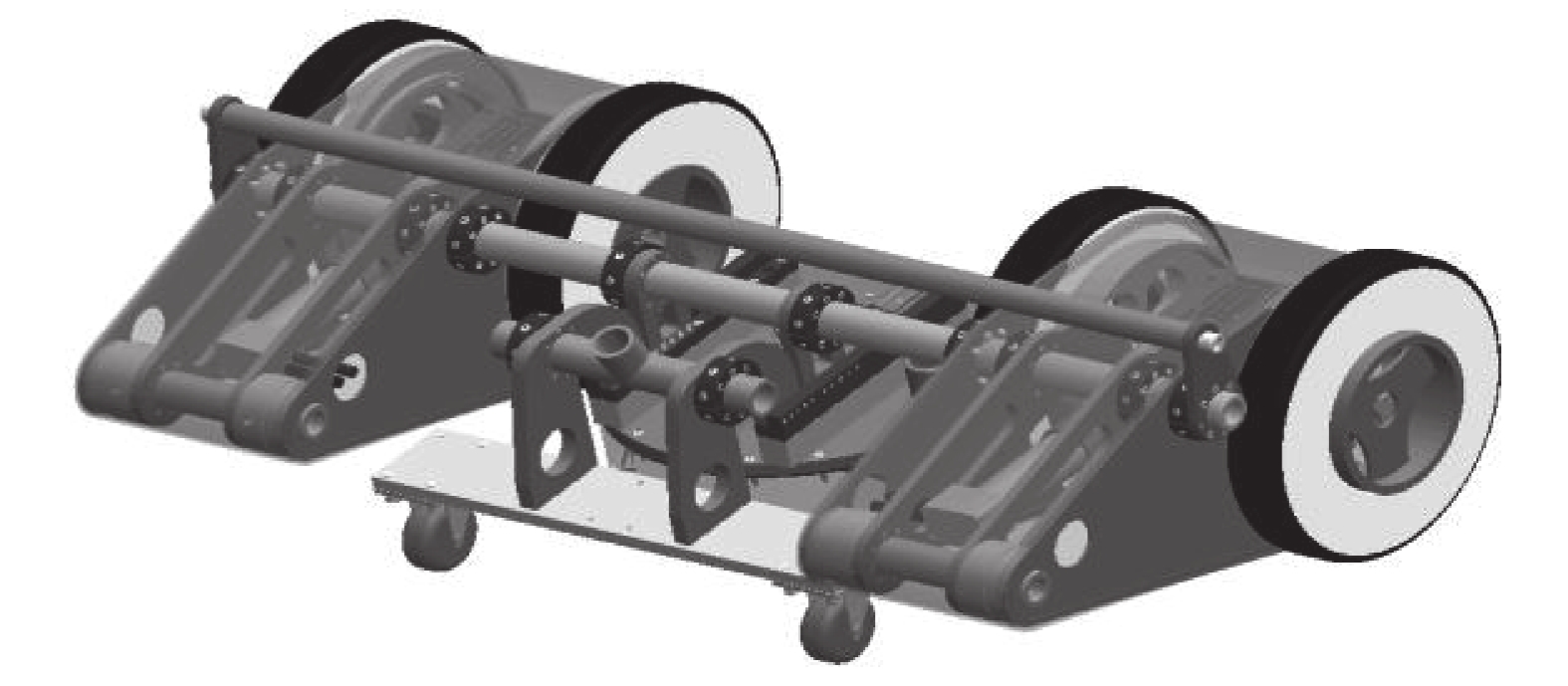
1 爬壁机器人结构如图1所示为设计的爬壁机器人三维结构. 该机器人在两侧各有一套磁吸附爬壁轮,以实现壁面吸附和行走;中间是一个由旋转喷杆、真空清洗盘和毛刷而组成的清除回收组件;前部有2个万向轮构成的从动轮,且2个从动轮之间安装有防止倾覆的小磁吸附组件. 分别介绍磁吸附爬壁轮和清洗回收组件的结构.
|
图 1 爬壁机器人的三维结构 Fig. 1 Three-dimensional model of wall-climbing robot |
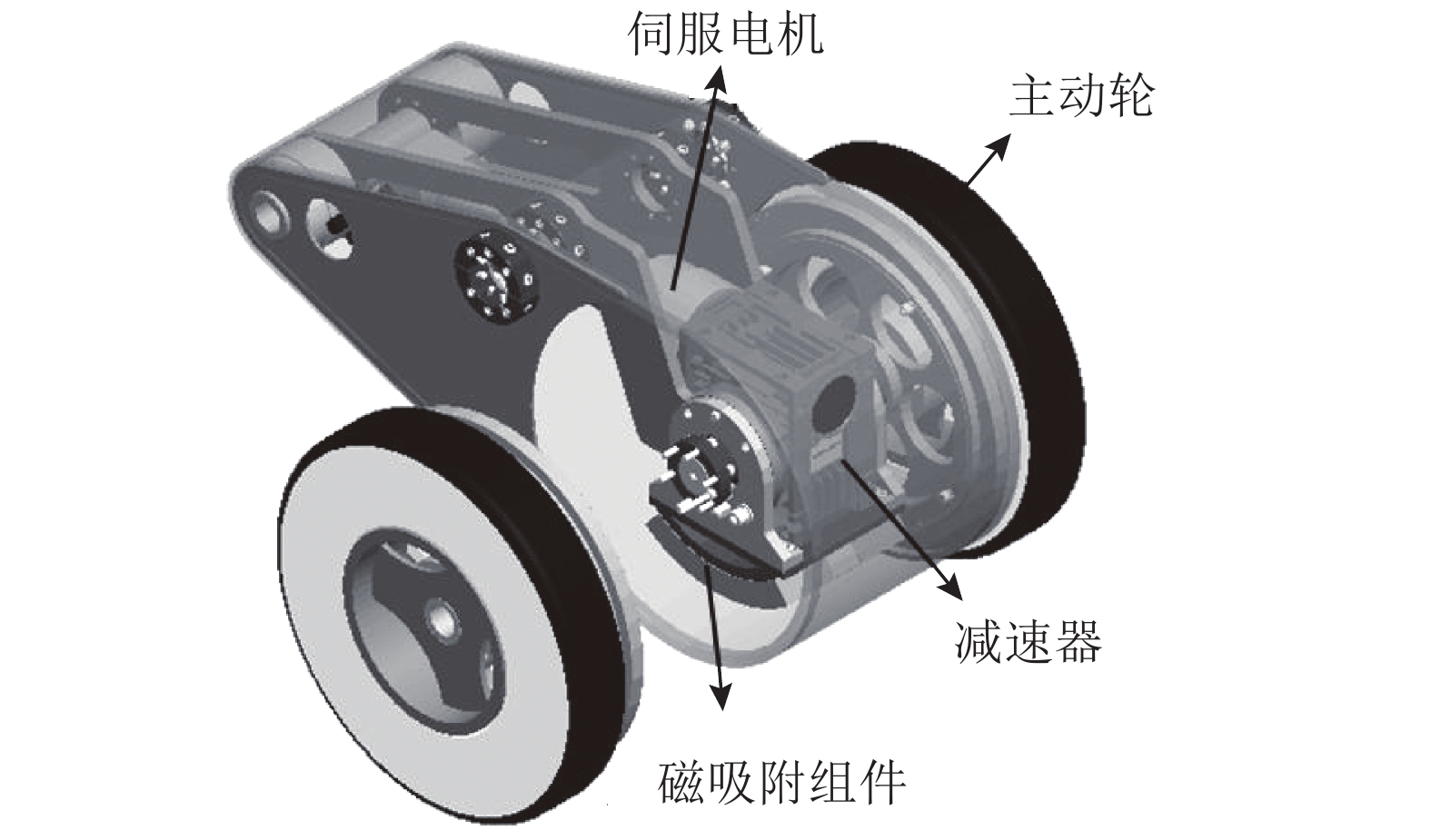
如图2所示,磁吸附爬壁轮主要包括伺服电机、减速器、磁吸附组件和主动轮. 伺服电机经过减速器而驱动主动轮,从而克服摩擦力来实现爬壁机器人在壁面上的运动. 磁吸附组件产生足够的吸附力,保证机器人能够可靠地在作业壁面上工作.
|
图 2 磁吸附爬壁轮的组成 Fig. 2 Schematic diagram of magnetic wheel |
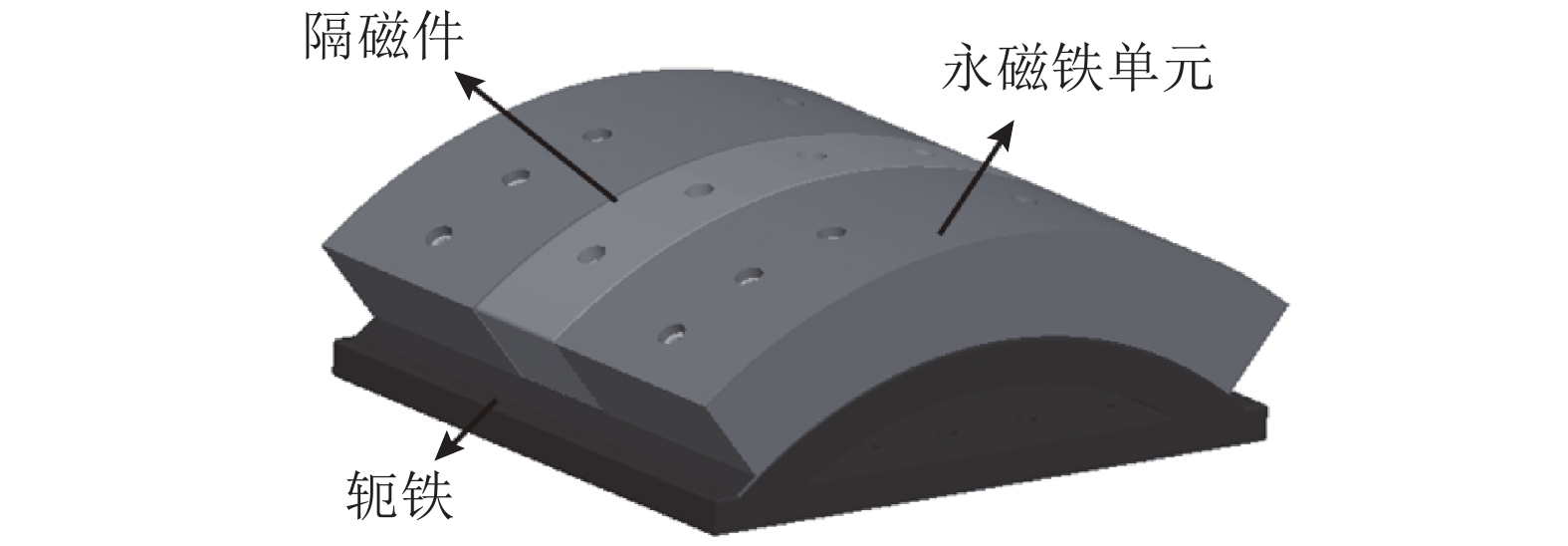
磁吸附组件由永磁铁单元、轭铁、隔磁件等组成(见图3),永磁铁单元和隔磁件通过螺钉固定在轭铁上,整个磁吸附组件通过轭铁安装于减速器下方. 永磁铁单元、隔磁件、轭铁与导磁的作业壁面形成磁回路,通过这种方式能够生成较大的单向磁吸附力.
|
图 3 磁吸附组件的结构 Fig. 3 Schematic diagram of magnetic components |
从动轮之间的小磁吸附组件结构与图3所示的基本一致,主要区别在于尺寸偏小,故未贴出小磁吸附组件的结构图.
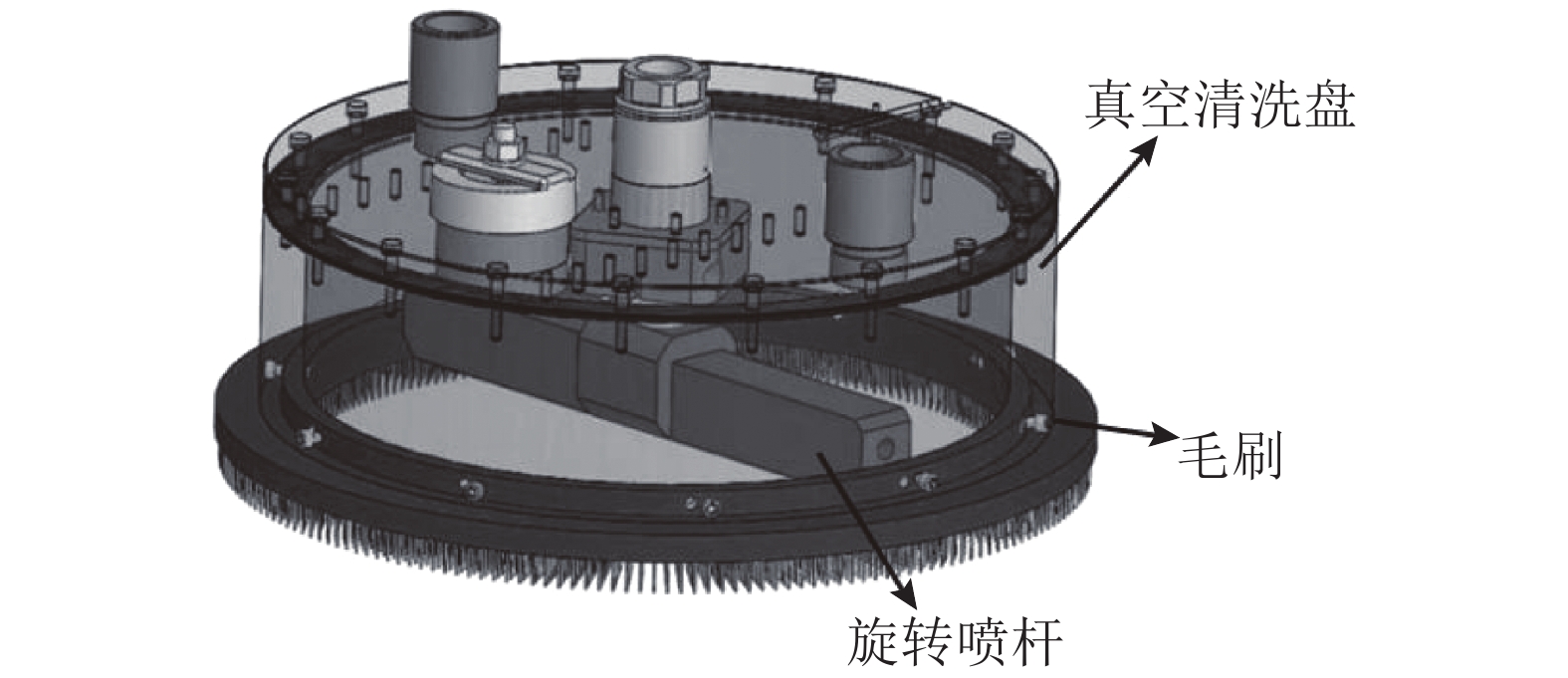
1.2 磁吸附爬壁轮清洗回收组件具备污垢清除和污水回收2个功能. 如图4所示,旋转喷杆安装于真空清洗盘的内部,高压水通过旋转喷杆上的喷嘴形成高速水射流来完成污垢的清除,并产生射流反冲力而使喷杆旋转,以产生更高效的清洗作用;真空清洗盘在毛刷与壁面的密封作用下,利用外部真空系统污水从作用壁面上抽出,以实现环保清洗作业.
|
图 4 清洗回收组件示意图 Fig. 4 Schematic diagram of cleaning and recycling components |
建立爬壁机器人力学模型的主要边界条件如下:1)爬壁机器人能够沿壁面行走而不滑移;2)爬壁机器人能够沿壁面行走而不倾覆;3)电机能够驱动爬壁机器人行走. 基于以上边界条件,可以建立爬壁机器人作业时的力学模型,如下式所示:
| $\left. \begin{array}{l}{F_{{\rm n}1}} + {F_{{\rm n}2}} + {F_{{\rm n}3}} + G\cos \,\beta = {N_1} + {N_2} + {N_3} + {F_{\rm j}},\\{F_{{\rm f}1}} + {F_{{\rm f}2}} + {F_{{\rm f}3}} = G\sin\, \beta ,\\({F_{\rm j}} - {F_{\rm v}} - G\sin \,\beta ){l_1} + ({N_3} - {F_{{\rm n}3}}){l_2} + G\cos \beta \times h < 0,\\{F_{{\rm n}1}} = {F_{{\rm n}2}},\\{F_{\rm j}} = 0.745Q\sqrt {{p_0}} ,\\{F_ {{\rm v}}} = \displaystyle\frac{\pi }{4}{d^2}p.\end{array} \right\}$ | (1) |
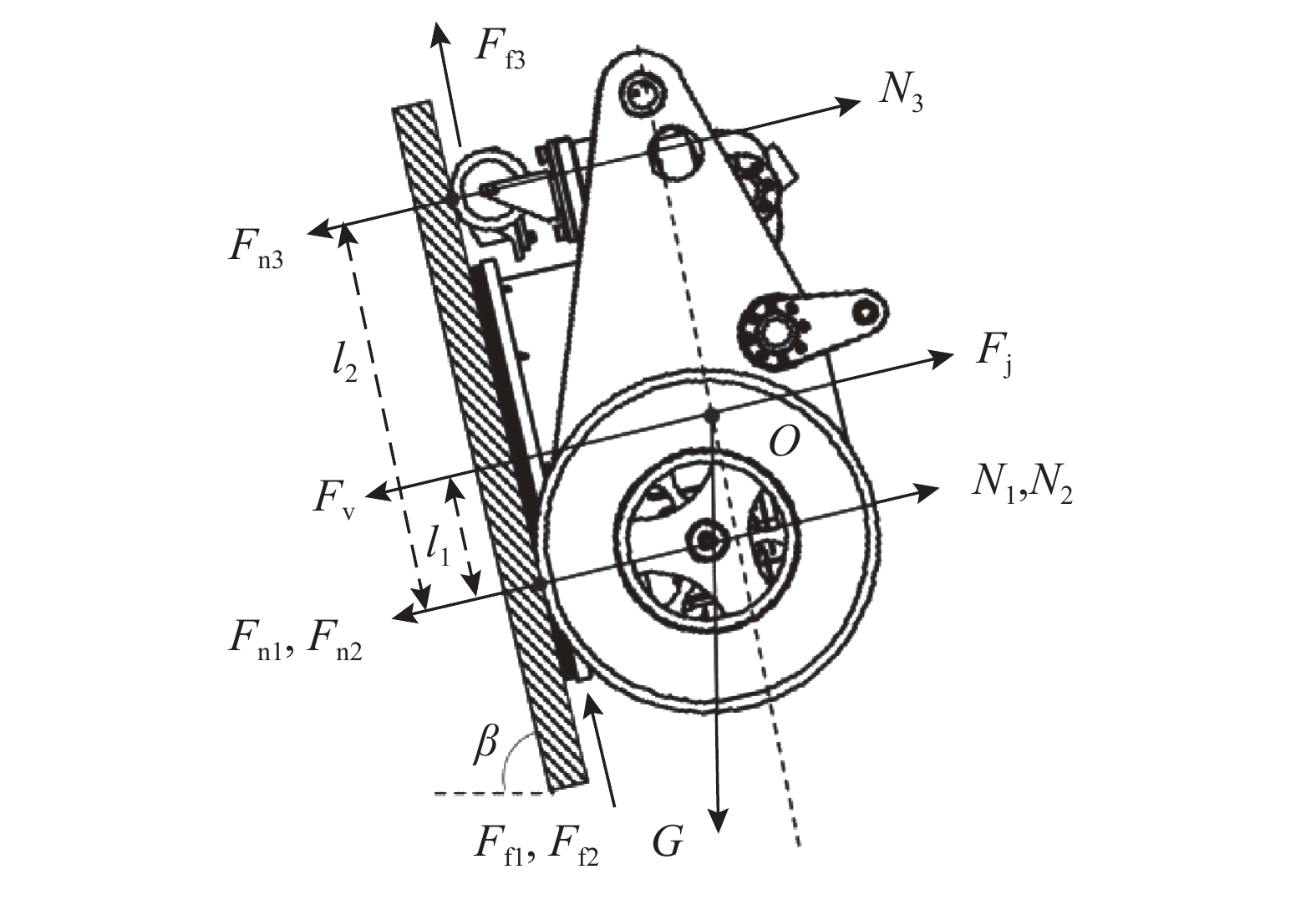
式中:Ff1、Ff2为主动轮处静摩擦力,Ff3为从动轮处静摩擦力,Fj为射流反冲力,Fn1、Fn2为主动轮处磁铁吸附力,Fn3为从动轮处磁铁吸附力,Fv为真空清洗盘内的真空吸附力,G为爬壁机器人重力,N1、N2为主动轮处支持力,N3为从动轮处支持力,Q为水射流的流量,h为重心O点与作业壁面的垂直距离,l1、l2为驱动轮与作业壁面的接触点分别与重心、从动轮中心沿作业壁面方向的距离,β为作业壁面的倾角. 考虑到真空清洗盘的毛刷较软,毛刷与钢板之间的接触力较小,忽略真空清洗盘处的支持力及对应的摩擦力作用. 如图5所示为对应的爬壁机器人静力学分析示意图[13].
|
图 5 爬壁机器人静力学建模 Fig. 5 Static mechanical model of wall-climbing robot |
为了保证爬壁机器人可靠地吸附在壁面上行走,须满足以下约束条件:1)爬壁机器人各接触点的支持力大于0;2)爬壁机器人主动轮所承受的静摩擦力小于最大静摩擦力. 由于从动轮不起到制动和驱动作用,从动轮处的静摩擦力较小而忽略,可以得到如下约束条件:
| $\left. \begin{array}{l}{N_1} > 0,\\{N_2} > 0,\\{N_3} > 0,\\{F_{{\rm f}1}} < {\mu _1}{N_1}, {F_{{\rm f}2}} < {\mu _2}{N_2}.\end{array} \right\}$ | (2) |
式中:μ1、μ2为主动轮与作业壁面之间的静摩擦系数.
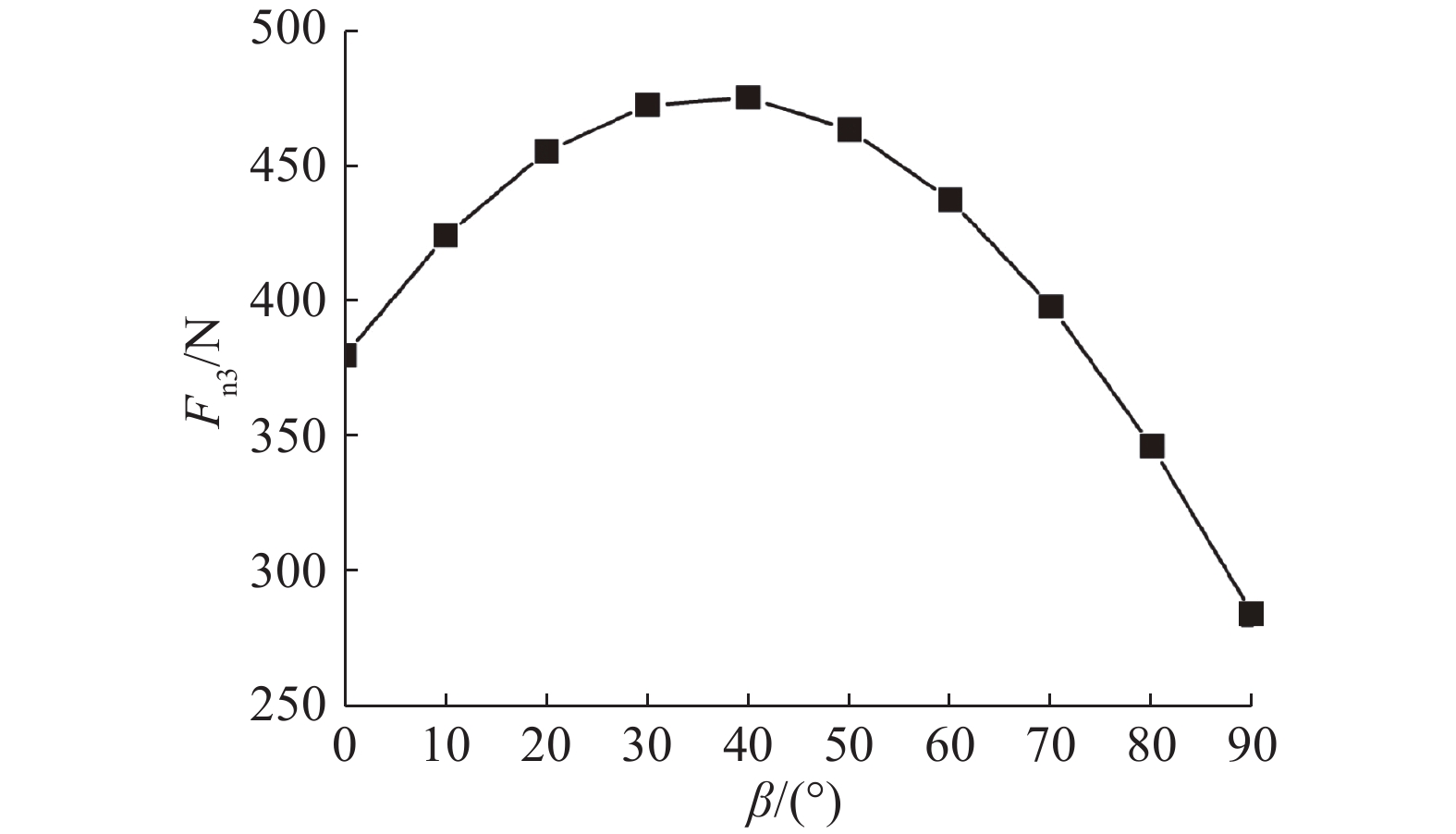
结合式(1)、(2),可以得到爬壁机器人正常作业所需要的磁吸附力,如图6、7所示. 可知,爬壁机器人为了防止滑移,(Fn1+Fn2+Fn3)max=3 000 N;爬壁机器人为了防止倾覆,(Fn3)max=480 N,即每个主动轮处的磁铁吸附力应达到1 260 N,从动轮处的磁铁吸附力应达到480 N,这为后续的磁组件优化设计提供了理论目标.

|
图 6 磁铁总吸附力-壁面倾角曲线图 Fig. 6 Curve of total magnetic adsorption force versus inclination angle of surface |
|
图 7 从动轮磁铁吸附力-壁面倾角曲线图 Fig. 7 Curve of driven wheel magnetic adsorption force versus inclination angle of surface |
爬壁机器人磁吸附组件的磁场为静态磁场,磁吸附力的计算满足Maxwell电磁场基本理论,如下:1)磁路高斯定理
式中:B为磁场磁感应强度,H为磁场强度,μ为磁导率.
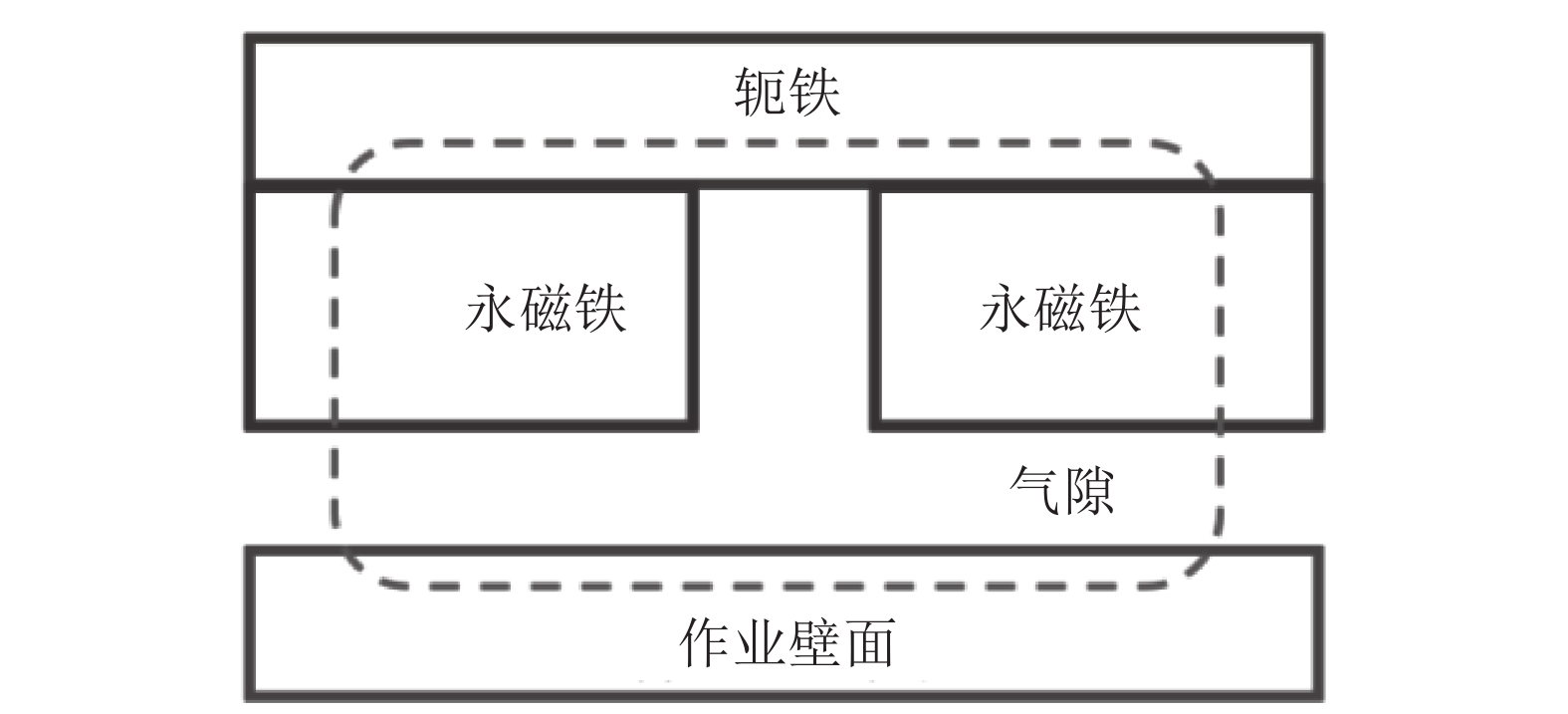
磁吸附组件产生的磁场经气隙进入导磁的作业壁面,然后穿越气隙回到磁吸附组件,形成完整的磁回路,如图8所示. 存在如下关系:
|
图 8 磁场回路图 Fig. 8 Magnetic circuit diagram |
| ${\phi _1} = {\phi _2} + {\phi _3}.$ | (3) |
式中:
| ${\phi _1} = {k_1}{\phi _2},$ | (4) |
其中,k1为漏磁系数,k1>1. 式(4)可以化为
| ${B_1}{S_1} = {k_{\rm{1}}}{\mu _0}{H_2}{S_2}.$ | (5) |
式中:B1为磁吸附组件磁感应强度,S1为磁吸附组件截面积,H2为气隙磁场强度,S2为气隙截面积,μ0为真空磁导率.
根据安培环路定理,有
| ${H_1}{L_1} + {H_2}{L_2} + {H_4}{L_4} = 0.$ | (6) |
式中:H1为磁吸附装置磁场强度,H4为作业壁面磁场强度,L1、L2、L4分别为磁吸附装置、气隙、磁阻的长度. 令
| ${H_1}{L_1} = {\rm{ - }}{k_2}{H_2}{L_2},$ | (7) |
其中,k2为磁阻系数,k2>1. 式(7)可以化为
| ${\left( {BH} \right)_2} = - \frac{1}{{{k_1}{k_2}}}{\mu _0}{\left( {BH} \right)_1}\frac{{{V_1}}}{{{L_2}{S_2}}}.$ | (8) |
根据虚功原理可知,磁吸附力为
| $F = \frac{{\partial W}}{{\partial L}}.$ | (9) |
针对永磁体能量W,存在W=气隙体积×单位体积的磁能[14],则
| $W = {L_2}{S_2}{\left( {BH} \right)_2} = - \frac{{\mu _0}{\left( {BH} \right)_1}{V_1}}{{{k_1}{k_2}}}.$ | (10) |
将式(10)代入式(9),有
| $F = - \frac{{{\mu _0}{{\left( {BH} \right)}_1}{V_1}}}{{{k_1}{k_2}{L_2}}}.$ | (11) |
式中:(BH)1为磁能积,V1为永磁铁的体积。由式(11)可知,F受到μ0、(BH)1、V1、k1、k2及L2等多个因素的影响. 针对特定的磁铁材料,μ0、(BH)1、k1、k2等为恒定值,因此磁吸附力主要与V1及L2有关.
3.2 磁吸附组件优化目标[15-20]当永磁材料、气隙及作业壁面厚度等确定时,磁吸附力主要受到永磁铁自身结构尺寸的影响. 在一定的边界条件下,永磁铁结构尺寸与磁吸附力正相关,但永磁铁结构尺寸的增加会导致永磁铁质量的增加,提高了对磁吸附力的要求. 永磁铁结构尺寸与磁吸附力之间存在一定的耦合关系[16],磁吸附组件设计的目标为:在一定质量下的磁吸附力最大. 引入变量γ来表征磁吸附力与质量的比值,简称磁质比,定义为
| $\gamma = \frac{{{F_{\rm n}}}}{{{m_{\rm n}}}}.$ | (12) |
式中:Fn为磁吸附力,mn为磁吸附组件质量.
由2章的静力学模型求解可知,主动轮磁吸附组件的吸附力远大于从动轮磁吸附组件的吸附力,而且2个磁吸附组件在结构上相同的,只存在尺寸的差异. 为了本文篇幅的精简,以下部分只涉及对主动轮磁吸附组件的优化设计,提及的 “磁吸附组件”均指主动轮处的磁吸附组件.
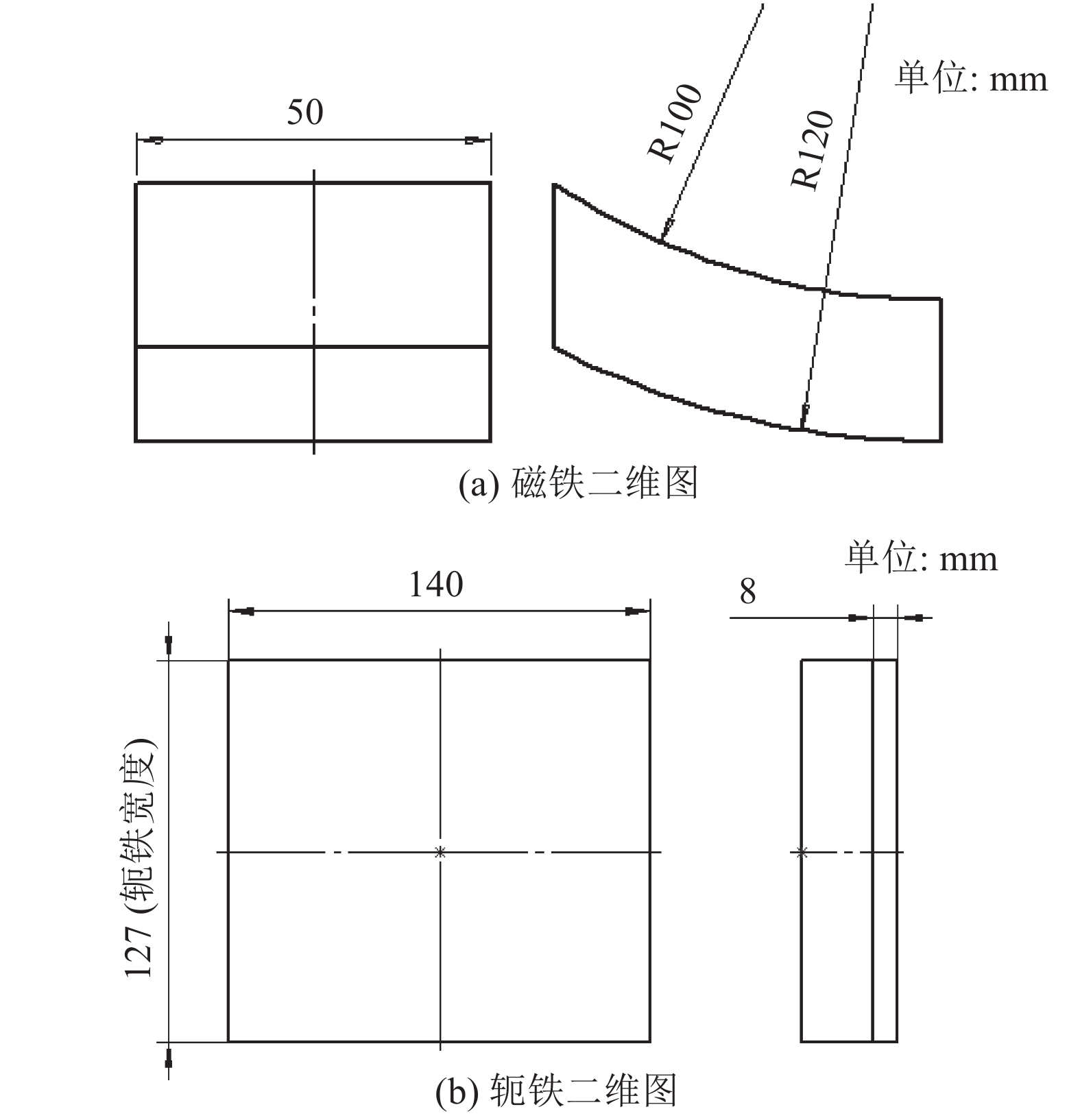
由于爬壁机器人总体尺寸和安装空间的限制,磁吸附组件的部分尺寸已经确定,如图9所示. 对永磁铁厚度、轭铁厚度和永磁铁宽度3个参数进行优化分析,分别用字母h1、h2和h3来表示,这3个参数的初始值分别为20、8和50 mm.
|
图 9 磁吸附组件的结构尺寸 Fig. 9 Dimensions of magnetic components |
利用Ansoft Maxwell软件,完成不同结构参数下磁吸附力和磁质比的计算. 在分析某个结构参数时,其他参数的数值保持不变. 其中,永磁材料为N38钕铁硼,隔磁件材料为铝,轭铁材料为电工纯铁,气隙为10 mm,永磁铁的布置方式和充磁方向如图10所示.
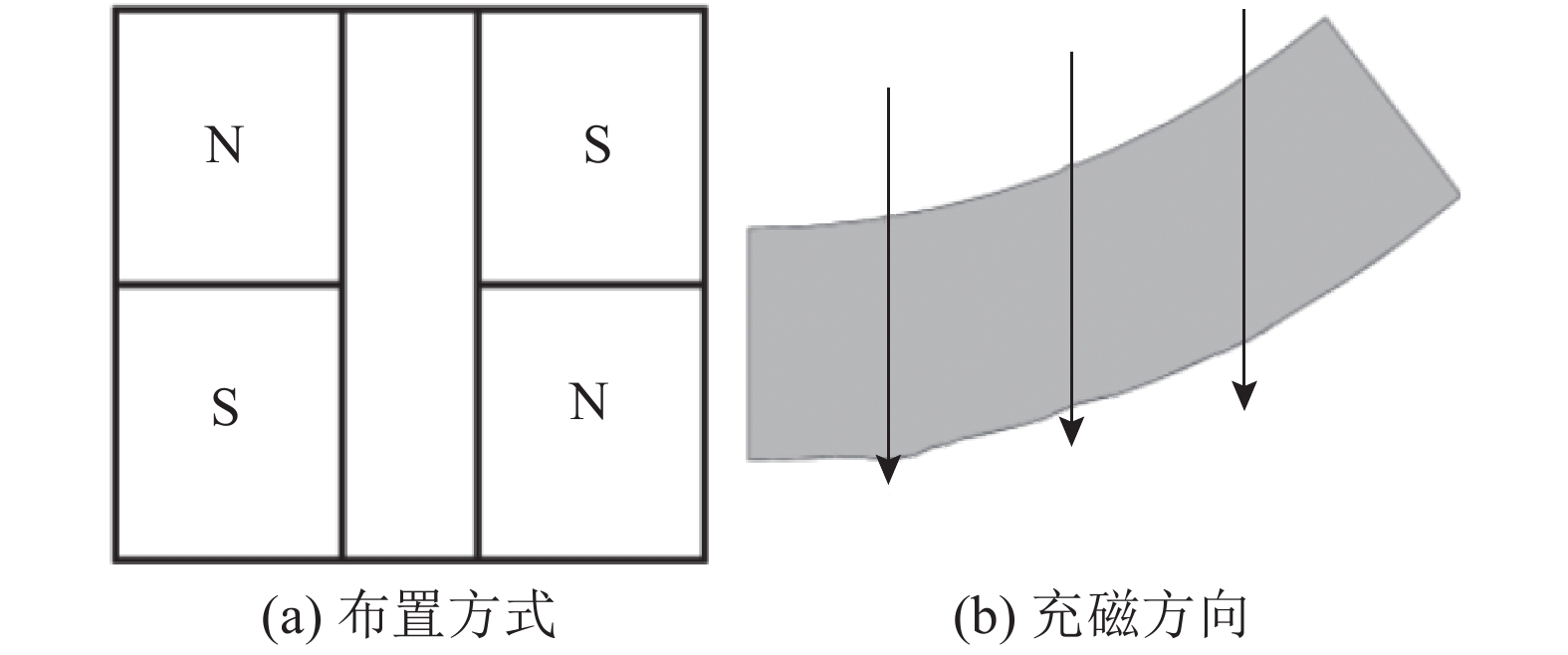
|
图 10 永磁铁布置方式与充磁方向 Fig. 10 Layout and magnetizing direction of permanent magnet |
如图11所示,永磁铁厚度的增加会增大吸附力,当磁铁增厚Δh1达到10 mm后,磁铁吸附力几乎不再变化;随着Δh1的增加,γ增大,当Δh1达到10 mm后,γ的变化较小. 综合考虑磁吸附力和磁质比,将磁铁厚度增加10 mm,对应的吸附力为1 448 N,满足要求.

|
图 11 永磁铁增厚对磁吸附力和磁质比的影响 Fig. 11 Effect of permanent magnet thickening on magnetic adsorption force and γ |
如图12所示,增大永磁铁宽度可以显著提高吸附力和磁质比. 图中,Δh3为永磁铁增宽。永磁铁宽度的增加受爬壁机器人内安装空间的限制. 隔磁件需要一定的宽度,为安装螺钉提供安装空间. 可知,永磁铁宽度增加5 mm,对应的吸附力为1 284.5 N,满足要求.

|
图 12 永磁铁增宽对磁吸附力和磁质比的影响 Fig. 12 Effect of permanent magnet broadening on magnetic adsorption force and γ |
如图13所示,增大轭铁厚度可以提高磁吸附力,在轭铁增厚Δh2达到10 mm后,吸附力的变化非常小. 磁质比随着轭铁增厚的增加而减小,说明轭铁增厚可以减小磁阻而增大磁吸附力,但轭铁增厚使轭铁质量增加得更多,降低了磁质比;因此,轭铁厚度选择保持不变.
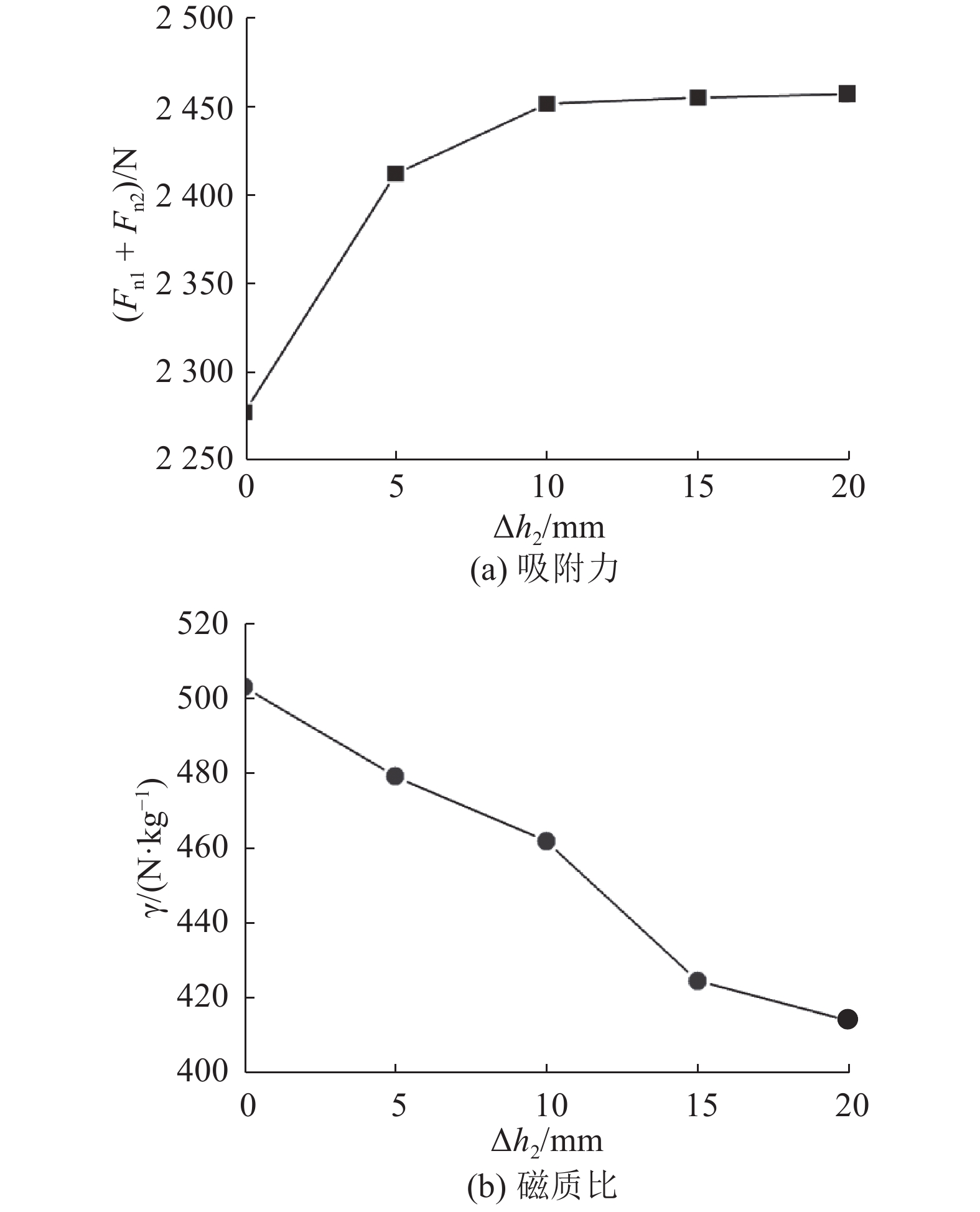
|
图 13 轭铁增厚对磁吸附力和磁质比的影响 Fig. 13 Effect of yoke thickening on magnetic adsorption force and γ |
根据上述分析,结合爬壁机器人的结构,确定磁吸附组件的基本结构尺寸,如图14所示. 为了验证优化设计的可行性,开展磁吸附组件和爬壁机器人的工作性能实验.
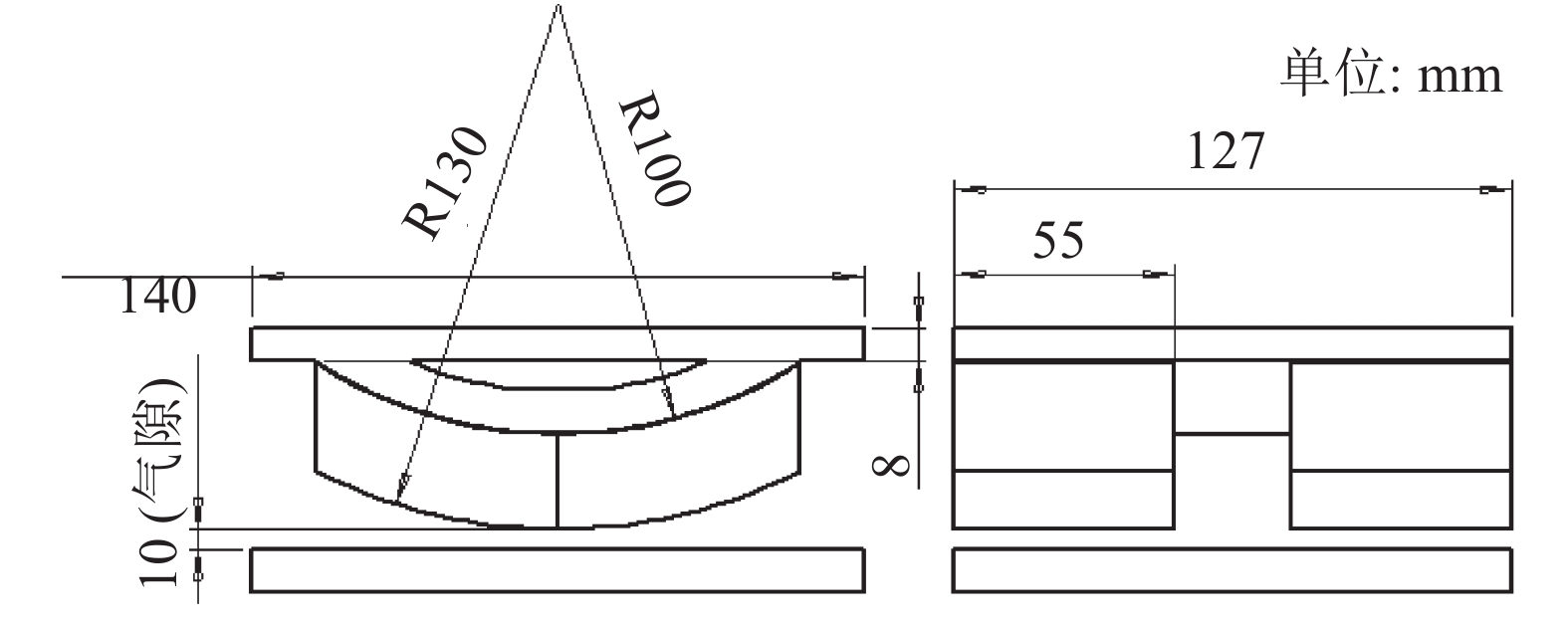
|
图 14 磁吸附组件的结构尺寸 Fig. 14 Dimensions of magnetic components |
磁吸附组件的主要性能是磁吸附力,采用WDW电子式万能拉力试验机,测量不同气隙下的磁吸附力,如图15所示. 实验时,磁吸附组件放置在拉力机台面上,通过塞纸的方法来确定磁铁圆弧最低点与台面之间的距离,即塞纸的厚度可以认为是磁铁的气隙. 为了减少误差的影响,气隙的确定采用5次测量求均值的方式. 气隙确定后,调节拉力头匀速上移,直接读取拉力,即磁吸附力.

|
图 15 磁吸附组件的性能测试 Fig. 15 Performance testing of magnetic components |
图16中,δ为磁铁气隙,实验结果与仿真结果的变化趋势基本一致,仿真结果比实验结果稍大. 这是因为仿真数据是在理想边界情况下得到的数值,实际磁铁材料的磁力性能比理论小. 由于实验值与仿真值的比值在一个较小的范围内变化,在实际设计中,可以引入系数n对仿真数值进行修正,以判断磁吸附力的实际数值,指导爬壁机器人的设计. 如图16所示,n为0.73~0.77,可取均值0.75.
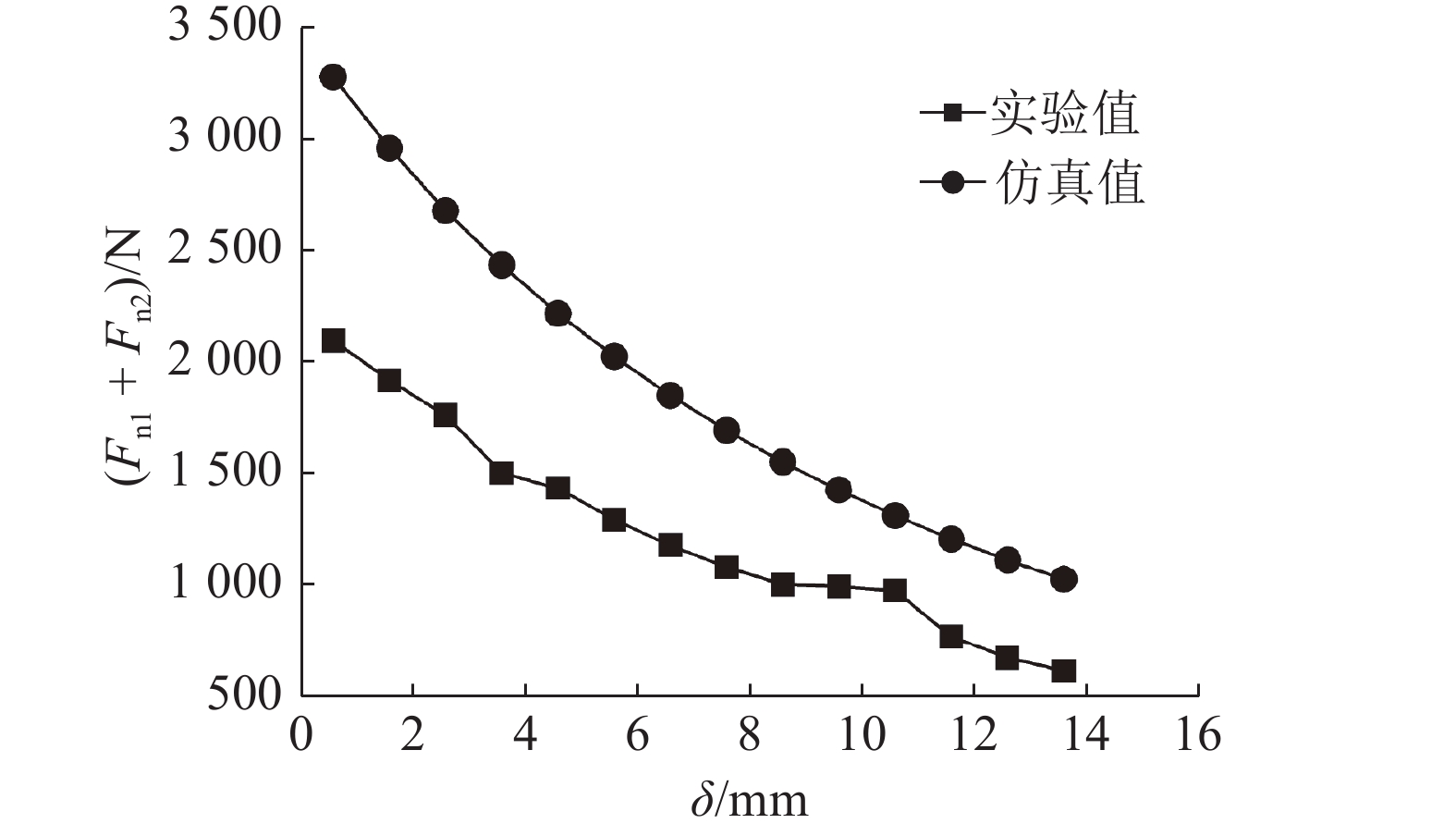
|
图 16 磁铁气隙对磁吸附力的影响 Fig. 16 Effect of magnet gap on magnetic adsorption force |
测量爬壁机器人在作业壁面潮湿、干燥等工况下的最大负载能力. 实验过程如图17、18所示,实验数据如表1所示.

|
图 17 机器人负载测试图 Fig. 17 Diagram of robot load testing |

|
图 18 钢板表面喷水图 Fig. 18 Diagram of steel surface watering |
| 表 1 爬壁机器人的负载 Table 1 Load of wall-climbing robot |
由表1可知,干燥壁面比湿润壁面具有更大的负载能力,主动轮胎压增加会减弱负载能力. 与湿润壁面相比,干燥壁面具有较大的摩擦系数,故具有更大的负载能力;胎压增加会减小轮胎变形,一方面减小轮胎与作业壁面的接触面积,另一方面增大磁吸附组件与作业壁面之间的气隙,这都会导致摩擦力的下降,即负载能力的下降.
如图19所示为爬壁机器人的转向运动测试. 结果表明,爬壁机器人的运动灵活,能够保持可靠吸附.

|
图 19 爬壁机器人的转向运动 Fig. 19 Movement of wall-climbing robot |
(1)设计磁吸附爬壁机器人,介绍机械结构及工作原理,阐述磁吸附组件的结构及重要性.
(2)完成爬壁机器人的力学建模,得到正常工作对磁吸附力的要求,为后续的磁吸附组件优化设计提供边界条件.
(3)结合理论分析和有限元工具,开展磁吸附组件的优化设计,以实现磁质比最大的优化目标,确定磁吸附组件的结构尺寸.
(4)基于磁吸附组件的样机实验和爬壁机器人的样机实验,验证了磁吸附组件的吸附力与仿真分析基本一致,且爬壁机器人具有较大的负载能力和较灵活的运动能力.
(5)由于条件限制,未加工不同结构尺寸的多组磁吸附组件,完成对优化设计的验证. 仅以爬壁机器人样机试验,说明优化设计的可行性. 后续将针对优化设计的验证试验,开展深入的研究.
| [1] |
OCHAN A. Robotics moves onwards and upwards[J]. Industrial Robot, 2003, 30(3): 225-230. DOI:10.1108/01439910310473933 |
| [2] |
ELKMANN N, FELSCH T, SACK M, et al. Modular climbing robot for service-sector applications[J]. Industrial Robot, 1999, 26(6): 460-465. DOI:10.1108/01439919910296692 |
| [3] |
桂仲成, 陈强, 孙振国, 等. 爬壁机器人永磁吸附组件的优化设计[J]. 电工技术学报, 2006, 21(11): 32-40. GUI Zhong-cheng, CHEN Qiang, SUN Zhen-guo, et al. Optimization of permanent-magnetic adhesion device for wall-climbing robot[J]. Transactions of China Electrotechnical Society, 2006, 21(11): 32-40. |
| [4] |
陈勇, 王昌明, 包建东. 新型爬壁机器人磁吸附单元优化设计[J]. 兵工学报, 2012, 33(12): 1539-1544. CHEN Yong, WANG Chang-ming, BAO Jian-dong. Optimization of a novel magnetic adsorption unit for wall-climbing robot[J]. Acta Armanentarii, 2012, 33(12): 1539-1544. |
| [5] |
衣正尧. 用于搭载船舶除锈清洗器的爬壁机器人研究[D]. 大连: 大连海事大学, 2010. YI Zheng-yao. Research on a wall climbing robot for boarding ship rust removal cleaner [D]. Dalian: Dalian Maritime University, 2010. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1837016 |
| [6] |
薛胜雄, 任启乐, 陈正文, 等. 磁隙式爬壁机器人的研制[J]. 机械工程学报, 2011, 47(21): 37-42. XUE Sheng-xiong, REN Qi-le, CHEN Zheng-wen, et al. Design on magnetic gap adhesion typed crawler[J]. Journal of Mechanical Engineering, 2011, 47(21): 37-42. |
| [7] |
YAO P, LI D. The magnetic field analysis and optimization of permanent magnetic adhesion device for a novel wall climbing robot [C] // IEEE International Technology and Innovation Conference. Xi’an: IEEE, 2009: 1–5. http://ieeexplore.ieee.org/document/5518593/
|
| [8] |
HU B. A miniature wall climbing robot with biomechanical suction cups[J]. Industrial Robot, 2009, 36(6): 551-561. DOI:10.1108/01439910910994623 |
| [9] |
SHEN W, GU J, SHEN Y. Permanent magnetic system design for the wall-climbing robot [C] // IEEE International Conference on Mechatronics and Automation. Niagara Falls: IEEE, 2005: 2078–2083. http://www.tandfonline.com/doi/abs/10.1533/abbi.2006.0024
|
| [10] |
LI X, LI D, CHONG C. The study of magnetic circuit control technology for permanent magnet hump rail brake [C] // 6th International Symposium on Instrumentation and Control Technology: Sensors, Automatic Measurement, Control, and Computer Simulation. Beijing: SPIE, 2006: 635842–635848. http://spie.org/Publications/Proceedings/Paper/10.1117/12.718184
|
| [11] |
KOCHAN A. Robotics moves onwards and upwards[J]. Industrial Robot, 2003, 30(3): 225-230. DOI:10.1108/01439910310473933 |
| [12] |
WANG X, YI Z, GONG Y, et al. Ultra-high pressure water jetting removal rust model and analysis of removal rust capability [C] // The 7th International Conference on Fluid Power Transmission and Control. Hangzhou: ICFP, 2009: 503–506.
|
| [13] |
MANIERE E, SIMMONES R. Architecture, the backbone of robotic system [C] // 2000 IEEE International Conference on Robotic and Automation. San Francisco: IEEE, 2000: 505–513.
|
| [14] |
YOSHIDA Y, TAKEIRI Y. The use of magnetic fields in a partial-coaxial microwave cavity a holey-plate ion source[J]. Review of Scientific Instruments, 2000, 71(1): 66-69. DOI:10.1063/1.1150162 |
| [15] |
衣正尧, 弓永军, 王兴如, 等. 船舶除锈爬壁机器人设计方案研究[J]. 机床与液压, 2010, 38(7): 65-72. YI Zheng-yao, GONG Yong-jun, WANG Xing-ru, et al. Research on design scheme of a wall climbing robot for rust removal[J]. Machine Tool and Hydraulics, 2010, 38(7): 65-72. DOI:10.3969/j.issn.1001-3881.2010.07.021 |
| [16] |
钟文定. 铁磁学[M]. 北京: 科技出版社, 1987: 463.
|
| [17] |
王峰. 水下船体表面清刷机器人磁吸附驱动装置的研究[D]. 哈尔滨: 哈尔滨工程大学, 2003. WANG Feng. Research on underwater ship hull cleaning robot magnetic absorbing and driving technology [D]. Harbin: Harbin Engineering University, 2003. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y544865 |
| [18] |
王军波, 陈强, 孙振国. 爬壁机器人变磁力吸附单元的优化设计[J]. 清华大学学报: 自然科学版, 2003, 43(2): 214-217. WANG Jun-bo, CHEN Qiang, SUN Zhen-guo. Optimization of attracting devices with variable magnetic force for wall-climbing robots[J]. Journal of Tsinghua University: Science and Technology, 2003, 43(2): 214-217. |
| [19] |
HAM C, KO W, HAN Q. Analysis and optimization of a Maglev system based on the Halbach magnet arrays[J]. Journal of Applied Physics, 2006, 99(8): 510-513. |
| [20] |
LIU J, CHOI H, WALMER M. Design of permanent magnet systems using finite element analysis[J]. International Journal of Iron and Steel Research, 2006, 13(supple.1): 383-387. |



