电磁轴承(又称主动电磁轴承,active magnetic bearings, AMB)通过对电磁铁线圈中电流的实时控制,使其产生受控的电磁力来实现对转子的非接触悬浮[1],具有无接触、适合高速、动力特性易于控制等特点,目前已成为高速旋转机械的关键支撑单元。对于开环电磁轴承系统,对应的机械刚度为负值[1],即AMB-刚性转子系统是一个开环不稳定系统,其动力学特性与所采用的控制规律密切相关,因此研究AMB转子系统的控制规律具有重要意义。
对于支承在AMB上的刚性转子来讲,转子的轴向运动与转子径向运动之间的耦合较小,轴向运动可简化为1个单自由度系统,而径向运动为1个相互耦合的四自由度系统。为了在相互耦合的径向四自由度系统中使用单自由度控制技术,就提出多种解耦控制理论。目前AMB–刚性转子系统的解耦主要分为交叉反馈解耦控制、智能解耦控制以及逆系统法解耦控制等。
交叉反馈解耦控制物理概念清楚且便于计算[2],因此早期AMB–刚性转子系统的解耦控制多采用该方法。Ahrens等[3]设计了抑制转子陀螺效应的交叉反馈解耦器;沈钺等[4]从理论上证明了当转子的转速超过某临界转速时交叉反馈控制能够对陀螺效应进行完全补偿;田希晖等[5]在传统位移交叉反馈的基础上提出了一种可以分别针对章动和进动进行相位补偿的增益预调交叉反馈控制。交叉反馈解耦只实现了转子径向2个转动自由度之间的解耦,并没有实现径向4个自由度间的完全解耦。
智能解耦控制算法凭借不依赖控制对象模型、具有自学习能力、鲁棒性强等优点[6],也被用于AMB-刚性转子系统的解耦控制。Ouyang等[7]设计了基于滑模控制的交叉解耦控制器;Li等[8]将滑模理论应用于状态反馈控制以实现解耦;Guo等[9]设计了自适应模糊解耦控制器。然而智能解耦控制算法设计难度大,对控制器硬件要求高,实用性受到限制。
逆系统法具有物理概念清晰、易于理解、易于实现等特点[10],成为目前较多采用的解耦控制。Fang等[11]利用逆系统法实现了AMB–刚性转子系统各自由度的动态解耦;Hutterer等[12]将卡尔曼滤波器应用于逆系统,以改善解耦效果;Li等[13]将最小二乘法应用于逆系统解耦器,实现了对AMB–刚性转子系统的解耦。然而,逆系统模型非常复杂,难于构造,且抵抗外部干扰的能力较差。
针对AMB–刚性转子系统径向相互耦合的四自由度问题,本文设计一种易于计算的前馈解耦控制器. 针对解耦后系统,设计不平衡量辨识器对转子不平衡量进行辨识,并对辨识结果进行补偿;利用最速跟踪微分器(time-optimal tracking differentiator, TOTD)来获取前馈解耦控制及不平衡量辨识器所需的微分信号,以改善噪声环境下解耦和不平衡补偿的效果;对前馈解耦控制及不平衡补偿的解耦效果、不平衡补偿能力以及抗噪能力进行仿真及试验研究。
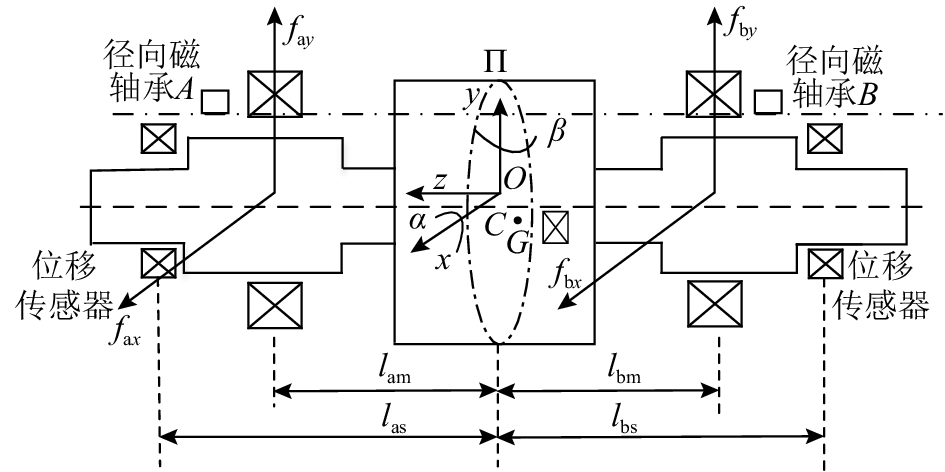
1 电磁轴承–刚性转子系统的力学模型如图1所示为由 AMB支撑的刚性转子的典型结构。实验测得的转子系统的一阶弯曲临界转速为472 Hz (即28 320 r/min),而转子的转速范围为0~24 000 r/min,故认为转子为刚性转子。如果不考虑轴向与径向的耦合,那么转子的径向就具有4个自由度。
|
图 1 AMB–刚性转子系统结构 Fig. 1 Structure of AMB-high speed motor rotor system |
为了描述转子、传感器和AMB间的相互位置,设平衡转子质心
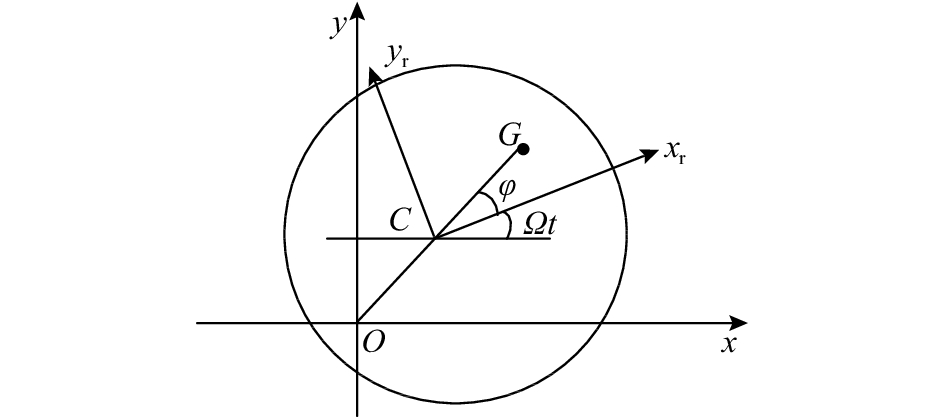
为了考虑转子不平衡对系统动力学行为的影响,将不平衡质量等效为在平衡转子质心
|
图 2 转子不平衡模型 Fig. 2 Model of rotor imbalance |
设转子的质量为
由于不平衡质量相对于转子的质量很小,不足以影响转子的质心位置,不平衡转子的运动状态仍然用平衡转子质心C沿
| $\left. \begin{aligned}&{l}m\ddot x = {f_{{\rm{a}}x}} + {f_{{\rm{b}}x}} + m\varepsilon {\varOmega ^2}\cos \;(\varOmega t + \varphi ),\\&J\ddot \beta + {J_z}\varOmega ( - \dot \alpha ) = {l_{{\rm{am}}}}{f_{{\rm{a}}x}} - {l_{{\rm{bm}}}}{f_{{\rm{b}}x}} + m{\varepsilon _{{z}}}\varepsilon {\varOmega ^2}\cos \;(\varOmega t + \varphi ),\\&m\ddot y = {f_{{\rm{a}}y}} + {f_{{\rm{b}}y}} + m\varepsilon {\varOmega ^2}\sin \;(\varOmega t + \varphi ) - mg,\\&J( - \ddot \alpha ) - {J_z}\varOmega \dot \beta = {l_{{\rm{am}}}}{f_{{\rm{a}}y}} - {l_{{\rm{bm}}}}{f_{{\rm{b}}y}} + m{\varepsilon _z}\varepsilon {\varOmega ^2}\sin \;(\varOmega t + \varphi ).\end{aligned} \right\}$ | (1) |
式中:
假设AMB的电磁力采用线性化模型,那么电磁力的表达式[1]为
| $\left. \begin{aligned} {f_{{\rm{a}}x}} = {k_{{\rm{ia}}}}{i_{{\rm{a}}x}} - {k_{{\rm{sa}}}}{x_{{\rm{am}}}},\; \\ {f_{{\rm{b}}x}} = {k_{{\rm{ib}}}}{i_{{\rm{b}}x}} - {k_{{\rm{sb}}}}{x_{{\rm{bm}}}},\; \\ {f_{{\rm{a}}y}} = {k_{{\rm{ia}}}}{i_{{\rm{a}}y}} - {k_{{\rm{sa}}}}{y_{{\rm{am}}}},\; \\ {f_{{\rm{b}}y}} = {k_{{\rm{ib}}}}{i_{{\rm{b}}y}} - {k_{{\rm{sa}}}}{y_{{\rm{bm}}}}.\; \\ \end{aligned} \right\}$ | (2) |
式中:(
AMB处转子在
| $\left. \begin{aligned} {x_{{\rm{am}}}} = x + {l_{{\rm{am}}}}\beta ,\; \\ {x_{{\rm{bm}}}} = x - {l_{{\rm{am}}}}\beta ,\;\\ {y_{{\rm{am}}}} = y - {l_{{\rm{am}}}}\alpha ,\; \\ {y_{{\rm{bm}}}} = y + {l_{{\rm{bm}}}}\alpha .\; \\ \end{aligned} \right\}$ | (3) |
将式(2)和(3)代入式(1),并令
| ${\dot{ X}} = {{AX}} + {{BU}} + {{G}} + {{W}}.$ | (4) |
式中:
| ${{A}} = \left[ {\begin{array}{*{20}{c}} {\bf{0}}&{{E}} \\ {{{{A}}_{21}}}&{{{{A}}_{22}}}\end{array}} \right]{\text{,}} $ |
| ${{{A}}_{21}} = \left[ {\begin{array}{*{20}{c}} {{{{{A}}'}_{11}}}&{\bf{0}} \\ {\bf{0}}&{{{{{A}}'}_{22}}} \end{array}} \right]{\text{,}} $ |
| ${{{A}}_{22}} = \left[ {\begin{array}{*{20}{c}} {\bf{0}}&{{{{{A}}''}_{12}}} \\ {{{{{A}}''}_{21}}}&{\bf{0}} \end{array}} \right]{\text{,}} $ |
| ${{{A}}'_{11}} ={{{A}}'_{22}} =- \left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{{ {{k_{{\rm{sa}}}} + {k_{{\rm{sb}}}}} }}{m}}&{\displaystyle\frac{{ {{k_{{\rm{sa}}}}{l_{{\rm{am}}}} - {k_{{\rm{sb}}}}{l_{{\rm{bm}}}}} }}{m}} \\ {\displaystyle\frac{{ {{k_{{\rm{sa}}}}{l_{{\rm{am}}}} - {k_{{\rm{sb}}}}{l_{{\rm{bm}}}}} }}{J}}&{\displaystyle\frac{{ {{k_{{\rm{sa}}}}l_{{\rm{am}}}^{\rm{2}} + {k_{{\rm{sb}}}}l_{{\rm{bm}}}^2} }}{J}} \end{array}} \right]{\text{,}} $ |
| $ {{{A}}''_{12}} = - {{{A}}''_{21}} = \left[ {\begin{array}{*{20}{c}} 0&0 \\ 0&{ - \displaystyle\frac{{{J_z}}}{J}\Omega } \end{array}} \right]{\text{,}}$ |
| $ {{{B'}}_{11}} = {{{B'}}_{22}} = \left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{{{k_{{\rm{ia}}}}}}{m}}&{\displaystyle\frac{{{k_{{\rm{ib}}}}}}{m}} \\ {\displaystyle\frac{{{l_{{\rm{am}}}}{k_{{\rm{ia}}}}}}{J}}&{ - \displaystyle\frac{{{l_{{\rm{bm}}}}{k_{{\rm{ib}}}}}}{J}} \end{array}} \right]{\text{,}}$ |
| $ {{B}} = \left[ {\begin{array}{*{20}{c}} {\bf{0}} \\ {{{{B}}_2}} \end{array}} \right]{\text{,}}{{{B}}_2} = \left[ {\begin{array}{*{20}{c}} {{{{{B'}}}_{11}}}&{\bf{0}} \\ {\bf{0}}&{{{{{B'}}}_{22}}} \end{array}} \right]{\text{,}}$ |
| ${{G}} = \left[ {\begin{array}{*{20}{c}} {\bf{0}} \\ {{{{G}}_2}} \end{array}} \right]{\text{,}}{{W}} = \left[ {\begin{array}{*{20}{c}} {\bf{0}} \\ {{{{W}}_2}} \end{array}} \right]{\text{,}}$ |
| ${{{G}}_2} = {\left[ {\begin{array}{*{20}{c}} 0&0&{ - g}&0 \end{array}} \right]\rm ^T}{\text{,}}$ |
| ${{U}} = {\left[ {\begin{array}{*{20}{c}} {{i_{{{\rm a}x}}}}&{{i_{{{\rm b}x}}}}&{{i_{{{\rm a}y}}}}&{{i_{{{\rm b}y}}}} \end{array}} \right]\rm ^T}{\text{,}}$ |
| ${{{W}}_2} = \left[ {\begin{aligned}\quad& {\varepsilon {\varOmega ^2}\cos\; (\varOmega t + \varphi )} \\ & {\displaystyle\frac{{m{\varepsilon _z}\varepsilon }}{J}{\varOmega ^2}\cos\; (\varOmega t + \varphi )} \\ & {\varepsilon {\varOmega ^2}\sin\; (\varOmega t + \varphi )} \\ & {\displaystyle\frac{{m{\varepsilon _z}\varepsilon }}{J}{\varOmega ^2}\sin\; (\varOmega t + \varphi )}\quad \end{aligned}} \right]{\text{,}}$ |
E为相应维数的单位矩阵.
传感器处转子在
| $\left. \begin{aligned} {x_{{\rm{as}}}} = x + {l_{{\rm{as}}}}\beta ,\; \\ {x_{{\rm{bs}}}} = x - {l_{{\rm{as}}}}\beta ,\; \\ {y_{{\rm{as}}}} = y - {l_{{\rm{as}}}}\alpha ,\; \\ {y_{{\rm{bs}}}} = y + {l_{{\rm{bs}}}}\alpha .\; \\ \end{aligned} \right\}$ | (5) |
同样地,可以得到用矩阵形式表示的输出方程为
| ${{Y}} = {{CX}}.$ | (6) |
式中:Y=[xas xbs yas ybs ] 为输出变量,C=[C1 0],
| ${{{C}}_1} = \left[ {\begin{array}{*{20}{c}} {{{{{C}}'}_{11}}}&{\bf{0}} \\ {\bf{0}}&{{{{{C}}'}_{22}}} \end{array}} \right], {{{C}}'_{11}} = {{{C}}'_{22}} =\left[ {\begin{array}{*{20}{c}} 1&{{l_{{\rm{as}}}}} \\ 1&{ - {l_{{\rm{bs}}}}} \end{array}} \right].$ |
为便于分析,将式(4)及(6)用分块矩阵表示为
| ${{\dot{ X}}_1} = {{{X}}_2},\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\;\;\;$ | (7) |
| ${{\dot{ X}}_2} = {{{A}}_{21}}{{{X}}_1} + {{{A}}_{22}}{{{X}}_2} + {{{B}}_2}{{U}} + {{{W}}_2} + {{{G}}_2},$ | (8) |
| ${{Y}} = {{{C}}_1}{{{X}}_1}.\quad\quad\quad\quad\quad\quad\quad\quad\quad\;\;\quad\quad$ | (9) |
将式(7)代入(8)可得
| ${{\ddot{ X}}_1} = {{{A}}_{21}}{{{X}}_1} + {{{A}}_{22}}{{\dot{ X}}_1} + {{{B}}_2}{{U}} + {{{W}}_2} + {{{G}}_2}.$ | (10) |
可见,AMB–刚性转子系统各变量之间的耦合由矩阵
矩阵
矩阵
为了进行前馈解耦控制,先将AMB–刚性转子系统关于状态变量的微分方程转化为关于输出变量的微分方程,将式(9)代入式(10)得
| $\begin{split} {\ddot{ Y}} = &\left( {{{{\overline{ A}}}_{21\left( 1 \right)}} + {{{\overline{ A}}}_{21\left( 2 \right)}}} \right){{Y}} + \left( {{{{\overline{ A}}}_{22\left( 1 \right)}} + {{{\overline{ A}}}_{22\left( 2 \right)}}} \right){\dot{ Y}} + \\&\left( {{{{\overline{ B}}}_{2\left( 1 \right)}} + {{{\overline{ B}}}_{2\left( 2 \right)}}} \right){{U}} + {{{\overline{ W}}}_2} + {{{\overline{ G}}}_2}. \end{split} $ | (11) |
式中:
为了达到使4个输出变量之间解耦的目的,就需要消除矩阵
| ${{{v}}_0}(t) = {{KY}}(t) + {{M}}{\dot{ Y}}(t) + {{U}}(t) + {{SU}}(t).$ | (12) |
式中:
用
| $\begin{split} {\ddot{ Y}} = &{{{\overline{ A}}}_{21(1)}}{{Y}} + [{{{\overline{ A}}}_{21(2)}} - {{{\overline{ B}}}_{2(1)}}{{K}}]{{Y}} + [{{{\overline{ A}}}_{22(2)}} - {{{\overline{ B}}}_{2(1)}}{{M}}]{\dot{ Y}} + \\&{{{\overline{ A}}}_{22(1)}}{\dot{ Y}} + [{{{\overline{ B}}}_{2(2)}} - {{{\overline{ B}}}_{2(1)}}{{S}}]{{U}} + {{{\overline{ B}}}_{2(1)}}{{{v}}_0}(t) + {{{\overline{ W}}}_2} + {{{\overline{ G}}}_2}. \\ \end{split} $ | (13) |
为了消除系统重力的影响,引入补偿矩阵
| $\begin{split} {\ddot{ Y}} = &{{{\overline{ A}}}_{21(1)}}{{Y}} + [{{{\overline{ A}}}_{21(2)}} - {{{\overline{ B}}}_{2(1)}}{{K}}]{{Y}} + [{{{\overline{ A}}}_{22(2)}} - {{{\overline{ B}}}_{2(1)}}{{M}}]{\dot{ Y}} + \\&{{{\overline{ A}}}_{22(1)}}{\dot{ Y}} + [{{{\overline{ B}}}_{2(2)}} - {{{\overline{ B}}}_{2(1)}}{{S}}]{{U}} + {{{\overline{ B}}}_{2(1)}}{{v}}(t) + {{{\overline{ W}}}_2}.\end{split} $ | (14) |
为了消除矩阵
| ${{\overline{ A}}_{21(2)}} = {{\overline{ B}}_{2(1)}}{{K}},$ | (15) |
| ${{\overline{ A}}_{22(2)}} = {{\overline{ B}}_{2(1)}}{{M}},$ | (16) |
| ${{\overline{ B}}_{2(2)}} = {{\overline{ B}}_{2(1)}}{{S}}.$ | (17) |
将式(15) ~ (17)代入式(14)得
| ${\ddot{ Y}} = {{\overline{ A}}_{21(1)}}{{Y}} + {{\overline{ A}}_{22(2)}}{\dot{ Y}} + {{\overline{ B}}_{2(2)}}{{v}}(t) + {{\overline{ W}}_2}.$ | (18) |
矩阵
可见,只要根据式(15) ~ (17),分别求得
为了抑制由转子的不平衡引起的不平衡同频振动,需要对转子的不平衡进行补偿。
不平衡力矩阵
| ${{v}}(t) = - {{PY}}(t) - {{D}}{\dot{ Y}}(t) - {{I}}\int {{{Y}}(t)} {\rm d}t.$ | (19) |
其中,
| ${{P}} = {\rm{diag\;[}}{P_{{\rm a}x}} \;\; {P_{{\rm b}x}}\;\;{P_{{\rm a}y}}\;\;{P_{{\rm b}y}}],$ |
| $ {{I}} = {\rm{diag\;[}}{I_{{\rm a}x}} \;\; {I_{{\rm b}x}} \;\; {I_{{\rm a}y}} \;\; {I_{{\rm b}y}}],$ |
| ${{D}} = {\rm{diag\;[}}{D_{{\rm a}x}} \;\; {D_{{\rm b}x}} \;\; {D_{{\rm a}y}} \;\; {D_{{\rm b}y}}].$ |
分别为PID控制器的3个参数。
将式(19)代入式(18)得
| $\begin{split} {{{\overline{ W}}}_2} = &{\ddot{ Y}} + \left[{{{\overline{ B}}}_{2(1)}}{{P}} - {{{\overline{ A}}}_{21(1)}}\right]{{Y}} + \\ &\left[{{{\overline{ B}}}_{2(1)}}{{D}} - {{{\overline{ A}}}_{22(1)}}\right]{\dot{ Y}} + {{{\overline{ B}}}_{2(1)}}{{I}}\int {{Y}} {\rm d}t. \end{split} $ | (20) |
由式(20)得出
| $\begin{split}\frac{{{Y}}}{{{{{\overline{ W}}}_2}}} =&s \times\left\{{}{s^3} + \left[{{{\overline{ B}}}_{2(1)}}{{D}} - {{{\overline{ A}}}_{22(1)}}\right]{s^2} +\right.\\ &\left.\left[{{{\overline{ B}}}_{2(1)}}{{P}} - {{{\overline{ A}}}_{21(1)}}\right]s + {{{\overline{ B}}}_{2(1)}}{{I}}\right\}^{-1}.\end{split}$ | (21) |
显然,只要合理地选择矩阵
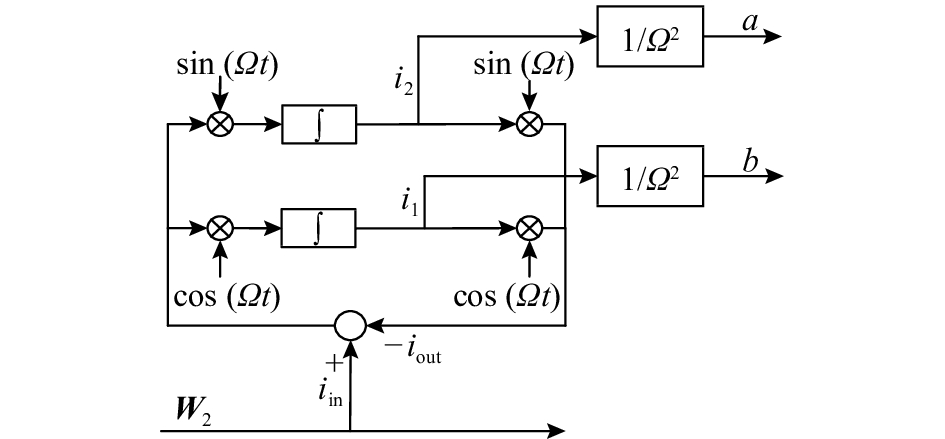
|
图 3 陷波滤波器结构原理图 Fig. 3 Block diagram of notch filter |
由陷波滤波器的结构可知:
| $\displaystyle\frac{{{i_{{\rm{out}}}}}}{{{i_{{\rm{in}}}}}} = \displaystyle\frac{s}{{{s^2} + s + {\varOmega ^2}}}.$ | (22) |
以
| ${i_{{\rm{in}}}} = \varepsilon \;{\varOmega ^2}\cos \;(\varOmega t + \varphi ).$ | (23) |
式中:
将
| $\begin{split} {i_{{\rm{out}}}} =& {i_{{\rm{in}}}} = \varepsilon {\varOmega ^2}\cos\; (\varOmega t + \varphi ) =\\ & \varepsilon {\varOmega ^2}\cos\; \varphi \cos\; (\varOmega t) - \varepsilon {\varOmega ^2}\sin\; (\varphi )\sin\; (\varOmega t). \\ \end{split} $ | (24) |
又由于
| ${i_{{\rm{out}}}} = {i_1}\cos \;(\varOmega t) + {i_2}\sin \;(\varOmega t).$ | (25) |
则有
| $\left. \begin{array}{l} {i_1} = \varepsilon {\varOmega ^2}\cos \;\varphi ,\;a = \varepsilon \cos \;\varphi {\text{,}} \\ {i_2} = - \varepsilon {\varOmega ^2}\sin \;\varphi ,\;b = - \varepsilon \sin \;\varphi . \\ \end{array} \right\}$ | (26) |
陷波滤波器内积分器的收敛需要一定的时间,设所需收敛时间为
| $\varepsilon {\rm{ = }}\sqrt {{a^2} + {b^2}} , \; \varphi {\rm{ = }} - \arctan\; (b/a).$ | (27) |
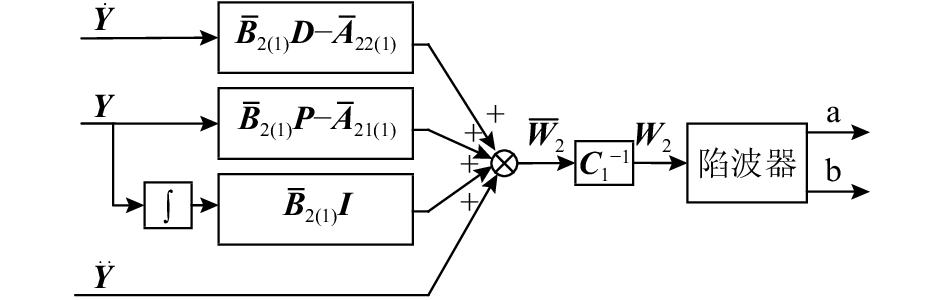
|
图 4 不平衡辨识器结构原理示意图 Fig. 4 Block diagram of observer about imbalance |
至此,就完成了对
| $\begin{split} {{{\dot{ X}}}_2} = &{{{A}}_{21}}{{{X}}_1} + {{{A}}_{22}}{{{X}}_2} + {{{B}}_2}[{{U}} - {{{U}}_{\rm{W}}}] + {{{W}}_2} {\rm{ = }}\\ &{{{A}}_{21}}{{{X}}_1} + {{{A}}_{22}}{{{X}}_2} + {{{B}}_2}{{U}}. \end{split} $ | (28) |
显然,这时转子的不平衡量得到了完全补偿。另外,该方法是在系统的输入
在前馈解耦控制器以及转子不平衡量辨识器中,需要利用输出位移信号
在经典控制理论中,通常利用经典微分器(classical differentiator,CD)来获取给定信号的微分信号,其具体的运算过程为
| ${\dot x_{{\rm{(CD)}}}}(t) = \displaystyle\frac{s}{{Ts + 1}}x(t).$ | (29) |
式中:
如果给定信号
| ${\dot x_{{\rm{(CD)}}}}(t) \approx \displaystyle\frac{1}{T}[x(t) - x(t - T)] + \displaystyle\frac{1}{T}n(t).$ | (30) |
可见,经典微分器的输出信号叠加了一个对原信号中的噪声放大了
采用经典微分器的前馈解耦控制以及不平衡补偿存在的主要问题如下:
1) 前馈解耦控制需要利用输出位移信号
2) 式(20)中,把不平衡力矩
3) 对于经典的PID控制器,需要用到误差的微分信号,若微分信号是利用经典微分器获取的,那么PID控制器也会存在噪声的放大效应,不利于系统的稳定。
4.2 离散最速跟踪微分器由于离散最速跟踪微分器具有很好的噪声抑制能力,且对噪声的放大效应低[18],为了改善噪声环境下AMB–刚性转子系统的解耦和不平衡补偿的效果,本文利用最速跟踪微分器代替经典微分器来计算广义速度及广义加速度。
为了说明跟踪微分器的工作原理,任选一路解耦后系统的输出位移信号,如
| $\left. \begin{aligned}&{l}{{\ddot x}_{{\rm{(TO)}}}}(k) = {f_{{\rm{han}}}}[{x_{{\rm{(TO)}}}}(k) - {h_1}{{\dot x}_{{\rm{(TO)}}}}(k) -\; \\ &\,\;\quad\quad\quad\quad{x_{{\rm{as}}\left( {\rm{d}} \right)}}(k),{{\dot x}_{{\rm{(TO)}}}}(k),r,{h_0}],\; \\& {{\dot x}_{{\rm{(TO)}}}}(k + 1) = {{\dot x}_{{\rm{(TO)}}}}(k) + h{{\ddot x}_{{\rm{(TO)}}}}(k),\; \\ & {x_{{\rm{(TO)}}}}(k + 1) = {x_{{\rm{(TO)}}}}(k) + h{{\dot x}_{{\rm{(TO)}}}}(k).\; \\ \end{aligned} \right\}$ | (31) |
式中:
由跟踪器的特性[18]可知,按式(31)递推,
若令
| $p(k) = {x_{({\rm{TO}})}}(k) - {h_1}{\dot x_{({\rm{TO}})}}(k) - {x_{{\rm{as}}\left( {\rm{d}} \right)}}(k),$ |
则最速控制综合函数定义为
| ${f_{{\rm{han}}}}[p(k),{\dot x_{({\rm{TO}})}}(k),r,{h_0}] = - \left\{ \begin{split} r \cdot {\rm sign}\;\left( a \right),\;\;&\left| a \right| > r{h_0}; \\ {a / {{h_0}}},\quad\quad \;\;\;\; &\left| a \right| \leqslant r{h_0}. \end{split} \right.$ | (32) |
其中,
| $a = \left\{ \begin{aligned}&\begin{aligned}{{\dot x}_{({\rm{TO}})}}& + \displaystyle\frac{1}{2}\left( {\sqrt {{r^2}h_0^2 + 8r\left| {p + {h_0}{{\dot x}_{({\rm{TO}})}}} \right|} - r{h_0}} \right) \times\\ &{\rm sign}\left( {p + {h_0}{{\dot x}_{({\rm{TO}})}}} \right),\;\;\;\left| {p + {h_0}{{\dot x}_{({\rm{TO}})}}} \right| > rh_0^2;\end{aligned}\\&2{{\dot x}_{({\rm{TO}})}} + p/{h_0}{\rm{,}}\;\;\;\left| {p + {h_0}{{\dot x}_{({\rm{TO}})}}} \right| \leqslant rh_0^2.\end{aligned} \right.$ |
同理,将
定义
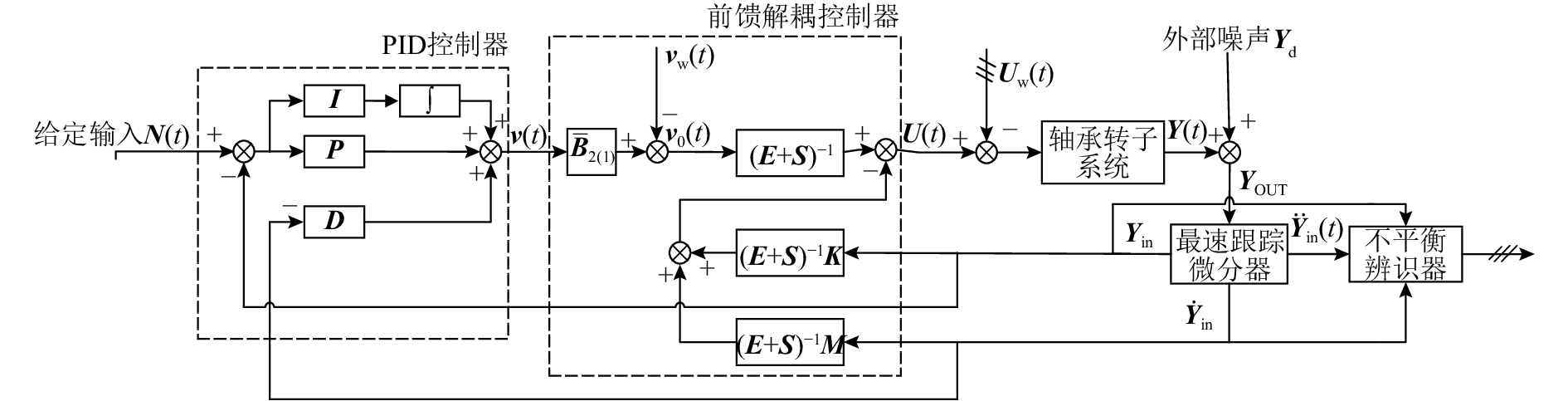
如图5所示为AMB–刚性转子系统前馈解耦控制及不平衡补偿结构框图,主要包括被控对象、前馈解耦器、跟踪微分器、PID控制器、不平衡辨识器等。由于跟踪微分器良好的噪声抑制能力和优秀的微分跟踪能力,将
|
图 5 前馈解耦控制及不平衡补偿框图 Fig. 5 Diagram of decoupling control system and imbalance compensation |
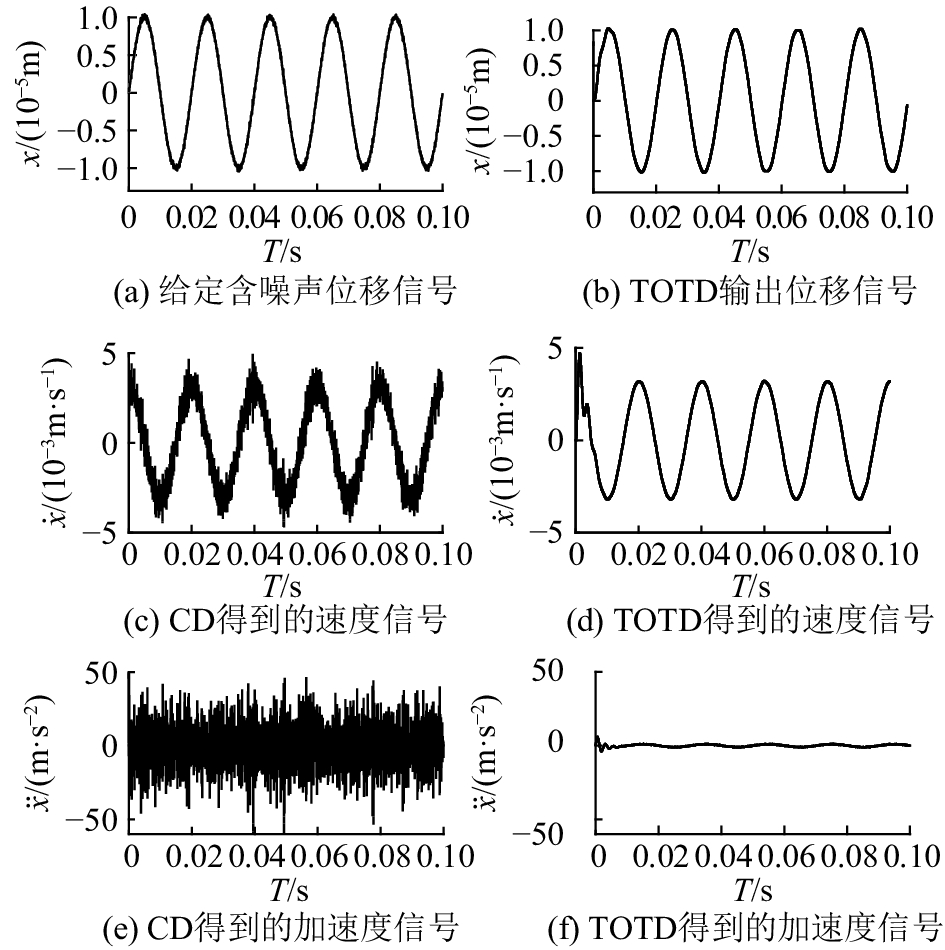
理论上,跟踪微分器具有良好的滤波特性,并且能够克服经典微分器严重的噪声放大效应,因此在噪声环境下能够更加真实地获得速度及加速度信号。如图6所示为在噪声环境(
|
图 6 存在噪声时CD与TOTD性能比较 Fig. 6 Comparison chart of CD and TOTD with noises |
在Matlab仿真软件上搭建了AMB–刚性转子系统前馈解耦控制及不平衡补偿模型,并对其进行理论仿真,以验证所设计的控制系统的解耦效果、不平衡补偿效果以及对测量噪声的抗扰能力。表1为AMB–刚性转子系统的相关参数。
| 表 1 AMB–刚性转子系统的相关参数 Table 1 Parameters of an AMB-rotor system |
首先在无噪声干扰的理想情况下进行仿真,即
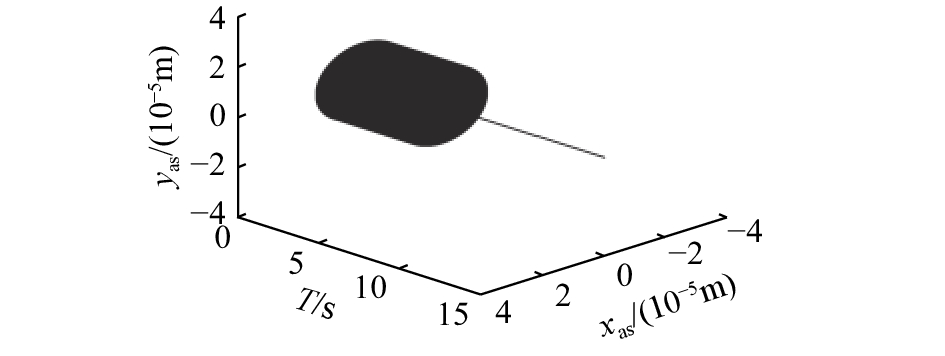
如图7所示为当额定转速为24 000 r/min时,转子稳定悬浮5 s后,将辨识得到的不平衡补偿矩阵
|
图 7 实施不平衡补偿前、后的转子位移轨迹 Fig. 7 Motion orbits of rotor without and with imbalance compensation |
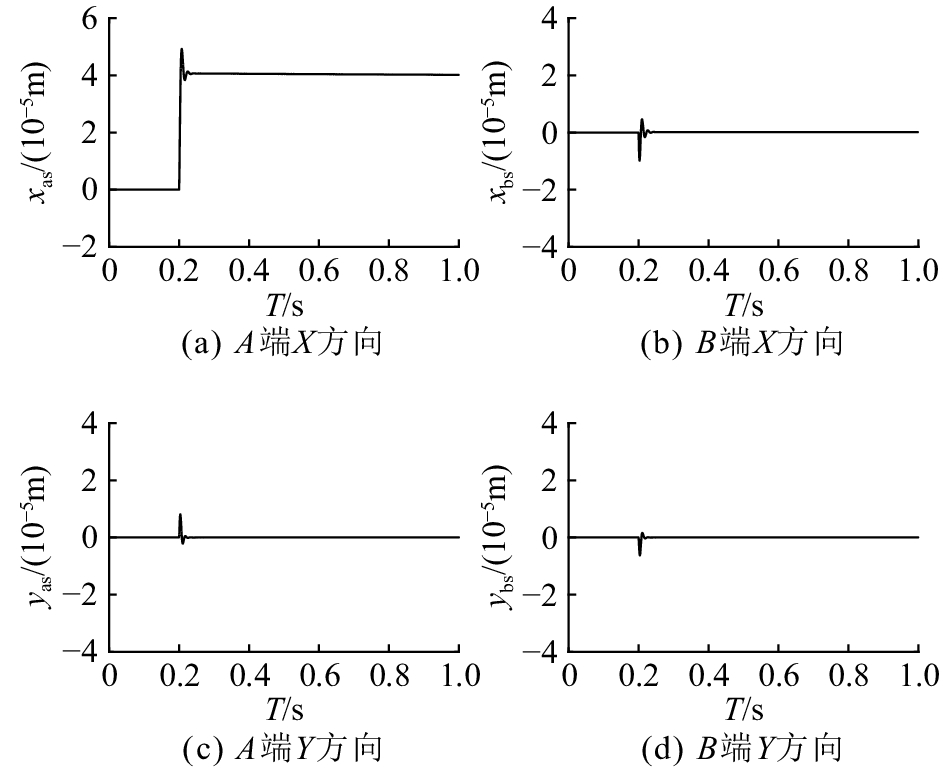
如图8和9所示分别为额定转速24 000 r/min下,转子的不平衡振动已经得到补偿后,在0.2 s给A端位移传感器处转子x方向位移产生一个0.04 mm的阶跃后,不采用与前馈解耦控制情况下系统径向各自由度方向的输出位移响应曲线。
|
图 8 未采用前馈解耦控制时转子系统的阶跃响应 Fig. 8 Step response performance of rotor system without feedforward decoupling control |
|
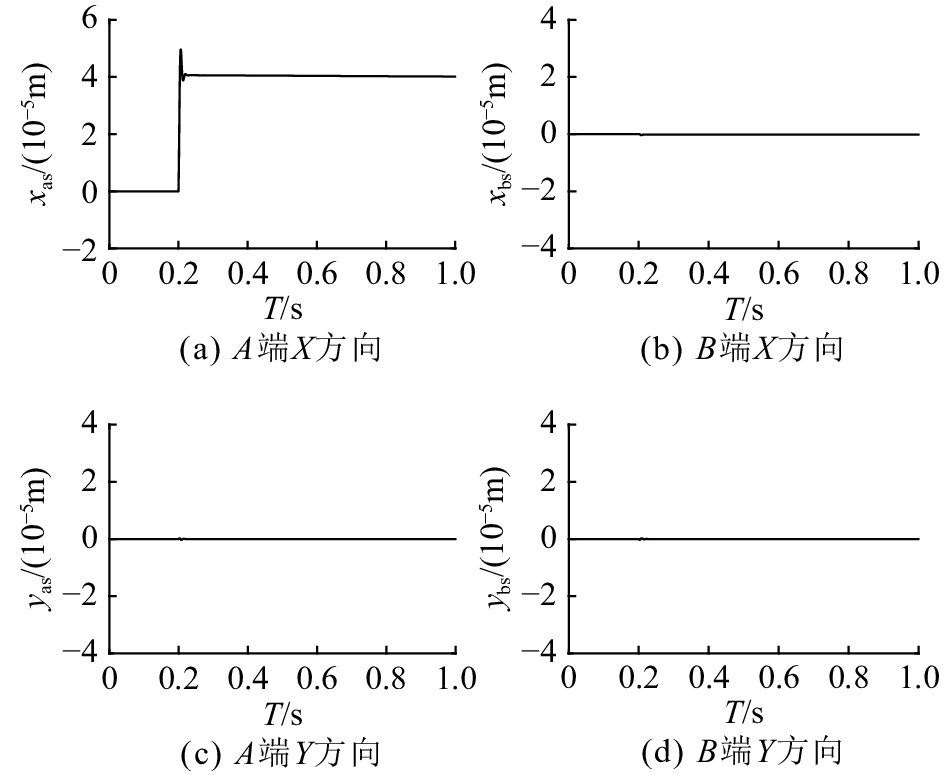
图 9 采用前馈解耦控制时转子系统的阶跃响应 Fig. 9 Step response performance of rotor system with feedforward decoupling control |
在未采用前馈解耦控制时,转子系统某方向上的位移阶跃变化,都会引起其他方向上位移的变化,可见4个输出变量之间存在耦合。但在采用前馈解耦控制后,转子系统某方向上的位移阶跃变化,并不会引起其他方向上的位移变化,AMB–刚性转子径向原来相互耦合的四自由度系统被解耦为4个单自由度的系统。
6.3 扰动抑制能力经典微分器对噪声的放大效应会降低前馈解耦控制器和不平衡量辨识器的精度。当输出位移中存在噪声,即测量噪声
|
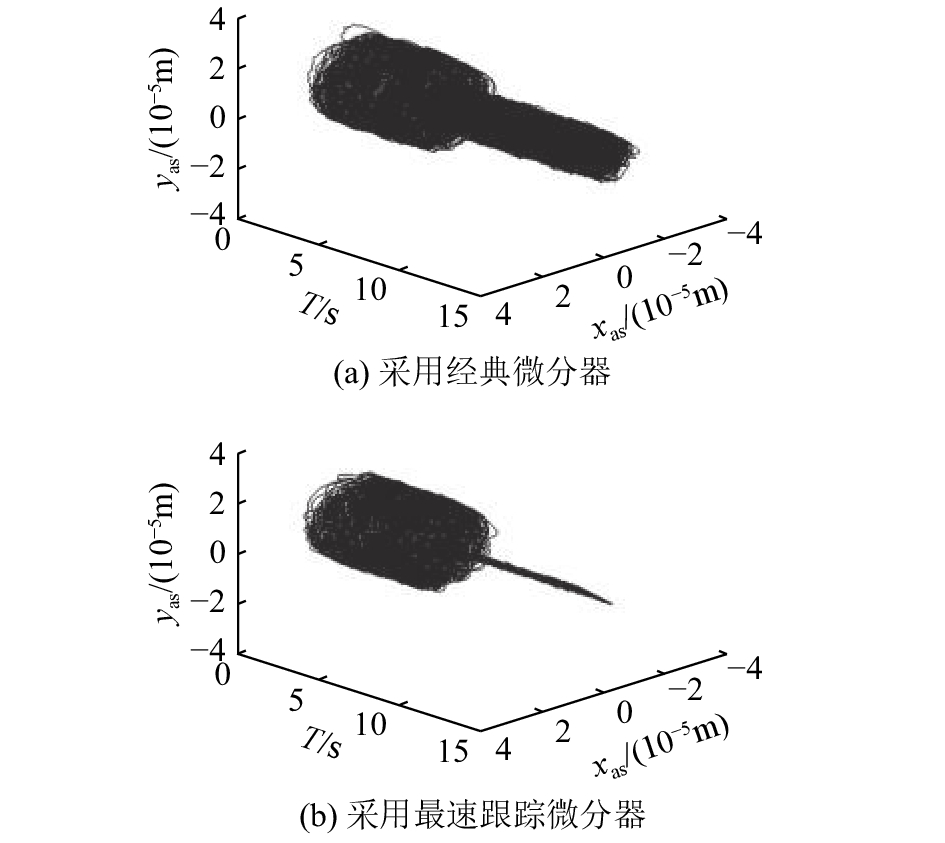
图 10 采用不同微分器的不平衡补偿前、后转子的运动轨迹 Fig. 10 Motion orbits of rotor without and with imbalance compensation by using different differentiators |
在系统存在噪声干扰的情况下,如果使用经典微分器,会严重影响不平衡辨识器的辨识精度,无法实现转子不平衡振动的完全补偿,补偿后转子的振动仍然很大。如果采用最速跟踪微分器,则明显提高了不平衡量的辨识精度,改善了转子不平衡振动的补偿效果,补偿后转子的振动得到有效控制。
在24 000 r/min的稳态转速下,在0 s时开启不平衡补偿且系统已进入稳定状态,在0.2 s后A端位移传感器处转子在x方向上的位移从0阶跃为0.04 mm,此时采用2种微分器得到转子径向各自由度方向的输出位移响应曲线,如图11和图12所示。
|
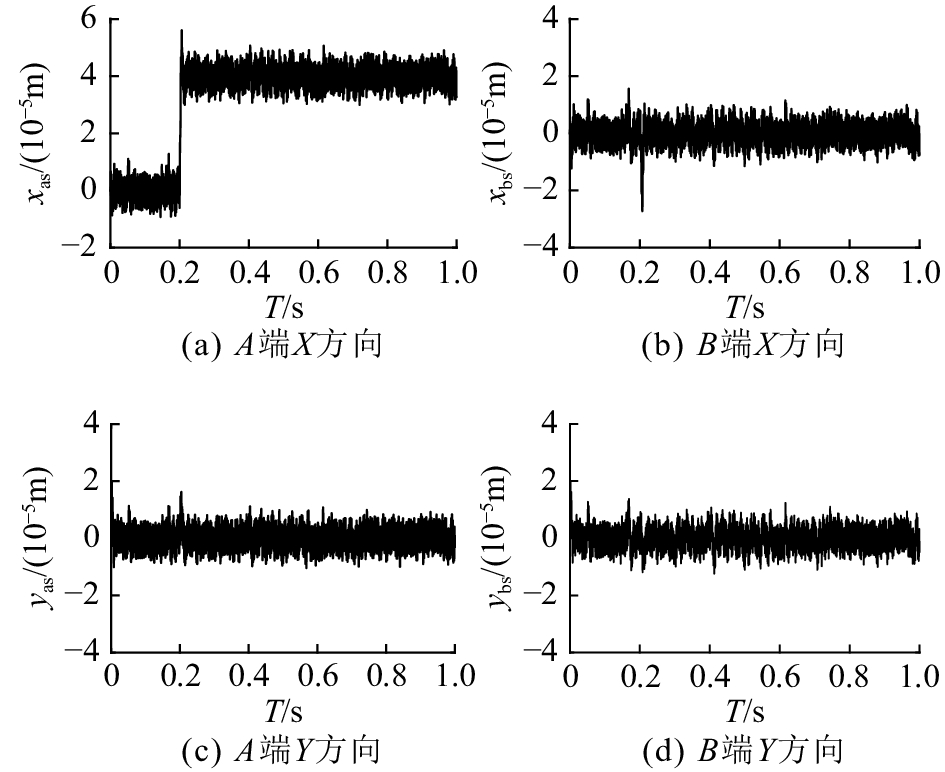
图 11 采用经典微分器(CD)的前馈解耦控制抗扰能力 Fig. 11 Anti-interference of feedforward decoupling controller using classical differentiator (CD) |
|
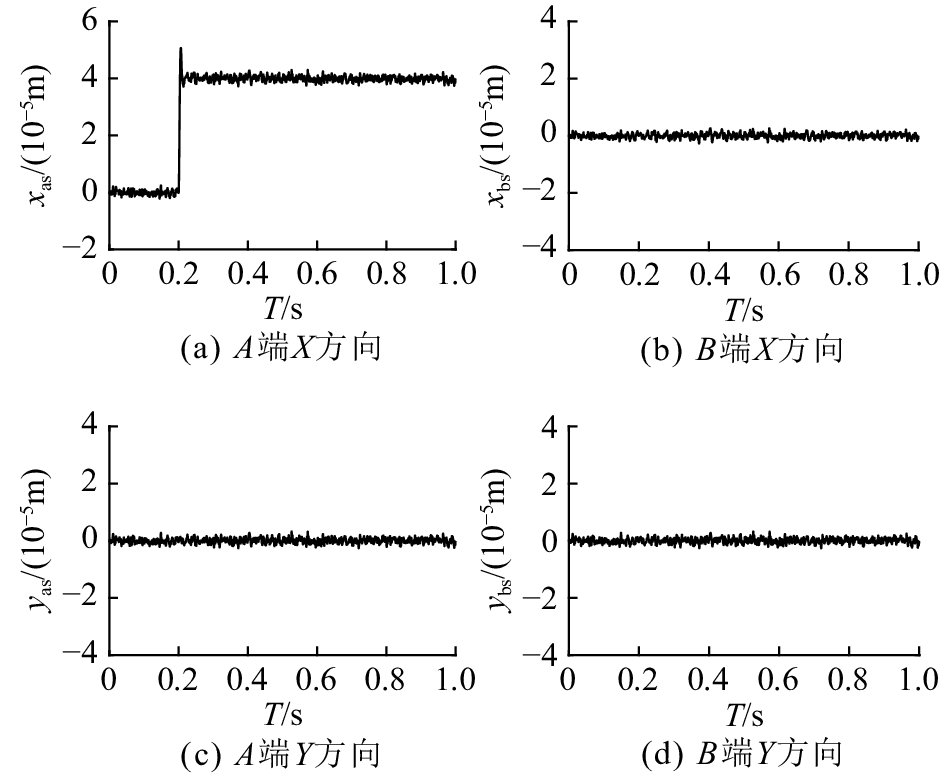
图 12 采用最速跟踪微分器(TOTD)的前馈解耦控制抗扰能力 Fig. 12 Anti-interference of feedforward decoupling controller using time-optimal tracking differentiator (TOTD) |
在系统存在噪声干扰的情况下,如果采用经典微分器的前馈解耦控制,则当转子系统上某一方向上发生位移阶跃时,其他方向上的位移都会出现波动,噪声干扰对系统解耦效果产生了明显的影响;如果采用最速跟踪微分器的前馈解耦控制,则当转子系统上某一方向上发生位移阶跃时,其他方向上的位移几乎没有出现波动,解耦效果明显。此外,采用最速跟踪微分器的转子系统各方向上的位移输出波形也明显好于经典微分器,滤波效果明显。
7 实验结果及分析为验证本文提出的前馈控制的解耦效果、不平衡补偿效果以及对测量噪声的抗扰能力,在如图13所示的某磁悬浮高速电机系统上进行实验研究。实验系统主要由电源、变频器、dSPACE测控平台、传感器、开关功放、电机和上位机等组成。电机的转子径向由2个AMB支撑,轴向由1对永磁轴承支撑。

|
图 13 AMB–高速电机试验装置 Fig. 13 Rig of AMB-high speed motor |
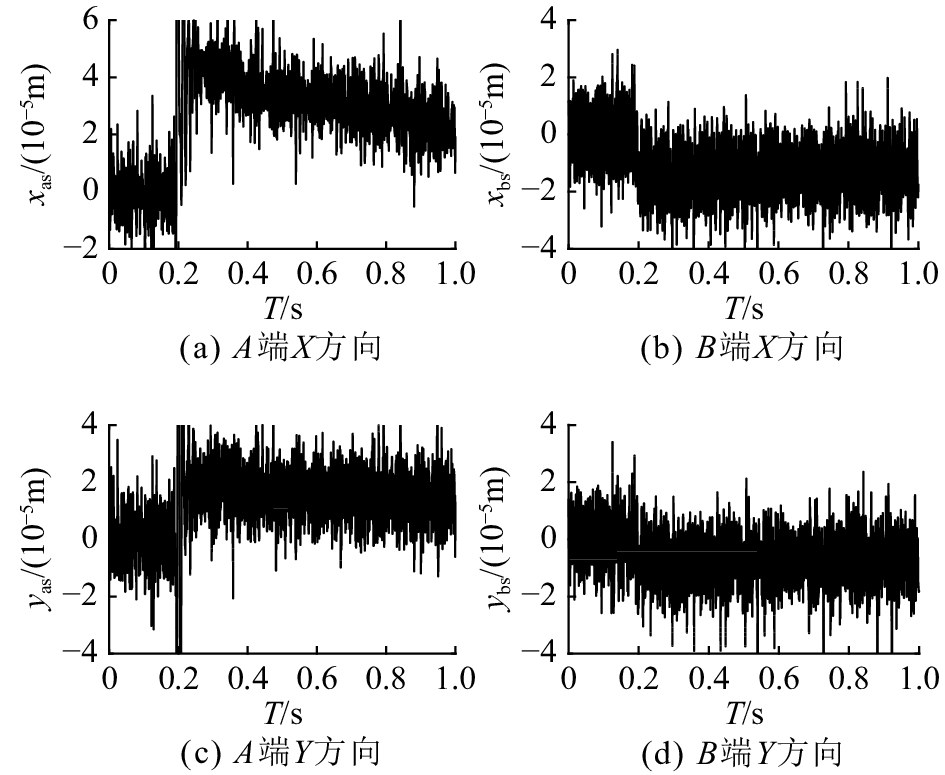
首先验证实验用AMB–刚性转子系统的耦合特性。如图14所示为在5 000 r/min的稳态转速下,A端传感器处转子x方向位移阶跃为0.04 mm,转子径向其他自由度方向上的输出位移响应曲线。结果表明,转子系统在某方向的位移阶跃变化,会引起其他方向位移的明显变化,无法对各方向位移进行独立控制。
|
图 14 未采用前馈解耦控制系统性能 Fig. 14 Performance of system without feedforward decoupling control |
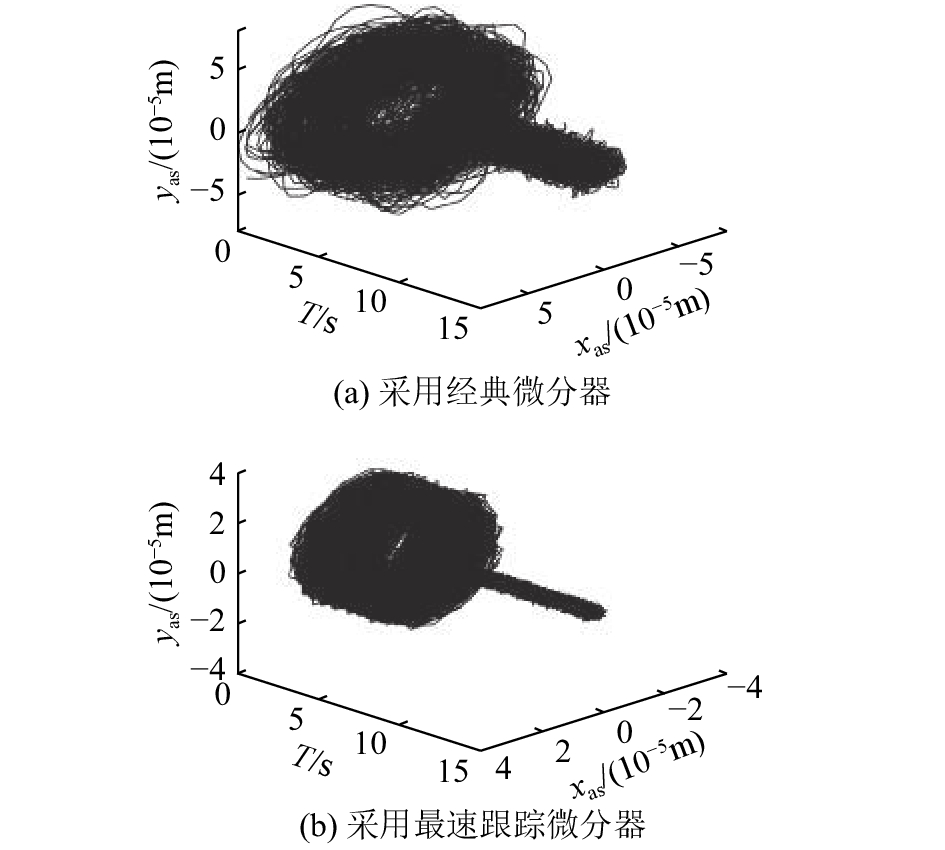
如图15所示分别为5 000 r/min的稳态转速下,当转子稳定悬浮5 s后,采用不同微分器的不平衡补偿前后A端位移传感器处转子的运动轨迹。如图16和17所示分别为开启不平衡补偿待系统稳定后,A端传感器处转子x方向位移阶跃为0.04 mm,采用不同微分器得到的转子径向各自由度方向的输出位移响应曲线。
|
图 15 采用不同微分器的不平衡补偿前、后转子位移轨迹 Fig. 15 Track of axes displacement with imbalance compensation by using different differentiators |
|
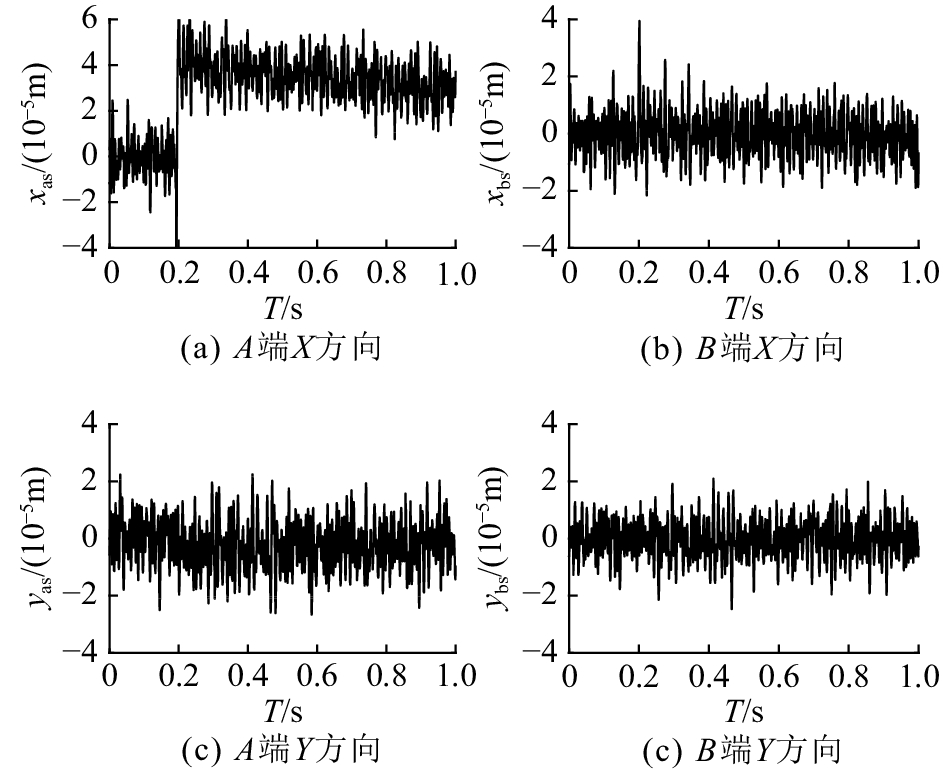
图 16 采用经典微分器 (CD) 的解耦控制性能 Fig. 16 Anti-interference of decoupling controller using CD |
|
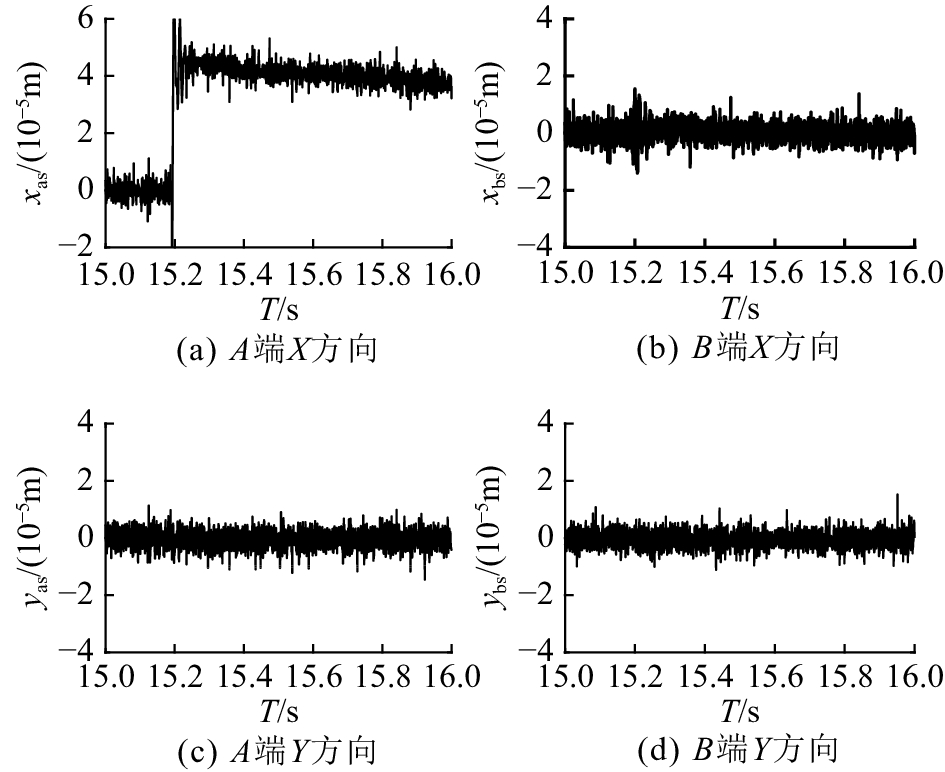
图 17 采用最速跟踪微分器 (TOTD) 的解耦控制抗扰能力 Fig. 17 Anti-interference of decoupling controller using TOTD |
结果表明,基于所设计不平衡量辨识器的不平衡补偿方法能够有效地抑制转子不平衡振动。采用前馈解耦控制,当转子系统在某个方向上的位移发生阶跃响应时,仅在该方向上出现扰动,对其他方向上的位移均没有产生明显影响,因此原来互相耦合的四自由度系统就可以按照4个独立的单自由度系统分别进行控制。并且,用最速跟踪微分器取代经典微分器,能够明显地改善解耦效果和不平衡补偿效果。
图17中B端位移传感器处的位置在x方向上仍然存在的微小扰动,可能原因[19] 如下:1) 本文提出的前馈解耦控制策略,是针对AMB线性化模型,而在实际中AMB的非线性影响了解耦控制效果。2) 求解前馈解耦控制器需要实际AMB–刚性转子系统精确的参数,但是实际上很难获得完全准确的转子系统参数。3) 虽然最速跟踪微分器具有良好的滤波特性,但并不能完全消除外部噪声对系统的影响。
8 结 论(1) 所设计的前馈解耦控制器能够将AMB–刚性转子径向四自由度耦合系统解耦为4个单自由度系统。
(2) 对于解耦后系统,利用所设计的不平衡量辨识器辨识出转子不平衡量并对其进行不平衡补偿,能够明显地抑制转子系统的不平衡振动。
(3) 最速跟踪微分器对输出的波形具有良好的滤波特性,提高了系统抗扰能力,削弱了外部测量噪声对解耦效果及不平衡补偿效果的影响。
| [1] |
BLEULER H, COLE M, KEOGH P. Magnetic bearings: theory, design and application to rotating machinery [M]. New York: Springer, 2009: 150–154. https://books.google.com/books/about/Magnetic_Bearings.html?id=1Kyg5dWyBasC
|
| [2] |
章琦, 祝长生. 电磁悬浮飞轮转子系统的模态解耦控制[J]. 振动工程学报, 2012, 25(3): 302-310. ZHANG Qi, ZHU Chang-sheng. Modal decoupling control for active magnetic bearing-supported flywheel rotor system[J]. Journal of Vibration Engineering, 2012, 25(3): 302-310. DOI:10.3969/j.issn.1004-4523.2012.03.012 |
| [3] |
AHRENS M, KUCERA L. Cross feedback control of a magnetic bearing system controller design considering gyroscopic effects [C] // Proceedings of the 3rd International Symposium on Magnetic Suspension Technology. Pennsylvania: Technomic Publishing Company Inc, 1995: 177–194. https://core.ac.uk/display/42776058
|
| [4] |
沈钺, 孙岩桦, 王世琥, 等. 磁悬浮飞轮系统陀螺效应的抑制[J]. 西安交通大学学报, 2003, 37(11): 1105-1109. CHEN Yue, SUN Yan-hua, WANG Shi-hi, et al. Reduction of gyroscopic effect of a magnetic bearing-supported flywheel system[J]. Journal of Xi'an Jiaotong University, 2003, 37(11): 1105-1109. DOI:10.3321/j.issn:0253-987X.2003.11.002 |
| [5] |
田希晖, 房建成, 刘刚. 一种磁悬浮飞轮增益预调交叉反馈控制方法[J]. 北京航空航天大学学报, 2006, 32(11): 1299-1303. TIAN Xi-hui, FANG Jian-cheng, LIU Gang. Gain scheduling cross feedback control approach for magnetic suspending flywheel[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(11): 1299-1303. DOI:10.3969/j.issn.1001-5965.2006.11.009 |
| [6] |
刘金琨. 智能控制[M]. 北京: 电子工业出版社, 2017: 3–5.
|
| [7] |
OUYANG H, LIU F, ZHANG G, et al. Vibration suppression for rotor system of magnetic suspended wind turbines using cross-feedback-based sliding mode control[C] // IEEE/SICE International Symposium on System Integration. Tokyo: IEEE, 2015: 112–115. http://ieeexplore.ieee.org/document/7404963/
|
| [8] |
LI H, YANG S, REN H. Dynamic decoupling control of DGCMG gimbal system via state feedback linearization[J]. Mechatronics, 2016, 36: 127-135. DOI:10.1016/j.mechatronics.2016.04.004 |
| [9] |
GUO X, WANG Q, LI G, et al. Adaptive fuzzy decoupling control for permanent magnet spherical motor dynamic system [C] // International Conference on Electrical Machines and Systems. Hangzhou: IEEE, 2014: 2192–2196. http://ieeexplore.ieee.org/document/7013866/
|
| [10] |
李春文, 冯元琨. 多变量非线性控制的逆系统方法[M]. 北京: 清华大学出版社, 1991: 6–7.
|
| [11] |
FANG J, REN Y. Decoupling control of magnetically suspended rotor system in control moment gyros based on an inverse system method[J]. IEEE/ASME Transactions on Mechatronics, 2012, 17(6): 1133-1144. DOI:10.1109/TMECH.2011.2159618 |
| [12] |
HUTTERER M, HOFER M, SCHRODL M. Decoupled control of an active magnetic bearing system for a high gyroscopic rotor [C] // IEEE International Conference on Mechatronics. Nagoya: IEEE, 2015: 210-215. http://ieeexplore.ieee.org/articleDetails.jsp?arnumber=7083976
|
| [13] |
LI Y, ZHU H. Decoupling control of three degrees of freedom hybrid magnetic bearing based on LS-SVM[J]. Applied Mechanics & Materials, 2014, 29: 534-538. |
| [14] |
富月, 李婧怡. 线性多变量系统有限时间最优解耦控制[J]. 控制与决策, 2016, 12(31): 2271-2273. FU Yue, LI Jing-yi. Finite-time optimal decoupling control for linear multi-variable systems[J]. Control and Decision, 2016, 12(31): 2271-2273. |
| [15] |
ZHENG S, HAN B, FENG R, et al. Vibration suppression control for AMB-supported motor driveline system using synchronous rotating frame transformation[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5700-5708. DOI:10.1109/TIE.2015.2407857 |
| [16] |
JIANG K, ZHU C, CHEN L. Imbalance compensation by recursive seeking imbalance mass position in active magnetic bearing-rotor system[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5655-5664. DOI:10.1109/TIE.2015.2405893 |
| [17] |
FANG J, XU X, XIE J. Active vibration control of rotor imbalance in active magnetic bearing systems[J]. Journal of Vibration and Control, 2013, 21(4): 684-700. |
| [18] |
韩京清. 自抗扰控制技术[M]. 北京: 国防工业出版社, 2008: 69–71 http://www.cnki.com.cn/Article/CJFDTOTAL-QYKX200701004.htm
|
| [19] |
戴先中. 多变量非线性系统的神经网络逆控制方法[M]. 北京: 科学出版社, 2005: 94. https://book.douban.com/subject/1750849/
|



