正交频分复用技术(orthogonal frequency division multiplexing, OFDM)[1-2]如今广泛应用于移动通信系统中,具备高传输速率和抗频选衰落的优点. 然而随着近年来无线通信应用场景的愈发复杂,快时变信道引起更多关注,其快时变特性对OFDM系统的信道估计提出了新的挑战. 压缩感知(compressed sensing,CS)[3]理论是一种可行的方法,通过更少的测量值还原整个稀疏信号,主要应用于信号处理领域. 在信道估计方面,文献[4]指出常见的无线多径信道普遍具有稀疏特性,在此基础上,研究者们结合压缩感知算法进行信道估计,提出了压缩信道感知(compressed channel sensing)估计方法[4-5]. Taubock等[6-7]详细论证了双选择信道的稀疏性特性,并给出了通用的信道系数基扩展模型,通过组稀疏特性进行信道估计. 利用信道内在的组稀疏特性,用更少的导频符号获得更精确可靠的估计结果,提高了系统的带宽利用率,适用于快时变信道估计.
在导频放置方面,稀疏信道估计的导频选取是通过构建相应的感知矩阵,使其更好地满足限制等距特性(restricted isometry property,RIP)以提高CSI恢复概率. 文献[8]表明,互相关性越小,感知矩阵越满足RIP. 理论上应穷尽搜索所有可能的导频模式以找出最佳感知矩阵,然而限于实际OFDM系统中的载波和导频数量,穷尽搜索在计算量上是不现实的,因此需要尽可能准确、快速的次优导频搜索方案. He等[9]提出了基于随机搜索的导频模式优化方案,Qi等[10-13]提出了离散随机近似方法和交叉熵优化(cross-entropy optimization,CEO)方法,然而上述方法无法保证收敛时间,文献[14-15]基于进化算法中的遗传算法(genetic algorithm,GA)搜索导频,缺点是可能陷入局部最小值. 因此,可采用分布估计算法(estimation of distribution algorithm,EDA)[16] 优化导频模式,通过从概率分布中抽取个体,不会陷入局部最小值,效果优于GA.
本文首先对OFDM系统信道进行建模,研究信道的组稀疏特性. 考虑到组稀疏特性和导频位置对压缩信道估计性能的重要作用,利用组稀疏更小的搜索空间,结合分布估计算法的高鲁棒性,对传统的导频放置模式进行改进,针对组稀疏算法优化导频位置,提高其重构水平. 最后,通过仿真证明该算法有更好的性能.
1 系统模型在高速应用场景中,随着多普勒频移的变大,时间选择性衰落也变得更为严重,此时,需将信道建模成双选择性衰落信道模型:
| $h(t,\tau ) = \sum\limits_{p = 1}^{P(t)}\, {\left[ {{\eta _p}(t)\delta (\tau - {\tau _p}(t))\exp \left( {{\rm j}2{\rm{\pi }}{v_p}(t)t} \right)} \right]} .$ | (1) |
式中:δ为冲激函数,
收发端的函数关系式可以写成:
| $r(t) = \int_{ - \infty }^\infty {h(t,\tau )s(t - \tau ){\rm{d}}\tau } + z\left( t \right).$ | (2) |
式中:
| $r[n] = \sum\limits_{m = 0}^{M - 1} {\Big\{ {h[n,m]s[n - m]} \Big\}} + z[n].$ | (3) |
其中,
本文采用的是单天线带有循环前缀(cyclic prefix, CP)的OFDM系统,发送信号
| $\begin{array}{l}\!\!s[n]\!\! =\! \!\displaystyle\frac{1}{{\sqrt K }}\displaystyle\sum\limits_{l = 0}^{L - 1}{\left\{ {\displaystyle\sum\limits_{k = 0}^{k - 1}{\left[ {{a_{l,k}}\exp \left( {{\rm j}2{\rm{\pi }}kn/K} \right)} \right]g[n - lN]} } \right\}} .\end{array}$ | (4) |
式中:
| $\begin{array}{l}{r_{l,k}} = \displaystyle\frac{1}{{\sqrt k }}\displaystyle\sum\limits_{n = - \infty }^\infty {\Big\{ {r[n]\exp \left( { - {\rm j}2{\rm{\pi }}k(n - lN)/K} \right)\gamma [n - lN]} \Big\}} .\end{array}$ | (5) |
其中,
发送端数据符号
| ${r_{l,k}} = {H_{l,k}}\,{a_{l,k}} + {z_{l,k}}.$ | (6) |
式中:
| ${H_{l,k}} = \sum\limits_{m = 0}^{K - 1}\; {\sum\limits_{i = - L/2}^{L/2 - 1} \,{\left[ {{F_{m,i}}\exp \left( { - {\rm j}2\pi \left(\frac{{km}}{K} - \frac{{li}}{L}\right)} \right)} \right]} } ,$ | (7) |
| ${F_{m,i}} = \sum\limits_{q = 0}^{N - 1}\, {\left\{ {{S_h}[m,i + qL]A_{\gamma ,g}^*\left(m,\frac{{i + qL}}{{{N_0}}}\right)} \right\}} .$ | (8) |
式中:
在许多实际情况中,稀疏信号的非零分量趋向于出现在簇中. 为了利用这种结构提高重建质量,引入组稀疏压缩感知(group sparse compressed sensing, GSCS)的方法. GSCS与块稀疏CS和基于模型的CS密切相关.
令
| $ \cup _{b = 0}^{B - 1}{I_b} = \{ 0, 1,\cdots ,N - 1\},$ |
| $ \displaystyle\sum\nolimits_{b = 0}^{B - 1} {|{I_b}|} = N.$ |
例如

|
图 1 组稀疏压缩感知(GSCS)信号模型 Fig. 1 Signal model for group sparse compressed sensing (GSCS) method |
与CS理论相似,GSCS方法从下式中重构信号
| ${{y}} = {{\varPhi x}} + {{z}}.$ | (9) |
式中:
| $\mathop {\arg \min }\limits_{{x}} {\left\| {{x}} \right\|_{2|\cal{J}}},\;{\rm s}.{\rm t}.\,{\left\| {{{y}} - {{\varPhi x}}} \right\|_2} \leqslant \varepsilon. $ |
根据第2章的信道模型,为了求得完整信道响应
| ${\cal{G}}: = \left[ (\lambda \Delta L,\,\kappa \Delta K)\,|\,\lambda = 0,1, \cdots ,J - 1;\kappa = 0,1, \cdots, D - 1\right] ,$ |
满足
| $\begin{split}&{H_{\lambda \Delta L,\kappa \Delta K}} =\\ & \displaystyle\sum\limits_{m = 0}^{K - 1} \;{\displaystyle\sum\limits_{i = - L/2}^{L/2 - 1} \,{\left[ {{F_{m,i}}\exp \,\left( { - {\rm j}2\pi \left(\displaystyle\frac{{\kappa \Delta Km}}{D} - \displaystyle\frac{{\lambda \Delta Li}}{L}\right)} \right)} \right]} } = \\ & \displaystyle\sum\limits_{m = 0}^{D - 1} \;{\displaystyle\sum\limits_{i = - J/2}^{J/2 - 1}\, {\left[ {{F_{m,i}}\exp \,\left( { - {\rm j}2\pi \left(\displaystyle\frac{{\kappa m}}{D} - \displaystyle\frac{{\lambda i}}{J}\right)} \right)} \right]} } .\end{split}$ | (12) |
式中:
| ${\cal{B}_b} = \left\{ {{k_b}\Delta m, \cdots ,\left( {{k_b} + 1} \right)\Delta m} \right\} \times \left\{ {{l_b}\Delta i, \cdots ,\left( {{l_b} + 1} \right)\Delta i} \right\}.$ |
其中,
| $\begin{split}&{k_b} \in \{ 0, \cdots ,(K/\Delta m) - 1\} ,\\ &{l_b} \in \{ - L/(2\Delta i), \cdots ,(({N_0} - L/2)/\Delta i) - 1\}. \end{split}$ |
再定义集合
| $\cal{J}{\rm{ = }}\left\{ {{I_b}} \right\}_{b = 0}^{{B_D}{B_J} - 1},$ |
有
对式(10)进行2-D基扩展:
| ${H_{\lambda \Delta L,\kappa \Delta K}} = \sum\limits_{m = 0}^{D - 1} \;{\sum\limits_{i = - J/2}^{J/2 - 1} \left({{G_{m,i}}\,{u_{m,i}}[\lambda ,\kappa ]} \right)} .$ | (13) |
式中:
| ${u_{m,i}}\left[ {\lambda ,\kappa } \right] = \left( {1/JD} \right)\exp \left( { - {\rm j}2{\rm{\pi }}\left( {\displaystyle\frac{{\kappa m}}{D} - \displaystyle\frac{{ i}}{J}} \right)} \right)$ |
是一个二维正交基,
| $\begin{aligned}&{\left[ {{{{h}}_\Delta }} \right]_{\kappa J + \lambda ,(i + J/2)D + m}} = {H_{\lambda \Delta L,\kappa \Delta K}},\\ & {\left[ {{g}} \right]_{(i + J/2)D + m}} = {G_{m,i}},\\ & {\left[ {{{{u}}_{m,i}}} \right]_{\kappa J + \lambda }} = {u_{m,i}},\end{aligned}$ |
其中,
| ${{{h}}_\Delta } = \sum\limits_{m = 0}^{D - 1} \;{\sum\limits_{i = - J/2}^{J/2 - 1} {\left( {{G_{m,i}}{{{u}}_{m,i}}} \right) = } } {{Ug}}.$ | (18) |
其中
至此得到信道系数的稀疏表达式,由压缩感知理论可知,可以通过较少的观测值来重构原信号,但是对需要的最少样本数有要求,即对导频数量有最低要求,假设导频的位置已确定为
| ${{{h}}_{(p)}} = {{\varPhi x}} + {{{z}}_{(p)}}.$ | (19) |
式中:
基于组稀疏压缩感知的信道估计具体步骤如下:
1)通过
2)利用现有的GSCS算法重构出
3)通过向量g的估计值和矩阵
适用于GSCS的重构算法G-OMP的算法流程如下:
输入:
初始化:
当
重复以下操作
1.
2.
3.
4.
5.
6.
结束循环
输出:
由上文可知,基于GSCS方法进行信道估计需要先求得导频位置处
| ${{f}} = {\left[ {f\left( 0 \right), f(1) ,f\left( {N - 1} \right)} \right]^{\rm T}}$ |
为一个个体,
导频放置问题即为求解优化问题:
| ${Q_1}:{\rm{ }}\mathop {\rm{min}}\limits_{{{f}} \in \cal{S}}\, \mu \left( {{{A}}\left( {{f}} \right)} \right),\;{\rm{ s}}{\rm{.t}}{\rm{. }}\sum\limits_{n = 0}^{N - 1} \,\,{f\left( n \right)} = P.$ | (22) |
式中:
| $\mu \left( {{A}} \right) = \mathop {\rm{max}}\limits_{d \in \cal{D}} \frac{1}{P}\left| {\sum\limits_{i = 1}^P\, {{\omega ^{{k_i}d}}} } \right|.$ | (23) |
其中,
适用于组稀疏压缩感知EDA导频放置模式算法流程如下:
初始化:i=0,生成包含M个随机个体的总体
重复以下操作
1. 对当前总体
2. 按1中排序选取总体中前T个个体
按如下方法得到
对
| ${N_0} = \arg \mathop {\rm{max}}\limits_{{{n}} = 0,1, \cdots ,N - 1} \left\{ {{g_t}\left( n \right),{g_{t,{\rm{flip}}}}\left( n \right)} \right\}.$ |
将
3. 得到新总体
4. 计算导频概率向量
| ${{ p}^{\left( i \right)}}\left( n \right) = \frac{1}{T}\sum\limits_{t = 1}^T\, {{{{\tilde f}}^{\left( i \right)}}\left( n \right)}; \; \; {n = 0,1, \cdots ,N - 1} .$ |
得到概率分布
5. 保留
当概率向量
结束循环
返回:导频索引集合
本文通过Matlab对算法进行仿真,基于500次蒙特卡洛实验,采用4-QAM调制,设置子载波数为512,符号个数为32,CP长度为128,载波频率5 GHz,导频个数为128.
文中双选信道通过IlmProp工具产生. 收发端距离为1 500 m,其中包含10个簇,每个簇又包含了10个散射体. 其中3个簇围绕在接收端,这些簇的直径在5~30 m,每个簇的增益服从高斯分布,并且具有随机的速度和随机的加速度,速度和加速度对应的上限分别为50和7 m/s.
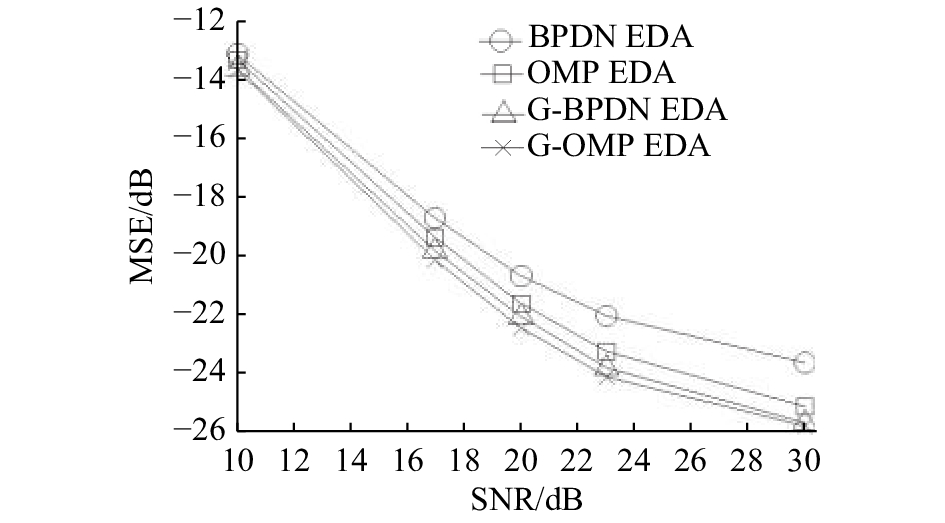
本文采用G-BPDN和G-OMP算法重构稀疏信号,采用不同的导频放置模式进行对比,组大小取(4, 1),仿真结果如图2~5所示,其中MSE为均方误差,SNR为信噪比.
|
图 2 组稀疏与传统稀疏信道估计方法对比(采用G-OMP和G-BPDN重构算法) Fig. 2 Compressive channel estimation utilizing group sparsity compared to conventional compressive channel estimation (using G-OMP and G-BPDN reconstruction technique) |
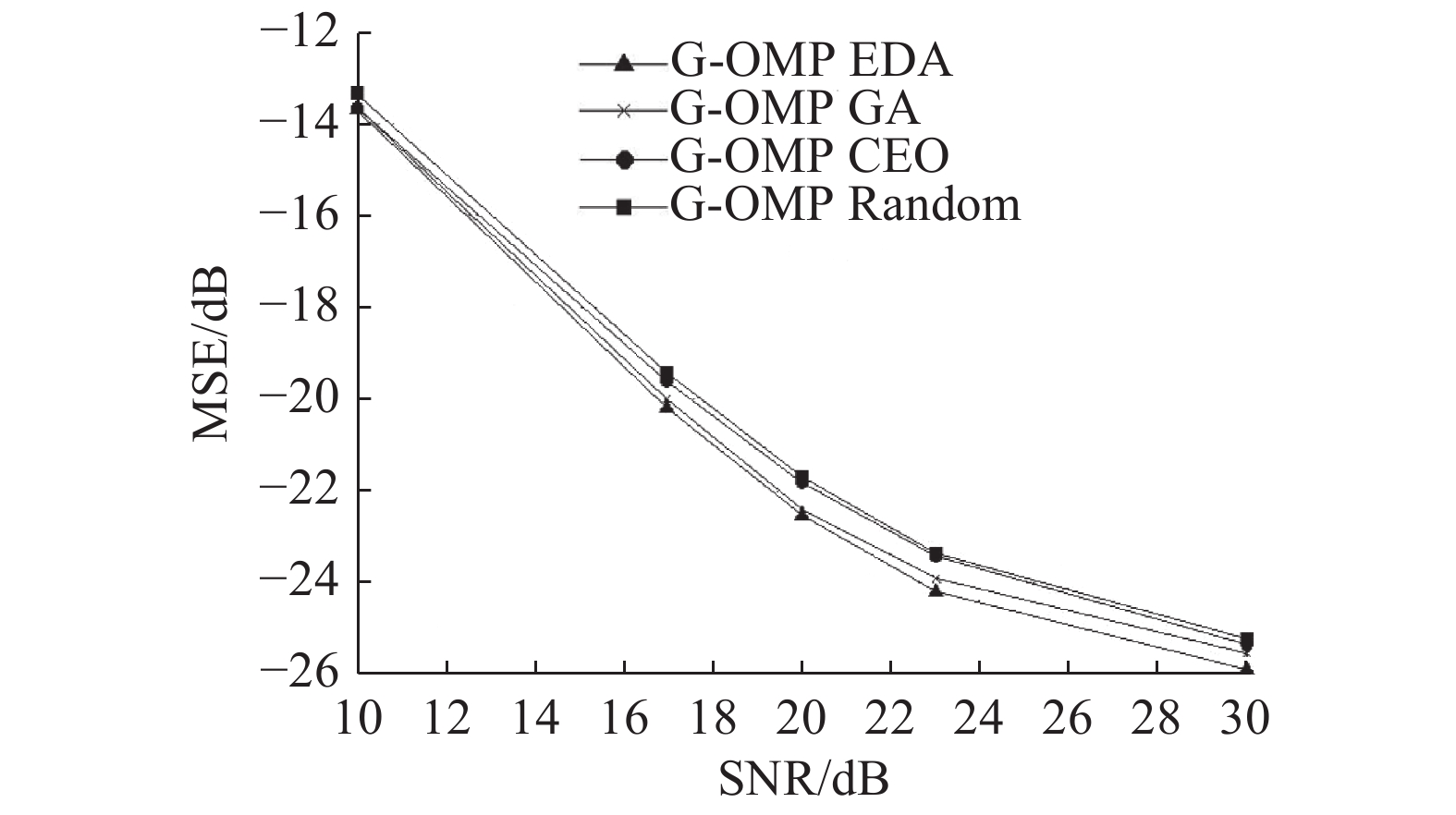
|
图 3 基于不同优化方案的组稀疏信道估计方法对比(均采用G-OMP重构算法) Fig. 3 Comparison of group sparsity channel estimation based on different optimization schemes (using G-OMP reconstruction technique) |
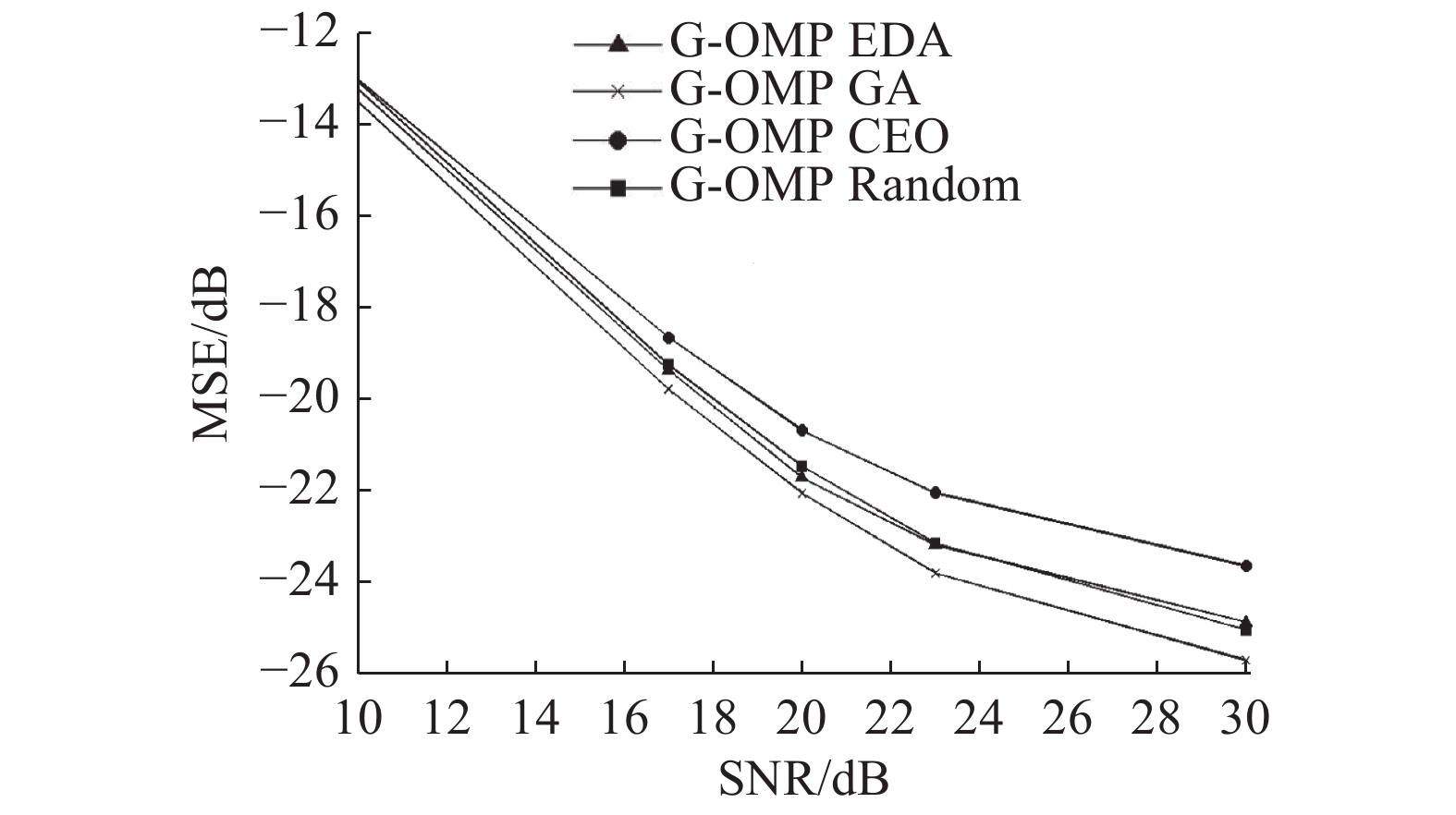
|
图 4 基于不同优化方案的组稀疏信道估计方法对比(均采用G-BPDN重构算法) Fig. 4 Comparison of group sparsity channel estimation based on different optimization schemes (using G-BPDN reconstruction technique) |
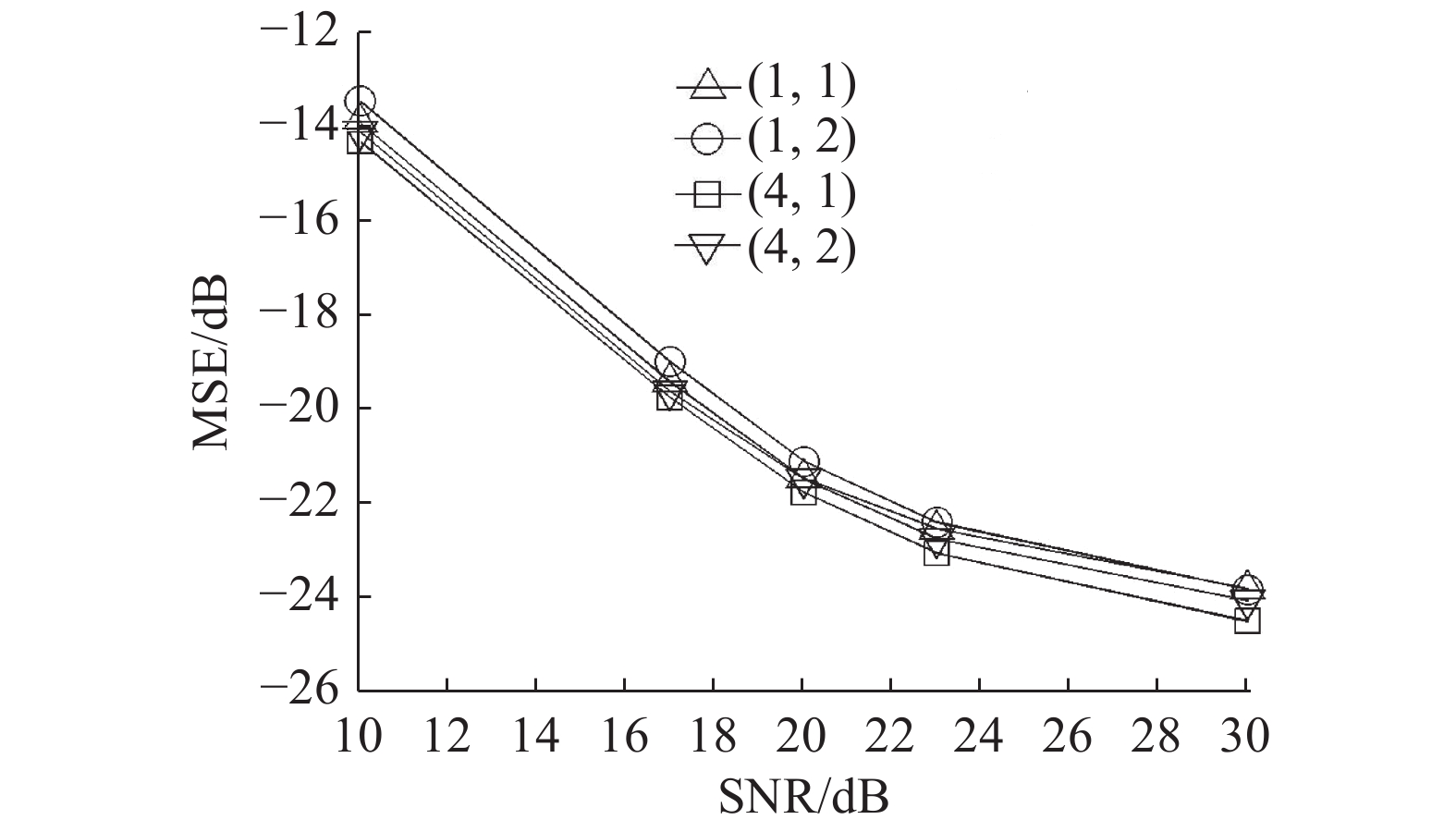
|
图 5 采用不同块大小的组稀疏信道估计性能对比 Fig. 5 Performance of compressive channel estimator utilizing group sparsity for various block sizes |
由仿真结果可看出,采用组稀疏压缩感知的信道估计方法性能明显优于同种重构算法的传统压缩感知方法. 对导频进行优化后的估计方案略优于传统方法,采用G-BPDN重构算法时,高信噪比条件下G-BPDN EDA改进方案具有较明显的优势,CEO和GA方法效果相仿,采用G-OMP时则没有较明显的改善,总体性能仍略有提升,G-BPDN EDA具有最优性能. 而在组稀疏估计块的大小选择方面,仿真结果表明,在一定范围内,频域分组选取较大时有较好的效果.
下面对GSCS算法的复杂度进行分析.
1)组稀疏算法复杂度取决于相应的CS算法,GSCS算法复杂度记为
2)计算式(11)、(12)中
3)式(7)做快速傅里叶变换(fast Fourier transformation, FFT),复杂度为
4)总复杂度为
易得,第三项复杂度远低于第二项,第一项无法给出复杂度的明确界限,根据不同CS算法具体分析. G-BPDN的具体值尚无法确定,文献[18]论述了BPDN算法有多种实现算法,且各有不同的计算复杂度. G-OMP复杂度分别为
| $O({\rm{GSCS}}){\rm{ = }}O(M{(n{'_{{\rm{G{\text{-}}OMP}}}})^2} + {n_{{\rm{G{\text{-}}OMP}}}}{{\varPhi }}). $ |
其中,
综上所述,一般情况下
本文基于压缩感知理论,研究了OFDM系统中的双选衰落信道估计方法,利用信号的组稀疏性提升重建效果. 为了获取准确的估计信息,压缩感知理论要求观测矩阵与稀疏基具有不相关性. 基于这一原则,本文结合分布估计算法对导频的优化,改进了组稀疏压缩感知的导频放置模式. 本文在设计导频时,建立了一个优化的概率分布模型,由该模型抽样得到新的导频图案个体,从而迭代收敛到优化的导频模式. 该方法得到的观测矩阵的互相关性更小,能更好地满足约束等距性,因此所得优化导频模式在组稀疏信道估计方面表现更好,且由于概率分布模型的特性,具有更好的鲁棒性. 仿真结果同样表明,该导频优化方案在均方误差性能方面优于传统方法,采用G-BPDN重构算法时,改进方案具有较明显的优势;采用G-OMP时虽没有较明显的改善,总体性能仍略有提升.
| [1] |
ENGELS M. Wireless OFDM systems: How to make them work? [M]. Norwell: Springer Science & Business Media, 2002: 33–36.
|
| [2] |
BERTHOLD U, JONDRAL F K, BRANDES S, et al. OFDM-based overlay systems: a promising approach for enhancing spectral efficiency [Topics in radio communications][J]. IEEE Communications Magazine, 2007, 45(12): 52-58. DOI:10.1109/MCOM.2007.4395365 |
| [3] |
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [4] |
BAJWA W U, HAUPT J, RAZ G, et al. Compressed channel sensing [C] // 2008 42nd Annual Conference on Information Sciences and Systems. New Jersey: IEEE, 2008: 5–10.
|
| [5] |
BAJWA W U, HAUPT J, SAYEED A M, et al. Compressed channel sensing: a new approach to estimating sparse multipath channels[J]. Proceedings of the IEEE, 2010, 98(6): 1058-1076. DOI:10.1109/JPROC.2010.2042415 |
| [6] |
TAUBOCK G, HLAWATSCH F, EIWEN D, et al. Compressive estimation of doubly selective channels in multicarrier systems: leakage effects and sparsity-enhancing processing[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 255-271. DOI:10.1109/JSTSP.2010.2042410 |
| [7] |
EIWEN D, TAUBÖCK G, HLAWATSCH F, et al. Group sparsity methods for compressive channel estimation in doubly dispersive multicarrier systems [C] // 2010 IEEE 11th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC). Marrakech: IEEE, 2010: 1–5.
|
| [8] |
TROPP J A. Greed is good: algorithmic results for sparse approximation[J]. IEEE Transactions on Information Theory, 2004, 50(10): 2231-2242. DOI:10.1109/TIT.2004.834793 |
| [9] |
HE X, SONG R. Pilot pattern optimization for compressed sensing based sparse channel estimation in OFDM systems [C] // 2010 International Conference on Wireless Communications & Signal Processing (WCSP). Suzhou: IEEE, 2010: 1–5.
|
| [10] |
QI C, WU L. Optimized pilot placement for sparse channel estimation in OFDM systems[J]. IEEE Signal Processing Letters, 2011, 18(12): 749-752. DOI:10.1109/LSP.2011.2170834 |
| [11] |
QI C, WU L. A study of deterministic pilot allocation for sparse channel estimation in OFDM systems[J]. IEEE Communications Letters, 2012, 16(5): 742-744. DOI:10.1109/LCOMM.2012.032612.112553 |
| [12] |
QI C, YUE G, WU L, et al. Pilot design schemes for sparse channel estimation in OFDM systems[J]. IEEE Transactions on Vehicular Technology, 2015, 64(4): 1493-1505. DOI:10.1109/TVT.2014.2331085 |
| [13] |
QI C, YUE G, WU L, et al. Pilot design for sparse channel estimation in OFDM-based cognitive radio systems[J]. IEEE Transactions on Vehicular Technology, 2014, 63(2): 982-987. DOI:10.1109/TVT.2013.2280655 |
| [14] |
NAJJAR L. Pilot allocation by Genetic Algorithms for sparse channel estimation in OFDM systems [C] // 21st European Signal Processing Conference (EUSIPCO 2013). Marrakech: IEEE, 2013: 1–5.
|
| [15] |
HE X, SONG R, ZHU W P. Pilot allocation for sparse channel estimation in MIMO-OFDM systems[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2013, 60(9): 612-616. DOI:10.1109/TCSII.2013.2268433 |
| [16] |
LARRAÑAGA P., LOZANO J. A. Estimation of distribution algorithms: a new tool for evolutionary computation [M]. New York: Springer Science & Business Media, 2001: 58–59
|
| [17] |
FLANDRIN P. Time-frequency/time-scale analysis [M]. Orlando: Academic Press, 1998: 237–240.
|
| [18] |
FORNASIER M. Theoretical foundations and numerical methods for sparse recovery [M]. New York: Walter de Gruyter, 2010: 108–111.
|



