工业控制系统在许多领域(如:电力、石油、化工、交通)的关键基础设施中广泛使用,其安全性对工业生产运行和国家经济安全意义重大. 近年来随着互联网技术的发展与成熟,控制系统与信息系统的集成度不断提高,导致广泛存在于IT系统的信息安全问题也出现在工业控制系统. 工控系统与传统IT系统的最大区别在于工控系统与物理世界存在实时交互关系[1],针对工控系统的攻击,最终将会对物理世界产生影响,如造成设备故障,生产过程中断,人员伤亡等严重后果. 工控系统若遭受攻击,可能会对国家造成重大的经济损失与社会影响. 研究工控系统攻击检测算法是保护工控系统安全的一种必要而且有效的手段.
工控系统中主要研究的攻击有拒绝服务攻击 (denial of service, DoS)攻击和欺骗攻击两大类,DoS攻击的目的是破坏系统网络的可用性;欺骗攻击通过篡改网络中传输的数据,从而破坏系统服务的完整性. 目前研究的欺骗攻击[2]主要有3种,分别是偏差攻击、浪涌攻击、几何攻击,这3种攻击都是在攻击时间段内向控制系统过程变量注入不同幅值的偏差. 无论DoS攻击还是欺骗攻击,都是通过诱导系统进入异常状态,从而实现攻击目的.
针对DoS攻击和欺骗攻击检测算法的研究目前已经比较成熟,Barbosa等[3]对SCADA(supervisory control and data acquisition)流量的特性进行研究分析,利用快速傅里叶变换(fast Fourier transformation, FFT)和滑动窗口形成可视化的检测模型,成功检测到网络中的DoS攻击. Hong等[4]提出了一种基于主机和网络的集成式异常检测系统,在变电站WSU(Washington State University)网络安全试验台上的测试结果表明,提出的异常检测算法可以检测出重放攻击、DoS攻击等. Kwon等[5]提出了基于行为的IDS(intrusion detection systems),通过对智能变电站网络流量特性进行统计分析,可以检测出DoS等多种攻击. DoS攻击可改变工控网络流量,破坏系统的可用性,以上检测算法均通过统计网络流量特征,发现流量异常. 张云贵等[6]基于高炉拱顶温度控制系统的对象模型,采用序贯检测方法在较短的时间内检测到偏差攻击. Amin等[7]利用水利灌溉SCADA系统的故障诊断系统进行欺骗攻击检测. Mo等[8-10]采用卡尔曼滤波器进行状态估计,并利用残差检测控制系统中的隐身欺骗攻击. 张环宇等[11]通过建立工控系统安全模型,设计了基于残差滤波的预测攻击集的集中式攻击识别监测器,仿真结果表明:该方法可以在一定程度上增强系统的鲁棒性. 甄玉磊等[12]针对网络控制系统中数据包丢失可能干扰重放攻击检测器问题,基于卡尔曼滤波器,提出了一种使用状态递推器的重放攻击检测方法. 对于欺骗攻击,以上检测算法主要是基于状态估计的方法,利用系统状态的残差进行攻击检测.
由于工控网络具有确定、静态和数据流量可以预见等特性[13],传统的入侵检测算法对DoS攻击具有良好的检测效果. 欺骗攻击的效果与攻击幅值及时间有关,在对控制系统造成破坏之前,攻击很可能已被检测出来. 基于上述情况,DoS攻击和欺骗攻击的目的很难实现,于是理性攻击者会采取更隐蔽的正弦欺骗攻击手段,攻击者对相关过程变量注入一定幅值和频率的正弦信号,通过控制系统状态始终在正常范围内小幅波动,加快现场控制设备的磨损速度,最终破坏控制系统. 正弦攻击同时考虑了幅值和频率特性,不会造成系统运行状态异常,攻击能力和隐蔽性比DoS攻击等更强. 现有的DoS攻击检测算法仅统计网络流量特性,没有考虑攻击变量幅值及频率的变化;欺骗攻击检测算法大多是通过对系统状态残差的估计来检测异常,只考虑了攻击的幅值特性. 另外这类基于状态估计的方法都依赖较为准确的物理模型,实际上对动态系统很难建立精确的模型,使用这些算法检测正弦攻击的效果并不理想. 基于数据驱动的检测方法利用数据中包含的信息检测控制系统是否存在异常,不依赖于物理模型,简单而且有效,因此使用数据驱动方法检测正弦攻击是一种可行的手段.
多尺度主成分分析(multi-scale principal component analysis,MSPCA)是基于数据驱动的一类异常检测方法,被广泛的用于多变量过程监视. 该方法将主成分分析和小波分析的优点相互结合[14],利用主成分分析去除线性变量相关性,利用小波分析提取变量局部特征和近似分解变量自相关性的能力. MSPCA将PCA的单尺度建模推广到多尺度建模,既能捕捉过程变量大范围的变化,也能捕捉过程变量的细小波动,在过程异常监视中具有良好的应用前景.
针对工控系统中存在的正弦攻击,本文首先以控制系统的典型回路为研究对象,建立其数学模型;利用傅里叶变换、小波分析从频域和时间-尺度域对正弦攻击的攻击能力和隐蔽性进行分析,并与偏差攻击等欺骗攻击进行比较,验证常规主成分分析无法有效检测出该攻击. 接着将多尺度主成分分析用于正弦攻击检测,并提出其在线检测算法;在Tennessee Eastman (TE)过程上进行仿真研究,分析正弦攻击对被控过程产生的影响,然后使用本文提出的攻击检测算法检测正弦攻击,与PCA方法相比,显示出更强的攻击检测能力.
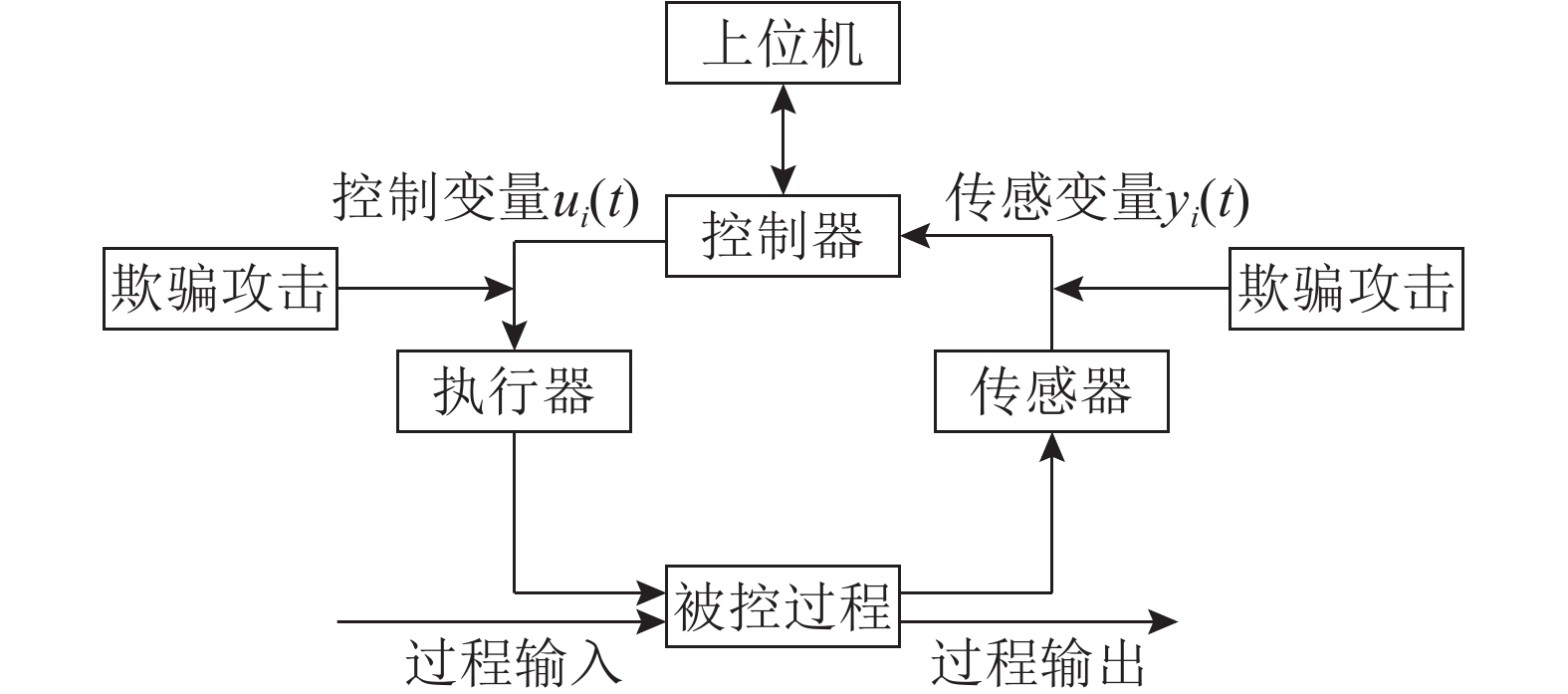
1 正弦欺骗攻击建模工业过程控制系统包括传感器、执行器、控制器和物理系统4个部分. 传感器检测物理系统并发送测量信息给控制器,控制器发送控制信号给执行器,执行器在接收到控制信号后,执行一个动作(如:打开阀门),形成闭环控制,如图1所示.
|
图 1 工业控制系统控制回路结构图 Fig. 1 Structure chart of control loop in industrial control system |
在控制回路中,攻击者通过对传感器测量值
工控系统中存在的欺骗攻击[2]主要有偏差攻击、浪涌攻击、几何攻击,这3种攻击都是在攻击时间段内向
定义1 攻击时间段(
定义2 传感变量偏差攻击模型定义如下:
| ${\hat y_i}(t) = \left\{ \begin{array}{l}{y_i}(t), \;\; t \notin {T_{\rm{a}}};\\{y_i}(t) + {E_i}, \;\; t \in {T_{\rm{a}}}.\end{array} \right.$ | (1) |
式中:
攻击者在攻击时间段内对每个时刻的数据添加一个非零常数
偏差攻击通过改变过程变量值,使执行器开度不在正常的工作范围,最终导致控制系统状态异常,但不会在攻击过程中对执行器等现场控制设备直接造成损害. 基于以上分析,由于常规欺骗攻击能力有限以及防御者的检测手段较成熟,欺骗攻击很可能无法实现攻击目的. 此外,“震网”病毒通过改变离心机转子的速率[15],让转速忽高忽低,通过长时间的攻击,对离心机造成物理损坏[16]. 因此,在图1的典型控制回路中,理性攻击者会根据先验系统知识,对欺骗攻击进行变种,实施更隐蔽的正弦攻击. 在正弦攻击过程中,攻击者向相关过程变量注入一定幅值和频率的正弦信号,控制过程变量始终在工作范围小幅波动,系统不会偏离正常工作状态. 但是攻击信号的频率会致使与变量相关的执行器开度以一定幅值正弦震荡,加快执行器中调节阀等元件的磨损,通过长时间的攻击,直接损坏执行器等现场控制设备,造成系统停车等严重后果. 与偏差攻击等不同,正弦攻击通过其频率特性损坏相关传感执行设备,最终导致控制系统无法正常运行;由于偏差攻击检测算法只考虑了幅值特性,而正弦攻击综合考虑幅值和频率特性,这些算法不能有效地检测出正弦攻击,正弦攻击的隐蔽性更强.
正弦攻击建模过程具体如下,这里仅以传感变量建模为例. 对传感变量和控制变量进行正弦攻击,攻击效果类似,控制器如果是带有抑制扰动的控制律,则可以通过增大攻击幅值等措施,来实现相同的攻击目的. 本文的目的在于提出这一类攻击方法,为了叙述简便,且便于读者理解,只分析传感变量.
定义3 传感变量正弦攻击模型定义如下:
| ${\hat y_i}(t) = \left\{ \begin{array}{l}{y_i}(t),\;\;t \notin {T_{\rm{a}}};\\{y_i}(t) + {E_i}\sin \,{\omega _i}t,\;\;t \in {T_{\rm{a}}}.\end{array} \right.$ | (2) |
式中:
当幅值
由傅里叶变换可知,对于任何非周期信号,可以将其用一段连续频谱的不同频率的正弦信号进行叠加. 偏差攻击实际上是阶跃信号,通过傅里叶变换可以分解为多个不同频率及幅值的正弦信号,信号的有效带宽在低频部分,不会对原始信号的频带产生影响,是幅值类攻击. 其能量分布在所有频率中,单个频率分量的攻击能力有限. 与偏差攻击不同,正弦攻击与幅值和频率2个变量有关,是频率攻击. 由于其频谱单一,攻击信号的能量集中在单个频率分量上,攻击能力强,能产生更大的威胁;此外,若攻击信号频率很高,会直接影响过程变量的频带. 因此正弦攻击比偏差攻击的攻击能力更强,可以严重损坏现场控制设备.
2 基于多尺度主成分分析(MSPCA)的正弦欺骗攻击检测 2.1 正弦攻击小波变换及分析小波分析是一种信号的时间-尺度分析方法,在时频两域都具有表征信号局部特征的能力. 时间窗和频率窗都可改变,在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率,实际上就是一种窗口大小可调的傅里叶变换方法.
设
| ${W_f}{\rm{(}}a,b{\rm{) = }}\left\langle {f(t),\,{\psi _{a,\,b}}(t)} \right\rangle {\rm{ = }}\displaystyle\frac{1}{{\sqrt {|a|} }}{\rm{ }}\int\limits_R {f(t)\,\overline {\psi \left(\displaystyle\frac{{t - b}}{a}\right)} }\, {\rm{ d}}t.$ | (3) |
式中:
由小波变换的定义可知,原始传感变量
| ${W_y}{\rm{(}}a,b{\rm{) = }}\displaystyle\frac{1}{{\sqrt {|a|} }}{\rm{ }}\int\limits_R {{y_i}(t)\,\overline {\psi \left(\displaystyle\frac{{t - b}}{a}\right)} } {\rm{ }}\,{\rm d}t.$ | (4) |
正弦攻击信号
| ${W_{\hat y}}{\rm{(}}a,b{\rm{) = }}{W_y}{\rm{(}}a,b{\rm{) + }}\displaystyle\frac{1}{{\sqrt {|a|} }}{\rm{ }}\int\limits_R {{E_i}\sin \left({\omega _i}t\right)\overline {\psi \left(\displaystyle\frac{{t - b}}{a}\right)} } {\rm{ }}\,{\rm d}t.$ | (5) |
对比
| ${W_y}{\rm{(}}a,b{\rm{)}} \approx {\rm{0}},\displaystyle\frac{1}{{\sqrt {|a|} }}{\rm{ }}\int\limits_R {{E_i}\sin \left({\omega _i}t\right)\overline {\psi \left(\displaystyle\frac{{t - b}}{a}\right)} } {\rm{ }}\,{\rm d}t > > 0,$ |
则
PCA是单尺度建模方法,只适用于分析异常存在于某一固定尺度上的数据. 由于正弦攻击信号
多尺度主成分分析是由Bakshi于1998年提出的[17],将主成分分析去除变量间相关性、小波分析去除变量的自相关性的优势相结合,在各尺度上计算小波系数的PCA,既减少了误差,消除了数据间的相关性,又顾及到数据的多尺度特性.
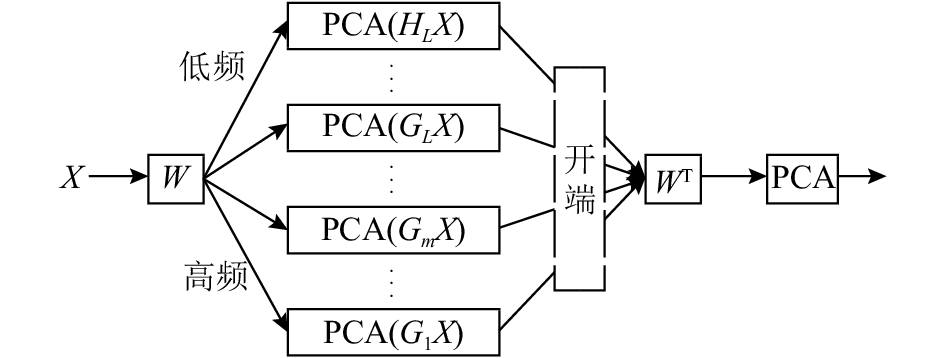
MSPCA从多尺度的角度出发,首先利用小波多尺度分解对采样数据 X 的每个变量进行
|
图 2 多尺度主元分析(MSPCA)实施过程 Fig. 2 Methodology for multi-scale principal component analysis (MSPCA) |
多尺度主成分模型建立后,对于新的待检测数据,要检测数据中是否存在正弦攻击,可以通过建立统计指标进行假设检验,判断过程数据是否背离了主成分模型. 通常的方法是在主成分子空间建立
定义4
| ${T^2}{\rm{ = }}\sum\limits_{a = 1}^k \,{\frac{{t_a^2}}{{{\lambda _a}}}} .$ | (6) |
式中:
正常工控下,
| ${T^2} < T_\alpha ^2.$ | (7) |
| $T_\alpha ^2\,{\rm{ = }}\,\frac{{k(n - 1)}}{{n - k}}\,{F_{k,\,n - k,\,a}}.$ | (8) |
其中,
定义5
| ${\rm{SPE = }}\sum\limits_{j = 1}^m \,{{{({{{x}}_j} - {{\hat {{x}}}_j})}^2}} .$ | (9) |
式中:
正常工控下,SPE应满足下式:
| ${\rm{SPE}} < {\rm{SP}}{{\rm{E}}_{\rm{\alpha }}}.$ | (10) |
| $\begin{aligned}&{\rm{SP}}{{\rm{E}}_{\rm{\alpha }}}{\rm{ = }}{\theta _1}{\left( {\displaystyle\frac{{{C_\alpha }\sqrt {2{\theta _2}h_0^2} }}{{{\theta _1}}} + 1 + \frac{{{\theta _2}{h_0}({h_0} - 1)}}{{\theta _1^2}}} \right)^{{1}/{{{h_0}}}}};\\&{\theta _i} = \displaystyle\sum\limits_{j = k + 1}^m {\lambda _j^i} {\rm{ }}\,i = 1,2,3;\\&{h_0} = 1 - \displaystyle\frac{{2{\theta _1}{\theta _3}}}{{3\theta _2^2}}.\end{aligned}$ | (11) |
其中 ,
正常工控下,SPE和
| ${\rm{SPE < SP}}{{\rm{E}}_{\rm{\alpha }}}, \;\; {T^2} < T_\alpha ^2.$ | (12) |
若其中至少有一个统计量超出了控制限,则表明控制系统遭受正弦攻击.
2.3 基于多尺度主成分分析的正弦攻击在线检测法基于多尺度主成分分析的正弦攻击在线检测算法分为2个阶段:MSPCA模型训练阶段和正弦攻击在线检测阶段. MSPCA模型训练阶段使用正常工况下的数据样本训练得到各尺度PCA模型及攻击检测统计指标的控制限;正弦攻击检测阶段使用PCA模型对可能存在正弦攻击的新数据进行主成分分析,根据统计指标进行正弦攻击在线检测,具体步骤如下:
1)选取正常工况下的
2)对经过小波去噪样本的每一列进行小波
3)对
4)根据
5)对矩阵
6)确定数据窗口宽度
7)对窗口内的数据进行标准化处理,经小波去噪后对数据进行小波分解,通过系数组合可得到矩阵
8)根据训练阶段得到的PCA模型对
9)若步骤3)中多个尺度有攻击事件发生,则将相应尺度小波系数进行组合,得到综合尺度矩阵
算法的步骤1)~步骤5)为MSPCA模型训练阶段,步骤6)~步骤9)为正弦攻击在线检测阶段,模型训练阶段和在线检测阶段是分离实施的. 算法的检测环节具体过程如下:在进行攻击检测前,首先根据检测性能要求确定样本数
时间复杂度是在线异常检测算法的重要指标,经过分析,MSPCA在线检测算法的单步执行的时间复杂度是
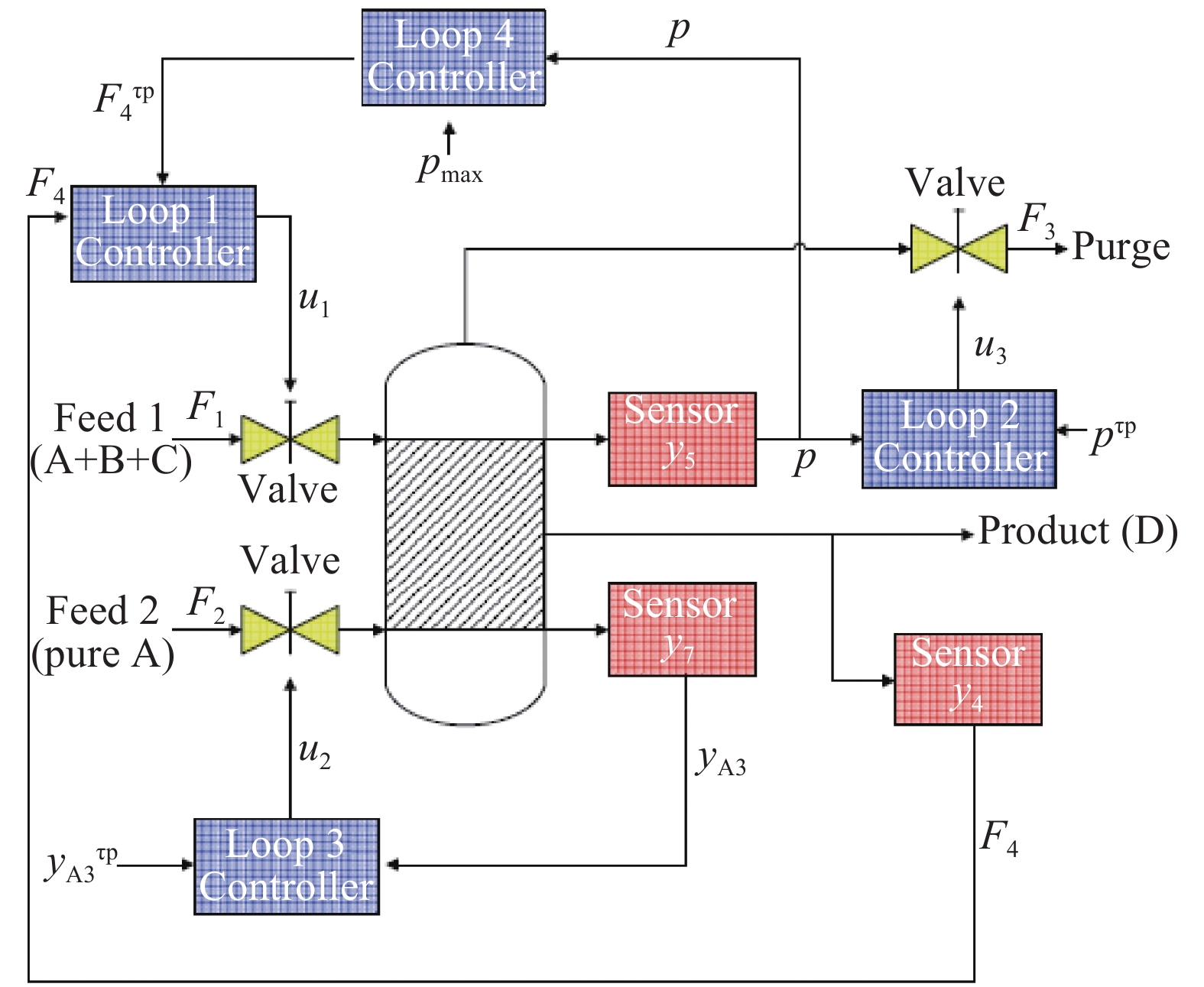
为了验证正弦攻击的攻击效果及检测算法的有效性,在TE过程上进行仿真验证. TE 过程的原型是 Eastman 化学公司的一个实际的工艺流程,该过程由反应器、冷凝器、循环压缩机、气液分离器和汽提塔等主要操作单元组成,是一个复杂的非线性过程,被广泛用于多变量控制、最优化、非线性控制、故障诊断等领域. 该过程包括 12 个作为操纵变量的阀门和 41 个可测量变量,其详细的工艺流程图和过程描述见文献[19],简化的工艺流程图如图3所示.
|
图 3 TE过程流程图 Fig. 3 Tennessee Eastman (TE) process flow chart |
TE过程检测的主要参数包括反应物进料流量、反应器温度、压力、液位、产物
通过研究分析可知,压强
这里选择对TE过程反应器的压强
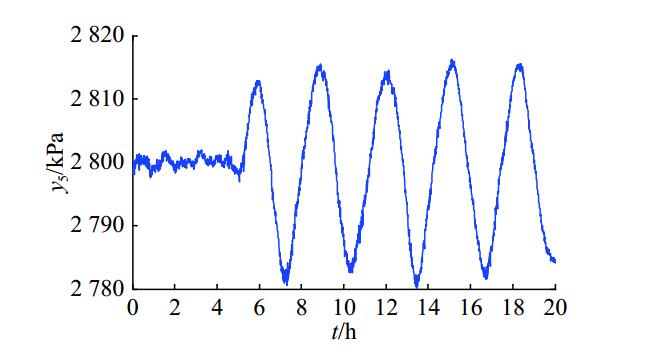
第一组攻击对反应器压强和放空阀的影响如图4和5所示,t为运行的时间. 观察可知,当对压强实施正弦攻击时,压强会呈现正弦变化趋势,但始终在正常工作范围内;压强会对放空阀的开度产生影响,使其也呈现出正弦变化规律. 放空阀开度量程为0~100%,0对应全关,100%对应全开. 正弦攻击致使阀门开度在0~20%范围内不停变化,加速其磨损过程,最终导致反应器不能正常工作.
|
图 4 攻击频率 ω=2 时的反压器压力变化图 Fig. 4 Pressure change when attack frequency ω=2 |
|
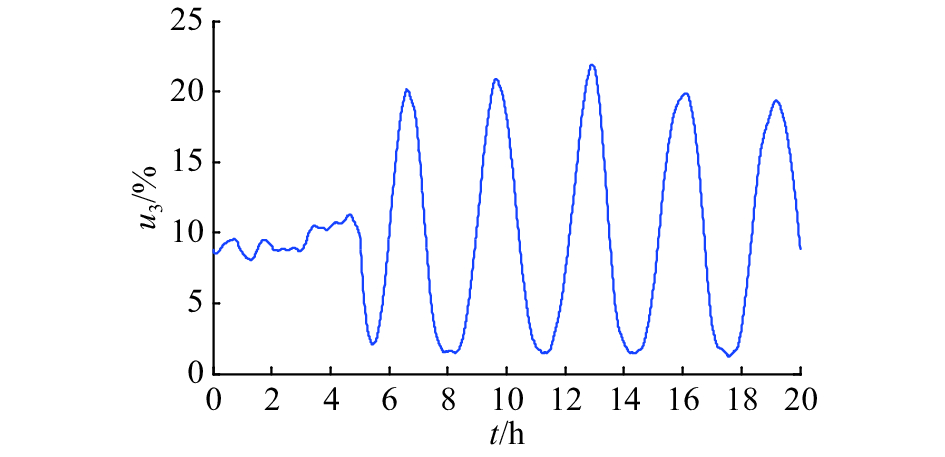
图 5 攻击频率 ω=2 时的阀门开度变化图 Fig. 5 Purge valve change when attack frequency ω=2 |
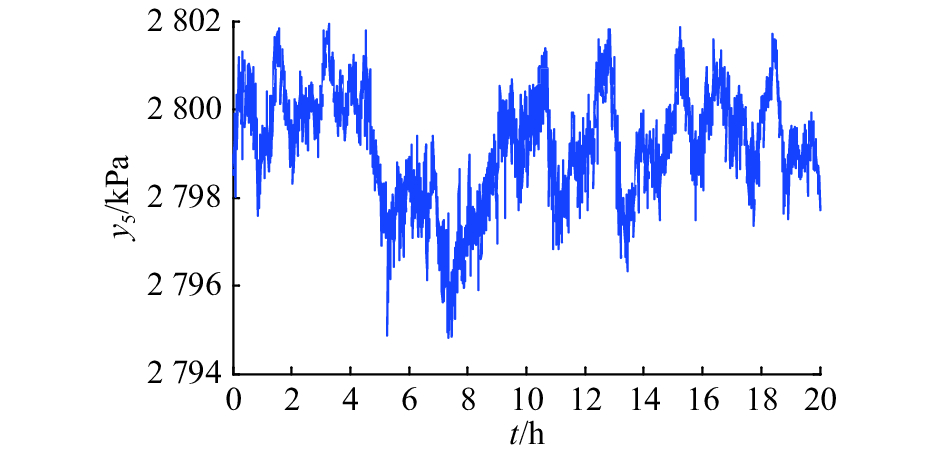
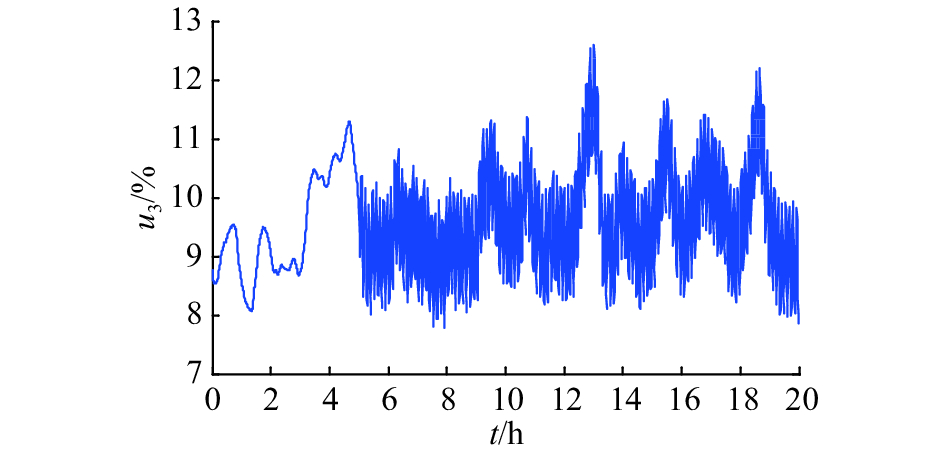
第二组攻击对反应器压强和放空阀的影响如图6和7所示,由于攻击的频率加大,导致阀门处于高频正弦震荡过程中. 虽然开度的振幅减小了,但是震荡的频率增大,这可能会对放空阀造成更加严重的损坏.
|
图 6 攻击频率 ω=50 压力变化图 Fig. 6 Pressure change when attack frequency ω=50 |
|
图 7 攻击频率 ω=50 阀门开度变化图 Fig. 7 Purge valve change when attack frequency ω=50 |
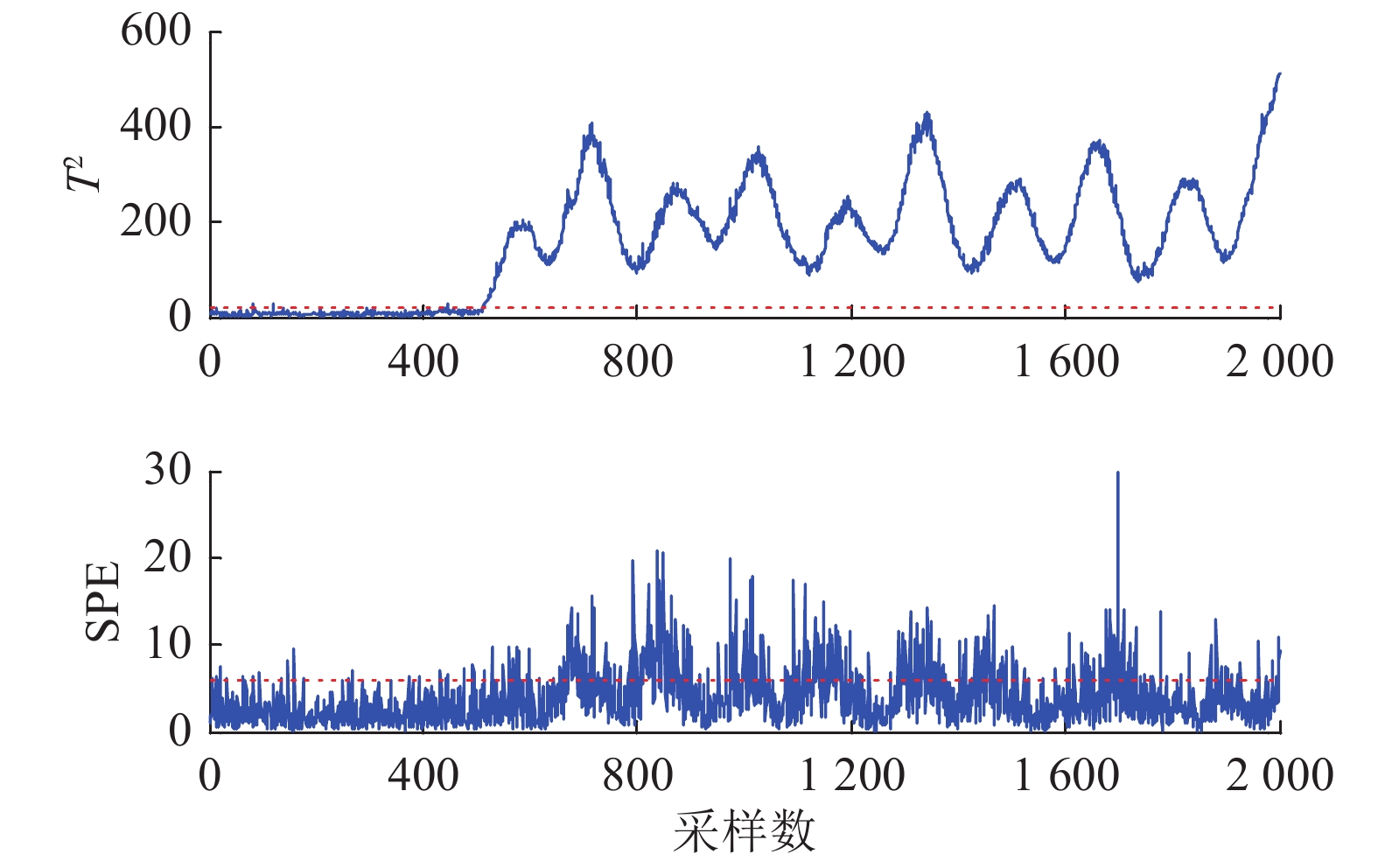
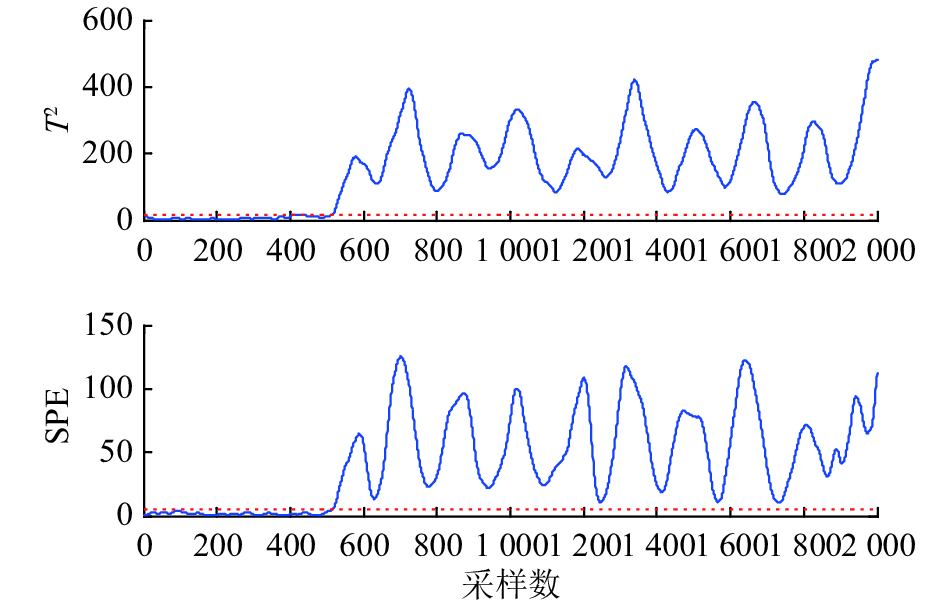
对第一组正弦攻击进行分析,实施正弦攻击后,分别使用PCA和MSPCA进行攻击检测,检测结果如图8和9所示. 图中上下两个子图的蓝色实线分别表示
|
图 8 攻击频率 ω=2 时PCA检测结果 Fig. 8 PCA detection when attack frequency ω=2 |
|
图 9 攻击频率 ω=2 时的MSPCA检测结果 Fig. 9 MSPCA detection when attack frequency ω=2 |
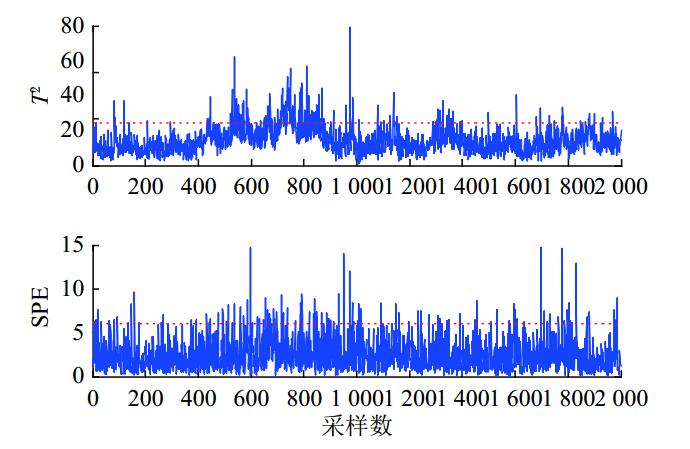
对第二组正弦攻击进行分析,实施正弦攻击后,对测量数据分别使用PCA和MSPCA进行攻击检测,检测结果如图10和11所示.
|
图 10 攻击频率 ω=50 时的PCA检测结果 Fig. 10 PCA detection when attack frequency ω=50 |
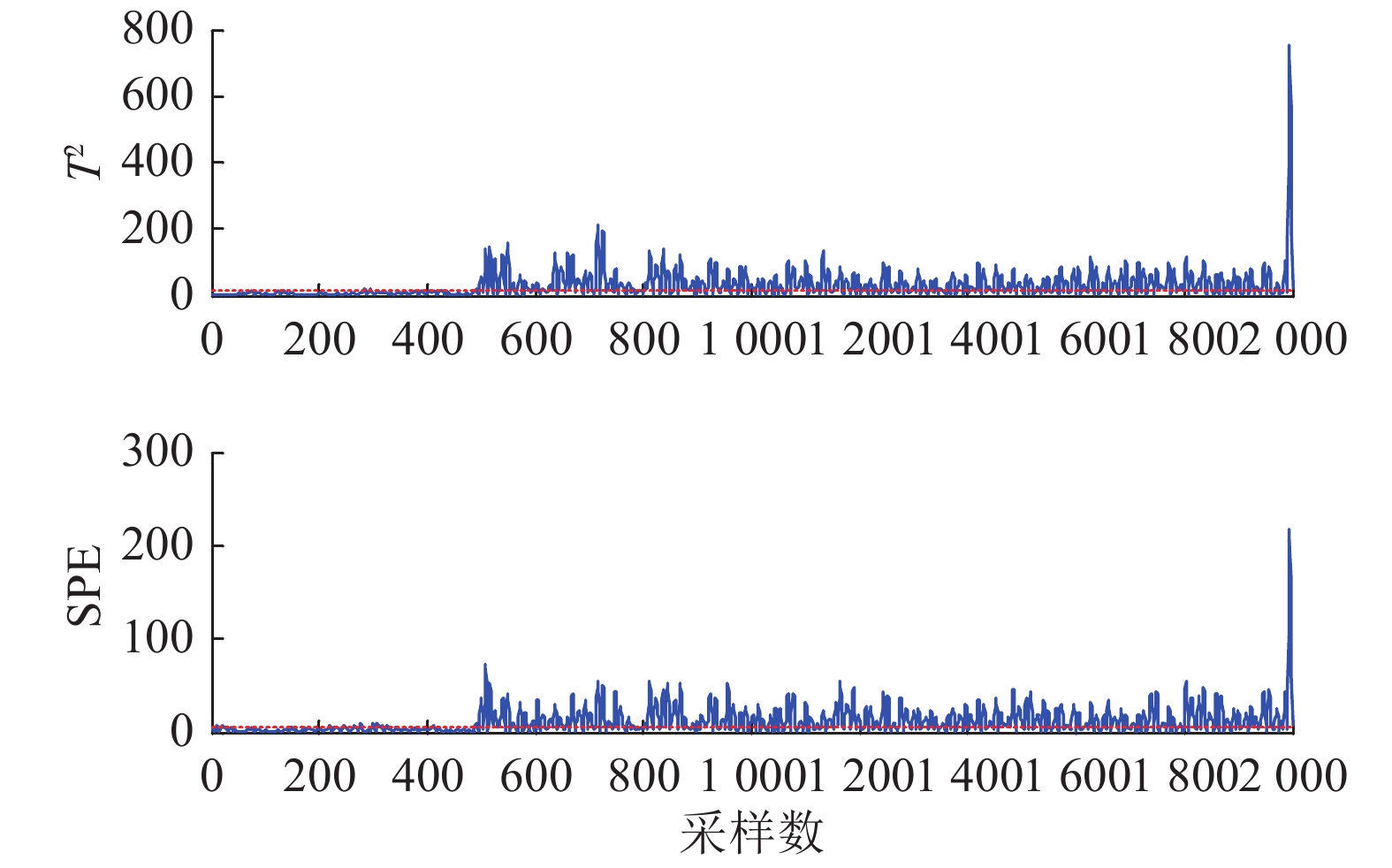
|
图 11 攻击频率 ω=50 时的D4尺度高频系数MSPCA检测结果 Fig. 11 MSPCA D4 level detection when attack frequency ω=50 |
当对压强实施频率
由以上结果可以得出如下结论:对于低频正弦攻击,由于测量数据的尺度特性没有改变,PCA能检测出攻击,MSPCA也能检测出攻击;对于高频正弦攻击,测量数据的尺度特性被改变,PCA基本不能检测出攻击,而MSPCA在相应的高频尺度上可以准确、快速地检测出攻击. 这一结论说明PCA只能检测出单尺度下的欺骗攻击,而MSPCA可以检测出不同尺度的正弦攻击,证明了MSPCA在检测正弦欺骗攻击方面的优越性.
4 结 语本文针对复杂多变量化工过程中存在的正弦攻击,建立了数学模型,并从频域的角度分析了其特性,提出了将多尺度主成分分析用于正弦攻击的检测,并建立在线检测算法. 仿真实例表明:正弦攻击会对化工过程的执行器等现场控制设备造成损害,同时在进行欺骗攻击检测时,对于多尺度类型的攻击,PCA方法存在明显的缺陷,会存在无法检测出攻击的情况;而MSPCA能及时检测出不同尺度类型的攻击,可以有效地保护工业控制系统的安全. 本文仅提出了将MSPCA算法用于正弦欺骗攻击的检测,并在TE平台上验证其性能,并没有考虑到多种欺骗攻击共存时,MSPCA算法能否检出各种攻击,以及漏报率、误报率等指标的性能好坏,这是本文的不足之处,也是接下来的重点研究方向之一.
| [1] |
AMIN S, LIN Z S, HUANG Y L, et al. Attacks against process control systems: risk assessment, detection, and response [C] // Proceedings of the 6th ACM Symposium on Information, Computer and Communications Security. Hong Kong: ACM, 2011: 355–366.
|
| [2] |
HUANG Y L, CARDENAS A A, AMIN S, et al. Understanding the physical and economic consequences of attacks on control systems[J]. International Journal of Critical Infrastructure Protection, 2009, 2(3): 73-83. DOI:10.1016/j.ijcip.2009.06.001 |
| [3] |
BARBOSA R R R, SADRE R, PRAS A. Towards periodicity based anomaly detection in SCADA networks [C] // Emerging Technologies & Factory Automation. Krakow: IEEE, 2012: 1–4.
|
| [4] |
HONG J, LIU C C, GOVINDARASU M. Integrated anomaly detection for cyber security of the substations[J]. IEEE Transactions on Smart Grid, 2014, 5(4): 1643-1653. DOI:10.1109/TSG.2013.2294473 |
| [5] |
KWON Y J, KIM H K, YONG H L, et al. A behavior-based intrusion detection technique for smart grid infrastructure [C] // PowerTech, 2015 IEEE Eindhoven. Eindhoven: IEEE, 2015: 1–6.
|
| [6] |
张云贵, 佟为明, 赵永丽. CUSUM异常检测算法改进及在工控系统入侵检测中的应用[J]. 冶金自动化, 2014(5): 1-5. ZHANG Yun-gui, TONG Wei-ming, ZHAO Yong-li. Improvement of CUSUM algorithm and its application in intrusion detection for industry control systems[J]. Metallurgical Industry Automation, 2014(5): 1-5. DOI:10.3969/j.issn.1000-7059.2014.05.001 |
| [7] |
AMIN S, LITRICO X, SASTRY S, et al. Cyber security of water SCADA systems—Part I: analysis and experimentation of stealthy deception attacks[J]. IEEE Transactions on Control Systems Technology, 2013, 21(5): 1963-1970. DOI:10.1109/TCST.2012.2211873 |
| [8] |
MO Y, CHABUKSWAR R, SINOPOLI B. Detecting integrity attacks on SCADA systems[J]. IEEE Transactions on Control Systems Technology, 2014, 22(4): 1396-1407. DOI:10.1109/TCST.2013.2280899 |
| [9] |
LIU Y, NING P, REITER M K. False data injection attacks against state estimation in electric power grids[J]. ACM Transactions on Information & System Security, 2009, 14(1): 21-32. |
| [10] |
KWON C, LIU W, HWANG I. Security analysis for cyber-physical systems against stealthy deception attacks [C] // American Control Conference (ACC), 2013. Washington: IEEE, 2013, pp. 3344–3349.
|
| [11] |
张环宇, 陈凯. 基于零动态的工控系统攻击检测识别安全模型[J]. 计算机工程, 2017, 43(10): 98-103. ZHANG Huan-yu, CHEN Kai. Industrial control system security model of attack detection and identification based on zero dynamics[J]. Computer Engineering, 2017, 43(10): 98-103. DOI:10.3969/j.issn.1000-3428.2017.10.017 |
| [12] |
甄玉磊. 网络控制系统中重放攻击的检测与对策[D]. 北京: 北京交通大学, 2016. ZHEN Yu-lei, Detection and countermeasure of replay attack in networked control system [D]. Beijing: Beijing Jiaotong University, 2016. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CMFD&dbname=CMFD201701&filename=1016303045.nh&v=MDIwMzZXcnJQVkYyNkdMQzRIZEhJcXBFYlBJUjhlWDFMdXhZUzdEaDFUM3FUcldNMUZyQ1VSTEtmYnVSdkZ5cms= |
| [13] |
BARBOSA R R R, SADRE R, PRAS A. A first look into SCADA network traffic [C] // Network Operations and Management Symposium. IEEE, 2017: 518–521. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CMFD&dbname=CMFD201701&filename=1016303045.nh&v=MDIwMzZXcnJQVkYyNkdMQzRIZEhJcXBFYlBJUjhlWDFMdXhZUzdEaDFUM3FUcldNMUZyQ1VSTEtmYnVSdkZ5cms=
|
| [14] |
MIRIN S N S, WAHAB N A. Fault detection and monitoring using multiscale principal component analysis at a sewage treatment plant[J]. Jurnal Teknologi, 2014, 70(3). |
| [15] |
LANGNER R. Stuxnet: dissecting a cyberwarfare weapon[J]. IEEE Security & Privacy, 2011, 9(3): 49-51. |
| [16] |
FUBEERF. 深度: 震网病毒的秘密(二)[EB/OL]. (2013-12-26). [2017-07-18]. http://www.freebuf.com/news/19199.html.
|
| [17] |
BAKSHI B R. Multiscale PCA with application to multivariate statistical process monitoring[J]. AIChE Journal, 1998, 44(7): 1596-1610. DOI:10.1002/(ISSN)1547-5905 |
| [18] |
钱叶魁, 陈鸣, 叶立新, 等. 基于多尺度主成分分析的全网络异常检测方法[J]. 软件学报, 2012, 23(2): 361-377. QIAN Ye-kui, CHEN M, YE Li-xin, et al. Network-Wide anomaly detection method based on multiscale principal component analysis[J]. Journal of Software, 2012, 23(2): 361-377. |
| [19] |
CHIANG L H, RUSSELL E L, BRAATZ R D. Fault detection and diagnosis in industrial systems [M]. 2nd ed. London: Springer-Verlag, 2001.
|



