子空间辨识包括N4SID、MOESP和CVA等经典子空间辨识方法,主要优点是利用鲁棒计算工具,如:QR分解和奇异值分解(singular value decomposition, SVD),可直接获得被辨识对象的状态空间方程[1],因此被广泛应用于工业过程的辨识建模[2-3]以及控制监测[4-6]. 在工业应用中,在线子空间辨识技术具有巨大的潜力[7-10].
在线子空间辨识的主要难点在于如何递归更新QR和SVD. 早期为了减少计算量,通常采用近似方法来实现QR和SVD的更新问题. Verhaegen等[11]采用SVD的一阶更新策略来实现子空间辨识的递归,但是该方法只有满足严格的噪声条件才能获得无偏估计. 近年来,子空间跟踪技术如近似投影子空间跟踪(projection approximation subspace tracking,PAST)和基于传播的方法(propagator-based method,PM)被引入在线子空间辨识方法. Lovera等[12]将PAST方法用于递归更新SVD,实现在线子空间辨识. Mercère[13]则将基于传播的方法用于SVD的递归实现. 杨华等[14]构造具有遗忘因子的输入输出数据矩阵,将梯度型算法引入基于遗忘因子的状态子空间跟踪中,实现对广义能观矩阵的估计.除此之外,有学者采用直接更新QR和SVD,设计在线子空间辨识方法. Kameyama等[15]采用bona-fide算法,直接更新QR分解中的分量,从而实现QR分解的递归更新. 谢磊等[16]通过将Updating和Downdating操作有效结合,利用快速滑窗QR分解算法,减少了不必要的重复步骤. Alenany等[17]引入递归约束最小二乘法,直接构建在线子空间辨识方法. 随着现代计算能力越来越强,利用Hessenberg QR等算法直接对QR和SVD更新,具有更大的工业应用潜力.
基于主成分分析的子空间辨识方法(SIMPCA),由于采用主成分分析作为主要的子空间分解手段,能够很好地处理变量含误差(Error-In-Varibles, EIV)过程的建模和监测问题[18-21]. 典型的基于主成分分析的子空间辨识方法一般都利用辅助变量来消除噪声项,但在主成分分析过程中会出现较大的偏差,导致系统参数得不到较为精确的估计. 为此,Wu等[22]提出了SIMPCA-E算法,该方法先估计并消除噪声项,然后采用主成分分析,提取系统相关子空间矩阵.
本文在SIMPCA-E算法的基础上,利用Hessenberg QR算法对QR分解的R分量进行递归更新,并采用特征值分解代替SVD分解,减少辨识过程的计算量;采用遗忘因子机制,实现对时变过程的辨识.
1 问题描述考虑如下EIV线性离散系统:
| ${{x}}(k \,+\, 1) \,=\, {{Ax}}(k) \,+\, {{Bu}}_0(k) \,+\, {{w}}(k),$ | (1) |
| ${{y}}(k) \,=\, {{Cx}}(k) \,+\, {{Du}}_0(k) \,+\, {{v}}(k).\;\;\;\;\;\;\;\;$ | (2) |
其中,
| ${{u}}(k){\rm{ \,=\, }}{{{u}}_0}(k){\rm{ \,+\, }}{{\mu}} (k).$ |
为了辨识的统计一致性,一般考虑如下假设:
假设1:系统渐进稳定,如A的特征值在单位圆内.
假设2:(A,C)是可观的.
假设3:噪声
假设4:所有噪声序列不相关.
本文旨在通过在线采集输入输出对
过去和未来时刻的栈向量和Hankel矩阵定义如下:
| ${{{y}}_p}(k) \,=\, \left[ {\begin{array}{*{20}{c}} {{y}}(k \,-\, p) \\ {{y}}(k \,-\, p \,+\, 1) \\ \vdots \\{{y}}(k \,-\,) \\ \end{array}} \right] ,\;{{{y}}_f}(k) \,=\, \left[ {\begin{array}{*{20}{c}} {{y}}(k) \\ {{y}}(k \,+\, 1) \\ \vdots \\ {{y}}(k \,+\, f \,-\, 1) \\ \end{array}} \right] ,$ |
| ${{{Y}}_{p,N}} \,=\, \left[ {{{{y}}_p}(k)\;\;\;{{{y}}_p}(k \,+\, 1)\;\;\;\; \cdots \;\;\;\,{{{y}}_p}(k \,+\, N \,-\, p \,-\, f \,-\, 1)} \right],$ |
| ${{{Y}}_{f,N}} \,=\, \left[ {{{{y}}_f}(k)\;\;{{{y}}_f}(k \,+\, 1)\;\;\; \cdots \;\;\,{{{y}}_f}(k \,+\, N \,-\, f \,-\, 1)} \right].$ |
式中:p和f为用户自定义的过去和未来时刻,一般都大于系统阶次n. 同理定义
通过迭代式(1)和(2),构建输入输出矩阵方程:
| $\begin{split}{{{Y}}_{f,N}} \,=\, &{{{\varGamma}} _f}{{{X}}_{f,N}} \,+\, {{{H}}_f}{{{U}}_{f,N}} \,-\, {{{H}}_f}{{{M}}_{f,N}} \,+\, \\ &{{{G}}_f}{{{W}}_{f,N}} \,+\, {{{V}}_{f,N}}.\end{split}$ | (3) |
式中:
| ${{{\varGamma}} _f} \,=\, {\left[ {{{{C}}^{\rm T}}\;\;{{({{CA}})}^{\rm T}}\;\; \cdots \;\;{{({{CA}}^{f \,-\, 1})}^{\rm T}}} \right]^{\rm T}}.$ |
定义如下三角矩阵
| ${{{H}}_f} \,=\, \left[ {\begin{array}{*{20}{c}} {{D}}& {\bf 0}& \cdots & {\bf 0} \\ {{CB}}& {{D}}& \cdots & {\bf 0} \\ \vdots & \vdots & {\rm{}} & \vdots \\{{CA}}^{f - 2}{{B}}&{{CA}}^{f - 3}{{B}} &\cdots & {{D}} \\ \end{array}} \right],$ |
| ${{{G}}_f} \,=\, \left[ {\begin{array}{*{20}{c}} {\bf 0}& {\bf 0}& \cdots & {\bf 0} \\ {{C}}& {\bf 0}& \cdots & {\bf 0} \\ \vdots & \vdots & {\rm{}} & \vdots \\ {{CA}}^{f - 2}&{{CA}}^{f - 3}& \cdots &{\bf 0} \\ \end{array}} \right].$ |
通过选择较大的p,可得
| ${{{X}}_{f,N}} \,\approx\, {{{L}}_z}{{{Z}}_{p,N}}.$ | (4) |
式中:
结合式(3)和(4),可得
| ${{{Y}}_{f,N}} \,=\, {{{\varGamma}} _f}{{{L}}_z}{{{Z}}_{p,N}} \,+\, {{{H}}_f}{{{U}}_{f,N}} \,+\, {{{E}}_{f,N}}.$ | (5) |
式中:
| $\begin{aligned}\left[ {\begin{array}{*{20}{c}} {{{Z}}_{p,N}} \\ {{{U}}_{f,N}} \\ {{{Y}}_{f,N}} \\ \end{array}} \right] \,=\, \left[ {\begin{array}{*{20}{l}} {{{R}}_{11,N}}&{}&{} \\ {{{R}}_{21,N}}&{{{R}}_{22,N}} &{} \\ {{{R}}_{31,N}}&{{{R}}_{32,N}}&{{{R}}_{33,N}} \\ \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{{Q}}_{1,N}} \\ {{{Q}}_{2,N}} \\ {{{Q}}_{3,N}} \\ \end{array}} \right].\end{aligned}$ | (6) |
定义:
| $\begin{aligned}{{{R}}_{k,N}} \,=\, \left[ {\begin{array}{*{20}{c}} {{{R}}_{11,N}}&{}&{} \\ {{{R}}_{21,N}}&{{{R}}_{22,N}} &{} \\ {{{R}}_{31,N}}&{{{R}}_{32,N}}&{{{R}}_{33,N}} \\ \end{array}} \right] .\end{aligned}$ |
通过QR分解的结果,可得噪声项
| ${\hat {{E}}_{f,N}} \,=\, {{{R}}_{33,N}}{{{Q}}_{3,N}}.$ | (7) |
将
| ${{{Y}}_{f,N}} \,-\, {\hat {{E}}_{f,N}} \,=\, {{{\varGamma}} _f}{{{X}}_{f,N}} \,+\, {{{H}}_f}{{{U}}_{f,N}}.$ | (8) |
定义:
| $\begin{aligned}&{\tilde {{Y}}_{f,N}} \,=\, {{{Y}}_{f,N}} - {\hat {{E}}_{f,N}},\\&\left[ {{{I}} \,-\, {{{H}}_f}} \right]\left[ {\begin{array}{*{20}{c}} {{\tilde Y}_{f,N}} \\ {{{U}}_{f,N}} \\ \end{array}} \right] \,=\, {{{\varGamma}} _{f,N}}{{{X}}_{f,N}}.\end{aligned}$ | (9) |
式(9)两边乘以
| ${({{\varGamma}} _f^ \bot )^{\rm T}}\left[ {{{I}} \,-\, {{{H}}_f}} \right]\left[ {\begin{array}{*{20}{c}} {{\tilde Y}_{f,N}} \\ {{{U}}_{f,N}} \\ \end{array}} \right] = 0.$ | (10) |
进行如下主成分分析:
| $\left[ {\begin{array}{*{20}{c}} {{\tilde Y}_{f,N}} \\ {{{U}}_{f,N}} \\ \end{array}} \right] \,=\, {{PT}}^{\rm T} \,+\, \overline {{P}}\,{\overline {{T}}^{\rm T}}.$ | (11) |
式中:
| $\left[ {\begin{array}{*{20}{c}} {{\varGamma}} _{_f}^ \bot \\ - {({{{H}}_f})^T}{{\varGamma}} _{_f}^ \bot \\ \end{array}} \right] \,=\, \overline {{P}} {{F}}{\rm{ \,=\, }}\left[ {\begin{array}{*{20}{l}} \overline {{{{P}}_\Gamma }} \\ \overline {{{{P}}_U}} \\ \end{array}} \right] .$ | (12) |
式中:F为任意非奇异矩阵.一般选取F为单位矩阵,系统矩阵可与参考文献[23]类似,从
离线SIMPCA-E算法的关键是,如何估计噪声项
在QR分解中,可得如下等式:
| ${{{U}}_{f,N}}{\rm{ \,=\, }}{{{R}}_{{\rm{21,}}N}}{{{Q}}_{1,N}} \,+\, {{{R}}_{{\rm{22,}}N}}{{{Q}}_{2,N}},$ | (13) |
| ${{{Y}}_{f,N}}{\rm{ \,=\, }}{{{R}}_{{\rm{31,}}N}}{{{Q}}_{1,N}} \,+\, {{{R}}_{{\rm{32,}}N}}{{{Q}}_{2,N}} \,+\, {{{R}}_{{\rm{33,}}N}}{{{Q}}_{3,N}}.$ | (14) |
因此,可构建如下矩阵:
| $\begin{align} &\left[ {\begin{array}{*{20}{l}} {{{Y}}_{f,N}} \,-\, {{\hat {{E}}}_{f,N}} \\ {{{U}}_{f,N}} \\ \end{array}} \right] \left[ {{{({{{Y}}_{f,N}} \,-\, {{\hat {{E}}}_{f,N}})}^{\rm T}} {{U}}_{f,N}^{\rm T}} \right]\,=\, \\& \left[ {\begin{array}{*{20}{l}} {({{{Y}}_{f,N}} \,-\, {{\hat {{E}}}_{f,N}}){{({{{Y}}_{f,N}} \,-\, {{\hat {{E}}}_{f,N}})}^{\rm T}}}&{({{{Y}}_{f,N}} \,-\, {{\hat {{E}}}_{f,N}}){{U}}_{f,N}^{\rm T}} \\ {{{{U}}_{f,N}}{{({{{Y}}_{f,N}} \,-\, {{\hat {{E}}}_{f,N}})}^{\rm T}}}&{{{{U}}_{f,N}}{{U}}_{f,N}^{\rm T}} \end{array}} \right]. \\ \end{align} $ | (15) |
通过替代QR分解中的R矩阵,可得
| $\begin{split}&({{{Y}}_{f,N}} \,-\, {\hat {{E}}_{f,N}}){({{{Y}}_{f,N}} \,-\, {\hat {{E}}_{f,N}})^{\rm T}} \,=\,\\ &{{{R}}_{31,N}}{{R}}_{31,N}^{\rm T} \,+\, {{{R}}_{32,N}}{{R}}_{32,N}^{\rm T},\end{split}$ | (16) |
| $({{{Y}}_{f,N}} \,-\, {\hat {{E}}_{f,N}}){{{U}}_{f,N}}^{\rm T} \,=\, {{{R}}_{31,N}}{{R}}_{21,N}^{\rm T} \,+\, {{{R}}_{32,N}}{{R}}_{22,N}^{\rm T},$ | (17) |
| ${{{U}}_{f,N}}{({{{Y}}_{f,N}} \,-\, {\hat {{E}}_{f,N}})^{\rm T}} \,=\, {{{R}}_{21,N}}{{R}}_{31,N}^{\rm T} \,+\, {{{R}}_{22,N}}{{R}}_{32,N}^{\rm T},$ | (18) |
| ${{{U}}_{f,N}}{{U}}_{f,N}^{\rm T} \,=\, {{{R}}_{21,N}}{{R}}_{21,N}^{\rm T} \,+\, {{{R}}_{22,N}}{{R}}_{22,N}^{\rm T}.$ | (19) |
式(15)可转换为
| $\begin{aligned} &\left[ \!\!\!\! {\begin{array}{*{20}{l}} {{{Y}}_{f,N}} \,-\, {{\hat {{E}}}_{f,N}} \\ {{{U}}_{f,N}} \\ \end{array}} \right]\left[ {{{({{{Y}}_{f,N}} \,-\, {{\hat {{E}}}_{f,N}})}^{\rm T}} {{U}}_{f,N}^{\rm T}} \right] \,=\, \\ &\left[ \!\!\!\!{\begin{array}{*{20}{l}} {{{{R}}_{31,N}}{{R}}_{31,N}^{\rm T} \,+\, {{{R}}_{32,N}}{{R}}_{32,N}^{\rm T}}\quad\;\;\; \!{{{{R}}_{31,N}}{{R}}_{21,N}^{\rm T} \,+\, {{{R}}_{32,N}}{{R}}_{22,N}^{\rm T}} \\ {{{({{{R}}_{31,N}}{{R}}_{21,N}^{\rm T} \,+\, {{{R}}_{32,N}}{{R}}_{22,N}^{\rm T})}^{\rm T}}}\;\;\! {{{{R}}_{21,N}}{{R}}_{21,N}^{\rm T} \,+\, {{{R}}_{22,N}}{{R}}_{22,N}^{\rm T}}\end{array}}\!\!\!\! \right]. \\\end{aligned} $ | (20) |
进行如下特征值分解:
| $\left[ {\begin{array}{*{20}{c}} {{\tilde Y}_{f,N}} \\ {{{U}}_{f,N}} \\ \end{array}} \right] \left[ {{{\tilde Y}_{f,N}}^{\rm T} \quad {{U}}_{f,N}^{\rm T}} \right] \,=\, [{ \varPi _{1}}\quad { \varPi _{2}}]\left[ {\begin{array}{*{20}{c}} {{{{\varLambda}} _1}}&{\bf 0} \\ {\bf 0}&{{{{\varLambda}} _2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\tilde { \varPi}}_1}} \\ {{{\tilde { \varPi}}_2}} \end{array}} \right].$ | (21) |
式中:
| $\left[ {\begin{array}{*{20}{l}} {{\varGamma}} _{_f}^ \bot \\ - {({{{H}}_f})^T}{{\varGamma}} _{_f}^ \bot \\ \end{array}} \right] \,=\, { \varPi _2}{{F}}{\rm{ \,=\, }}\left[ {\begin{array}{*{20}{l}} { \varPi} _{2\varGamma } \\ { \varPi} _{2U} \\ \end{array}} \right] .$ | (22) |
从2.2.1节可知,QR分解的更新是在线实现SIMPCA-E算法的关键是
假设已采集初始数据
当获取了新的输入输出对
| $\begin{aligned}&\left[ \!\!\!\! \begin{array}{l}{{ Z}_{p,N}} \quad { z_p}(k \,+\, N \,-\, p \,-\, f)\\{{ U}_{f,N}} \quad {u_f}(k \,+\, N \,-\, f) \\{{ Y}_{f,N}} \quad {y_f}(k \,+\, N \,-\, f)\end{array} \!\!\!\! \right]\,=\,\\& \left[ \!\!\!\! \begin{array}{l}{{ {z}}_p}(k \,+\, N \,-\, p \,-\, f) \,\,\, \,\,\,\, {{ R}_{11,N}}\;\;\;\\{{ u}_f}(k \,+\, N \,-\, f) \quad \quad {{ R}_{21,N}}\;\;\;\; {{ R}_{22,N}}\\{{ y}_f}(k \,+\, N \,-\, f) \quad \quad {{ R}_{31,N}}\;\;\;\;\;{{ R}_{32,N\;\;\;\;\;\;\;\;\;\;}}{{ R}_{33,N}}\end{array} \!\!\!\! \right]\left[ \!\!\!\! \begin{array}{l}{\bf{0}} \quad \,\,\,\,\,\, {\bf 1} \\{{ \bar { Q}}_1} \quad {\bf{0}}\\{{ \bar { Q}}_2} \quad {\bf{0}}\end{array} \!\!\!\! \right].\end{aligned}$ | (23) |
式中:
| ${{{z}}_p}(k \,+\, N) \,=\, \left[ {\begin{array}{*{20}{c}} {{{y}}_p}(k \,+\, N \,-\, p \,-\, f) \\ {{{u}}_p}(k \,+\, N \,-\, p \,-\, f) \\ \end{array}} \right] .$ |
定义:
| $\begin{aligned}&{{{H}}_{k,N \,+\, 1}} \,=\,\\ &\left[{\begin{array}{*{20}{l}}{{{z}}_p}(k \,+\, N \,-\, p \,-\, f){}& {{{R}}_{11,N}}&{}&{} \\ {{{u}}_f}(k \,+\, N \,-\, f) &{{{R}}_{21,N}}&{{{R}}_{22,N}}&{} \\ {{{y}}_f}(k \,+\, N \,-\, f)& {{{R}}_{31,N}}&{{{R}}_{32,N}}&{{{R}}_{33,N}} \\ \end{array}} \right] .\end{aligned}$ | (24) |
R矩阵可以利用式(23)通过Hessenberg QR法进行更新,即利用一系列Givens旋转
| $\begin{aligned}&{{{H}}_{k,N + 1}}\times{{{q}}_1}{{{q}}_2} \cdots {{{q}}_x} \,=\, \\&\left[ {\begin{array}{*{20}{c}} {{{R}}_{11,N \,+\, 1}}&{}&{}& {\bf 0} \\ {{{R}}_{21,N \,+\, 1}}&{{{R}}_{22,N \,+\, 1}} &{}&{\bf 0} \\ {{{R}}_{31,N \,+\, 1}}&{{{R}}_{32,N \,+\, 1}}&{{{R}}_{33,N \,+\, 1}} &{\bf 0} \\ \end{array}} \right] .\end{aligned}$ | (25) |
去除最后一列,设置
| ${{{R}}_{k,N{\rm{ \,+\, 1}}}} \,=\, \left[ {\begin{array}{*{20}{c}} {{{R}}_{11,N \,+\, 1}}&{}&{} \\ {{{R}}_{21,N \,+\, 1}}&{{{R}}_{22,N \,+\, 1}} &{} \\ {{{R}}_{31,N \,+\, 1}}&{{{R}}_{32,N \,+\, 1}}&{{{R}}_{33,N \,+\, 1}} \\ \end{array}} \right] .$ |
由此可得R矩阵的更新:
| $\begin{split}&({{{Y}}_{f,N \,+\, 1}} - {\hat {{E}}_{f,N \,+\, 1}}){({{{Y}}_{f,N \,+\, 1}} - {\hat {{E}}_{f,N \,+\, 1}})^{\rm T}} =\\& {{{R}}_{31,N \,+\, 1}}{{R}}_{31,N \,+\, 1}^{\rm T} \,+\, {{{R}}_{32,N{\rm{ \,+\, 1}}}}{{R}}_{32,N \,+\, 1}^{\rm T},\end{split}$ | (26) |
| $\begin{split}&({{{Y}}_{f,N \,+\, 1}} - {\hat {{E}}_{f,N \,+\, 1}}){{{U}}_{f,N \,+\, 1}}^{\rm T}= \\& {{{R}}_{31,N \,+\, 1}}{{R}}_{21,N{\rm{ \,+\, 1}}}^{\rm T} + {{{R}}_{32,N{\rm{ + 1}}}}{{R}}_{22,N \,+\, 1}^{\rm T},\end{split}$ | (27) |
| $\begin{split}&{{{U}}_{f,N \,+\, 1}}{({{{Y}}_{f,N \,+\, 1}} \,-\, {\hat {{E}}_{f,N \,+\, 1}})^{\rm T}}\,=\, \\& {{{R}}_{21,N \,+\, 1}}{{R}}_{31,N \,+\, 1}^{\rm T} \,+\, {{{R}}_{22,N \,+\, 1}}{{R}}_{32,N{\rm{ \,+\, 1}}}^{\rm T},\end{split}$ | (28) |
| $\begin{split}&{{{U}}_{f,N \,+\, 1}}{{U}}_{f,N \,+\, 1}^{\rm T} \,=\,\\ &{{{R}}_{21,N \,+\, 1}}{{R}}_{21,N \,+\, 1}^{\rm T} \,+\, {{{R}}_{22,N \,+\, 1}}{{R}}_{22,N \,+\, 1}^{\rm T}.\end{split}$ | (29) |
当R矩阵更新后,可从式(20)~(22)获取扩展观测矩阵.
2.2.3 主要结果综上所示,本文提出的在线SIMPCA-E算法可归纳为如下步骤.
算法1(OSIMPCA-E):
1)利用初始数据序列
2)当采集到最新的输入输出
3)如式(21)所示,应用特征值分解,估计残差子空间
4)从
5)置
本文所提方法的计算量主要包括QR更新和特征值分解,见(21)和(25). 当f和p相同时,Hessenberg QR算法的计算量为
为了能够跟踪时变过程,类似于文献[23],本文将遗忘因子机制引入所提的OSIMPCA-E算法,直接代替式(24):
| $\begin{split}&{{{H}}_{k,N \,+\, 1}} =\\ &\left[ {\begin{array}{*{20}{l}} {{{z}}_p}(k \,+\, N \,-\, p \,-\, f) &\lambda {{{R}}_{11,N}}&{}&{} \\ {{{u}}_f}(k \,+\, N \,-\, f) &\lambda {{{R}}_{21,N}}&\lambda {{{R}}_{22,N}} &{} \\ {{{y}}_f}(k \,+\, N \,-\, f) &\lambda {{{R}}_{31,N}}&\lambda {{{R}}_{32,N}}&\lambda {{{R}}_{33,N}} \\ \end{array}} \right] .\end{split}$ | (30) |
式中:
遗忘因子
假设
| ${{H}}_{_{k,N}}^{\rm T} \,=\, \left[ \begin{array}{*{20}{c}} {h_{11,1}} &\cdots &{h_{11,N}} \\ & \ddots & \vdots \\& {} & {}{h_{nn,N}} \end{array} \right],$ |
则可得
| $\overline {{H}}_{_{k,N \,+\, 1}}^{\rm T} \,=\, \left[ {\begin{array}{*{20}{c}} \lambda {h_{11,1}}& \cdots &\lambda {h_{11,N}} \\& \ddots & \vdots \\&{}& \lambda {h_{nn,N}} \\ {x_1} & \cdots &{x_n} \\ \end{array}} \right] .$ |
经过Givens转换后,可得
| ${{H}}_{_{k,N + 1}}^{\rm T} \,=\, \overline {{H}}_{_{k,N \,+\, 1}}^{\rm T}{{{Q}}^{\rm T}} \,=\, \left[ {\begin{array}{*{20}{c}} {x_1}& \cdots & {x_n} \\ \lambda {h_{11,1}}& \cdots&\lambda {h_{11,N}} \\&\ddots & \vdots \\&{}& \lambda {h_{nn,N}} \\ 0 &\cdots &0 \\ \end{array}} \right] $ |
由
| ${{{R}}_{31,N \,+\, 1}}{{R}}_{31,N + 1}^{\rm T} \,=\, {\lambda ^2}{{{R}}_{31,N}}{{R}}_{31,N}^{\rm T} \,+\, {{{\varDelta}} _{N \,+\, 1}}.$ |
这里
为了表明所提方法的有效性,采用文献[24]的模型,系统描述如下:
| $\begin{aligned}{{x}}(t + 1) =& \left[ {\begin{array}{*{20}{c}}& 0.8 \;&- 0.4 \;&0.{\rm{2}} \\ &0&0.{\rm{3}} &- 0.5 \\ &0&0& 0.5 \\ \end{array}} \right] {{x}}(t) + \\ &\left[ {\begin{array}{*{20}{c}} &0 &0 \\ &0 &- 0.6 \\& 0.5 &0 \\ \end{array}} \right] {{u}}(t) +\left[ {\begin{array}{*{20}{c}} 0 .055 \\ 0.040 \\ 0.045 \\ \end{array}} \right] {{w}}(t),\end{aligned}$ |
| $ {{y}}(t) = \left[ {\begin{array}{*{20}{l}} 0.5 \;\;\;0.5\;\;\;\;\;0 \\ 0\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;1 \\ \end{array}} \right] {{x}}(t) + \left[ {\begin{array}{*{20}{l}} 0.025 \\ 0.030 \\ \end{array}} \right] {{v}}(t).$ |
为了能够评估OSIMPCA-E算法的性能,考虑系统矩阵A不变化、缓慢变化、突变等3种情况. 假设已知系统阶次,为3. 将过去时刻p和未来时刻f设置为6. 针对每种情况,共做100 蒙特卡洛实验. 每次实验采集2 000个数据. 初始数据长度为200. 噪声信号设定如下:
1) 系统矩阵A不变. 首先,针对线性时不变系统测试所提方法,选择
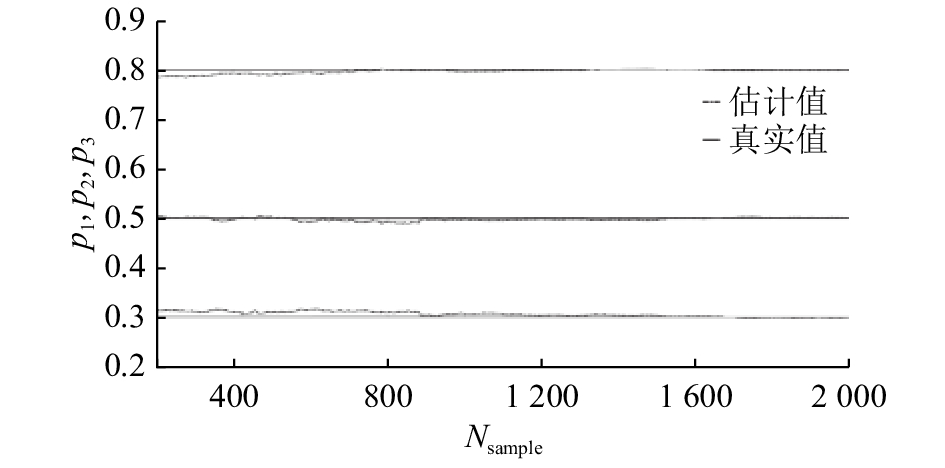
|
图 1 系统矩阵A不变:100次蒙特卡洛实验系统特征平均值 Fig. 1 Ture and estimated poles of OSIMPCA-E algorithm for 100 Monte-Carlo experiments with same system matrix A. |
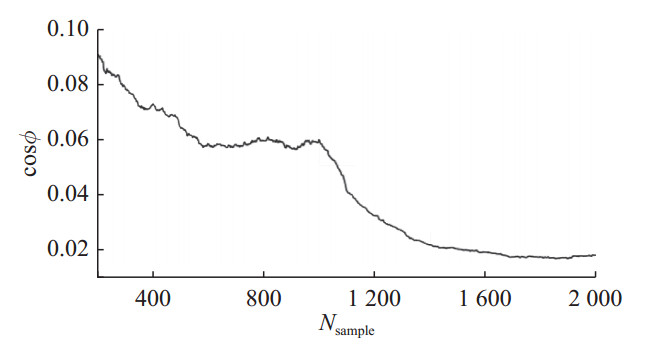
|
图 2 系统矩阵A不变:100次蒙特卡洛实验主子空间夹角平均值 Fig. 2 Principal subspace angles computed with OSIMPCA-E algorithm for 100 Monte-Carlo experiments with same system matrix A |
2) 系统矩阵A缓慢变化
当采样1 000个数据后, 系统矩阵A如下:
| $\begin{aligned}&{{A}} =\left[ {\begin{array}{*{20}{c}} 0{\rm{.8}} - 0.2 M & - 0.4 & 0.{\rm{2}} \\ 0& 0.{\rm{3}} - 0.2 M & - 0.5 \\ 0& 0& 0.5 + 0.1 M \\ \end{array}} \right] .\end{aligned}$ |
式中:
| $\begin{aligned}&{\displaystyle{M={{{\rm \exp} \left.\left( - \frac{{t - 1\,000}}{{2\,000}}\right)\right/}}{{{{\rm e}^{ - 1}} - 1}}}}\end{aligned}$ |
这里选择λ= 0.920. 图3表示了针对缓慢时变过程,OSIMPCA-E算法所辨识的系统极点与真实系统极点的对比。从图3可知,虽然在精度上还有待提高,OSIMPCA-E算法针对缓慢时变过程,能够较快的跟踪系统矩阵的变化。同时,所辨识的扩展观测矩阵也能够匹配真实扩展观测矩阵的变化,如图4所示。
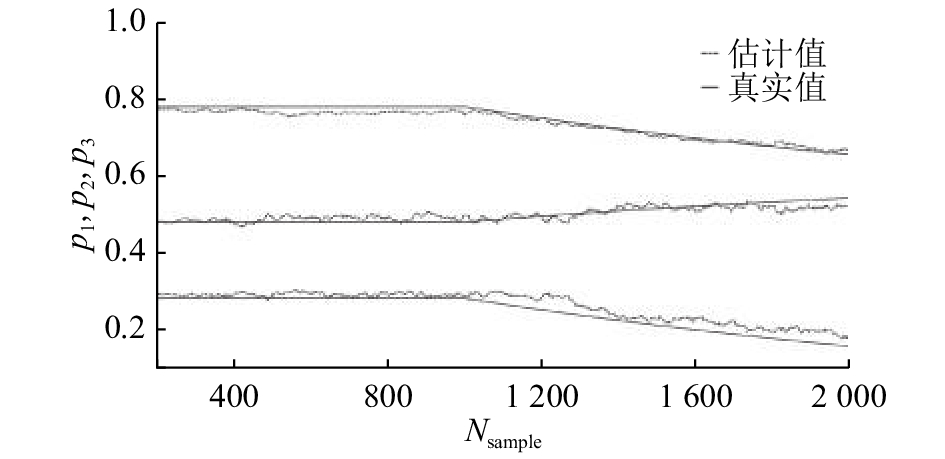
|
图 3 系统矩阵A缓慢变化:100次蒙特卡洛实验系统特征平均值 Fig. 3 Ture and estimation poles of OSIMPCA-E algorithm for 100 Monte-Carlo experiments with slow varying system matrix A |
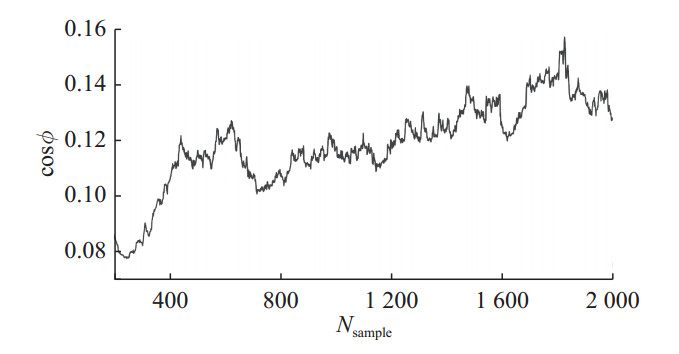
|
图 4 系统矩阵A缓慢变化:100次蒙特卡洛实验主子空间夹角平均值 Fig. 4 Principal Subspace angles computed with OSIMPCA-E algorithm for 100 Monte-Carlo experiments with slow varying system matrix A. |
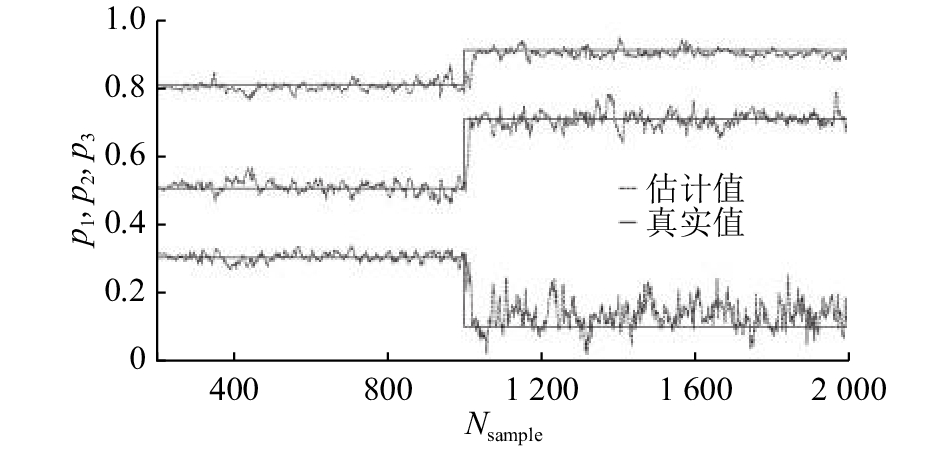
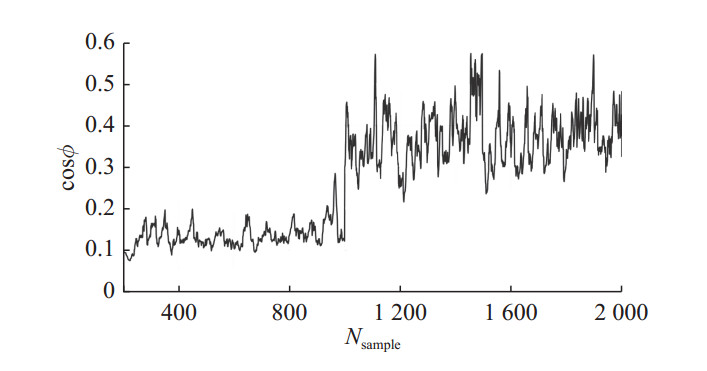
3) 系统矩阵A突变
当采样1 000个数据后,系统矩阵A如下:
| ${{A}} = \left[ {\begin{array}{*{20}{l}} 0{\rm{.9}} & - 0.4 &0.{\rm{2}} \\0&0.{\rm{1}}& - 0.5\\ 0&0&0.{\rm{7}} \\ \end{array}} \right] .$ |
这里选择
|
图 5 系统矩阵A突变:100次蒙特卡洛实验系统特征平均值 Fig. 5 Ture and estimation poles of OSIMPCA-E algorithm for 100 Monte-Carlo experiments with abrupt change in system matrix A |
|
图 6 系统矩阵A突变:100次蒙特卡洛实验主子空间夹角平均值 Fig. 6 Principal Subspace angles computed with OSIMPCA-E algorithm for 100 Monte-Carlo experiments with abrupt change in system matrix A |
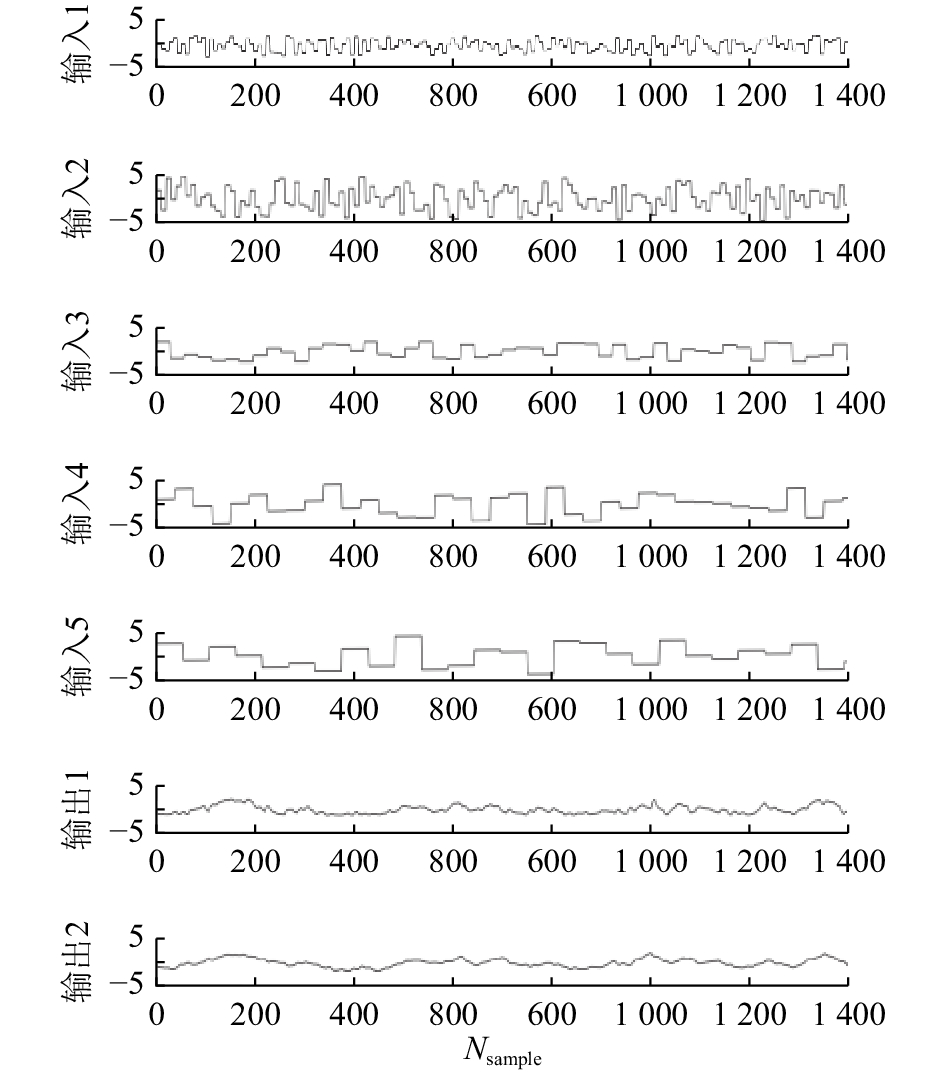
本文将考虑一个工业Benchmark模型来表明所提算法的有效性. 该模型为污水处理模型所采用的过程为巴西圣保罗大学所建(Activated Sludge Wastewater Treatment Plant-University of Sao Paulo,ASWWTP-USP)[25]. 该过程的辨识目标是建立一定工况下厌氧区和好氧区的氮含量. 本文采用伪随机二进制序列信号(Pseudo-random binary sequences,PRBS)作为激励输入. 共产生1 400组数据,预处理后的数据如图7所示. 采用前300组数据进行初始建模,系统阶次选为3,过去时刻和未来时刻选为6,
|
图 7 ASWWTP-USP模型预处理后的过程数据 Fig. 7 Process data of ASWWTP-USP benchmark |
图8显示了在线辨识的后1 000个数据. 结果表明OSIMPCA-E方法能够获得良好的性能,可以快速跟踪过程的变化. 为了进一步比较所提方法的性能,采用相对平均误差指标

|
图 8 ASWWTP-USP模型的在线辨识结果 Fig. 8 Online estimation for ASWWTP-USP benchmark |
| ${\eta _{{\rm{MRSE}}}} = \frac{1}{l}{\sum_{i = 1}^l} {\;\;{{\left\{ {\frac{{{\displaystyle\sum\nolimits_{j = 1}^N} {\;{{\left[ {{y_i}(j) - {{\hat y}_i}(j)} \right]}^2}} }}{{\displaystyle\sum\nolimits_{j = 1}^N {\;{y_i}^2(j)} }}} \right\}}^{1/2}}} .$ |
式中:yi表示真实输出,
| 表 1 不同辨识算法的MRSE比较 Table 1 Performance comparison using MRSE of different algorithms % |
本文提出了一种基于主成分分析和噪声估计的在线子空间辨识方法. 为了减少计算量,该方法采用Hessenberg QR方法更新QR,通过主成分分析实现残差子空间的在线估计,并利用遗忘因子机制实现时变系统的辨识. 仿真结果表明,所提方法能够很好地估计时不变、时变以及突变线性EIV系统. 未来研究方向将包括基于在线子空间辨识方法构建时变过程的故障检测与诊断.
| [1] |
HUANG B, KADALI R. Dynamic modeling, predictive control and performance monitoring: a data-driven subspace approach [M]. London: Springer Verlag, 2008: 2-3.
|
| [2] |
齐晓慧, 王俭臣. 固定翼飞机动力学模型的子空间辨识方法[J]. 上海交通大学学报, 2016, 50(4): 613-618. QI Xiao-hui, WANG Jian-chen. Subspace model identification method for flight dynamics of fixed-wing airplane[J]. Journal of Shanghai Jiaotong University, 2016, 50(4): 613-618. |
| [3] |
JUILLET F, SCHMID P J, HUERRE P. Control of amplifier flows using subspace identification techniques[J]. Journal of Fluid Mechanics, 2013, 725(5): 522-565. |
| [4] |
孙磊, 金晓明. 基于子空间辨识的模型预测控制策略及其应用[J]. 控制理论与应用, 2009, 26(3): 313-315. SUN Lei, JIN Xiao-ming. Model-predictive-control based on subspace identification and its application[J]. Control Theory & Applications, 2009, 26(3): 313-315. |
| [5] |
OLOFSSON K E J, SOPPELSA A, BOLZONELLA T, et al. Subspace identification analysis of RFX and 430 T2R reversed-field pinches[J]. Control Engineering Practice, 2013, 21(7): 917-929. DOI:10.1016/j.conengprac.2013.03.004 |
| [6] |
CORBETT B, MHASKAR P. Subspace identification for data-driven modeling and quality control of batch processes[J]. AIChE Journal, 2016, 62(5): 1581-1601. |
| [7] |
AKHENAK A, DUVIELLA E, BAKO L, et al. Online fault diagnosis using recursive subspace identification: application to a dam-gallery open channel system[J]. Control Engineering Practice, 2013, 21(6): 797-806. |
| [8] |
NEZAM S A, VENKATASUBRAMANIAN V. Electromechanical mode estimation using recursive adaptive stochastic subspace identification[J]. IEEE Transactions on Power Systems, 2013, 29(1): 349-358. |
| [9] |
HOUTZAGER I, VAN WINGERDEN J, VERHAEGEN M. Recursive predictor-based subspace identification with application to the real-time closed-loop tracking of flutter[J]. IEEE Transactions on Control Systems Technology, 2012, 20(4): 934-949. DOI:10.1109/TCST.2011.2157694 |
| [10] |
GILA P, SANTOS F, PALMA L, CARDOSO A. Recursive subspace system identification for parametric fault detection in nonlinear systems[J]. Applied Soft Computing, 2015, 37: 444-455. DOI:10.1016/j.asoc.2015.08.036 |
| [11] |
VERHAEGEN M, DEPRETTERE E. A fast, recursive MIMO state space model identification algorithm [C] // Proceedings of the 1991 Conference on Decision and Control. Brighton: IEEE, 1991:1349–1354.
|
| [12] |
LOVERA M, GUSTAFSSON T, VERHAEGEN M. Recursive subspace identification of linear and non-linear Wiener state-space models[J]. Automatica, 2000, 36(11): 1639-1650. DOI:10.1016/S0005-1098(00)00103-5 |
| [13] |
MERCÈRE G, BAKO L, LECOEUCHE S. Propagator based methods for recursive subspace model identification[J]. Signal Processing, 2008, 88(3): 468-491. DOI:10.1016/j.sigpro.2007.09.012 |
| [14] |
杨华,李少远. 一种新的基于遗忘因子的递推子空间辨识算法[J]. 控制理论与应用, 2009, 26(1): 69-72. YANG Hua, LI Shao-yuan. A novel recursive MOESP subspace identification algorithm based on forgetting factor[J]. Control Theory & Applications, 2009, 26(1): 69-72. |
| [15] |
KAMEYAMA K, OHSUMI A, MATSUURA Y, et al. Recursive 4SID-based identification algorithm with fixed input-output data size[J]. International Journal of Innovative Computing Information and Control, 2005, 1(1): 17-33. |
| [16] |
谢磊, 梁武星, 张泉灵, 等. 基于快速滑窗QR分解的自适应子空间辨识[J]. 化工学报, 2008, 59(6): 1448-1453. XIE Lei, LIANG Wu-xing, ZHANG Quan-ling, et al. Adaptive subspace identification baised on fast foving window QR decomposition[J]. Journal of Chemical Industry and Engineering, 2008, 59(6): 1448-1453. DOI:10.3321/j.issn:0438-1157.2008.06.018 |
| [17] |
ALENANY A, SHANG H. Recursive subspace identification with 0prior information using the constrained least squares approach[J]. Computers & Chemical Engineering, 2013, 54(54): 174-180. |
| [18] |
YIN S, DING S X, HAGHANI A, et al. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process[J]. Journal of Process Control, 2012, 22(9): 1567-1581. DOI:10.1016/j.jprocont.2012.06.009 |
| [19] |
DING S X, YIN S, PENG K X, et al. A novel scheme for key performance indicator prediction and diagnosis with application to an industrial hot strip mill[J]. IEEE Transactions on Industrial Informatics, 2013, 9(4): 2239-2247. DOI:10.1109/TII.2012.2214394 |
| [20] |
CHEN Z X, FANG H J, CHANG Y. Weighted data-driven fault detection and isolation: a subspace-based approach and algorithms[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3290-3298. DOI:10.1109/TIE.2016.2535109 |
| [21] |
NAIK A S, YIN S, DING S X, ZHANG P. Recursive identification algorithms to design fault detection systems[J]. Journal of Process Control, 2010, 20(8): 957-965. DOI:10.1016/j.jprocont.2010.06.018 |
| [22] |
WU P, PAN H P, REN J, YANG C J. A new subspace identification approach based on principal component analysis and noise estimation[J]. Industrial & Engineering Chemistry Research, 2015, 54(8): 5106-5114. |
| [23] |
OKU H. Recursive subspace model identification algorithms for slowly time-varying systems in closed loop[C] // 2007 European Control Conference. Greece: IEEE, 2007: 5715–5720.
|
| [24] |
WANG J, QIN S J. A new subspace identification approach based on principal component analysis[J]. Journal of Process Control, 2002, 12(8): 841-855. DOI:10.1016/S0959-1524(02)00016-1 |
| [25] |
SOTOMAYOR O A Z, PARK S W, GARCIA C. Multivariable identification of an activated sludge process with subspace-based algorithms[J]. Control Engineering Practice, 2003, 11(8): 961-969. DOI:10.1016/S0967-0661(02)00210-1 |


