2. 国家海洋局第二海洋研究所 卫星海洋环境动力学国家重点实验室,浙江 杭州 310058
2. State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, Hangzhou 310058, China
杭州湾位于杭州、上海和宁波之间,西北湾顶与著名的钱塘江相连,东部湾口与东海相通,湾口南部散落着舟山群岛. 杭州湾位于中国经济最发达的长三角经济区内,两岸有着重要的工业园区,并且分布着中国乃至全球最大的港口.
水利专家提出多种方案保护海岸经济的发展,比如在钱塘江建闸和建潜坝减小潮量降低破坏;但是考虑到淤积、防洪、通航和旅游因素,最终按照“缩窄固定江堤”和“弯曲河道”的原则在钱塘江和杭州湾两岸进行围垦造地[1]. 20世纪50年代,杭州湾南岸和北岸大部分处于自然演变的状态,60年代开始围海造田,工业填海和围海造田是造成岸线向海迁移的主要原因[2]. 1974—2014年,杭州湾围垦面积达到851.03 km2,其中1974—2005 年围垦537.47 km2,2005—2014年围垦313.56 km2 [3]. 围垦潮滩主要位于湾顶和南岸庵东附近潮滩(如图1所示),陆地向杭州湾水域延伸直接导致杭州湾顶部断面缩窄,水流在湾顶被急剧压缩,流速显著增大,水位快速抬升. 黄赛花等[4]建立杭州湾的2D潮流数学模型,结果表明杭州湾大桥的修建对北岸深槽流场的影响不明显,但是南岸的围垦对北岸深槽的维系不利.
采用实地测量的方式研究杭州湾岸线变化对潮汐过程的影响不仅耗时费力,而且年份越早拥有的实测资料越少,不利于全面研究杭州湾潮汐情况. 最近十几年由于计算机技术的发展,数学模型蓬勃发展. 李身铎等[5]建立杭州湾三维水动力数值模型,研究该区域的潮流和分潮,再现该区域的潮流潮波特征. 吴修广等[6]基于有限体积海岸海洋模型(finite volume community ocean model,FVCOM),建立杭州湾三维潮流泥沙数值模型,再现杭州湾海域潮流过程和泥沙运输过程. Guo等[7]使用FVCOM模拟1981—2005年的岸线,研究杭州湾围垦工程对台风引起的风暴潮的影响,发现围垦工程区域会产生更高的风暴潮. 鲁友鹏等[8]采用 FVCOM 模拟1984年、2010年和2020年3个不同时期杭州湾南岸区域的岸线地形,分析金塘水道3个时期水动力场的显著变化. Song等[9]使用最新版本的美国普林斯顿大学海洋模型(Princeton ocean model,POM)对中国沿海潮滩围垦的远场效应进行研究,结果表明局部的潮滩围垦对整个东海的潮能分布、分潮的振幅迟角和涨落潮历时不对称性等潮汐动力特性都会产生深刻的影响.
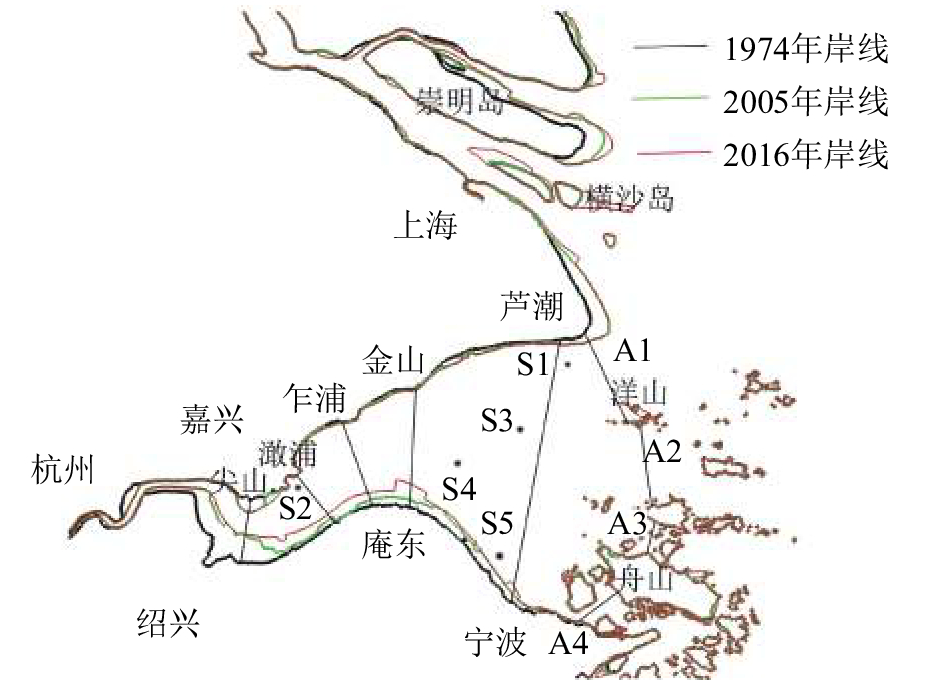
杭州湾内平均水深约为11 m,水深从南往北、自西向东逐渐增大. 杭州湾呈漏斗状,对湾内潮汐具有放大作用,从湾口至湾顶水位逐渐升高,流速逐渐增大[10]. 从20世纪60年代开始,为了兴利除害,钱塘江-杭州湾水域不断减少,尤其是钱塘江河口和杭州湾南岸,曹娥江口两侧陆地向钱塘江延伸近15 km,相当于钱塘江河口横断面长度的一半[11]. 与此同时,南岸向水域延伸5 km左右[12],图1显示长江口和杭州湾交接处的南汇也向海延伸近10 km;由于自然淤积和围垦,崇明岛、长兴岛和横沙岛面积明显扩大.
杭州湾、长江口和舟山群岛岸线的累积变化,使得附近海域的潮汐过程发生改变. 为了研究1974—2016年杭州湾及附近海域的岸线变化对杭州湾及长江口潮汐过程的影响,基于海图数据提取2005年、2009年、2016年岸线. 由于1974年海图目前不可获取,基于卫星图片获取数据,考虑潮位过程线、卫星图片成像时间等综合因素[13-14] 提取1974年岸线. 在提取得到的各年份岸线数据基础上,基于FVCOM建立杭州湾海域高分辨率三维水动力数值模型分析1974年以来杭州湾-长江口海域岸线变化对杭州湾海域潮流、潮能和潮汐不对称等潮汐特征的影响,为沿海岸线规划使用提供参考.
1 FVCOM水动力数值模型FVCOM在水平方向上采用三角形网格,能够很好地适应有众多岛屿的区域;垂直方向上采用σ坐标系,有助于处理水深变化显著的情况. 模型采用有限体积方法,有效结合有限元方法处理复杂边界的优点和有限差分方法高计算效率的优点. FVCOM采用判断干湿网格的方法,更适合模拟杭州湾南岸具有大面积滩涂的区域,充分体现海水 “淹没”以及“露出”该区域的过程.
|
图 1 杭州湾-长江口岸线变化及验潮站位置分布 Fig. 1 Coastline changes of Hangzhou Bay-Changjiang Estuary and stations distribution |
FVCOM水动力模型主要控制方程为
| $ \begin{split} \frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} + w\frac{{\partial u}}{{\partial z}} &- fv = - \frac{1}{\rho }\frac{{\partial P}}{{\partial x}} + \\ \frac{\partial }{{\partial z}}\left({K_{\rm m}}\frac{{\partial u}}{{\partial z}}\right) + F_u, \end{split}$ | (1) |
| $\begin{split} \frac{{\partial v}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}}+ w\frac{{\partial v}}{{\partial z}}&+ fu = - \frac{1}{\rho}\frac{{\partial P}}{{\partial y}} + \\ \frac{\partial }{{\partial z}}\left({K_{\rm m}}\frac{{\partial v}}{{\partial z}}\right) + {F_v}, \end{split} $ | (2) |
| $\frac{{\partial P}}{{\partial z}} = - \rho g,$ | (3) |
| $\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0.$ | (4) |
式中:x、y、z分别为坐标轴东向、北向和垂向的分量,u、v、w分别为x、y、z方向上的速度,P为压强,f为科氏力参数,ρ为海水密度,g为重力加速度. Fu、Fv分别为x、y方向上的动量扩散项,Km为垂直涡动黏性系数.
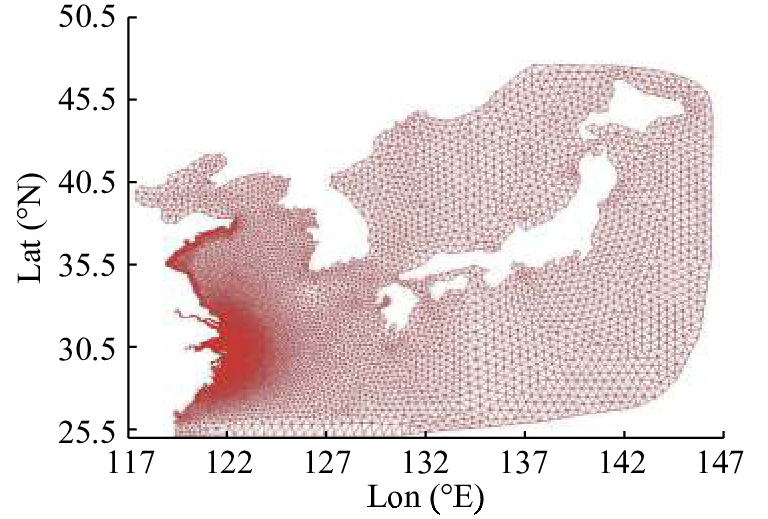
1.2 模型配置模型网格如图2所示,大区域范围为117.5°E~146.6°E,25.5°N~45.9°N,包括渤海、黄海、东海、日本海和日本列岛南部琉球群岛东部的部分西太平洋海域. 大区域计算网格为长江口-杭州湾-三门湾小区域计算网格提供高分辨率的驱动数据. 大范围的水深提取与Earth Topography (ETOPO)水深为2011年杭州湾、长江口和象山港的精确水深. 5组实验网格使用上述水深插值,实验1为控制实验,实验2~5为对比实验. 5组实验的网格参数如表1所示,实验1与实验5的驱动为2009年2月26日到3月16日使用tpxo7.2模型的潮位时间序列和长江与钱塘江的径流,实验2、3、4采用2005年8月20日到10月20日的潮位时间序列和长江与钱塘江的径流. 实验2、3、4研究岸线改变产生的潮汐动力变化,实验5研究潮滩减少对分潮的影响,用以排除岸线改变后潮滩减少对分潮影响的干扰. 模型最小分辨率约为100 m,最大分辨率约为50 km,垂向为均匀的6个σ层,外模时间步长为0.2 s,内模时间步长为2 s. 模型使用冷启动,起始潮位和流速都为0,温度和盐度为常数,分别为20 ℃和30 psu.
| 表 1 5组实验网格的年份、网格数和节点数 Table 1 Year, element number and node number of 5 experiments mesh |
|
图 2 总区域的模型网格 Fig. 2 Mesh of model domain |
模型验证采用2009年2月和3月的实测潮位和流速数据,S1位于芦潮港附近,S2位于澉浦附近,S3位于滩浒附近,S4和S5位于宁波杭州湾新区附近,验潮站的具体位置分布如图1所示. 实测数据分为2部分,2月27日到28日大潮时期,3月4日到5日小潮时期,时间间隔为0.5 h或1.0 h. 模型验证包括水位验证和流速验证. 验证结果的量化评价根据均方根误差(root mean squared error,RMSE)、标准均方根误差(normalized root mean squared error,NRMSE)、相关系数(correlation coefficent,CC)和预报能力(skill score,SS),计算公式如下:
| $ {\rm RMSE}= {{{\left[ {\frac{1}{N}\sum\limits_{i = 1}^N {{{({M_i} - {O_i})}^2}} } \right]}^{1/2}}} ,$ | (5) |
| ${\rm{NRMSE}} = {\left[ {\frac{{\displaystyle\sum\limits_{i = 1}^N {{{({M_i} - {O_i})}^{1/2}}} }}{{\displaystyle\sum\limits_{i = 1}^N {{O_i}^2}}}} \right]^{1/2}}, $ | (6) |
| ${\rm{CC}} = \frac{1}{N}\displaystyle\sum\limits_{i = 1}^N {\frac{{({M_i} - \bar M)({O_i} - \bar O)}}{{{S_{{M}}}{S_{{O}}}}}} ,$ | (7) |
| $ { \rm{SS}} = 1 - \frac{{\displaystyle\sum\limits_{i = 1}^N {{{({M_i} - {O_i})}^2}} }}{{\displaystyle\sum\limits_{i = 1}^N {{{({O_i} - \bar O)}^2}} }}.$ | (8) |
式中:Mi为模拟结果,Oi为实测结果,SM和SO分别为模拟结果和实测结果的标准偏差,
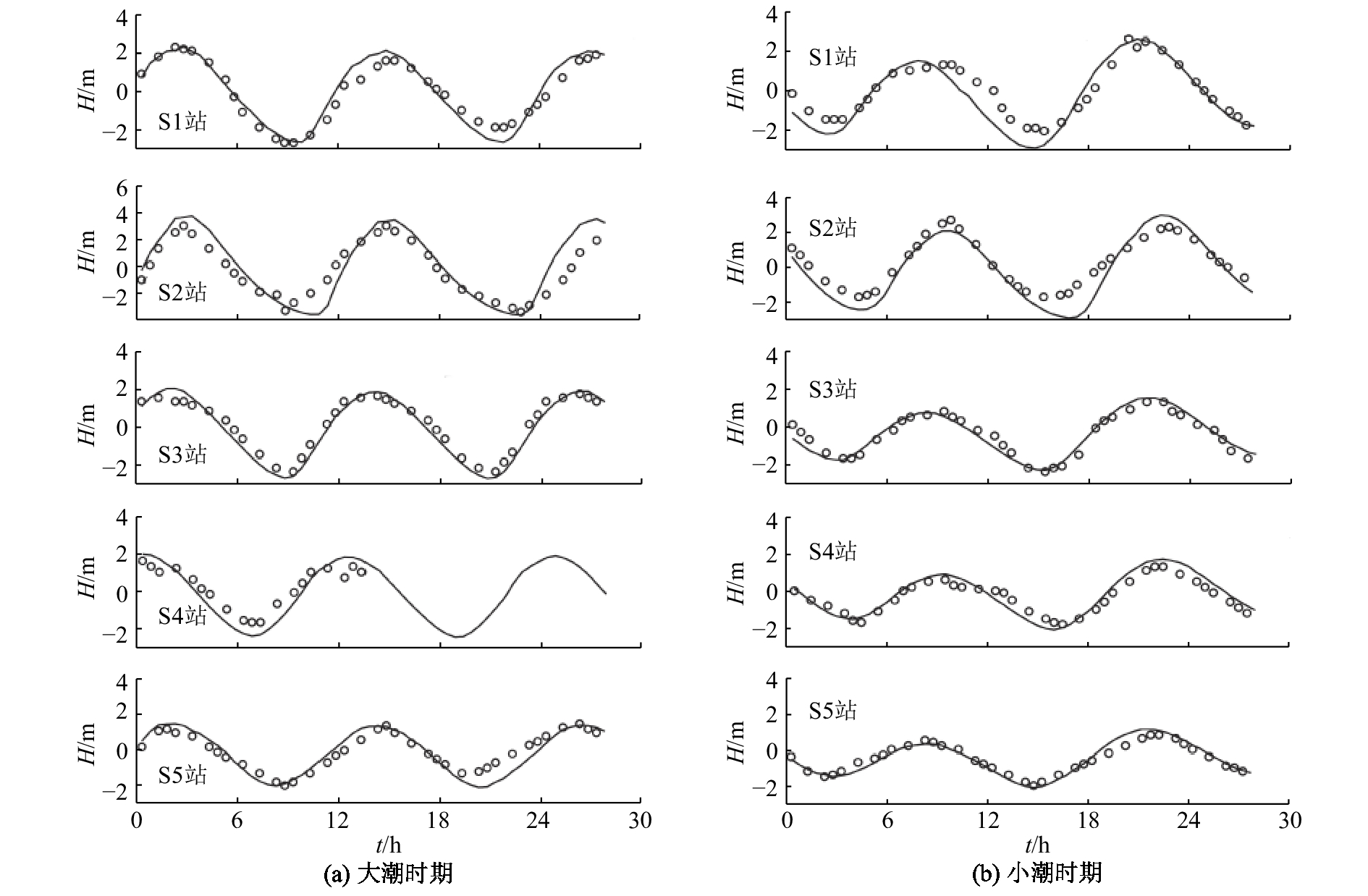
模拟结果与实测水位数据的比较如图3所示,H为水位,t为时间,大潮时的实测水位为2009年2月27日的实测数据,小潮时的实测水位为2009年3月5日的实测数据. 从图3可以看到,模拟结果与实测水位数据整体趋势比较吻合,S2小潮期间最低水位偏大,S4大潮最低水位偏大. 5个验潮站的误差分析(见表2)显示,S5的均方根误差最小,为0.4 m;S2的均方根误差最大,为0.94 m;S3的标准均方根误差最小,为0.29;S2的标准均方根误差最大,为0.55. 5个站的相关系数均大于0.90. 潮位验证结果良好.
| 表 2 实测潮位与模拟结果误差分析 Table 2 Error analysis between observed tidal level and model result |
|
图 3 五个测站模拟与实测水位对比结果 Fig. 3 Comparison between model results and observed values of tidal level at five stations |
采用5个验潮站大潮期间和小潮期间表(0.2H)、中(0.6H)、底(1.0H)三层的流速实测数据验证流速大小和流向. 图4为5个验潮站分别在大小潮时段的对比拟合结果,V表示流速大小,D表示流向. 流速大小和流向的整体趋势吻合. 量化误差分析结果如表3所示. S5站流速验证最理想,流速和流向的均方根误差分别为0.16 ~0.18 m/s和37.6°~41.3°;S2站最不理想,流速和流向的均方根误差分别为0.57 ~0.63 m/s和46.9°~65.9°.

|
图 4 5个测站模拟与实测流速流向对比 Fig. 4 Comparison between model and observed values of velocity and direction at 5 stations |
| 表 3 流速和流向实测数据与模拟结果误差分析 Table 3 Error analysis of flow velocity and direction between observation and model result |
杭州湾和附近海域的涨落潮过程中潮位和垂向平均潮流分布如图5所示. 图5以滩浒为参考点,RGB表示潮位,箭头表示流速. 涨急时刻(图5(a)),湾口潮位大、湾内潮位小,湾顶水位为3~4 m,海水从外海流进湾内,湾内流速较大,为1~2 m/s. 涨停时刻,湾口附近流向大海,湾顶潮位达到最大,最大潮位为4 m左右,流速为1 m/s,湾口流速接近0 m/s(图5(b)). 落急时刻(图5(c)),湾内水流整体流向外海,在湾口出现最小潮位,最小潮位为3 m左右.落停时刻(图5(d)),湾内整体潮位较小,为–2 m左右,湾口附近流速接近0 m/s,湾内流速为1 m左右.

|
图 5 4个时刻潮位和垂向平均潮流分布 Fig. 5 Distribution of tidal level and averaged vertical velocity of 4 moments |
M2分潮和M4分潮分别为杭州湾及附近海域的主要分潮和主要浅水分潮[16],因此主要分析M2和M4分潮的变化. 杭州湾内M2振幅较大,除舟山群岛以西区域,振幅都为1.5 m以上. M2分潮振幅从湾口北部的1.5 m左右,逐渐增大到湾顶的2.2 m左右,从湾口南岸的1.2 m左右逐渐增大到北岸的1.7 m左右. M2分潮北岸的传播速度大于南岸,从北岸湾口传播至湾顶澉浦附近历时约为2.4 h(图6(a),实验1).
M4振幅在湾顶约为0.3 m,逐渐减小到湾口北岸的0.2 m和湾口南部的0.1 m以下,同时长江口M4分潮振幅为0.2 m左右. M4分潮北岸的传播速度大于南岸,从北岸湾口传播至湾顶澉浦附近历时1.5 h(图6(b),实验1).

|
图 6
杭州湾海域M2、M4同潮图、潮能通量和潮汐不对称
|
使用一个潮周期的单宽潮能通量来计算杭州湾及附近海域的潮能分布,将北向和东向流速分开计算来确定潮能传播方向,计算公式如下[9]:
| ${ { E}_{\rm f}} = \frac{1}{T}\int_0^T {\rho D\left(g\zeta + \frac{1}{2}{{\left| { v} \right|}^2}\right) {{ v}{\rm d}}}t .$ | (9) |
式中:
舟山群岛中间的水道单宽潮能较大(图6(c),实验1),尤其是螺头水道中为3×105 W/m以上,进入湾内和长江口由于水深变浅而迅速减小,总体上北部大于南部,岛屿间大于开阔海域. 湾内的潮能主要从螺头水道和岱山岛与洋山附近水道传入,其中大部分都在湾口损耗,湾内较大潮能汇集到从金山到乍浦的北部深槽潮内,最大为2.5×105 W/m左右. 杭州湾与外海相通有4个断面,图1中的A1、A2、A3和A4断面的潮能通量分别为2.29×106 、2.90×106、1.29×106 和2.11×106 kW.
3.1.4 潮汐不对称潮汐不对称性是海岸潮汐过程中最重要的性质之一,影响潮汐河口和海湾中物质输运和积累. 由于M2分潮和M4分潮分别为杭州湾及附近海域的主要分潮和主要浅水分潮,使用M2-M4分潮组合研究该区域的潮汐不对称特征.
| ${\gamma _{{{{{{\rm M}}}2}/{{{{\rm M}}}4}}}} = \displaystyle\frac{{\displaystyle\frac{3}{2}{a{^2_{{{\rm M2}}}{a_{{{\rm M}4}}}}}\sin \left( {2{\varphi _{{{\rm M}2}}} - {\varphi _{{{\rm M}4}}}} \right)}}{{{{\left[ {\displaystyle\frac{1}{2}(a^2 _{{{\rm M2}}}+ 4a^2_{{{\rm M4}}})} \right]}^{3/2}}}}.$ | (10) |
式中:
杭州湾内
1974—2005年,M2分潮振幅在金山到湾顶增加最大达0.6 m(图7(a)),湾内2005年比1974年M2分潮晚到,但是到达湾顶相差不大. 2005—2016年,M2分潮振幅从金山到澉浦增幅为0.05 m左右(图7(b)),在金山断面以上2016年晚于2005年,但是金山断面以下2016年早于2005年. 1974—2016年为以上2个时段的累积变化,M2振幅从金山附近增加0.1 m左右逐渐到尖山附近增加0.6 m左右(图7(c)),2016年M2分潮从湾口至乍浦断面都落后于1974年,而乍浦至澉浦段2016年M2分潮反超1974年.
1974—2005年,尖山断面急剧缩窄使得附近水域潮汐作用增大,导致尖山断面附近M2振幅增加. 2005—2016年,乍浦断面和金山断面缩窄较大,使得附近水域M2分潮振幅增加.

|
图 7 各实验之间M2振幅之差与相位对比 Fig. 7 Difference in M2 amplitude and phase between experiments |
|
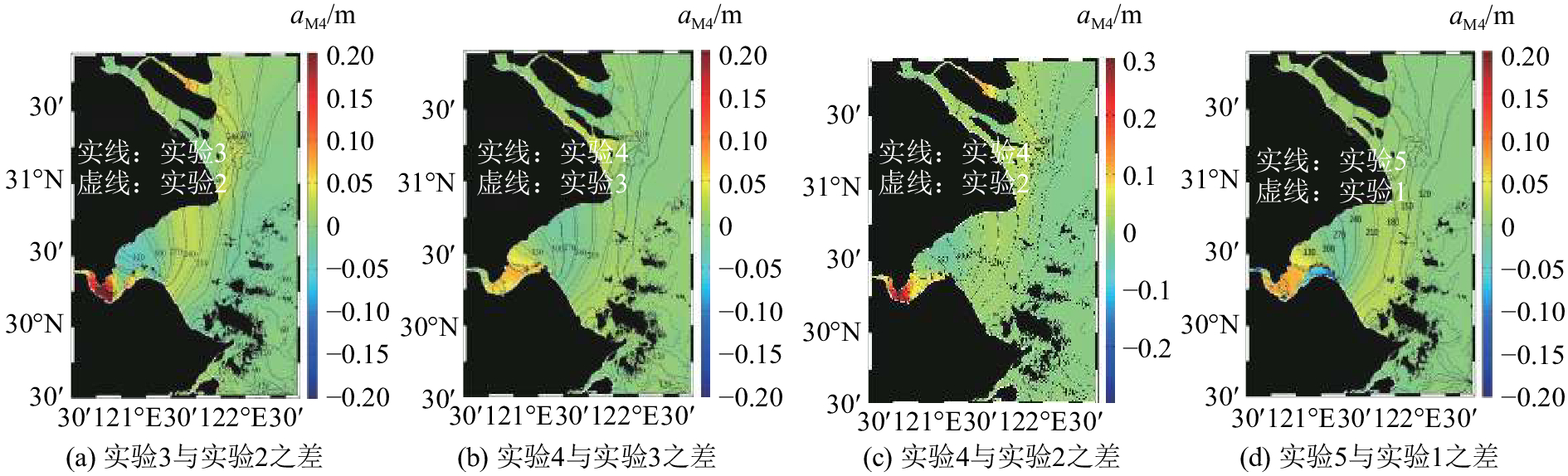
图 8 各实验之间M4振幅之差与相位对比 Fig. 8 Difference in M4 amplitude and phase between experiments |
1974—2005年,M4分潮振幅变化最大约为0.2 m(图8(a)),湾上部略微小于0 m,湾下部略微大于0 m,幅度范围为0~0.05 m,湾口南和湾顶M4滞后到达,金山断面附近提前到达. 2005—2016年,M4分潮振幅的变化如图8(b)所示,杭州湾湾顶值增加0.05 m左右,金山减少0.03 m左右;长江南港增加0.02 m左右和北支中部增加0.03 m左右,湾口南提前而金山断面以上滞后. 1974—2016年M4分潮振幅的总变化如图8(c)所示,尖山附近增加0.25 m左右,长江北支增加0.1 m左右,其他区域相对于以上2个区域的变化值较小,主要是湾顶M4分潮滞后较大.
潮滩减少使得M4振幅增加(图8(d),实验5与实验1对比),表明该区域潮滩对M4分潮底摩擦的耗损值大于对流的增加值. M4分潮是M2分潮传播到近岸浅水区域产生的,所以M4振幅在以上区域增加与M2振幅增加正相关. 潮滩的消失也减少了底摩阻,导致M4分潮的振幅在以上区域增加.
3.2.3 潮能通量对比1974—2005年,潮能通量从澉浦断面中部到金山断面中部减小较为明显,其中减小值最大约为3×104 W/m(图9(a)). 2005—2016年,潮能通量在庵东浅滩正北和东部水域的变化较为明显,减小值最大约为3×104 W/m(图9(b)). 1974—2016年,潮能通量从金山到澉浦段明显减小,累积减小值最大约为5×104 W/m(图9(c)). 螺头水道(图1)潮能减少值最大约为2×104 W/m,其他水域的潮能变化相比以上区域并不明显. 岸线改变使得潮位增加,流速减小导致潮能通量的减少.

|
图 9 各实验之间潮能通量对比 Fig. 9 Difference in tidal energy flux between experiments |

|
图 10
各实验之间
|
1974—2005年,杭州湾尖山断面
2005—2016年,澉浦断面
1974—2016年杭州湾-钱塘江河口和长江口的岸线变化导致的尖山断面、杭州湾口和长江口门处海域涨潮更有优势,而乍浦断面和金山断面之间涨潮优势减弱(图10(c)). 1974—2016年M2和M4振幅和相位的变化导致
由于在杭州湾水域
1974—2016年,长江口-杭州湾-三门湾海域的岸线逐渐向海域推进,导致岸线走向和过水断面等地形发生较大改变,扭曲了水流. 遥感图片分析结果显示,曹娥江口向水域推进15 km,尖山向水域推进近7 km,杭州湾南岸向水域推进约7 km,长江口与杭州湾之间的南汇推进10 km,长江口内的崇明岛、长兴岛和横沙岛围填面积很大.
1974—2005年岸线变化导致M2分潮振幅从金山到杭州湾湾顶和长江口北支内增加. M4分潮振幅在澉浦以上最大增幅达0.2 m,澉浦到金山略有减小,金山断面至湾口M4振幅增加0.05 m左右. 从单宽潮能通量来看,澉浦断面中部到金山断面中部减小值最大约为3×104 W/m. 岸线改变使得尖山断面附近和湾口涨潮优势增强,乍浦-庵东断面附近涨潮优势减弱. 2005—2016年岸线变化引起M2振幅在金山断面到澉浦断面之间水域增加0.05 m左右. 杭州湾湾顶M4振幅增加0.04 m左右,金山附近海域减小0.03 m左右. 从单宽潮能来看,庵东浅滩正北、东部水域潮能通量减少最大达3×104 W/m. 同时,岸线改变使得湾顶澉浦断面附近和舟山群岛海域涨潮更有优势,金山断面到芦潮断面和长江口北支口处涨潮优势有所减弱.
1974—2016年岸线改变使得M2振幅从金山附近增加0.1 m左右,逐渐增大到尖山附近增加0.6 m左右,从长江口北支从口门处增加0.1 m到中部增加0.3 m. M4振幅在尖山附近增加0.25 m左右,其次是长江北支增加0.1m左右. 潮能通量在金山到澉浦之间减小值最大约为5×104 W/m. 尖山断面、杭州湾口和长江口门处海域,涨潮更有优势,乍浦断面和金山断面之间涨潮的优势减弱.
建立的杭州湾-长江口海域水动力数值模型仅考虑了潮波动力和径流作用,没有考虑风场及波浪作用,研究结果具有一定的局限性. 同时岸线变化势必也会对杭州湾海域泥沙动力、海床冲淤变化产生影响,下阶段将考虑多种动力要素,建立杭州湾水动力泥沙数值模型,对岸线变化影响下杭州湾泥沙动力特征的变化展开研究.
| [1] |
韩曾萃, 潘存鸿. 钱塘江河口治导线探索[J]. 浙江水利科技, 2017, 209(1): 58-63. HAN Zeng-cui, PAN Cun-hong. The exploration of the regulation line for Qiantang estuary[J]. Zhejiang Hydrotechnics, 2017, 209(1): 58-63. |
| [2] |
杨金中, 李志中, 赵玉灵. 杭州湾南北两岸岸线变迁遥感动态调查[J]. 国土资源遥感, 2002, 51(1): 23-28. YANG Jin-zhong, LI Zhi-zhong, ZHAO Yu-ling. The remote sensing monitoring of Hangzhouwan banks[J]. Remote Sensing for Land and Resources, 2002, 51(1): 23-28. DOI:10.3969/j.issn.1001-070X.2002.01.006 |
| [3] |
花一明. 杭州湾滩涂围垦及利用动态遥感监测研究[D]. 杭州: 浙江大学, 2016: 79 HUA Yi-ming. Study on the expansion of reclamation and land use changes in Hangzhou Bay [D]. Hangzhou: Zhejiang University, 2016: 79 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2980747 |
| [4] |
黄赛花, 吴彦坤, 孙志林. 海湾工程对杭州湾北岸深槽潮流的影响[J]. 浙江大学学报: 理学版, 2015, 42(5): 605-611. HUANG Sai-hua, WU Yan-kun, SUN Zhi-lin. Impact of the gulf projects on the tidal currents of deep channel in the northern coast of Hangzhou Bay[J]. Journal of Zhejiang University: Science Edition, 2015, 42(5): 605-611. |
| [5] |
李身铎, 顾思美. 杭州湾潮波三维数值模拟[J]. 海洋与湖沼, 1993, 24(1): 7-15. LI Shen-duo, GU Si-mei. 3D numerical simulation of tidal wave in Hangzhou Bay[J]. Oceanologia et Limnologia Sinica, 1993, 24(1): 7-15. |
| [6] |
吴修广, 刘光生, 程文龙. 基于FVCOM的杭州湾三维泥沙数值模拟[J]. 水利水运工程学报, 2011, 4(4): 86-96. WU Xiu-guang, LIU Guang-sheng, CHENG Wen-long. 3D numerical simulation of sediment in the Hangzhou Bay based on FVCOM[J]. Hydro-Science and Engineering, 2011, 4(4): 86-96. DOI:10.3969/j.issn.1009-640X.2011.04.014 |
| [7] |
GUO Y K, ZHANG J S, ZHANG L X, et al. Computational investigation of typhoon-induced storm surge in Hangzhou Bay, China[J]. Estuarine, Coastal and Shelf Science, 2009, 130(4): 530-536. |
| [8] |
鲁友鹏, 梁书秀, 孙昭晨, 等. 湾南岸岸线变化对水动力的影响累积效应[J]. 海洋环境科学, 2015, 34(3): 384-390. LU You-peng, LIANG Shu-xiu, SUN Zhao-chen, et al. Cumulative efects of topography change on waterway's hydrodynamic along the southern coast of Hangzhou Bay[J]. Marine Environmental Science, 2015, 34(3): 384-390. |
| [9] |
SONG D, WANG X H, ZHU X, et al. Modeling studies of the far-field effects of tidal flat reclamation on tidal dynamics in the East China Seas[J]. Estuarine, Coastal and Shelf Science, 2013, 133: 147-160. DOI:10.1016/j.ecss.2013.08.023 |
| [10] |
谢东风, 潘存鸿, 吴修广. 基于FVCOM模式钱塘江河口涌潮三维数值模拟研究[J]. 海洋工程, 2011, 29(1): 47-52. XIE Dong-feng, PAN Cun-hong, WU Xiu-guang. Three-dimensional numeriacal modeling of tidal bore in Qiantang base on FVCOM[J]. The Ocean Engineering, 2011, 29(1): 47-52. DOI:10.3969/j.issn.1005-9865.2011.01.007 |
| [11] |
冯利华, 鲍毅新. 曹娥江出口江道的演变与整治[J]. 水科学进展, 2005, 16(1): 52-55. FENG Li-hua, BAO Yi-xin. Evolvement of water outlet of Cao'e River and its dredging[J]. Advances in Water Science, 2005, 16(1): 52-55. DOI:10.3321/j.issn:1001-6791.2005.01.011 |
| [12] |
邵明明. 围垦工程对杭州湾潮波动力过程的影响研究[D]. 杭州: 浙江大学, 2016: 87 SHAO Ming-ming. Impacts of reclamation on tidal dynamics in Hangzhou Bay [D]. Hangzhou: Zhejiang University, 2016: 87 http://xuewen.cnki.net/CMFD-1016182974.nh.html |
| [13] |
冯永玖, 袁佳宇, 宋丽君, 等. 杭州湾海岸线信息的遥感提取及其变迁分析[J]. 遥感技术与应用, 2015, 30(2): 345-352. FENG Yong-jiu, YUAN Jia-yu, SONG Li-jun, et al. Coastline mapping and change detection along Hangzhou Bay using remotely sensed imagery[J]. Remote Sensing Technology and Application, 2015, 30(2): 345-352. |
| [14] |
贾明明, 刘殿伟, 王宗明, 等. 面向对象方法和多源遥感数据的杭州湾海岸线提取分析[J]. 地球信息科学学报, 2013, 15(2): 262-269. JIA Ming-ming, LIU Dian-wei, WANG Zong-ming, et al. Coastline changes in Hangzhou Bay based on object-oriented method using multi-source remote sensing data[J]. Journal of Geo-information Science, 2013, 15(2): 262-269. |
| [15] |
ZHU L, HE Q, SHEN J, et al. The influence of human activities on morphodynamics and alteration of sediment source and sink in the Changjiang Estuary[J]. Geomorphology, 2016, 273: 52-62. DOI:10.1016/j.geomorph.2016.07.025 |
| [16] |
曹颖, 林炳尧. 杭州湾潮汐特性分析[J]. 浙江水利水电专科学校学报, 2000, 12(3): 14-16. CAO Ying, LIN Bing-yao. Tidal characteristics of Hangzhou Bay[J]. Journal of Zhejiang University of Water Resources and Electric Power, 2000, 12(3): 14-16. DOI:10.3969/j.issn.1008-536X.2000.03.008 |


