2. 贵州省水利水电勘测设计研究院,贵州 贵阳 550002;
3. 贵州省喀斯特地区水资源开发利用工程技术研究中心,贵州 贵阳 550002
2. Guizhou Survey/Design Research Institute for Water Resources and Hydropower, Guiyang 550002, China;
3. Guizhou Engineering Technology Research Center for Exploitation and Utilization of Water Resources in Karst region, Guiyang 550002, China
混凝土坝体开裂长期困扰工程界,大量研究表明,大体积混凝土的结构失效和耐久性问题大多是因早龄期开裂引起的[1]. 由于混凝土材料的早期抗拉强度非常低,混凝土构件在热应力、自收缩以及外荷载作用下极易产生裂缝. 在混凝土完全硬化之前,整个结构的耐久性和工作寿命会由于混凝土早龄期阶段产生的各种裂缝而受到严重影响. 因此,对大体积混凝土结构的早龄期开裂及裂缝扩展演化过程进行分析就显得尤为重要[2-3].
混凝土的早龄期是其各项性能形成和发展最为关键的时期. 伴随着水化反应的进行,混凝土细观结构发生剧烈演变,材料强度迅速形成和发展. 因此,有必要考虑结构内部温度、水化热生成速率以及强度增长速率之间的直接联系,以一种更合理的方式模拟早龄期混凝土热、力学性能的发展进程. 然而,常规计算分析通常简化了混凝土早龄期阶段的水化过程,也没有考虑水化度对混凝土材料性能(如弹性模量、抗压强度、抗拉强度等)的影响[4],在预测混凝土的力学性质过程中存在较大偏差.
国外关于早龄期混凝土性能的相关研究中,Cervera等[5-6]提出一种水化度模型以模拟混凝土的化学-热-力耦合行为,可以采用有限单元法实现并且预测水化度和水化热随时间的演化规律. Lackner等[7]找到了用于描述本构方程的材料断裂能与水化度之间的关系,提出另一种多项式描述水化反应化学亲和力的公式. Klemczak[8]利用程序 TEMWIL 结合水化度模型模拟大体积混凝土的热量及水分传输的过程,实质上,水化度模型是基于等效时间的,并不能完全考虑热-化学耦合因素. Hilaire 等[9]研究水化过程中混凝土在拉、压荷载下的基础徐变规律.
国内关于水化数值计算模型的研究在近几年发展较快. 黄耀英等[10]采用基于等效时间成熟概念的绝热温升模型,研究混凝土在考虑水管冷却效应条件下的等效热传导过程. 杜明月等[11]基于Krustlovi-Dabi水化动力学方程式,分析混凝土温度场和湿度场的耦合效应. Zhou等[12-13]针对Cervera等[5-6]提出的水化度模型做出一定修正,与Cervera等提出的水化度模型和试验数据相比,修正后的水化度模型更为精确.
混凝土结构的开裂行为是材料本身在外荷载作用下和周围环境约束下的损伤破坏行为. 以往的研究主要可分为2类:一类从宏观层次出发,结合各种类型的屈服准则,探讨混凝土损伤或断裂过程,但是无法反映混凝土材料的组成对力学响应的影响;另一类从细观层次出发,区分混凝土的骨料、砂浆以及界面过渡区(internal transition zone, ITZ)三相介质,不仅考虑混凝土材料的不均匀性,而且结合一些简单的损伤模型或屈服准则后可以探讨混凝土内裂纹萌生、扩展、贯通的全过程. 在混凝土细观力学特性研究中,刘光廷等[14]对混凝土随机骨料模型生成投放方法进行研究. 马怀发等[15]采用凸多面体骨料模型对混凝土细观力学性质进行计算分析. 有研究考虑混凝土细观结构组成的非均匀性,采用连续介质力学研究思路,通过物理试验与数值试验相结合的方法,模拟混凝土类材料的损伤断裂过程[16].
通常,采用细观力学的方法更能深入探讨混凝土裂缝发生的机理. 然而,细观力学方法存在局限性. 力学参数的确定是细观力学中的难点之一,各相介质的材料属性不论取为定值或是随机分布都是不全面的,无法真实地反映混凝土内部材料属性的空间分布特性. 混凝土的化学-热-力耦合模型是从本质的化学反应出发,可以很好地预测混凝土材料特性的发展情况. 将混凝土化学-热-力耦合的性能演变模型引入细观力学损伤特性研究中,根据混凝土的温度边界情况及养护条件合理预测混凝土力学性能的分布特性,在细观层次上实现早龄期混凝土单轴拉伸试验的数值模拟,并研究裂缝扩展情况及损伤特性.
1 化学-热-力耦合模型 1.1 化学-热耦合过程以Arrhenius化学反应动力学理论为基础的水化度模型被学术界广泛接受[17]. 根据Arrhenius定律,与时间相关的水化过程可用式(1)进行描述. 水化度模型中,水化反应速率与温度、化学反应亲和力
| $\displaystyle\frac{{\partial \xi }}{{\partial t}} = {A_\xi }\left( \xi \right){\rm{exp}}\left( { - \displaystyle\frac{{{E_{\rm a}}}}{{RT}}} \right).$ | (1) |
式中:
| ${A_\xi }\left( \xi \right) = {\beta _1}\left( {{\beta _2} + {\beta _3}\xi + {\xi ^2}} \right)\left( {{\xi _\infty } - \xi } \right)\exp\; \left( { - \bar \eta \displaystyle\frac{\xi }{{{\xi _\infty }}}} \right).$ | (2) |
式中:
修正后的水化度模型的优点在文献[12]中有所讨论. 特别地,由于大体积混凝土结构的施工期相当长(通常为数月甚至数年),考虑到长期的水化过程,将最终水化度
混凝土的瞬态热传导过程如下:
| $\rho c\displaystyle\frac{{\partial T\left( {x,y,z,t} \right)}}{{\partial t}} = {\lambda _T}\Delta T\left( {x,y,z,t} \right) + \displaystyle\frac{{\partial Q}}{{\partial t}},$ | (3) |
| $\displaystyle\frac{{\partial Q}}{{\partial t}} = {Q_\infty }\displaystyle\frac{{\partial \xi }}{{\partial t}}.$ | (4) |
式中:
为描述混凝土力学性质随水化程度的演变过程,准确地获取混凝土的力学参数,并且模拟水化过程中混凝土在荷载作用下的损伤演化过程,引入水化度损伤模型[19-20]. 模型可以较好地预测混凝土材料在损伤过程中抗拉性能的退化,但是在双轴或三轴高围压条件下适用性较差. 考虑到混凝土的开裂主要发生在早龄期阶段,应力水平较低,类似于低围压状态,采用这一模型进行数值模拟是合适的.
混凝土材料的表观应力为
| ${{\sigma }} = \left( {1 - D} \right){\tilde{ \sigma }},$ | (5) |
| $ \dot {\tilde \sigma} = \mathit{\boldsymbol{E}}\left( \xi \right){\mathit{\boldsymbol{\dot \varepsilon }}_{\rm{e}}} = \mathit{\boldsymbol{E}}\left( \xi \right)\left( {\mathit{\boldsymbol{\dot \varepsilon }} - {{\mathit{\boldsymbol{\dot \varepsilon }}}_{{\rm{as}}}} - {{\mathit{\boldsymbol{\dot \varepsilon }}}_{{\rm{th}}}}} \right). $ | (6) |
假设泊松比
| $E\left( \xi \right) = {E_\infty }{\bar \xi ^\beta },$ | (7) |
| $\bar \xi = {\left\langle {\displaystyle\frac{{\xi - {\xi _0}}}{{{\xi _\infty } - {\xi _0}}}} \right\rangle _ + }.$ | (8) |
式中:
由于压应力相对于混凝土抗压强度来说非常小,只考虑混凝土的拉裂损伤. 混凝土抗拉强度随水化度的变化关系[19]为
| ${f_{\rm t}}\left( \xi \right) = {f_{{\rm t}\infty }}{\bar \xi ^\gamma }.$ | (9) |
式中:
损伤因子D可以由弹性等效拉伸应变
| $\hat \varepsilon = \sqrt {{{\left\langle {{{{\varepsilon }}_{{\rm{e}}}}} \right\rangle }_ + }:{{\left\langle {{{{\varepsilon }}_{{\rm{e}}}}} \right\rangle }_ + }} .$ | (10) |
由Mazars[20]提出的损伤准则:
| $f = \hat \varepsilon - \kappa .$ | (11) |
式中:
| $f \leqslant 0,\;\;\;\dot \kappa \geqslant 0,\;\;\;\dot \kappa f = 0.$ | (12) |
上述关系表明,如果
| $D\left( \xi \right) = 1 - \displaystyle\frac{{{\varepsilon _0}}}{\kappa }{\rm {ex}}{\rm p} \left( { - \displaystyle\frac{{\kappa - {\varepsilon _0}}}{{{\varepsilon _{\rm f}}}}} \right),\;\;\;\kappa \geqslant {\varepsilon _0},$ | (13) |
| ${\varepsilon _0}\left( \xi \right) = \frac{{{{\rm f}_{\rm t}}\left( \xi \right)}}{{E\left( \xi \right)}} = \displaystyle\frac{{{{\rm f}_{{\rm t}\infty }}}}{{{E_\infty }}}{\bar \xi ^{\gamma - \beta }},$ | (14) |
| ${\varepsilon _f}\left( \xi \right) = \displaystyle\frac{{{\varepsilon _0}\left( \xi \right)}}{2} + \displaystyle\frac{{{G_{{\rm ft}}}\left( \xi \right)}}{{{{\rm f}_{\rm t}}\left( \xi \right){l_{\rm f}}}}.$ | (15) |
式中:lf为特征长度. 混凝土材料抗拉性能的软化主要由抗拉强度
| ${G_{{\rm ft}}}\left( \xi \right) = {G_{{\rm ft}}}{\bar \xi ^\delta }.$ | (16) |
式中:
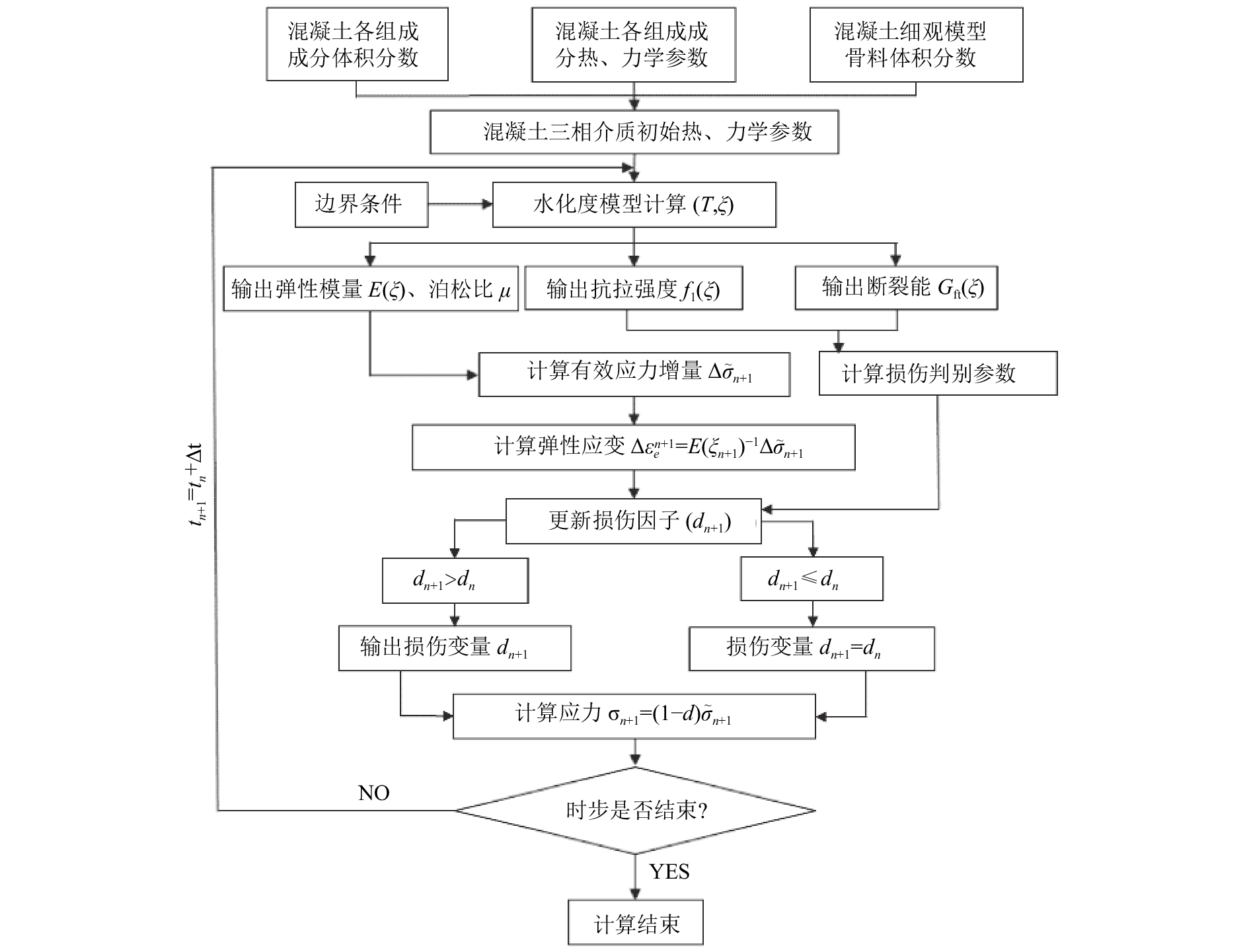
模型的细观参数率定、水化度计算、损伤更新过程和边界条件加载等如图1所示.
|
图 1 水化度损伤模型计算流程 Fig. 1 Algorithm of hydration damage model |
在化学-热-力耦合模型中,水化度是决定混凝土材料热学性能的中间变量. 结合相关文献的研究,采用适用于各向异性材料的均匀化方法来估算混凝土材料三相介质相应的比热容和导热系数.
在水泥、水和骨料各自的比热容和体积分数已知的情况下,砂浆基质的比热容用下式进行估算[26]:
| $\left. \begin{array}{l}{c_{{\rm{freshpaste}}}} = {c_{{\rm{water}}}}{\phi_{{\rm{water}}}} + {c_{{\rm{cement}}}}{\phi_{{\rm{cement}}}},\\{c_{{\rm{paste}}}}\left( \xi \right) = {c_{{\rm{freshpaste}}}}\left\{ {1 - A\left[ {1 - {\rm ex}{\rm p}\; \left( { - B\xi } \right)} \right]} \right\},\\{c_{{\rm{concrete}}}} = {c_{{\rm{paste}}}}{\phi_{{\rm{paste}}}} + {c_{{\rm{agg}}}}{\phi_{{\rm{agg}}}} + {c_{{\rm{filler}}}}{\phi_{{\rm{filler}}}}. \end{array} \right\}$ | (17) |
式中:
砂浆基质的导热系数采用Hashin-Shtrikman界限进行估算,主要由试验测得的细观各相的导热系数(
| $\left. \begin{aligned}{\lambda _{l}} = {\lambda _1} + \displaystyle\frac{{{\phi_2}}}{{\displaystyle\frac{1}{{{\lambda _2} - {\lambda _1}}} + \displaystyle\frac{{{\phi_1}}}{{3{\lambda _1}}}}},\\{\lambda _{u}} = {\lambda _2} + \displaystyle\frac{{{\phi_1}}}{{\displaystyle\frac{1}{{{\lambda _1} - {\lambda _2}}} + \displaystyle\frac{{{\phi_2}}}{{3{\lambda _2}}}}}. \end{aligned} \right\}$ | (18) |
两相复合材料的有效导热系数
| ${\lambda _{\hom }} = \displaystyle\frac{{{\lambda _{l}} + {\lambda _{u}}}}{2}.$ | (19) |
根据文献[26-27],水泥浆的导热系数是体积分数的函数并且与水化度不相关. 因此,忽略导热系数的非线性行为.
研究所用混凝土为大岗山大坝C180 36混凝土,配比如表1所示. 混凝土各组分的热学参数见表2. 采用式(17)~(19)得到的混凝土材料三相介质相应的热学参数如表3所示,界面过渡区的热学参数与砂浆取为一致.
| 表 1 混凝土各组成成分的质量浓度 Table 1 Content of the composition of concrete |
| 表 2 混凝土各组分热学参数 Table 2 Thermal parameters of concrete components |
| 表 3 骨料、砂浆及界面过渡区的热学参数 Table 3 Thermal parameters of aggregate, cement and ITZ |
混凝土的弹性模量与抗拉强度是影响混凝土变形及抗拉性能的主要指标,参数取值准确对研究混凝土的拉裂损伤性能及裂纹扩展规律起着至关重要的作用. 影响因素主要有水泥品种、水胶比、掺和料、骨料级配及种类、龄期以及外界温度等.
使用Hashin-Shtrikman界限来推求混凝土的细观力学参数. 目前业内关于界面过渡区的力学参数取值有很多研究. Yang[28]发现,当界面厚度为20 μm时,过渡区平均弹性模量是砂浆弹性模量的20%~40%;当界面厚度为40 μm时,过渡区平均弹性模量是砂浆弹性模量的50%~70%. 将界面过渡区的弹性模量和抗拉强度取为砂浆基质的0.6倍.
表4列出了由大岗山施工现场物理时测得的C180 36混凝土7、28、90、180 d龄期时的弹模和抗拉强度值. 结合骨料的相关参数及质量浓度,采用式(18)、(19)推算砂浆基质、ITZ各龄期相应的弹性模量及抗拉强度值,具体计算结果如表4所示. 在计算过程中,骨料的弹性模量为50 GPa、抗拉强度为8 MPa.
| 表 4 混凝土、砂浆及界面过渡区的弹性模量及抗拉强度值 Table 4 Elastic modulus and tensile strength values of concrete, cement paste and ITZ |
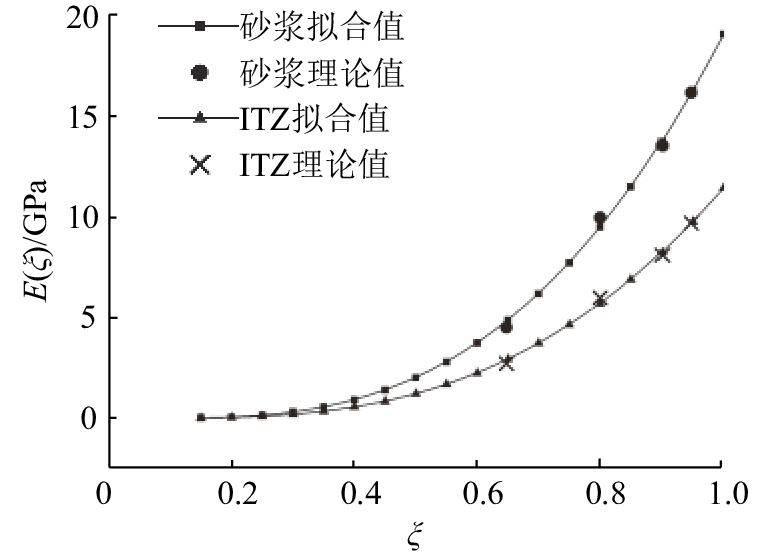
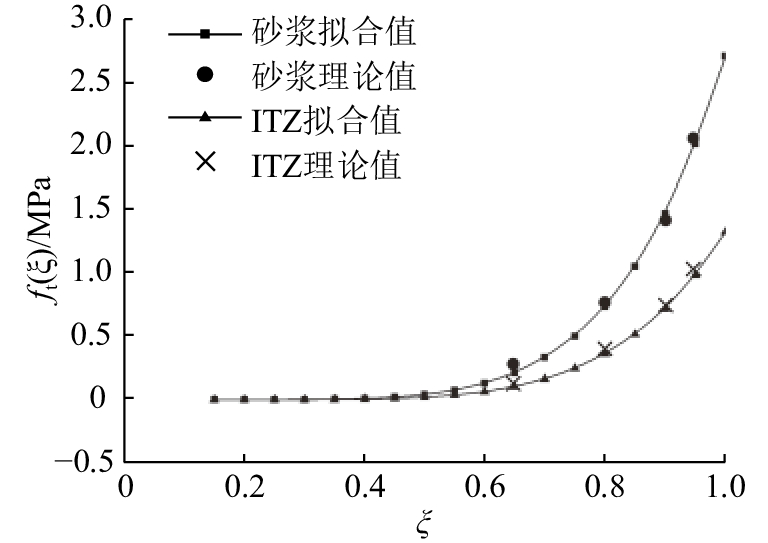
由表4砂浆基质和ITZ不同龄期时的弹性模量、抗拉强度值,结合式(7)~(9)拟合相应的力学参数如表5所示. 参考唐欣薇[29]的研究,骨料、砂浆基质和界面过渡区的断裂能和泊松比参数取值也列于表5中. 图2、3显示了砂浆和界面过渡区的弹性模量、抗拉强度随水化度的发展规律.
| 表 5 混凝土、砂浆及界面过渡区的力学参数 Table 5 Mechanical parameters of aggregate, cement and ITZ |
|
图 2 砂浆、界面过渡区的弹性模量变化曲线 Fig. 2 Elastic modulus evolution of cement paste and ITZ |
|
图 3 砂浆、界面过渡区的抗拉强度变化曲线 Fig. 3 Tensile strength evolution of cement paste and ITZ |
在单轴拉伸数值试验中采用二维平面应变模型,数值试样尺寸为200 mm×200 mm. 结合细观力学随机骨料模型生成方法,按照Fuller级配理论将混凝土划分为由凸多边形骨料、砂浆和界面过渡区组成的三相介质. 单轴拉伸数值试验中混凝土骨料最大粒径为40 mm,与常规室内湿筛试件最大骨料粒径相同,随机骨料面积填充率为50%.
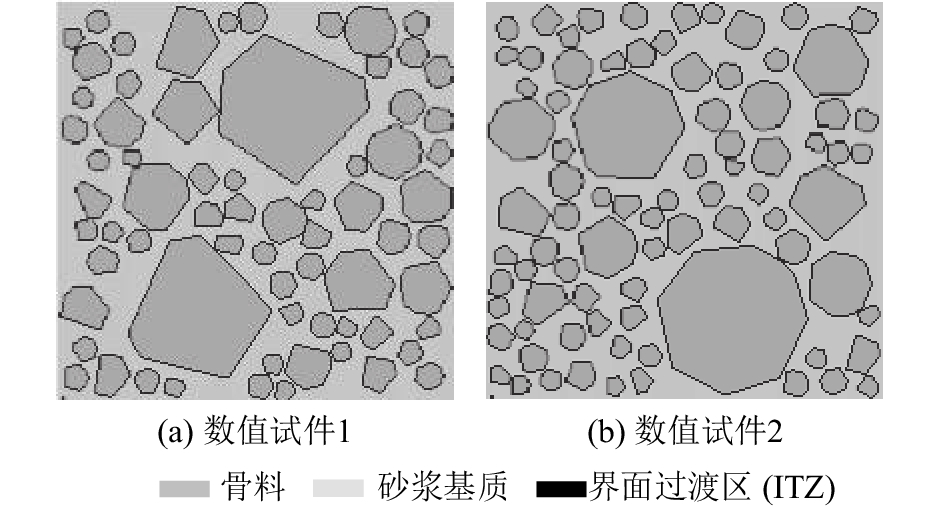
考虑到不同的凸多边形骨料形状、数目以及在平面内的投放位置对试件的力学响应有一定影响,进行数值试验时,根据相同的骨料填充率随机生成2组数值试件,数值试件1和2均为40 000个单元,具体骨料分布情况如图4所示.
依据文献[6]可知,混凝土破坏过程中,损伤和断裂主要发生在骨料和砂浆的薄弱胶结面处,随后往骨料和砂浆内扩展. 除高性能混凝土外,由于骨料强度往往高于混凝土基质,裂纹主要产生在砂浆和界面过渡区. 因此,将骨料单元作弹性处理,在砂浆和界面过渡区单元中引入1.2节介绍的水化度损伤模型来模拟裂缝的演化扩展过程.
在数值试验过程中,试件底部采用两向全约束,试件左侧及右侧自由,位移荷载施加于试件顶部,最大加载位移控制为
|
图 4 单轴拉伸数值试件 Fig. 4 Numerical specimens in uniaxial tensile test |
| 表 6 砂浆、界面过渡区的水化度模型参数 Table 6 Parameters for hydro-thermal model of cement paste and ITZ |

|
图 5 7 d龄期时不同试件的水化性态 Fig. 5 Hydration degree of different specimens at age of 7 d |
2组数值试件在7 d龄期时砂浆水化程度的分布情况如图5所示. 两组试件水化度分布存在一定的差异. 依据弹性模量以及抗拉强度与水化度之间的正比关系,试件1、2中弹性模量和抗拉强度的分布也存在空间上的差异性,这对研究早龄期混凝土的力学性能演化有重要的作用.
|
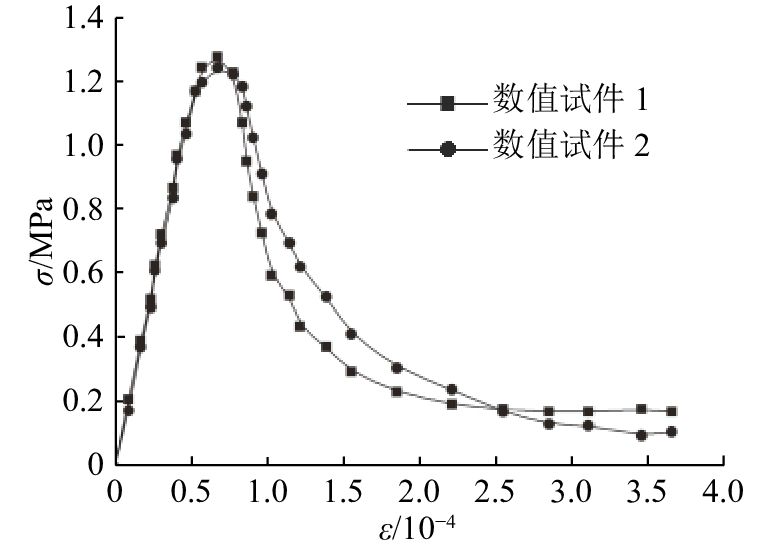
图 6 7 d龄期时数值试件1和2的单轴拉伸应力-应变曲线 Fig. 6 Stress-strain curves of uniaxial tensile test of specimen 1 and 2 at age of 7 d |
图 6显示2组试件7 d龄期时在单轴拉伸加载下的应力-应变关系. 即使采用同一套数值试验参数和同样的骨料填充率,由于骨料位置和形状分布的随机性,每组试验中所用试件均具有不同的细观结构,所得到的应力-应变关系曲线也存在一定差异. 但是不同的试件在加载过程中都先后经历了线弹性、初始裂纹萌生、裂纹稳定扩展和试件失稳破坏4个阶段. 在加载初期,数值试件均表现出线弹性,应力-应变关系基本为直线. 随着加载的进行,由于骨料与砂浆胶结面处强度低,部分界面过渡区单元首先出现损伤,应力-应变关系逐渐偏离直线,表现出非线性特性. 当试件达到峰值抗拉强度后,部分砂浆单元逐渐出现损伤,微裂纹逐步发展成宏观裂纹,最后相互贯通,试件呈现出整体断裂的特点. 数值试件1在7 d龄期进行加载时得到的最大拉应力略大于试件2,但是试件1断裂后,表现出更大的残余强度.
|
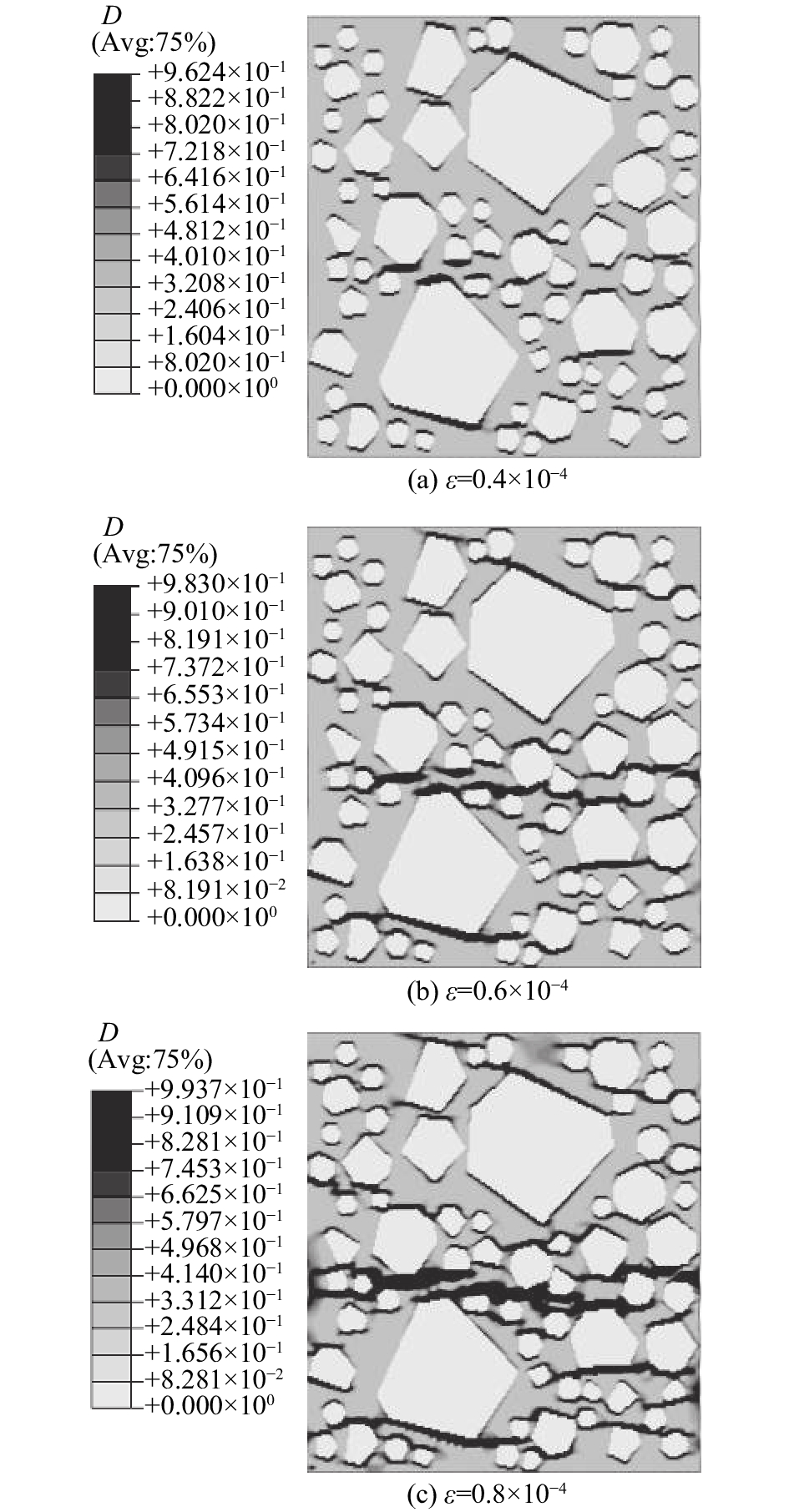
图 7 7 d龄期时数值试件1拉伸破坏过程 Fig. 7 Failure process of specimen 1 at age of 7 d |

|
图 8 7 d龄期时数值试件2拉伸破坏过程 Fig. 8 Failure process of specimen 2 at age of 7 d |
图7和8分别为数值试件1、2在7 d龄期进行加载时的破坏过程. 对比图7、8可以看出,由于2组数值试件细观结构的差异,2组试件在相同加载条件下所呈现的渐进损伤破坏过程也不相同. 试件1的拉伸破坏过程为在加载初期,大部分骨料与砂浆的胶结面位置均出现一定程度的损伤,随着加载继续进行,试件内部微裂纹萌生并且逐步由中心向两侧扩展、贯通,最终在试件的中部位置形成一条完整的宏观裂缝,导致试件失稳破坏. 试件2在加载初期呈现的损伤状态与试件1基本一致,但是随着单轴拉伸试验的进行,微裂纹在试件2中多个位置出现,最后在试件上、中、下部区域共形成4条宏观意义上的裂缝,此时试件已丧失承载能力.
| 表 7 不同数值试件各龄期抗拉强度值 Table 7 Tensile strength of two numerical specimens |
|
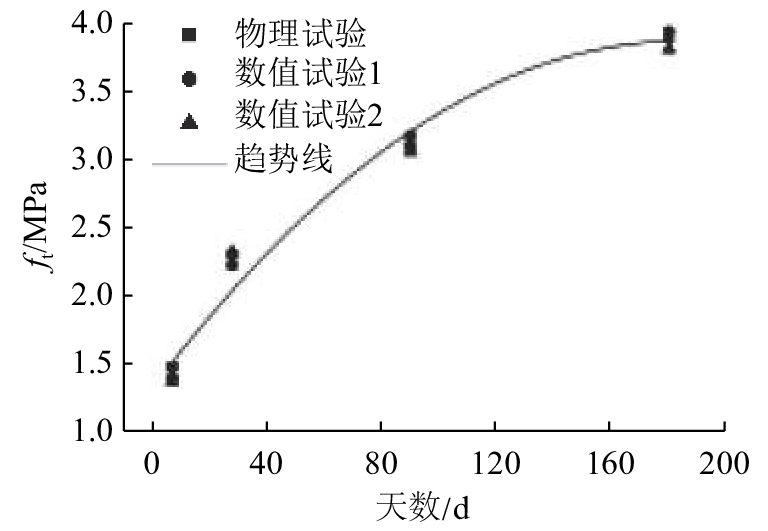
图 9 不同试件各龄期的抗拉强度值及拟合的增长曲线 Fig. 9 Tensile strength and fitting growth curve of different specimens at different ages |
表7列出了2组数值试件分别在7、28、90和180 d龄期进行加载后得到的相应龄期的抗拉强度值. 图9将单轴拉伸数值试验得到的2组抗拉强度值与宏观物理试验数据进行对比,并且拟合出拉伸强度增长过程. 表7及图9的结果显示,在单轴拉伸试验的数值模拟中引入水化度损伤模型后,2组试件各龄期的抗拉强度值与宏观物理试验结果吻合良好,因此,模型较为准确地模拟了早龄期混凝土试件的单轴拉伸破坏过程.
3 结 语有效结合混凝土细观力学方法与混凝土性能演变理论的优点,将性能演变过程引入细观力学研究中. 借助随机骨料模型研究方法,将混凝土视为由凸多边形骨料、砂浆和界面过渡区组成的三相介质,在砂浆和界面过渡区单元中引入水化度损伤模型,通过定义损伤因子实现早龄期混凝土损伤开裂过程的数值模拟. 主要的工作与结论总结如下.
1)不同于常规的随机力学特性的分布模型,混凝土试件材料参数来源于混凝土化学-热-力耦合的性能演变模型,模型可以考虑试件养护条件(温度历史)对试件材料特性的影响.
2)在混凝土配合比及各组分材料参数的基础上开展参数研究. 首先,结合绝热温升物理试验对混凝土化学-热-力学特性的水化度模型进行参数率定;其次,结合混凝土各个龄期的弹性模量及抗拉强度试验结果建立这些力学参数与水化度的联系.
3)在合理的参数研究基础上,采用随机骨料模型进行细观计算. 结果显示水化度的空间分布差异性对早龄期混凝土的弹性模量、抗拉强度、断裂能等力学参数的取值存在显著影响.
4)在单轴拉伸数值试验中引入水化度损伤模型,结果表明,试件各龄期抗拉强度值与宏观物理试验结果吻合良好. 损伤因子直观反映了混凝土试件中微裂缝萌生、扩展直至贯通的全过程,模型可以为早龄期混凝土结构的拉伸损伤断裂过程分析提供有力的数值工具.
5)即使采用同一套材料参数和同样的骨料填充率,由于骨料位置和形状分布的随机性,每组数值试验中所用试件仍然具有不同的细观结构. 在相同的加载条件下,应力-应变关系曲线和试件损伤开裂状态也存在一定差异. 但是不同试件在加载过程中,都先后经历了线弹性、初始裂纹萌生、裂纹稳定扩展和试件失稳破坏4个阶段.
6)目前细观力学数值模拟离替代物理试验还有相当长的距离,但是将性能演变的理念引入细观力学,无疑是混凝土研究中一个重要的方向. 水化度损伤模型的本构、跨尺度连接混凝土宏细观力学性质的方法、全级配混凝土荷载响应、长期加载条件下混凝土的损伤过程(需考虑徐变效应)等,是目前研究领域较少涉及的.
水化过程中的损伤存在可逆的可能性,然而数值模拟的实现难度较大,损伤修复机制也缺乏大量的实践作为支撑. 损伤研究采用单轴拉伸模型,选取合适龄期(如7 d、28 d等)的模型后,因为拉伸破坏持续时间很短,损伤过程的时效可以忽略,因此没有涉及损伤修复. 目前存在的不足之处值得在下一步工作中深入探讨.
| [1] |
BENBOUDJEMA F, TORRENTI J M. Early-age behaviour of concrete nuclear containments[J]. Nuclear Engineering and Design, 2008, 238(10): 2495-2506. DOI:10.1016/j.nucengdes.2008.04.009 |
| [2] |
GASCH T, MALM R, ANSELL A. A coupled hygro-thermo-mechanical model for concrete subjected to variable environmental conditions[J]. International Journal of Solids and Structures, 2016, 91: 143-156. DOI:10.1016/j.ijsolstr.2016.03.004 |
| [3] |
JENDELE L, SMILAUER V, CERVENKA J. Multiscale hydro-thermo-mechanical model for early-age and mature concrete structures[J]. Advances in Engineering Software, 2014, 72(2): 134-146. |
| [4] |
CHU I, YUN L, AMIN M N, et al. Application of a thermal stress device for the prediction of stresses due to hydration heat in mass concrete structure[J]. Construction and Building Materials, 2013, 45(13): 192-198. |
| [5] |
CERVERA M, FARIA R, OLIVER J, et al. Numerical modelling of concrete curing, regarding hydration and temperature phenomena[J]. Computers and Structures, 2002, 80(18/19): 1511-1521. |
| [6] |
CERVERA M, OLIVER J, PRATO T. Thermo-chemo-mechanical model for concrete. II: Damage and creep[J]. Journal of Engineering Mechanics, 1999, 125(9): 1028-1038. DOI:10.1061/(ASCE)0733-9399(1999)125:9(1028) |
| [7] |
LACKNER R, MANG H A. Chemoplastic material model for the simulation of early-age cracking: from constitutive law to numerical analyses of massive concrete structures[J]. Cement and Concrete Composites, 2004, 26(5): 551-562. DOI:10.1016/S0958-9465(03)00071-4 |
| [8] |
KLEMCZAK B. Prediction of coupled heat and moisture transfer in early-age massive concrete structures[J]. Numerical Heat Transfer, Part A: Applications, 2011, 60(3): 212-233. DOI:10.1080/10407782.2011.594416 |
| [9] |
HILAIRE A, BENBOUDJEMA F, DARQUENNES A, et al. Modeling basic creep in concrete at early-age under compressive and tensile loading[J]. Nuclear Engineering and Design, 2014, 269(4): 222-230. |
| [10] |
黄耀英, 郑宏, 夏开文, 等. 基于等效时间的混凝土水管冷却等效热传导[J]. 华中科技大学学报: 自然科学版, 2012, 40(2): 45-48. HUANG Yao-ying, ZHENG Hong, XIA Kai-wen, et al. Study on equivalent heat conduct of concrete using pipe cooling and equivalent time[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2012, 40(2): 45-48. |
| [11] |
杜明月, 田野, 金南国, 等. 基于水泥水化的早龄期混凝土温湿耦合[J]. 浙江大学学报(工学版), 2015, 49(8): 1410-1416. DU M Y, TIAN Y, JIN N G, et al. Coupling of hygro-thermal field in early-age concrete based on cement hydration[J]. Journal of Zhejiang University: Engineering Science, 2015, 49(8): 1410-1416. |
| [12] |
ZHOU W, FENG C, LIU X, et al. A macro-meso chemo-physical analysis of early-age concrete based on a fixed hydration model[J]. Magazine of Concrete Research, 2016, 68(19): 81-994. |
| [13] |
ZHOU W, FENG C, LIU X, et al. Contrastive numerical investigations on thermo-structural behaviors in mass concrete with various cements[J]. Materials, 2016, 9(5): 378. DOI:10.3390/ma9050378 |
| [14] |
刘光廷, 高政国. 三维凸型混凝土骨料随机投放算法[J]. 清华大学学报: 自然科学版, 2003, 43(8): 1120-1123. LIU Guang-ting, GAO Zheng-guo. Random 3-D aggregate structure for concrete[J]. Journal of Tsinghua University: Science and Technology, 2003, 43(8): 1120-1123. |
| [15] |
马怀发, 陈厚群, 吴建平等. 大坝混凝土三维细观力学数值模型研究[J]. 计算力学学报, 2008, 25(2): 241-247. MA Huai-fa, CHEN Hou-qun, WU Jian-ping, et al. Study on numerical algorithm of 3D meso-mechanics model of dam concrete[J]. Chinese Journal of Computational Mechanics, 2008, 25(2): 241-247. |
| [16] |
唐春安, 朱万成. 混凝土损伤与断裂—数值试验 [M]. 北京: 科学出版社, 2003: 10-143
|
| [17] |
SCHUTTER G D, TAERWE L. General hydration model for portland cement and blast furnace slag cement[J]. Cement and Concrete Research, 1995, 25(3): 593-604. DOI:10.1016/0008-8846(95)00048-H |
| [18] |
BENTZ D P, WALLER V, LARRARD F D. Prediction of adiabatic temperature rise in conventional and high-performance concretes using a 3-D microstructural model[J]. Cement and Concrete Research, 1998, 28(2): 285-297. DOI:10.1016/S0008-8846(97)00264-0 |
| [19] |
SCHUTTER G D. Degree of hydration based Kelvin model for the basic creep of early age concrete[J]. Materials and Structures, 1999, 32(4): 260-265. DOI:10.1007/BF02479595 |
| [20] |
MAZARS J. A description of micro-and macroscale damage of concrete structures[J]. Engineering Fracture Mechanics, 1986, 25(5/6): 729-737. |
| [21] |
TORRENTI J M, BENBOUDJEMA F. Mechanical threshold of cementitious materials at early age[J]. Materials and Structures, 2005, 38(3): 299-304. DOI:10.1007/BF02479294 |
| [22] |
SCHUTTER G D, TAERWE L. Degree of hydration-based description of mechanical properties of early age concrete[J]. Materials and Structures, 1996, 29(6): 335-344. DOI:10.1007/BF02486341 |
| [23] |
SCHUTTER G D, TAERWE L. Fracture energy of concrete at early ages[J]. Materials and Structures, 1997, 30(2): 67-71. DOI:10.1007/BF02486306 |
| [24] |
PIJAUDIER-CABOT G, BAŽANT Z P. Nonlocal damage theory[J]. Journal of Engineering Mechanics, 1987, 113(10): 1512-1533. DOI:10.1061/(ASCE)0733-9399(1987)113:10(1512) |
| [25] |
JIRÁSEK M, BAUER M. Numerical aspects of the crack band approach[J]. Computers and Structures, 2012, 110(10): 60-78. |
| [26] |
BENTZ D P. Transient plane source measurements of the thermal properties of hydrating cement pastes[J]. Materials and Structures, 2007, 40(10): 1073-1080. DOI:10.1617/s11527-006-9206-9 |
| [27] |
ZHANG Y, PICHLER C, YUAN Y, et al. Micromechanics-based multifield framework for early-age concrete[J]. Engineering Structures, 2014, 47(1): 16-24. |
| [28] |
YANG C C. Effect of the transition zone on the elastic moduli of mortar[J]. Cement and Concrete Research, 1998, 28(5): 727-736. DOI:10.1016/S0008-8846(98)00035-0 |
| [29] |
唐欣薇. 基于宏细观力学的混凝土破损行为研究[D]. 北京: 清华大学, 2009: 23-57 TANG Xin-wei. Study on damage and fracture behavior of concrete based on macro and meso mechanics [D]. Beijing: Tsinghua University, 2009: 23-57 http://cdmd.cnki.com.cn/Article/CDMD-10003-2009224204.htm |



