互承结构[1-2]中杆件间的主次等级不明显,严格意义上的互承构型是搭承式互承构型,直杆在连接处不开槽,任意相邻两杆的间距等于两杆截面半厚的和. 在几何上,搭承式互承构型中每一单元的位置由邻近单元决定. 在具有大量单元的互承系统中,确定每一单元的位置时需要同时考虑所有的单元. 大量几何约束的客观存在导致互承结构的构型困难[3]. 如果能控制所有单元间的间距(偏心距),就能控制整体形状和单元的几何参数. 控制偏心距成为解决搭承式互承构型复杂几何约束的途径.
控制偏心距主要有两类方案. 第一类是直接转换方法,将单元从交汇于一个节点并且无偏心距的原始构型转化成两两承接于多个节点的互承构型,从标准网格转化成互承网格. 通过转换公式,得到偏心距表达式,在控制偏心距的情况下反过来求得满足几何约束的初始参数. Baverel[4] 使用解析几何方法,研究基于初始网格的平移法、旋转法、扩展平移法的构型过程,并且实现了旋转法对5种柏拉图多面体、5种截角多面体和1种平面多面体的偏心距控制. Senechal等[5]使用一般分析方法给出由标准构型经旋转法生成互承构型过程中的几何约束方程,并且使用表达式明晰了参数对最终构型的影响,但是限于正多面体. Rizzuto[6]进一步研究了螺栓连接的偏心角度与旋转角度关系等应用问题. 由于各节点空间关系同等,转换规则多面体实际上是节点的几何约束问题. 第二类是通过遗传算法[7]、复合优化[8-9]、映射法[10]等不同方法初步得到互承构型后,通过优化迭代逼近目标偏心距. Song等[11-14]用不同的构型方法得到几何不协调的互承构型后,通过构建不同的误差函数,不同程度地生成复杂互承构型. 其中包括采用弹簧-质子模型,直接利用Kangaroo Engine下的动态迭代物理求解器[15]迭代. Anastas等[16]利用动态迭代物理求解器迭代提出针对自由曲面的基于单元区块算法的互承构型生成方法;Corio等[17]采用同样的算法在比萨罗马失事船残骸遗址上生成了互承屋盖. 算法的实质是对目标曲面上划分所得的单元区块采取边线放缩、取中点、连线等一系列参数化步骤,保持最终的互承构型与目标曲面的关联. 优化法所得互承构型往往不满足目标曲面的设定,并且单元上下关系难以预判.
基于现有网壳结构的网格几何划分型式生成互承构型,是对上述两类方案的补充. 一方面,网格几何型式在网壳结构中广泛应用,比规则多面体的工程适用性更广泛,特别是以常用柱面网壳网格为初始构型转换得到的互承构型,更容易被工程人员识别和推广. 另一方面,将目标曲面设定为解析曲面,以直接转换法获得互承构型,避免优化计算的复杂性和无法预知最终形态的问题,在获得偏心距与转换参数解析关系的基础上,可以通过控制转换参数,得到预想的构件尺寸和互承构型. 直接转换法包括上述扩展平移法、旋转法和源自Anastas等[16]提出的基于单元区块算法的新方法(简称为“收缩法”).
以控制偏心距为目标,采用平面预判定,第一层次为单元块偏心距和差的零值判定、第二层次为节点单元物理判定和第三层次为所有节点几何协调性判定的三层次判定法,系统地分析常用柱面网格[18]. 通过3种直接转换法,探讨生成互承构型的可行性;得到3种可行方案及解析式,证明光滑曲线挤出曲面上的四边形网格经扩展平移可生成互承构型.
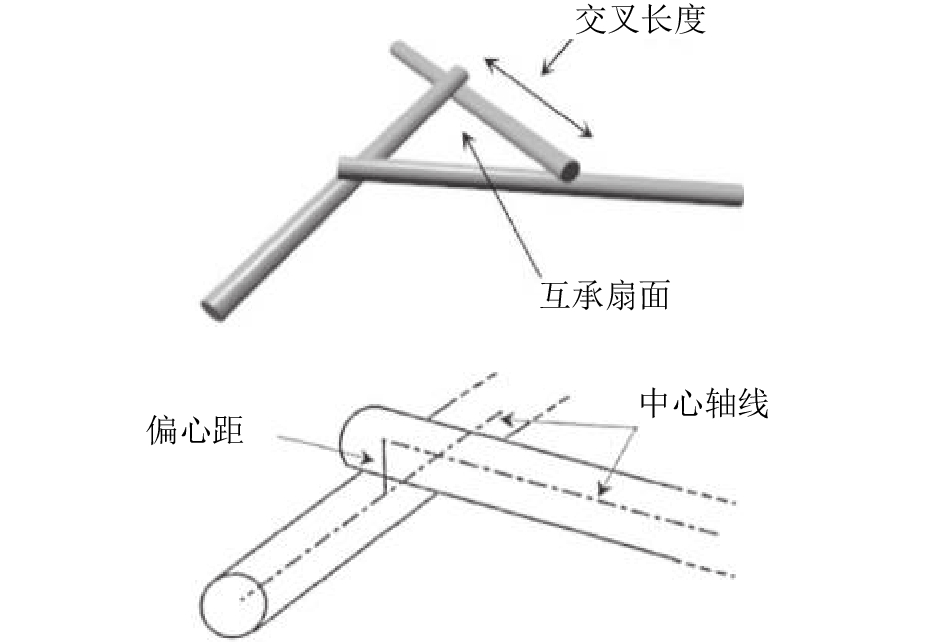
1 互承构型及直接转换法 1.1 搭承式互承构型如图1所示,搭承式互承构型由互承单元块按互承原则组合而成. 在任一单元块中,邻近单元间两两支承于非端点部位,一个单元可以在另一个单元上面或下面;不同于一般网格结构中单元构件的轴线相交于一点,互承单元块中由于构件厚度的存在,单元的轴线在空间中错位,自然形成一个平面外的“扇面”. 错位程度为“偏心距”,扇面边长为“交叉长度”. 杆件空间位置由偏心距和交叉长度决定,偏心距由杆件几何尺寸所决定,构型上的“几何约束”是设计互承结构的首要障碍. 构件有不同的截面形式,以圆截面为例. 为了简化分析,将单元杆件抽象为杆件的中心轴线,以杆件中心轴线组成的互承网格作为互承构型的抽象模型. 当两杆搭承时,两中心轴线的最短间距(偏心距)为两单元杆件的截面半径之和.
|
图 1 三单元的互承单元块 Fig. 1 Reciprocal unit block with three members |

|
图 2 单层柱面网壳的常用型式 Fig. 2 Common patterns of single-layer cylindrical reticulated shell |
常用柱面网格型式[18]有人字型、单向斜杆、交叉斜杆、四边形、联方网格型、三向网格I型和三向网格II型(见图2). 按照不同的作法,将7种网格型式分为3类. 前4种以四边形网格为基础,归为一类. 将圆柱圆弧等分成割线,通过等分点作平行的纵向直线,然后将直线等分,作平行于割线的横线,形成四边形网格. 按照不同布置方式增加斜撑,形成人字型、单向斜杆正交正放和交叉斜杆正交正放的网格型式. 联方网格型和三向网格II型为一类. 联方型网格是在圆柱上按相同间距作相同导程的左、右螺旋线,过交点作螺旋线的割线,形成菱形网格. 当菱形网格加上纵向或横向线段变成三角形网格时,形成三向网格II型. 根据新增线段的方向,将三向网格II型细分为2种:当新增为纵向时,称为三向网格II型1;横向时为三向网格II型2. 三向网格I型是以平面三向网格为基础,将节点垂直映射到柱面形成的. 平面三向网格将长方形的四边等分,用直线连接横向和纵向的等分点,形成2个方向的平行线,再加上纵向或横向直线,形成三角形网格. 与三向网格II型一样,三向网格I型也分2种:第三向为纵向的称为三向网格I型1,横向的为三向网格I型2.
相对于互承网格,转换前的网格称为标准网格. 在标准网格中,一个节点连接的数条线段为一个单元组,单元组内单元个数称为原子价. 柱面网格节点的原子价多为4和6;在四边形网格基础上加斜撑的网格形式,如人字型、单向斜杆、交叉斜杆存在8原子价节点,或者由多种偶数价态节点组合而成,如人字型网格除1个8原子价节点外,其余是6原子价节点.
1.3 转换方法 1.3.1 旋转法旋转法指标准网格中的每一单元绕中点在切平面内旋转一定的角度,得到节点离散、相邻单元间存在偏心距的互承网格,如图3所示. 一般规定,包含单元自身并且垂直于次法线的面为单元旋转所在的切平面;所有单元的旋转角度θ相同,θ的取值范围为(0, π). 柱面网格中所有单元的次法线均过圆柱轴线上的某一点.
|
图 3 4原子价节点和6原子价节点旋转生成互承单元块 Fig. 3 Reciprocal frames generated by rotation of members around node with four or six valence |
|
图 4 柱面上四边形网格的扩展平移 Fig. 4 Extended translation applied on quadrilateral grid on cylinder |
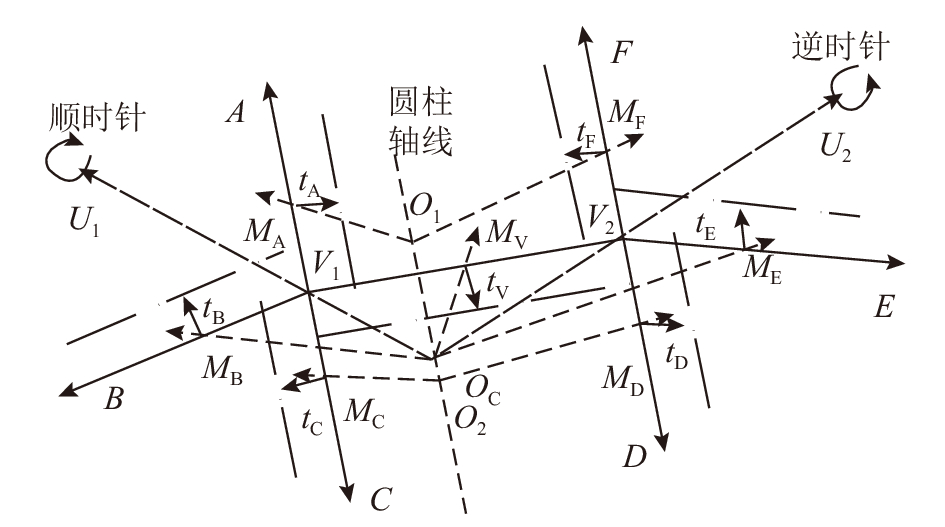
扩展平移法是指标准网格中每一单元在包含自身并且垂直于次法线的平面内平移,得到节点离散、相邻单元间存在偏心距的互承网格. 标准网格各单元移动的距离可以不同,但是单元组内所有单元的移动方向的取向一致,而且任意相邻节点单元组的取向相反. 以四边形网格(见图4)为例,B、V1、V2、E是柱面上同一环向上4点,OC为该环向圆弧的圆心;A、V1、C及D、V2、F所在的网格线方向为柱面轴向. MA、MB、MC、···、MF、MV分别是网格线段V1A、V1B、V1C、···、V2F、V1V2的中点. 对于柱面网格,各网格线的次法线是指网格线中点M所在环向圆弧的圆心O与M的连线OM,如图中O1MA、OCMB、O2MC、OCMV等. 线段V1A平移方向为线段向量
| ${{{t}}_{\rm{A}}} = {t_{\rm{A}}} \cdot \displaystyle\frac{{\mathop {{{{V}}_{\rm{1}}}{{A}}} \times \mathop {{{O}}_{\rm{1}}{{{M}}_{\rm{A}}}} }}{{|\mathop {{{{V}}{\rm_{1}}}{{A}}} \times \mathop {{{O}}{\rm_{1}}{{{M}}_{\rm{A}}}} |}}.$ |
其余各线段VP的平移方式同线段V1A 需要注意的是,线段向量的表示需由节点V指向端点P,次法线向量需要从O指向M;当某一节点周边各线段平移向量为
| ${{{t}}_{\rm{P}}} = {t_{\rm{P}}} \cdot \displaystyle\frac{{\mathop {{{{V}}_{\rm{1}}}{{P}}} \times \mathop {{{O}}_{\rm{1}}{{{M}}_{\rm{P}}}} }}{{|\mathop {{{{V}}{\rm_{1}}}{{P}}} \times \mathop {{{O}}{\rm_{1}}{{{M}}_{\rm{P}}}} |}},\;\left(t_{\rm P}>0\right).$ |
邻近节点的平移取向相反,平移向量为
| ${{{t}}_{\rm{P}}} = -{t_{\rm{P}}} \cdot \displaystyle\frac{{\mathop {{{{V}}_{\rm{1}}}{{P}}} \times \mathop {{{O}}_{\rm{1}}{{{M}}_{\rm{P}}}} }}{{|\mathop {{{{V}}{\rm_{2}}}{{P}}} \times \mathop {{{O}}{\rm_{2}}{{{M}}_{\rm{P}}}} |}}.$ |
当绕交点V2的4条线段平移取向满足以向量
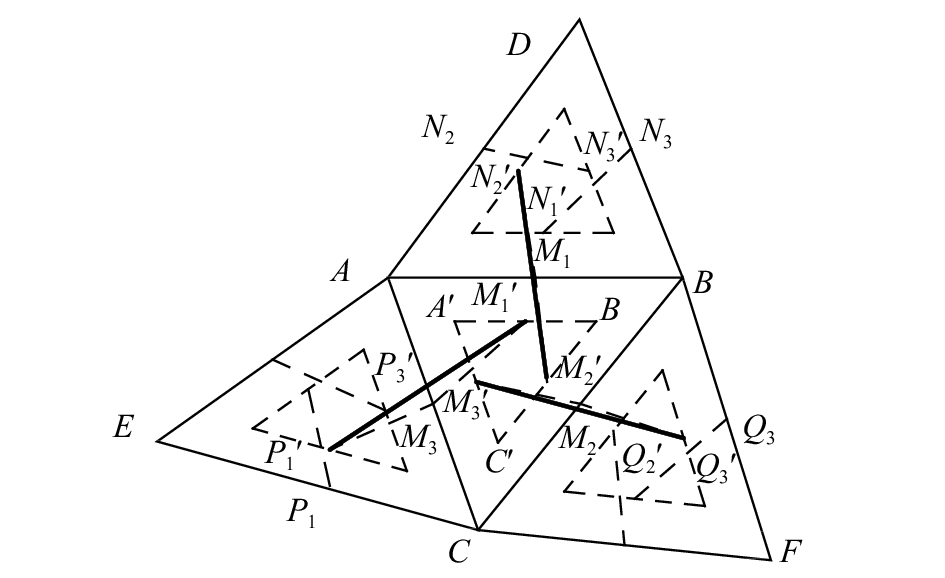
收缩法是基于单元区块算法的互承构型生成法[8],有三角形和四边形2种单元区块类型. 以三角形区块(见图5)为例,收缩法对所有单元区块均匀收缩,根据单元区块几何中心和设定的收缩系数s,以原单元区块为放射空间,作位似变换. 三角形ABC收缩后得到三角形A'B'C'. 将变换前后2三角形的三边中点M1、M2、M3与M1'、M2'、M3'按旋转顺序相连,即M1与M2'对应、M2与M3'对应、M3与M1'对应. 对相邻的三角形ABD作相同变换,得到M1与N2'对应. 其次,将同时对应于M1的M2'与N2'连接,作为互承单元块的一个单元. 同理得另2个单元M1'P1'和M3'Q3'. 3个单元形成一个扇,为一个基本互承单元块. 对其余区块作收缩、取中点、连线,得到互承网格.
|
图 5 基于三角形区块的收缩法 Fig. 5 Contraction method based on triangular pattern |
由于互承构型要求所有连接是2个构件的搭接,并且3种转换方法本身对初始网格有特定的要求,不是所有网格型式都适用于某种转换. 三维网格可以某种映射方式投影在平面上并且保持网格边线的相对关系,因此如果二维平面网格转换得到的平面互承网格边线走向不协调,或者存在三条边线交点过近的情况,可以预判对应三维网格的转换会存在类似问题. 初步确定旋转法、扩展平移法和收缩法的使用范围.
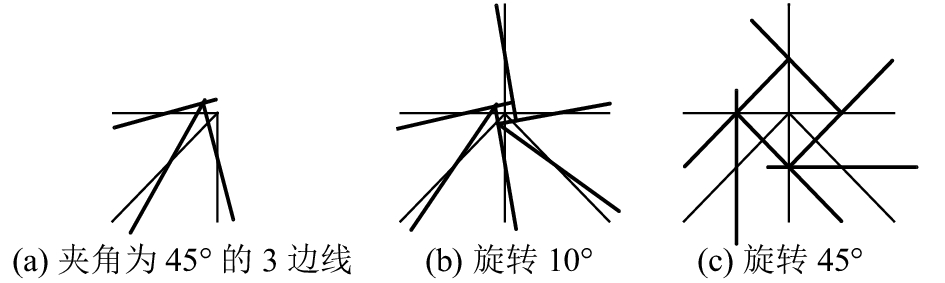
旋转法对于人字型、单向斜杆、交叉斜杆等在四边形网格基础上加斜撑的网格型式不可行(见图6). 在平面上,互成45°的三条边线在旋转时总是相交于一点. 因此,8原子价节点不作考虑.
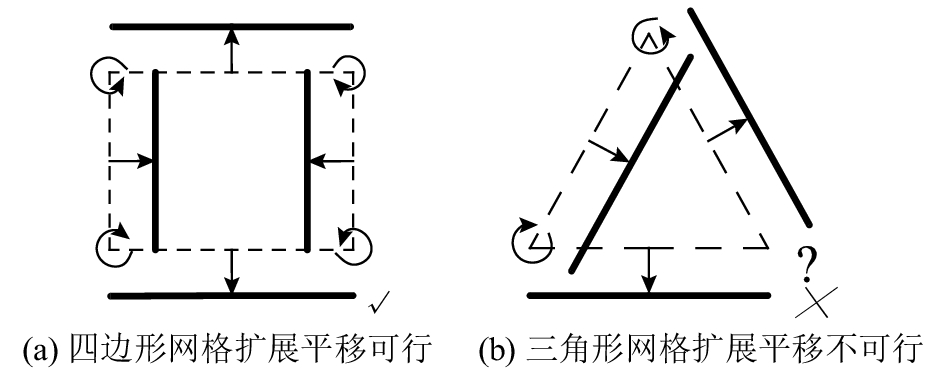
Baverel[4]指出对于多面体,扩展平移法只适用于每一面具有偶数边的情况. 此对柱面网壳同样成立,具有偶数边的网格单元才能够实现扩展平移. 排除三角形的网格划分形式,只有节点原子价为4的标准网格适用于扩展平移法(见图7).
对人字型、单向斜杆、交叉斜杆的平面投影网格运用收缩法,转换后网格的单元块区分不明显,某一单元块的一端可能进入另一单元块的扇面内. 因此,不对这3种网格型式的收缩法作深入研究. 平面预判定的结果表明,旋转法和收缩法适用于四边形网格、联方型网格、三向网格I型和三向网格II型,扩展平移法只适用于四边形网格和联方型网格.
|
图 6 夹角为45°的3条边线在旋转时总是相交于一点 Fig. 6 3 sidelines united at an angle of 45°always meet in a bit during rotation |
|
图 7 四边形网格和三角形网格的扩展平移 Fig. 7 Extended translation of quadrilateral pattern and triangular pattern |
为了判定各种柱面网格型式转换后所得互承网格是否符合互承原则,在预判定基础上,提出三层次判定法. 三层次判定法的目的是获得满足任意相邻两单元间的偏心距等于两单元的半径之和要求的互承构型.
2.1 判定一:单元块偏心距和差的零值判定在互承单元块中,按顺时针或逆时针次序,依次记杆件编号为A, B, C, ···, Xn,序号为1, 2, 3, ···, n;1、2杆之间的偏心距为e1, 依次顺推,e2, e3, ···, en–1, en为首尾两杆n和1杆之间的偏心距. 根据定义,偏心距e1~en与杆件半径RA~ RXn满足:
对于4原子价的单元块,
| $\left. {\begin{array}{*{20}{c}}{{R_{\rm{A}}} + {R_{\rm{B}}} = {e_1},}\\{{R_{\rm{B}}} + {R_{\rm{C}}} = {e_2},}\\{{R_{\rm{C}}} + {R_{\rm{D}}} = {e_3},}\\{{R_{\rm{D}}} + {R_{\rm{A}}} = {e_4}.}\end{array}} \right\}$ | (1) |
对于6原子价单元块,
| $\left. {\begin{array}{*{20}{c}}{{R_{\rm{A}}} + {R_{\rm{B}}} = {e_1},}\\{{R_{\rm{B}}} + {R_{\rm{C}}} = {e_2},}\\{{R_{\rm{C}}} + {R_{\rm{D}}} = {e_3},}\\{{R_{\rm{D}}} + {R_{\rm{E}}} = {e_4},}\\{{R_{\rm{E}}} + {R_{\rm{F}}} = {e_5},}\\{{R_{\rm{F}}} + {R_{\rm{A}}} = {e_6}.}\end{array}} \right\}$ | (2) |
由式(1)和(2)分别可得恒等式:
| $D = {e_{\rm{1}}} - {e_{\rm{2}}} + {e_{\rm{3}}} - {e_{\rm{4}}} = 0,\quad n = 4,\quad\quad\quad\;$ | (3) |
| $D = {e_{\rm{1}}} - {e_{\rm{2}}} + {e_{\rm{3}}} - {e_4} + {e_5} - {e_6} = 0,\quad n = 6.$ | (4) |
式中:n为节点原子价,D为偏心距和差值(单元块中所有杆件偏心距顺次加减的结果).
式(3)和(4)构成第一层次的判据:在每一节点处都有偏心距和差值等于0.
|
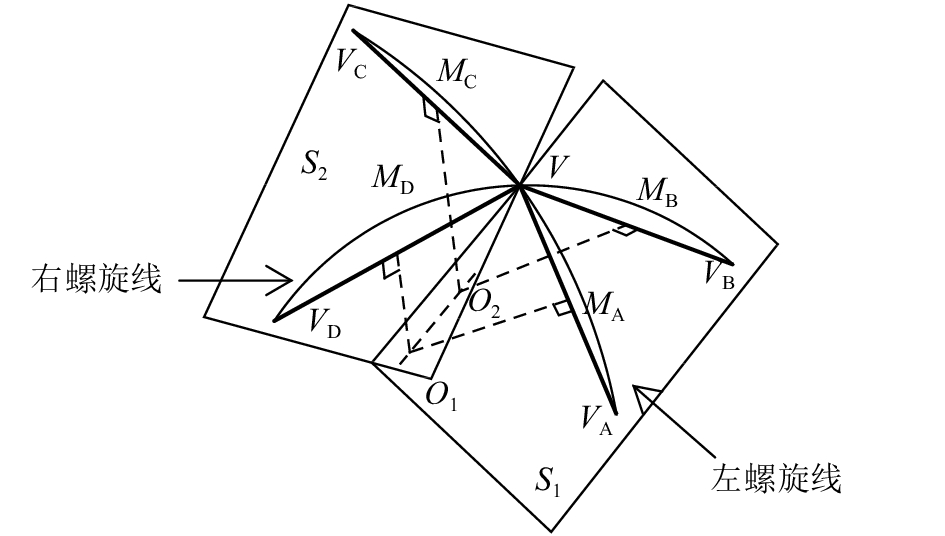
图 8 联方型网格中单元的扩展平移面和旋转面 Fig. 8 Extended translation plane and rotation plane of members in lamella grid |
联方型网格不满足第一层次判据. 如图8所示,节点V、VA、VC、VB、VD在同一圆柱的左、右螺旋线上,以V为中心构成一个4原子价节点,VA、VB、VC、VD距V的环向弧度值和纵向距离均相等(O1O2为柱面轴线). 经推理,左螺旋线过线段VVA中点MA的主法线
式(1)和(2)中RA, RB, RC,···, RXn表示杆件半径,根据物理意义均大于0. 在式(1)或(2)基础上,加设n个不等式条件,并且转化为关于RA的不等式:
对于4原子价的单元块,
| ${\rm{max}}\;\{ 0,\;{e_{\rm{1}}} - {e_{\rm{2}}}\} < {R_{\rm{A}}} < {\rm{min}}\;\{ {e_{\rm{1}}},\;{e_{\rm{1}}} - {e_{\rm{2}}} + {e_{\rm{3}}},\;{e_4}\}.$ | (5) |
对于6原子价的单元块,
| $\begin{array}{l}{\rm{max}}\;\{ 0,\;{e_{\rm{1}}} - {e_{\rm{2}}},\;{e_{\rm{1}}} - {e_{\rm{2}}} + {e_{\rm{3}}} - {e_4}\} < {R_{\rm{A}}}< \\\;\;\;{\rm{min}}\;\{ {e_{\rm{1}}},\;{e_6},\;{e_{\rm{1}}} - {e_{\rm{2}}} + {e_{\rm{3}}},\;{e_{\rm{1}}} - {e_{\rm{2}}} + {e_{\rm{3}}} - {e_4} + {e_5}\} .\end{array}$ | (6) |
当标准网格的单元组二度旋转对称时,经过扩展平移、旋转或收缩变换后,互承网格的单元块仍保持二度旋转对称. 空间位置相对的偏心距相等,即对于4原子价节点,满足e1=e3,e2=e4;6原子价节点满足e1=e4,e2=e5,e3=e6. 式(5)和(6)简化为
| ${\rm{max}}\;\{ 0,\;{e_{\rm{1}}} - {e_{\rm{2}}}\} < {R_{\rm{A}}} < {\rm{min}}\;\{ {e_{\rm{1}}},\;{e_{\rm{2}}},\;2{e_{\rm{1}}} - {e_{\rm{2}}}\} ,\quad n{\rm{ = 4}},$ | (7) |
| $\begin{split}&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\;\;\,{\rm{max}}\;\left\{ {{\rm{0}},\;{e_{\rm{1}}} - {e_{\rm{2}}},\;\, {e_3} - {e_{\rm{2}}}} \right\} < {R_{\rm{A}}} < \\ &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\;\;\;\;\;\,{\rm{min}}\;\left\{ {{e_{\rm{1}}},\; {e_{\rm{1}}} - {e_{\rm{2}}} + {e_{\rm{3}}},\; {e_{\rm{3}}}} \right\},\quad n{\rm{ = 6}}.\end{split}$ | (8) |
内部单元组绕各自中心节点的轴旋转180°后与初始单元组重合的网格称为二度旋转对称网格. 长方形、联方网格型和三向网格II型都属于二度旋转对称网格,三向网格I型不属于. 原子价为6的二度旋转对称网格满足e1=e4,e2=e5,e3=e6,有D=e1–e2+e3–e4+e5–e6=0,满足判定一.
取式(7)和(8)不等式的两边,得到二度旋转对称网格的第二层次不等式判据:
| ${\rm{max}}\;\{ 0,\;{e_{\rm{1}}} - {e_{\rm{2}}}\} < {\rm{min}}\;\{ {e_{\rm{1}}},\;{e_{\rm{2}}},\;2{e_{\rm{1}}} - {e_{\rm{2}}}\} ,\quad n{\rm{ = 4}},\;\;\;$ | (9) |
| $\begin{split}&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\;\;\;\;\;\;{\rm{max}}\;\left\{ {{\rm{0}},\;{e_{\rm{1}}} - {e_{\rm{2}}},\;{e_3} - {e_{\rm{2}}}} \right\} <\\ &\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \;\;\;\;\;\;\;\;\;\,{\rm{min}}\;\left\{ {{e_{\rm{1}}},\;{e_{\rm{1}}} - {e_{\rm{2}}} + {e_{\rm{3}}},\;{e_{\rm{3}}}} \right\},\;\quad n{\rm{ = 6}}{\rm{.}}\end{split}$ | (10) |
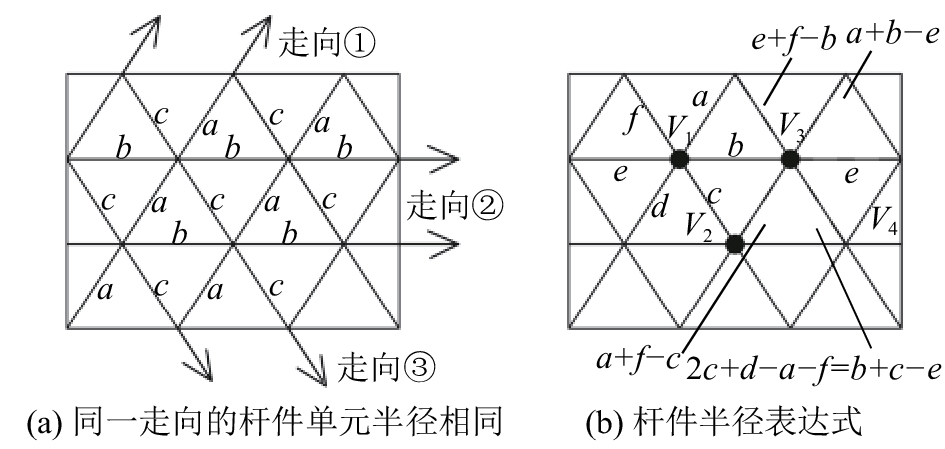
对于6原子价二度旋转对称网格,为了保证互承构型整体上几何协调,当所有节点的偏心距数组[e1, e2, e3, e4, e5, e6]相同,并且满足式(10)时,初始构型中同一走向的杆件单元半径必须相同(见图9(a)),至多有3种截面尺寸的单元杆件. 构成关于杆件截面几何尺寸分布的第三层次判据.
判据三的证明如下:已知节点V1周边6杆的半径分别是a、b、c、d、e、f,由所有节点的偏心距数组[e1, e2, e3, e4, e5, e6]相同,可得节点V2、V3周边杆件半径的表达式(见图9(b)).
| ${{{V}}_{\rm{3}}}{{{V}}_4} = 2c + d - a - f = b + c - e,$ | (11) |
| ${\text{若}}\;\;\left. {\begin{array}{*{20}{c}}{{e_{\rm{1}}} = {e_4}},\\{{e_{\rm{2}}} = {e_5}},\\{{e_{\rm{3}}} = {e_6}}.\end{array}} \right\}\;\;{\text{则}}\;\left. {\begin{array}{*{20}{c}}{a + b = d + e},\\{b + c = e + f},\\{c + d = f + a}.\end{array}} \right\}$ | (12) |
由上式(11)和(12)得
| $d = a,\;e = b,\;f = c. $ | (13) |
|
图 9 不同规格的单元构件在网格中的分布 Fig. 9 Distribution of different size of members in grid |
| 表 1 6种网格3种转换方法的可行性判定结果 Table 1 Results of judgement between six kinds of network and three conversion methods |
对半径为10 m的柱面,以四边形网格、联方型网格、三向网格I型和三向网格II型为初始网格,旋转法、扩展平移法、收缩法为转换方法,对转换结果应用三层次判定法,得到表1的判定结果. 三向网格I型和三向网格II型的扩展平移法在平面预判定中已被排除,实际上是对表中14种方案运用三层次判定法. 编制Matlab程序能够实现三层次判定法对14种方案的判定. 第一层次判定,以偏心距和差值-转换参数曲线为依据,偏心距-转换参数曲线为辅助,转换参数包括旋转角度θ、扩展平移量t和收缩系数s. 第二层次判定,在通过判定一的基础上,以是否成功搜索到满足判据二不等式的RA为依据. 满足以上两层次判定的一般是空间上规则的网格,单元杆件尺寸的分布均匀,第三层次判定以找出合适的杆件半径为目标;如果有那么互承构型成立,反之不成立.
3.1 未通过判定一的方案在旋转法中,不满足偏心距和差零值条件的有四边形网格、联方型网格、三向网格I型1和三向网格I型2. 联方型网格的旋转法和扩展平移法已经在2.1.1节中说明. 其余3种网格的偏心距和差值与变换参数的关系如图10和11所示.
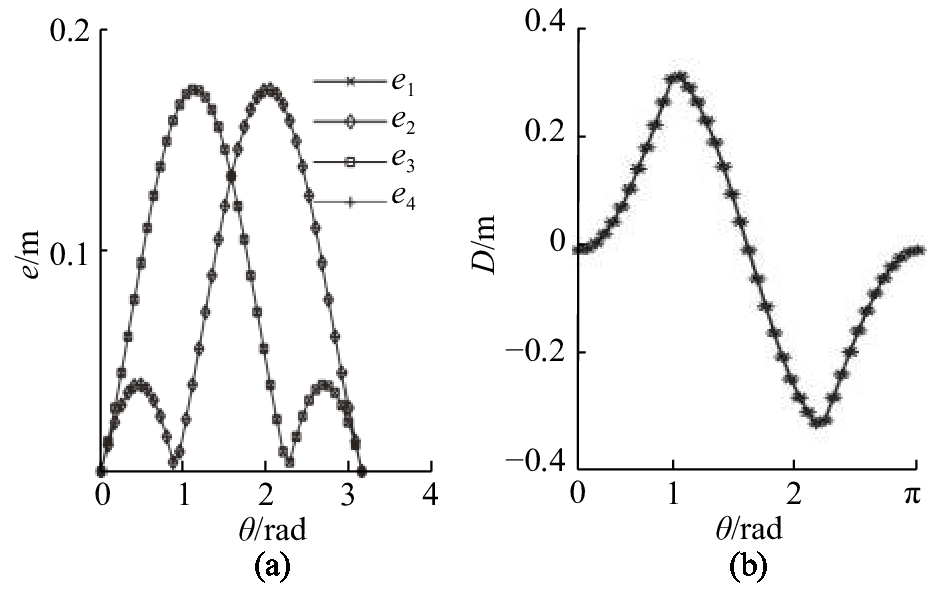
四边形网格旋转后,所有节点的偏心距数组[e1, e2,e3, e4]相等,并且满足e1=e3, e2=e4,但是偏心距和差D=e1–e2+e3–e4=2(e1–e2)≠0,呈现图10右图的类正弦函数的规律. 在(0, π)的定义域内,当旋转弧度值为π/2时,图中对应D=0,但是变换后的网格仍为四边形,不存在对应的互承构型.
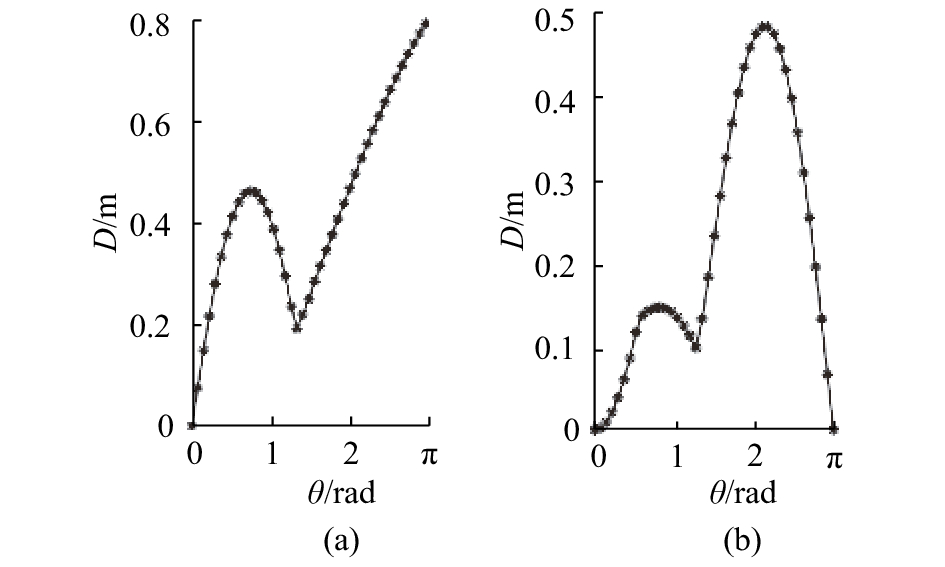
对于三向网格I型,各个节点的偏心距数组不同. 且由图11(b)中某一节点的 D-θ图可知,无论是I型1还是I型2,在定义域内都不存在D=0的值.
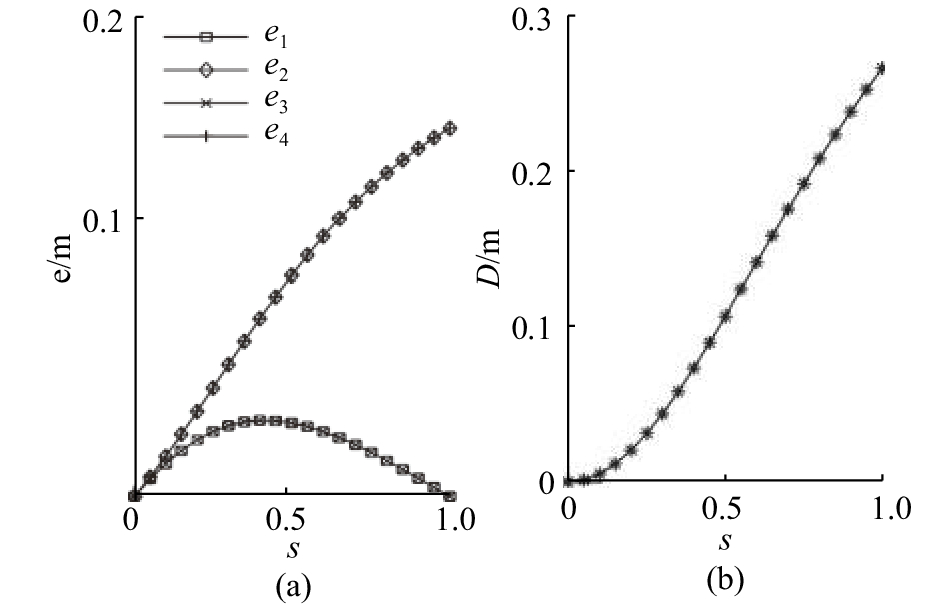
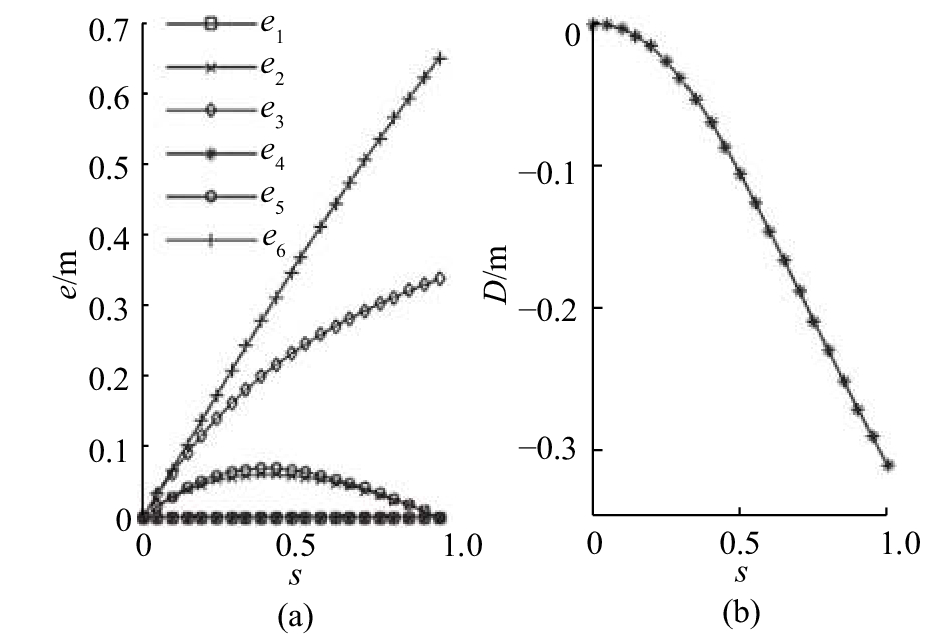
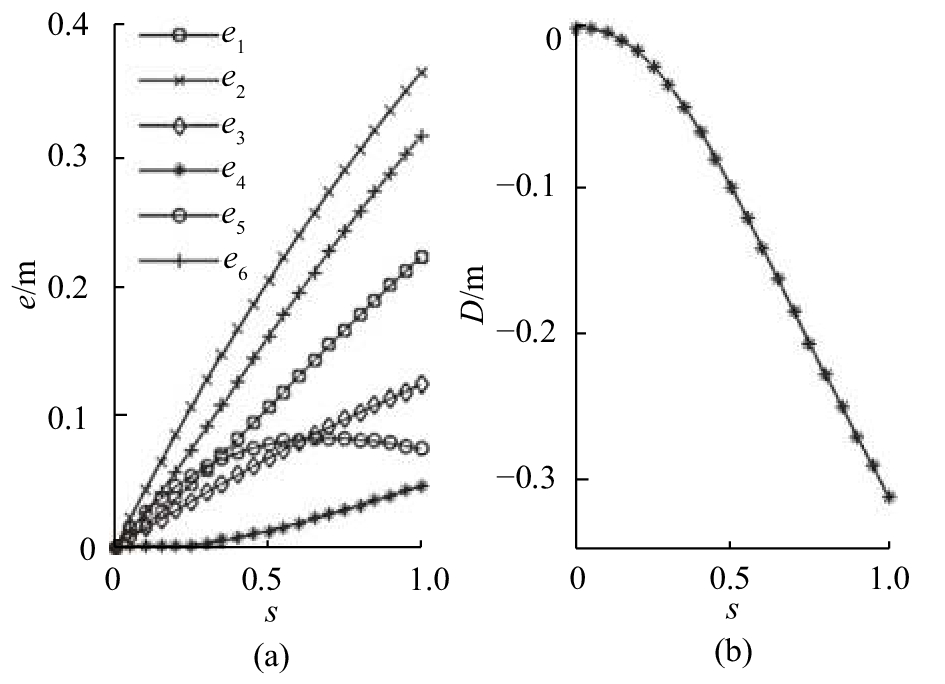
在收缩法中,四边形网格、联方型网格、三向网格I型的1和2都不满足判据一. 四者偏心距值与收缩系数的关系曲线规律类似:偏心距和差的绝对值随收缩系数的增大而增大(图12~15). 不同的是,四边形网格和联方型网格的所有节点的偏心距数组相等并且满足e1=e3, e2=e4;三向网格I型1在所有节点除保持e1=e4=0外,其余偏心距各不相同(见图14);三向网格I型2,除了所有节点偏心距数组不同外,同一节点的偏心距也各不相同(见图15).
|
图 10 四边形网格的偏心距-旋转角度(e-θ)、偏心距和差值-旋转角度(D-θ)曲线 Fig. 10 Curves for eccentricity-rotation angle (e-θ) and difference-rotation angle (D-θ) of quadrilateral grid |
|
图 11 三向网格I型某节点的偏心距和差值-旋转角度曲线 Fig. 11 Curves for D-θ of one node in three-way-I grids |
|
图 12 四边形网格的偏心距-收缩系数(e-s)、偏心距和差值-收缩系数(D-s)曲线 Fig. 12 Curves for eccentricity-contraction coefficient (e-s) and difference-contraction coefficient (D-s) of quadrilateral grid |

|
图 13 联方型网格的偏心距-收缩系数、偏心距和差值-收缩系数曲线 Fig. 13 Curves for e-s and D-s of lamella grid |
|
图 14 三向网格I型1的偏心距-收缩系数、偏心距和差值-收缩系数曲线 Fig. 14 Curves for e-s and D-s of three-way-I-1 grid |
|
图 15 三向网格I型2的偏心距-收缩系数、偏心距和差值-收缩系数曲线 Fig. 15 Curves for e-s and D-s of three-way-I-2 grid |
|
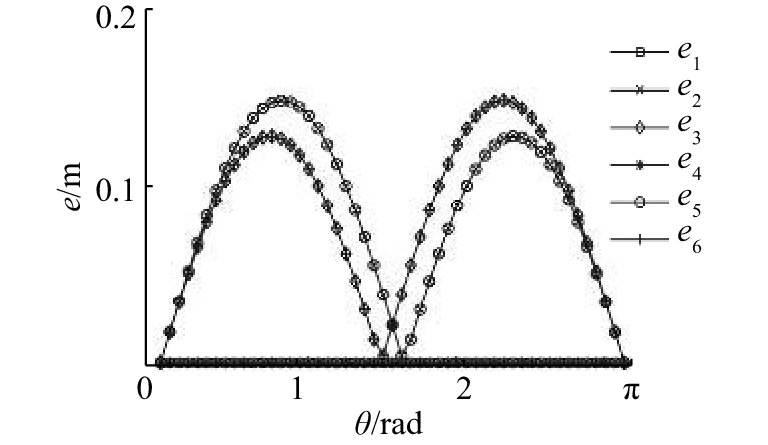
图 16 三向网格II型1的偏心距-旋转角度曲线 Fig. 16 Curve for e-θ of three-way-II-1 grid |
|
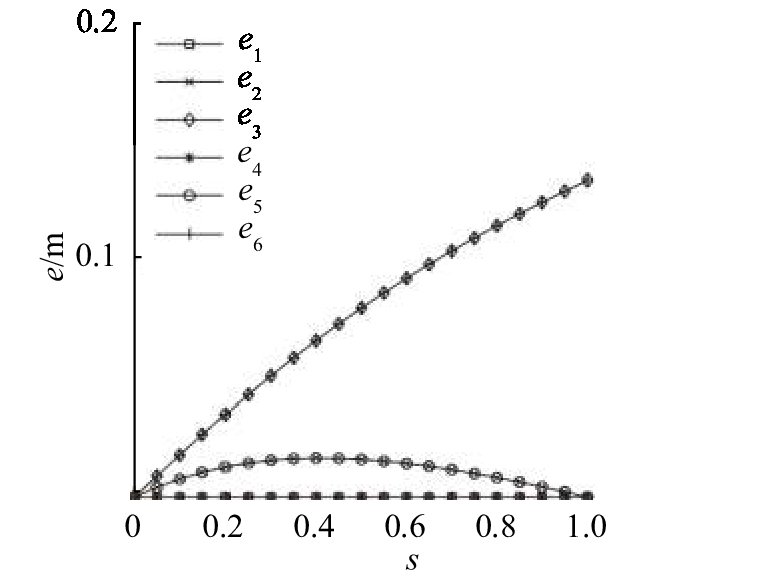
图 17 三向网格II型1的偏心距-收缩系数曲线 Fig. 17 Curve for e-s of three-way-II-1 grid |
三向网格II型1的旋转法和收缩法满足判据一,但是没有能通过第二层次物理判定. D-θ、D-s的函数关系图呈现接近零的无序散点分布,偏差在计算机精度范围内,满足判定一的零值条件. 两者的偏心距与转换参数的关系具有相似的规律:节点的偏心距数组不随节点位置的变化和改变,不同位置的单元块具有空间相似性;如图16和17所示,偏心距数组各元素满足:
| $\left. {\begin{array}{*{20}{c}}{{e_{\rm{1}}} = {e_4} = 0},\\{{e_{\rm{2}}} = {e_5} \ne 0},\\{{e_{\rm{3}}} = {e_6} \ne 0}.\end{array}} \right\}$ | (14) |
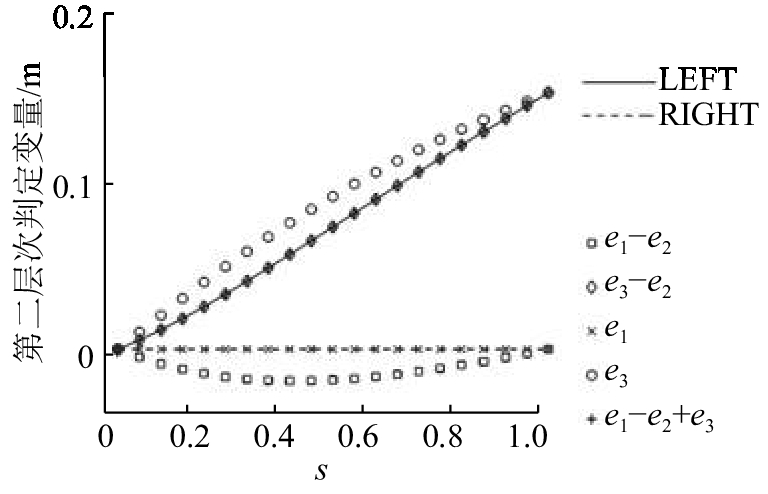
由于物理判定要求e1=RA+RB,RA>0,RB>0,即e1>0,三向II型1经旋转法和收缩法转换后e1=0,所以2种方法生成的互承网格均不是互承构型. 如果从判定二的条件出发,可得出相同的结论. 论证如下. 对于6原子价二度旋转对称网格,判定二要求满足上式(10),令
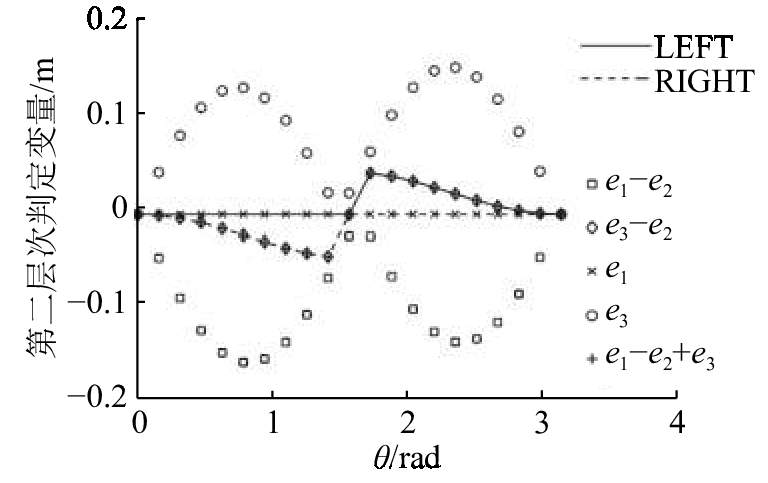
| $\left. \begin{array}{l}{{\rm LEFT}} {\rm{ = max}}\;\{ 0,\;{e_{\rm{1}}}{\rm{ - }}{e_{\rm{2}}},\;{e_{\rm{3}}}{\rm{ - }}{e_{\rm{2}}}\} ,\\{{\rm RIGHT}} = {\rm{min}}\;\{ {e_{\rm{1}}},\;{e_{\rm{1}}}{\rm{ - }}{e_{\rm{2}}}{\rm{ + }}{e_{\rm{3}}},\;{e_{\rm{3}}}\} .\end{array} \right\}$ | (15) |
需要满足LEFT<RIGHT. 实际结果如图18和19所示:2种转换方法都满足LEFT始终大于等于RIGHT,不满足判据二. 三向网格II型1的旋转法和收缩法无法得到满足物理条件的RA.
|
图 18 三向网格II型1旋转法的第二层次判定图 Fig. 18 Diagram of Level 2 determination through rotation method of three-way-II-1 grid |
|
图 19 三向网格II型1收缩法的第二层次判定图 Fig. 19 Diagram of Level 2 determination through contraction method of three-way-II-1 grid |
三层次判定均通过的3种方案是四边形网格的扩展平移法、三向网格II型2的旋转法和三向网格II型2的收缩法. 四边形网格扩展平移的参数关系明确,可行性将在第4章通过关系式说明,不做具体讨论. 三向网格II型2旋转法和收缩法的判定结果如下.
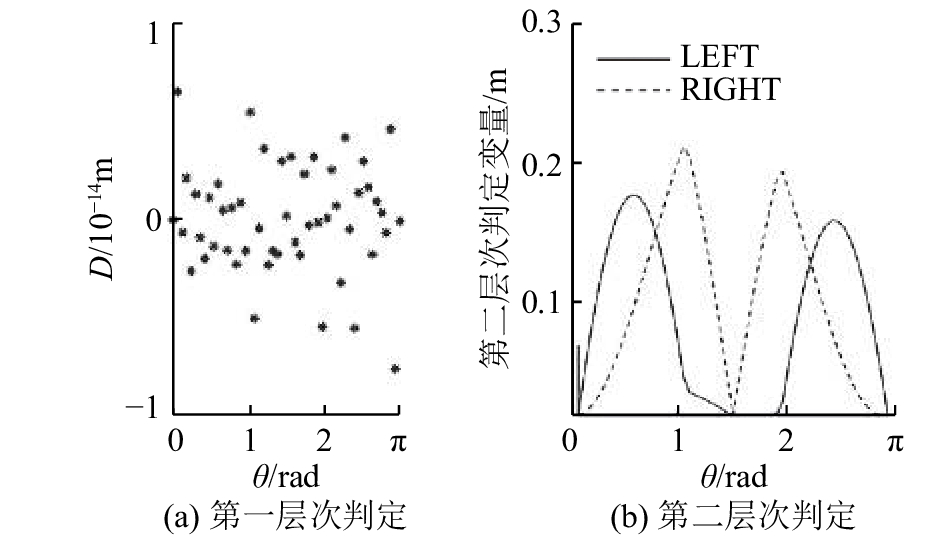
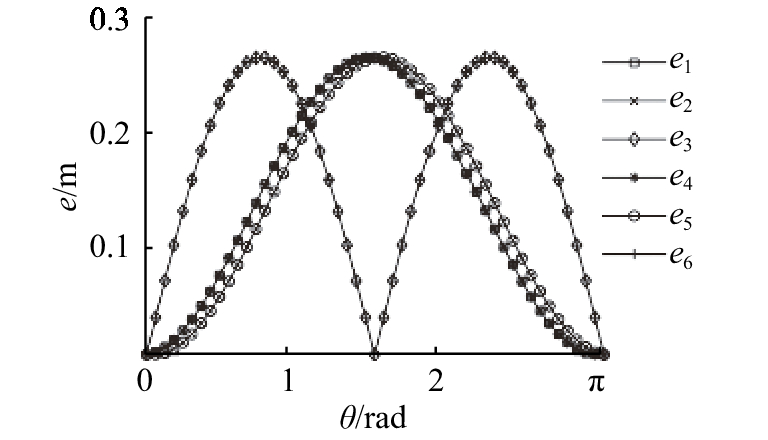
三向网格II型2在每向杆件截面半径相同时,可以通过旋转一定的角度,生成互承构型. 图20表明三向网格II型2的第一层次和第二层次判定均通过. 其中图20(b)表明,只有当θ∈(0.75, 2.30)时,LEFT<RIGHT,满足判据二. 无论旋转多大角度,所有节点偏心距数组保持相同,并且e1=e4, e2=e5, e3=e6( 见图21). 因此,根据判据三,当各向杆件半径相同时,互承构型存在.
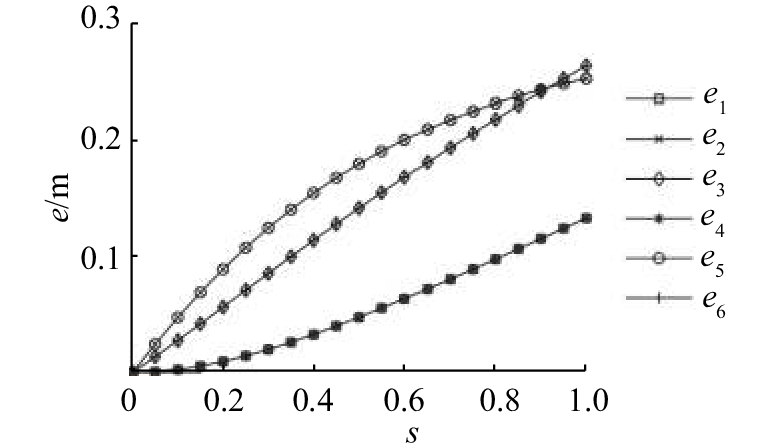
三向II型2收缩法的结果与旋转法类似. 如图22(b)所示,当收缩系数s∈(0.5, 1.0)时,互承构型存在. 各节点偏心距数组相等,并且e1=e4, e2=e5, e3=e6(见图23),当各向杆件半径相同时,判据三成立.
|
图 20 三向网格II型2旋转法的第一、二层次判定图 Fig. 20 Diagrams of Level 1 and Level 2 determination through rotation method of three-way-II-2 grid |
|
图 21 三向网格II型2的偏心距-旋转角度曲线 Fig. 21 Curves for e-θ of three-way-II-2 grid |

|
图 22 三向网格II型2收缩法的第一、二层次判定图 Fig. 22 Diagrams of Level 1 and Level 2 determination through contraction method of three-way-II-2 grid |
|
图 23 三向网格II型2的e-s曲线 Fig. 23 Curve for e-s of three-way-II-2 grid |
对14种方案中的3种可行方案提出偏心距与初始网格参数和转换参数的解析关系,便于根据工程需要通过调整转换参数,获得所需的互承构型. 四边形网格的扩展平移法具有简单的e-t关系,并且对光滑曲线挤出的曲面适用;三向网格II型2的旋转法和收缩法的偏心距代数表达式具有相似的形式,但是不对等.
4.1 挤出曲面上的四边形的扩展平移法 4.1.1 四边形网格扩展平移的参数关系由几何关系可得,轴向、环向杆件间的偏心距只与轴向杆件的平移距离t1有关:
| ${e_1} = {e_2} = {t_1}\sin \alpha = e.\;$ | (16) |
交叉长度为
| ${\lambda _1} = 2\;{t_2},\;{\lambda _2} = 2{t_1} \cos \alpha .$ | (17) |
互承构型杆长为
| ${L_1} = L_{10} + {\lambda _1},\;{L_2} = L_{20} + {\lambda _2}.$ | (18) |
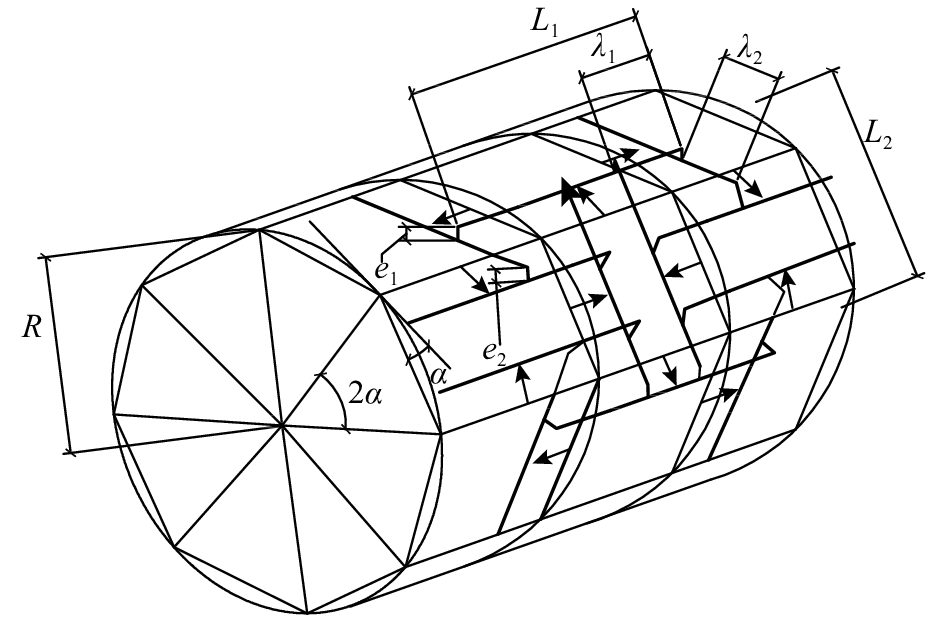
式中:α为环向圆弧上一点的割线与该点处圆弧切线的夹角,L10、L20为初始网格单元轴向和环向的边线长度;t1、t2为轴向和环向线段的平移距离;e1、e2为偏心距,λ1、λ2为交叉长度(扇面轴向和环向的边长),L1、L2为互承构型轴向和环向的杆件长度(见图24).
设柱面壳半径为R,轴向杆半径为R1、环向杆半径为R2,当R1+R2=e时,判据一、二、三都成立. 对于任意满足R1+R2=e,R1>0,R2>0 的R1和R2都能生成互承构型.
当L10=L20=2Rα,t2/t1=cosα时,L1=L2并且λ1=λ2,限定杆件截面半径R1=R2,此时杆件规格统一. 建立跨度参数与交叉长度之间简单而具工程意义的数量关系:
| ${R_{{\rm{incy}}}} = \frac{{\lambda L - {\lambda ^2}}}{{4e}}.$ | (19) |
式中:
|
图 24 四边形网格扩展平移后的互承构型 Fig. 24 Configuration of quadrilateral grid by extended translation method |
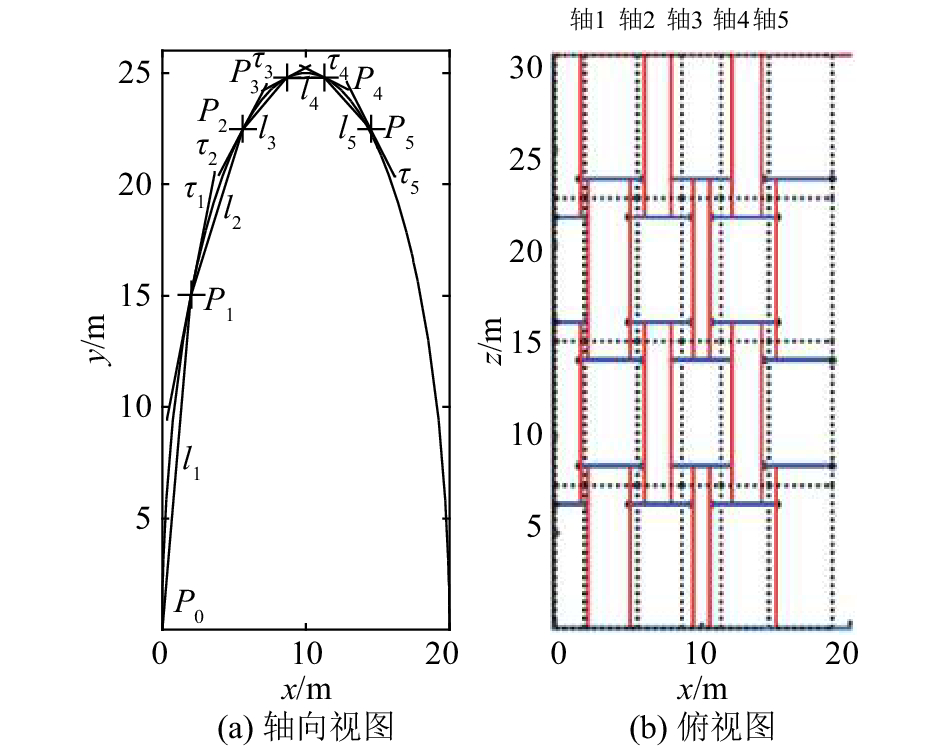
对于一般光滑曲线挤出曲面上的四边形网格经扩展平移法生成的互承构型,式(16)~(18)同样成立. 网格的特征是任意相邻两根横向线段在其公共点处关于曲线的法线对称;纵向线段平行于挤出方向,并且等长. 如图25和26所示,前图的横向曲线是两段相切圆弧的组合曲线,后图是椭圆弧.
如图26所示,以椭圆弧挤出曲面为例,说明四边形网格的作法. 二维曲线沿垂直于曲线所在平面的导轨直线方向挤出,生成零高斯曲率的曲面;在横向曲线上逐次取特定点,依次连接作出曲线的割线;过特定点作导轨直线的平行线,同时将导轨直线等分,过等分点作横向割线的平行线,形成四边形网格. 在特定点Pi处曲线的切线τi与左、右两条割线li、li+1的夹角相同,记夹角为αi. 圆弧是常曲率曲线,所有特定点处的αi相等;对于一般的光滑曲线,不同位置的特定点处αi往往不同. 为了使单元杆件规格尽可能少,调整不同Pi处的轴向杆件的平移量

|
图 25 双圆弧挤出曲面上的四边形互承构型 Fig. 25 Quadrilateral reciprocal configuration on biarc extrusion surface |
|
图 26 椭圆弧挤出曲面上的四边形互承构型 Fig. 26 Quadrilateral reciprocal configuration on elliptic arc extrusion surface |
经推算,得到三向网格II型2由旋转法和收缩法得到的偏心距e1~e6、交叉长度λA~λF和杆件长度LA~LF等互承构型参数的解析式,其中偏心距的解析式如表2所示,其他参数从略. 互承构型参数与柱面初始网格参数半径R、初始网格的环向等分角度φ和轴向等分长度z(或柱面跨度B、矢高f、轴向长度Len、环向等分数和轴向等分数)相关,由转换参数决定.
杆件截面半径RA~RF由偏心距e1~e3计算得到. 3.3节以6原子价互承单元块为研究对象,分析得到:三向网格II型2的互承构型由1种6原子价节点单元块沿轴向和环向扩展而成,并且杆件截面半径只有3种类型;对于单元块内6根杆件,偏心距满足e1=e4, e2=e5, e3=e6,截面半径满足RA=RD, RB=RE, RC=RF. 实际上,三向网格II型2的互承构型也可以看作由3原子价互承单元块组合而成,如图27所示. 以三角形为研究对象作单元块,三角形3条边线依次对应杆件截面半径RA~RC和e1~e3,由偏心距定义得到杆件的截面半径RA、RB、RC为
| $\left. \begin{array}{l}{R_{\rm{A}}} + {R_{\rm{B}}} = {e_1} ,\\{R_{\rm{B}}} + {R_{\rm{C}}} = {e_2} ,\\{R_{\rm{C}}} + {R_{\rm{A}}} = {e_3} .\end{array} \right\} \Rightarrow \left. \begin{array}{l}{R_{\rm{A}}} = ({e_1} - {e_2} + {e_3})/2 ,\\{R_{\rm{B}}} = ({e_1} + {e_2} - {e_3})/2 ,\\{R_{\rm{C}}} = ( - {e_1} + {e_2} + {e_3})/2 .\end{array} \right\}$ | (20) |
三向网格II型2旋转法和收缩法得到的互承构型的网格形式相似,但是不对等. 一方面,两种构型偏心距的解析表达式(见表2)的结构存在相似性,但是表达式细部完全不同,分别由转换参数旋转角度θ或收缩系数s所决定. 另一方面,同一初始参数的三向II型2网格,经过旋转一定的比例系数或相同大小的收缩系数如0.58,旋转角度θ=0.58π rad,收缩系数s=0.58,得到的互承网格虽然几何形式相似,但是杆件尺寸、交叉长度和杆件间上下位置关系不同,如图27(a)、(b)所示. 图27对应的初始网格参数如下,跨度B=18 m,矢高f =5.5 m,纵向总长度Len=18 m,环向等分数为12,纵向等分数为6;旋转0.58π rad或者收缩到原来的0.58倍后,得到的互承构型的参数如表3所示,λA~λF为杆件A~F的交叉长度,LA~LF为杆件A~F的长度. 由图27和表3可知,2种方法得到的是不同的构型.
在已知三向网格II型2柱面壳的初始网格参数和转换参数后,根据推导的解析关系,方便地获得所需的互承构型,为该类互承结构的工程应用提供几何基础.
| 表 2 三向网格II型2由旋转法和收缩法得到的偏心距解析式 Table 2 Analytical formulas of eccentricities from three-way-II-2 grid by rotation method and contraction method |
| 表 3 旋转法和收缩法所得互承构型参数的对比结果 Table 3 Geometrical parameters comparison of reciprocal configurations by rotation method and contraction method m |

|
图 27 三向网格II型2分别采用旋转法(旋转角度为0.58π rad)和收缩法(收缩系数为0.58)的互承构型 Fig. 27 Reciprocal configurations by rotation angle of 0.58π rad in rotation method and contraction coefficient of 0.58 in contraction method based on three-way-II-2 grid. |
基于常用柱面网格型式和3种直接转换方法,提出三层次判定法,系统分析柱面网格生成互承构型的可行性. 结果表明,只有四边形网格的扩展平移法、三向网格II型2的旋转法和收缩法可以直接转换成搭承式互承构型;一般光滑曲线挤出曲面上的四边形网格,经扩展平移可转换成互承构型,偏心距-平移量的关系式与柱面网格的相同;四边形和三向网格II型2的互承构型可以实现快速搭建,通常挤出曲面四边形互承构型只需要单一截面尺寸(长度不同)的杆件实现搭建,三向网格II型2的互承构型最多需要3种规格的杆件.
提出的三层次判定法采用基于单元块的分析思路,对于由同一单元块扩展而成的柱面网格形式具有一定的适用性. 当节点原子价为6时,判据二采用简化形式,实际上只对二度旋转对称的网格成立,对于其他网格形式,应根据判定二的依据,对判据二作出修正. 研究结果表明,单元块几何单一并且二度旋转对称、整体形态规则的网格系统,更有可能生成互承构型.
互承构型仅仅是互承结构实际应用的第一步,结构的实际应用包括几何、材料、力学和节点等等,研究仅仅涉及常用柱面壳网格向互承构型转化的几何可能性.
下一步的工作将对符合上述条件、更普遍的柱面阿基米德铺砌网格生成互承构型的可行性进行研究,以丰富柱面互承构型的形式,同时展开力学模型分析和节点构造研究.
| [1] |
PUGNALE A, SASSONE M. Structural reciprocity: critical overview and promising research/design issues[J]. Nexus Network Journal, 2014, 16(1): 9-35. DOI:10.1007/s00004-014-0174-z |
| [2] |
PARIGI D, PUGNALE A. Three-dimensionality in reciprocal structures: concepts and generative rules[J]. Nexus Network Journal, 2014, 16(1): 151-177. DOI:10.1007/s00004-014-0183-y |
| [3] |
PARIGI D, KIRKEGAARD P H. Design and fabrication of free-form reciprocal structures[J]. Nexus Network Journal, 2014, 16(1): 69-87. DOI:10.1007/s00004-014-0177-9 |
| [4] |
BAVEREL O L S. Nexorades: a family of interwoven space structures [D]. Guildford: University of Surrey, 2000 Nexorades: a family of interwoven space structures
|
| [5] |
SENECHAL B, DOUTHE C, BAVEREL O. Analytical investigations on elementary nexorades[J]. International Journal of Space Structures, 2011, 26(4): 313-320. DOI:10.1260/0266-3511.26.4.313 |
| [6] |
RIZZUTO J P. Eccentricity orientation of bolted connections in space structure configurations using reciprocally supported elements[J]. Journal of the International Association for Shell and Spatial Structures, 2014, 55(1): 49-62. |
| [7] |
BAVEREL O, NOOSHIN H, KUROIWA Y. Configuration processing of nexorades using genetic algorithms[J]. Journal of the International Association for Shell and Spatial Structures, 2004, 45(2): 99-108. |
| [8] |
PARIGI D, KIRKEGAARD P H, SASSONE M. Hybrid optimization in the design of reciprocal structures [C/OL] // Proceedings of the IASS Symposium. Seoul: IASS-APCS, 2012. [2018-05-24]. https://www.researchgate./netprofile/Mario_Sassone/publication
|
| [9] |
邹丁, 肖南. 互承型结构构型生成优化研究[J]. 空间结构, 2016, 22(3): 17-26. ZOU Ding, XIAO Nan. Morphogenesis of reciprocal structure by optimization methods[J]. Spatial Structures, 2016, 22(3): 17-26. |
| [10] |
SONG P, FU C W, GOSWAMI P, et al. Reciprocal frame structures made easy[J]. ACM Transactions on Graphics (TOG), 2013, 32(4): 94. |
| [11] |
SONG P, FU C W, GOSWAMI P, et al. An interactive computational design tool for large reciprocal frame structures[J]. Nexus Network Journal, 2014, 16(1): 109-118. DOI:10.1007/s00004-014-0173-0 |
| [12] |
MELLADO N, SONG P, YAN X, et al. Computational design and construction of notch-free reciprocal frame structures [M] // Block P, Knippers J, Mitra N J, et al. Advances in Architectural Geometry 2014. Cham: Springer International Publishing, 2015: 181-197
|
| [13] |
THONNISSEN U. A form-finding instrument for reciprocal structures[J]. Nexus Network Journal, 2014, 16(1): 89-107. DOI:10.1007/s00004-014-0172-1 |
| [14] |
PARIGI D, KIRKEGAARD P H. The reciprocalizer: an agile design tool for reciprocal structures[J]. Nexus Network Journal, 2014, 16(1): 61-68. DOI:10.1007/s00004-014-0176-x |
| [15] | |
| [16] |
ANASTAS Y, RHODE-BARBARIGOS L, ADRIAENSSENS S. Design-to-construction workflow for cell-based pattern reciprocal free-form structures[J]. Journal of the International Association for Shell and Spatial Structures, 2016, 57(2): 159-176. DOI:10.20898/j.iass.2016.188.737 |
| [17] |
CORIO E, LACCONE F, PIETRONI N, et al. Conception and parametric design workflow for a timber large-spanned reversible grid shell to shelter the archaeological site of the roman shipwrecks in Pisa[J]. International Journal of Computational Methods and Experimental Measurements, 2017, 5(4): 551-561. DOI:10.2495/CMEM |
| [18] |
钱若军, 杨联萍, 胥传熹, 等. 空间格构结构设计 [M]. 南京: 东南大学出版社, 2007: 22-25
|











