2. 浙江大学超重力研究中心,浙江 杭州 310058;
3. 中国水利水电科学研究院岩土工程研究所,北京 100048;
4. 浙江大学 流体动力与机电系统国家重点实验室,浙江 杭州 310027;
5. 中国中铁工程装备集团有限公司,河南 郑州 450016
2. Hypergravity Research Center of Zhejiang University, Hangzhou 310058, China;
3. Department of Geotechnical Engineering, China Institute of Water Resources and Hydropower Research, Beijing 100048, China;
4. State Key Laboratory of Fluid Power Transmission and Control, Zhejiang University, Hangzhou 310027, China;
5. China Railway Engineering Equipment Group Co. Ltd, Zhengzhou 450016, China
全断面隧道掘进机(TBM)具有低扰动、自动控制、开挖快和安全环保等优点,在我国越来越多地应用在交通、水利和矿山工程领域,显示出巨大的技术和经济优势. 在TBM施工过程中,掘进速率至关重要,直接决定工程经济效益. TBM掘进速率由机械设计、围岩条件和施工管理共同决定,核心问题是掘进机与围岩的相互作用. 目前研究者从刀具破岩机制、围岩性质影响和优化破岩效率等方面对掘进速率开展了大量的研究,研究方式主要包括室内切割试验、数值仿真和现场掘进试验.
室内切割试验可以直观地反映岩石破碎特征,对滚刀破岩理论力学模型进行检验和修正,同时可以研究刀具形状、间距和岩体条件对掘进速率的影响. 美国科罗拉多矿业学院通过一系列不同类型岩石的滚刀线性切割试验,分析岩石破裂机制和滚刀破岩规律,建立了刀具贯入力学模型[1]. Chen等[2]和姚羲和等[3]分别研究了滚刀压力、滚刀线性切割次数与岩石破碎区大小的关系. 在刀具影响方面,Chang等[4]和龚秋明等[5]通过在线性切割时改变刀间距和贯入度,得出存在最优刀间距和切深比使破岩效率达到最高的结论;莫振泽等[6]使用不同刃角的楔形刀具对花岗岩进行贯切试验,结果表明尖刃刀具比钝刃刀具产生的贯入度更大,破岩效果更好. 在岩体条件方面,马洪素等[7-8]研究了围压、节理倾向对破岩规律的影响;刘泉声等[9]比较分析了有、无侧限条件下泥岩的贯入特征. 由于室内试验多基于小尺寸完整试样,所以试验结果存在尺寸效应,无法反映岩体的复杂情况,并且单刀或双刀切割与实际刀盘整体旋转切割存在一定差异.
相比于室内试验的装置复杂、成本高的缺点,数值仿真具有操作简便、成本低的优点. Cho等[10]利用AUTODYN-3D有限元软件,基于线性的D-P材料岩石模型,模拟盘形滚刀直线切割岩石,得出岩石破碎不连续力机理;满林涛等[11]利用ABAQUS,根据Drucker-Prager塑性屈服准则和岩石力学特性,建立滚刀破岩三维模型,分析滚刀破岩机理. 蒋明镜等[12]和莫振泽等[13]采用离散元模拟滚刀破岩过程,均得出滚刀下岩石破坏主要包括张拉破坏和剪切破坏的结论. 除破岩机理分析外,数值仿真还可以用来研究岩体条件对破岩模式和速率的影响. 张魁等[14-15]利用UDEC软件研究节理条件和围压条件下滚刀破岩的基本破碎模式;孙金山等[16]和施文俊等[17]分别利用颗粒流、非连续变形分析(discontinuous deformation analysis, DDA)研究结构面对滚刀下岩石破坏过程的影响;卢谨等[18]利用三维离散单元程序(three-dimensional distinct element codes, 3DEC)离散元程序建立了TBM滚刀破岩三维仿真模型,分析了TBM掘进速率随岩石单轴抗压强度、弹性模量和泊松比的变化关系.
TBM现场掘进试验综合考虑地质因素、机器因素和施工管理因素,真实反映TBM的掘进破岩情况. 挪威科技大学[19]基于大量的TBM隧道掘进数据,对岩体参数和机械参数进行回归分析,建立了掘进速率的综合预测模型. 宋克志等[20]利用施工现场采集的数据,分析了泥岩、砂岩中盾构掘进效能与岩石强度、刀盘推力及刀盘扭矩的关系. Gong等[21]通过在现场开展掘进试验,研究TBM贯入度随刀盘推力与扭矩的变化关系,并通过渣片筛分研究不同滚刀推力下的破岩效率. 杜立杰等[22]基于TBM现场数据,通过建立贯入度指数FPI与岩石单轴抗压强度和完整性系数的多元回归关系式,以及贯入度与FPI的拟合关系式,进行贯入度和所需推力的预测.
TBM施工现场数据是在特定地质条件下掘进机与围岩相互作用情况的真实反映. 通过对现场数据的分析计算,能够更全面、准确地探讨TBM隧道岩-机作用规律,提出更加符合工程实际的掘进速率模型,优化设计,指导施工. 然而,目前对TBM施工现场掘进数据的搜集和利用比较少. 本研究基于吉林引松供水隧道工程TBM3标段,通过中铁工程装备集团TBM混合云管理平台,对掘进现场数据进行全方位实时采集和存储,并加以分析计算,开展对TBM掘进速率的研究.
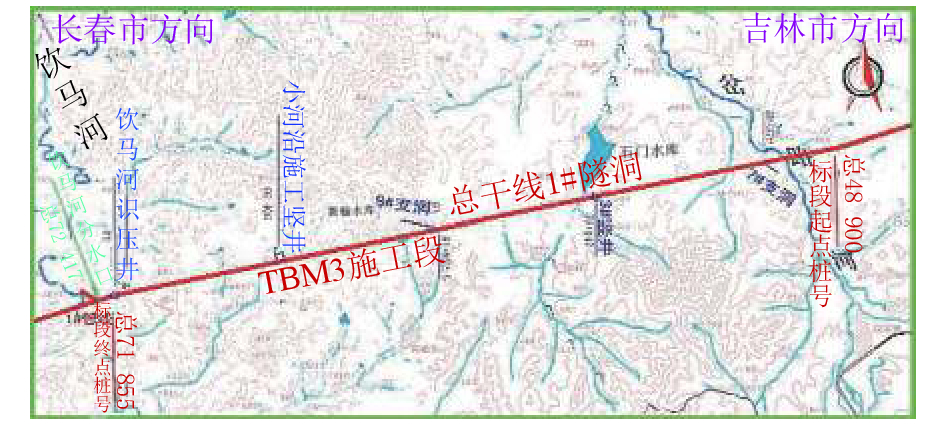
1 吉林引松供水工程 1.1 工程概况吉林引松供水工程总干线TBM段为自流输水隧洞,全长69.855 km,埋深主要集中在50~100 m,最大埋深为260 m,取水口位于丰满水库,途经温德河、岔路河到饮马河分水口. 根据TBM施工台数和线路特点划分为:TBM1、TBM2、TBM3共3个标段,本研究基于TBM3标段. TBM3标段位于吉林市岔路河至饮马河之间,线路桩号48 900 m~71 855 m,总长度为22 955 m,其中TBM施工段总长20 198 m,开挖断面为圆形,开挖成洞的洞径不小于7.65 m. TBM3标段地理位置见图1.
|
图 1 TBM3标段地理位置平面图 Fig. 1 Location map of TBM3 section |
TBM3施工段内岩石种类以三叠系上统、石炭系下统和中下统、泥盆系中下统灰岩,以及燕山期花岗岩为主,含少量凝灰岩、闪长岩和凝灰质砂岩;岩石饱和单轴抗压强度以40~80 MPa为主,Ⅲ级围岩居多、Ⅳ-Ⅴ级围岩次之,岩石强度和围岩级别相应的洞段长度占比情况如图2所示. 本研究选取灰岩段掘进数据. 灰岩段共10条断层,大部分与线路大角度相交. 灰岩岩溶较发育,垂直分带性不明显,溶洞多沿沟谷、断层呈北东或南北向分布,洞径大小不一,多充填. 沿沟谷地表水发育,容易出现溶洞突水、突泥问题.

|
图 2 岩石强度占比和围岩级别占比 Fig. 2 Proportion of rock strength and classification |
TBM3标段采用开挖直径为7.93 m的开敞式TBM,TBM主要技术参数如表1所示。其中,TBM在额定扭矩8 410 kN·m下运行时可以实现的最大转速为3.97 r/min,当刀盘扭矩小于额定扭矩运行时,可以实现的最大转速为7.6 r/min.
| 表 1 TBM主要技术参数 Table 1 TBM specifications |
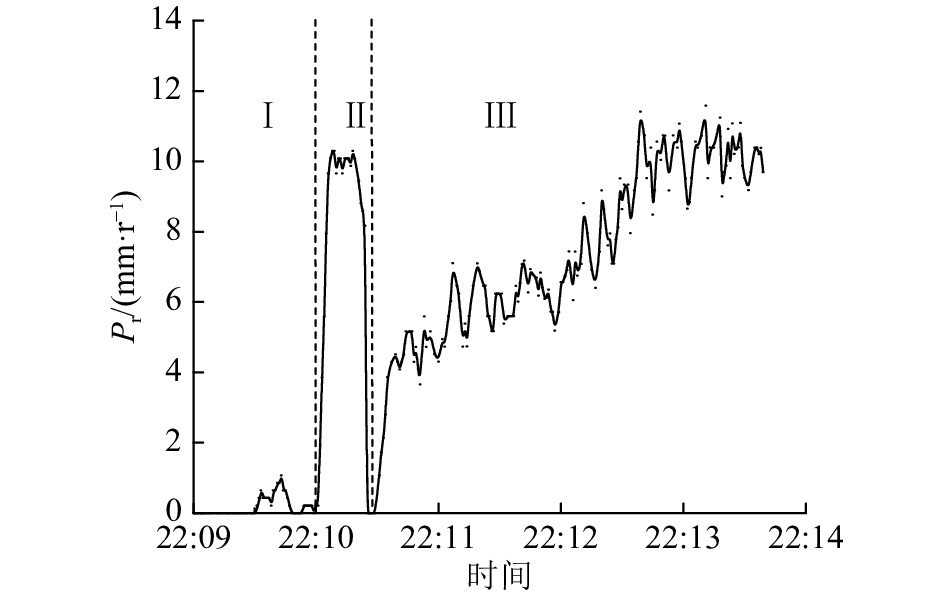
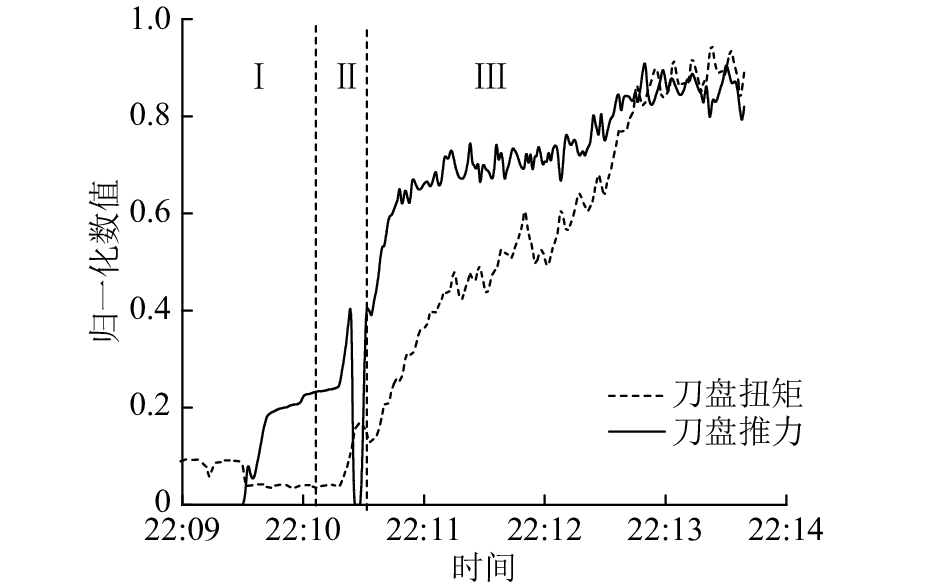
TBM依靠刀盘上分布的滚刀进行破岩,滚刀在推力作用下对掌子面挤压破碎,同时滚刀绕刀盘中心轴公转及绕自身刀轴自转,在刀盘螺旋推进下,实现对岩石的连续滚压、侵入和剥落,从而向前掘进. 刀盘掘进速率采用贯入度Pr(刀盘每转1圈的切深,mm/r)表示,图3、4为刀盘接触岩石施加推力至破碎岩石过程中贯入度、推力F和扭矩T的时程特征曲线(以桩号70 686为例). 其中,为便于显示,对刀盘推力、扭矩进行最大最小归一化处理. 如图3、4所示,TBM刀盘破岩可以分为3个阶段:挤压阶段、起裂阶段和破碎阶段.
|
图 3 贯入度特征曲线 Fig. 3 Time-curve of penetration rate |
|
图 4 刀盘推力和扭矩归一化特征曲线 Fig. 4 Time-curves of normalized cutterhead thrust and torque |
Ⅰ挤压阶段. 刀盘推力从零开始增加,贯入度很小(小于2 mm/r),增加缓慢. 该阶段刀盘推力较小,刀具对岩面产生挤压变形,刀具下方岩石产生压碎区,但是压碎区周边应力小于岩石的抗拉、抗剪强度,无岩片剥落。由于刀具并未贯入岩石,滚刀沿岩面滚动所受阻力小,刀盘扭矩小,维持在空转扭矩左右.
Ⅱ起裂阶段. 贯入度突然增大(最大达10.3 mm/r)后回落,刀盘推力、扭矩变化亦然. 这是因为刀盘推力增加至破岩门槛值,滚刀下方中央裂纹扩展,压碎区周边应力大于岩石的抗拉或抗剪强度,产生径向裂纹,滚刀侵入岩石,从而使贯入度突然增大,当裂缝继续发展造成刀具脱空,刀盘推力急剧下降;此阶段切割槽初步形成,滚刀滚动受阻,刀盘扭矩同步增加和下降.
Ⅲ破碎阶段. 贯入度随推力、扭矩增大而增大. 岩石裂缝在刀具作用下继续发展,刀具间岩石径向裂纹贯通,表面岩体被裂缝分割,在扭矩协同作用下形成碎片剥落,此时刀具再次脱空,滚刀推力、滚动力骤降. 随着刀盘继续滚压,刀盘推力、扭矩重复以上特征,呈连续间断性的“跃进式”破碎.
3 TBM掘进速率分析由于挤压阶段和起裂阶段均未能实现有效破岩,根据特征曲线将前两阶段数据过滤掉,掘进速率分析以破碎阶段为主. 掘进速率的大小主要受机器因素和围岩地质条件的影响,可以表示为
| ${P_{\rm r}} = f\left( {F,T,{\rm RMBI}} \right). $ | (1) |
式中:Pr为刀盘贯入度,代表掘进速率;F为刀盘推力,忽略盾壳与洞壁摩擦力、后配套拉力等的影响;T为刀盘扭矩,忽略空转扭矩影响;RMBI为岩体可掘性指数,由岩体强度、节理和磨蚀性等共同决定. 由于工程现场条件限制,岩体性质参数获取困难,选用由点荷载试验值换算的岩石饱和单轴抗压强度Rc和完整性系数Kv共同表示岩体可掘性. 文中所用数据均为掘进机刀具磨损正常、运行状态正常时的数据. 围岩情况如表2所示.
| 表 2 岩体性质参数 Table 2 Parameters of rock mass |
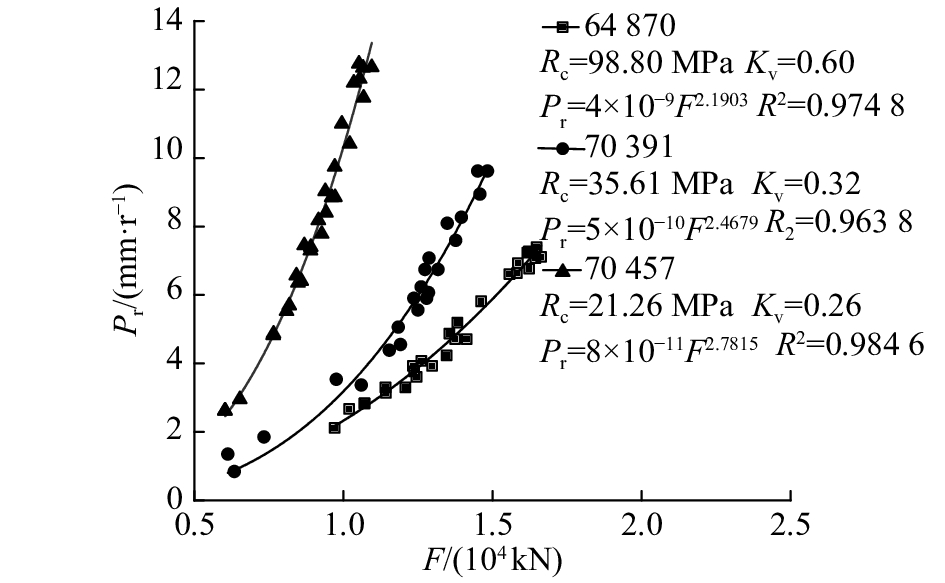
刀盘推力是产生贯入度的主要因素之一,推力越大,贯入度越大. 图5为TBM在不同刀盘推力作用下的掘进曲线图(以桩号64 870、70 391、70 457为例). 可以看出,岩石强度越高、完整性越好,同一贯入度时所需要的刀盘推力越大,并且贯入度随刀盘推力增长越缓. 例如当刀盘推力由9 000 kN增加至10 000 kN时,TBM在岩石饱和单轴抗压强度为分别为21.26、35.61、98.80 MPa,对应完整性系数分别为0.26、0.32、0.60的情况下,贯入度增长率分别为34%、31%、26%. 从单条掘进曲线看,随着刀盘推力增大,对于不同强度、完整性的岩石,贯入度均呈幂函数(相关系数均大于0.95)增长趋势,即随着刀盘推力的增大,贯入度的增长率增大,这与龚秋明等[7, 20, 23]的研究结果相符. 因为当推力较大时,滚刀推力在岩石内的应力传播范围更广,形成压碎区的面积更大,产生的裂缝数量更多,深度和宽度更大,相较推力较小时更容易实现宏观裂缝的贯通和岩片的形成. 同时,刀盘破岩实际是能量集聚与释放的过程,当推力较大时,相同时间内刀盘给予岩石的应变能越多,转化为岩石碎片的动能越多,即产生岩石碎片越多. 根据挪威科技大学[19]的研究,贯入度与刀盘推力的关系可以表示为
|
图 5 贯入度与刀盘推力的关系 Fig. 5 Relationship between penetration rate and cutterhead thrust |
| ${P_{\rm r}}= {\left( F/F_1\right)^\alpha }\text{.}$ | (2) |
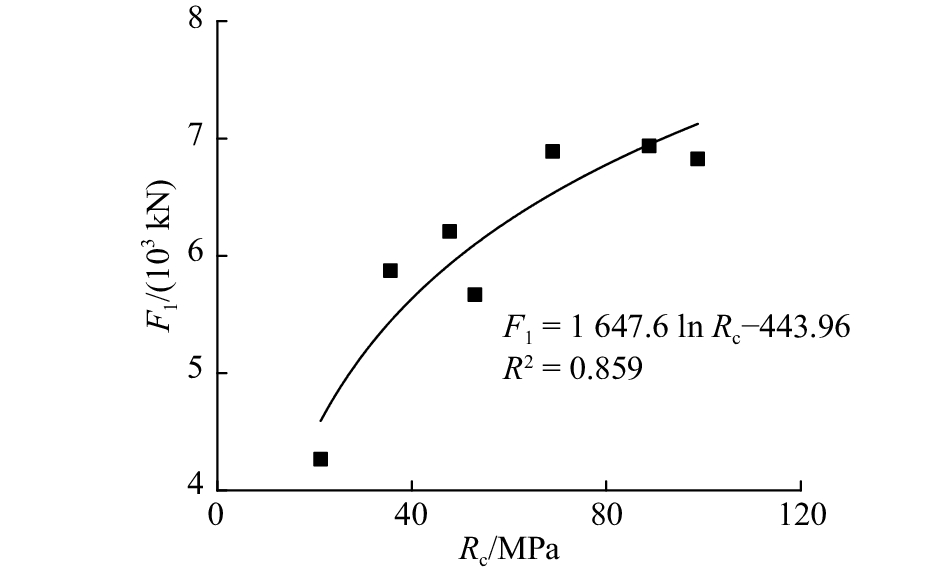
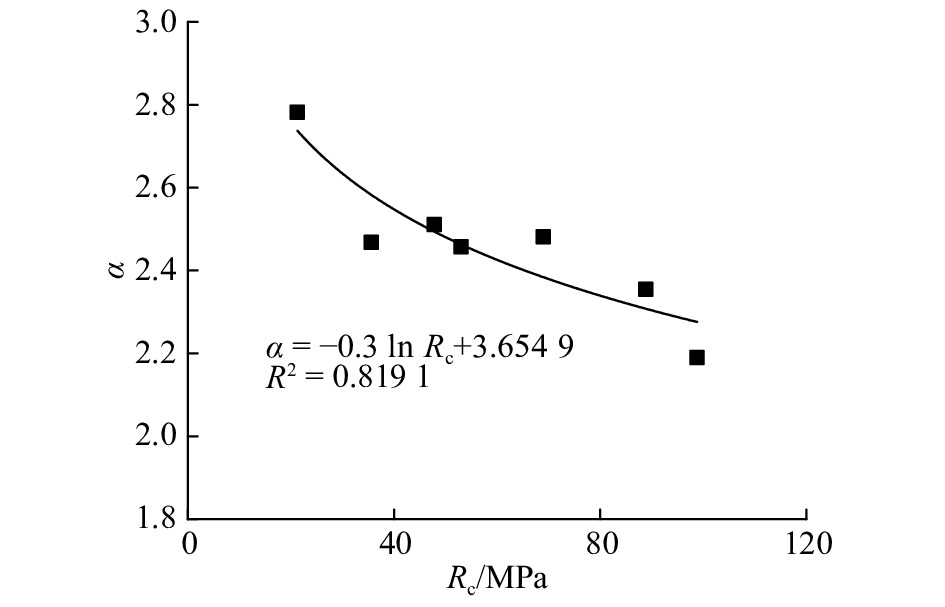
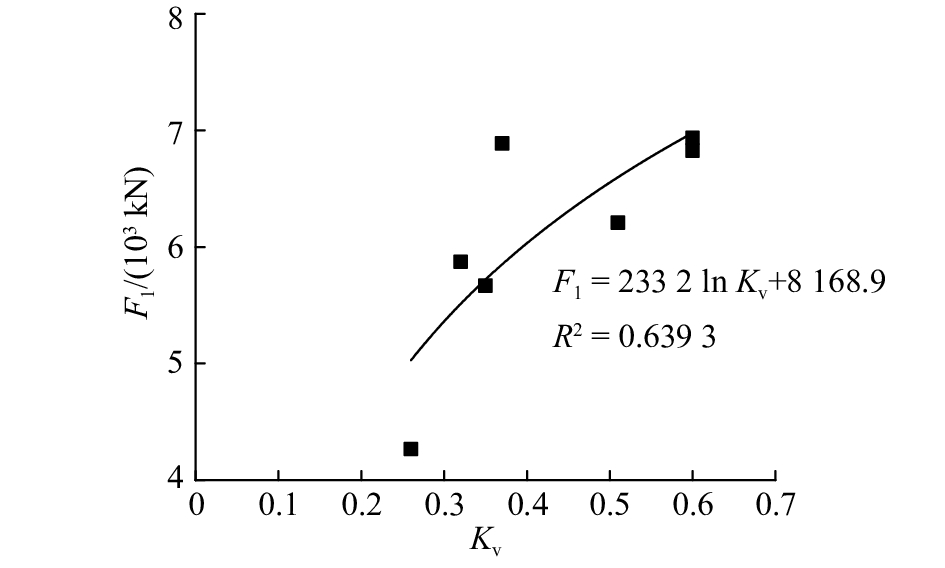
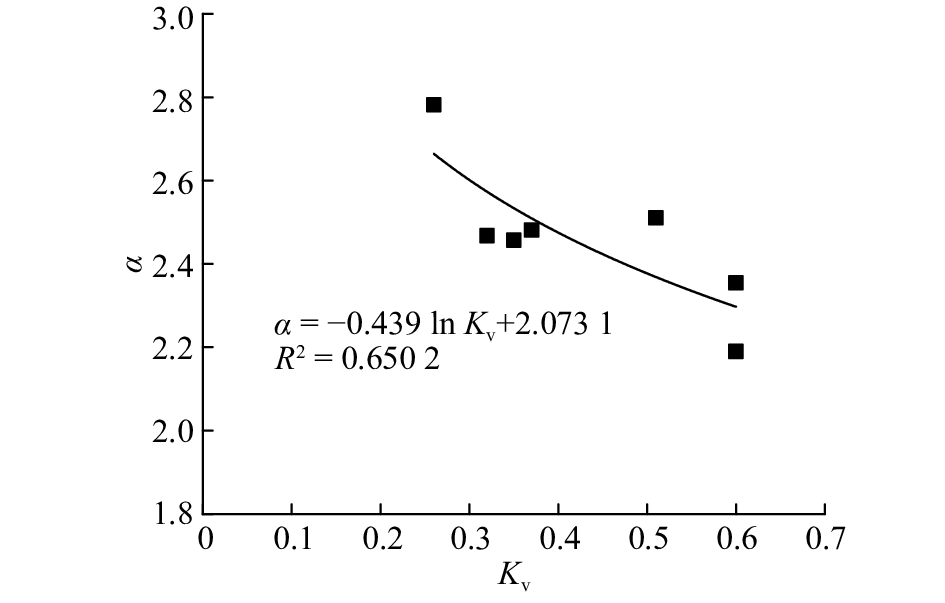
式中:F1为贯入度等于1 mm/r时的刀盘推力;α为刀盘侵入系数,描述刀盘推力对贯入度的影响大小. 为了分析不同岩石情况下F1、α的变化规律,对表2中所有围岩情况的掘进曲线进行统计回归分析,结果如表3、图6~9所示.
从图6~9可以看出,F1随岩石强度Rc、完整性系数Kv增大而增大,α随岩石强度、完整性系数增大而减小,从而导致贯入度增长率随两者增加而减小. 同时,F1、α随岩体质量变好而变化率逐渐减小,大约在Rc=50 MPa时变化率出现明显区分. 原因在于,当Rc>50 MPa时,一般岩体完整性较好,岩石裂缝发展困难,岩石难以切割,F1、α的增长和降低趋势比较平缓;当Rc<50 MPa时,一般岩体完整性差,节理裂隙发育,岩石更易被刀具切割和形成片、块状剥落. 但是当岩体呈较破碎、破碎状态时,掌子面容易坍塌,洞顶容易发生掉块塌落、TBM容易卡机,应当降低刀盘推力、减速稳定推进,必要时可以采取预埋注浆管进行回填加固等措施. 根据图6~9的回归分析结果,进行二元回归,可以得出F1、α与岩石单轴饱和抗压强度、完整性系数的关系式为
| ${F_1} \!=\! 1{\rm{ \,\,}}600\ln \,\,{R_{\rm{c}}}{\rm{ + }}91.50\ln \,\,{K_{\rm{v}}} \!-\! 173.60, \,{R^2} \!=\! 0.859,$ | (3) |
| $ \alpha \!=\!\! {\rm{ - }}0.265\ln {R_{\rm{c}}}{\rm{ - }}0.067{\rm{ \,\,}}8\ln {K_{\rm{v}}} \!+\! 3.454{\rm{ \,\,}}7,\,{R^2} \!=\! 0.823{\rm{ \,\,}}3. $ | (4) |
| 表 3 贯入度与刀盘推力关系曲线的参数统计结果 Table 3 Statistical results of curve parameters of penetration rate and cutterhead thrust |
|
图 6 当Pr=1 mm/r时刀盘推力与岩石饱和单轴抗压强度的关系 Fig. 6 Relationship between cutterhead thrust and rock saturated uniaxial compressive strength with Pr=1 mm/r |
|
图 7 刀盘侵入系数与岩石饱和单轴抗压强度的关系 Fig. 7 Relationship between cutterhead penetration coefficient and rock saturated uniaxial compressive strength |
|
图 8 当Pr=1 mm/r时刀盘推力与岩体完整性系数的关系 Fig. 8 Relationship between cutterhead thrust and rock mass integrity coefficient with Pr=1 mm/r |
|
图 9 刀盘侵入系数与岩体完整性系数的关系 Fig. 9 Relationship between cutterhead penetration coefficient and rock mass integrity coefficient |
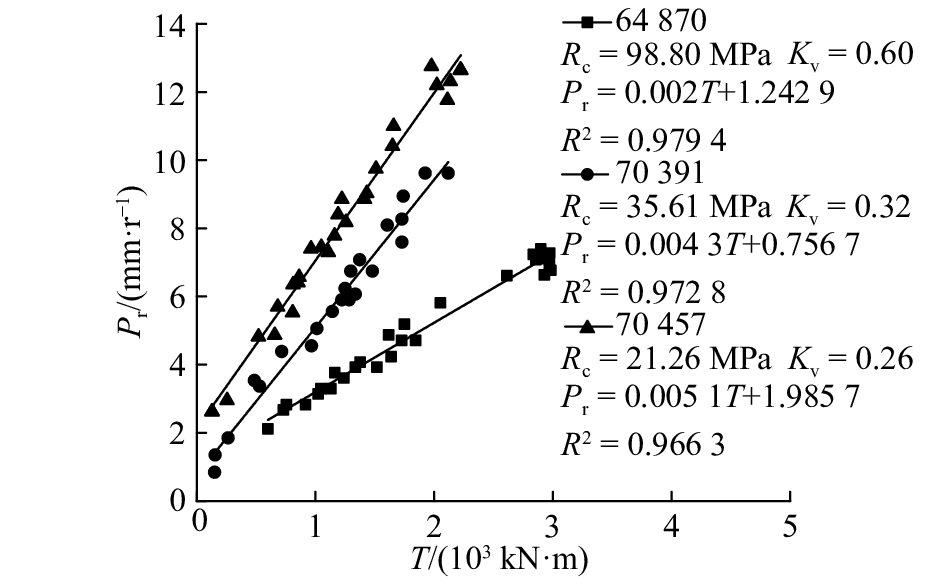
刀盘扭矩是TBM另一主要破岩动力,来源于滚刀在高低起伏的切割槽中滚动时刀刃与岩石的滚动摩擦力. 图10为TBM在不同刀盘扭矩作用下的掘进曲线(以桩号64 870、70 391、70 457为例). 可以看出,在不同岩石饱和单轴抗压强度、完整性系数的条件下,刀盘贯入度随刀盘扭矩均呈线性(相关系数均大于0.95)变化趋势,这与宋克志等[20]的研究结果一致. 岩石强度越小、完整性越差,直线斜的率越大,刀盘贯入度随刀盘扭矩增长越快. 同时,3条直线的截距均大于零,这是由于在挤压和起裂阶段已致使岩面产生了一定贯入度. 根据曲线回归结果,可以将贯入度与刀盘扭矩之间的关系式表示为
| ${P_{\rm r}} = kT + b. $ | (5) |
式中:k为刀盘滚动系数,描述刀盘扭矩对贯入度的影响大小;b为初始贯入度,即挤压和起裂阶段产生的贯入度. 为了分析不同岩石情况下k、b的变化规律,对表2中所有围岩情况下的Pr-T曲线进行统计回归分析,结果如表4、图11~12所示.
|
图 10 贯入度与刀盘扭矩的关系 Fig. 10 Relationship between penetration rate and cutterhead torque |
| 表 4 贯入度与刀盘扭矩关系曲线的参数统计结果 Table 4 Statistical results of curve parameters of penetration rate and cutterhead thrust |
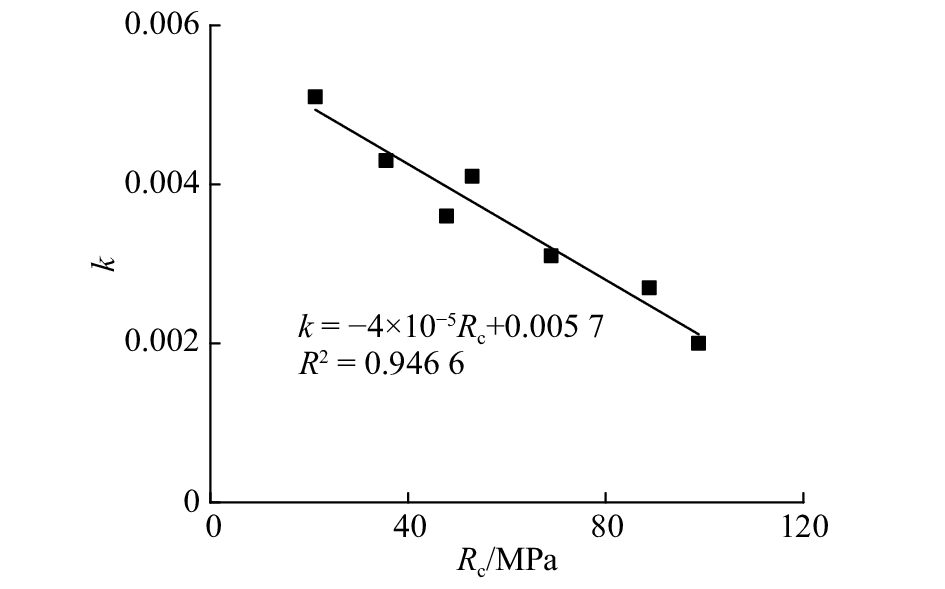
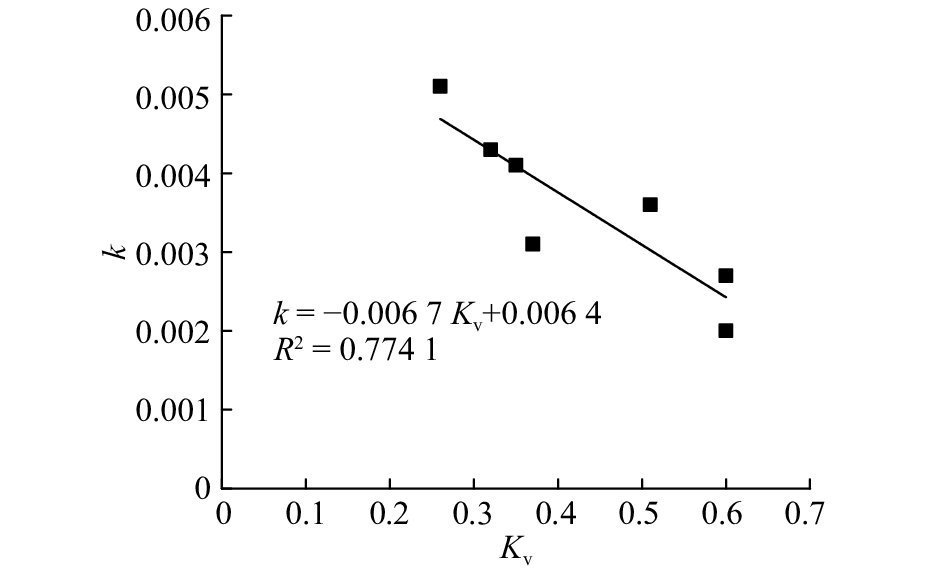
从表4可以发现,初始贯入度b为0~2 mm/r,与贯入度特征曲线分析结果相符. 在实际隧道掘进中,正常情况下,一般要求初始贯入度从1 mm/r开始增加,故取b值为1 mm/r. 从图11、12可以看出,滚动系数k随岩石强度、完整性系数的增加而线性降低,说明岩石质量越好,刀盘扭矩对破岩的贡献占比越低,此时需要推力发挥更大的作用. 根据图11、12的回归结果,进一步进行二元回归,可得到滚动系数与岩石饱和单轴抗压强度、完整性系数的关系式为
| $ k = {\rm{ - 3}} \times 10^{-5}{R_{\rm{c}}} - 0.001{\rm{ }}\,\,4\,\;{K_{\rm{v}}} + 0.006, \, {R^2} = 0.956 \,\, 4. $ | (6) |
|
图 11 刀盘滚动系数与岩石饱和单轴抗压强度的关系 Fig. 11 Relationship between cutterhead rolling coefficient and rock saturated uniaxial compressive strength |
|
图 12 刀盘滚动系数与岩体完整性系数的关系 Fig. 12 Relationship between cutterhead rolling coefficient and rock mass integrity coefficient |
TBM的施工预测主要包括掘进速率和刀具磨损的预测,不仅为项目可行性研究阶段进行经济评估和施工方法选择提供重要依据,还可以有效帮助施工方进行进度和成本管理;通过推力、扭矩等操作参数的预测,可以判断掘进机运行是否正常,状态是否良好,并且可以反映掌子面前方地质条件的变化情况,从而实现操作参数的优化调整,安全、高效地掘进. 所以TBM施工预测研究一直是行业内的热门课题. 但由于掘进机与岩体相互作用的复杂性,很难从理论上全面解释TBM性能与地质条件的相关性. 刘泉声等[24]在总结分析国内外已有的TBM施工预测模型的基础上,建议对TBM施工现场数据和地质资料进行收集和利用,开发经验性TBM施工预测模型.
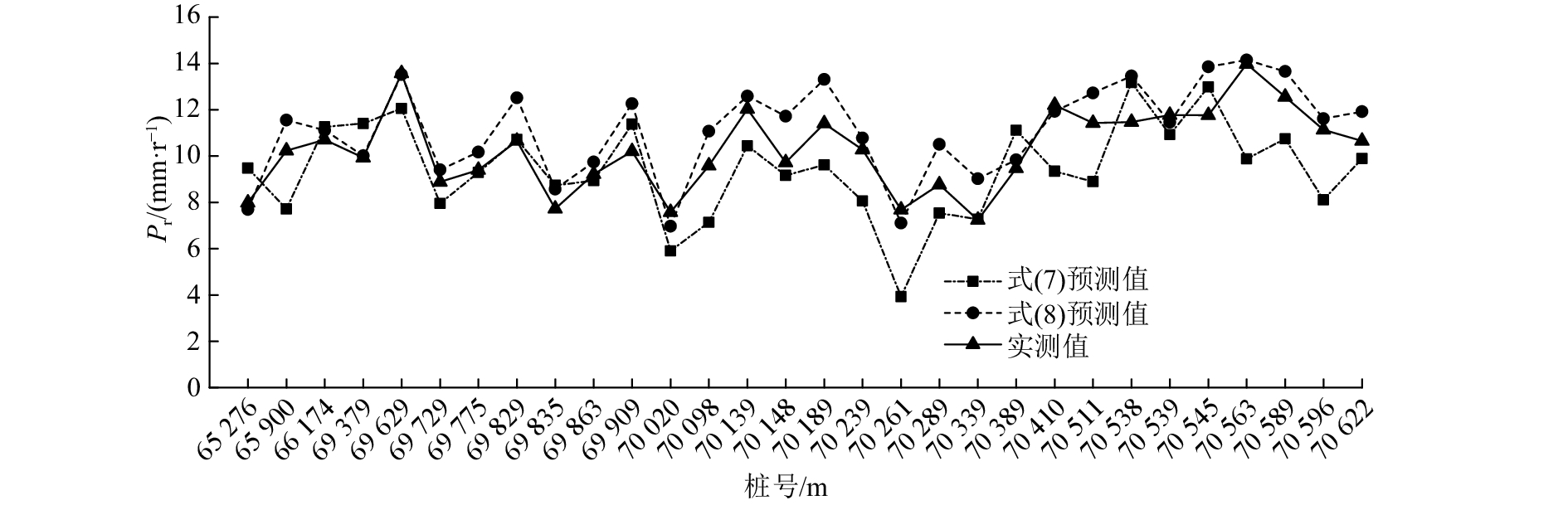
由式(2)~(6)建立TBM掘进速率模型如下:
| ${P_{\rm r}} = {\left( {\frac{F}{{1 \,\, 600\ln {R_{\rm c}}{\rm{ + }}91.50\ln {K_{\rm v}} - 173.60}}} \right)^\alpha },$ | (7) |
| ${P_{\rm{r}} = (-3 \times 10^{-5}{R_{\rm{c}}} - 0.001\,\,4\,\,{K_{\rm{v}}} + 0.006} )T + 1. $ | (8) |
式中:
|
图 13 刀盘贯入度预测值与实测值对比 Fig. 13 Comparison between actual and predicted penetration rates |
|
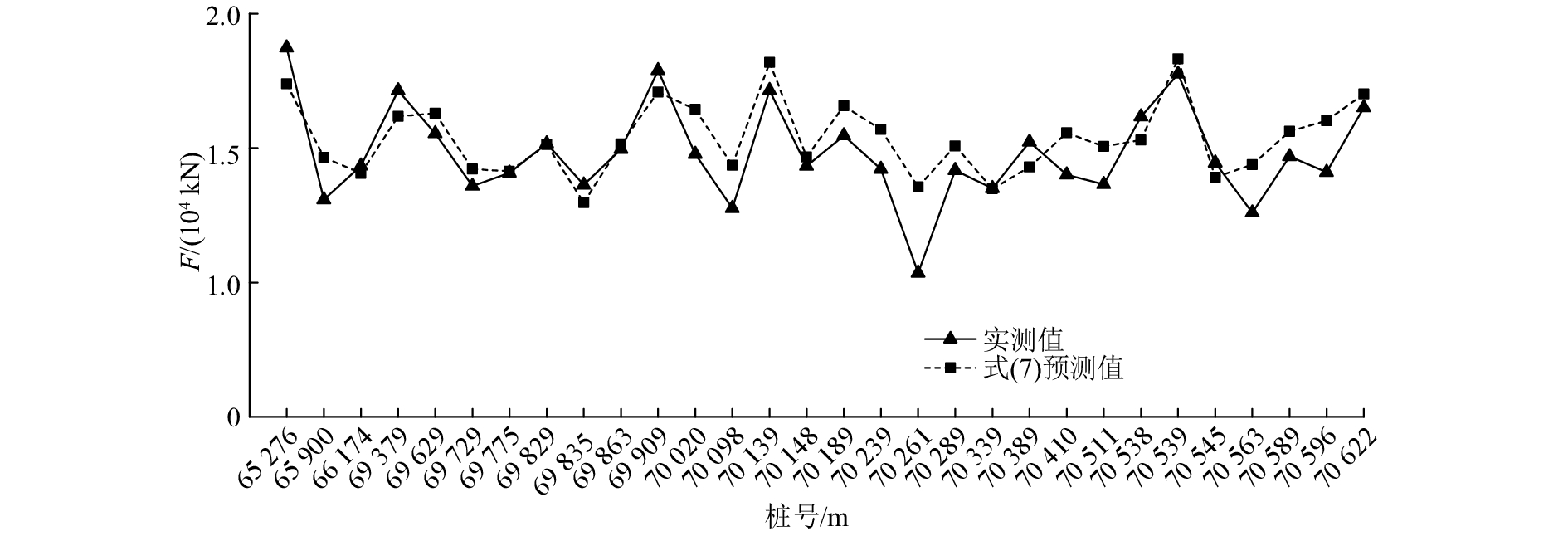
图 14 刀盘推力预测值与实测值对比 Fig. 14 Comparison between actual and predicted cutterhead thrusts |
|
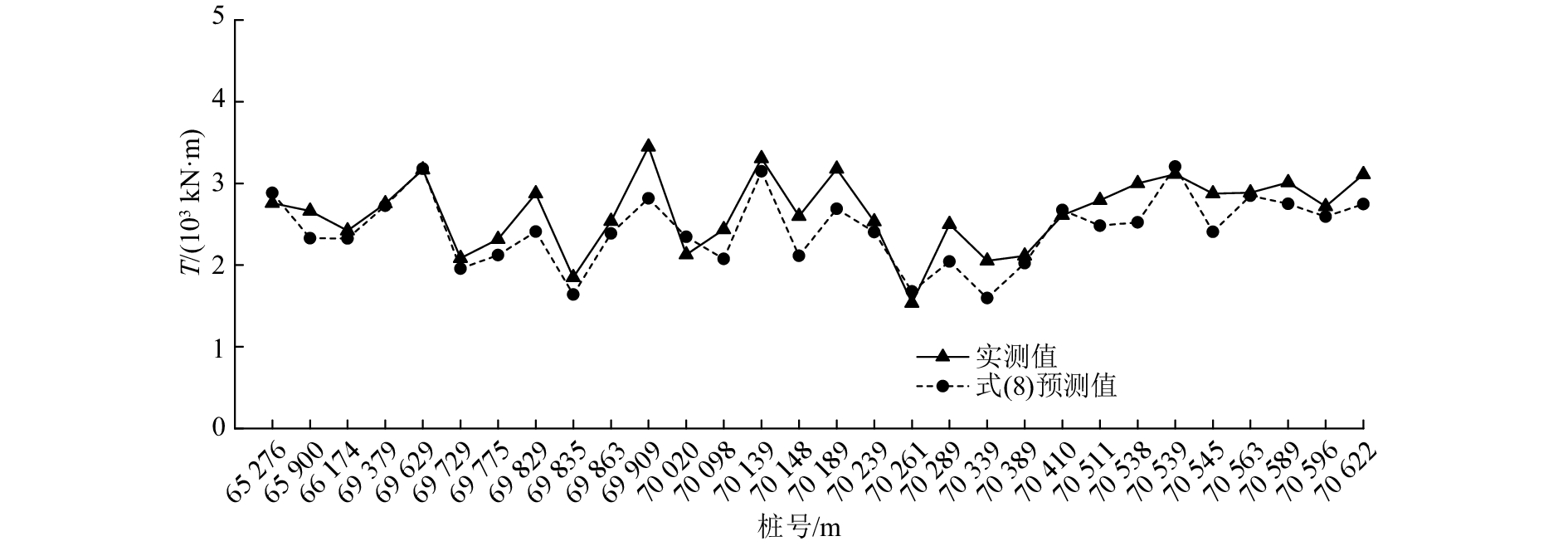
图 15 刀盘扭矩预测值与实测值对比 Fig. 15 Comparison between actual and predicted cutterhead torques |
基于吉林引松供水工程TBM3标段隧道灰岩地层现场掘进数据,分析TBM刀盘破岩过程,研究刀盘贯入度与刀盘推力、扭矩及岩石强度、完整性之间的关系,主要得到以下结论.
1)TBM刀盘破岩分为挤压、起裂和破碎3个阶段. 挤压阶段贯入度约为1~2 mm,当刀盘推力达到破岩门槛值时进入起裂阶段,起裂阶段贯入度、刀盘推力和扭矩同步突变;破碎阶段贯入度增长快,破岩迅速.
2)破碎阶段刀盘贯入度随刀盘推力增大呈幂函数增长,增长率与岩石饱和单轴抗压强度、岩体完整性系数呈复杂的对数关系;而随刀盘扭矩加大呈线性增长,增长率随岩石饱和单轴抗压强度、岩体完整性系数增加而线性降低.
3)随着TBM施工信息化程度提高,施工数据采集利用条件得以改善,对于某一特定的设备、施工条件和工程地质条件,可以建立类似式(7)、(8)的经验模型,预测掘进机运行参数,并可据此捕捉不良地质条件.
由于涉及的岩体、机液影响因素比较少,工程数据量有待增加,尤其是岩体参数有限,施工预测模型有很大的完善空间,预测精度和适用性有待进一步提高,将在后续工作中研究.
| [1] |
ROSTAMI J. Development of a force estimation model for rock fragmentation with disc cutters through theoretical modeling and physical measurement of crushed zone pressure [D]. Colorado: Colorado School of Mines, 1997 https://www.researchgate.net/publication/307167689_DEVELOPMENT_OF_A_FORCE_ESTIMATION_MODEL_FOR_ROCK_FRAGMENTATION_WITH_DISC_CUTTERS_THROUGH_THEORETICAL_MODELING_AND_PHYSICAL_MEASUREMENT_OF_CRUSHED_ZONE_PRESSURE
|
| [2] |
CHEN L H, LABUZ J F. Indentation of rock by wedge-shaped tools[J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(7): 1023-1033. DOI:10.1016/j.ijrmms.2006.03.005 |
| [3] |
姚羲和, 赵晓豹, 龚秋明, 等. 滚刀线性侵入试验中岩石破裂模式研究[J]. 岩土工程学报, 2014, 36(9): 1705-1713. YAO Xi-he, ZHAO Xiao-bao, GONG Qiu-ming, et al. Linear cutting experiments on crack modes of rock under indentation of a single disc cutter[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(9): 1705-1713. |
| [4] |
CHANG S H, CHOI S W, BAE G J, et al. Performance prediction of TBM disc cutting on granitic rock by the linear cutting test[J]. Tunnelling and Underground Space Technology, 2006, 21(3): 271-285. |
| [5] |
龚秋明, 何冠文, 赵晓豹, 等. 掘进机刀盘滚刀间距对北山花岗岩破岩效率的影响实验研究[J]. 岩土工程学报, 2015, 37(1): 54-60. GONG Qiu-ming, HE Guan-wen, ZHAO Xiao-bao, et al. Influence of different cutter spacings on rock fragmentation efficiency of Beishan granite by TBM[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(1): 54-60. |
| [6] |
莫振泽, 李海波, 周青春, 等. 楔刀作用下岩石微观劣化的试验研究[J]. 岩土力学, 2012, 33(5): 1333-1340. MO Zhen-ze, LI Hai-bo, ZHOU Qing-chun, et al. Experimental study of rock microscopic deterioration under wedge cutter[J]. Rock and Soil Mechanics, 2012, 33(5): 1333-1340. DOI:10.3969/j.issn.1000-7598.2012.05.009 |
| [7] |
马洪素, 龚秋明, 王驹, 等. 围压对TBM滚刀破岩影响规律的线性切割试验研究[J]. 岩石力学与工程学报, 2016, 35(2): 346-355. MA Hong-su, GONG Qiu-ming, WANG Ju, et al. Linear cutting tests on effect of confining stress on rock fragmentation by TBM cutter[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(2): 346-355. |
| [8] |
马洪素, 纪洪广. 节理倾向对TBM滚刀破岩模式及掘进速率影响的试验研究[J]. 岩石力学与工程学报, 2011, 30(1): 155-163. MA Hong-su, JI Hong-guang. Experimental study of the effect of joint orientation on fragmentation modes and penetration rate under TBM disc cutters[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(1): 155-163. |
| [9] |
刘泉声, 潘玉丛, 孔晓璇, 等. TBM滚刀贯入过程中泥岩破坏特征试验研究[J]. 岩土力学, 2016, 37(S1): 166-174. LIU Quan-sheng, PAN Yu-cong, KONG Xiao-xuan, et al. Experimental investigation on mudstone fragmentation characteristics in indentation process by TBM disc cutter[J]. Rock and Soil Mechanics, 2016, 37(S1): 166-174. |
| [10] |
CHO J W, JEON S, YU S H, et al. Optimum spacing of TBM disc cutters: a numerical simulation using the three-dimensional dynamic fracturing method[J]. Tunnelling and Underground Space Technology, 2010, 25(3): 230-244. DOI:10.1016/j.tust.2009.11.007 |
| [11] |
满林涛, 李守巨. 盘形滚刀破岩过程有限元数值模拟[J]. 工程建设, 2011, 43(4): 1-5. MAN Lin-tao, LI Shou-ju. Finite element numerical simulation of process of rock breaking by disc cutter[J]. Engineering Construction, 2011, 43(4): 1-5. |
| [12] |
蒋明镜, 孙亚, 王华宁, 等. 全断面隧道掘进机破岩机理离散元分析[J]. 同济大学学报: 自然科学版, 2016, 44(7): 1038-1044. JIANG Ming-jing, SUN Ya, WANG Hua-ning, et al. Rock failure mechanism analysis with discrete element method by using tunnel boring machine[J]. Journal of Tongji University: Natural Science, 2016, 44(7): 1038-1044. |
| [13] |
莫振泽, 李海波, 周青春, 等. 基于UDEC的隧道掘进机滚刀破岩数值模拟研究[J]. 岩土力学, 2012, 33(4): 1196-1202. MO Zhen-ze, LI Hai-bo, ZHOU Qing-chun, et al. Research on numerical simulation of rock breaking using TBM disc cutters based on UDEC method[J]. Rock and Soil Mechanics, 2012, 33(4): 1196-1202. DOI:10.3969/j.issn.1000-7598.2012.04.035 |
| [14] |
张魁, 夏毅敏, 林赉贶, 等. TBM刀具作用下节理岩石破碎模式研究[J]. 现代隧道技术, 2016, 53(2): 148-156. ZHANG Kui, XIA Yi-min, LIN Lai-kuang, et al. Breaking modes of jointed rock under a TBM cutter[J]. Modern Tunnelling Technology, 2016, 53(2): 148-156. |
| [15] |
张魁, 夏毅敏, 谭青, 等. 不同围压条件下TBM刀具破岩模式的数值研究[J]. 岩土工程学报, 2010, 32(11): 1780-1787. ZHANG Kui, XIA Yi-min, TAN Qing, et al. Numerical study on modes of breaking rock by TBM cutter under different confining pressures[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1780-1787. |
| [16] |
孙金山, 陈明, 陈保国, 等. TBM滚刀破岩过程影响因素数值模拟研究[J]. 岩土力学, 2011, 32(6): 1891-1897. SUN Jin-shan, CHEN Ming, CHEN Bao-guo, et al. Numerical simulation of influence factors for rock frag mentation by TBM cutters[J]. Rock and Soil Mechanics, 2011, 32(6): 1891-1897. DOI:10.3969/j.issn.1000-7598.2011.06.048 |
| [17] |
施文俊, 袁宝远. DDA模拟TBM破岩机理[J]. 科学技术与工程, 2012, 12(20): 5101-5104. SHI Wen-jun, YUAN Bao-yuan. TBM failure rock mechalism with DDA simulation[J]. Science Technology and Engineering, 2012, 12(20): 5101-5104. DOI:10.3969/j.issn.1671-1815.2012.20.053 |
| [18] |
卢瑾, 高捷, 梅稚平. 岩石力学参数对TBM掘进速率的影响分析[J]. 水电能源科学, 2010, 28(7): 44-46. LU Jin, GAO Jie, MEI Zhi-ping. Influence analysis of rock mechanical parameters on TBM penetrating rate[J]. Water Resources and Power, 2010, 28(7): 44-46. DOI:10.3969/j.issn.1000-7709.2010.07.013 |
| [19] |
BRULAND A. Hard rock tunnel boring [D].Trondheim: Norwegian University of Science and Technology, 1998
|
| [20] |
宋克志, 孙谋. 复杂岩石地层盾构掘进效能影响因素分析[J]. 岩石力学与工程学报, 2007, 26(10): 2092-2096. SONG Ke-zhi, SUN Mou. Analysis of influencing factors of shield tunneling performance in complex rock strata[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(10): 2092-2096. DOI:10.3321/j.issn:1000-6915.2007.10.019 |
| [21] |
GONG Q M, ZHAO J, JIANG Y S. In situ TBM penetration tests and rock mass boreability analysis in hard rock tunnels[J]. Tunnelling and Underground Space Technology, 2007, 22(3): 303-316. DOI:10.1016/j.tust.2006.07.003 |
| [22] |
杜立杰, 齐志冲, 韩小亮, 等. 基于现场数据的TBM可掘性和掘进性能预测方法[J]. 煤炭学报, 2015, 40(6): 1284-1289. DU Li-jie, QI Zhi-chong, HAN Xiao-liang, et al. Prediction method for the boreability and performance of hard rock TBM based on boring data on site[J]. Journal of China Coal Society, 2015, 40(6): 1284-1289. |
| [23] |
龚秋明, 佘祺锐, 侯哲生, 等. 高地应力作用下大理岩岩体的TBM掘进试验研究[J]. 岩石力学与工程学报, 2010, 29(12): 2522-2532. GONG Qiu-ming, SHE Qi-rui, HOU Zhe-sheng, et al. Experimental study of TBM penetration in marble rock mass under high geostress[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(12): 2522-2532. |
| [24] |
刘泉声, 刘建平, 潘玉丛, 等. 硬岩隧道掘进机性能预测模型研究进展[J]. 岩石力学与工程学报, 2016, 35(S1): 2766-2786. LIU Quan-sheng, LIU Jian-ping, PAN Yu-cong, et al. Research advances of tunnel boring machine performance prediction models for hard rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(S1): 2766-2786. |



