颗粒物质是由大量相互作用的颗粒组成的复杂体系. 颗粒物质广泛存在于食品、制药、化工、能源等领域[1]. 颗粒在回转装置中的混合是农业及工业生产中的一个重要过程,混合质量直接影响产品的质量. 当使用固体热载体法进行油页岩干馏时,油页岩和固体热载体良好混合才能保证有效的热量传递,获得比较高的干馏效率[2]. 因此有必要对回转干馏炉内的颗粒混合进行研究.
二元颗粒在回转装置中的运动和混合受到多种因素的影响,例如颗粒的黏结性、密度、尺寸、形状等. 高红利等[3]通过数值模拟比较二元湿颗粒体系和干颗粒体系的混合过程,结果表明,二元湿颗粒在液桥力的作用下不易分离,湿颗粒体系的混合效果优于干颗粒体系. 黄德财等[4]采用分子动力学方法研究颗粒密度对二元颗粒体系混合分离的影响,发现增大小颗粒密度使二元颗粒体系出现巴西果分离,增大大颗粒密度使二元颗粒体系出现反巴西果分离. Yamamoto等[5]通过研究发现,在二元颗粒体系中,颗粒的密度比越大,2种颗粒的混合程度越低,混合速度越慢. 陈辉等[6]研究尺寸差异和密度差异对回转窑内二元颗粒混合的影响,分析表明,合理配置体积比和密度比,可以使渗流和凝聚作用相互平衡,使颗粒物料混合均匀. Nielsen等[7]对二元颗粒在滚筒中混合过程的研究表明,相对于小颗粒和高密度颗粒,大颗粒和低密度颗粒更集中地分布在物料的上部. Hohner等[8]研究球形颗粒和多面体颗粒在滚筒内的运动混合情况,结果表明球形颗粒的混合速度比多面体颗粒快. 耿凡等[9]采用离散单元法对杆状颗粒和球形颗粒在滚筒干燥器内的混合过程进行数值模拟,结果发现,杆状颗粒的混合速率和混合效果均优于球形颗粒.
在回转装置中设置内构件可以破坏涡心区,提高颗粒系统的混合程度,不少学者对设置内构件的回转装置进行了研究. 李少华等[10]采用离散单元法研究了直抄板、直角抄板、弯抄板对回转式干馏炉内颗粒混合质量的影响. Karali等[11]通过图像分析法处理实验结果,研究直角抄板的切向径向长度比对滚筒最佳物料装载量的影响. Machado等[12]研究边界条件对内置单一直角抄板滚筒内颗粒流动特性的影响. Sunkara等[13]通过实验和建立数学模型的方法研究直角抄板切向径向长度比对抄板搬运量、抄板卸料速度和颗粒物料分布的影响. Bhattacharya等[14]分别在水平滚筒混合器中心安装C形、S形、反S形和直抄板,以此来抑制颗粒的分离作用,通过模拟和实验的方法探索最优的挡板设计. 赵永志等[15]通过在圆形滚筒中心设置十字形内构件来增强颗粒的混合,十字内构件存在一个最优尺寸,内构件过小和过大都不利于颗粒间的混合.
虽然不少学者研究安装内构件回转装置内颗粒的运动混合,但是大多数研究在回转装置圆周筒壁或者圆心区域安装内构件,很少根据涡心区(颗粒混合较差的区域)的尺寸和位置设置内构件. 根据无挡板回转炉内颗粒涡心区的尺寸和位置,在距离回转炉圆心21 mm处分别设置一边形、二边形、三边形、四边形和半圆形(无穷边形)挡板,各形状挡板的外接圆半径相等. 研究挡板形状对挡板卸料特性、颗粒速度矢量分布和颗粒混合程度的影响. 为确定合适的挡板形状以提高颗粒的混合质量提供理论依据,为回转干馏炉的优化设计提供参考.
1 DEM模型的建立离散单元法(discrete element method,DEM)由Cundall和Strack提出[16],建立在基本的牛顿运动定律上,用于研究非连续性颗粒物质的结构和运动规律. 颗粒在回转炉中的运动属于密集颗粒流,采用基于软球模型的离散单元法. 软球模型将颗粒间的法向力简化为弹簧和阻尼器,切向力简化为弹簧、阻尼器和滑动器. 不考虑颗粒表面变形,依据颗粒间的法向重叠量和切向位移计算接触力.
颗粒之间以及颗粒和回转炉之间的接触力模型选用Hertz-Mindlin (No Slip)模型. 接触力主要有3种计算模型:线性接触力模型、Hertz-Mindlin模型和Hertz-Mindlin (No Slip)模型. 在密集颗粒流中采用Hertz-Mindlin (No Slip)模型来计算接触力不仅能够保证计算精度,而且能够避免计算量过大[17]. 回转炉中的颗粒运动属于密集颗粒运动,选用Hertz-Mindlin (No Slip)模型. 在Hertz-Mindlin (No Slip)模型中,法向力基于Hertz接触理论,切向力基于Mindlin-Deresiewicz理论[17].
法向力为
| ${{{F}}_{\rm{n}}} = {\rm{(}} - {K_{\rm{n}}}{\alpha ^{3/2}} - {C_{\rm{n}}}{v _{\rm{n}}}){{n}}.$ | (1) |
式中:Kn为法向弹性系数,α为法向重叠量,Cn为法向阻尼系数,νn为法向相对速度,n为颗粒球心间的单位矢量.
切向力为
| ${{{F}}_{\rm{t}}} = \min \; ( - {K_{\rm{t}}}\eta - {C_{\rm{t}}}{v _{\rm{t}}}, \; - \mu \left| {{{{F}}_{\rm{n}}}} \right|){{t}}. $ | (2) |
式中:Kt为切向弹性系数,η为接触点的切向位移,Ct为切向阻尼系数,νt为接触点的滑移速度,μ为滑动摩擦系数,t为切向单位矢量.
模拟中的回转炉采用圆柱形回转炉,半径为42 mm,深度为19 mm,回转炉及挡板材料为钢材,泊松比ν=0.3,剪切模量G=7.5×1010 Pa,密度ρ=7 800 kg/m3. 考虑到计算机计算量以及实验室规模下回转炉模型为小尺度回转炉[2],对小尺度物理模型下二元颗粒在回转炉中的运动及混合进行数值模拟. 王瑞芳等[1]和陈辉等[17]同样对小尺度物理模型下的颗粒运动进行了研究. 随着转速的提高,颗粒在回转装置中的运动模式依次经历滑移、阶梯、滚落、泄落、抛落、离心等运动模式[18]. 滚落模式为工业中的常用模式[7],因此主要研究颗粒在滚落模式下的混合及运动状态. 根据之前的工作[19],设置滚筒转速为25 r/min时,颗粒运动模式为滚落模式. 在仿真中,对于大颗粒粒径以及大小颗粒整体体积比,参考前期的工作[20],大颗粒直径为3 mm,2种颗粒的整体体积比为1 : 1. 小颗粒直径为变量. 大颗粒和小颗粒的粒径比δ=dlarge : dsmall,分别参考笔者[20]和Bhattacharya等[14]的研究,设置最大粒径比和最小粒径比分别为3.0和1.5;δ的间隔为0.5,选用的δ分别为3.0、2.5、2.0、1.5. 在农业及工业生产中,回转装置内常用的物料填充率为1/3~1/2[21],因此设置颗粒的填充率为1/3. 填充完成后大颗粒数量为626. 大、小颗粒的密度参考油页岩和页岩灰颗粒的密度[22]. 参考王恭等[23]的研究,设置颗粒的相关参数,如表1和2所示. 在回转炉中安装n边形挡板(n=1, 2, 3, 4, ∞),挡板自身各边长相等,挡板厚度为1 mm. 挡板外接圆直径为12 mm,如图1所示. 涡心区中心大约位于距离回转炉圆心21 mm处,挡板外接圆圆心距离回转炉圆心21 mm. 只研究挡板形状的影响,因此挡板的数量是固定的. 挡板数量参考Yamamoto等[5]的工作,同一回转炉内均匀安装4个挡板. 0~1 s为颗粒生成时间,先生成小颗粒再生成大颗粒. 当粒径比为1.5时颗粒填充完成后的回转炉截面图如图2所示. 从1 s开始,回转炉以25 r/min的转速顺时针转动,30 s时数值模拟停止.
在前期工作中,研究二元球形颗粒在圆周筒壁安装抄板的回转干馏炉内的混合[20]以及柱状生物质颗粒在无内构件回转炉中的运动[24],通过实验和离散单元法数值模拟对颗粒分布和混合形态进行对比,实验结果和模拟结果吻合得较好,验证了数值模拟的合理性. 在数据提取方面,数值模拟比实验更具优势. 借助离散单元法进行数值模拟,初步探索回转炉内挡板形状对二元颗粒运动混合的影响.
| 表 1 油页岩颗粒和页岩灰颗粒的物理性质 Table 1 Physical properties of oil shale particles and oil shale ash particles |
| 表 2 大小颗粒间及颗粒与回转炉之间的力学性质 Table 2 Mechanical properties of large and small particles and between particles and rotary retort |
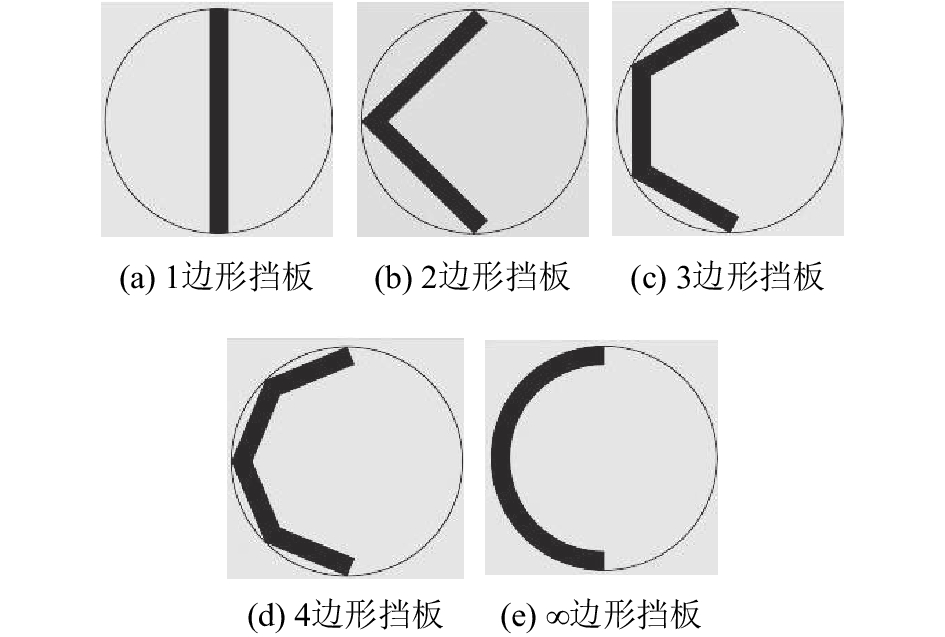
|
图 1 外接圆半径相同及边数不同的挡板示意图 Fig. 1 Flights with different sides and same radius of circumcircle |
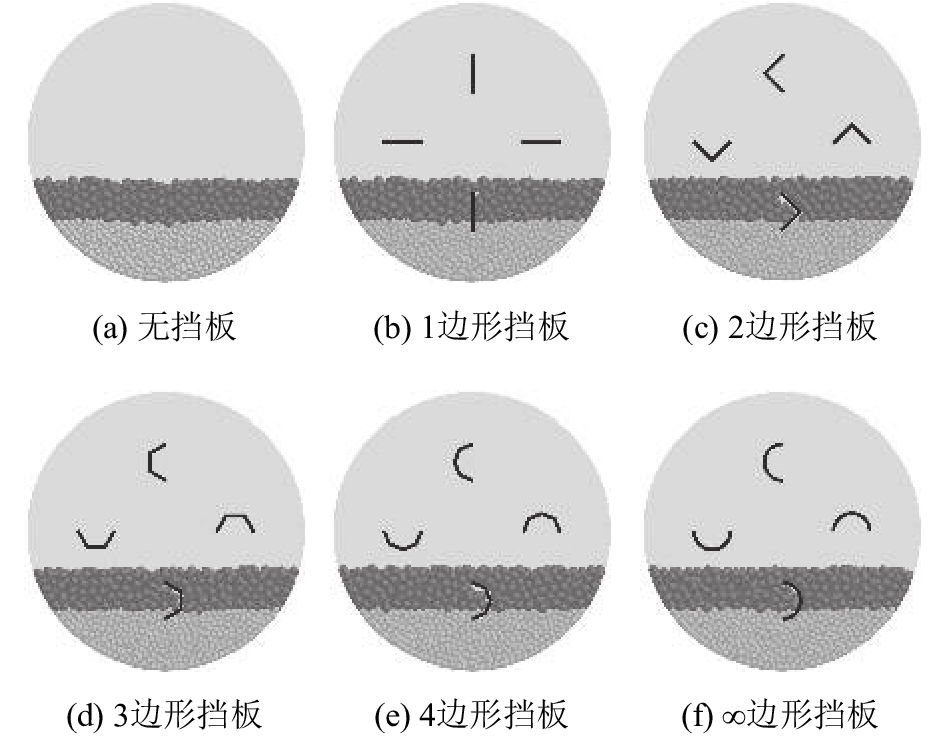
|
图 2 当粒径比为1.5时颗粒填充完成状态 Fig. 2 States after generating all particles for particle diameter ratio of 1.5 |
2种或2种以上颗粒在回转炉的带动下运动时,受到混合机制和分离机制的共同作用. 混合机制使不同种颗粒的分布趋于均匀,分离机制使颗粒的分布趋于不均匀. 分离机制包括渗流作用和凝聚作用,渗流作用指体积偏小的颗粒在物料表层运动时会渗流至物料的中心区域,凝聚作用指密度偏大的颗粒在物料表层运动时逐渐下沉,向物料的中心区域集中[12]. 在Machado等 [12]的研究中,体积较小的颗粒密度较小,渗流作用和凝聚作用相互竞争,合理配置密度比和体积比可以平衡2种作用,使物料接近均匀混合,只有一种作用占优时会产生径向分离. 体积较小的颗粒密度较大(ρlarge : ρsmall=2 200 : 2 600),渗流和凝聚作用相互促进,2种作用都使小颗粒向中心区域集中. 在回转炉运行一段时间后,混合机制和分离机制达到动态平衡,颗粒系统呈现出稳定的分布特点. 图3为30 s时颗粒的混合形态,可以看出,小颗粒集中分布在颗粒物料的涡心区,大颗粒集中分布在物料的外围区域.
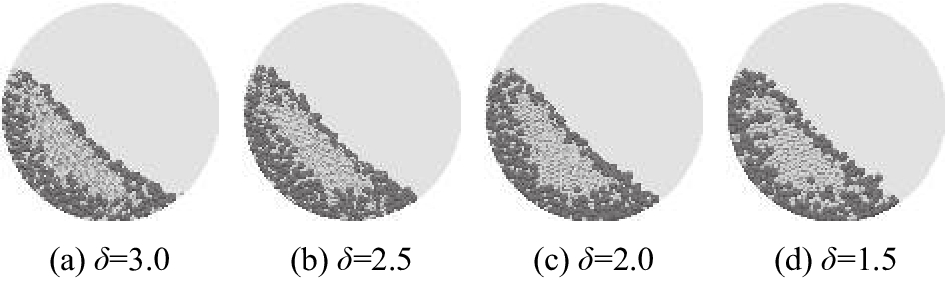
|
图 3 在无挡板、各粒径比下二元颗粒30 s时的混合形态 Fig. 3 Mixing forms of binary particles in rotary retorts without flights at 30 s for different particle diameter ratios |
使用接触数指标来定量评价2种颗粒的混合程度,接触数指标[10]为
| $M = \frac{{{c_{{\rm{ls}}}}}}{{{c_{{\rm{ll}}}} + {c_{{\rm{ls}}}} + {c_{{\rm{ss}}}}}}.$ | (3) |
式中:
图4为接触数指标M随时间t的变化曲线,8 s后各曲线进入稳定波动阶段,对8 s后的M取时间平均值. 当δ分别为3.0、2.5、2.0、1.5时,时均M值分别为0.157、0.175、0.205、0.288. 当渗流和凝聚作用相互促进,即较小的颗粒密度较大时,固定颗粒密度和一种颗粒的粒径,2种颗粒粒径相差越大,混合程度越低.
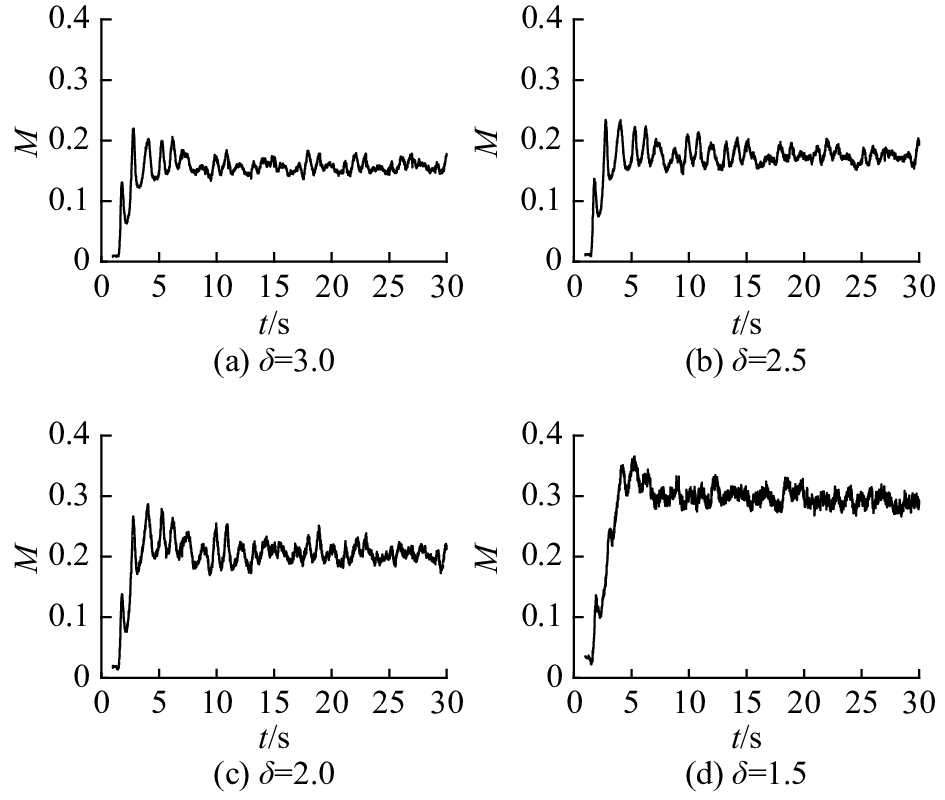
|
图 4 在无挡板、不同粒径比下接触数指标随时间的变化曲线 Fig. 4 Variations of contact number index with time in rotary retorts without flights for different particle diameter ratios |
以δ=1.5为例,在回转炉中设置挡板,探索挡板形状对二元颗粒运动混合的影响. 如果没有特殊说明,讨论δ=1.5的情况.
2.2 挡板对颗粒运动混合的影响 2.2.1 挡板对颗粒运动模式的影响探讨δ=1.5时挡板对颗粒运动模式的影响. 当回转炉内不安装挡板时,颗粒的运动模式为滚落模式,颗粒从左上方流出,进入物料表层,在物料表层颗粒从左上方向右下方流动,同时不断有颗粒从右下方流入颗粒群主体内部.
当回转炉内安装挡板时,滚落模式被破坏,最明显的特征是产生了颗粒瀑布流. 颗粒瀑布流可以分为主体颗粒瀑布流和悬空颗粒瀑布流. 以安装半圆挡板为例进行说明,当挡板未脱离颗粒群主体时形成的颗粒瀑布流为主体颗粒瀑布流,当挡板脱离了颗粒群主体时形成的颗粒瀑布流为悬空颗粒瀑布流,如图5所示.
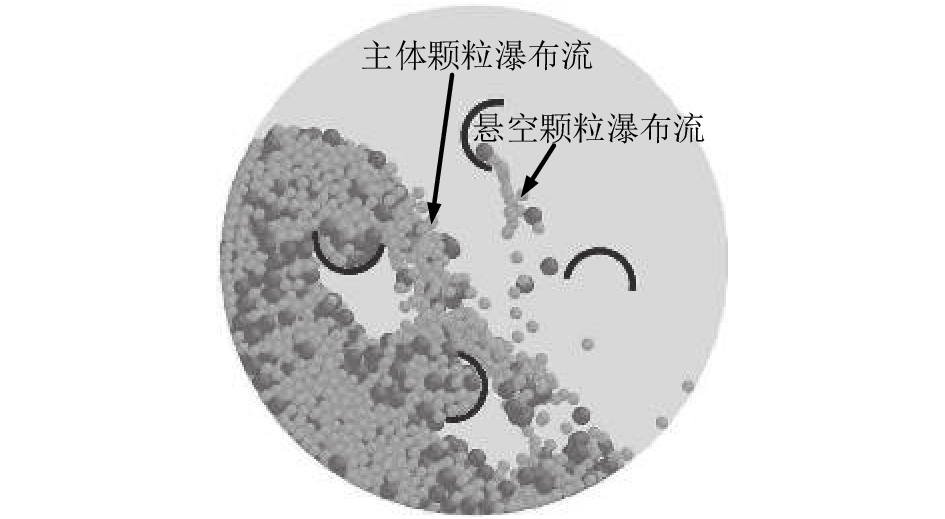
|
图 5 ∞边形挡板在卸料过程中产生的2种颗粒瀑布流 Fig. 5 Two kinds of cascading curtains of particles formed during unloading processes with ∞ side flight |
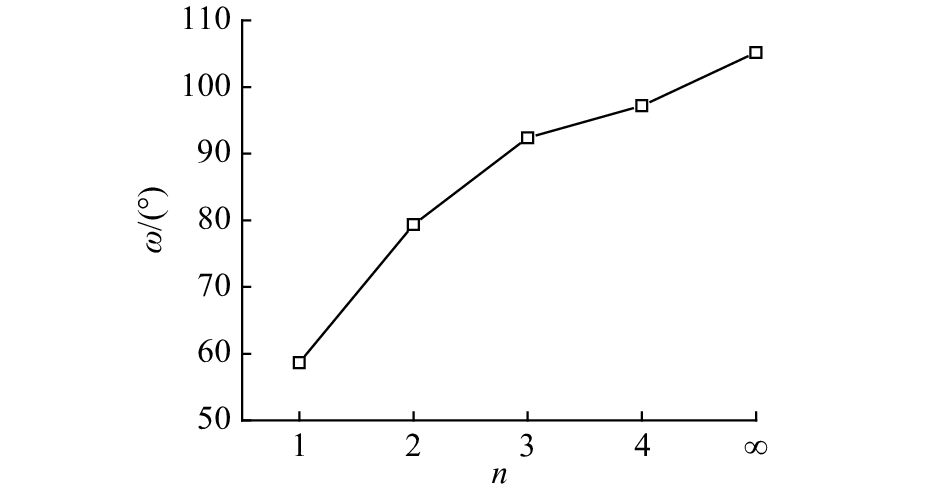
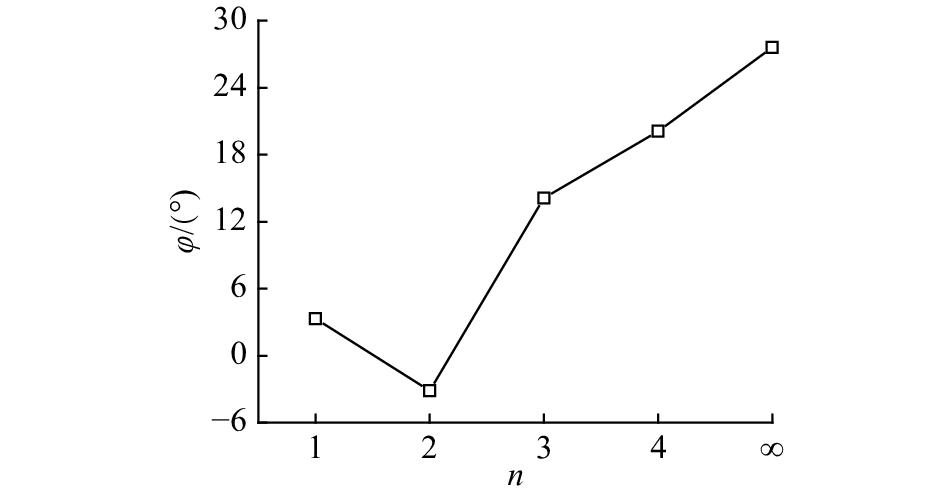
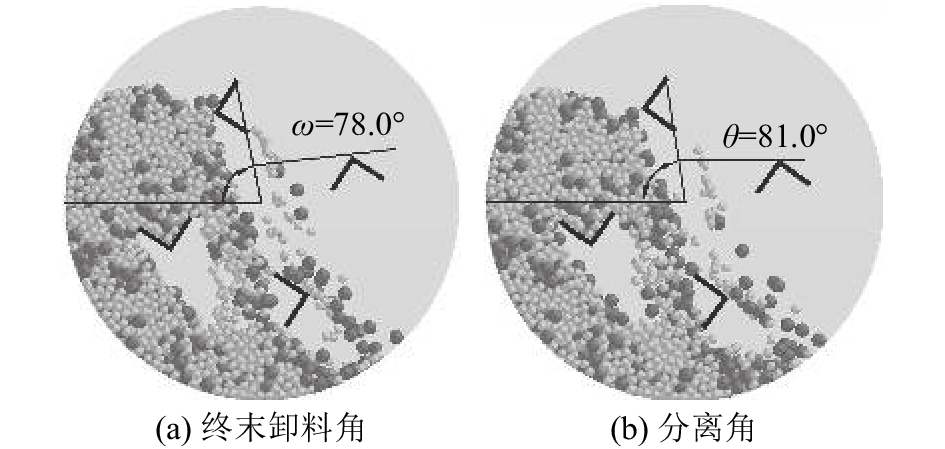
定义挡板与颗粒群主体刚分离时,挡板外接圆直径与回转炉左侧水平射线之间的夹角为分离角θ,如图6(a)所示;定义挡板上方的最后一个颗粒离开挡板时,挡板外接圆直径与回转炉左侧水平射线之间的夹角为终末卸料角ω,如图6(b)所示;定义在挡板的一次卸料过程中,终末卸料角与分离角之差为悬空扫角φ. 对各个回转炉运行过程中挡板的最后10次卸料过程中的终末卸料角进行测量,求取平均值,平均终末卸料角与挡板边数n的关系如图7所示. 图7表明,挡板边数越多,平均终末卸料角越大. 原因是边数越多,挡板内能容纳的颗粒越多;挡板边数越少,颗粒越容易从挡板中流出. 挡板边数越多,卸下全部颗粒所需要的时间越多,平均终末卸料角越大. 对各个回转炉运行过程中挡板的最后10次卸料过程中的分离角进行测量,计算出悬空扫角,求取平均值. 图8为平均悬空扫角随挡板边数n的变化曲线. 当悬空扫角为正值时,未完成卸料的挡板存在悬空状态,在挡板卸料的后期,挡板脱离颗粒群主体,在颗粒群主体的上方完成卸料,形成悬空颗粒瀑布流. 当悬空扫角为负值时,说明挡板还没脱离颗粒群主体时已经完成卸料,仅存在主体颗粒瀑布流. 当挡板边数为2时,平均悬空扫角为–3.2°. 如图9所示为随机选取的2边形挡板卸料过程,分离角大于终末卸料角,悬空扫角为负. 如果悬空扫角为负值,当挡板内部已经没有颗粒时,挡板底部仍然没有完全脱离颗粒群主体. 在回转炉运行过程中,仅存在主体颗粒瀑布流. 对于安装其他边形挡板,平均悬空扫角为正,在回转炉运行过程中,主体颗粒瀑布流和悬空颗粒瀑布流共存.
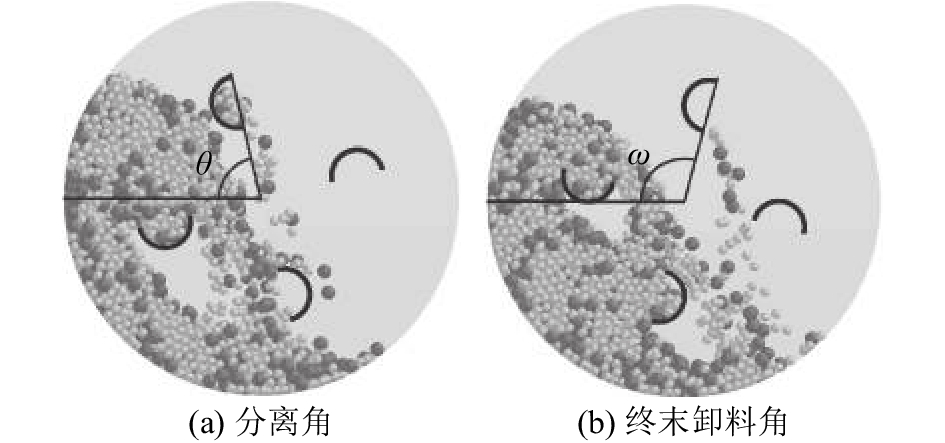
|
图 6 采用∞边形挡板时随机选取的卸料过程中的分离角和终末卸料角 Fig. 6 Angle of separation and terminal angle of unloading formed during randomly selected unloading processes with ∞ side flight |
|
图 7 当粒径比为1.5时平均终末卸料角与挡板边数的关系 Fig. 7 Variation in averaged terminal angle of unloading with number of flight’s sides for particle diameter ratio of 1.5 |
|
图 8 当粒径比为1.5时平均悬空扫角与挡板边数的关系 Fig. 8 Variation in averaged sweep angle of hovering with number of flight’s sides for particle diameter ratio of 1.5 |
|
图 9 2边形挡板卸料过程的分离角和终末卸料角 Fig. 9 Angle of separation and terminal angle of unloading in one unloading process of flight with two sides |
探讨当δ=1.5时挡板对颗粒速度矢量的影响. 图10为30 s时安装不同形状挡板的回转炉内颗粒的速度(线速度)矢量图,长度表示速度大小,箭头表示速度方向. 深灰色的为大颗粒,浅灰色的为小颗粒. 当回转炉内不安装挡板时,如图10(a)所示,根据速度矢量将颗粒群分成5个区域:涡心区(A)、流出区(B)、流动区(C)、流入区(D)和稳定区(E). 在涡心区,基本都是小颗粒,极少出现大颗粒;颗粒的速度较小,运动方向各不相同. 在流出区、流动区、流入区和稳定区,小颗粒和大颗粒共存;颗粒的速度均比涡心区的大. 在稳定区,颗粒在回转炉的带动下从右下方向左上方运动,颗粒与炉壁之间保持相对静止. 颗粒可以看成绕圆心做圆周运动,运动方向与颗粒到圆心的连线垂直. 因为稳定区颗粒的角速度相同,所以离回转炉圆心越远的颗粒,速度越大. 因此,沿炉壁到圆心的方向,颗粒的速度矢量的长度逐渐变短. 在流动区,颗粒从左上方向右下方运动,各个颗粒的速度大小较为接近,运动方向比较一致. 流出区为稳定区到流动区的过渡,流入区为流动区到稳定区的过渡. 因为稳定区和流动区中颗粒的运动方向相反,所以作为过渡区,流入区和流出区中颗粒的速度大小、运动方向各不相同.

|
图 10 在粒径比为1.5时安装不同挡板下30 s时颗粒的速度矢量 Fig. 10 Velocity vectors of particles while installing different flights at 30 s for particle diameter ratio of 1.5 |
当回转炉内安装挡板时,对于不同形状的挡板,颗粒的速度矢量分布相似. 如图10(b)~(f)所示. 以1边形挡板为例进行说明,如图10(b)所示. 从整体上看,已经不存在小颗粒集中分布的涡心区. 2种颗粒交错分布,比不安装挡板的颗粒分布均匀. 根据速度矢量将颗粒主体分成3个区域:稳定区(α)、流动区(β)和抛洒区(γ). 在稳定区(α),颗粒的速度矢量与前述不安装挡板时稳定区(E)的速度矢量分布特点相似. 颗粒的运动方向与颗粒到回转炉圆心的连线垂直,沿炉壁到回转炉圆心的方向,颗粒的速度逐渐减小. 在抛洒区(γ),因为挡板随回转炉转动,使得颗粒在离开挡板时存在水平速度,因此颗粒离开挡板后作平抛运动. 在抛洒区,颗粒的运动方向较为统一,速度矢量指向右下方. 颗粒离挡板(卸出此颗粒的挡板)越远,速度越大,重力加速度使离开挡板后的颗粒速度不断增大. 在流动区(β),颗粒的速度大小不一,方向各异. β1区为稳定区和抛洒区的过渡,速度矢量各异. 在β2区,向抛洒区流动的颗粒与挡板推动的往左上运动的颗粒相互挤压、碰撞,使得颗粒的速度矢量各不相同. 在β3区,从挡板左侧漏下的颗粒与回转炉壁带动往上运动的颗粒相互挤压碰撞,颗粒的速度大小不一,运动方向较为随机. 在β4区,颗粒与上方抛落的颗粒发生剧烈碰撞,由于碰撞的随机性颗粒的速度矢量指向各个方向,速度大小也各不相同.
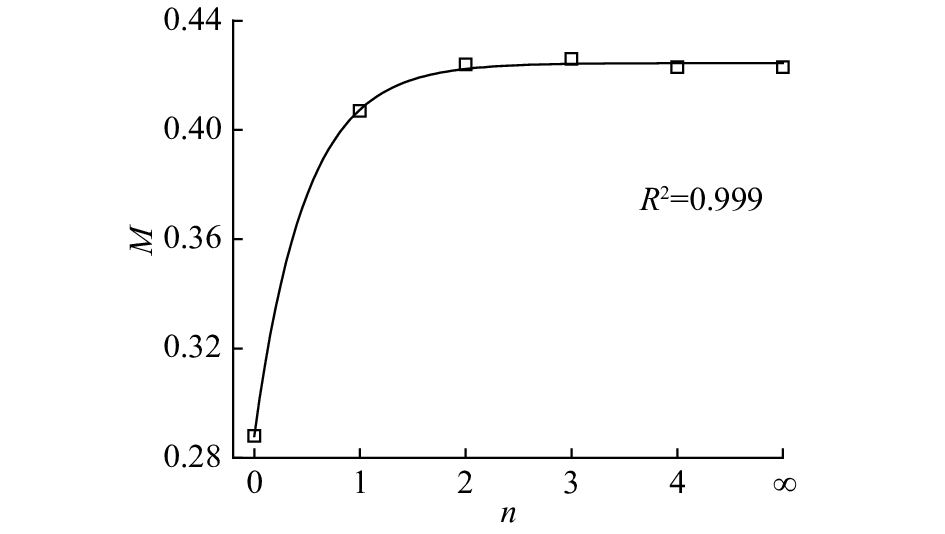
2.2.3 挡板对颗粒混合程度的影响探讨当δ=1.5时挡板对颗粒混合程度的影响. 图11为安装各形状挡板时接触数指标随时间的变化曲线. 可以看出,8 s后各曲线均进入稳定波动段,不再上升. 对8~30 s的接触数指标取时间平均值. 各形状挡板下稳定后时均接触数指标如图12中的散点所示. 当挡板边数分别为0、1、2、3、4、∞时,稳定段的时均接触数指标分别为0. 288、0. 407、0. 424、0. 426、0. 423、0. 423. 当挡板边数从0增加到2时,时均接触数指标的提高较为明显,颗粒的混合质量变好. 对于2、3、4、∞边形挡板,时均接触数指标的差别较小,颗粒的混合质量相差较小.

|
图 11 当粒径比为1.5、安装不同挡板时接触数指标随时间的变化曲线 Fig. 11 Variations of contact number index with time while installing different flights for particle diameter ratio of 1.5 |
|
图 12 当粒径比为1.5、稳定后时均接触数指标与挡板边数关系 Fig. 12 Variation of averaged contact number index of stable fluctuation regime with number of flight’s sides for particle diameter ratio of 1.5 |
以
| $M = - 0.136 \exp \;( - n/0.48) + 0.424. $ | (4) |
式中:x∈[0, 1, 2,···,∞). R2为仿真数据和拟合曲线的相关系数,R2为0~1.0,R2越大,表明相关性越好. R2=0.999表明相关性非常好. 图12中的曲线为拟合曲线.
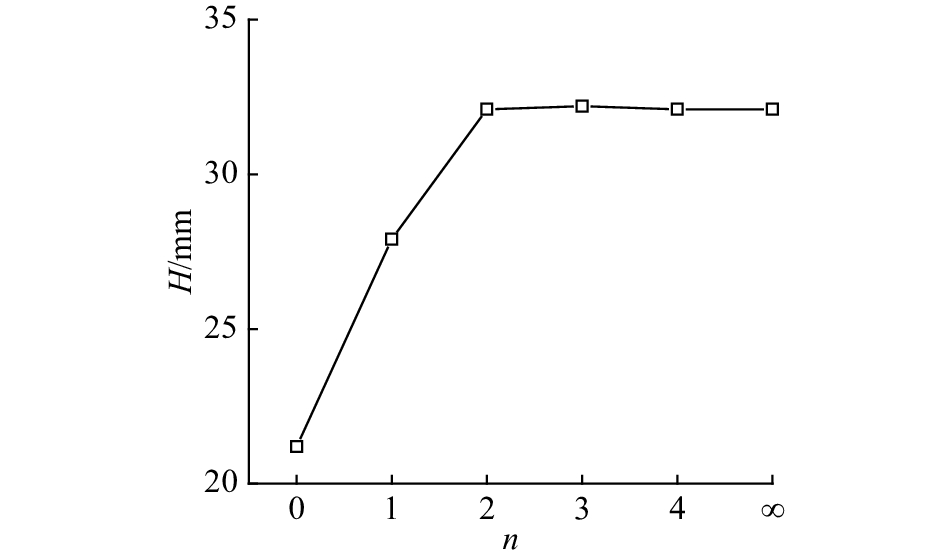
在回转炉中安装挡板可以有效增强颗粒间混合机制的作用,使颗粒系统达到混合程度更高的平衡态. 挡板主要依靠推送和抛洒2种作用来增强二元颗粒之间的混合. 当回转炉内不安装挡板时,大颗粒集中分布在颗粒群主体的外围区域,很难运动到涡心区,挡板的推送作用可以将外围的大颗粒推送到涡心区. 抛洒作用是指挡板将颗粒抬升后以颗粒瀑布流的形式将颗粒卸下. 形成的颗粒瀑布流与下方的颗粒发生碰撞、掺混,增强颗粒之间的混合. 各形状挡板的外接圆直径均为12 mm,有效推送长度均为12 mm,各形状挡板推送作用的强度差别较小. 各形状挡板增混效果不同主要是因为抛洒作用的强度存在差异. 如图13所示,设颗粒到x轴的垂直距离为颗粒的高度h,回转炉最低点a的高度为0 mm,定义回转炉运行过程中颗粒达到的最大高度为颗粒上升高度H. n与H的关系如图14所示. 当挡板边数分别为0、1、2、3、4、∞时,对应的颗粒上升高度分别为21.2、27.9、32.1、32.2、32.1、32.1 mm. 从0到2边形挡板,颗粒上升高度增加明显,当安装2、3、4、∞边形挡板时,颗粒上升高度差别很小. 变化趋势与稳定段时均接触数指标随挡板边数的变化趋势一致. 较高的颗粒上升高度有利于挡板产生较为强烈的抛洒作用,得到较好的增混效果. 当单板边数增加到2时,不能使颗粒上升高度产生明显的变化,挡板边数为2以及更高时,颗粒接触数指标差别不大.

|
图 13 颗粒高度及颗粒上升高度 Fig. 13 Height of particle and rising height of particles |
|
图 14 当粒径比为1.5、颗粒上升高度与内构件边数的关系 Fig. 14 Variation in rising height of particles with number of flight’s sides for particle diameter ratio of 1.5 |
1)挡板边数越多,平均终末卸料角越大. 当挡板边数为2时,在回转炉运行过程中,仅存在主体颗粒瀑布流. 对于安装其他边形挡板,在回转炉运行过程中,主体颗粒瀑布流和悬空颗粒瀑布流共存.
2)当回转炉中安装挡板时,比起无挡板,不存在小颗粒集中分布的涡心区. 2种颗粒交错分布,比不安装挡板的颗粒分布均匀.
3)当挡板边数从0增加到2时,时均接触数指标的提高较为明显,颗粒的混合质量变好. 对于2、3、4、∞边形挡板,时均接触数指标的差别较小,颗粒的混合质量相差较小. 挡板主要依靠推送和抛洒2种作用来增强二元颗粒之间的混合.
| [1] |
王瑞芳, 李占勇, 窦如彪, 等. 水平转筒内大豆颗粒随机运动与混合特性模拟[J]. 农业机械学报, 2013, 44(6): 93-99. WANG Rui-fang, LI Zhan-yong, DOU Ru-biao, et al. Simulation on random motion and mixing characteristic for soybean in rotary drum[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(6): 93-99. |
| [2] |
王擎, 肖冠华, 孔祥钊, 等. 固体热载体干馏桦甸油页岩试验研究[J]. 东北电力大学学报, 2013, 33(5): 15-21. WANG Qing, XIAO Guan-hua, KONG Xiang-zhao, et al. Experimental investigation of solid heat carrier retorting of Huadian oil shale[J]. Journal of Northeast Dianli University, 2013, 33(5): 15-21. DOI:10.3969/j.issn.1005-2992.2013.05.004 |
| [3] |
高红利, 陈友川, 赵永志, 等. 薄滚筒内二元湿颗粒体系混合行为的离散单元模拟研究[J]. 物理学报, 2011, 60(12): 330-337. GAO Hong-li, CHEN You-chuan, ZHAO Yong-zhi, et al. Simulation of mixing process for size-type binary wet particulate systems in a rotating horizontal drum by discrete element method[J]. Acta Physica Sinica, 2011, 60(12): 330-337. |
| [4] |
黄德财, 冯耀东, 解为梅, 等. 颗粒密度对旋转筒内二元颗粒体系分离的影响[J]. 物理学报, 2012, 61(12): 372-378. HUANG De-cai, FENG Yao-dong, XIE Wei-mei, et al. Effect of particle density on the segregation of binary granular systems in a rotating drum[J]. Acta Physica Sinica, 2012, 61(12): 372-378. |
| [5] |
YAMAMOTO M, ISHIHARA S, KANO J. Evaluation of particle density effect for mixing behavior in a rotating drum mixer by DEM simulation[J]. Advanced Powder Technology, 2015, 27: 864-870. |
| [6] |
陈辉, 肖友刚, 赵先琼, 等. 回转窑内二元颗粒物料的径向混合[J]. 工程科学学报, 2016, 38(2): 194-199. CHEN Hui, XIAO You-gang, ZHAO Xian-qiong, et al. Transverse mixing of binary solid materials in a rotating kiln[J]. Chinese Journal of Engineering, 2016, 38(2): 194-199. |
| [7] |
NIELSEN A R, ANIOL R W, LARSEN M B, et al. Mixing large and small particles in a pilot scale rotary kiln[J]. Powder Technology, 2011, 210(3): 273-280. DOI:10.1016/j.powtec.2011.03.029 |
| [8] |
HÖHNER D, WIRTZ S, SCHERER V. Experimental and numerical investigation on the influence of particle shape and shape approximation on hopper discharge using the discrete element method[J]. Powder Technology, 2013, 235(2): 614-627. |
| [9] |
耿凡, 徐大勇, 袁竹林, 等. 滚筒干燥器中杆状颗粒混合特性的三维数值模拟[J]. 东南大学学报: 自然科学版, 2008, 38(1): 116-122. GENG Fan, XU Da-yong, YUAN Zhu-lin, et al. Three dimensional numerical simulation of mixing characteristics of slender particles in rotary dryer[J]. Journal of Southeast University: Natural Science Edition, 2008, 38(1): 116-122. |
| [10] |
李少华, 张立栋, 张轩, 等. 回转式干馏炉内影响颗粒混合运动因素的数值分析[J]. 中国电机工程学报, 2011, 32(2): 32-38. LI Shao-hua, ZHANG Li-dong, ZHANG Xuan, et al. Numerical analysis of particle mixing and movement in rotary retorting[J]. Proceedings of the CSEE, 2011, 32(2): 32-38. |
| [11] |
KARALI M A, HERZ F, SPECHT E, et al. Comparison of image analysis methods to determine the optimum loading of flighted rotary drums[J]. Powder Technology, 2016, 291: 147-153. DOI:10.1016/j.powtec.2015.11.053 |
| [12] |
MACHADO M V C, NASCIMENTO S M, DUARTE C R, et al. Boundary conditions effects on the particle dynamic flow in a rotary drum with a single flight[J]. Powder Technology, 2017, 311: 341-349. DOI:10.1016/j.powtec.2017.01.076 |
| [13] |
SUNKARA K R, HERZ F, SPECHT E, et al. Transverse flow at the flight surface in flighted rotary drum[J]. Powder Technology, 2015, 275: 161-171. DOI:10.1016/j.powtec.2015.01.058 |
| [14] |
BHATTACHARYA T, HAJRA S K, MCCARTHY J J. A design heuristic for optimizing segregation avoidance practices in horizontal drum mixers[J]. Powder Technology, 2014, 253(2): 107-115. |
| [15] |
赵永志, 张宪旗, 刘延雷, 等. 滚筒内非等粒径二元颗粒体系增混机理研究[J]. 物理学报, 2009, 58(12): 8386-8393. ZHAO Yong-zhi, ZHANG Xian-qi, LIU Yan-lei, et al. Augmenting the mixing of size-type binary granular systems in a rotating horizontal drum[J]. Acta Physica Sinica, 2009, 58(12): 8386-8393. |
| [16] |
CUNDALL P A, STRACK O L. A discrete numerical model for granular assemblies[J]. Geotechnique, 1979, 29(1): 47-65. DOI:10.1680/geot.1979.29.1.47 |
| [17] |
陈辉, 刘义伦, 赵先琼, 等. 一元散体颗粒物料在回转窑截面上的运动与混合[J]. 中国有色金属学报, 2015, 25(5): 2575-2581. CHEN Hui, LIU Yi-lun, ZHAO Xian-qiong, et al. Motion and mixing of mono-disperse granular material in cross section of rotary kiln[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(5): 2575-2581. |
| [18] |
MELLMANN J. The transverse motion of solids in rotating cylinders: forms of motion and transition behavior[J]. Powder Technology, 2001, 118(3): 251-270. DOI:10.1016/S0032-5910(00)00402-2 |
| [19] |
张立栋, 李连好, 程硕, 等. 颗粒在圆形偏心滚筒内的运动模式[J]. 化工进展, 2015, 34(9): 3244-3247. ZHANG Li-dong, LI Lian-hao, CHENG Shuo, et al. Motion mode of particles in a circular eccentric drum[J]. Chemical Industry and Engineering Progress, 2015, 34(9): 3244-3247. |
| [20] |
张立栋, 李少华, 朱明亮, 等. 回转干馏炉内抄板形式与双组元颗粒混合过程冷模数值研究[J]. 中国电机工程学报, 2012, 32(11): 72-78. ZHANG Li-dong, LI Shao-hua, ZHU Ming-liang, et al. Cold mode numerical analysis of flights forms and two component particles mixing in rotary retorting[J]. Proceedings of the CSEE, 2012, 32(11): 72-78. |
| [21] |
JIANG M, ZHAO Y, LIU G, et al. Enhancing mixing of particles by baffles in a rotating drum mixer[J]. Particuology, 2011, 9(3): 270-278. DOI:10.1016/j.partic.2010.06.008 |
| [22] |
钱家麟, 尹亮. 油页岩: 石油的补充能源[M]. 北京: 中国石化出版社, 2011: 49, 319
|
| [23] |
王恭, 苗宇, 孙灵芳, 等. 回转干馏炉内颗粒停留时间的计算机模拟研究[J]. 东北电力大学学报, 2012, 32(3): 37-41. WANG Gong, MIAO Yu, SUN Ling-fang, et al. Computer simulation of particles' residence time in rotary dry distillation furnace[J]. Journal of Northeast Dianli University, 2012, 32(3): 37-41. |
| [24] |
张立栋, 韦庆文, 秦宏, 等. 柱状生物质颗粒与钢球颗粒在滚筒中的混合特性[J]. 化工进展, 2016, 35(10): 3057-3064. ZHANG Li-dong, WEI Qing-wen, QIN Hong, et al. Mixing characteristics in a rotary drum filled with cylindrical biomass and spherical steel particles[J]. Chemical Industry and Engineering Progress, 2016, 35(10): 3057-3064. |


