2. 中航成飞民用飞机有限责任公司,四川 成都 610073
2. Chengdu Civil Aircraft Co. Ltd, Chengdu 610073, China
飞机交点孔(如机翼与机身连接孔、起落架与机身连接孔等)的加工质量对飞机的机动性能和疲劳寿命有重要影响. 交点孔的材料一般为高强度钢和钛合金,要求表面粗糙度Ra≤0.8. 飞机上各个交点孔位置特殊,空间分布范围广,飞机装配现场工装设备复杂,操作空间狭小,使得传统机床精加工十分困难. 机器人镗孔具有高机动性和高灵活性等特点,成为飞机交点孔加工的理想选择. 然而,与传统机床相比,机器人镗孔系统的弱刚性导致加工中容易产生振动[1],影响加工质量和刀具寿命.
课题组前期研究发现,机器人镗孔过程中主要存在2种振动形式:强迫振动[2]和颤振[3]. 强迫振动的振动主体为机器人,振动频率等于主轴旋转频率;颤振的振动主体为镗杆,颤振频率接近镗杆的固有频率. 强迫振动使工件表面出现螺旋状振纹,通过施加压脚压力能够有效抑制螺旋状振纹;颤振使工件表面出现网状振纹,难以被抑制. 为了避免颤振的发生,需要建立机器人镗孔系统的动力学模型,获得系统稳定性叶瓣图,从中选取合适的加工参数. 然而,准确识别机器人镗孔系统的动力学参数十分困难,一旦系统中某个因素发生变化,比如机器人位姿改变,稳定性叶瓣图也会发生变化,原本可以稳定加工的参数下也会发生颤振. 因此,需要研究对机器人镗孔颤振的早期识别,通过及时改变加工参数等方法避免颤振的发生,实现高效高质量加工交点孔.
识别机器人镗孔颤振时,需要采集能够反映加工状态的信号,并且用合适的信号处理方法提取颤振特征. 在颤振识别中常用的信号包括切削力信号[4-5]、加速度信号[6-7]和声信号[8-9]等. 处理这些信号需要考虑传感器的安装问题,在机器人镗孔加工中适用性比较差. 利用镗孔执行器原有的内置光栅尺,采集加工中的压脚位移信号进行颤振识别,能够解决安装问题,并且降低颤振识别的成本. 压脚信号能够快速反映当前加工状态,已经被逐步用于加工精度控制[10]和加工监控[11],是实现颤振识别的理想选择. 在信号处理方面,传统的时域分析[12]和频域分析[13-14]方法存在局限性,不能同时在时、频域内进行分析,并且难以有效处理颤振等复杂的非平稳时变信号,不利于提取颤振特征. 以Hilbert-Huang变换(HHT)[15-16]为代表的时频分析方法不仅弥补了传统方法的不足,而且能对颤振信号进行多层分解,揭示颤振发展过程中信号的时频变化细节,目前已广泛应用于机械故障诊断[17-18]、颤振识别[19-20]等领域.
以机器人镗孔系统中光栅尺采集的压脚位移信号为对象,对颤振前后的信号进行时域和频域分析,得到颤振发生的频段. 对信号进行HHT,将信号分解成一系列不同频段的固有模态函数(intrinsic mode function, IMF). 提取与颤振相关的IMF,分析IMF的瞬时频率的变化规律,提出新的颤振特征提取方法,实现颤振的快速识别.
1 机器人镗孔系统机器人镗孔系统如图1所示,主要由ABB-IRB6600-175/2.55型工业机器人和镗孔末端执行器组成,镗孔末端执行器通过快换法兰安装于工业机器人末端. 镗孔末端执行器如图2所示,主要由压脚、气缸、光栅尺、镗杆、电主轴和进给丝杆等组成. 压脚通过末端执行器两侧的气缸驱动,实现伸出和缩回两个动作,压脚压力通过气缸中的气压值调节,为了避免加工中出现剧烈振动,压脚压力始终维持在0.4 MPa. 光栅尺位于压脚附近,可以实时监测压脚位移信号. 光栅尺的最小分辨率为7.812 5×10–5 mm,采样频率为2 kHz.

|
图 1 机器人镗孔系统 Fig. 1 Robotic boring system |

|
图 2 机器人镗孔末端执行器 Fig. 2 End-effector of robotic boring |
试验中为了保证交点孔轴心与镗杆轴心的同轴度,调节机器人姿态,机器人各关节角度分别为α1=–48.38°,α2=54.82°,α3=6.86°,α4=–54.16°,α5=107.43°,α6=–21.95°,位姿在试验中始终不变.
镗孔加工时,压脚伸出压紧工件表面,通过电主轴的自转和沿导轨的轴向进给运动实现镗孔加工. 在压脚作用下,机器人镗孔系统由悬臂梁结构转变为类简支梁结构,提高系统的稳定性和刚性;如果加工参数不合适,镗孔系统仍会发生颤振. 在颤振发生时,压脚随机器人镗孔系统一起振动,通过压脚位移信号的变化监测振动.
2 颤振信号分析及传统识别方法 2.1 颤振信号的时域和频域分析为了分析颤振发生时的压脚位移信号,采用不同的加工参数进行机器人镗孔试验. 试验中工件材料为高强度钢,镗杆直径为31 mm,镗孔直径加工范围为42~48 mm,镗刀片参数如表1所示. 每次试验前对工件表面进行预加工以消除上次切削痕迹.
| 表 1 镗刀片几何参数 Table 1 Geometry parameters of boring cutter |
观察试验后的工件表面,大部分工件表面光滑无振纹,表面粗糙度Ra≤0.8;小部分试验产生颤振,对应工件表面出现明显的颤振振纹. 为了分析机器人镗孔系统在颤振发生时的压脚位移信号,取一组典型的颤振信号进行分析. 试验的加工参数如下:主轴转速nr=800 r/min,进给量f=0.05 mm/r,切削深度ap=0.35 mm. 试验加工后的工件表面如图3所示.

|
图 3 颤振时的工件表面质量 Fig. 3 Surface quality of workpiece when chatter occurs |
根据图3的工件表面质量,将加工依次分为3个阶段:平稳阶段、过渡阶段和颤振阶段. 在平稳阶段,工件表面光滑没有振纹;在过渡阶段,工件表面出现微小振纹,但是没有严重损害工件表面;在颤振阶段,工件表面出现细密的网状振纹,严重破坏了工件表面. 如果能够在颤振不严重的过渡阶段实现颤振识别,可以有效避免颤振发生.
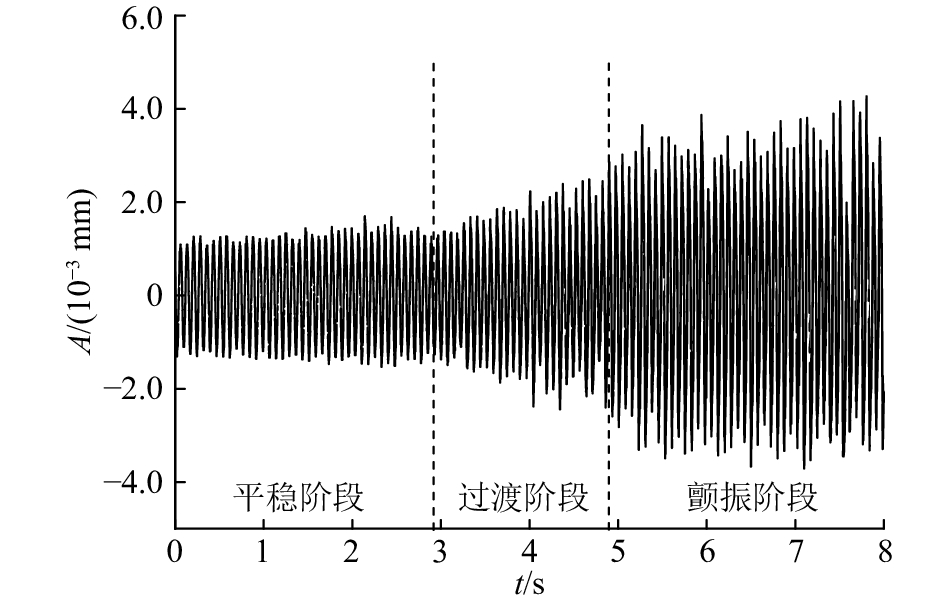
图4为试验的压脚位移信号,纵坐标为幅值A. 在平稳阶段,幅值平稳并且较小;在过渡阶段,幅值呈上升趋势;在颤振阶段,幅值达到最大并且趋于平稳. 放大压脚位移信号的3个阶段,观察并且比较时域的变化,通过FFT分析比较频域的变化,结果如图5~7所示.
|
图 4 颤振时的压脚位移信号 Fig. 4 Pressure foot displacement signal when chatter occurs |
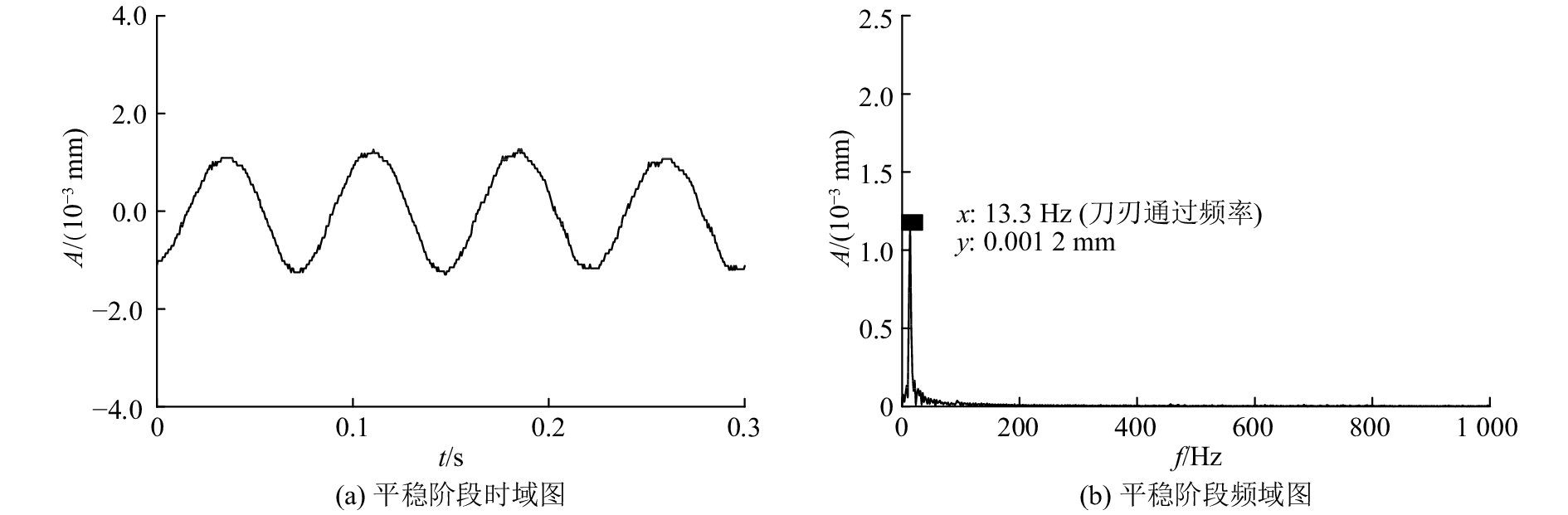
图5(a)、5(b)分别为平稳阶段的时域信号和频域信号. 由图5可知,平稳阶段信号为明显的正弦波,仅在13.3 Hz的低频处出现了明显的频域集中. 频率为刀刃通过频率,与主轴转速和刀具齿数相关. 试验中机器人镗孔为单刃加工,刀刃通过频率与主轴旋转频率相等.
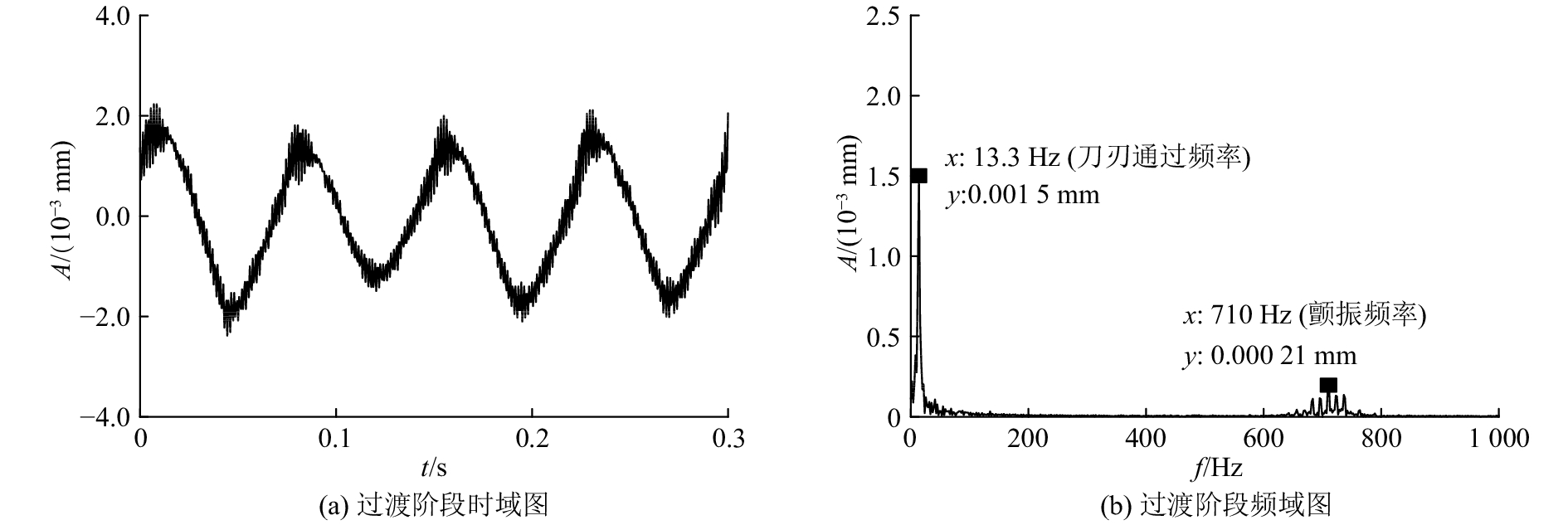
图6(a)、6(b)分别为过渡阶段的时域信号和频域信号. 在图6(a)中,正弦波幅值增大,并出现大量的高频小波;图6(b)在13.3 Hz的频域幅值明显增大,并且在710 Hz左右的高频段出现明显的频域集中. 由文献[3]知,新出现的高频小波信号是颤振信号,对应频率为颤振频率. 颤振频率处于高频段,与刀刃通过频率的低频段明显不同.
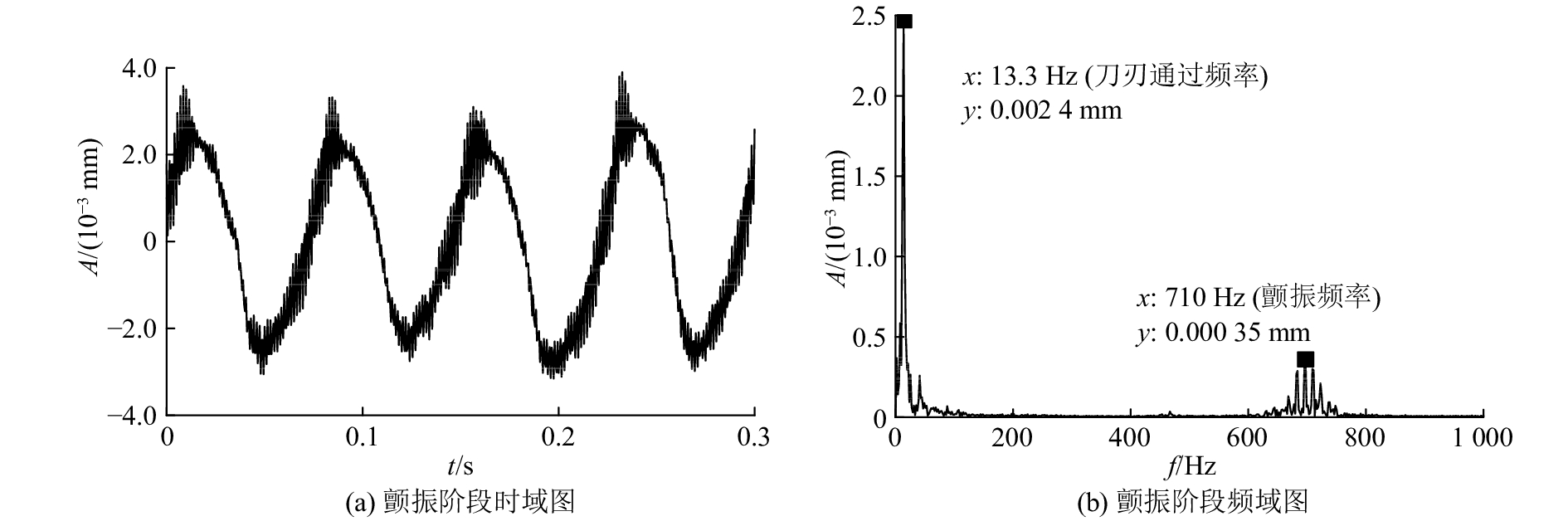
图7(a)、7(b)分别为颤振阶段的时域信号和频域信号. 图7(a)的正弦波幅值和高频小波幅值进一步增大并且趋于稳定. 图7(b)在13.3 Hz和710 Hz附近的频域幅值进一步增大并且趋于稳定,出现少量二阶刀刃通过频率. 随着颤振的加剧,压脚位移信号的能量进一步增强.
将压脚位移信号x(t)简化为
| $x(t) = A\sin \;(2{\rm{\pi }}{f_{\rm{a}}}t) + B\sin \;(2{\rm{\pi }}{f_{\rm{b}}}t) + {\rm{rand}}\;(t).$ | (1) |
式中:fa和A分别为刀刃通过频率和幅值,fb和B分别为颤振频率和幅值,rand (t)为随机噪声信号.
比较不同阶段的压脚位移信号 x (t),颤振信号的特点为:1)在时域上,随着颤振的发生和加剧.幅值明显增大;2)在频域上,随着颤振的发生和加剧.能量出现频移,颤振发生时高频小波大量出现.对应的频率 fb在 710 Hz 左右的高频段,为颤振频率.
|
图 5 压脚位移信号平稳阶段时频图 Fig. 5 Time and frequency domain plot of pressure foot displacement signal in stable state |
|
图 6 压脚位移信号过渡阶段时频图 Fig. 6 Time and frequency domain plot of pressure foot displacement signal in transition state |
|
图 7 压脚位移信号颤振阶段时频图 Fig. 7 Time and frequency domain plot of pressure foot displacement signal in chatter state |
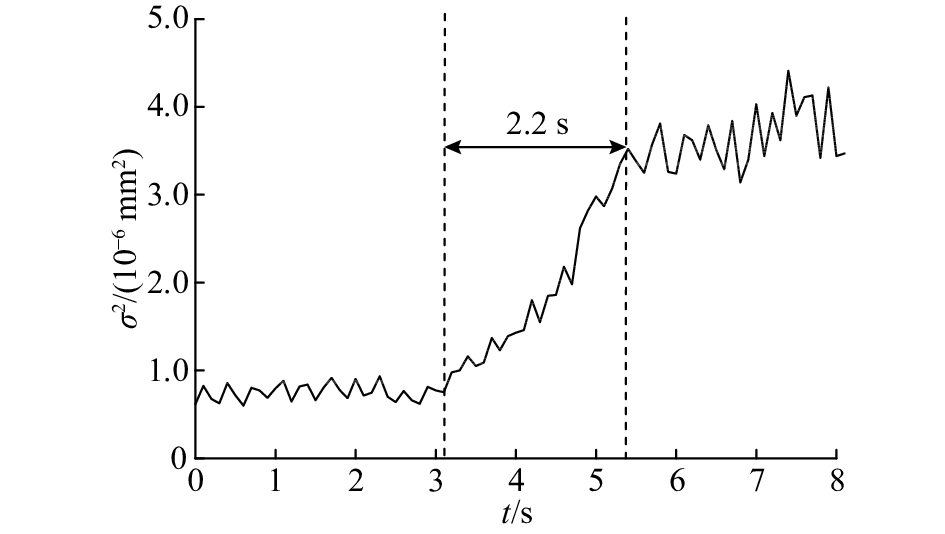
传统的颤振识别根据信号在颤振发生时时域幅值增大的特点,分析时域信号的幅值方差实现颤振识别[21]. 使用传统方法识别机器人镗孔颤振,需要每隔0.1 s采集压脚位移信号作为一个样本,计算各样本的方差均值,拟合压脚位移信号的方差曲线,结果如图8所示,纵坐标为方差σ2. 由图8可知,0~3.1 s时,方差较小并且平稳;3.1~5.3 s时,方差快速上升;5.3 s之后,方差增至最大并且趋于稳定. 用时域方差进行颤振识别,在3.1 s监测到颤振发生,需要2.2 s进行颤振识别,识别时间较长,识别效果不佳. 因此不适合采用时域方法对机器人镗孔颤振进行识别.
根据压脚位移信号在颤振发生时能量频移的特点来识别颤振. 由于原始信号中除了包含与颤振频率相关的信号外,还包含大量与刀刃通过频率和其他频率相关的信号,导致频率的成分和变化规律比较复杂. 需要对原始信号进行分解. 采用HHT对压脚位移信号进行分解,提取与颤振相关的信号分量,选择合适的颤振特征,实现颤振识别.
|
图 8 压脚位移信号方差 Fig. 8 Variance of pressure foot displacement signal |
HHT主要包含经验模态分解(empirical mode decomposition,EMD)和Hilbert变换.
EMD将一个复杂的非平稳信号分解为若干个IMF和残余分量(residual,RES). 各个IMF分别包含原信号由高频段到低频段的不同成分,RES代表原信号的平均趋势. EMD将非平稳信号进行平稳化处理,在分解时保留原始信号的特性,分解是自适应的,反映颤振的本质信息. Hilbert变换指将信号与1/(πt)作卷积,对各个IMF信号做Hilbert变换,得到各个IMF的幅值、相位和频率随时间的变化函数. HHT通过MATLAB的HHT工具箱实现.
HHT适用于分析非线性非平稳信号;无须选择基函数,具有完全自适应性;不受Heisenberg测不准原理制约,在时频域分析上能够达到很高的精度.
3.2 颤振信号的HHT分析为了提取与颤振相关的信号分量,对压脚位移信号进行EMD,获得一系列IMF,对各IMF作FFT,分析频率成分,结果如图9所示. 由图9可知,EMD将压脚位移信号按频率成分从高到低依次分解为IMF1~IMF11及RES. IMF4、IMF5为幅值最大的分量,对应频率为刀刃通过频率,与颤振无关;IMF1的幅值次之,对应频率为710 Hz左右,与颤振频率相一致.

|
图 9 压脚位移信号的EMD及各IMF的FFT Fig. 9 EMD of pressure foot displacement signal and FFT of each IMF |
为了进一步分析各IMF的重要程度,求解各IMF与原始信号的相关系数,结果如表2所示. 由表2可知,IMF4、IMF5与原始信号的相关系数比较大,IMF1的相关系数次之,IMF1与颤振相关. IMF1蕴含大量与颤振相关的信号分量,对IMF1进行特征提取利于颤振的识别.
| 表 2 各IMF与原始信号的相关系数 Table 2 Correlation coefficient between each IMF and original signal |
根据颤振发生时信号能量频移的特点,通过Hilbert变换计算IMF1的瞬时频率,分析瞬时频率在颤振前后的变化规律,结果如图10所示,纵坐标为瞬时频率f. 由图10可知,在颤振发生前,瞬时频率在0~1 000 Hz内均有分布;当颤振发生时,瞬时频率短时间内大量集中在560~860 Hz的高频段,其他频段分布较少,瞬时频率的分布范围与颤振频率相对应. 本研究根据该规律进行颤振识别.

|
图 10 IMF1的瞬时频率 Fig. 10 Instantaneous frequency of IMF1 |
根据IMF1的瞬时频率在颤振前后的变化规律,提出基于HHT的颤振特征提取方法,利用IMF1瞬时频率中颤振频段的概率变化进行颤振识别. 具体步骤如下.
1)采集镗孔时的压脚位移信号x(n),n为时间t的离散变量. 对x(n)进行HHT,得到IMF1的瞬时频率f(n).
2)每隔时间Ts截取f(n)中的数据为一个样本,每个样本的数据量为
| $S = {T_{\rm{s}}} \cdot {F_{\rm{s}}}.$ | (2) |
式中:Fs为光栅尺的采样频率.
3)对第i个样本的fi(n)的值进行判别,得到fi(n)中颤振频段[f1,f2]的数据量为
| ${S_i} = {\rm{count}}\;[{f_i}(n)],\;\;{f_1} \leqslant {f_i}(n) \leqslant {f_2}.$ | (3) |
式中:count为计数函数,计算fi(n)在区间[f1,f2]的数据量.
4)计算第i个样本中,颤振频段数据量Si占样本数据量S的概率Pi:
| ${P_i} = {S_i}/S.$ | (4) |
5)将各样本的Pi依次连接,得到IMF1瞬时频率中颤振频段[f1,f2]的概率P的变化规律,作为识别颤振的依据.
将IMF1的瞬时频率每隔0.1 s作为一个样本,以710 Hz为频率中心,绘制瞬时频率中颤振频段[560,860] Hz 的概率P随时间的变化曲线,如图11所示. 由图11可知,在0~0.8 s,概率P为0.55左右较为平稳;在0.8~1.3 s,概率P急剧上升至0.9左右;在1.3 s之后,概率P趋于平稳. 以概率P的变化为依据,能够在0.8 s时监测到颤振的发生,颤振识别只需要0.5 s左右.

|
图 11 IMF1的瞬时频率中[560,860] Hz 的概率变化 Fig. 11 Probability variation of IMF1’s instantaneous frequency between [560, 860] Hz |
对比图11与8可知,当颤振将发生时,能量频移比时域幅值增加更早发生,达到峰值并且稳定的时间更短. 通过监测能量频移,即瞬时频率的变化规律能够更好地对颤振进行识别. 对比工件的加工表面,在工件出现颤振振纹之前,概率P已经增加到最大,能够及时对颤振进行识别,避免颤振进一步破坏加工.
为了实现良好的颤振识别效果,预先设定颤振频段[f1,f2]的大小及概率P的阈值. 在机器人镗孔系统下,根据试验中颤振频率出现的范围,将颤振频段设定为[560,860] Hz ,频段包含颤振频率的高频段,避开刀刃通过频率的低频段,能够避免产生误判和漏判. 由图11可知,颤振时IMF1瞬时频率中颤振频段[560,860] Hz 的概率P>0.8,将概率P=0.8作为判别颤振发生的阈值,对颤振进行识别.
4 试验验证为了验证本文方法对不同加工参数下颤振识别的有效性,将所有试验中的压脚位移信号进行HHT,每隔0.1 s分析IMF1瞬时频率中[560,860] Hz 的概率P的变化,进行颤振识别. 试验共25组,试验参数及颤振识别结果如表3所示.
| 表 3 试验参数及颤振识别结果 Table 3 Test parameters and results of chatter identification |
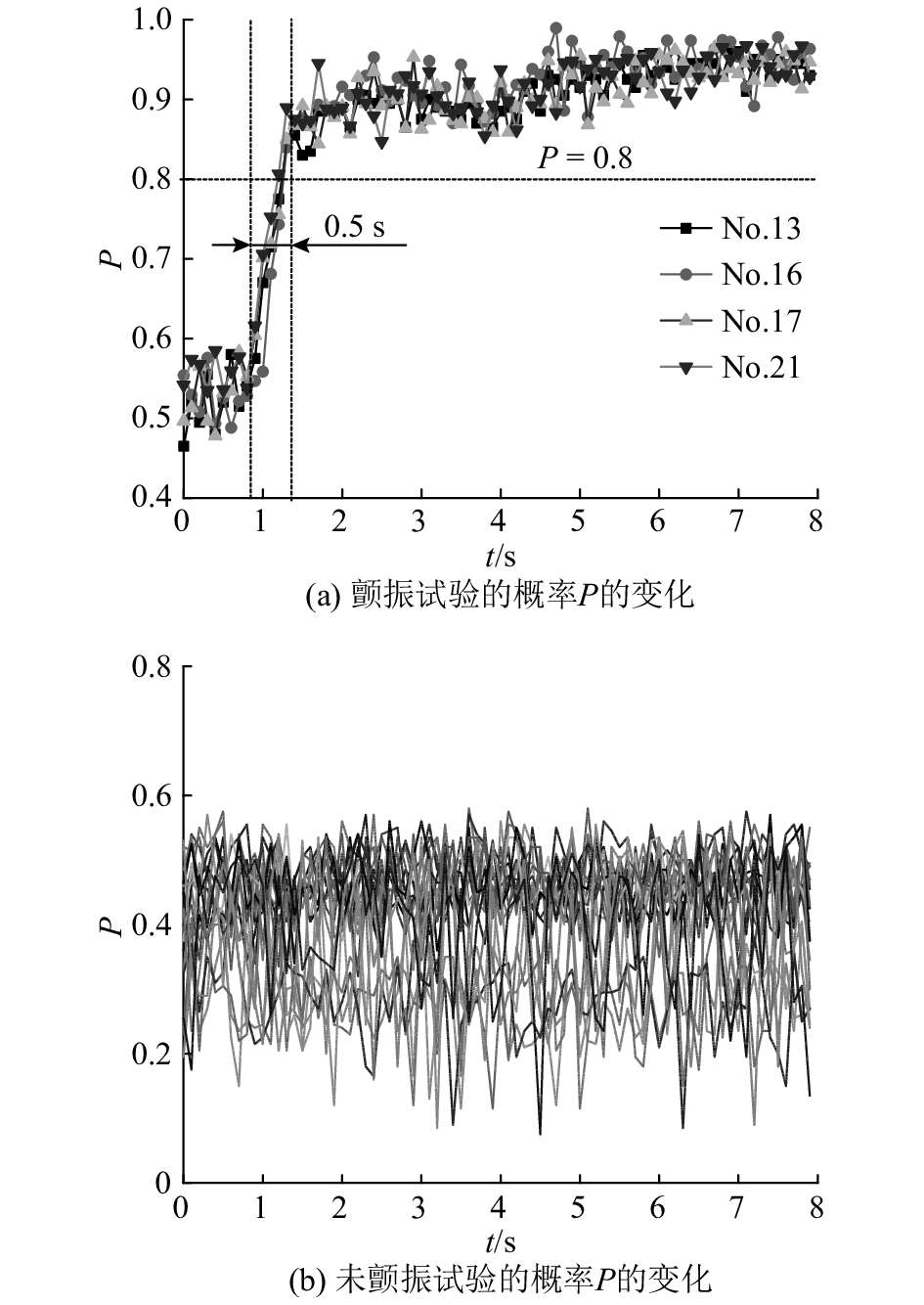
为了进一步分析颤振识别结果的准确性,绘制各组试验的概率P的变化趋势图,结合工件的加工表面进行分析. 结果表明,只有发生颤振的4组试验加工表面出现颤振振纹,概率P达到了0.8的阈值,识别时间为0.5 s左右,结果如图12(a)所示. 未发生颤振的21组试验加工表面无颤振振纹,概率P均在0.6以下,没有达到0.8的阈值,结果如图12(b)所示. 颤振识别方法能够在机器人镗孔颤振发生前0.5 s左右实现颤振准确、快速的识别.
|
图 12 颤振与未颤振试验的概率P的变化 Fig. 12 Variation of probability P in chatter and non-chatter experiments |
以机器人镗孔颤振为研究对象,通过采集分析压脚位移信号分析与识别颤振. 研究结论如下.
1) 与平稳切削时相比,在颤振发生时,压脚位移信号的时域幅值增大,并且出现大量高频小波,高频小波对应的频率即为颤振频率.
2) 在颤振发生时,能量频移比时域幅值增大更早发生,达到峰值并且稳定的时间更短. 通过能量频移能够及时地识别颤振.
3) 固有模态函数IMF1中蕴含大量与颤振相关的信号分量,对应的瞬时频率在颤振发生前后有明显的变化. 将IMF1作为颤振特征的提取对象,分析IMF1瞬时频率中颤振频段的概率分布变化,实现颤振识别.
4) 利用HHT提取颤振特征是实现机器人镗孔颤振识别的有效手段,在颤振形成前0.5 s及时对颤振进行识别,大大缩短识别时间.
5) 颤振识别方法的本质是针对颤振时能量频移的特点,对颤振时新出现的颤振能量进行分离,观察该颤振能量在颤振前后的变化规律来实现颤振识别. 目前已经验证该方法在机器人镗孔颤振识别中的有效性,可以将方法进一步推广到有类似颤振特征的其他加工系统的颤振识别中.
| [1] |
PAN Z, ZHANG H, ZHU Z, et al. Chatter analysis of robotic machining process[J]. Journal of Materials Processing Technology, 2006, 173(3): 301-309. DOI:10.1016/j.jmatprotec.2005.11.033 |
| [2] |
GUO Y, DONG H, WANG G, et al. Vibration analysis and suppression in robotic boring process[J]. International Journal of Machine Tools and Manufacture, 2016, 101: 102-110. DOI:10.1016/j.ijmachtools.2015.11.011 |
| [3] |
WANG G, DONG H, GUO Y, et al. Chatter mechanism and stability analysis of robotic boring [J/OL]. The International Journal of Advanced Manufacturing Technology, 2017, 91: 411-421. [2017-06-05]. https://link.springer.com/article/10.1007/s00170-016-9731-9
|
| [4] |
FAASSE R P H, VAN D W N, OOSTERLING J A J, et al. Prediction of regenerative chatter by modelling and analysis of high-speed milling[J]. International Journal of Machine Tools and Manufacture, 2003, 43(14): 1437-1446. DOI:10.1016/S0890-6955(03)00171-8 |
| [5] |
TOH C K. Vibration analysis in high speed rough and finish milling hardened steel[J]. Journal of Sound and Vibration, 2004, 278(1): 101-115. |
| [6] |
LAMRAOUI M, THOMAS M, BADAOUI M E. Cyclostationarity approach for monitoring chatter and tool wear in high speed milling[J]. Mechanical Systems and Signal Processing, 2014, 44(1): 177-198. |
| [7] |
LI X Q, WONG Y S, NEE A Y C. Tool wear and chatter detection using the coherence function of two crossed accelerations[J]. International Journal of Machine Tools and Manufacture, 1997, 37(4): 425-435. DOI:10.1016/S0890-6955(96)00030-2 |
| [8] |
THALER T, POTOCNIK P, BRIC I, et al. Chatter detection in band sawing based on discriminant analysis of sound features[J]. Applied Acoustics, 2014, 77: 114-121. DOI:10.1016/j.apacoust.2012.12.004 |
| [9] |
SCHMITZ T L. Chatter recognition by a statistical evaluation of the synchronously sampled audio signal[J]. Journal of Sound and Vibration, 2003, 262(3): 721-730. DOI:10.1016/S0022-460X(03)00119-6 |
| [10] |
费少华, 方强, 孟祥磊, 等. 基于压脚位移补偿的机器人制孔锪窝深度控制[J]. 浙江大学学报: 工学版, 2012, 46(7): 1157-1161. FEI Shao-hua, FANG Qiang, MENG Xiang-lei, et al. Countersink depth control of robot drilling based on pressure foot displacement compensation[J]. Journal of Zhejiang University: Engineering Science, 2012, 46(7): 1157-1161. |
| [11] |
OLSSON T, HAAGE M, KIHLMAN H, et al. Cost-efficient drilling using industrial robots with high-bandwidth force feedback[J]. Robotics and Computer-Integrated Manufacturing, 2010, 26(1): 24-38. DOI:10.1016/j.rcim.2009.01.002 |
| [12] |
HUANG P, LI J, SUN J, et al. Vibration analysis in milling titanium alloy based on signal processing of cutting force[J]. The International Journal of Advanced Manufacturing Technology, 2013, 64(5-8): 613-621. DOI:10.1007/s00170-012-4039-x |
| [13] |
李茂月, 韩振宇, 富宏亚, 等. 基于开放式控制器的铣削颤振在线抑制[J]. 机械工程学报, 2012, 48(17): 172-182. LI Mao-yue, HAN Zhen-yu, FU Hong-ya, et al. Online milling chatter suppression based on open architecture controller[J]. Journal of Mechanical Engineering, 2012, 48(17): 172-182. |
| [14] |
CAO H, LI B, HE Z. Chatter stability of milling with speed-varying dynamics of spindles[J]. International Journal of Machine Tools and Manufacture, 2012, 52(1): 50-58. DOI:10.1016/j.ijmachtools.2011.09.004 |
| [15] |
HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A: Mathematical Physical and Engineering Sciences, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 |
| [16] |
HUANG N E, SHEN Z, LONG S R. A new view of nonlinear water waves: the Hilbert Spectrum[J]. Annual Review of Fluid Mechanics, 1999, 31(1): 417-457. DOI:10.1146/annurev.fluid.31.1.417 |
| [17] |
SOUALHI A, MEDJAHER K, ZERHOUNI N. Bearing health monitoring based on Hilbert–Huang transform, support vector machine, and regression[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(1): 52-62. DOI:10.1109/TIM.2014.2330494 |
| [18] |
唐贵基, 向玲, 朱永利. 基于HHT的旋转机械油膜涡动和油膜振荡故障特征分析[J]. 中国电机工程学报, 2008, 28(2): 77-81. TANG Gui-ji, XIANG Ling, ZHU Yong-li. Fault analysis of oil whirl and oil whip based on Hilbert-Huang transform for rotor system[J]. Proceedings of the Chinese Society for Electrical Engineering, 2008, 28(2): 77-81. DOI:10.3321/j.issn:0258-8013.2008.02.014 |
| [19] |
李欣, 梅德庆, 陈子辰. 基于经验模态分解和希尔伯特-黄变换的精密孔镗削颤振特征提取[J]. 光学精密工程, 2011, 19(6): 1291-1297. LI Xin, MEI De-qing, CHEN Zi-chen. Feature extraction of chatter for precision hole boring processing based on EMD and HHT[J]. Optics and Precision Engineering, 2011, 19(6): 1291-1297. |
| [20] |
CAO H, LEI Y, HE Z. Chatter identification in end milling process using wavelet packets and Hilbert–Huang transform[J]. International Journal of Machine Tools and Manufacture, 2013, 69: 11-19. DOI:10.1016/j.ijmachtools.2013.02.007 |
| [21] |
YEH L J, LAI G J. A study of the monitoring and suppression system for turning slender workpieces[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 1995, 209(3): 227-236. DOI:10.1243/PIME_PROC_1995_209_077_02 |



