水下滑翔机是一种新型的海洋水文要素观测平台,通过浮力调节装置实现自身浮力改变,在净浮力、阻力及升力的作用下,实现锯齿形滑翔观测运动. 自1989年Stommel[1]提出水下滑翔机的概念,水下滑翔机发展迅速,比较著名的有美国Webb研究所的Slocum水下滑翔机[2]、华盛顿大学的Seaglider水下滑翔机[3]和Scripps海洋研究所的Spray 水下滑翔机[4].
水下滑翔机的制造和运营成本较低且续航力强,被广泛应用于海洋科学研究和海洋观测任务中. 但是由于水下滑翔机仅仅依靠浮力调节装置进行驱动,限制了水下滑翔机的航速与机动性,对于一些需要快速追踪与捕捉的海洋现象难以观测. 将滑翔机的浮力调节装置与传统螺旋桨推进器结合的一种混合驱动水下滑翔机,兼具传统自助式水下航行器(autonomous underwater vehicle, AUV)与水下滑翔机的优点. 目前研制的混合驱动水下滑翔机有Memorial大学的Slocum AUV[5],Bachmayer等设计的 Hybrid Glider[6],Monterey Bay研究中心研制的Tehys AUV[7],天津大学研制的Petrel-II Hybrid Glider[8],和浙江大学研制的ZJU Glider[9-12]. 这类混合驱动水下滑翔机多采用外置的螺旋桨推进器,推进效率较低,对水下滑翔机艉部流场有影响. 喷水推进型水下滑翔机采用内置在艉部的喷水推进泵驱动,结构紧凑,推进效率高且水下噪声低,可实现水下滑翔机不同观测范围和不同观测精度的要求,应用前景广阔.
对水平翼的优化是混合驱动水下滑翔机设计的关键. 在滑翔模式下,水平翼为混合驱动水下滑翔机提供升力,对滑翔经济性和稳定性有决定性作用.在AUV模式下,水平翼对航行效率和机动性有十分重要的影响. Liu等[13]基于计算流体力学(CFD)方法,以升阻比为优化目标,对滑翔模式混合驱动水下滑翔机水平翼的几个简单外形布局进行比较,得到局部范围内的最优解,但未对水平翼要素进行全面分析. Sun等[14]以水下滑翔机的滑翔范围为优化目标,建立滑翔运动模型,对翼身融合水下滑翔机进行外形优化. Sugimoto[15]基于遗传算法,以滑翔速度为优化目标,对Hang-Glider的水平翼进行简单优化,算法设计较为复杂. 总的来说,目前针对混合驱动水下滑翔机水平翼优化的研究较少.
本文以喷水推进型水下滑翔机为研究对象,采用数值仿真方法对水下滑翔机的性能进行预测,通过分析水平翼参数对喷水推进型水下滑翔机的滑翔效率和静稳特性的影响,确定水平翼的最优配置. 建立喷水推进型水下滑翔机的运动模型,对喷水推进型水下滑翔机的定常滑翔运动、水平面回转运动进行仿真分析.
1 数值仿真方法常用的获取水动力系数的方法有:理论计算、试验和CFD方法. 理论计算方法主要采用经验公式进行计算,仅对于细长体外形及运动过程较为简单的模型有效[16]. 试验方法主要包括风洞试验、拖曳试验等,是目前最为有效且准确的手段,但是试验成本高并且耗时较长. CFD方法以计算机为硬件基础,通过各类数学方法,能够解决各种流体力学难题,近年来应用广泛. Bettle等[17]采用CFD 中RANS求解器计算潜艇在不同横滚角下的不稳定性,验证了初始横滚角对稳定性的影响较大. Jagadeesh等[18]对比拖曳试验与CFD方法计算得到的AUV壳体的阻力、升力和力矩,验证CFD方法的准确性. Zhao等[19]基于CFD方法,运用动网格技术对带附体的AUV进行多自由度的运动仿真,得到各个方向上的阻力. Yu等[20]基于CFD方法,采用RANS方程,计算得到微型AUV的速度场分布及压力分布. 本文采用计算机工程与制造集成代码(the integrated computer engineering and manufacturing code,ICEM)进行网格划分,采用FLUENT 16.0作为仿真工具.
1.1 阻力计算模型水阻通常由3部分组成:摩擦阻力、形状阻力和兴波阻力[21],由于水下滑翔机航行在深海,离水面较远,兴波阻力可忽略. 摩擦阻力主要是由于水的黏性产生,在湍流条件下,水下滑翔机壳体摩擦阻力系数的计算采用国际船模拖曳水池会议(1957,ITTC)推荐公式[22]:
| ${C_{D{\rm _h}}} = \frac{{0.075}}{{{{\left( {{\rm{lg}}{Re} - 2} \right)}^2}}}. $ | (1) |
式中:
形状阻力主要由主体外形决定,一般认为形状阻力系数与摩擦阻力系数的比是一个常数k,模型的总阻力系数CD可由形状因子1+k计算得到:
| ${C_{D}} = \left( {1 + k} \right){C_{D{\rm _h}}}. $ | (2) |
水下滑翔机采用流线型回转体外形,形状因子通过Hoerner (1965)推荐公式[23]:
| $1{\rm{ + }}k{\rm{ = 1 + }}1.5{\left( {{d}/{l}} \right)^{1.5}}{\rm{ + }}7{\left( {{d}/{l}} \right)^3}. $ | (3) |
式中:d、l分别为水下滑翔机的回转体直径和长度.
喷水推进型水下滑翔机的水平翼和尾翼采用美国国家航空咨询委员会(National Advisory Committee for Aeronautics,NACA)翼型. 由Re计算公式判定水平翼和尾翼的外流场为层流状态. 水平翼和尾翼的摩擦阻力系数参考平板层流状态的Blasius精确解[24]:
| ${C_{D{\rm _w}}} = 1.328/\sqrt {{\mathop{Re}\nolimits} } . $ | (4) |
式中:
水下滑翔机的总阻力为
| $\begin{split} D\! =& {D_{\rm h}} + {D_{\rm w}} + {D_{\rm{tw}}} = \frac{1}{2}\rho {V^2}{A_{\rm{h}}}{\rm{(}}1 + k{\rm{)}}{C_{D{\rm _h}}} + \\& \frac{1}{2}\rho {V^2}{A_{\rm{w}}}{\rm{(}}1 + k{\rm{)}}{C_{D{\rm w}}} + \frac{1}{2}\rho {V^2}{A_{{\rm{tw}}}}{\rm{(}}1 + k{\rm{)}}{C_{D_{\rm tw}}}. \end{split} $ | (5) |
式中:
计算域如图1(a)所示,为一长5l、直径为3l的包围滑翔机的圆柱体,其旋转轴与滑翔机模型的对称轴重合,进流边界面(入口)为圆柱体的前端面,距模型首端的距离为l,出流边界面(出口)为圆柱体的后端面,距模型尾端的距离为3l. 整个计算域采用结构化网格,网格总数为240万,以保证求解精度.
水下滑翔机外部采用外O网格,要求第一层网格节点位于湍流核心区内,节点分布律采用Exponential,网格边界层节点数取10. 第一层网格距离
| ${y^ + } = \frac{{\Delta y}}{\mu }\sqrt {{\tau _\omega }/\rho } ,$ | (6) |
| $\Delta y = {y^ + }\mu \sqrt {\rho/{\tau _\omega }} . $ | (7) |
式中:
流场中水的流动状态通常由雷诺数来判定,Re计算公式如下:
| $Re = \rho vc/\mu . $ | (8) |
式中:
当
| 表 1 喷水推进型水下滑翔机在不同速度下的雷诺数 Table 1 Reynolds numbers at different speeds of water-jet hybrid glider |
1)数值计算:经过多次调试及经验积累,采用RNG k -
2)速度入口(velocity inlet):滑翔机艏部向前1l,设定来流速度的大小与方向;
3)压力出口(pressure outlet):滑翔机艉部向后3l,认为流动在该处已经充分发展,故边界条件使用压力出口;
4)壁面(wall):滑翔机外表面,包括水平翼,设定无滑移条件;
5)外场:因为流域外表面距离滑翔机足够远,所以可以认为在该面上没有法向速度,可以取边界条件为滑移壁面(slip wall),壁面粗糙度设置为0,剪切力为0.
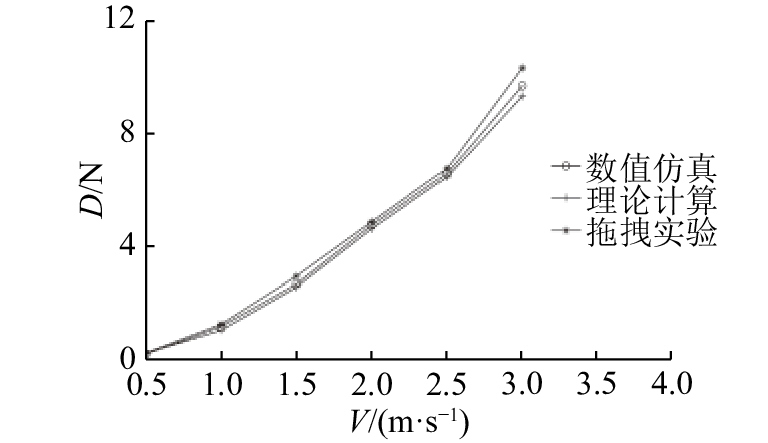
1.4 结果分析为了对理论计算和数值仿真方法的准确性进行验证,将已经进行拖曳试验的喷水推进型水下滑翔机I代的理论计算、数值仿真与拖曳试验结果进行对比,图1(a)为喷水推进型水下滑翔机I代仿真模型,图1(b)为拖曳试验模型. 图2为水下滑翔机在0.5~3.0 m/s航速下V的阻力曲线. 理论计算与拖曳试验的阻力值最大误差为12%,其余误差均小于8%;数值仿真与拖曳试验的阻力值最大误差为10%,其余误差均小于5%. 综上所述,数值仿真结果精度较高,该数值仿真方法可用于喷水推进型水下滑翔机水动力系数计算.

|
图 1 喷水推进型水下滑翔机I代模型 Fig. 1 Model of water-jet hybrid glider I |
|
图 2 喷水推进型水下滑翔机I代阻力对比曲线 Fig. 2 Resistance comparison curves of water-jet hybrid glider I |
喷水推进型水下滑翔机的动力装置有浮力调节装置和喷水推进泵,姿态调整装置主要有质心调节装置和尾舵. 纵剖面的主要运动方式为滑翔运动,与传统滑翔机的滑翔运动类似,通过浮力调节装置和质心调节装置实现纵剖面锯齿形滑翔运动. AUV模式用来观测高速、高机动性的对象,与传统AUV水平面运动类似,通过喷水推进泵和尾舵实现水平面的快速机动航行.
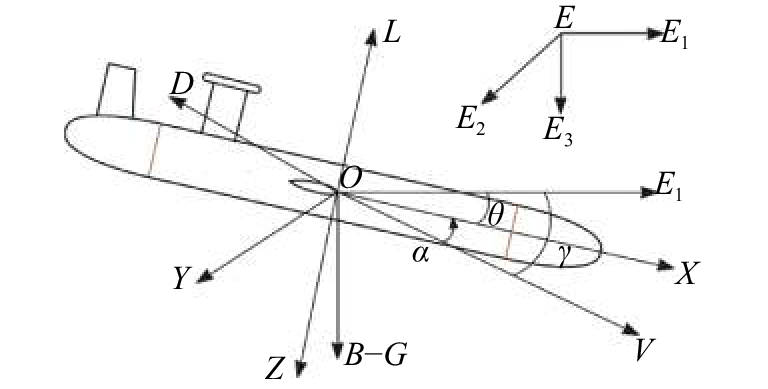
如图3所示,喷水推进型水下滑翔机常用的坐标系主要包括大地坐标系E-E1E2E3,和机体坐标系O-XYZ,原点O位于机体浮心处,OX轴指向机体艏部方向,OY轴指向机体右舷方向,OZ轴垂直于水平翼向下[26].
|
图 3 喷水推进型水下滑翔机坐标系 Fig. 3 Coordinate system of water-jet hybrid glider |
喷水推进型水下滑翔机的主要运动模式为锯齿形滑翔运动,选择NACA00112为水平翼翼型,水平翼参数包括展弦比、弦长、后掠角及安装位置,在机体坐标系X轴上,浮心之前为正,浮心之后为负. 正交试验工况为:航速为0.5m/s,攻角为8°[27]. 水平翼正交试验的重要评价指标为滑翔效率和静稳定性.
在单个滑翔周期内,水平滑翔距离一定的情况下,滑翔角越小,表示滑翔运动坡度越缓,垂直滑翔距离越小,滑翔运动消耗的能量越少,滑翔效率越高. 滑翔角与升阻比(L/D)成正比:
| $\gamma {\rm{ = }}\theta - \alpha, $ | (9) |
| ${\rm{tan}}\, \gamma = - {\left( {{L}/{D}} \right)^{ - 1}}{\rm{ = }}{{2h}}/{s}. $ | (10) |
式中:
静稳定性分为水平面静稳定性和纵剖面静稳定性,通常用静稳定系数来表示[28]:
| $\left. \begin{array}{l}l_\beta ' = N_v'/Y_v',\\ l_\alpha ' = - M_w'/Z_w'. \end{array} \right\}$ | (11) |
式中:
研究水平翼参数对滑翔效率和稳定性的影响,通过一次变化法进行敏感性分析,敏感性系数定义为[29]
| ${s_i} = \partial {y_j}/\partial {x_i}. $ | (12) |
式中:
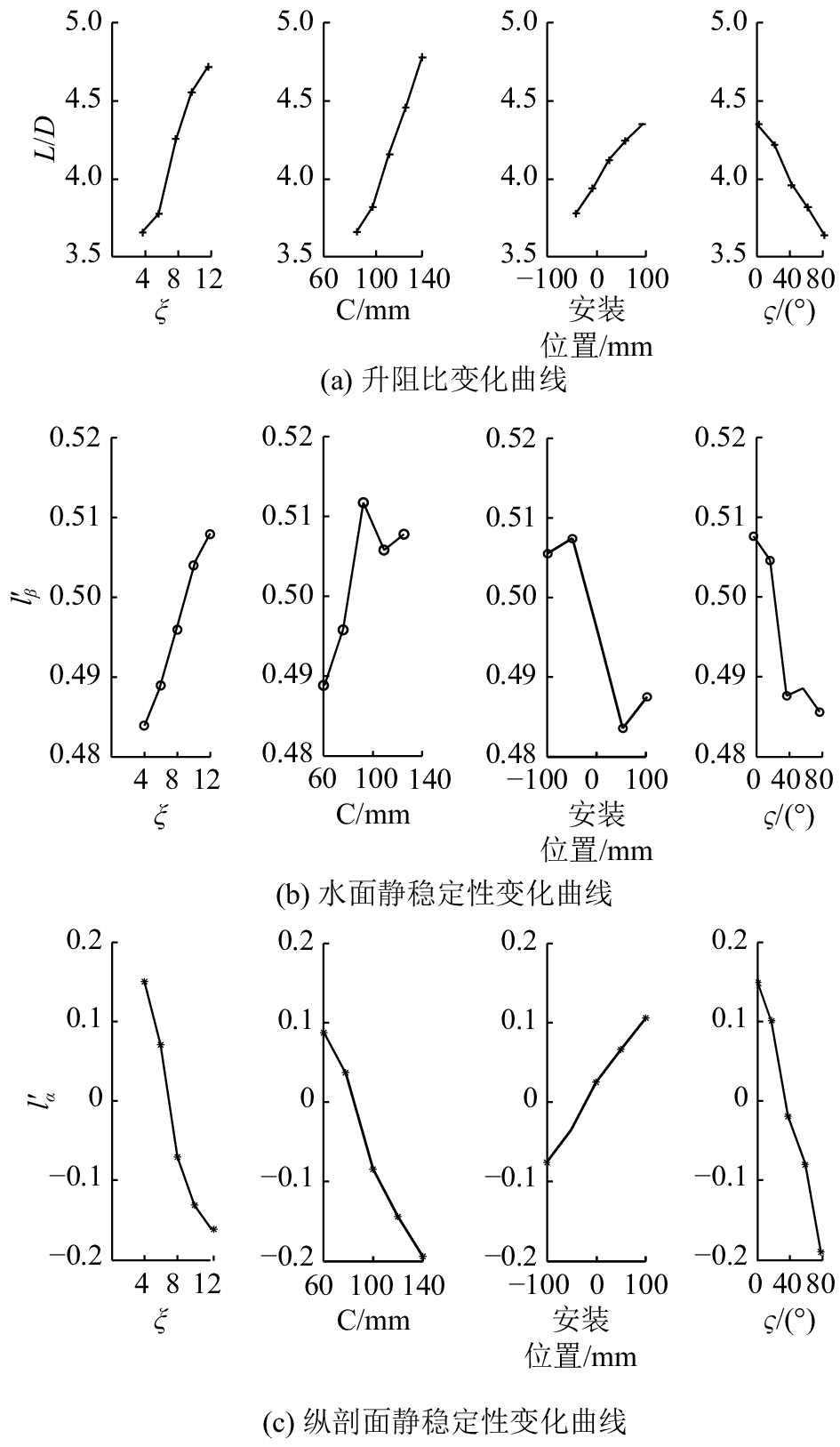
|
图 4 水平翼参数的正交试验结果 Fig. 4 Orthogonal test results of wing parameters |
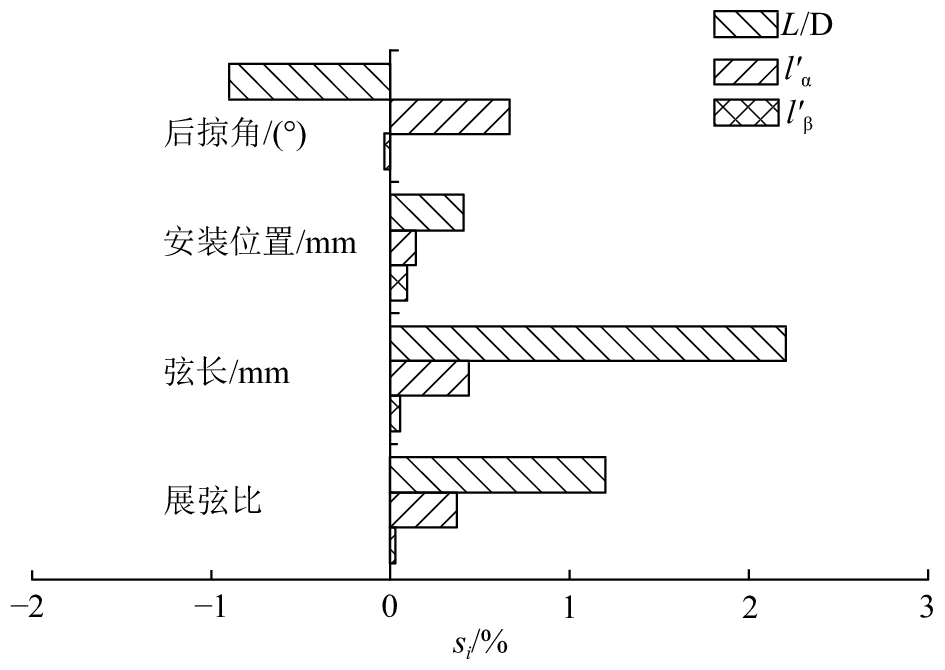
|
图 5 水平翼参数的敏感性分析结果 Fig. 5 Sensitivity analysis results of wing parameters |
仿真结果如图4和5所示,得到以下结论:1)升阻比随着弦长C、展弦比ξ、安装位置的增大而增大,随后掠角
水平翼安装位置对滑翔效率和静稳定性影响较小,可确定水平翼安装位置在浮心. 增大后掠角可以提高纵剖面稳定性,但是会降低升阻比,需要确定合适的水平翼后掠角.
2.3 水平翼参数配置水平翼的弦长是影响水平翼表面流场Re的重要因素,Re增大会导致流场变化更加剧烈,边界层厚度减小,湍流显著增加. 试验数据表明,当NACA00112水平翼流场的Re<
| $c \geqslant \frac{{Re \cdot \mu }}{{\rho V}}.$ | (13) |
喷水推进型水下滑翔机最大航速为2.5 m/s,由式(13)可得,
水下滑翔机的阻力主要由主体的湿表面积和外形决定,升力由水平翼提供,水平翼的升阻比计算公式为
| $\left. \begin{array}{l}{L_{\rm w}} = \rho {C_{L_{\rm w}}}{A_{\rm w}}{V^2}/2,\\{D_{\rm w}} = \rho {C_{D_{\rm w}}}{A_{\rm w}}{V^2}/2,\\{\lambda _{\rm w}} = {L_{\rm w}}/{D_{\rm w}}. \end{array} \right\}$ | (14) |
式中:
根据Whicker公式[31],得到水平翼升阻比与攻角、后掠角和展弦比的关系.
| $\left. \begin{array}{l}{C_{L_{\rm w}}} = \displaystyle\frac{{1.8\pi \xi }}{{{\rm{cos}}\,\varsigma \sqrt {4 + \displaystyle\frac{{{\xi ^2}}}{{{\rm{co}}{{\rm{s}}^4}\,\varsigma }}} + 1.8}}\alpha + \displaystyle\frac{{{C_{\rm{DC}}}}}{\xi }{\alpha ^2},\\{C_{D_{\rm w}}} = {C_{\rm{D0_w}}} + \displaystyle\frac{{{{\left( {{C_{\rm{L_w}}}} \right)}^2}}}{{0.9\pi \xi }}. \end{array} \right\}$ | (15) |
式中:
|
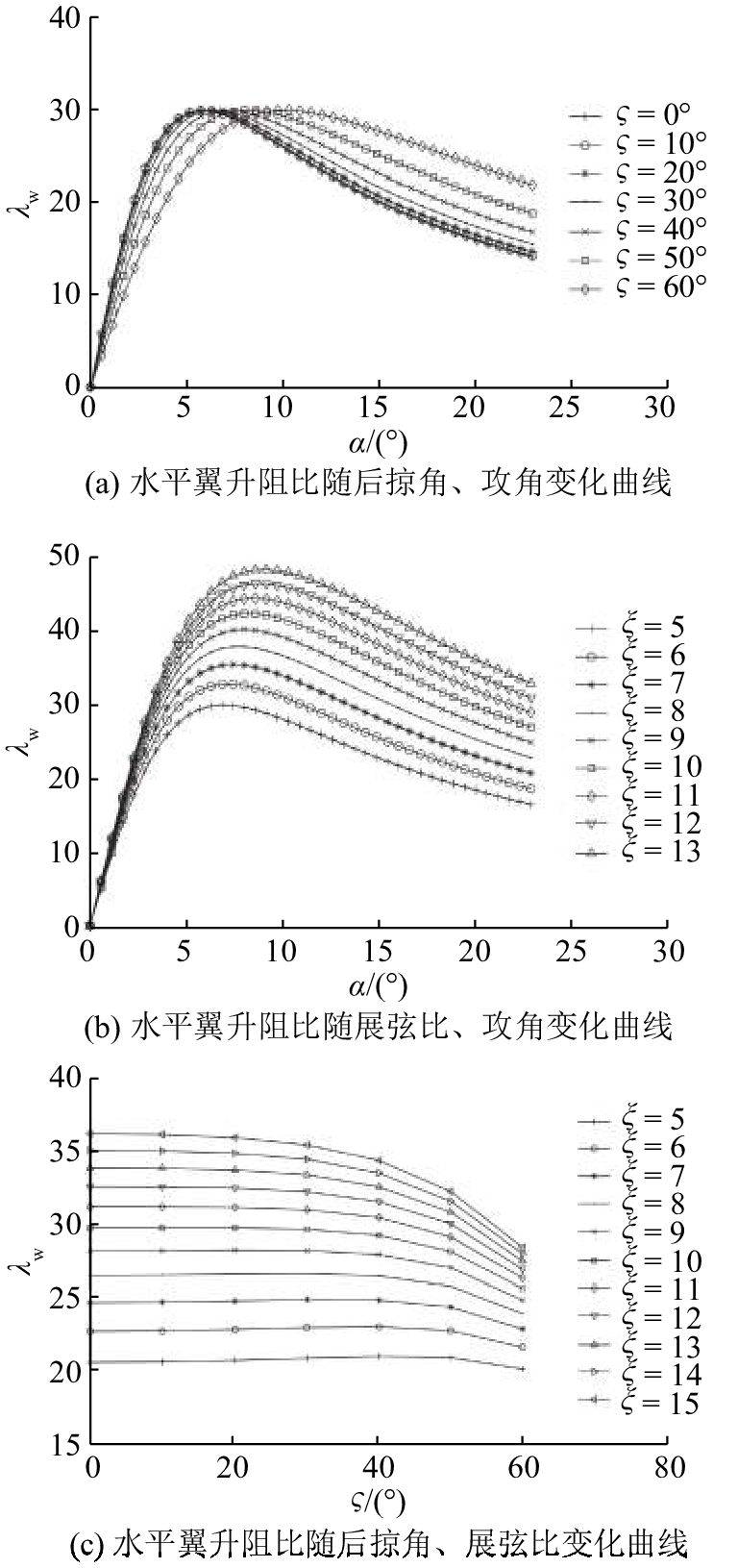
图 6 不同水平翼参数下水平翼升阻比变化曲线 Fig. 6 Curves of lift-to-drag ratio of horizontal tail under different wing parameters |
由图6(a)可知,展弦比一定,水平翼的升阻比随攻角先增后减;且随着后掠角增大,最大升阻比不变,对应攻角增大,一般为6°~8°.
由图6(b)可知,后掠角一定,水平翼的升阻比随攻角先增后减;随着展弦比增大,最大升阻比增大,对应攻角增大,一般为6°~8°. 展弦比增大会导致升力和阻力同时增大,在小攻角范围内,阻力增大的速度比升力增大的速度快,因此对于小攻角、大滑翔角的滑翔运动,减小阻力对提升滑翔效率更有帮助.
由图6(c)可知,攻角一定,当展弦比小于10时,升阻比随后掠角先增后减;当展弦比大于10时,水平翼的升阻比随后掠角增大而减小. 这是由于展弦比较大时,随着后掠角增大,阻力增大的速度比升力增大的速度快. 当展弦比较小时,在0°~40°,随后掠角增大,升力增大的速度比阻力增大的速度快.
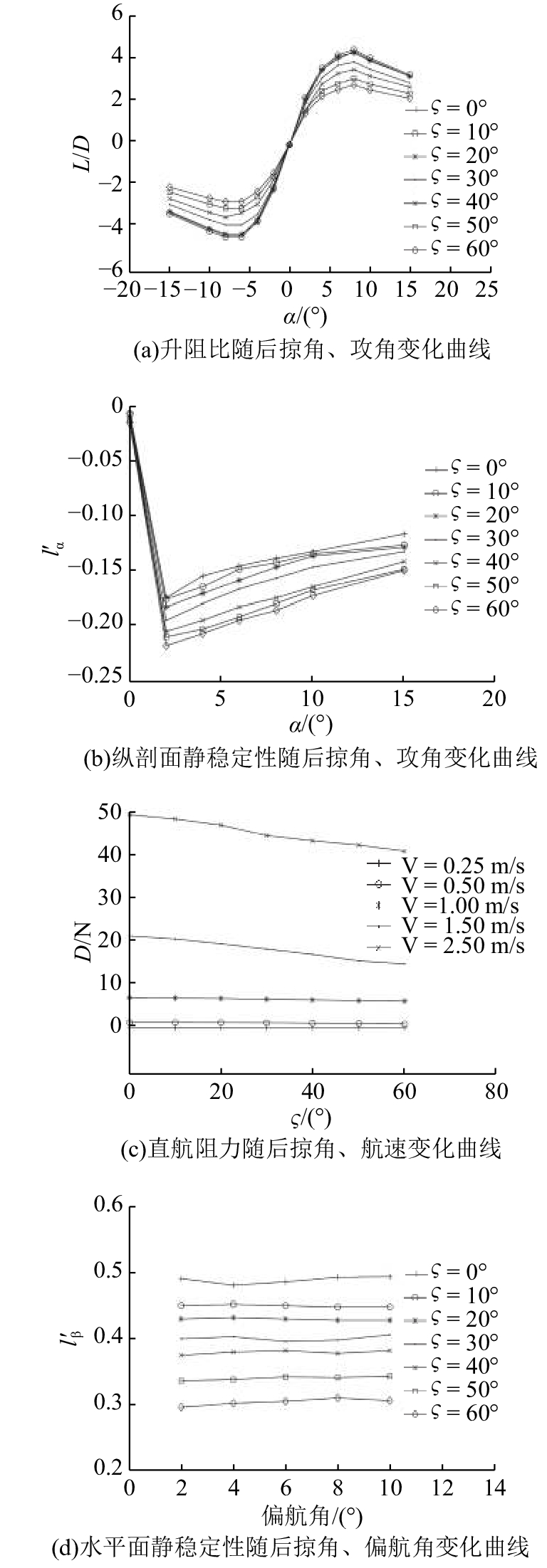
取水平翼的攻角为8°,弦长为100 mm,展弦比为10,安装位置为浮心处,对水下滑翔机不同水平翼后掠角进行数值仿真,探究后掠角对滑翔效率、直航阻力和静稳定性的影响,结果如图7所示.
|
图 7 滑翔效率、直航阻力和静稳定性与后掠角关系曲线 Fig. 7 Relationship curve between sweep angle and gliding efficiency, direct route resistance, and static stability |
由图7(a)可知,随着攻角增大,水下滑翔机的升阻比先增大后减小,在8°攻角附近升阻比最大,与Whicker公式计算结果相符. 负攻角下的升阻比正攻角下的升阻比大,这是由于喷水推进型水下滑翔机的上下表面不对称,负攻角时,迎流面积增大,导致阻力增大,升阻比减小.
由图7(a)可知,在不同后掠角下,水下滑翔机的升阻比随攻角的变化规律相同. 当后掠角为10°时,升阻比最大,随后掠角增大,升阻比减小,这是由于随着后掠角增大,水平翼迎流面积减小,导致升力减小,升阻比减小.
由图7(b)可知,随攻角增大,水下观测平台纵剖面静稳定系数先减小后增大. 在2°攻角下,纵剖面静稳定系数最小,表面纵剖面静稳定性最好. 随后掠角增大,水下观测平台的纵剖面稳定性系数减小,纵剖面静稳定性更好. 这表明水下观测平台以小攻角状态进行滑翔运动时更稳定,在受到水流的强扰动时,可以增大水平翼后掠角,增强纵剖面静稳定性.
由图7(c)可知,在不同速度下,水下观测平台的阻力随后掠角变化的规律一致,随着后掠角增大,阻力略微减小. 随着后掠角增大,水平翼迎流面积逐渐减小,但是由于水平翼迎流面积较小,对总阻力的影响较小.
由图7(d)可知,水下观测平台水平面静稳定系数不随偏航角变化而改变,随着后掠角增大而减小.
综上所述,在锯齿形滑翔模式下,当水平翼后掠角为10°时,滑翔效率最高,静稳定性较好.
3 运动分析 3.1 滑翔运动分析根据以上得到的水平翼配置,对喷水推进型水下滑翔机的滑翔运动进行分析,得到运动方程[32]:
| $\left. \begin{aligned}&{r}\dot u = \dot v = \dot w = \dot p = \dot q = \dot r,\\&v = p = q = r = \phi = 0,\\&u = w = \psi = \theta = C\left({\rm {cons\tan t}} \right), \end{aligned} \right\}$ | (16) |
| $\left. \begin{aligned}&\bar mg\left( {{x_{\rm{G}}}{\rm{cos}}\,\theta {\rm{ + }}{z_{\rm G}}{\rm{sin}}\,\theta } \right) = M,\\&L{\rm{sin}}\,\alpha - D{\rm{cos}}\,\alpha = \left( {B - G} \right){\rm{sin}}\,\theta ,\\&L{\rm{cos}}\,\alpha + D{\rm{sin}}\,\alpha = \left( {B - G} \right){\rm{cos}}\,\theta . \end{aligned} \right\}$ | (17) |
式中:
喷水推进型水下滑翔机以大滑翔角、小攻角状态航行,水动力表示为
| $\left. \begin{array}{l}D{\rm{ = }}\displaystyle\frac{{{C_D}}}{2}\rho {V^2}S = \displaystyle\frac{{{C_{D0}} + KC_{L\alpha }^2{\alpha ^2}}}{2}\rho {V^2}S,\\L{\rm{ = }}\displaystyle\frac{{{C_L}}}{2}\rho {V^2}S = \displaystyle\frac{{C_{L\alpha }^{}{\alpha ^2}}}{2}\rho {V^2}S, \end{array} \right\}$ | (18) |
| $\begin{gathered} \left[ \begin{gathered} 0 \\ B - G \\ \end{gathered} \right]{\rm{ = }} \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}\,\theta }&{{\rm{sin}}\,\theta } \\ { - {\rm{sin}}\,\theta }&{{\rm{cos}}\,\theta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\rm{cos}}\,\theta }&{ - {\rm{sin}}\,\theta } \\ {{\rm{sin}}\,\theta }&{{\rm{cos}}\,\theta } \end{array}} \right]\left[ \begin{gathered} D \\ L \\ \end{gathered} \right] \\ \end{gathered} . $ | (19) |
式中:S为喷水推进行水下滑翔机湿表面积. CD0为直航阻力系数(α=0);
| $\tan\,\gamma = - \frac{{{C_D}}}{{{C_L}}} = - \frac{{{C_{D0}} + KC_{L\alpha }^2{\alpha ^2}}}{{{C_{L\alpha }}\alpha }},$ | (20) |
| $KC_{L\alpha }^2{\alpha ^2} + \tan\, \gamma\cdot{C_{L\alpha }}\alpha + {C_{D0}} = 0. $ | (21) |
上述方程若想得到实解,则需满足
| ${\rm{ta}}{{\rm{n}}^2}\,\gamma\geqslant 4K{C_{D0}}. $ | (22) |
滑翔角
| $\gamma = \pm {\rm{arctan }}\left( {2\sqrt {K{C_{D0}}} } \right). $ | (23) |
由以上方程可知,
攻角与水动力系数的关系式为
| $\alpha {\rm{ = }} \mp \frac{1}{{{C_{L\alpha }}}}\sqrt {\frac{{{C_{D0}}}}{K}} {\rm{ = }} \mp \frac{1}{{2K{C_{L\alpha }}}}{\rm{tan}}\,\gamma . $ | (24) |
基于式(18)和(19),得到滑翔速度
| $V = \sqrt {\frac{{B - G}}{{ {{\rm{cos}}\, \gamma {C_L} - {\rm{sin}} \,\gamma {C_D}} }} \times \frac{2}{{\rho S}}} , $ | (25) |
| $ {V_{{X}}} = V{\rm{cos}}\, \gamma ,\\{V_{{Z}}} = V{\rm{sin}}\, \gamma . $ | (26) |
式中:
水下观测平台俯仰角与质心调节重量块的关系如下:
| $\theta = {\rm{arctan}}\,\left( {\frac{{{m_{\rm m}}{x_{\rm m}}}}{{hm}}} \right). $ | (27) |
式中:
| 表 2 喷水推进型水下滑翔机的水动力系数表 Table 2 Hydrodynamic coefficient of water-jet hybrid glider |
表2为数值仿真得到的喷水推进型水下滑翔机的水动力系数表. 当航速为0.25 m/s时,滑翔角范围为(19°,90°),攻角范围为(0°,11°). 当航速为0.5 m/s时,滑翔角范围为(17.6°,90°),攻角范围为(0°,8.7°).
浮力调节装置的浮力调节范围为(–7.5 ~7.5)N.图8(a)表示攻角随滑翔角和俯仰角增大而减小,滑翔角较大时,攻角较小. 图8(b)表示滑翔角和俯仰角随质心调节位移量增大而增大,攻角随质心调节位移量增大而减小. 图8(c)表示滑翔速度

|
图 8 喷水推进型水下滑翔机的定常滑翔运动分析 Fig. 8 Steady gliding motion analysis of water-jet hybrid glider |
尾舵的水动力分解后得到沿Y轴方向的升力
| $\left. \begin{array}{l}{L_{\rm R}} = \displaystyle\frac{1}{2}{C_{L_{\rm R}}}\rho {A_{\rm R}}{V^2},\\{D_{\rm R}} =\displaystyle \frac{1}{2}{C_{D_{\rm R}}}\rho {A_{\rm R}}{V^2}. \end{array} \right\}$ | (28) |
式中:
在AUV模式下,采用喷水推进泵推进,喷水推进型水下滑翔机的水平面运动方程为[33]
| $\left. \begin{array}{l}X = m\left( {\dot u - vr - {X_g}{r^2} - {Y_g}{r^2}} \right),\\Y = m\left( {\dot v + ur - {Y_g}{r^2} - {X_g}\dot r} \right),\\N = {I_Z}\dot r + m\left[ {{X_g}\left( {\dot v + ur} \right) - {Y_g}\left( {\dot u - vr} \right)} \right]. \end{array} \right\}$ | (29) |
式中:(Xg,Yg)为水下滑翔机重心在XOY平面上坐标;r为绕Z轴转动角速度,IZg为滑翔机绕过重心Z轴的转动惯量,IZ为滑翔机绕过浮心原点Z轴的转动惯量.
尾舵的仿真曲线如图9所示,根据尾舵的安装位置可求出尾舵对喷水推进型水下滑翔机的力矩.
依据数值仿真结果,对喷水推进型水下滑翔机进行水平面运动仿真. 首先进行直航运动仿真,喷泵推力值设定为8.6和48.6N. 结果如图10所示.
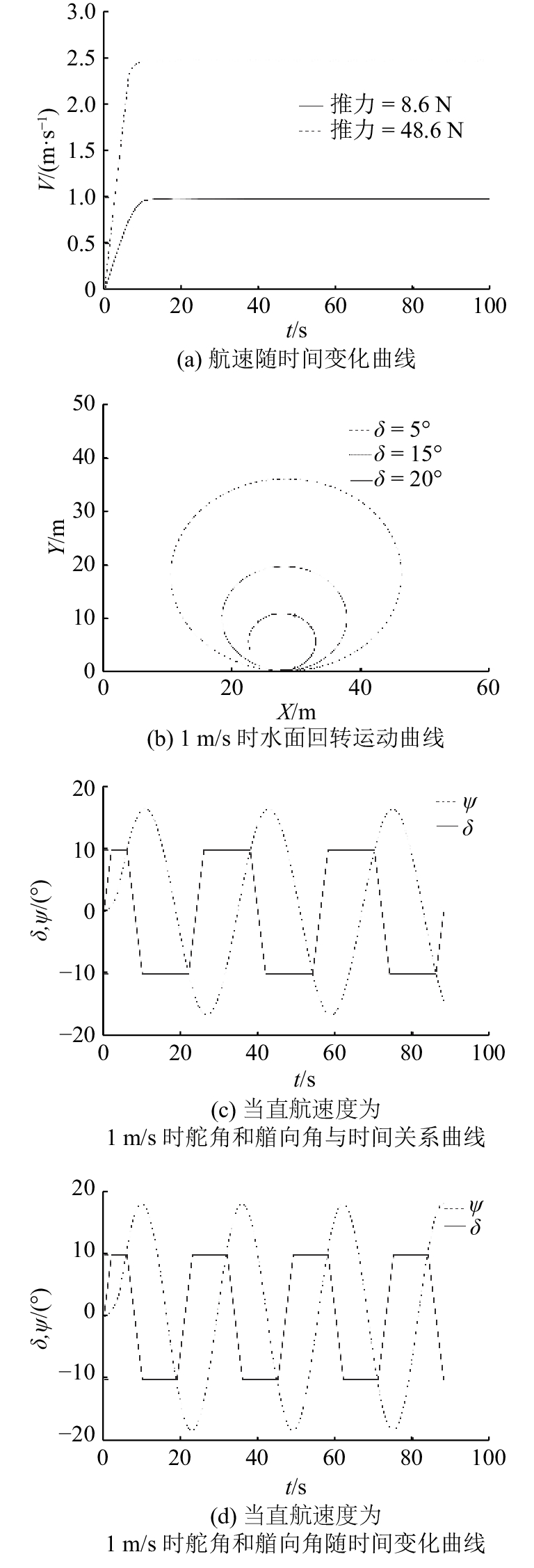
图10(a)表示随着推力的增大,加速时间缩短,航速最终趋于稳定. 定常回转运动是衡量水平面机动性的一种基本运动,直接反映操控尾舵时水下航行器航向改变的能力. 喷水推进型水下滑翔机以直航速度1 m/s前进30 s,等航速稳定后打舵角,试验舵角依次为5°、10°和20°. 图10(b)表示航速稳定,随着舵角增大,回转直径、纵距以及回转周期数值都会减小,且随着舵角增大,减小的趋势逐渐变缓. 回转直径是水平面机动性的重要衡量指标,在20°舵角时,回转直径为12.5 m,回转周期为42 s.
传统AUV在航行过程中,完成完整的水平面回转运动的情况较少,经常由一个航向变为另一个航向. 转向过程中回转角度不大,为了评价喷水推进型水下滑翔机的航向改变性能,进行水平面Z形运动仿真试验,试验速度分别采用1.0 和2.5 m/s,操舵角
如图10(c)、(d)所示,当航速为1 m/s时,Z形运动的周期为32 s,超越艏向角为16.6°. 当航速为2.5 m/s时,Z形运动的周期为26 s,超越艏向角为18.2°. 当舵角一定时,随着航速的增大,初转期、超越时间及周期均有增大. 这说明舵效与速度有关,速度越大,舵效越好. 当航速增大时,超越艏向角增大,这是由于惯性使喷水推进型水下滑翔机在原方向上继续行驶了一段距离.

|
图 9 舵的升力系数和阻力系数与舵角的关系曲线 Fig. 9 Relationship between rudder angle and lift coefficient as well as resistance coefficient |
|
图 10 喷水推进型水下滑翔机的水平面运动分析 Fig. 10 Horizontal motion analysis of water-jet hybrid glider |
首先验证数值仿真方法的准确性,结合多种方法对水平翼参数进行配置,在刚体六自由度动力学模型基础上,建立喷水推进型水下滑翔机的定常运动模型,并且进行仿真分析,得到以下结论.
1)通过对比理论计算、数值仿真和拖曳试验的结果,验证数值仿真方法的准确性,说明该数值仿真方法可以用于喷水推进型水下滑翔机的水动力计算.
2)当喷水推进型水下滑翔机水平翼翼型为NACA0012,弦长为100 mm,展弦比为10,安装位置在浮心处,后掠角为10°时,升阻比最大,静稳定性较好.
3)滑翔模式下,喷水推进型水下滑翔机滑翔角为38°,攻角为1.5°时,水平滑翔速度最快,单周期的滑翔距离最远;喷水推进型水下滑翔机的最大滑翔角和俯仰角为83.9°. 当浮力调节量为7.5 N时,垂向最大滑翔速度为1.1 m/s;AUV模式下,水平面的机动性较好,在1 m/s航速、20°舵角的条件下,喷水推进型水下滑翔机回转直径为12.5 m,回转周期为42 s.
| [1] |
STOMMEL H. The Slocum mission [J]. Oceanography, 1989, 2(1): 22-25 https://tos.org/oceanography/article/the-slocum-mission
|
| [2] |
SCHOFIELD O, KOHUT J, ARAGON D, et al. Slocum gliders: robust and ready[J]. Journal of Field Robotics, 2010, 24(6): 473-485. |
| [3] |
ERIKSEN C C, OSSE T J, LIGHT R D, et al. Seaglider: a long-range autonomous underwater vehicle for oceanographic research[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 424-436. DOI:10.1109/48.972073 |
| [4] |
RUDNICK D L, DAVIS R E, SHERMAN J T. Spray underwater glider operations[J]. Journal of Atmospheric and Oceanic Technology, 2016, 33(6): 1113-1122. DOI:10.1175/JTECH-D-15-0252.1 |
| [5] |
EICHHORN M, WILLIAMS C D, BACHMAYER R, et al. A mission planning system for the AUV "SLOCUM Glider" for the Newfoundland and Labrador Shelf[J]. Journal of Petrology, 2017, 27(6): 1331-1364. |
| [6] |
BACHMAYER R, LEONARD N E, GRAVER J, et al. Underwater gliders: recent developments and future applications [C] // International Symposium on Underwater Technology. [S. l.]: IEEE, 2004: 195-200 http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1405540
|
| [7] |
HOBSON B W, BELLINGHAM J G, KIEFT B, et al. Tethys-class long range AUVs-extending the endurance of propeller-driven cruising AUVs from days to weeks [C] // Autonomous Underwater Vehicles. [S. l.]: IEEE, 2012: 1-8 http://ieeexplore.ieee.org/document/6380735/
|
| [8] |
WANG S X, SUN X J, WANG Y H, et al. Dynamic modeling and motion simulation for a winged hybrid-driven underwater glider[J]. China Ocean Engineering, 2011, 25(1): 97-112. DOI:10.1007/s13344-011-0008-7 |
| [9] |
YANG C, PENG S, FAN S. Performance and stability analysis for ZJU glider[J]. Marine Technology Society Journal, 2014, 48(3): 88-103. DOI:10.4031/MTSJ.48.3.6 |
| [10] |
PENG S, YANG C, FAN S, et al. Hybrid underwater glider for underwater docking: modeling and performance evaluation[J]. Marine Technology Society Journal, 2014, 48(6): 112-124. DOI:10.4031/MTSJ.48.6.5 |
| [11] |
FAN S S, YANG C J, PENG S L, et al. Underwater glider design based on dynamic model analysis and prototype development[J]. Journal of Zhejiang University Science C, 2013, 14(8): 583-599. DOI:10.1631/jzus.C1300001 |
| [12] |
PENG S, YANG C, FAN S, et al. A hybrid underwater glider for underwater docking [C] // Oceans. San Diego: IEEE, 2014, 152(2): 1-7 http://ieeexplore.ieee.org/document/6741166/
|
| [13] |
LIU F, WANG Y, NIU W, et al. Hydrodynamic performance analysis and experiments of a hybrid underwater glider with different layout of wings [C] // Oceans. San Diego: IEEE, 2014, 152(1): 1-5 http://ieeexplore.ieee.org/document/6964512/citations
|
| [14] |
SUN C, SONG B, WANG P, et al. Shape optimization of blended-wing-body underwater glider by using gliding range as the optimization target[J]. International Journal of Naval Architecture and Ocean Engineering, 2017, 9(6): 693-704. DOI:10.1016/j.ijnaoe.2016.12.003 |
| [15] |
SUGIMOTO T. Wing design for hang-gliders having minimum induced drag[J]. Journal of Aircraft, 2015, 29(4): 730-731. |
| [16] |
HESS J L. Calculation of potential flow about arbitrary three-dimensional lifting bodies [M]. Long Beach: Douglas Aircraft Company, 1969: 8
|
| [17] |
BETTLE M C, GERBER A G, WATT G D. Unsteady analysis of the six DOF motion of a buoyantly rising submarine[J]. Computers and Fluids, 2009, 38(9): 1833-1849. DOI:10.1016/j.compfluid.2009.04.003 |
| [18] |
JAGADEESH P, MURALI K, IDICHANDY V G. Experimental investigation of hydrodynamic force coefficients over AUV hull form[J]. Ocean Engineering, 2009, 36(1): 113-118. DOI:10.1016/j.oceaneng.2008.11.008 |
| [19] |
ZHAO J, SU Y, JU L, et al. Hydrodynamic performance calculation and motion simulation of an AUV with appendages [C] // International Conference on Electronic and Mechanical Engineering and Information Technology. Harbin: IEEE, 2011: 657-660 http://ieeexplore.ieee.org/document/6023135/
|
| [20] |
YU X, SU Y. Hydrodynamic performance calculation of mini-AUV in uneven flow field [C] // IEEE International Conference on Robotics and Biomimetics. Tianjin: IEEE, 2011: 868-872 http://ieeexplore.ieee.org/abstract/document/5723440/
|
| [21] |
姜次平, 邵世明. 船舶阻力[M]. 上海: 上海交通大学出版社, 1985: 35-42
|
| [22] |
RAMAMURPHY A V. Wall slip in viscous fluids and influence of materials of construction[J]. Journal of Rheology, 1986, 30(2): 337-357. DOI:10.1122/1.549852 |
| [23] |
CHONG-BEN N I, ZHU R C, MIAO G P, et al. A method for ship resistance prediction based on CFD computation[J]. Chinese Journal of Hydrodynamics, 2010, 25(5): 579-586. |
| [24] |
VELDMAN A E P, VOOREN A I V D. Drag of a finite flat plate [C]//Proceedings of the Fourth International Conference on Numerical Methods in Fluid Dynamics. Berlin: Springer, 1975: 423-430 https://link.springer.com/chapter/10.1007%2FBFb0019783
|
| [25] |
ISA K, ARSHED M R, ISHAK S. A hybrid-driven underwater glider model, hydrodynamics estimation, and an analysis of the motion control[J]. Ocean Engineering, 2014, 81(2): 111-129. |
| [26] |
BHATTA P. Nonlinear stability and control of gliding vehicles[J]. Recent Developments in Ruminant Nutrition, 2006, 4(10): 325-352. |
| [27] |
WU J, ZHANG M, SUN X. Hydrodynamic characteristics of the main parts of a hybrid-driven underwater glider PETREL [M]. [S. l.]: Autonomous Underwater Vehicles, 2011
|
| [28] |
施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1999: 123-129
|
| [29] |
KIM S H. Comparison of sensitivity analysis methods for building energy simulations in early design phases: once-at-a-time (OAT) vs. variance-based methods[J]. KIEAE Journal, 2016, 16(2): 17-22. DOI:10.12813/kieae.2016.16.2.017 |
| [30] |
WEBB D C, SIMONTTI P J, JONES C P. SLOCUM: an underwater glider propelled by environmental energy[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 447-452. DOI:10.1109/48.972077 |
| [31] |
BRESHEARS D D, WHICKER J J, JOHANSEN M P, et al. Wind and water erosion and transport in semi-arid shrubland, grassland and forest ecosystems: quantifying dominance of horizontal wind-driven transport[J]. Earth Surface Processes and Landforms, 2003, 28(11): 1189-1209. DOI:10.1002/(ISSN)1096-9837 |
| [32] |
朱雨时, 杨灿军, 吴世军, 等. 水柱测量中的水下滑翔机转向性能[J]. 浙江大学学报: 工学版, 2016, 50(9): 1637-1645. ZHU Yu-shi, YANG Can-jun, WU Shi-jun, et al. Water glider steering performance in water column measurement[J]. Journal of Zhejiang University: Engineering Science, 2016, 50(9): 1637-1645. |
| [33] |
GRAVER GRADY J. Underwater gliders: dynamics, control and design[J]. Journal of Fluids Engineering, 2005, 127(3): 523-528. DOI:10.1115/1.1899169 |



