2. 上海飞机设计研究院,上海200436
2. Shanghai Aircraft Design and Research Institute, Shanghai 200436, China
组合导航系统使用2种或2种以上的不同导航系统对同一导航信息进行测量和解算以形成量测量,根据量测量计算和校正各导航系统的误差[1]. 捷联惯性导航系统(strapdown inertial navigation system, SINS)与全球定位系统(global positioning system, GPS)的组合导航是目前应用广泛的组合导航系统,通过对多传感器量测信息的融合,得到更优的状态估计. 经典卡尔曼滤波在解决组合导航的信息融合问题中发挥了重要的作用. 卡尔曼滤波利用高斯状态空间将观测噪声建模为高斯分布,在噪声参数已知并保持不变的融合场景下效果显著[2-3].
在实际应用中,将噪声直接设定为固定的高斯白噪声存在局限性,比如在组合导航的应用过程中,系统本身可能存在摄动或受到外界未知噪声干扰等多种因素,导致观测噪声在滤波过程中是变化的,经典卡尔曼滤波算法的精度会大幅下降[4]. 为了提高系统的自适应性,通常考虑通过改变参数以减弱时变噪声对滤波效果的影响. 贝叶斯方法是目前使用最为广泛的方法,利用贝叶斯定理可以求取待估计量的后验概率,但是变量维数的增多会导致积分计算量大幅增加. 为了简化对于贝叶斯公式中积分项的求取,Beal[5]提出变分贝叶斯学习的概念,在此之前,Attias[6]曾在计算机科学领域详细阐述过相关理论框架. 参数个数较多或者观测量的维度增加会使边缘似然函数的求解极为复杂,导致计算量急剧增大,甚至无法直接计算[7]. 变分贝叶斯学习的精髓是使用简单可求的分布来逼近真实的后验分布,大大降低计算的难度,使得高精度滤波成为可能.
变分贝叶斯方法最早提出是用于解决机器学习和模式识别中的参数估计和模型选择问题,考虑到其强大的自适应能力,许多学者将其用于解决状态估计中噪声自适应的问题. Sarkka 等[8]最早提出将变分贝叶斯学习和卡尔曼滤波方法结合,用于时变噪声的状态估计. 基于变分贝叶斯学习的滤波方法,研究者分别提出了针对不同系统的噪声模型. Dong等[9]提出基于Wishart分布的噪声自适应变分贝叶斯容积信息滤波器,将测量噪声逆矩阵建模为Wishart分布;Li等[10]提出具有自适应性和鲁棒性的无迹卡尔曼滤波器,通过运用变分贝叶斯方法对时变的测量噪声协方差进行估计,从而实现自适应;Mohammed等[11]提出基于代谢血流动力学模型对血液氧合水平依赖进行测量的状态空间方法,基于扩展卡尔曼滤波器和变分贝叶斯方法来推断隐藏状态和参数;Feng等[12]提出鲁棒的概率假设密度(probability hypothesis density, PHD)滤波器,将变分贝叶斯方法应用于状态的联合递归预测和时变测量噪声参数估计;沈锋等[13]提出自适应的变分贝叶斯容积卡尔曼滤波算法,在非线性系统的滤波问题中能够较好地跟踪变化的观测噪声方差;徐定杰等[14]利用变分贝叶斯学习算法进行模型的参数估计,通过最大化边缘似然函数的下界,不断逼近真实后验分布,实现混合高斯分布的参数估计;陈金广等[15]假设系统过程噪声方差和量测噪声方差之间的函数关系已知,利用假设的函数关系获得新的过程噪声方差,配合变分贝叶斯学习进行多次迭代,以得到最优状态估计.
随着变分贝叶斯方法的成熟,应用领域逐渐拓宽,近年来,在处理组合导航噪声自适应问题时发挥了很大的作用. 沈忱等[7]针对SINS/GPS组合导航的线性模型提出并且推导了基于变分贝叶斯学习的自适应卡尔曼滤波算法,消除了时变噪声对卡尔曼滤波方法的影响;郝燕玲等[16]针对SINS/GPS组合导航中量测噪声统计特性不准确引起卡尔曼滤波精度下降的问题,提出基于变分贝叶斯自适应无迹卡尔曼滤波(variational Bayesian unscented Kalman filtering, VB-UKF)的非线性融合方法;Li等[17]提出了强跟踪容积卡尔曼滤波(strong tracking cubature Kalman filtering, STCKF)方法,使得在非线性SINS/GPS组合导航系统中数值计算多变量矩的积分成为可能;徐健等[18]提出基于变分贝叶斯的平方根容积卡尔曼滤波算法,并且用于水下无人航行器(unmanned underwater vehicle, UUV)的航位推算导航方法(dead reckoning, DR)和水下应答器(underwater transponder, UTP)组合导航系统中.
在实际问题中,GPS用户接收器会受到来自各方的噪声和干扰,观测噪声存在野值,导致噪声分布表现出厚尾特性,比如闪烁噪声通常为厚尾的非高斯分布[19]. 直接使用上述滤波方法会导致算法性能降低,滤波精度大幅下降. 为了处理具有厚尾特性的非高斯噪声,Zhu等[19]和Piche等[20]提出用T分布来近似观测噪声分布,T分布相比高斯分布具有厚尾特性可以使滤波算法对野值的敏感度降低,提高滤波精度,当较多野值出现时,能够很好地进行噪声跟踪.
设计针对GPS/SINS组合导航模型的滤波器,以T分布模拟观测噪声分布,使用变分贝叶斯学习和高斯滤波算法解决噪声为T分布的状态估计问题. 提出针对SINS/GPS组合导航系统的变分贝叶斯高斯滤波(variational Bayesian Gaussian filtering, VBGF)算法,并且通过仿真实验与传统算法进行对比,验证算法在处理野值问题上的有效性.
1 T分布和组合导航模型 1.1 T分布T分布相较于高斯分布具有厚尾特性,对野值的包容度较高,概率密度函数为
| $S({ v}\left| {{ \mu} ,{{\varLambda}} } \right.,\lambda ) \propto {\left[ {1 + \frac{1}{\lambda}{{({ v} - { \mu} )}^{\rm{T}}}{{\varLambda}} ({ v} - { \mu} )} \right]^{ - \displaystyle ({{d{\rm{ + }}\lambda }})/{{\rm{2}}}}}. $ | (1) |
式中:
T分布尾的厚度由
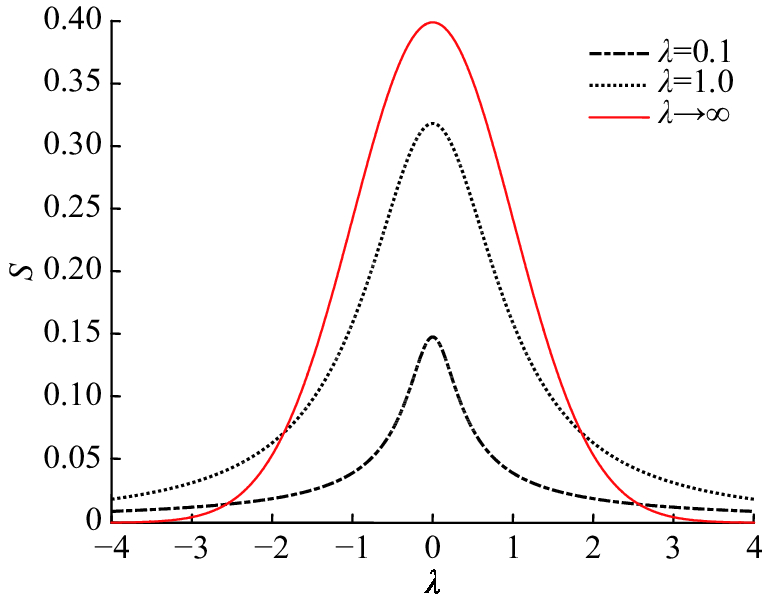
|
图 1
T分布概率密度函数随
|
由于T分布的最大似然估计很难得到闭式解,通常将T分布看作多个相同均值的高斯分布的积分:
| $S({ v}\left| {{ \mu} ,{{\varLambda}} } \right.,\lambda ) = \int_0^\infty {N({ v}{{\left| {{ \mu} ,\left({u}{{\varLambda}} \right)} \right.}^{ - 1}})} \,{\rm Gamma}\;\left({u}\left| {\frac{\lambda }{2},\frac{\lambda }{2}} \right.\right){\rm{d}}{ u}. $ | (2) |
式中:
研究对象为零输入、线性离散时间的SINS/GPS 组合导航系统,模型通常表述为
| $\left. \begin{array}{l}{{ x}_k} = {{ \varPhi} _k}{{ x}_{k - 1}} + {{ w}_k},\\{{ z}_k} = {{ H}_k}{{ x}_k} + {{ v}_k}. \end{array} \right\}$ | (3) |
式中:
| $\begin{split}{{{x}}_k} =& [{\varphi _{\rm E}},{\varphi _{\rm N}},{\varphi _{\rm U}},\Delta {v_{\rm E}},\Delta {v_{\rm N}},\Delta {v_{\rm U}},\Delta \sigma ,\Delta L,\Delta h,\\&{\varepsilon _{{\rm b}{\rm E}}},{\varepsilon _{{\rm b}{\rm N}}},{\varepsilon _{{\rm b}{\rm U}}},\;{\nabla _{{\rm b}{\rm E}}},{\nabla _{{\rm b}{\rm N}}},{\nabla _{{\rm b}{\rm U}}}]{\rm ^T}.\end{split}$ | (4) |
式中:E、N、U表示东北天3个方向,
观测向量
| ${{ z}_k} = [{{ \sigma} _{\rm G}} - {{ \sigma} _{\rm S}},{L_{\rm G}} - {L_{\rm S}},{h_{\rm G}} - {h_{\rm S}}]. $ | (5) |
式中:σ、L、h分别表示纬度、经度和高度.
使用T分布来模拟噪声分布,噪声模型的后验概率密度可以表示为
| $p(\left. {{{ z}_k}} \right|{{ H}_k}{{ x}_k},{{\varLambda}_k} ,\lambda ) = S(\left. {{{ z}_k}} \right|{{ H}_k}{{ x}_k},{{\varLambda}_k} ,\lambda ). $ | (6) |
根据式(2),引入自举变量
| $\left.\begin{array}{l}p\left(\left. {{{ z}_k}} \right|{{ H}_k}{{ x}_k},{{\varLambda}_k} ,{{u}_k}) = N(\left. {{{ z}_k}} \right|{{ H}_k}{{ x}_k},{({{u}_k}{{\varLambda}_k} )^{ - 1}}\right),\\p(\left. {{{u}_k}} \right|\lambda ) = {\rm Gamma}\left(\left. {{{u}_k}} \right|\displaystyle\frac{\lambda }{2},\displaystyle\frac{\lambda }{2}\right).\end{array}\right\}$ | (7) |
依据文献[19]的计算方法,噪声模型的联合概率密度可以表示为
| $p({{{z}}_k},{{{x}}_k},{{{u}}_k},{{\varLambda}_k} ) = p(\left. {{{{z}}_k}} \right|{{{x}}_k},{{{u}}_k},{{\varLambda}_k} )p(\left. {{{{x}}_k}} \right|{{{z}}_{1:k - 1}})p(\left. {{{{u}}_k}} \right|\lambda ). $ | (8) |
式中:
针对上述组合导航模型,选择系统状态量
| $p( \varPsi \left| {{{{z}}_{1:k}}} \right.) = \frac{{p( \varPsi ,{{{z}}_k})}}{{p({{{z}}_{1:k}})}}{\rm{ = }}\frac{{p(\left. {{{{z}}_k}} \right| \varPsi ,{{{z}}_{1:k - 1}})p(\left. \varPsi \right|{{{z}}_{1:k - 1}})}}{{p(\left. {{{{z}}_k}} \right|{{{z}}_{1:k - 1}})}}. $ | (9) |
式中:
| $p( \varPsi \left| {{{ z}_{1:k}}} \right.){\rm{ = }}\frac{{p(\left. {{{ z}_k}} \right| \varPsi )p( \varPsi ,{{ z}_{1:k - 1}})}}{{p(\left. {{{ z}_k}} \right|{{ z}_{1:k - 1}})}}. $ | (10) |
变分贝叶斯方法可以看作最大期望方法的延伸,采用极大后验估计,核心观点是使用新的函数
| $\ln \;q( \varPsi ){\rm{ = }}\frac{{\ln \;\left[p(\left. {{{{z}}_k}} \right| \varPsi )p( \varPsi ,{{ z}_{1:k - 1}})\right]}}{{\ln p(\left. {{{ z}_k}} \right|{{ z}_{1:k - 1}})}}. $ | (11) |
式中:
| $q( \varPsi ){\rm{ = }}q({{ x}_k})q({{u}_k}). $ | (12) |
得到参数的估计的重点是求取式(10)中分母的值,也称为边缘似然函数或证据. 依据Beal[5]的计算,边缘似然函数可以表示为
| $\ln p(\left. {{{{z}}_k}} \right|{{{z}}_{1:k - 1}}) = F\left[ {q( \varPsi )} \right] + {D_{{\rm KL}}}\left[ {\left. {q( \varPsi )} \right\|p(\left. \varPsi \right|{{ {{z}}}_{1:k}})} \right].$ | (13) |
式中:
| $F\left[ {q( \varPsi )} \right] = \int {q( \varPsi )} \log \frac{{p(\left. {{{ z}_k}} \right| \varPsi )p(\left. \varPsi \right|{{ z}_{1:k - 1}})}}{{q( \varPsi )}}{\rm d} \varPsi .$ | (14) |
| ${D_{{\rm KL}}}\left[ {\left. {q( \varPsi )} \right\|p(\left. \varPsi \right|{{ z}_{1:k}})} \right] = \int {q( \varPsi )} \log \frac{{q( \varPsi )}}{{p(\left. \varPsi \right|{{ z}_{1:k}})}}{\rm d} \varPsi . $ | (15) |
当KL散度达到最小值0时,
| $\ln q({ \varPsi _i}) \propto {E_{{ \varPsi _i}}}\left[ {\ln p(\left. {{{ z}_k}} \right| \varPsi )p(\left. \varPsi \right|{{ z}_{1:k - 1}})} \right].$ | (16) |
式中:
根据式(8)可知,zk和
| $\begin{split}\ln p&(\left. {{{{z}}_k}} \right| \varPsi )p(\left. \varPsi \right|{{{z}}_{1:k - 1}}) = \ln p(\left. {{{{z}}_k}} \right|{{{x}}_k},{{{u}}_k},{{\varLambda}_k} ){\rm{ + }}\\&\ln p(\left. {{{{x}}_k}} \right|{{{z}}_{1:k - 1}}) + \ln p(\left. {{{{u}}_k}} \right|\lambda ).\end{split}$ | (17) |
由Beal[5]的证明可知,如果在共轭指数函数分布域(conjugate-exponential family,CE)内选取合适的待估计参数的先验分布,近似得到的新分布与先验分布是同样的形式,只是参数有所变化,对比先验分布可以得到新的分布相关参数的表达式[7]. 由于变量
依据式(15)和(16)可知,对
| $\begin{split}&\ln q({{u}_k}) \propto {E_{{{ x}_k}}}\left[ {\ln p(\left. {{{ z}_k}} \right| \varPsi )p(\left. \varPsi \right|{{ z}_{1:k - 1}})} \right] \propto {E_{{{ x}_k}}}\\ &\left[ {\ln p(\left. {{{ z}_k}} \right|{ H}{{ x}_k},{{u}_k},{{\varLambda}_k} )} \right] + \ln p(\left. {{{u}_k}} \right|\lambda ) \propto {E_{{{ x}_k}}}\\ &\ln \left[ {N(\left. {{{ z}_k}} \right|{ H}{{ x}_k},{{({{u}_k}{{\varLambda}_k} )}^{ - 1}})} \right]\;\; + {\rm Gamma}\left(\left. {{{u}_k}} \right|\displaystyle\frac{\lambda }{2},\displaystyle\frac{\lambda }{2}\right)\\ &\propto \left(\displaystyle\frac{{\lambda + d}}{2} - 1\right)\ln {{u}_k} - \displaystyle\frac{{\lambda + {{\bar \gamma }_k}}}{2}{{u}_k}.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\end{split}$ | (18) |
式中:d为观测向量的维数.
| $\begin{split}{{\bar \gamma }_k}{\rm{ = }}&{E_{ x}}\left[ {{{({{ z}_k} - { H}{{ x}_k})}^{\rm T}}{{\varLambda}_k} ({{ z}_k} - { H}{{ x}_k})} \right]=\\ &{\rm{Trace}}\left[ {{E_{ x}}({{ z}_k} - { H}{{ x}_k}){{({{ z}_k} - { H}{{ x}_k})}^{\rm T}}{{\varLambda}_k} } \right].\end{split}$ | (19) |
| $q({{u}_k}) \sim {\rm Gamma}\left(\frac{{\lambda + d}}{2},\frac{{\lambda + {{\bar \gamma }_k}}}{2}\right).$ | (20) |
所以,自举变量
| ${\bar u_k}{\rm{ = }}\frac{{\lambda + d}}{{\lambda + {{\bar \gamma }_k}}}. $ | (21) |
同理,
| $\begin{aligned}\ln &q({{ x}_k}) \propto {E_{{{u}_k}}}\left[ {\ln p(\left. {{{ z}_k}} \right| \varPsi )p(\left. \varPsi \right|{{ z}_{1:k - 1}})} \right]\\&\propto {E_{{{ u}_k}}}\left[ {\ln p(\left. {{{ z}_k}} \right|{ H}{{ x}_k},{{u}_k},{{\varLambda}_k} )} \right] + \ln p(\left. {{{ x}_k}} \right|{{ z}_{1:k - 1}})\\ & \propto {E_{{{ x}_k}}}\ln \left[ {N(\left. {{{ z}_k}} \right|{ H}{{ x}_k},{{({{u}_k}{{\varLambda}_k} )}^{ - 1}})} \right] + N\left(\left. {{{ x}_k}} \right|{ x}_k^ - ,{{P}}_k^ - \right)\\& \propto - \displaystyle\frac{1}{2}{{\bar {u}}_k}{({{ z}_k} - { H}{{ x}_k})^{\rm T}}{{\varLambda}_k} ({{ z}_k} - { H}{{ x}_k}) - \\&\displaystyle\frac{1}{2}{\left({{ x}_k} - { x}_k^ - \right)^{\rm T}}{\left({{P}}_k^ - \right)^{ - 1}}\left({{ x}_k} - { x}_k^ - \right).\quad\quad\quad\quad\;\;\;\,\quad\quad\quad\quad(22)\end{aligned}$ |
输入:初始状态
输出:
开始:
预测:
更新:
循环
结束
结束
3 实 验为了验证所提出VBGF方法的有效性,将VBGF算法、经典卡尔曼(Kalman filtering, KF)滤波方法和沈忱等[7]提出的变分贝叶斯自适应滤波(variational Bayesian adaptive Kalman fitering, VBAKF)算法的滤波效果进行比较,设置2组对比实验. 实验1为噪声不存在野值,当满足高斯分布时,上述3种算法滤波效果对比;实验2为噪声存在野值,当不满足高斯分布时,上述3种算法滤波效果对比.
仿真实验以1.2节中给出的GPS/SINS组合导航系统为模型,在MATLAB环境下依据飞行动力学仿真飞行器的理想飞行轨迹,并生成相应的飞行数据. 飞行器理想运动轨迹如图2所示. 实验中将位置初值设置为纬度45°,经度120°,高度300 m,飞行器速度、加速度、姿态角和姿态角变化率均为0.
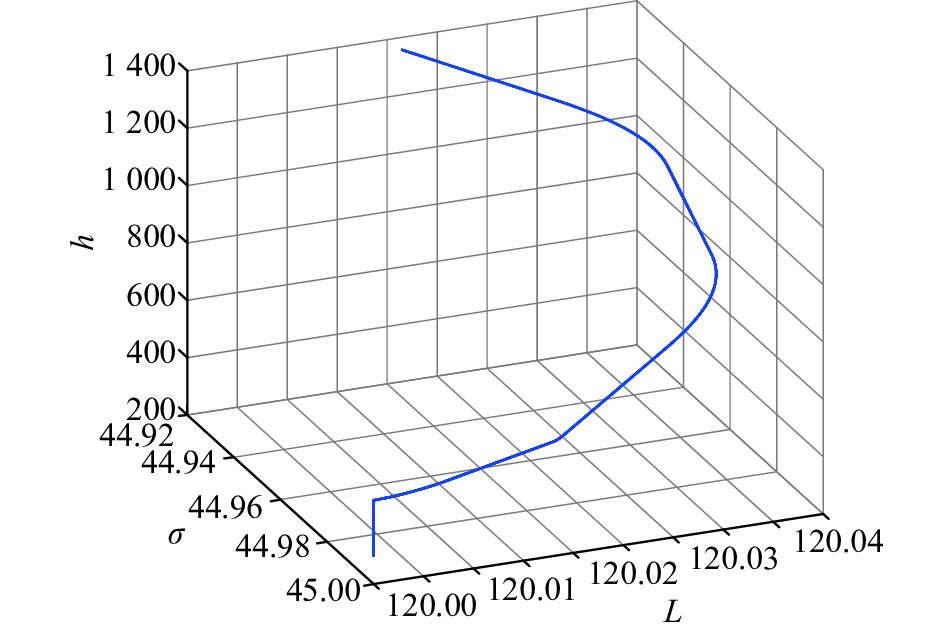
|
图 2 Matlab环境下飞行器的理想运动轨迹 Fig. 2 The ideal trajectory of aircraft in Matlab |
对比实验设定噪声方差
| ${{P}_0}(1,{\rm{1) = }}{{{P}}_{\rm{0}}}{\rm{(2,2) = }}{{{P}}_{\rm{0}}}{\rm{(3,3)}} = {\left( {\frac{{\rm{\pi }}}{{{\rm{180}}}}} \right)^{\rm{2}}},$ | (23) |
| ${{{P}}_{\rm{0}}}{\rm{(4,4) = }}{{{P}}_{\rm{0}}}{\rm{(5,5) = }}{{{P}}_{\rm{0}}}{\rm{(6,6) = 0}}{\rm{.}}{{\rm{1}}^{\rm{2}}},$ | (24) |
| ${{{P}}_{\rm{0}}}{\rm{(7,7) = }}{\left( {\frac{{{\rm{10}}}}{{{{R}_{\rm{e}}}}}} \right)^{\rm{2}}},$ | (25) |
| ${{{P}}_{\rm{0}}}{\rm{(8,8) = }}{\left( {\frac{{{\rm{10}}}}{{{{R}_{\rm{e}}}}}} \right)^{\rm{2}}},$ | (26) |
| ${{{P}}_{\rm{0}}}{\rm{(9,9) = 1}}{{\rm{0}}^{\rm{2}}},$ | (27) |
| ${{{P}}_{\rm{0}}}{\rm{(10,10) = }}{{{P}}_{\rm{0}}}{\rm{(11,11) = }}{{{P}}_{\rm{0}}}{\rm{(12,12) = }}{\left( {\frac{{{\rm{0}}{\rm{.1\pi }}}}{{{\rm{180 \times 3600}}}}} \right)^{\rm{2}}},$ | (28) |
| ${{{P}}_{\rm{0}}}{\rm{(13,13) = }}{{{P}}_{\rm{0}}}{\rm{(14,14) = }}{{{P}}_{\rm{0}}}{\rm{(15,15) = }}{\left( {{{g}_{\rm{0}}}{\rm{ \times 1}}{{\rm{0}}^{{\rm{ - 3}}}}} \right)^{\rm{2}}}.$ | (29) |
式中:地球半径
| ${{Q}_{\rm{t}}}{\rm{(1,1) = }}{{Q}_{\rm{t}}}{\rm{(2,2) = }}{{Q}_{\rm{t}}}{\rm{(3,3) = 8}}{\rm{.462 \times 1}}{{\rm{0}}^{{\rm{ - 14}}}},$ | (30) |
| ${{Q}_{\rm{t}}}{\rm{(4,4) = }}{{Q}_{\rm{t}}}{\rm{(5,5) = }}{{Q}_{\rm{t}}}{\rm{(6,6) = 9}}{\rm{.566 \times 1}}{{\rm{0}}^{{\rm{ - 9}}}}.$ | (31) |
其余元素全为零.
VBGF初始参数为
| $x_k^{{\rm{mean}}} = \frac{1}{{100}}\sum\limits_{i = 1}^{100} {({x_k} - \hat x_k^i)} ,$ | (32) |
| $x_k^{{\rm{rmse}}} = \sqrt {\frac{1}{{100}}\sum\limits_{i = 1}^{100} {{{({x_k} - \hat x_k^i)}^2}} } . $ | (33) |
式中:
图3和4分别表示上述3种算法在100次蒙特卡洛实验中所得位置估计误差的均值和均方根对比. 图中X1为纬度误差,X2为经度误差,X3为高度误差,t为时间. 当噪声不存在野值且满足高斯分布时,KF算法滤波精度很高,VBGF算法和VBAKF算法均能达到与KF算法精度相似的滤波效果.
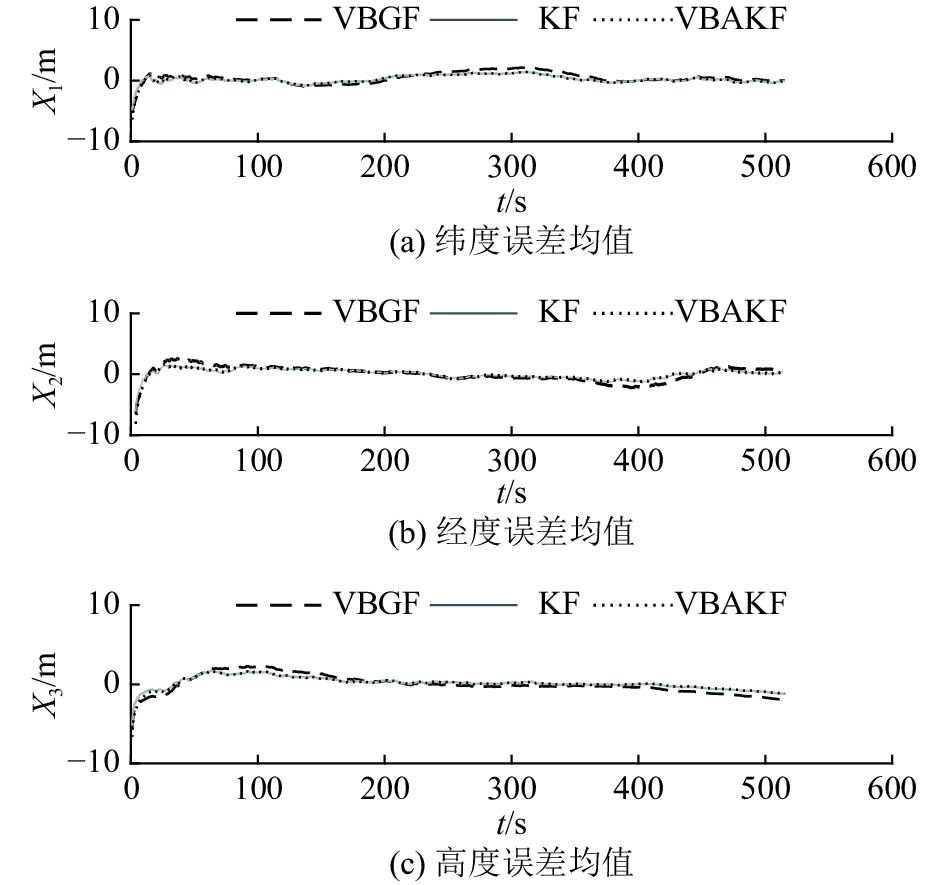
|
图 3 不存在野值的高斯噪声环境下VBGF、KF、VBAKF算法位置误差均值 Fig. 3 Mean error of position estimation of VBGF, KF and VBAKF in Gaussian noise environment without outliers |
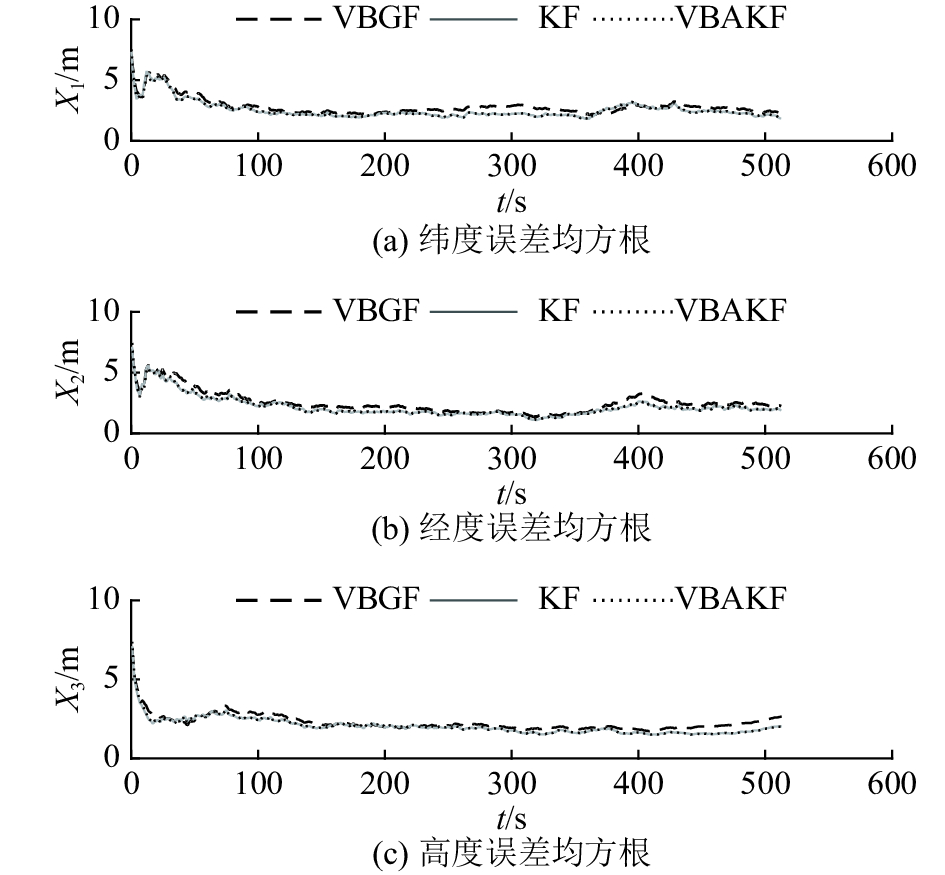
|
图 4 不存在野值的高斯噪声环境下VBGF、KF、VBAKF算法位置误差均方根 Fig. 4 Root mean square error of position estimation of VBGF, KF and VBAKF in Gaussian noise environment without outliers |
为了更直观地表现三者的滤波精度,求取高斯噪声下KF、VBAKF、VBGF 3种算法的均值误差和均方根误差,如表1所示.
| 表 1 高斯噪声下3种算法的均值误差和均方根误差 Table 1 Mean and RSME of estimation error of three algorithms under Gaussian noise |
为了模拟带有野值的噪声,参考Zhu等[19]提出的方法将噪声设置为
| ${ v}\sim (1 - \rho )N(0,{{{\varSigma}} _n}) + \rho f.$ | (34) |
式中:噪声野值的分布为
图5和6分别表示3种算法位置估计误差的均值和均方根对比. 可以观察到,由于野值存在,KF和VBAKF算法的误差均方根明显增加,滤波精度大幅降低,但是VBGF算法并没有受到野值影响,仍然能够进行稳定高精度的滤波. 存在野值使得观测噪声出现厚尾特性,不服从高斯分布,但是KF和VBAKF算法仍然将噪声建模为高斯分布. KF算法将噪声方差设置为固定值,对于野值造成的噪声方差的波动没有适应能力,导致滤波精度降低;VBAKF算法虽然能够自适应改变噪声方差,但是很难弥补模型的局限性,随着野值增多,自适应跟踪噪声的能力急剧下降. 相比前两种算法,VBGF算法充分考虑噪声可能存在的厚尾特性,建模为T分布,通过变分贝叶斯迭代改变模型参数,消除野值的影响,能够保持整体滤波结果的稳定.
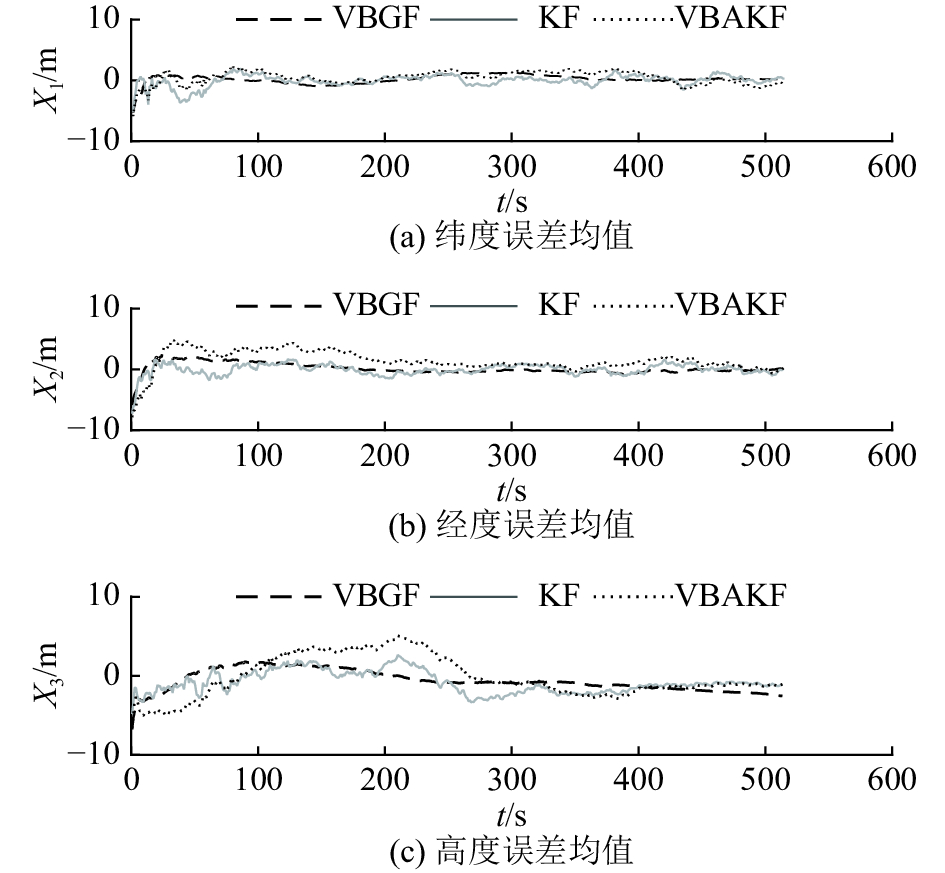
|
图 5 存在野值的非高斯噪声环境下VBGF、KF、VBAKF算法位置误差均值 Fig. 5 Mean error of position estimation of VBGF,KF and VBAKF in non-Gaussian noise environment with outliers |
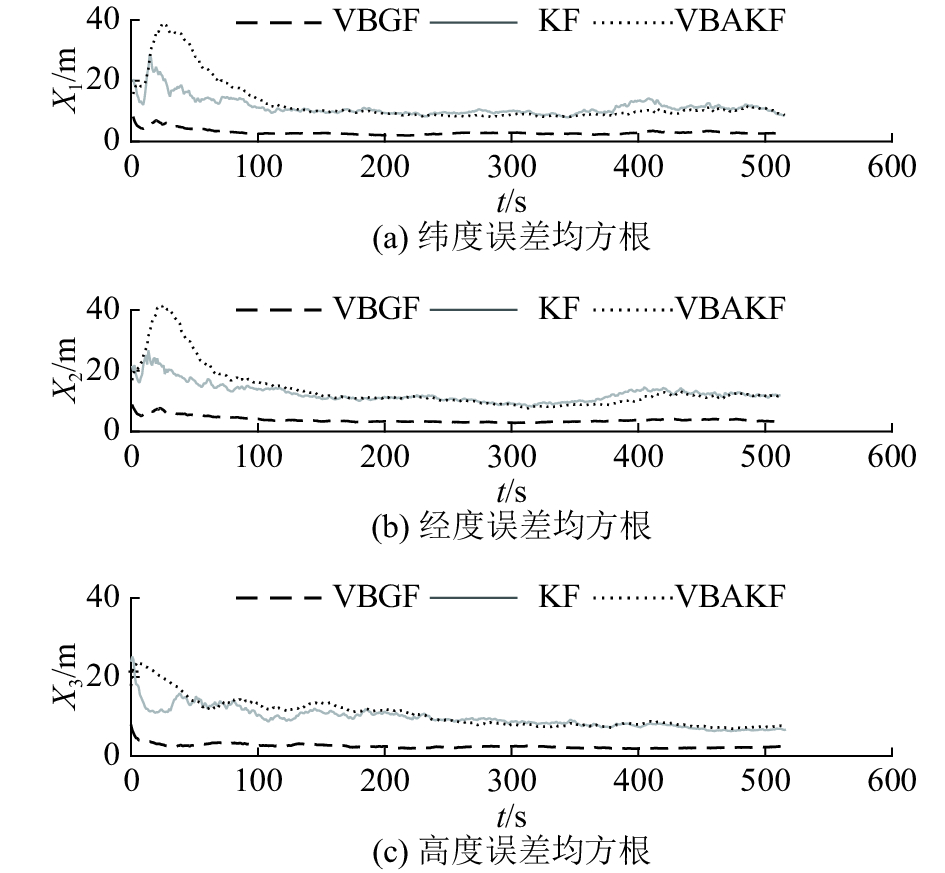
|
图 6 存在野值的非高斯噪声环境下VBGF、KF、VBAKF算法位置误差均方根 Fig. 6 Root mean square error of position estimation of VBGF,KF and VBAKF in non-Gaussian noise environment with outliers |
| 表 2 非高斯噪声下3种算法的均值误差和均方根误差 Table 2 Mean and RMSE of estimation error of three algorithms under non-Gaussian noise |
在实验2的噪声环境下,求取KF、VBAKF、VBGF 3种算法的均值误差和均方根误差,如表2所示.
4 结 语SINS/GPS组合导航系统在实际应用中面临噪声为非高斯分布并且存在野值的情况. 充分考虑野值导致的噪声厚尾特性,将观测噪声建模为T分布,针对SINS/GPS组合导航模型,提出基于T分布的变分贝叶斯高斯滤波算法. 算法利用变分贝叶斯方法对组合导航系统的状态和T分布参数的联合后验分布进行近似,当噪声存在野值时,能够实现对系统状态的鲁棒估计,相比传统组合导航滤波算法,可以实现更好的估计效果. 只讨论了SINS/GPS组合导航模型中量测噪声为厚尾分布时的滤波方法,仍然认为过程噪声服从高斯分布. 在实际应用中,过程噪声也可能因为系统扰动产生野值,呈现出厚尾的非高斯分布. 今后的研究方向倾向于研究新的鲁棒性Student-t滤波器以提高基础滤波器的估计精度.
| [1] |
秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理 [M]. 西安: 西北工业大学出版社, 2015: 3-4
|
| [2] |
DENG Z, ZHANG P, QI W, et al. Sequential covariance intersection fusion Kalman filter[J]. Information Sciences, 2012, 189: 293-309. DOI:10.1016/j.ins.2011.11.038 |
| [3] |
GAO J B, HARRIS C J. Some remarks on Kalman filters for the multisensor fusion[J]. Information Fusion, 2002, 3(3): 191-201. DOI:10.1016/S1566-2535(02)00070-2 |
| [4] |
HEWER G A, MARTIN R D, ZEH J. Robust preprocessing for Kalman filtering of glint noise[J]. IEEE Transactions on Aerospace and Electronic Systems, 1987(1): 120-128. |
| [5] |
BEAL M J. Variational algorithms for approximate Bayesian inference [M]. London: University of London, 2003: 53-70
|
| [6] |
ATTIAS H. Inferring parameters and structure of latent variable models by variational Bayes [C] // Proceedings of the Fifteenth Conference on Uncertainty in Artificial Intelligence. San Francisco: Morgan Kaufmann Publishers Inc., 1999: 21-30 http://ci.nii.ac.jp/naid/10021200959
|
| [7] |
沈忱, 徐定杰, 沈锋, 等. GPS/INS 组合导航的变分贝叶斯自适应卡尔曼滤波[J]. 哈尔滨工业大学学报, 2014, 46(5): 59-65. SHEN Chen, XU Ding-jie, SHEN Feng, et al. Variational Bayesian adaptive Kalman filtering for GPS/INS integrated navigation[J]. Journal of Harbin Institute of Technology, 2014, 46(5): 59-65. |
| [8] |
SARKKA S, NUMMENMAA A. Recursive noise adaptive Kalman filtering by variational Bayesian approximations[J]. IEEE Transactions on Automatic Control, 2009, 54(3): 596-600. DOI:10.1109/TAC.2008.2008348 |
| [9] |
DONG P, JING Z, LEUNG H, et al. Variational Bayesian adaptive cubature information filter based on wishart distribution[J]. IEEE Transactions on Automatic Control, 2017, 62(11): 6051-6057. DOI:10.1109/TAC.2017.2704442 |
| [10] |
LI K, CHAGN L, HU B. A variational Bayesian-based unscented Kalman filter with both adaptivity and robustness[J]. IEEE Sensors Journal, 2016, 16(18): 6966-6976. DOI:10.1109/JSEN.2016.2591260 |
| [11] |
MOHAMMED B, TOUFIK B. Joint variational Bayesian extended Kalman filter for the estimation of the metabolic/hemodynamic model [C] // 2015 4th International Conference on Electrical Engineering (ICEE). Boumerdes: IEEE, 2015: 1-6
|
| [12] |
FENG P, WANG W, NAQVI S M, et al. Variational Bayesian PHD filter with deep learning network updating for multiple human tracking [C] // 2015 Sensor Signal Processing for Defence (SSPD). Edinburgh: IEEE, 2015: 1-5 http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7288526
|
| [13] |
沈锋, 徐广辉, 桑靖. 一种自适应变分贝叶斯容积卡尔曼滤波方法[J]. 电机与控制学报, 2015, 19(4): 94-99. SHEN Feng, XU Guang-hui, SANG Jing. Adaptive variational Bayesian cubature Kalman filtering[J]. Electric Machines and Control, 2015, 19(4): 94-99. |
| [14] |
徐定杰, 沈忱, 沈锋. 混合高斯分布的变分贝叶斯学习参数估计[J]. 上海交通大学学报, 2013, 47(7): 1119-1125. XU Ding-jie, SHEN Chen, SHEN Feng. Variational Bayesian learning for parameter estimation of mixture of Gaussians[J]. Journal of Shanghai Jiao Tong University, 2013, 47(7): 1119-1125. |
| [15] |
陈金广, 李洁, 高新波. 双重迭代变分贝叶斯自适应卡尔曼滤波算法[J]. 电子科技大学学报, 2012, 41(3): 359-363. CHEN Jin-guang, LI Jie, GAO Xin-bo. Dual recursive variational Bayesian adaptive Kalman filtering algorithm[J]. Journal of University of Electronic Science and Technology of China, 2012, 41(3): 359-363. DOI:10.3969/j.issn.1001-0548.2012.03.006 |
| [16] |
郝燕玲, 张召友. 基于VB-UKF的SINS/GPS自适应融合技术[J]. 华中科技大学学报: 自然科学版, 2012, 40(1): 54-57. HAO Yan-ling, ZHANG Zhao-you. Adaptive fusion technology for SINS/GPS based on VB-UKF[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2012, 40(1): 54-57. |
| [17] |
LI Q, SUN F. Strong tracking cubature Kalman filter algorithm for GPS/INS integrated navigation system [C] // 2013 IEEE International Conference on Mechatronics and Automation. Takamatsu: IEEE, 2013: 1113-1117 http://europepmc.org/abstract/MED/29895815
|
| [18] |
徐健, 宋晓萍, 张宏瀚, 等. 基于变分贝叶斯的DR/UTP组合导航滤波方法[J]. 仪器仪表学报, 2016, 37(12): 2743-2749. XU Jian, SONG Xiao-ping, ZHANG Hong-han, et al. DR/UTP integrated navigation based on variational Bayes[J]. Chinese Journal of Scientific Instrument, 2016, 37(12): 2743-2749. |
| [19] |
ZHU H, LEUNG H, HE Z. A variational Bayesian approach to robust sensor fusion based on Student-t distribution[J]. Information Sciences, 2013, 221: 201-214. DOI:10.1016/j.ins.2012.09.017 |
| [20] |
PICHE R, SARKKA S, HARTIKAINEN J. Recursive outlier-robust filtering and smoothing for nonlinear systems using the multivariate Student-t distribution [C] // 2012 IEEE International Workshop on Machine Learning for Signal Processing. Santander: IEEE, 2012: 1-6 http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.298.183
|



