2. 中船重工第 709 研究所,湖北 武汉 430074
2. 709th Research Institute of China Shipbuilding Industry Corporation, Wuhan 430074, China
自主水下机器人(autonomous underwater vehicle, AUV)精确的路径跟踪能力是其作业任务(海洋地图测绘、水下工程检查)以及自身安全避障的重要技术保障[1-4]. 深海环境极其复杂、具有不可预知性,AUV高度自治并且自身携带的动力能源有限,因此为了保证AUV在有限的动力能源下安全航行并且高效地完成水下作业任务,针对AUV路径跟踪技术的研究是十分关键的[5-7]. AUV水平面运动是指AUV保持在某一固定深度航行,重心在水平面内运动. 当AUV实际航行时,受到风、浪、流等环境因素的影响,运动控制系统是一个带有不确定性的、耦合的典型非线性系统.
近年来,计算机技术的飞速发展及其在控制系统中的广泛应用使得适用于计算机系统的离散控制算法的研究得到了学者们的高度关注. 由于离散非线性系统理论的不完善性和复杂性,AUV控制问题的研究较少. AUV离散系统水平面路径跟踪控制的研究一般考虑以下3个问题. 1) AUV动力学的强非线性和不确定性. 在 AUV路径跟踪控制问题中,当运动速度和航行环境发生改变,AUV所受到的科里奥利向心力、水动力阻力和升力随之发生改变,造成AUV动力学模型的非线性和不确定性. 这就需要考虑系统的鲁棒性,并且采用更符合模型特点的非线性控制方法来研究. 自适应控制对处理模型参数不确定问题效果显著[8],神经网络具有任意逼近非线性函数的特点,因此基于神经网络的自适应控制算法是一种有效的控制方法[9-13]. 在AUV控制系统中,Qi等[14-17]利用神经网络技术对不确定非线性部分进行重构,进而通过网络参数的自适应学习,使得所设计的控制器具有较强的自适应性和鲁棒性等优点,但是以上研究都是针对AUV连续系统进行的. 2) 仅采用AUV的位置和姿态角量测信息进行控制,即采用输出反馈控制方法[18-21]. 与全状态反馈控制方法相比,输出反馈控制对减轻AUV重量、节约成本以及减少测量装置过多带来的测量误差和测量噪声等因素的影响有很好的作用. 3)AUV离散系统的稳定性分析. 离散非线性系统本身具有复杂性,理论体系不完善并且可用的数学工具不多,都为AUV的控制器设计带来很大的难度[22-23].
针对上述AUV离散系统水平面路径跟踪控制过程中需要解决的问题,提出了一种神经网络自适应输出动态反馈控制算法. 为了提高控制性能设计了一个动态反馈控制器镇定AUV离散误差动态系统线性部分. 对于AUV系统中的不确定非线性函数,利用神经网络理论对其重构. 设计一个鲁棒控制器来抑制重构误差及外界干扰,以提高系统鲁棒性. 最后基于离散Lyapunov理论分析跟踪误差系统的稳定性,并保证误差系统中的信号是最终一致有界的.
1 问题描述 1.1 AUV连续系统水平面模型AUV水平面三自由度(3-DOF)运动模型表示为
| $\left. \begin{array}{l}{\dot{ \eta }} = { J}\left( {{\eta }} \right){{\nu }},\\{{M}}{\dot{ \nu }} + {{C}}\left( {{ \nu }} \right){{ \nu }} + {{D}}\left( {{ \nu }} \right){{ \nu }} + { g}\left( {{\eta }} \right) + {{{\tau }}_{\rm d}} = {{\tau }}.\end{array}\right\} $ | (1) |
式中:
| ${ J}\left( {{\eta }} \right) = \left[ {\begin{array}{*{20}{c}} {\cos \psi }&{ - \sin \psi }&0 \\ {\sin \psi }&{\cos \psi }&0 \\ 0&0&1 \end{array}} \right].$ |
对AUV模型 (1)进行坐标变换. 对于光滑的期望,轨迹
| $\left.\begin{array}{l}{{\dot {\bar{ \xi}}_2}}= {{{\bar{ \xi }}}_2},\\{{\dot {\bar { \xi }}}_2} = \bar { f}\left( {{{{\bar{ \xi }}}_1},{{{\bar{ \xi }}}_2}} \right) + { J}\left( {{{{\bar{ \xi }}}_1}} \right){{{M}}^{ - 1}}\left( {{{\tau }} - {{{\tau }} _{\rm d}}} \right).\end{array} \right\}$ | (2) |
式中:
| $\begin{aligned} \bar { f}&\left( {{{{\bar{ \xi }}}_1},{{{\bar{ \xi }}}_2}} \right) = { J}\left( {{{{\bar{ \xi }}}_1}} \right){{ J}^{ - 1}}\left( {{{{\bar{ \xi }}}_1}} \right)\left( {{{{\bar{ \xi }}}_2} + {{{\dot{ \eta }}}_{\rm d}}} \right) + \\ &{ J}\left( {{{{\bar{ \xi }}}_1}} \right){{{M}}^{ - 1}}\left\{ - {{C}}\left[ {{{ J}^{ - 1}}\left( {{{{\bar{ \xi }}}_1}} \right)\left( {{{{\bar{ \xi }}}_2} + {{{\dot{ \eta }}}_{\rm d}}} \right)} \right]{{ J}^{ - 1}}\left( {{{{\bar{ \xi }}}_1}} \right)\left( {{{{\bar{ \xi }}}_2} + {{{\dot{ \eta }}}_{\rm d}}} \right) - \right. \\ & \left.{{D}}\left[ {{{ J}^{ - 1}}\left( {{{{\bar{ \xi }}}_1}} \right)\left( {{{{\bar{ \xi }}}_2} + {{{\dot{ \eta }}}_{\rm d}}} \right)} \right]{{ J}^{ - 1}}\left( {{{{\bar{ \xi }}}_1}} \right)\left( {{{{\bar{ \xi }}}_2} + {{{\dot{ \eta }}}_{\rm d}}} \right) - g\left( {{{{\bar{ \xi }}}_1}} \right)\right\} - {{{\ddot{ \eta }}}_{\rm d}}.\end{aligned}$ |
由于计算机技术的迅猛发展,动态系统的控制趋向数字控制方式. 在数字控制器上执行针对连续时间系统设计的控制算法时,受到采样时间的影响,一般很难达到满意的控制性能,甚至会出现离散化的系统不稳定的现象. 因此,在进行系统的控制设计时,建立系统的离散模型并直接对系统进行控制十分必要. 针对AUV水平面运动方程(2)建立离散模型,采用欧拉离散化方法,令
| ${\dot {\bar { \xi }}}\left( t \right) = {\left[{{\bar{ \xi }}}\left( {k + 1} \right)\right. -} {\left.{{\bar{ \xi }}\left( k \right)}\right]}/{T},$ |
离散化的AUV方程为
| $\left. \begin{aligned} & {{{\bar{ \xi }}}_1}\left( {k + 1} \right) = {{{\bar{ \xi }}}_1}\left( k \right) + T{{{\bar{ \xi }}}_2}\left( k \right), \\& {{{\bar{ \xi }}}_2}\left( {k + 1} \right) = {{{\bar{ \xi }}}_2}\left( k \right) + T\bar { f}\left( {{{{\bar{ \xi }}}_1}\left( k \right),{{{\bar{ \xi }}}_2}\left( k \right)} \right) + \\& \quad \quad \quad \quad \;\,T{ J}\left( {{{{\bar{ \xi }}}_1}\left( k \right)} \right){{{M}}^{ - 1}}\left[ {{{\tau }}\left( k \right) - {{{\tau }}_{\rm d}}\left( k \right)} \right]. \\ & \end{aligned} \right\}$ | (3) |
式中:T为采样时间.
下面对式(3)进行坐标变换. 令
| $ \begin{gathered} {{{\xi }}_1}\left( k \right) = {{{\bar{ \xi }}}_1}\left( k \right),\; {{{\xi }}_2}\left( k \right) = {{{\bar{ \xi }}}_1}\left( k \right) + T{{{\bar{ \xi }}}_2}\left( k \right). \end{gathered} $ | (4) |
令
| $\left. \begin{aligned}& {{{\xi }}_1}\left( {k + 1} \right) = {{{\xi }}_2}\left( k \right), \\& {{{\xi }}_2}\left( {k + 1} \right) = { f}\left( {{{\xi }}\left( k \right)} \right) + T{ J}\left( {{{{\xi }}_1}\left( k \right)} \right){{{M}}^{ - 1}}\left[ {{{\tau }}\left( k \right) - {{{\tau }}_{\rm d}}\left( k \right)} \right], \\& {{Y}}\left( k \right) = {{{\xi }}_1}\left( k \right). \\ \end{aligned} \right\}$ | (5) |
式中:
| $\begin{aligned}{ f}\left( {{{\xi }}\left( k \right)} \right) = & {T^{ - 1}}\left[ {{ J}\left( {{{{\xi }}_2}\left( k \right)} \right) - { J}\left( {{{{\xi }}_1}\left( k \right)} \right)} \right] \times \\ &{{ J}^{ - 1}}\left( {{{{\xi }}_1}\left( k \right)} \right)\left[ {{{{\xi }}_2}\left( k \right) - {{{\xi }}_1}\left( k \right)} \right] + { J}\left( {{{{\xi }}_1}\left( k \right)} \right){{{M}}^{ - 1}} \times \\ &\left\{ -{ C}\left[ {{{ J}^{ - 1}}\left( {{{{\xi }}_1}\left( k \right)} \right){T^{ - 1}}\left( {{{{\xi }}_2}\left( k \right) - {{{\xi }}_1}\left( k \right)} \right)} \right] \times \right.\\ &{{ J}^{ - 1}}\left( {{{{\xi }}_1}\left( k \right)} \right)\left( {{{{\xi }}_2}\left( k \right) - {{{\xi }}_1}\left( k \right)} \right) - \\ &{ D}\left[ {{{ J}^{ - 1}}\left( {{{{\xi }}_1}\left( k \right)} \right){T^{ - 1}}\left( {{{{\xi }}_2}\left( k \right) - {{{\xi }}_1}\left( k \right)} \right)} \right] \times \\ &\left.{{ J}^{ - 1}}\left( {{{{\xi }}_1}\left( k \right)} \right)\left( {{{{\xi }}_2}\left( k \right) - {{{\xi }}_1}\left( k \right)} \right) - { g}\left( {{{{\xi }}_1}\left( k \right)} \right)\right\} + {{{\xi }}_2}\left( k \right).\end{aligned}$ |
由于外界环境的影响,非线性函数
根据系统(5),控制器可以设计为
| ${{\tau }}\left( k \right) = {T^{ - 1}}{{M}}{{{J}}^{ - 1}} {{{{\xi }}_1}\left( k \right)} \left( {{{{u}}_1}\left( k \right) - {{{u}}_2}\left( k \right) + {{{u}}_3}\left( k \right)} \right).$ | (6) |
式中:
| $\left. \begin{array}{l}{{\zeta }}\left( {k + 1} \right) = {{{A}}_{\rm d}}{{\zeta}} \left( k \right) + {{{B}}_{\rm d}}{{{\xi}} _1}\left( k \right),\\{{{u}}_1}\left( k \right) = {{{C}}_{\rm d}}{{\zeta }}\left( k \right) + {{{D}}_{\rm d}}{{{\xi }}_1}\left( k \right).\end{array} \right\}$ | (7) |
并且u1(k)镇定下面的系统:
| $\left. \begin{array}{l}{{{\xi }}_1}\left( {k + 1} \right) = {{{\xi }}_2}\left( k \right),\\{{{\xi }}_2}\left( {k + 1} \right) = {{{u}}_1}\left( k \right).\end{array}\right\}$ | (8) |
其中,
| $\left. \begin{array}{l}{{{\xi }}_1}\left( {k + 1} \right) = {{{\xi }}_2}\left( k \right),\\{{{\xi }}_2}\left( {k + 1} \right) = {{{C}}_{\rm d}}{{\zeta }}\left( k \right) + {{{D}}_{\rm d}}{{{\xi }}_1}\left( k \right),\\{{\zeta }}\left( {k + 1} \right) = {{{A}}_{\rm d}}{{\zeta }}\left( k \right) + {{{B}}_{\rm d}}{{{\xi }}_1}\left( k \right).\end{array} \right\}$ | (9) |
由于系统(9)的状态未知,采用观测器对状态进行观测. 定义
| ${{E}}\left( k \right) = {\left[ {\begin{array}{*{20}{c}} {{{{\xi }}_1}\left( k \right)},&{{{{\xi }}_2}\left( k \right)},&{{{\zeta }}\left( k \right)} \end{array}} \right]^{\rm{T}}},\quad\quad\quad\quad\quad\quad\quad\quad$ |
| ${{b}} = {\left[ {\begin{array}{*{20}{c}}\!\!\! {{{\bf 0}_{3 \times 3}}}, & {{{{I}}_{3 \times 3}}} ,& {{{\bf 0}_{3 \times 3}}} \!\!\! \end{array}} \right]^{\rm{T}}},\;{{Z}}\left( k \right) = {\left[ {\begin{array}{*{20}{c}}\!\!\! {{{{\xi }}_1}\left( k \right)} ,& {{{\zeta }}\left( k \right)} \!\!\! \end{array}} \right]^{\rm{T}}},$ |
| ${{A}} = \left[ {\begin{array}{*{20}{c}}\!\!\! {{{\bf {0}}_{3 \times 3}}}&{{{{I}}_{3 \times 3}}}&{{{\bf {0}}_{3 \times 3}}} \!\!\! \\ \!\!\! {{{{D}}_{\rm d}}}&{{{{0}}_{3 \times 3}}}&{{{{C}}_{\rm d}}} \!\!\! \\ \!\!\! {{{{B}}_{\rm d}}}&{{{\bf {0}}_{3 \times 3}}}&{{{{A}}_{\rm d}}} \!\!\! \end{array}} \right] , \; {{c}} = \left[ {\begin{array}{*{20}{c}} \!\!\! {{{{I}}_{3 \times 3}}}&{{{\bf {0}}_{3 \times 3}}}&{{{\bf {0}}_{3 \times 3}}} \!\!\! \\ \!\!\! {{{\bf {0}}_{3 \times 3}}}&{{{\bf {0}}_{3 \times 3}}}&{{{{I}}_{3 \times 3}}} \!\!\! \end{array}} \right].$ |
式中:
根据式(5)、(7)和(8),建立
| $\left. \begin{aligned}&{\begin{aligned}{{E}}\left( {k + 1} \right) = &{{AE}}\left( k \right) +{{b}}\left[ {{\rm{ }}{{f}}\left( k \right) - {{{u}}_2}\left( k \right) + {{{u}}_3}\left( k \right) - {{{\tau }}_{\rm d}}\left( k \right)} \right],\end{aligned}}\\&{{Z}}\left( k \right) = {{cE}}\left( k \right).\end{aligned} \right\}$ | (10) |
对式(10)设计全维状态观测器以实现对AUV位姿、速度的估计,观测器形式如下:
| $\left.\begin{array}{l}{\hat{ E}}\left( {k + 1} \right) = {{A}}{\hat{ E}}\left( k \right) + {\bar{ K}}{\tilde{ Z}}\left( k \right),\\{\hat{ Z}}\left( k \right) = {{c}}{\hat{ E}}\left( k \right).\end{array} \right\}$ | (11) |
式中:状态
定义
| $\begin{split}{\tilde{ E}}\left( {k + 1} \right) = &{\tilde{ A}}{\tilde{ E}}\left( k \right){\rm{ + }}\\ &{{b}}\left[ {{\rm{ }}{ f}\left( {{{\xi }}\left( k \right)} \right) - {{{u}}_2}\left( k \right) + {{{u}}_3}\left( k \right) - {{{\tau }}_{\rm d}}\left( k \right)} \right].\end{split}$ | (12) |
| ${ f}\left( {{{\xi }}\left( k \right)} \right) = {{{W}}^{\rm T}}\phi \left( {{{\xi }}\left( k \right)} \right) + {{\varepsilon }}\left( k \right).$ | (13) |
式中:
设计AUV的神经网络自适应控制器为
| ${{{u}}_2}\left( k \right) = {{\hat{ W}}^{\rm T}}\left( k \right)\phi \left( {{\hat{ \xi }}\left( k \right)} \right).$ | (14) |
式中:
| ${\hat{ W}}\left( {k + 1} \right) = {\hat{ W}}\left( k \right)\, - \left[ {\phi \left( k \right){{{\hat{ E}}}^{\rm T}}\left( k \right){{{A}}^{\rm T}}{{Pb}} + \mu {\hat{ W}}\left( k \right)} \right].$ | (15) |
式中:
定义
| $\left\|{ f}\left( {{{\xi }}\left( k \right)} \right) - {{{u}}_2}\left( k \right)\right\|\; \leqslant \left\| {{\tilde{ W}}\left( k \right)} \right\|\phi _{\rm M} + \sigma .$ | (16) |
式中:
由于神经网络逼近非线性函数产生了重构误差
| ${{{u}}_3}\left( K \right) = {K_{\tilde { y}}}{\tilde{ y}}\left( k \right).$ | (17) |
式中:
根据鲁棒控制器
| $\left\| {{{{u}}_3}\left( k \right) + {{\varepsilon }}\left( k \right) + {{{\tau }}_{\rm d}}\left( k \right)} \right\| \leqslant K{_{{\tilde y}}}\left\| {{{\tilde{ y}}}\left( k \right)} \right\| + \gamma ,$\quad\quad\quad | (18) |
| $\begin{split}\left\| {{ f}\left( k \right)} - {{{u}}_2}\left( k \right) + {{{u}}_3}\left( k \right) + {{{\tau}}_{\rm d}}\left( k \right) \right\| \leqslant \\{\phi _{\rm{M}}}\left\| {{\tilde{ W}}\left( k \right)} \right\| + K{_{{\tilde y}}}\left\| {{\tilde{ y}}\left( k \right)} \right\| + \gamma .\quad\end{split}$ | (19) |
利用离散Lyapunov稳定性理论,对AUV水平面跟踪误差系统(10)和观测误差系统(12)进行稳定性分析. 为表示方便,变量
假设1 假设存在矩阵
定理1 令假设1成立. 在条件(27)~(29)下,AUV水平面运动系统(5),在观测器(12)、自适应律(15)、控制器(7)和(14)和(17)的作用下,水平面AUV离散系统中的
证明 构造如下的Lyapunov函数(
则
| $\Delta { V}\left( k \right) = \Delta {{ V}_1}\left( k \right) + \Delta {{ V}_2}\left( k \right) + \displaystyle\frac{1}{\alpha }\Delta {{ V}_3}\left( k \right).$ |
式中:
| $\quad \Delta {{ V}_1}\left( k \right) = {{{E}}^{\rm T}}\left( {k + 1} \right){{PE}}\left( {k + 1} \right) - {{{E}}^{\rm T}}\left( k \right){{PE}}\left( k \right),$ | (20) |
| $\quad \Delta {{ V}_2}\left( k \right) = {{\tilde{ E}}^{\rm T}}\left( {k + 1} \right){\tilde{ P}}{\tilde{ E}}\left( {k + 1} \right) - {{\tilde{ E}}^{\rm T}}\left( k \right){\tilde{ P}}{\tilde{ E}}\left( k \right),$ | (21) |
| $ \Delta {{ V}_3}\left( k \right) = {\rm tr}\left[ {{{{\tilde{ W}}}^{\rm T}}\left( {k + 1} \right){\tilde{ W}}\left( {k + 1} \right) - {{{\tilde{ W}}}^{\rm T}}\left( k \right){\tilde{ W}}\left( k \right)} \right].$ | (22) |
根据式 (14) 和 (17)可知,一定存在向量
| ${{f}} - {{{u}}_2} + {{{u}}_3} - {{\tau }}_{\rm d}\leqslant{\tilde { W}^{\rm{T}}}\phi+K_{{\tilde y}}{\tilde { E}}+{{\hat\gamma }}.$ |
把式(10)代入式(20),可得
| $\begin{aligned}& \Delta {{ V}_1} = - {{{E}}^{\rm T}}{{QE}} + 2{{{E}}^{\rm T}}{{{A}}^{\rm T}}{{b}}\left[ {{\rm{ }}{{f}} - {{{u}}_2} + {{{u}}_3} - {{{\tau }}_{\rm d}}} \right] + \\ & {\left[ {{\rm{ }}{{f}} - {{{u}}_2} + {{{u}}_3} - {{{\tau }}_{\rm d}}} \right]^{\rm T}}{{{b}}^{\rm T}}{{Pb}}\left[ {{\rm{ }}{{f}} - {{{u}}_2} + {{{u}}_3} - {{{\tau }}_{\rm d}}} \right] \leqslant \\ & - {{{E}}^{\rm T}}{{QE}} + 2{\left( {{\hat{ E}} - {\tilde{ E}}} \right)^{\rm T}}{{{A}}^{\rm T}}{{Pb}}\left[ {{{{\tilde{ W}}}^{\rm T}}\phi\left({\hat{ \xi }}\right) + {K_{{\tilde y}}}{\tilde{ E}} +{{ \hat\gamma}}} \right] + \\ & \,\left\| {{{{b}}^{\rm T}}{{Pb}}} \right\|{\left[ {{\phi _{\rm{M}}}\left\| {{\tilde{ W}}} \right\| + {K_{{\tilde y}}}\left\| {{\tilde{ E}}} \right\| + \gamma } \right]^2}.\quad\,\,\,\quad\quad\quad\quad\quad\quad\quad(23)\end{aligned}$ |
同理,把式(12)代入式(21),有
| $\begin{split}\Delta {{ V}_2} \leqslant - &{{{\tilde{ E}}}^{\rm T}}{\tilde{ Q}}{\tilde{ E}} + 2{{{\tilde{ E}}}^{\rm T}}{{{\tilde{ A}}}^{\rm T}}{\tilde{ P}}{{b}}\left[ {{{{\tilde{ W}}}^{\rm T}}{ {\phi}} + {K_{{\tilde y}}}{\tilde{ E}} + {{\hat\gamma}}} \right] + \\&\left\| {{{{b}}^{\rm T}}{\tilde{ P}}{{b}}} \right\|{\left[ {{\phi _{\rm{M}}}\left\| {{\tilde{ W}}} \right\| + {K_{{\tilde y}}}\left\| {{\tilde{ E}}} \right\| + \gamma } \right]^2}.\end{split}$ | (24) |
根据式(17),有
| $\begin{split}& \frac{1}{\alpha }\Delta {{ V}_3}\left( k \right) \leqslant \frac{{\mu ^2 - 2\mu }}{\alpha }{\left\| {{\tilde{ W}}} \right\|^2} + \frac{{2\left( {\mu ^2 - 2\mu } \right)}}{\alpha }\bar W\left\| {{\tilde{ W}}} \right\| + \\ & \alpha \phi _{\rm{M}}^2{\left\| {{{{A}}^{\rm T}}{{Pb}}} \right\|^2}{\left\| {{\hat{ E}}} \right\|^2} + \frac{{\mu ^2}}{\alpha }{{\bar W}^2} + \\ & 2\mu \phi _{\rm{M}}^{}\left\| {{{{A}}^{\rm T}}{{Pb}}} \right\|\left\| {{\hat{ E}}} \right\|\left( {\bar W + \left\| {{\tilde{ W}}} \right\|} \right) - 2{{{\hat{ E}}}^{\rm T}}{{{A}}^{\rm T}}{{Pb}}{{{\tilde{ W}}}^{\rm T}}\phi .\end{split}$ | (25) |
根据式(23)~(25)可得
| $\begin{aligned} \Delta {V}\left( k \right) \leqslant &- {{{E}}^{\rm T}}{{QE}} + 2\left\| {{{{A}}^{\rm T}}{{Pb}}} \right\|\left\| {{E}} \right\|\left( {{K_{{\tilde y}}}\left\| {{\tilde{ E}}} \right\| + \gamma } \right) + \\ & \left\| {{{{b}}^{\rm T}}{{Pb}}} \right\|{\left[ {{\phi _{\rm{M}}}\left\| {{\tilde{ W}}} \right\| + {K_{{\tilde y}}}\left\| {{\tilde{ E}}} \right\| + \gamma } \right]^2} - {{ \tilde {{E}}}^{\rm T}}{\tilde {{Q}}\tilde {{E}}} + \\ &2{\phi _{\rm{M}}}\left( {\left\| {{{{\tilde{ A}}}^{\rm T}}{\tilde{ P}}{{b}}} \right\| - \left\| {{{{A}}^{\rm T}}{{Pb}}} \right\|} \right)\left\| {{\tilde{ E}}} \right\|\left\| {{\tilde{ W}}} \right\| + \\ &2\left\| {{{{\tilde{ A}}}^{\rm T}}{\tilde{ P}}{{b}}} \right\|\left\| {{\tilde{ E}}} \right\|\left( {{K_{{\tilde y}}}\left\| {{\tilde{ E}}} \right\| + \gamma } \right) + \\ &\left\| {{{{b}}^{\rm T}}{\tilde{ P}}{{b}}} \right\|{\left[ {{\phi _{\rm{M}}}\left\| {{\tilde{ W}}} \right\| + {K_{\tilde y}}\left\| {{\tilde{ E}}} \right\| + \gamma } \right]^2} - \frac{{2\mu - \mu _{}^2}}{\alpha }{\left\| {{\tilde{ W}}} \right\|^2} + \\ &\alpha \phi _{\rm{M}}^2{\left\| {{{{A}}^{\rm T}}{{Pb}}} \right\|^2}{\left\| {{\hat{ E}}} \right\|^2} + \frac{{2\left( {\mu _{}^2 - 2\mu } \right)}}{\alpha }\bar W\left\| {{\tilde{ W}}} \right\| + \frac{{\mu _{}^2}}{\alpha }{{\bar W}^2} + \\ &2\mu \phi _{\rm{M}}^{}\left\| {{{{A}}^{\rm T}}{{Pb}}} \right\|\left\| {{\hat{ E}}} \right\|\left( {\bar W + \left\| {{\tilde{ W}}} \right\|} \right) \leqslant \\ & - {\kappa _1}{\left\| {{E}} \right\|^2} - {\kappa _2}{\left\| {{\tilde{ E}}} \right\|^2} - {\kappa _3}{\left\| {{\tilde{ W}}} \right\|^2} + 2{c_1}\left\| {{E}} \right\|\left\| {{\tilde{ W}}} \right\| + \\ &2{c_2}\left\| {{\tilde{ E}}} \right\|\left\| {{\tilde{ W}}} \right\| + 2{c_3}\left\| {{E}} \right\| + 2{c_4}\left\| {{\tilde{ E}}} \right\| + 2{c_5}\left\| {{\tilde{ W}}} \right\| + {c_6}.\end{aligned}$ |
式中:
| $\begin{aligned} {\kappa _1} = &{\lambda _{{\rm{min}}}}({{Q}}) - \left\| {{{{A}}^{\rm T}}{{Pb}}} \right\|{K_{{\tilde y}}} - {\left\| {{{{A}}^{\rm T}}{{Pb}}} \right\|^2}\alpha \phi _{\rm{M}}^2,\\{\kappa _2} = & {\lambda _{{\rm{min}}}}({\tilde{ Q}}) - \left\| {{{{A}}^{\rm T}}{{Pb}}} \right\|{K_{{\tilde y}}} - 2{K_{{\tilde y}}}\left\| {{{{\tilde{ A}}}^{\rm T}}{\tilde{ P}}{{b}}} \right\| - \\ & 3\left\| {{{{b}}^{\rm T}}{{Pb}}} \right\|K_{{\tilde y}}^2 - 3\left\| {{{{b}}^{\rm T}}{\tilde{ P}}{{b}}} \right\|K_{{\tilde y}}^2 - {\left\| {{{{A}}^{\rm T}}{{Pb}}} \right\|^2}\alpha \phi _{\rm{M}}^2,\\ {\kappa _3} = & - 3\phi _{\rm{M}}^2\left\| {{{{b}}^{\rm T}}{{Pb}}} \right\| + \frac{{2\mu - \mu _{}^2}}{\alpha } - 3\phi _{\rm{M}}^2\left\| {{{{b}}^{\rm T}}{\tilde{ P}}{{b}}} \right\|,\end{aligned}$ |
| $\begin{aligned} &\!\!\!\!\!\!\!\!\!\!\!\! {c_1} = \mu {\phi _{\rm{M}}}\left\| {{{{A}}^{\rm T}}{{Pb}}} \right\|,\\ & \!\!\!\!\!\!\!\!\!\!\!\!{c_2} = \mu {\phi _{\rm{M}}}\left\| {{{{A}}^{\rm T}}{{Pb}}} \right\| + {\phi _{\rm{M}}}\left( {\left\| {{{{\tilde{ A}}}^{\rm T}}{\tilde{ P}}{ b}} \right\| - \left\| {{{{A}}^{\rm T}}{{Pb}}} \right\|} \right),\\ & \!\!\!\!\!\!\!\!\!\!\!\!{c_3} = \left\| {{{{A}}^{\rm T}}{{Pb}}} \right\|\left( {\gamma + \mu {\phi _{\rm{M}}}\bar W} \right),\\ & \!\!\!\!\!\!\!\!\!\!\!\!{c_4} = \left\| {{{{\tilde{ A}}}^{\rm T}}{\tilde{ P}}{{b}}} \right\|\left( {\gamma + \mu {\phi _{\rm{M}}}\bar W} \right),\\ & \!\!\!\!\!\!\!\!\!\!\!\!{c_5} = \frac{{\mu \left( {\mu - 1} \right)\bar W}}{\alpha },\\ & \!\!\!\!\!\!\!\!\!\!\!\!{c_6} = {\gamma ^2}\left( {\left\| {{{{b}}^{\rm T}}{{Pb}}} \right\| + \left\| {{{{b}}^{\rm T}}{\tilde{ P}}{{b}}} \right\|} \right) + \frac{{\mu _{}^2{{\bar W}^2}}}{\alpha }.\end{aligned}$ |
其中,
| $ab \leqslant \displaystyle\frac{{{a^2} + {\kappa ^2}{b^2}}}{{2\kappa }},\quad\kappa > 0,$ |
则一定存在正数
| $\begin{aligned}& 2\left\| {{E}} \right\|\left\| {{\tilde{ W}}} \right\| \leqslant \frac{{{{\left\| {{\tilde{ W}}} \right\|}^2}}}{{{\kappa _4}}} + {\kappa _4}{\left\| {{E}} \right\|^2},\;2\left\| {{\tilde{ E}}} \right\|\left\| {{\tilde{ W}}} \right\| \leqslant \frac{{{{\left\| {{\tilde{ W}}} \right\|}^2}}}{{{\kappa _5}}} + {\kappa _5}{\left\| {{\tilde{ E}}} \right\|^2},\\ & 2{c_3}\left\| {{{ E}}} \right\| \leqslant \frac{{c_3^2}}{{{\kappa _6}}} + {\kappa _6}{\left\| {{E}} \right\|^2},\;2{c_4}\left\| {{\tilde{ E}}} \right\| \leqslant \frac{{c_4^2}}{{{\kappa _7}}} + {\kappa _7}{\left\| {{\tilde{ E}}} \right\|^2},\\ & 2{c_5}\left\| {{\tilde{ W}}} \right\| \leqslant \frac{{c_5^2}}{{{\kappa _8}}} + {\kappa _8}{\left\| {{\tilde{ W}}} \right\|^2},\end{aligned}$ |
则
| $\Delta { V} \leqslant - \sigma { V} + {c_7}.$ | (26) |
式中:
| $\sigma = \min \left\{ {\displaystyle\frac{{{{\kappa '}_1}}}{{{\lambda _{\operatorname{m} {\rm{ax}}}}\left( {{P}} \right)}},\; \displaystyle\frac{{{{\kappa '}_2}}}{{{\lambda _{\max }}\left( {{\tilde{ P}}} \right)}},\; \displaystyle\frac{{{{\kappa '}_3}}}{\alpha }} \right\},$ |
| ${c_7} = {c_6} + \displaystyle\frac{{c_3^2}}{{{\kappa _6}}} + \displaystyle\frac{{c_4^2}}{{{\kappa _7}}} + \displaystyle\frac{{c_5^2}}{{{\kappa _8}}},$ |
| ${\kappa '_1} = {\kappa _1} - {c_1}{\kappa _4} - {\kappa _6} > 0,$ | (27) |
| ${\kappa '_2} = {\kappa _2} - {c_2}{\kappa _5} - {\kappa _7} > 0,$ | (28) |
| ${\kappa '_3} = {\kappa _3} - \frac{{{c_1}}}{{{\kappa _4}}} - \frac{{{c_2}}}{{{\kappa _5}}} - {\kappa _8} > 0.$ | (29) |
所以水平面AUV离散系统中的
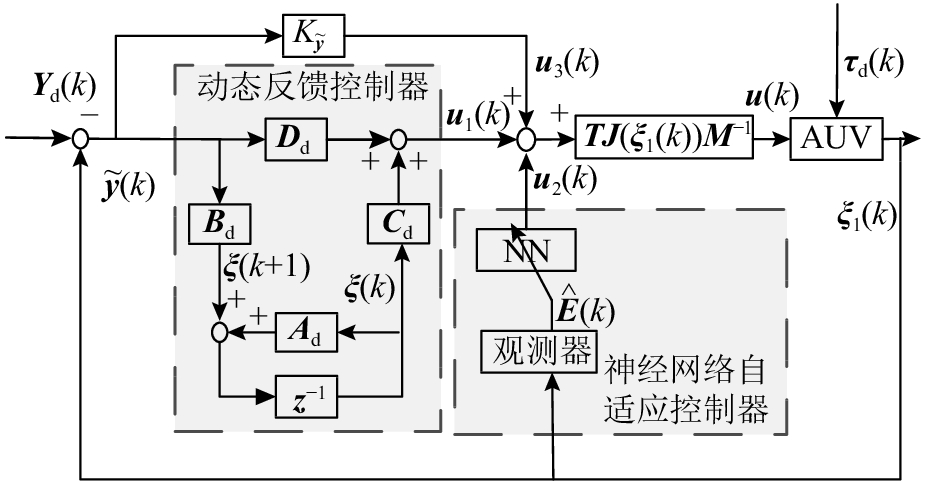
至此已经阐述了AUV水平面离散系统的控制器设计和稳定性分析过程,图1给出了控制器设计方法结构图. 可以看出控制器由三部分组成:第一部分
|
图 1 控制器详细设计结构图 Fig. 1 Detailed design framework of controller |
|
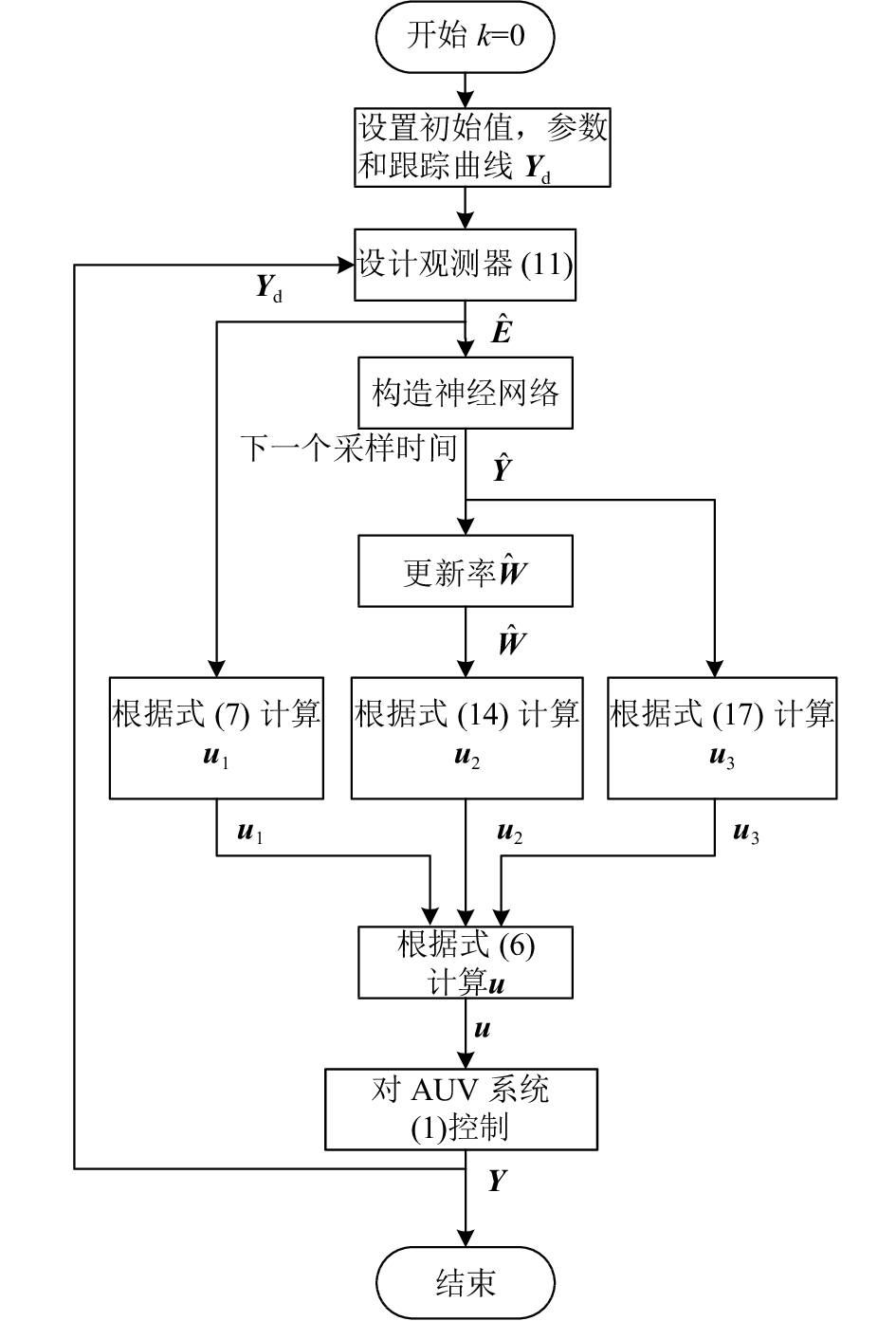
图 2 AUV水平面路径跟踪控制算法流程图 Fig. 2 Flow chart of path following control algorithm of AUV in the horizontal plane |
控制算法详细实现步骤如下.
1) 选择初始状态,适当的参数
2) 设计状态观测器(11),得到
3) 构造神经网络,得到
4) 根据式(14)和(17)计算
5) 根据式(7)计算控制器
6) 根据式(6)计算控制器
7) 对AUV系统(1)控制;
8) 回到步骤4进行下一次采样计算.
控制算法实现的流程图见图2.
3.2 仿真分析基于文献[1]的INFANTE AUV模型和数据进行数值仿真,INFANTE AUV长度为4.22 m,动态系统相关参数如下:
设AUV的初始位置为
动态补偿器的参数如下:
为了说明提出算法的有效性,对比研究基于动态反馈和没有动态反馈的控制器,仿真中使用的控制器有以下2种.
控制器1:式(6)、(7)、(14)和(17)表示的控制器.
控制器2:没有动态反馈的控制器,即
| ${{\tau }}\left( k \right) = {T^{ - 1}}{{M}}{{{J}}^{ - 1}}\left( {{{{\xi }}_1}\left( k \right)} \right)\left( {{{{u}}_1}\left( k \right) - {{{u}}_2}\left( k \right) + {{{u}}_3}\left( k \right)} \right).$ |
式中:
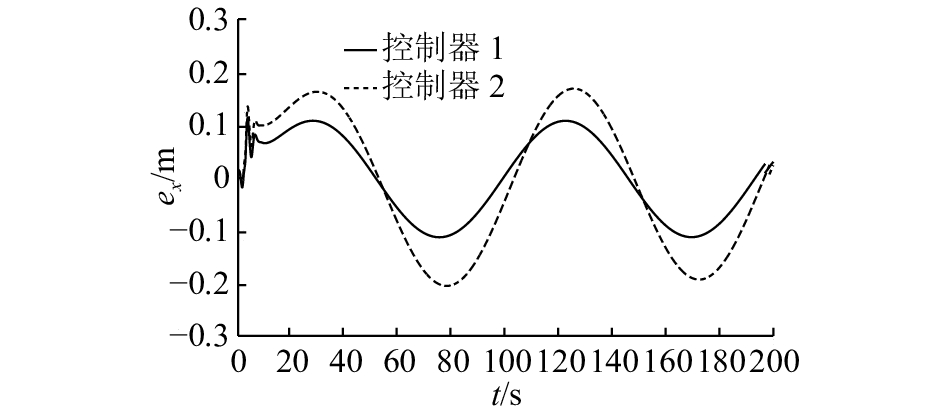
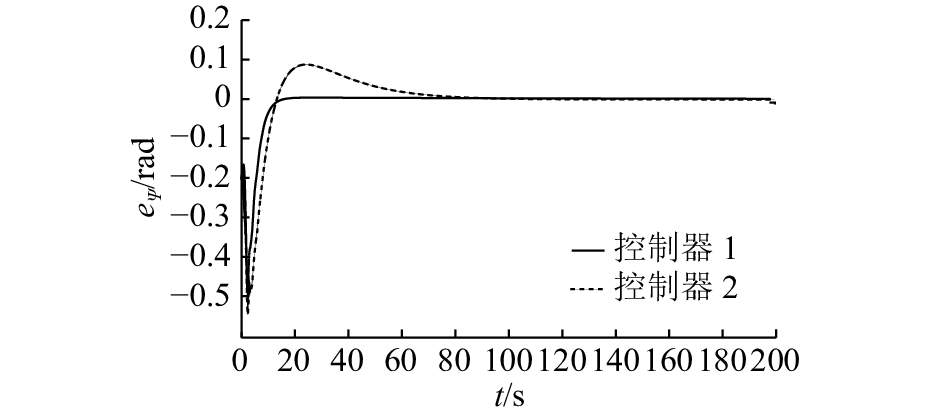
仿真结果如图3~9所示. 图中t表示时间. 图3~5分别表示AUV跟踪误差系统中
|
图 3 AUV路径跟踪误差系统中x方向的跟踪误差 Fig. 3 Tracking error in x of path tracking error system of AUV |
|
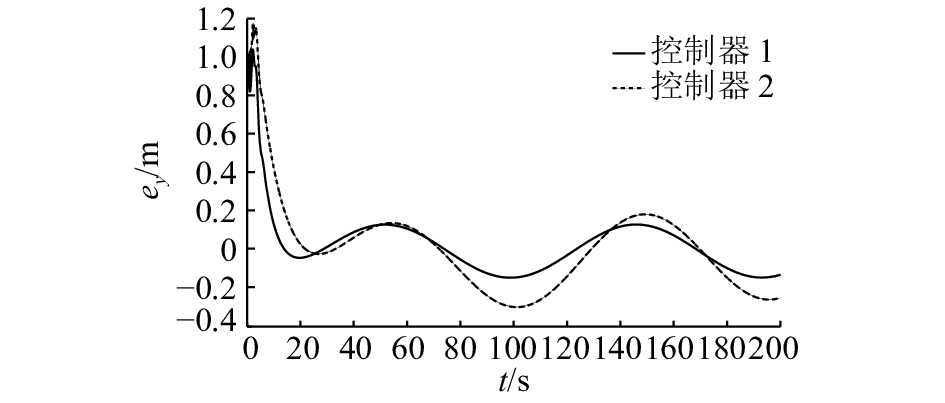
图 4 AUV路径跟踪误差系统中y方向的跟踪误差 Fig. 4 Tracking error in y of path tracking error system of AUV |
|
图 5 AUV路径跟踪误差系统中首摇角的跟踪误差 Fig. 5 Tracking error of yaw for path tracking error system of AUV |
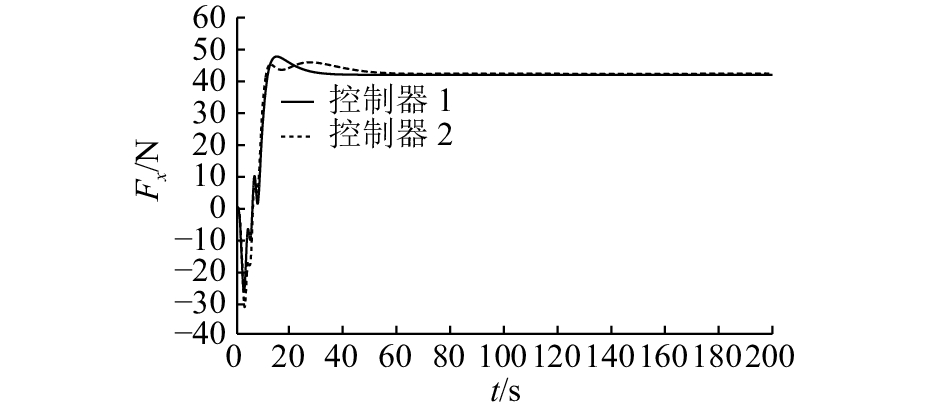
|
图 6 AUV路径跟踪误差系统中x方向控制力 Fig. 6 Control force in x of path tracking error system of AUV |
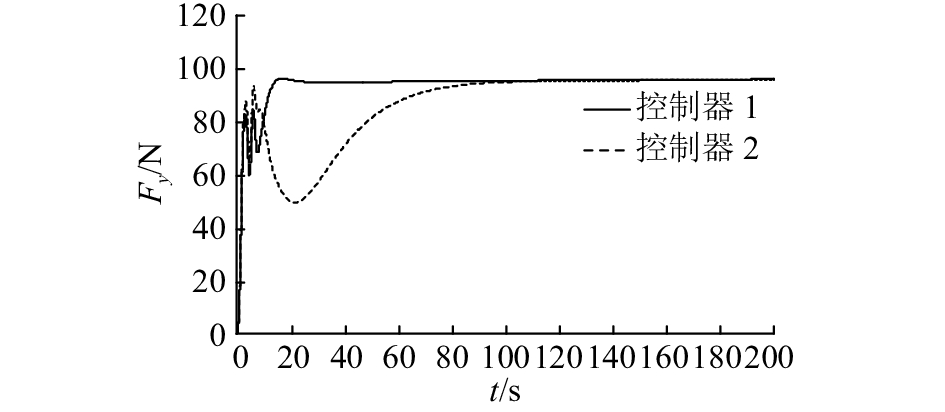
|
图 7 AUV路径跟踪误差系统中y方向控制力 Fig. 7 Control force in y of path tracking error system of AUV |
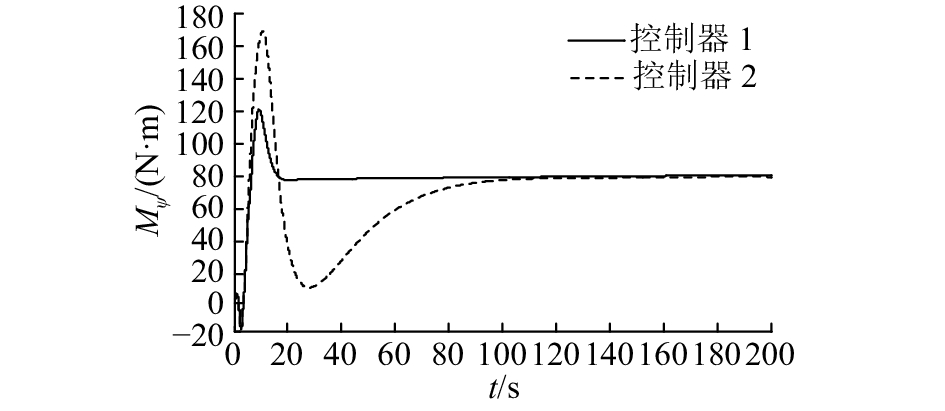
|
图 8 AUV路径跟踪误差系统中首摇角的控制力矩曲线 Fig. 8 Control torque of yaw for path tracking error system of AUV |
|
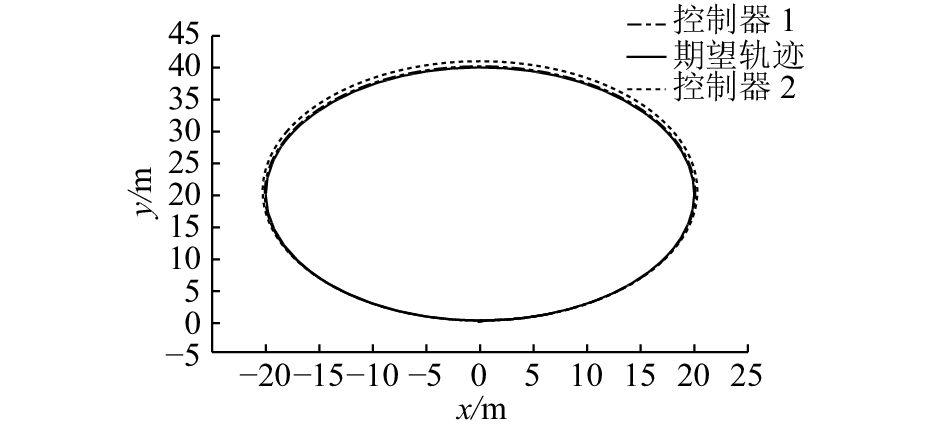
图 9 AUV在xy平面路径跟踪曲线 Fig. 9 Path tracking response in xy plane of AUV |
基于离散非线性系统理论对AUV水平面离散模型设计神经网络自适应的输出动态反馈控制器. 所提出的控制方法对模型精度的要求较低,对于AUV运动系统中的未知非线性结构具有很好的自适应性. 将控制系统看作是线性部分和非线性部分的累加,设计动态反馈控制器镇定AUV系统的线性部分以提高系统的控制性能,对非线性部分采用神经网络自适应方法进行控制. 仿真结果表明所设计的控制器对降低非线性阻尼及抑制外界干扰效果良好,所提出的控制方法具有良好的控制品质.
三维空间航行的AUV的路径控制问题及带有时滞的AUV控制问题需要进一步研究.
| [1] |
LAPIERRE L. Robust diving control of an AUV[J]. Ocean Engineering, 2009, 36(1): 92-104. DOI:10.1016/j.oceaneng.2008.10.006 |
| [2] |
徐玉如, 肖坤. 智能海洋机器人技术进展[J]. 自动化学报, 2007, 33(5): 518-521. XU Yu-ru, XIAO Kun. Technology development of autonomous ocean vehicle[J]. Acta Automatica Sinica, 2007, 33(5): 518-521. |
| [3] |
史剑光, 李德骏, 杨灿军, 等. 水下自主机器人接驳碰撞过程分析[J]. 浙江大学学报: 工学版, 2015, 49(3): 497-504. SHI Jian-guang, LI De-jun, YANG Can-jun, et al. Impact analysis during docking process of autonomous underwater vehicle[J]. Journal of Zhejiang University: Engineering Science, 2015, 49(3): 497-504. |
| [4] |
AGUIAR A, HESPANHA J. Trajectory-tracking and path-following of underactuated autonomous vehicles with parametric modeling uncertainty[J]. IEEE Transactions on Automatic Control, 2007, 52(8): 1362-1379. DOI:10.1109/TAC.2007.902731 |
| [5] |
魏清平, 王硕, 董翔, 等. 一种仿生水下机器人的设计与动力学分析[J]. 自动化学报, 2013, 39(8): 1330-1338. WEI Qing-ping, WANG Suo, DONG Xiang, et al. Design and kinetic analysis of a biomimetic underwater vehicle with two undulating long-fins[J]. Acta Automatica Sinica, 2013, 39(8): 1330-1338. |
| [6] |
LIANG X, WAN L, BLAKE J, et al. Path following of an underactuated AUV based on fuzzy backstepping sliding mode control[J]. International Journal of Advanced Robotic Systems, 2016, 13(122): 1-11. |
| [7] |
PEYMANI E, FOSSEN T I. Path following of underwater robots using Lagrange multipliers[J]. Robotics and Autonomous Systems, 2015, 67: 44-52. DOI:10.1016/j.robot.2014.10.011 |
| [8] |
初亮, 李天骄, 孙成伟. 面向再生制动优化的电动车自适应巡航控制策略[J]. 浙江大学学报: 工学版, 2017, 51(8): 1596-1602. CHU Liang, LI Tian-jiao, SUN Cheng-wei. Research on adaptive cruise control strategy for electric vehicle based on optimization of regenerative braking[J]. Journal of Zhejiang University: Engineering Science, 2017, 51(8): 1596-1602. |
| [9] |
唐志国, 李元春, 刘木林. 机械臂协调操作柔性负载鲁棒神经网络控制[J]. 浙江大学学报: 工学版, 2010, 44(7): 1394-1399. TANG Zhi-guo, LI Yuan-chun, LIU Mu-lin. Robust neural network control of dual-manipulator cooperative system handling flexible payload[J]. Journal of Zhejiang University: Engineering Science, 2010, 44(7): 1394-1399. |
| [10] |
ZHAO J. NN-adaptive predictive control for a class of discrete-time nonlinear systems with input-delay[J]. Neurocomputing, 2016, 173: 1832-1838. DOI:10.1016/j.neucom.2015.09.059 |
| [11] |
程鹏飞, 吴成富. 单侧机翼损伤飞机的神经网络自适应鲁棒非线性控制[J]. 系统工程与电子技术, 2016, 38(3): 607-617. CHENG Peng-fei, WU Cheng-fu. Neural network based robust adaptive nonlinear control for aircraft under one side of wing loss[J]. Systems Engineering and Electronics, 2016, 38(3): 607-617. |
| [12] |
CUI R, YANG C, LI Y, et al. Adaptive neural network control of AUVs with control input nonlinearities using reinforcement learning[J]. IEEE transactions on Systems, Man, and Cybernetics: Systems, 2017, 47(6): 1019-1029. DOI:10.1109/TSMC.2016.2645699 |
| [13] |
LIU Y, TONG S. Optimal control-based adaptive NN design for a class of nonlinear discrete-time block-triangular systems[J]. IEEE Transactions on Cybernetics, 2016, 46(11): 2670-2680. DOI:10.1109/TCYB.2015.2494007 |
| [14] |
QI X. Adaptive coordinated tracking control of multiple autonomous underwater vehicles[J]. Ocean Engineering, 2014, 91: 84-90. DOI:10.1016/j.oceaneng.2014.08.019 |
| [15] |
ZHANG L, QI X, PANG Y. Adaptive output feedback control based on DRFNN for AUV[J]. Ocean Engineering, 2009, 36(9): 716-722. |
| [16] |
PARK B. Adaptive formation control of underactuated autonomous underwater vehicles[J]. Ocean Engineering, 2015, 96: 1-7. DOI:10.1016/j.oceaneng.2014.12.016 |
| [17] |
张利军, 齐雪, 赵杰梅, 等. 垂直面欠驱动自治水下机器人定深问题的自适应输出反馈控制[J]. 控制理论与应用, 2012, 29(10): 1371-1376. ZHANG Li-jun, QI Xue, ZHAO Jie-mei, et al. Depth-keeping control for autonomous underwater vehicle in vertical plane using adaptive output feedback controller[J]. Control Theory and Applications, 2012, 29(10): 1371-1376. |
| [18] |
SUBUDHI B, MUKHERJEE K, GHOSH S. A static output feedback control design for path following of autonomous underwater vehicle in vertical plane[J]. Ocean Engineering, 2013, 63: 72-76. DOI:10.1016/j.oceaneng.2013.01.029 |
| [19] |
LI S, WANG X, ZHANG L. Finite-time output feedback tracking control for autonomous underwater vehicles[J]. IEEE Journal of Oceanic Engineering, 2015, 40(3): 727-751. DOI:10.1109/JOE.2014.2330958 |
| [20] |
LIU S, WANG D, POH E. Output feedback control design for station keeping of AUVs under shallow water wave disturbances[J]. International Journal of Robust and Nonlinear Control, 2009, 19(13): 1447-1470. DOI:10.1002/rnc.v19:13 |
| [21] |
PENG Z, WANG J. Output-feedback path-following control of autonomous underwater vehicles based on an extended state observer and projection neural networks[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 48(4): 535-544. DOI:10.1109/TSMC.2017.2697447 |
| [22] |
KUMAR R, KUMAR C, SEN D, et al. Discrete time-delay control of an autonomous underwater vehicle: theory and experimental results[J]. Ocean Engineering, 2009, 36(1): 74-81. DOI:10.1016/j.oceaneng.2008.07.011 |
| [23] |
SANTOS O, ROMERO H, SALAZAR S, et al. Optimized discrete control law for quadrotor stabilization: experimental results[J]. Journal of Intelligent and Robotic Systems, 2016, 84(1–4): 1-15. |
| [24] |
YU J, SHI P, DONG W, et al. Neural network-based adaptive dynamic surface control for permanent magnet synchronous motors[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(3): 640-645. DOI:10.1109/TNNLS.2014.2316289 |
| [25] |
HE W, CHEN Y, YIN Z. Adaptive neural network control of an uncertain robot with full-state constraints[J]. IEEE Transactions on Cybernetics, 2016, 46(3): 620-629. DOI:10.1109/TCYB.2015.2411285 |
| [26] |
MA J, GE S S, ZHENG Z, et al. Adaptive NN control of a class of nonlinear systems with asymmetric saturation actuators[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(7): 1532-1538. DOI:10.1109/TNNLS.2014.2344019 |


