2. 西安航空学院 电子工程学院,陕西 西安 710077;
3. 挪威科技大学奥勒松校区工程与科学学院 挪威 8730
2. School of Electronic Engineering, Xi'an Aeronautical University, Xi'an 710077, China;
3. Norwegian University of Science and Techchnology Aalesund, Norway 8730
智能优化算法已经成为当前的研究热点[1],被广泛应用于各个领域[2]. 通过模拟自然界物种的生存进化规律,不同类型的智能优化算法[3-5]相继被提出,为求解复杂全局优化问题提供了全新思路. 早熟收敛以及收敛效率不高是各种智能优化算法亟需解决的难题[6]. 对于高维度、多模态复杂优化问题,研究者围绕算法改进策略开展了系列深入研究. 改进方法主要围绕提高粒子个体学习对象多样性和扩展种群不同类型智能进化行为2个方面,通过采用特定知识模型对个体学习进化方向进行引导,或者引入不同算法协同进化实现大幅度提升算法求解性能的目的. Liang等[7]提出具有典型意义的改进策略,通过引入历史信息指导粒子进化方向,不仅使得个体具有“记忆功能”,而且学习对象更加多样化. 类似地,田瑾[8]提出的和声粒子群算法、马卫等[9]提出的改进布谷鸟优化算法,在种群现有进化规则的基础上,采用特定的知识模型引导个体进化方向,目的是让个体在保留自身搜索能力的同时具备改进策略带来的突出优势,提高算法跳出局部最优的概率. 但是,改进策略往往只对特定问题具有良好的优化效果,研究成果缺乏系统的理论分析支撑,可扩展性和通用性不强. 崔晓晖等[10]将粒子群算法与模拟退火算法相结合,在融合2种算法不同进化策略的基础上协同进化,有效改善算法的全局寻优能力. 但是,不同算法相互结合的形式只是简单融合了不同类型的智能优化算法,合理性需要进一步研究;此外,采用哪些类型的算法进行融合具有主观性,缺乏科学准确的判定规则. 大部分改进策略从算法本身出发,忽略了待求解问题对算法种群多样性的影响. 为了模拟碰撞过程中物体物理属性相互影响的变化过程,提出新的智能优化算法—弹性碰撞优化(elastic collision optimization,ECO)算法,引入改进的核模糊C均值聚类(fuzzy C-means, FCM)算法,从理论角度对算法种群多样性进行动态分析,针对性地提高粒子学习对象的合理性与多样性.
无线传感器网络(WSNs)是由大量低成本、具有无线通信和计算能力的传感器节点组成的自组织网络[11],为实时准确收集不同环境中所需的数据提供了可能. 随着WSNs规模不断扩大,需要处理的节点数据呈现爆炸式增长,给大规模WSNs管理带来严峻挑战. 不断成熟的云计算技术为解决WSNs面临的诸多问题开辟了新的研究思路[12],诞生了传感云(sensor cloud)系统. 传感云运用云计算技术进行WSNs数据采集、处理与存储,为用户提供全新的用户体验[13]. 云环境资源调度是云计算关键技术之一,Tian等[14]设计基于运行成本的云计算资源分配方案,能够确保云提供商效益最大化,但是不适用于动态变化的应用场景. Chohan等 [15]提出基于拍卖竞价策略的云资源调度算法,但是计算复杂度高.
传感云的研究处于起步阶段,国内外相关研究相对较少,为此以传感云资源调度为应用背景,在弹性碰撞优化算法研究的基础上,给出具有较高目标收益的传感云资源调度策略,并且利用多维复杂测试函数以及传感云资源调度实例,验证提出的ECO和传感云资源调度方案的有效性.
1 弹性碰撞优化算法智能优化算法隶属于随机启发式搜索技术范畴,在目标解空间内部署具有一定数量粒子的种群,粒子按照一定规则选择优秀的个体进行学习,使得种群能够向着全局最优解方向进化.
定义1 对于
| $ \left.\begin{aligned} & {{{X}}_i}\left( t+1 \right)={ \aleph} \left( {{{X}}_i}\left( t \right),{ \delta} \right),\quad{{{X}}_i}\left( t \right)\in \;{{P}}\left( t \right),\quad{{P}}\left( t \right)\in {{S}}; \\ & {{{X}}_i}=\left( {x_{i1}},{x_{i2}},\cdots ,{x_{in}} \right),\quad i=1,2,\cdots ,{{N}}; \\& {\xi _{j\min} }\leqslant{x_{ij}}\leqslant{\xi _{j\max} }, \quad j=1,2,\cdots ,{{n}}. \end{aligned}\right\}$ | (1) |
式中:t、
定义2 G收敛充分非必要条件. 对于算法G,种群
| $ \left.\begin{array}{l}p\left\{ {{P}\left( t \right)\left| {{P}\left( 1 \right),{P}\left( 2 \right), \cdots ,{P}\left( {t - 1} \right)} \right.} \right\} = \\ \quad p\left\{ {{P}\left( t \right)\left| {{P}\left( {t - 1} \right)} \right.} \right\},\\f\left( {\aleph \left( {{{X}_i},{{ \delta}} } \right)} \right) \leqslant f\left({{ \delta}} \right).\end{array}\right\}$ | (2) |
称
定义1给出智能优化算法的一般性数学描述,不同类型算法
|
图 1
|
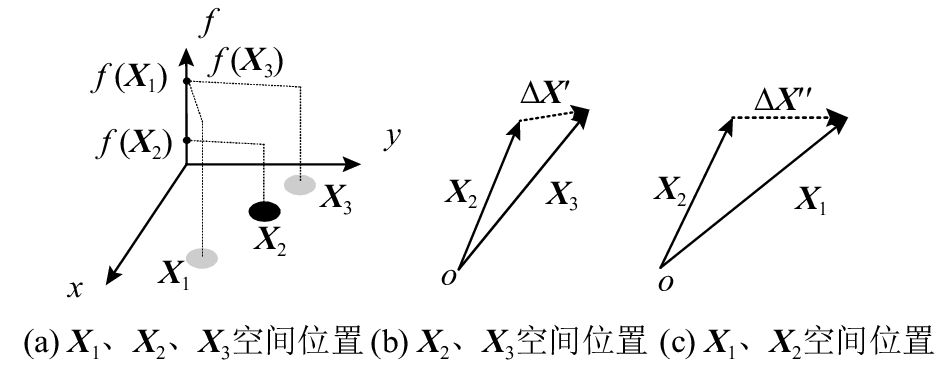
弹性碰撞融合了不同物体物理属性相互影响的变化过程,某种意义上来说碰撞过程具有一定的学习能力. 虽然碰撞后2个物体的动量变化的绝对值相同,但是碰撞前动量大的物体较大地影响了动量小的物体的空间位置,因此可以将弹性碰撞过程抽象为智能算法的粒子进化更新过程,对对心完全弹性(complete elastic,CE)碰撞、完全非弹性(complete inelastic,CI)碰撞和非完全弹性(non complete elastic,NCE)碰撞3种情形进行研究,分别将物体速度
定义3 碰撞更新. 对于粒子
| $\begin{aligned}\left. \begin{aligned} &mf\left( {{{{X}}_i}} \right) + mf\left( {{{X}}'} \right) = mf\left( {{{{X}}_{i,{\rm{new}}}}} \right) + mf\left( {{{{{X}}'}_{{\mathop{\rm \! \! \! \! new}\nolimits} }}} \right),\\ & \frac{1}{2}m{\left[ {f\left( {{{{X}}_i}} \right)} \right]^2} + \frac{1}{2}m{\left[ {f\left( {{{X}}'} \right)} \right]^2} = \\ & \quad\quad\;\; \frac{1}{2}m{\left[ {f\left( {{{{X}}_{i,{\rm{new}}}}} \right)} \right]^2} + \frac{1}{2}m{\left[ {f\left( {{{{{X}}'}_{{\rm{\!\!\!\!new}}}}} \right)} \right]^2},\end{aligned}\right\} \\\end{aligned}$ | (3) |
则
| $\begin{aligned}{{{X}}_{i,{\rm {new}}}} = & {\rm CE}\left( {{{{X}}_i},{{X}}'} \right) = \\ &{{{X}}_i}\displaystyle\frac{{2f\left( {{{X}}'} \right)}}{{f\left( {{{X}}'} \right) + f\left( {{{{X}}_i}} \right)}} + {{X}}'\displaystyle\frac{{f\left( {{{{X}}_i}} \right) - f\left( {{{X}}'} \right)}}{{f\left( {{{X}}'} \right) + f\left( {{{{X}}_i}} \right)}}.\end{aligned}$ |
同理,对于完全非弹性碰撞和非完全弹性碰撞:
CI:
| $\begin{array}{l}mf\left( {{{{X}}_i}} \right) + mf\left( {{{X}}'} \right) = 2mf\left( {{{{X}}_{i,{\rm{new}}}}} \right),\\{{{X}}_{i,{\rm{new}}}} = {\rm{CI}}\left( {{{{X}}_i},{{X}}'} \right) = \\\;\;\;\;{{{X}}_i}\displaystyle\frac{{3f\left( {{{X}}'} \right) - f\left( {{{{X}}_i}} \right)}}{{2\left( {f\left( {{{X}}'} \right) + f\left( {{{{X}}_i}} \right)} \right)}} + {{X}}'\displaystyle\frac{{3f\left( {{{{X}}_i}} \right) - f\left( {{{X}}'} \right)}}{{2\left( {f\left( {{{X}}'} \right) + f\left( {{{{X}}_i}} \right)} \right)}}.\end{array}$ | (4) |
NCE:
| ${{X}}_{i,{\rm{new}}}= {\rm{NCE}}\left( {{{X}_i},{X}'} \right) = \beta {\rm{CE}}\left( {{{X}_i},{X}'} \right);\; \beta \in \left( {0,1.0} \right).$ | (5) |
式(3)~(5)给出3种不同碰撞更新策略,为粒子提供了多种学习策略. 为了进一步改善算法收敛效率,保持种群样本多样性,定义ECO算法粒子更新策略如下.
定义4 ECO算法粒子更新. 在ECO算法中,对于粒子
| ${{X}_i}\left( {t + 1} \right) = \left\{ \begin{aligned}&{\rm{ECO}}\left( {{{X}_i}\left( t \right),{\delta }} \right),\quad{r_1} \geqslant \varepsilon ; \\&{{X}_i}\left( t \right),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{r_1} < \varepsilon . \\ \end{aligned}\quad\quad\quad \right.$ | (6) |
| $\begin{array}{l}{\rm{ECO}}\left( {{{{X}}_i}\left( t \right),{{\delta}} } \right) = \\\left\{ \begin{aligned}&{\rm{CE}}\left( {{{{X}}_i}\left( t \right),{{{G}}_i}\left( t \right)} \right),\;\;\;{r_2} \leqslant 0.5 ;\\&{\rm{CI}}\left( {{{{X}}_i}\left( t \right),{{B}}\left( t \right)} \right),\;\;\;\;\;0.5 <{r_2} \leqslant 0.5 + \xi ;\\&\alpha \left[{\rm{CE}}{\left( {{{{X}}_i}\left( t \right),{{{X}}_j}\left( t \right)} \right) + {\rm{CI}}\left( {{{{X}}_i}\left( t \right),{{{X}}_k}\left( t \right)} \right)} \right],\;{\text{其他}}.\end{aligned} \right.\end{array}$ | (7) |
式中:
从定义4可以看出,ECO更新过程实质是模拟弹性碰撞3种物理现象,而不是弹性碰撞恰好处于完全弹性碰撞和完全非弹性碰撞之间. 由于CE和CI具有明确的推导公式,因此引入比例系数可以将CE和CI转化为NCE. ECO更新涉及2个参数,算法实现相对简单,并且ECO以概率1–ε进行更新,更新策略融合3种碰撞更新机制,粒子分别在CE条件下“与种群最优碰撞”,使得粒子快速向种群最优解学习,提高算法进化速度;在CI条件下“与自身历史最优碰撞”,粒子增大逃离过去最优解的可能,增大算法跳出局部最优的概率;“随机碰撞”有效扩展了粒子学习空间,提高了群体样本多样性,算法收敛性能明显改善.
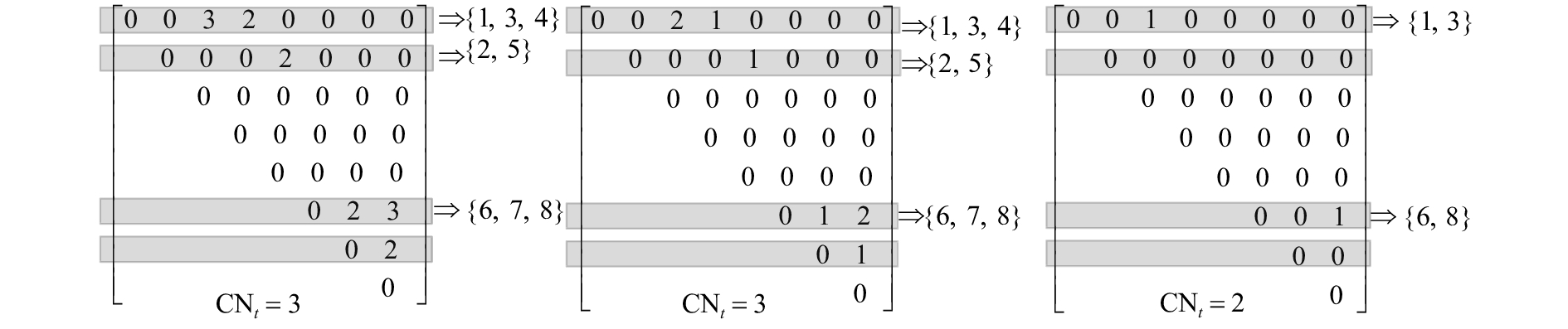
1.2 自适应核FCM模糊聚类算法FCM是目前应用最为广泛的聚类算法之一,通过隶属度矩阵
定义5 迭代比对矩阵. 当聚类数为
| ${{O}_{N \times N}} = {\left[ {{O_{ij}}} \right]_{N \times N}} = \sum\limits_{c = 2}^{{C_{\max }}} {{O}_{N \times N}^c} ,$ | (8) |
| $\begin{aligned} & { O}_{N\times N}^{c}={{\left[ o_{ij}^{c} \right]}_{N\times N}}, \\ & o_{ij}^{c}=\left\{ \begin{aligned} & \mu _{i}^{c} \mu _{j}^{c},\;\;\;{{X}_{i}}\;,\;{{X}_{j}}\in {{L}_{k}};\\ & 0,\;\;\;\;\;\;\;\;\;{\text{其他}}, \\ &\end{aligned} \right. \\ &{ O}_{N\times N}^{c}=\left[ \begin{aligned} \,\,& 0 & o_{12}^{c} &\quad \cdots & o_{1N}^{c} \\ & o_{21}^{c} & 0\,\,\, &\quad \cdots & o_{2N}^{c} \\ & \,\,\,\,\vdots & \vdots\,\,\,\, &\quad {} & \vdots \;\;\; \\ & o_{N1}^{c} & o_{N2}^{c} & \quad\cdots & 0 \;\; \end{aligned} \right]. \end{aligned}$ | (9) |
从定义5可以看出,
| $\begin{split}&{{O}'_{N \times N}} = {\left[ {{{O'}_{\!\!\!\!ij}}} \right]_{N \times N}},\\&O'_{ij} = \left\{ \begin{aligned}&\left\lceil{{O_{ij}}}\right\rceil ,\;{\rm{}}\;{O_{ij}} \geqslant \left( {{C_{\max }} - 1} \right){\mu _{\min }};\\& 0,\;\;\;\;\;\;\;\,{\text{其他}}. \\ \end{aligned} \right.\end{split}$ | (10) |
从式(10)可以看出,
AKFCM实现过程如下. 如图2所示为具体实例说明.
输入:KFCM初始化,
输出:最佳聚类结果
1. for
2. 利用KFCM将
3. end for
4. 根据式(9)得到迭代比对矩阵
5. while (
6. {
7.
8. for
9. for
10. if (
11. 将
12. else if (
13. else if (
14. 将
15. end for
16. end for
17. 更新
18. 对
19. }
20.
|
图 2 AKFCM 实现示意图 Fig. 2 AKFCM implementation diagram |
为了提高ECO粒子学习对象的合理性和针对性,将AKFCM算法引入ECO算法中,在每次迭代更新前对种群进行聚类分析,并且根据聚类结果合理选取粒子学习对象.
ECO算法实现过程如下.
输入:目标函数
输出:
1. 在解空间内随机生成群体
2. while (
3. {
4. 利用AKFCM算法对
5. for
6. 根据聚类结果为
7. 如果
8. 更新
9. end for
10. 更新种群最优解
11. }
12. 种群最优解
ECO在迭代进化过程中保留了优秀个体,ECO算法满足定义2的收敛充分非必要条件,因此ECO算法具有全局收敛性. 具体证明过程如下.
证明:令
| $p\left( {{Z}\left( {{P}\left( t \right)} \right) > 0\left| {{Z}\left( {{P}\left( {t - 1} \right)} \right) > 0} \right.} \right) > 0,\;\forall t \geqslant 1.$ | (11) |
设t时刻
| $\begin{split} &p( {{Z}}{\left( {{ P}\left( {t + 1} \right)} \right) = 0} ) =\\ &p\left({{Z}} {\left( {{ P}\left( {t + 1} \right)} \right) \!=\! 0\left| {{Z}}{\left( {{ P}\left( t \right)} \right) \!=\! 0} \right.} \right) \! \times p\left( {{Z}}{\left( {{ P}\left( t \right)} \right) = 0} \right) +\\ &p\left({{Z}} {\left( {{ P}\left( {t + 1} \right)} \right) = 0\left| {{Z}}{\left( {{ P}\left( t \right)} \right) \ne 0} \right.} \right) \times p\left( {{Z}}{\left( {{ P}\left( t \right)} \right) \ne 0} \right).\end{split}$ | (12) |
根据式(11)可知
| $\begin{split}p(& {Z}( {{P}( {t + 1}) )} = 0 ) = \\ &p( {Z}( {{P}( {t + 1} )}) = 0| {Z}( {{P}( t )} ) = 0 )\times p( {{Z}( {{P}( t )} ) = 0} ).\end{split}$ | (13) |
根据式(11)可知,对于
| $\begin{aligned}& p\left( {{Z}\left( {{P}\left( {t + 1} \right)} \right) = 0\left| {{Z}\left( {{P}\left( t \right)} \right) = 0} \right.} \right) =\\ & \quad 1 - p\left( {{Z}\left( {{P}\left( {t + 1} \right)} \right) > 0\left| {{Z}\left( {{P}\left( t \right)} \right) = 0} \right.} \right) \leqslant 1 - \gamma .\end{aligned}$ | (14) |
联立式(13)、(14)可以得到
| $\begin{gathered}\!\!\!\!\!\!p\left( {{Z}\left( {{P}\left( {t + 1} \right)} \right) = 0} \right) \leqslant \left( {1 - \gamma } \right)p\left( {{Z}\left( {{P}\left( t \right)} \right) = 0} \right) ,\\ \!\!\!\!\!\!p\left( {{Z}\left( {{P}\left( {t + 1} \right)} \right) = 0} \right) \leqslant \cdots \leqslant {\left( {1 - \gamma } \right)^{t + 1}}p\left( {{Z}\left( {{P}\left( 0 \right)} \right) = 0} \right). \\ \end{gathered} $ | (15) |
当
| $\mathop {\lim }\limits_{t \to \infty } p\left( {{Z}\left( {{P}\left( {t + 1} \right)} \right) = 0} \right) = 0.$ | (16) |
根据式(16),随着算法不断运行,
证毕.
1.3.2 ECO算法计算复杂度ECO种群初始化复杂度为
| $\begin{aligned}&\left( {{T_{\max }} + 1} \right)O\left( {nN} \right)+{T_{\max }}[ {T\left( {{C_{\max }} - 1} \right)} O\left( N \right) + \left.QO\left( {N^2} \right)\right] \approx\\ &{T_{\max }}QO\left( {{N^2}} \right).\end{aligned}$ |
式中:Tmax为KFCM最大迭代次数。
1.3.3 ECO算法种群多样性引入AKFCM能够增加种群样本多样性,而且有效避免算法陷入局部最优,为了定量分析算法种群样本多样性,给出ECO多样性评价指标.
定义6 定义ECO算法群体多样性评价指标
| ${\varGamma} \left( {{P}\left( t \right)} \right) = \frac{1}{{Nn}}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^n {{{\left[ {{x_{ij}}\left( t \right) - \frac{1}{N}\sum\limits_{i = 1}^N {{x_{ij}}\left( t \right)} } \right]}^2}} } .$ | (17) |
式中:xij(t)为粒子更新函数。
定理1 ECO算法能够有效保持群体多样性.
证明:由式(11)可知,
| $\begin{split}E&\left[ {{{P}}\left( t \right)} \right] = \frac{1}{{Nn}}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^n {E{{\left[ {{x_{ij}}\left( t \right) - \overline {{x_j}\left( t \right)} } \right]}^2}} } = \\ &\frac{1}{{Nn}}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^n {E{{\left[ ({{x_{ij}}\left( t \right) \!-\! E{x_{ij}}\left( t \right)) + (E{x_{ij}}\left( t \right)\! -\! {\overline {{x_j}\left( t \right)})} } \right]}^2}} }\!=\! \\ &\frac{1}{{Nn}}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^n {\left\{ {E{{\left[ {{x_{ij}}\left( t \right) - E{x_{ij}}\left( t \right)} \right]}^2} - } \right.} } \\ &2E \left( {\left[ {{x_{ij}}\left( t \right) - E{x_{ij}}\left( t \right)} \right]\left[ {E{x_{ij}}\left( t \right) - \overline {{x_j}\left( t \right)} } \right]} \right) + \\ &\left. {E{{\left[ {E{x_{ij}}\left( t \right) - \overline {{x_j}\left( t \right)} } \right]}^2}} \right\}.\quad\quad\quad\quad\quad\quad\quad\quad\quad(18)\end{split}$ |
令
| $\left.\begin{aligned}& \begin{aligned}&\left. E\left( {\left[ {{x_{ij}}\left( t \right) - E{x_{ij}}\left( t \right)} \right]\left[ {E{x_{ij}}\left( t \right) - \overline {{x_j}\left( t \right)} } \right]} \right) = \sigma _{ij}^2\left( t \right) \right/N,\\ & E{\left[ {\overline {{x_j}\left( t \right)} - E{x_{ij}}\left( t \right)} \right]^2} = \frac{1}{N}\sum\limits_{k = 1}^N {\sigma _{kj}^2\left( t \right)} + \\ & \quad\quad\quad\quad\quad\quad\quad\quad\;{\left[ {E{x_{kj}}\left( t \right) - \frac{1}{N}\sum\limits_{k = 1}^N {E{x_{kj}}\left( t \right)} } \right]^2},\end{aligned}\\ &E\left[ { {{{P}}\left( t \right)} } \right] = \frac{{N - 1}}{{{N^2}n}}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^n {\sigma _{ij}^2} } \left( t \right) + \varGamma \left( {E{x_{ij}}\left( t \right)} \right).\end{aligned}\right\}$ | (19) |
式中:
证毕.
2 传感云资源调度 2.1 问题描述与模型构建Tan[17]将传感云定义为WSNs云端服务平台,有机结合多种传感网络应用与云端,为用户提供远程控制、监测等云端服务. 传感云的出现改变了传统WSNs数据采集处理模式,WSNs只需要负责采集数据,而数据处理、分析等任务由云端完成. 传感云资源调度的目的是合理地为多个传感器网络服务请求配置云计算资源,并且使得效益最大化. 由于云资源架构的异构性,不同服务器处理相同任务的能耗和时长不同,并且研究表明系统能耗已经成为云端运营最大的开销,因此基于系统能耗和任务调度的传感云资源调度研究具有重要意义.
对于
定义7 定义传感云资源调度模型为在满足约束条件下,将任务集合
| $\begin{split}&f\left( {{{V}},{K}} \right):\min \; \left\{ {{\rm{WT}},{\rm{WE}}} \right\};\\&\left.{\rm{s.t.}} \begin{array}{l}\displaystyle\sum\limits_{j = 1}^g {{x_{ij}}} = 1,\; i = 1,2, \cdots ,m,\\{T_{\rm{st}}}\left( i \right) \geqslant {T_{\rm{fi}}}\left( j \right),\;{\rm{if}}\;{v_j} \in {{Z}}\left( i \right).\end{array}\right\}\end{split}$ | (20) |
式中:
推导1 设定任务
| ${T_{{\rm{st}}}}\left( i \right) = \left\{ \begin{aligned}&{\max} \; \left( {{T_a},\mathop {\max }\limits_{{v_j} \in {{Z}}\left( i \right)} \Big( {{T_{{\rm{fi}}}}\left( j \right) + {T_{{\rm{con}}}}\left( {i,j} \right)} \Big)} \right),\; {{Z}}\left( i \right) \ne {\bf 0}; \\& 0,\quad{{Z}}\left( i \right) = {\bf 0}. \\ \end{aligned} \right.$ | (21) |
式中:
| ${T_{{\rm{con}}}}\left( {i,j} \right) = \left\{ \begin{aligned}& {T_a} + {w_{ab}}/{q_{ab}},\quad &a \ne b; \\&0,\quad &a = b. \\ \end{aligned} \right.$ | (22) |
式中:wab为任务之间通信传输数据量,qab为任务之间通信传输速率。
| ${T_{{\rm{wor}}}}\left( {i,a} \right) = {l_i}/{I_a}.$ | (23) |
联立式(23)后得到
| $\begin{aligned}{T_{{\rm{fi}}}}\left( i \right) = {T_{{\rm{st}}}}\left( i \right) + {T_{{\rm{wor}}}}\left( {i,a} \right), \end{aligned}$ | (24) |
则
| $\begin{aligned}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{\rm{WT}} = \mathop {\max }\limits_{i = 1}^m \;\left( {{T_{{\rm{fi}}}}\left( i \right)} \right).\end{aligned}$ |
推导2 系统能耗分为执行任务能耗
| ${{\rm{WE}}_{{\rm{on}}}}\left( i \right) = \sum\limits_{{v_i}} {\left( {{l_i}/{I_i}} \right)} {P_{i,\operatorname{work} }},$ | (25) |
| ${{\rm{WE}}_{{\rm{off}}}}\left( i \right) = \left( {{\rm{WT}} - \sum\limits_{{v_i}} {\left( {{l_i}/{I_i}} \right)} } \right) {P_{i,{\rm{low}}}}.$ | (26) |
联立式(25)、(26)得到
| $\begin{gathered}{\rm{WE}} = \sum\limits_{i = 1}^g {\left( {{\rm W{E}_{{\rm{on}}}}\left( i \right) + {\rm W{E}_{{\rm{off}}}}\left( i \right)} \right)},\end{gathered} $ | (27) |
则
| $\begin{split}{\rm{WE}} =& \sum\limits_{i = 1}^g {\sum\limits_{{v_i}} {\left( {{l_i}/{I_i}} \right)} {P_{i,{\rm{work}}}}} +\\ &\sum\limits_{i = 1}^g {\left( {{\rm{WT}} - \sum\limits_{{v_i}} {\left( {{l_i}/{I_i}} \right)} } \right) {P_{i,{\rm{low}}}}} . \end{split}$ | (27) |
确定
传感云资源调度问题属于多目标离散优化问题,因此在Pareto最优解方法的基础上,对粒子编码和更新过程进行离散化处理,并且提出多目标离散ECO(multi-objective discrete ECO,MDECO)算法.
定义8 Pareto最优解. 对于
| ${f_1}\left( {{{X}_i}} \right) \leqslant {f_1}\left( {{{X}_j}} \right) \wedge {f_2}\left( {{{X}_i}} \right) \leqslant {f_2}\left( {{{X}_j}} \right),$ | (28) |
称
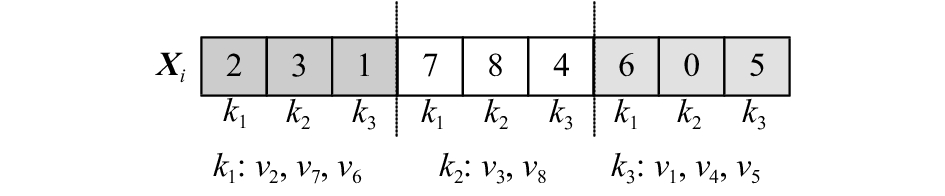
定义9 MDECO离散编码. 对于MDECO算法粒子
| ${{X}_i} = \left( {{v_1},{v_2}, \cdots ,{v_m},\overbrace {0, \cdots ,0}^{g\left\lceil {m/g} \right\rceil - m}} \right).$ | (29) |
式中:
|
图 3 粒子编码与资源调度示意图 Fig. 3 Particle coding and resource scheduling schematic diagram |
从图3列举实例可以看出,
离散粒子更新 对于采用“定义9”编码形式的粒子A、B、C,给出C更新公式为
| ${C} = \left\{ {b \otimes \left( {{A} \odot {B}} \right)} \right\} \to {A}.$ | (30) |
式中:
定义10 定义MDECO粒子更新公式为
| ${{X}_i}\left( {t + 1} \right) = \left\{ \begin{aligned} &{\rm{MDECO}}\left( {{{X}_i}\left( t \right),{\delta }} \right),\;&{r_1} \geqslant \varepsilon ; \\ &{{X}_i}\left( t \right), &{r_1} < \varepsilon , \end{aligned} \right.$ | (31) |
| $\begin{array}{l}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{\rm{MDECO}}\left( {{{X}_i}\left( t \right),{\delta } } \right) = \\\left\{ \begin{aligned}& \left\{ {\varphi \left( {1 - f\left( {{{G}_i}} \right)/\left( {f\left( {{{X}_i}} \right) + \zeta } \right)} \right) \otimes \left( {{{G}_i}\left( t \right) \odot {{X}_i}\left( t \right)} \right)} \right\} \to \\ & \quad\quad{{G}_i}\left( t \right),\quad{r_2} \leqslant 0.5;\\ & \left\{ {\varphi \left( {1 - f\left( {B} \right)/\left( {f\left( {{{X}_i}} \right) + \zeta } \right)} \right) \otimes \left( {{B}\left( t \right) \odot {{X}_i}\left( t \right)} \right)} \right\} \to \\ & \quad\quad{B}\left( t \right),\quad 0.5 < {r_2} \leqslant 0.5 + \xi ;\\ & \left\{ {\varphi \left( {1 - f\left( {{{X}_j}} \right)/\left( {f\left( {{{X}_i}} \right) + \zeta } \right)} \right) \otimes \left( {{{X}_j}\left( t \right) \odot {{X}_i}\left( t \right)} \right)} \right\} \to \\ & \quad\quad{{X}_j}\left( t \right),\quad {\text{其他}}.\end{aligned} \right.\end{array}$ | (32) |
式中:
基于MDECO算法的传感云资源调度算法实现过程可以描述如下.
输入:传感云系统相关参数,待处理任务数据、MDECO算法参数
输出:多个传感云资源调度方案
1. 根据定义9生成初始种群,并对Pareto最优解集初 始化;
2. while (
3. {
4. 执行AKFCM操作;
5. for
6. 为
7. 判定更新后粒子是否满足约束条件,如果满足则 进行支配性判定,即如果
8. 更新
9. end for
10. 更新Pareto最优解
11.
12. }
13. 输出Pareto最优解集,即多个传感云资源调度方案.
3 实验仿真 3.1 ECO算法验证实验为了分析ECO算法的全局寻优性能,采用
为了分析AKFCM聚类效果,分别采用真实数据和ECO种群数据进行实验测试. 真实数据测试实验中的数据来源于文献[18]提供的4组真实数据,分别采用文献[19]的自动确定聚类FCM算法和文献[20]的基于有效性函数的随机模糊聚类算法进行对比实验. 文献[19]通过图深度优先搜索方法获取出现次数的聚类个数,用来对比算法的迭代效率,文献[20]通过计算不同聚类个数下的最佳有效性函数以确定最佳聚类个数,用来对比算法的聚类准确性,聚类准确率

|
图 4 基于真实数据采用不同聚类算法的聚类结果对比 Fig. 4 Comparison of clustering results of different clustering algorithms for real data |

|
图 5 不同迭代次数下ECO种群聚类结果对比 Fig. 5 Comparison of ECO clustering results under different iterations |
| 表 1 3种聚类算法性能对比 Table 1 Performance comparison of three clustering algorithms |
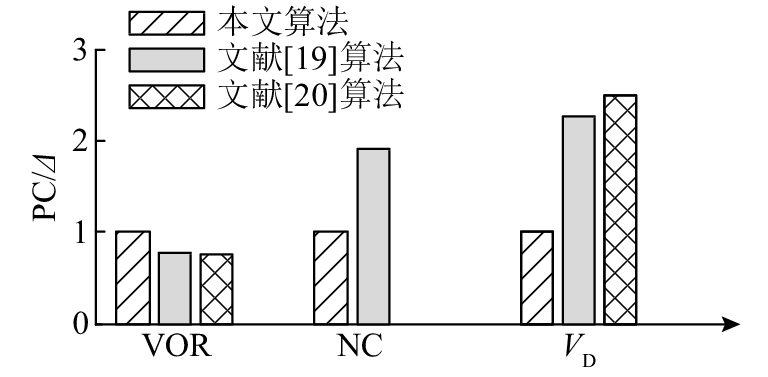
为了更加直观地分析本文聚类算法的性能,提出性能对比指标:
| ${\rm{PC}}\left(\varDelta \right) = \frac{1}{U}\sum\limits_{i = 1}^U {\frac{{I_{{\Theta _x}}^i - I_\Theta ^i}}{{I_\Theta ^i}}} .$ | (33) |
式中:
|
图 6 本文算法和文献[19]、文献[20]算法聚类结果比较 Fig. 6 Comparison of clustering results between the algorithm in this paper and literature [19] and [20] algorithm |
对于真实数据测试实验,从图4可以看出,虽然文献[19]的算法与AKFCM算法得到的最佳聚类个数相同,但是迭代次数几乎是AKFCM算法的2倍. 设定2种算法具有相同的
对于ECO种群数据实验,分别选取
为了进一步对比分析ECO收敛性能,选取布谷鸟优化算法[9]和量子粒子群优化(quantum-behaved particle swarm optimization,QPSO)算法[8]进行对比实验. 评价指标选取为求解成功率
| $ {\rm{Su}} = \frac{{\sum\limits_i^Z {{z_i}} }}{Z},\left\{ \begin{array}{l} {z_i} = 1,\left| {s - \widehat {{s_j}}} \right| > \gamma ;\\ {z_i} = 0,\left| {s - \widehat {{s_j}}} \right| \le \gamma . \end{array} \right. $ | (34) |
式中:
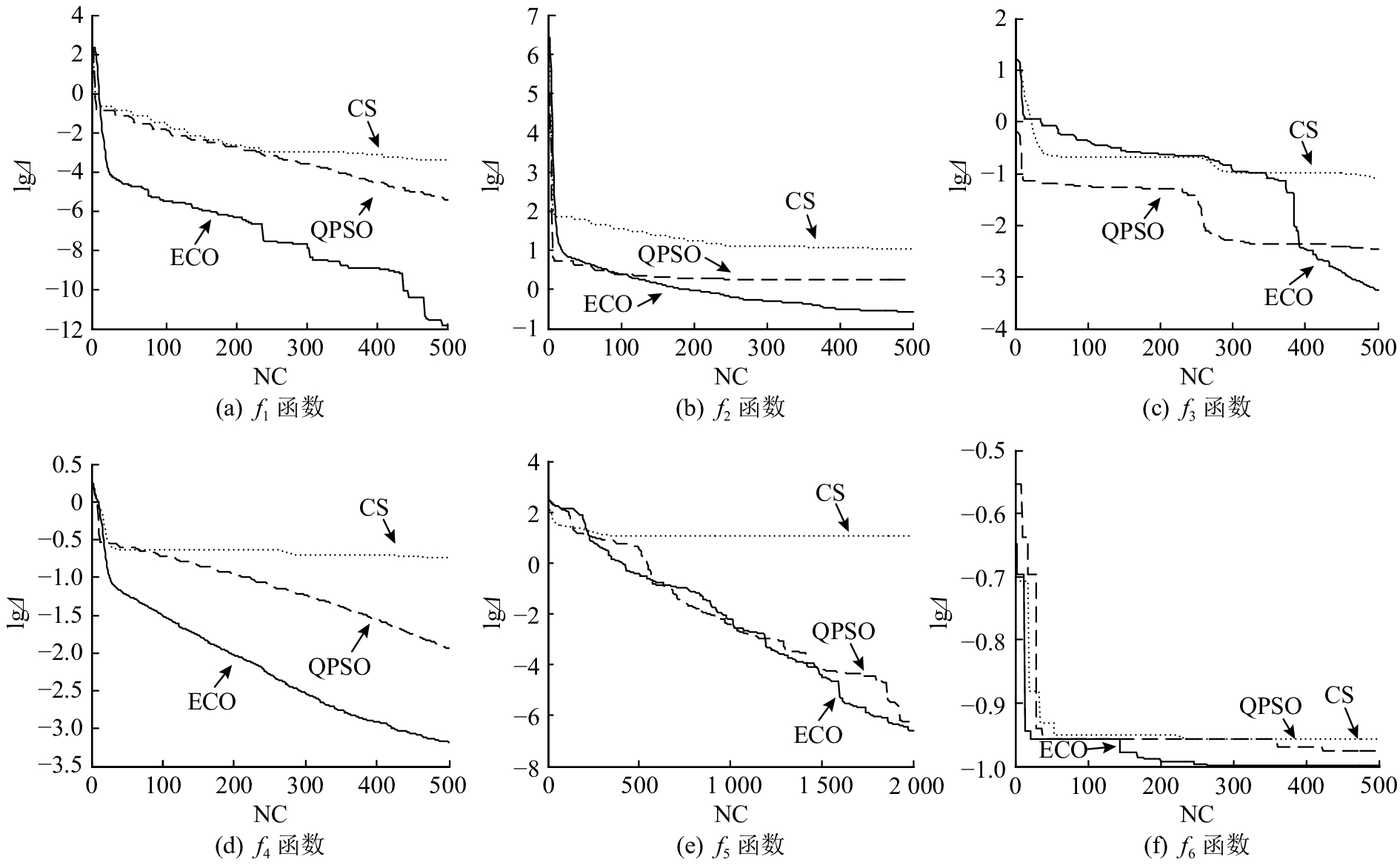
|
图 7 f1、f2、f3、f4、f5、f6函数的收敛曲线 Fig. 7 Function convergence curve of f1, f2, f3, f4, f5 and f6 |
| 表 2 不同算法评价指标对比 Table 2 Comparison of evaluation indexes of different algorithms |
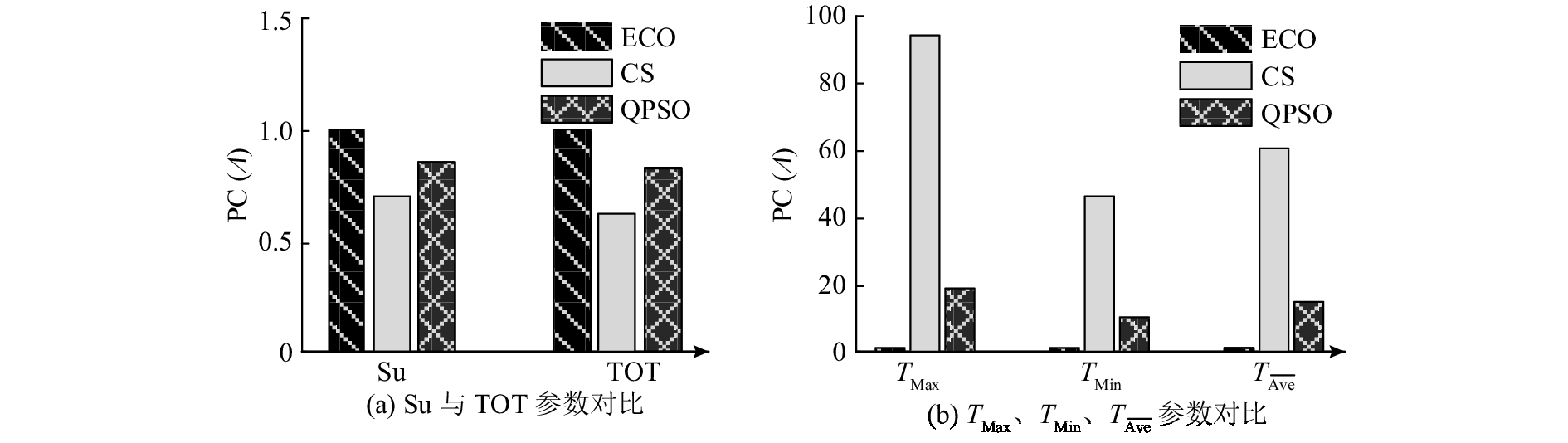
|
图 8 ECO与布谷鸟优化(CS)算法、量子粒子群优化(QPSO)算法的性能对比 Fig. 8 Porformance comparison between ECO and CS and QPSO |
从图7及表2可以看出,对于函数
AKFCM算法具有可靠的聚类稳定性和聚类效果,特别是对于动态变化的样本数据,AKFCM算法能够在较少迭代次数下实现较高水平的聚类分析,因为AKFCM算法在聚类过程中以样本隶属度为划分基础,迭代过程更符合模糊聚类实际情况.
ECO算法具有较高的收敛成功率和收敛精度. 这是因为ECO算法在迭代过程中,实时分析种群样本多样性,并且根据种群聚类结果选取更加合理的学习对象指导粒子进化,使得算法在后期仍具有较强的深度搜索能力和较高的跳出局部极值的概率,但是,引入AKFCM算法使得ECO算法需要消耗更多的时间进行迭代进化.
3.2 传感云资源调度测试实验利用NS2平台模拟80个具有不同规模、执行不同监测任务的无线传感器网络数据;利用CloudSim测试平台仿真15个云计算资源,由程序随机生成100个传感器网络数据处理任务对应的
由于MDECO属于多目标资源调度优化算法,目前大部分文献列举方法为单目标算法,为了能够进行对比实验,选取MDECO算法Pareto最优解集中与单目标算法任务长度接近的解对比2种算法能耗,并且用
| 表 3 MDECO与其他不同调度算法性能对比 Table 3 Performance comparison between MDECO and other different scheduling algorithms |
从表3可以看出,处理不同传感云资源任务调度规模时,MDECO算法的ET好于文献[22]、文献[23]和文献[24]算法,并且MDECO算法能耗最大能够降低44.29%,最少能够降低6.67%;同样,MDECO算法的
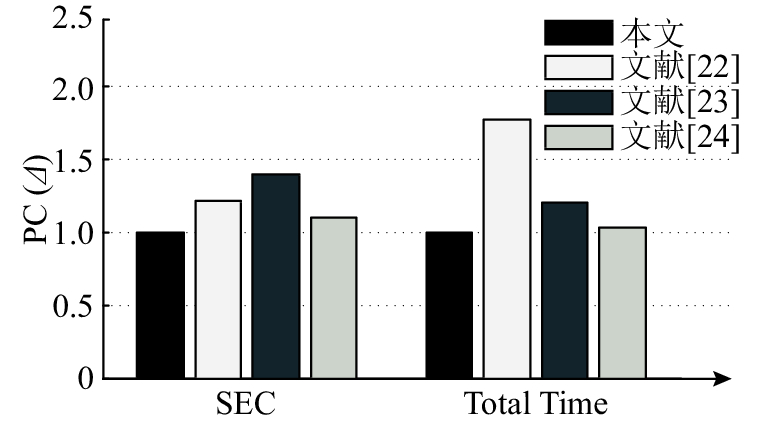
|
图 9 本文算法和文献[22]、文献[23]、文献[24]算法在系统能耗和任务执行时间方面的性能对比。 Fig. 9 Performance comparison in SEC and total time under the algorithm in this paper and literature [22], literature [23],and [24] algorithm. |
选取文献[1]提出的多目标Memetic优化算法、文献[6]提出的多目标分组遗传算法和多目标粒子群算法(multi-objective particle swarm optimization,MPSO)进行对比实验,评价指标选取文献[1]提出的
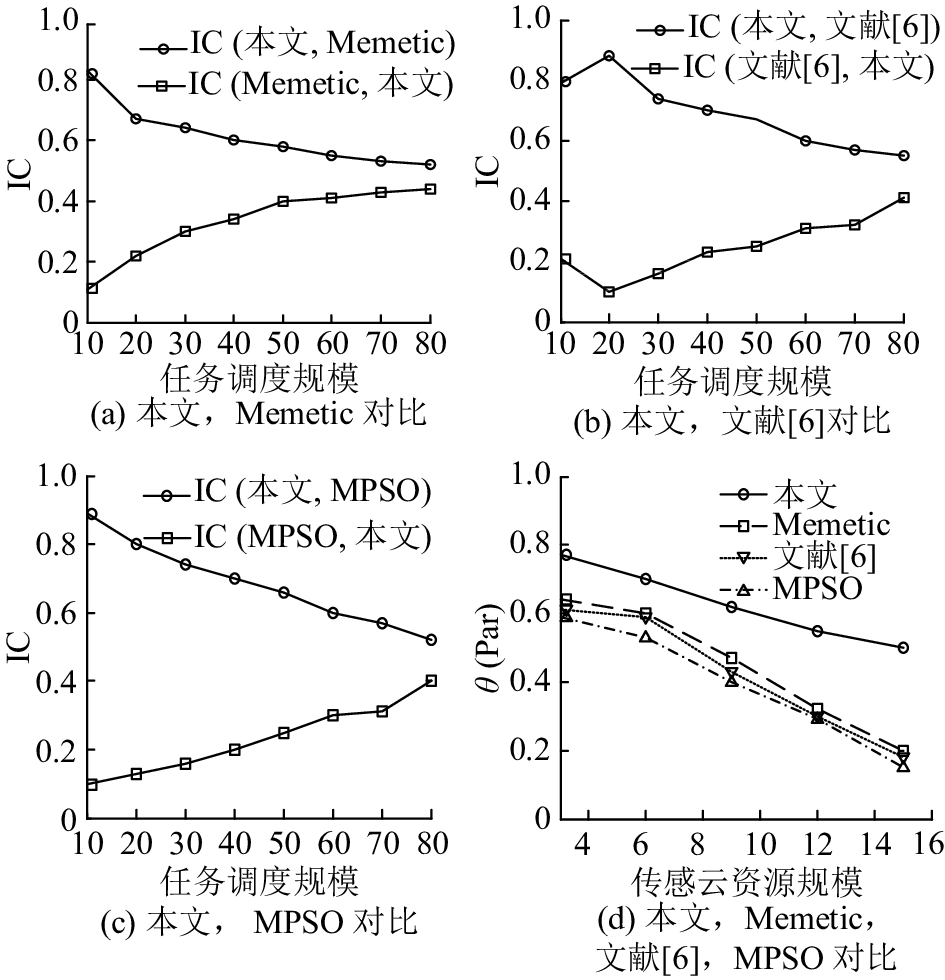
|
图 10
本文MDECO算法、文献[1]、文献[6]、MPSO算法下的关于 IC(X,Y)测度和Pareto最优解集多样度
|
从图10可以看出,对于不同传感云资源任务调度规模,IC(本文,Y)(Y表示为其他3种算法)都要大于IC(Y,本文). 例如,对于IC(本文,Memetic),MDECO算法(本文算法)支配Memetic算法最优解的概率分别为80.2%、64.3%、61.1%、59.4%、57.2%、54.3%、50.1%、49.9%,Memetic算法算法支配MDECO最优解的概率仅有14.5%、20.7%、29.4%、30.1%、37.3%、36.8%、40.2%、41.1%,MDECO算法能够得到更多优秀的解. 对于不同传感云资源规模,MDECO算法的最优解集多样度要好于其他3种算法,MDECO算法得到的Pareto最优解集更加均匀.
3.2.3 传感云资源调度测试实验结果分析从MDECO算法与单目标调度算法和多目标优化算法对比实验结果可以看出,基于MDECO算法的传感云资源调度方案更加合理,因为弹性碰撞优化算法优秀的全局寻优能力能够探索到更多潜在的任务调度问题最优解,有效降低系统能耗和任务处理时间,提高Pareto最优解集质量水平,并且MDECO算法采用多目标处理方式,不是简单地将多个优化目标加权成单目标,能够为决策者提供多种决策依据.
4 结 语对新的弹性碰撞优化算法进行了研究,提出了全新的智能优化算法,并且从种群多样的角度对智能优化算法改进策略进行分析探索,引入自适应核FCM模糊聚类算法实现对种群样本多样性的实时分析,使得种群进化方向更加合理科学. 种群样本多样性定量分析和测试函数仿真结果证明ECO在运算后期仍然具有较好的种群多样性. 从传感云资源调度应用研究入手,构建多目标传感云资源调度优化模型、设计符合工程实际的弹性碰撞优化算法实现流程,最后仿真实验验证传感云资源调度方案的有效性. 下一步将针对高维病态函数优化和提高传感云资源调度效率进行研究.
| [1] |
李智勇, 陈少淼, 杨波, 等. 异构云环境多目标Memetic优化任务调度方法[J]. 计算机学报, 2016, 39(2): 377-390. LI Zhi-yong, CHEN Shao-miao, YANG Bo, et al. Multi-objective Memetic algorithm for task scheduling on heterogeneous cloud[J]. Chinese Journal of Computers, 2016, 39(2): 377-390. |
| [2] |
王晓辉, 吴禄慎, 陈华伟, 等. 应用改进的粒子群优化模糊聚类实现点云数据的区域分割[J]. 光学精密工程, 2017, 25(4): 563-573. WANG Xiao-hui, WU Lu-shen, CHEN Hua-wei, et al. Region segmentation of point cloud data based on improved particle swarm optimization fuzzy clustering[J]. Optics and Precision Engineering, 2017, 25(4): 563-573. |
| [3] |
COLORNI A, DORIGO M, MANIEZZO V. Distributed optimization by ant colonies [C] // Proceedings of the First European Conference on Artificial Life. France: Elsevier Publishing, 1991: 134-142 https://www.researchgate.net/publication/216300484_Distributed_Optimization_by_Ant_Colonies
|
| [4] |
KENNEDY J, EBERHART R C. Particle swarm optimization [C] // Proceedings of the IEEE International Conference on Neural Networks. Perth: IEEE, 1995: 1942-1948 http://www.oalib.com/references/17655583
|
| [5] |
TAN Y, ZHU Y. Fireworks algorithm for optimization[C]// Proceedings of the 1st International Conference on Advances in Swarm Intelligence. Springer-Verlag, 2010:355-364 https://link.springer.com/chapter/10.1007/978-3-642-13495-1_44
|
| [6] |
李淑英, 潘亚, 费薇, 等. 基于分组遗传算法的虚拟机放置方法[J]. 南京理工大学学报, 2016, 40(6): 322-327. LI Shu-ying, PAN Ya, FEI Wei, et al. Virtual machine placement method based on grouping genetic algorithm[J]. Journal of Nanjing University of Science and Technology, 2016, 40(6): 322-327. |
| [7] |
LIANG J J, QIN A K, SUGANTHAN P N, et al. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J]. IEEE Transactions on Evolutionary Computation, 2006, 10(3): 281-295. |
| [8] |
田瑾. 高维多峰函数的量子行为粒子群优化算法改进研究[J]. 控制与决策, 2016, 31(11): 1967-1972. TIAN Jin. Improvement of quantum-behaved particle swarm optimization algorithm for high-dimensional and multi-modal functions[J]. Control and Decision, 2016, 31(11): 1967-1972. |
| [9] |
马卫, 孙正兴. 采用搜索趋化策略的布谷鸟全局优化算法[J]. 电子学报, 2015, 43(12): 2429-2439. MA Wei, SUN Zheng-xing. A global cuckoo optimization algorithm using coarse-to-fine search[J]. Chinese Journal of Electronics Acta Electronica Sinica, 2015, 43(12): 2429-2439. DOI:10.3969/j.issn.0372-2112.2015.12.013 |
| [10] |
崔晓晖, 印桂生, 董红斌. 面向服务匹配问题的协同演化算法[J]. 软件学报, 2015, 26(7): 1601-1614. CUI Xiao-hui, YIN Gui-sheng, DONG Hong-bin. Co-evolutionary algorithm for Web service matching[J]. Journal of Software, 2015, 26(7): 1601-1614. |
| [11] |
EBRAHIMI D, ASSI C. Network coding-aware compressive data gathering for energy-efficient wireless sensor networks[J]. ACM Transactions on Sensor Networks, 2015, 11(4): 1-24. |
| [12] |
曾建电, 王田, 贾维嘉, 等. 传感云研究综述[J]. 计算机研究与发展, 2017, 54(5): 925-939. ZENG Jian-dian, WANG Tian, JIA Wei-jia, et al. A survey on sensor-cloud[J]. Journal of Computer Research and Development, 2017, 54(5): 925-939. |
| [13] |
MADRIA S, KUMAR V, DALVI R. Sensor cloud: a cloud of virtual sensors[J]. IEEE Software, 2014, 31(2): 70-77. |
| [14] |
TIAN F G, CHEN K K. Towards optimal resource provisioning for running mapreduce programs in public clouds [C] // Proceedings of IEEE International Conference on Cloud Computing, Washington: IEEE, 2011: 155-162 http://ieeexplore.ieee.org/document/6008705/
|
| [15] |
CHohan N, Castillo C, Spreitzer M, et al. See spot run: using spot instances for map-reduce workflows[C]//Proceeding of the 2nd Usenix Conference on Hot Topics in Cloud Computing. USENIX Association, 2011: 7 http://dl.acm.org/citation.cfm?id=1863110
|
| [16] |
MA A L, ZHONG Y F, ZHANG L P. Adaptive multiplicative memetic fuzzy clustering algorithm for remote sensing imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(8): 4202-4217. |
| [17] |
TAN K L. What’s next?: sensor+cloud? [C]//Proceedings of the 7th ACM International Workshop on Data Management for Sensor Network. New York: ACM, 2010: 1 http://dl.acm.org/citation.cfm?id=1858160
|
| [18] |
KUNCHEVA L. Clustering date [DB/OL]. [2014-09–10]. http://pages.bangor.ac.uk/~mas00a/activities/artificial_data.html
|
| [19] |
陈海鹏, 申铉京, 龙建武, 等. 自动确定聚类个数的模糊聚类算法[J]. 电子学报, 2017, 45(3): 687-694. CHEN Hai-peng, SHEN Xuan-jing, LONG Jian-wu, et al. Fuzzy clustering algorithm for automatic identification of clusters[J]. Acta Electronica Sinica, 2017, 45(3): 687-694. DOI:10.3969/j.issn.0372-2112.2017.03.028 |
| [20] |
林济铿, 刘露, 张闻博, 等. 基于随机模糊聚类的负荷建模与参数辨识[J]. 电力系统自动化, 2013, 37(14): 50-57. LIN Ji-keng, LIU Lu, ZHANG Wen-bo, et al. Load modeling and parameter identification based on random fuzziness clustering[J]. Automation of Electric Power Systems, 2013, 37(14): 50-57. DOI:10.7500/AEPS201211019 |
| [21] |
朴尚哲, 超木日力格, 于剑. 模糊C均值算法的聚类有效性评价[J]. 模式识别与人工智能, 2015, 28(5): 452-461. PIAO Shang-zhe, CHAOMURILIGE, YU Jian. Cluster validity indexes for FCM clustering algorithm[J]. Pattern Recognition and Artificial Intelligence, 2015, 28(5): 452-461. |
| [22] |
魏蔚, 刘扬, 杨卫东. 一种通用云计算资源调度问题的快速近似算法[J]. 计算机研究与发展, 2016, 53(3): 697-703. WEI Wei, LIU Yang, YANG Wei-dong. A fast approximation algorithm for the general resource placement problem in cloud computing platform[J]. Journal of Computer Research and Development, 2016, 53(3): 697-703. |
| [23] |
XU Y, LI K, HE L, et al. A DAG scheduling scheme on heterogeneous computing systems using double molecular structure based chemical reaction optimization[J]. Journal of Parallel and Distributed Computing, 2013, 73(9): 1306-1322. DOI:10.1016/j.jpdc.2013.05.005 |
| [24] |
CAO J, LI K, STOJMENOVIC I. Optimal power allocation and load distribution for multiple heterogeneous multicore server processors across clouds and data centers[J]. IEEE Transactions on Computers, 2014, 63(1): 45-58. DOI:10.1109/TC.2013.122 |


