2. 瑞典皇家理工学院 建筑与建设环境学院, 瑞典 斯德哥尔摩 SE-100 44
2. Architecture and Civil Engineering, KTH Royal Institute of Technology, Stockholm SE-100 44, Kingdom of Sweden
随着城市人口以及交通需求的不断增加, 路网不畅、设施不足、交通拥堵等问题越来越突出.为了研究城市交通网络层面的拥堵演化规律, 城市路网交通流的宏观特性成为近年来的研究热点.Daganzo等[1-2]通过实测数据, 验证了现实交通网络中存在宏观基本图关系(macroscopic fundamental diagram, MFD).
针对MFD的研究大多基于仿真数据或微波数据, 随着GPS技术的发展与普及, 获取基于移动检测数据的MFD的可行性越来越高.Gayah等[3]通过获取道路网络中少量浮动车速度信息, 研究网络平均车辆密度的估计方法.Leclercq等[4]对不同的MFD估计方法进行对比和分析.Du等[5]在整个路网中浮动车渗透率非均衡分布的情况下, 从有限车辆中获取的信息对路网MFD进行估计.Ambühl等[6]融合线圈检测数据和浮动车数据, 建立MFD模型.Gayah等[7]分析交通需求分布和驾驶员的路径选择对MFD的影响.
在国内, 姬杨蓓蓓[8]采用VISSIM仿真实验方法, 验证了宏观基本图的存在.马万经等[9]对MFD的相关研究成果进行系统分析与总结.岳圆圆[10]利用浮动车数据和微波检测数据, 从路段、分等级路网和区域路网对北京多层次交通流基本图开展研究.许菲菲等[11]应用Paramics交通仿真软件, 对广州市海珠区路网进行建模, 通过采取不同的交通管控措施, 分析MFD的影响因素.韦薇[12]利用仿真参数研究流量-密度关系, 基于此推导路网MFD模型并探索模型参数的影响因素.朱琳等[13]利用实测数据, 证明了密度分布的不均匀性是影响路网宏观交通运行状态的根本因素.贺正冰等[14]利用高密度检测器数据, 绘制并分析北京市快速环路的宏观基本图.
综上所述, 目前对路网宏观基本图的研究主要是利用仿真数据开展, 密度在路网中的不均匀分布是影响MFD的重要因素, 但针对该问题的研究尚处于初级阶段.本文从出租车GPS数据出发, 利用微波数据对出租车GPS数据进行扩展处理, 研究基于移动检测数据的交通网络MFD特征, 对路网宏观交通状态进行评价.本文提出利用全部固定检测器和全部出租车轨迹数据的扩充系数估计方法, 考虑到扩充系数随时间、流量、密度等不同条件的变化而改变, 能够更好地反映宏观交通流的变化规律.
1 模型与方法MFD反映了交通网络层面的平均流量和密度关系, 主要应用于路网宏观交通状态识别与区域交通总量动态调控.分析如何利用移动检测数据构建MFD, 尤其是如何结合固定检测器数据, 将移动检测数据所得的MFD扩展为整个路网MFD.
1.1 基于移动检测数据的MFD若网络中的每一辆浮动车轨迹线数据已知, 则路网浮动车平均密度和流量可以分别由Edie提出的定义式给出:
| $ {K_{{\rm{probe}}}} = \sum\limits_{i = 1}^I {{t_i}} /\left( {{L_n}T} \right) = {\rm{TTT/}}\left( {{L_n}T} \right), $ | (1) |
| $ {Q_{{\rm{probe}}}} = \sum\limits_{i = 1}^I {{d_i}} /\left( {{L_n}T} \right) = {\rm{TTD/}}\left( {{L_n}T} \right). $ | (2) |
式中:Kprobe和Qprobe分别为路网浮动车平均密度和流量;I为固定时间间隔(例如:15 min)内总的出行次数;ti和di分别为第i条轨迹线的旅行时间和距离;Ln和T为路网总长度和分析时间段长度;TTT和TTD分别为一定时间段内所有浮动车的总行驶时间和总行驶距离.
在实际道路网络中, 很难获取所有车辆详细的轨迹线数据.若只能获得一部分轨迹线数据, 则不能采用式(1)、(2)对MFD进行估计.为了研究交通网络的MFD特性, Nagle等[15]提出以下近似估计方法:
| $ {{K'}_{{\rm{probe}}}} = \sum\limits_{i' = 1}^{I'} {{t_{i'}}} /\left( {\rho {L_n}T} \right), $ | (3) |
| $ {{Q'}_{{\rm{probe}}}} = \sum\limits_{i' = 1}^{I'} {{d_{i'}}} /\left( {\rho {L_n}T} \right). $ | (4) |
式中:K′probe和Q′probe分别为估计路网中所有车辆的平均密度和流量;ρ为浮动车平均渗透率;ti′和di′分别为第i′次出行的旅行时间和旅行距离;I′为分析时间段内的总浮动车辆数;对于浮动车和非浮动车, 假设平均旅行时间和旅行距离是相同的, 即浮动车渗透率在整个路网中都是一致的, 那么路网中所有车辆总的旅行时间和旅行距离可以通过浮动车和平均渗透率得到.
1.2 基于固定检测数据的MFD固定检测数据(例如来源于微波检测器)一般为单车道数据, 在计算基于固定检测器数据的宏观基本参数前, 需要将单车道数据整合成道路断面数据.提出以车道流量进行加权的计算方法如下:
| $ {{q'}_j} = \sum\limits_{k = 1}^{{n_j}} {{q_{jk}}} , $ | (5) |
| $ {{v'}_j} = \sum\limits_{k = 1}^{{n_j}} {{v_{jk}}{q_{jk}}} /\sum\limits_{k = 1}^{{n_j}} {{q_{jk}}} , $ | (6) |
| $ {{o'}_j} = \left( {\sum\limits_{k = 1}^{{n_j}} {{o_{jk}}{q_{jk}}} /\sum\limits_{k = 1}^{{n_j}} {{q_{jk}}} } \right) \times 100\% , $ | (7) |
| $ {{k'}_j} = {10^3}{{o'}_j}{n_j}/{l_{{\rm{eq}}}}. $ | (8) |
式中:q′j、v′j、o′j和k′j分别为断面流量、以车道流量进行加权的断面平均速度、断面平均时间占有率和断面密度, j为道路断面, qjk、vjk和ojk分别为第j个断面第k条车道的流量、速度和时间占有率, nj为断面j的总车道数, leq为等效车长.
根据断面加权流量, 对路网平均流量Qfixed、平均速度Vfixed和平均密度Kfixed进行估计, 计算方法如下:
| $ {Q_{{\rm{fixed}}}} = \sum\limits_{j = 1}^J {{{q'}_j}} /J, $ | (9) |
| $ {V_{{\rm{fixed}}}} = \sum\limits_{j = 1}^J {{{v'}_j}} /J, $ | (10) |
| $ {K_{{\rm{fixed}}}} = \sum\limits_{j = 1}^J {{{k'}_j}} /J. $ | (11) |
式中:J为布设有微波检测器的总断面数.
1.3 等效渗透率MFD的估计方法以所有浮动车从起点到终点的渗透率相同且已知为前提假设条件.虽然很容易为路网中的所有浮动车假设一个已知的渗透率, 但这与实际路网中的车辆运行状态不符, 配备有GPS设备的浮动车在路网中并非均匀分布.例如, 出租车在时间和空间分布上均具有明显的异质性.采用单一无差别的渗透率来估计浮动车辆的真实分布不准确.为了解决上述问题, 对估计浮动车的等效渗透率计算方法作出以下改进:
| $ \rho _{{\rm{eq}}}^k = {K_{{\rm{probe}}}}/{K_{{\rm{fixed}}}}, $ | (12) |
| $ \rho _{{\rm{eq}}}^q = {Q_{{\rm{probe}}}}/{Q_{{\rm{fixed}}}}. $ | (13) |
式中:Kfixed和Qfixed分别为基于固定检测数据得到的网络平均密度和平均流量, Kprobe和Qprobe分别为基于浮动车辆得到的路网密度和流量, ρeqk和ρeqq分别为密度等效渗透率和流量等效渗透率(扩展系数).
1.4 度量指标为了评估扩展系数准确性, 分别采用路网平均流量的均方根误差RMSEQ和密度的均方根误差RMSEK以及路网平均流量和密度的标准均方根误差NRMSEQ, K作为度量指标, 计算公式如下:
| $ {\rm{RMS}}{{\rm{E}}_Q} = \sqrt {\sum\limits_{t = 1}^N {\frac{{{{\left( {Q\left( t \right) - \hat Q\left( t \right)} \right)}^2}}}{N}} } , $ | (14) |
| $ {\rm{RMS}}{{\rm{E}}_K} = \sqrt {\sum\limits_{t = 1}^N {\frac{{{{\left( {K\left( t \right) - \hat K\left( t \right)} \right)}^2}}}{N}} } , $ | (15) |
| $ \begin{array}{l} {\rm{NRMS}}{{\rm{E}}_{Q,K}} = \\ \sqrt {\sum\limits_{t = 1}^N {\left[ {{{\left( {\frac{{Q\left( t \right) - \hat Q\left( t \right)}}{{{Q_{\rm{c}}}}}} \right)}^2} + {{\left( {\frac{{K\left( t \right) - \hat K\left( t \right)}}{{{K_{{\rm{jam}}}}}}} \right)}^2}} \right]} /N} . \end{array} $ | (16) |
式中:Q(t)和K(t)分别为微波检测器在t时刻所采集到的路网平均流量和平均密度观测值;
本文的数据来源包括:杭州市7 109辆出租车2015年6月22~30日连续9天的GPS数据;同一时间段的微波检测器数据.
1) 出租车GPS数据包含以下信息:日期、时间、出租车编号、产生数据时所在的经度、纬度、速度以及载客状态.每辆出租车经过固定时间间隔(20 s或60 s)产生一条数据, 以2015年6月22日为例, 当日共产生30 194 410条数据.剔除掉噪声数据, 剩余22 832 389条有效数据.统计出当天出租车总出行次数为113 095次, 有效车辆数为5 648辆, 平均每辆出租车一天完成20次载客出行.噪声数据的剔除方法如下:剔除车辆编号为空, 轨迹点时间间隔过大(根据统计结果, 设置为>60 s), 载客状态突变(例如载客状态从0到1, 再变回0为一次旅行)的异常数据.
2) 在杭州市路网中, 共布设286个微波检测器, 提供了每隔车道每5 min的车辆数、平均速度、时间占有率和时间戳等信息.以6月22日为例, 共有记录530 368条.
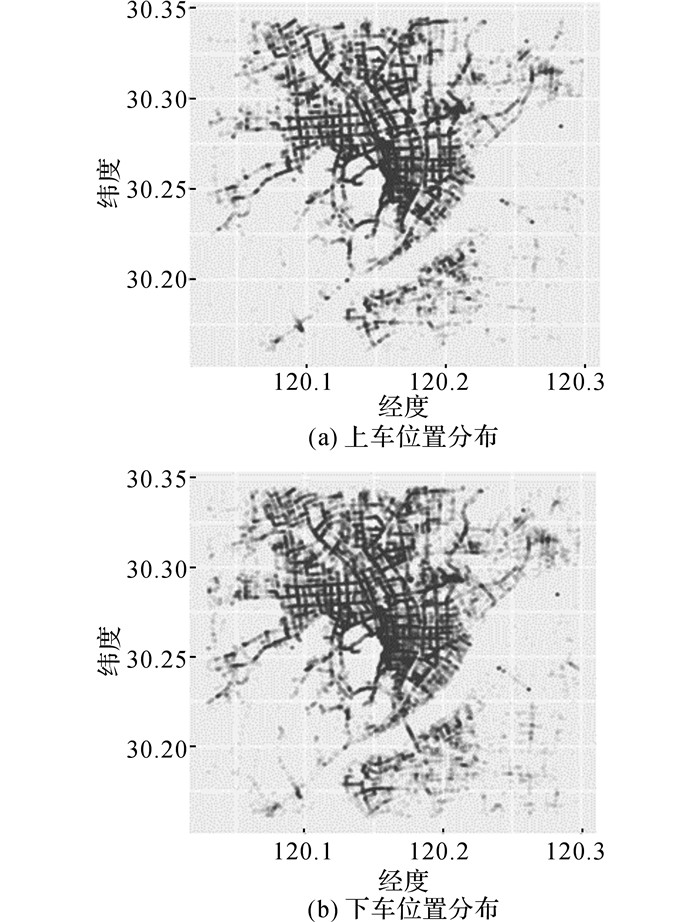
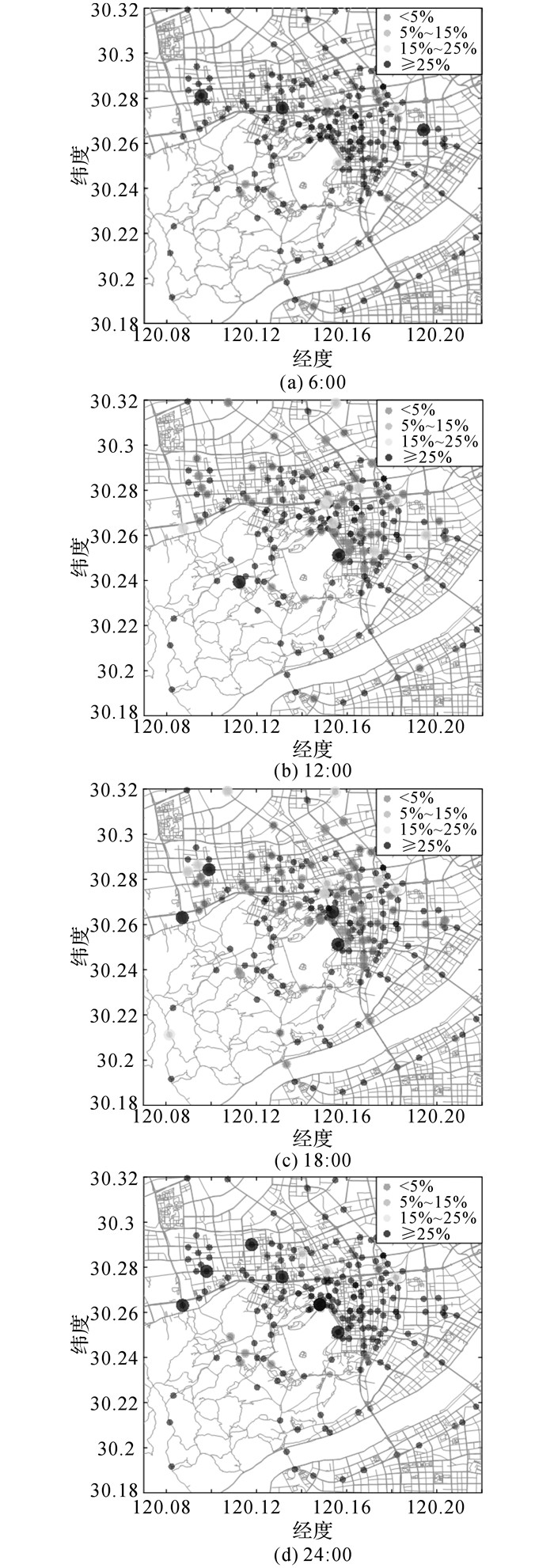
统计2015年6月22日出租车乘客上、下车位置分布, 如图 1所示.可以看出, 杭州市交通路网轮廓, 展示了市区与郊区的分布密度存在明显差异.如图 2所示为不同时刻微波检测器采集到的时间占有率的空间分布.西湖东北侧的时间占有率普遍较大, 交通需求较高.
|
图 1 出租车乘客上车、下车位置分布 Fig. 1 Distributions of taxi pick-up and drop-off locations of Hangzhou |
|
图 2 杭州市微波检测器时间占有率时空分布 Fig. 2 Spatio-temporal distributions of time occupanciesdetected by remote microwave sensors of Hangzhou |
应用Edie提出的通用定义式对路网平均密度和流量进行估计.其中分析时间间隔为300 s, 杭州市道路网总长度约为4 420.82 km.平均速度可以通过TTD/TTT计算得到.
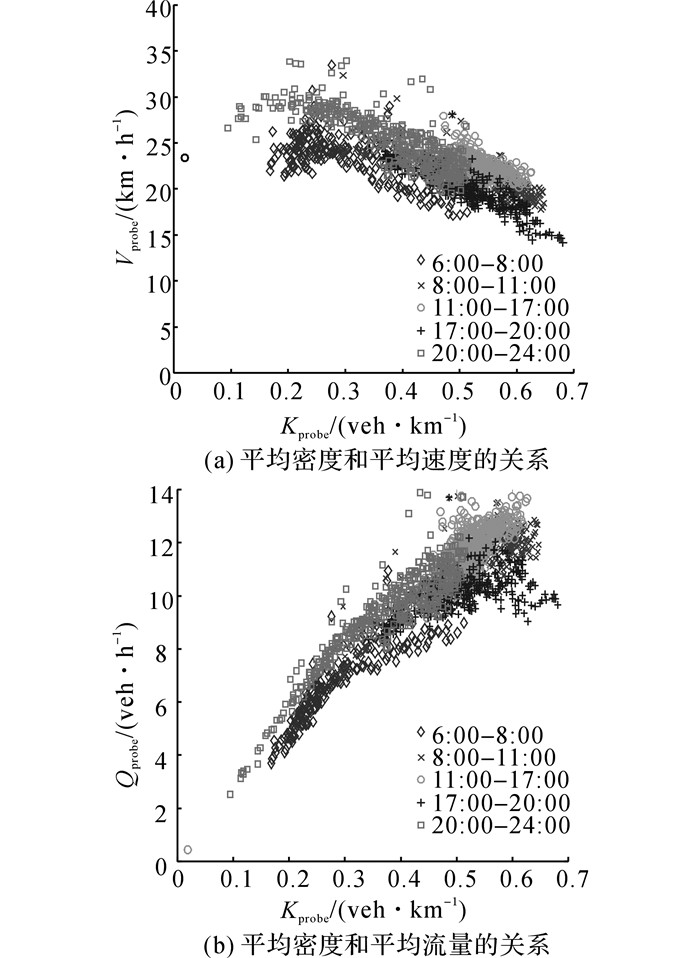
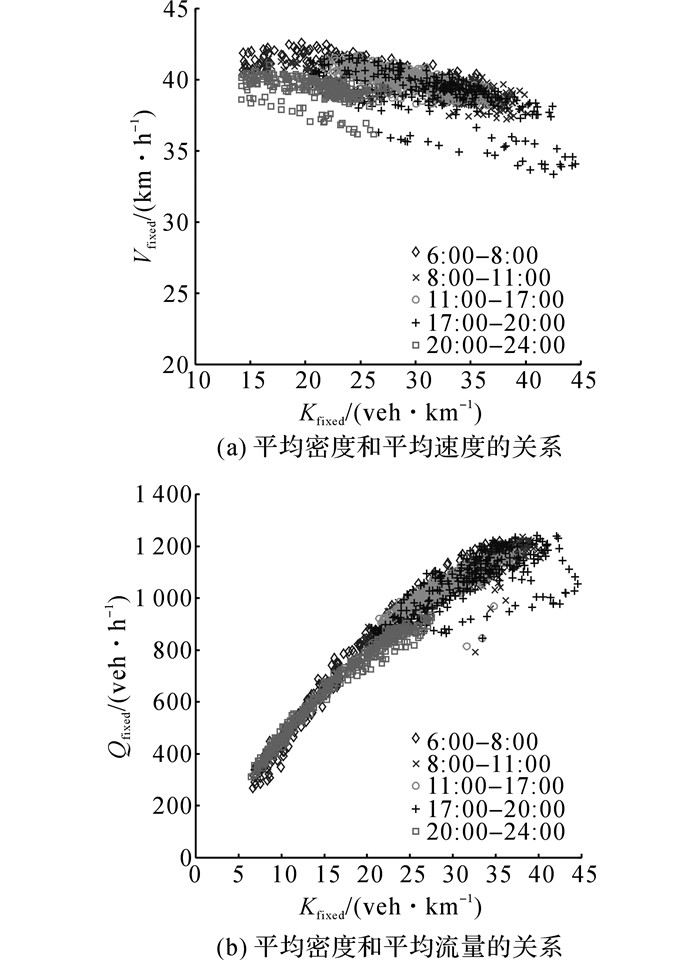
基于出租车GPS数据的宏观基本图如图 3所示.图中,Vprobe为平均速度.可以看出, 出租车平均速度与平均密度呈负相关性, 平均流量随平均速度的提高先增加, 而后呈下降趋势, 存在滞回现象, 符合此前研究中对宏观基本图形状的描述.早高峰和晚高峰虽然车辆密度相差不大, 但是晚高峰的流量与速度普遍低于早高峰.根据该浮动车宏观基本图, 可以判别杭州市路网的宏观交通状态.通过接入实时的出租车GPS数据, 可以计算得到对应于该时刻的MFD, 从而对当前时刻的道路网络交通状态进行实时判别.利用式(5)~(11), 建立基于固定微波检测数据的交通网络MFD如图 4所示.
|
图 3 基于出租车GPS数据构建宏观基本图 Fig. 3 MFDs based on taxi GPS data |
|
图 4 基于微波检测器数据构建宏观基本图 Fig. 4 MFDs based on remote microwave data |
对比基于移动检测数据(见图 3)和固定检测数据(见图 4)的MFD可知, 微波数据得到的平均速度约为出租车速度的2倍, 原因如下:1)由于出租车的运行特点, 大部分处于市中心较拥堵的地区, 所以平均速度低于微波平均速度;2)微波探测器点位一般设置于路中间, 没有将交叉口处较容易出现堵塞情况的速度计算在内, 造成平均速度比实际值高.微波数据的统计方法对于流量与密度这种非瞬时性的数据不会有太大影响.当评定扩展系数时, 仅评定出租车平均密度与流量的扩展系数.
2.3 误差和渗透率分析基于出租车GPS数据所构建的MFD是在渗透率ρ为固定数值的假设条件下, 然而在现实路网中, 出租车的空间分布是不均匀的.为了提高模型的适用性, 分别采用基于密度的等效渗透率ρeqk和基于流量的等效渗透率ρeqq来估计MFD.
取2015年6月22~26日共5天的微波检测器数据与出租车GPS数据, 将微波数据得到的宏观基本图参数与出租车数据得到的宏观基本图参数进行对比, 计算得到等效渗透率, 即扩展系数.对以下2种计算方法进行对比.
1) 根据平均值估计扩展系数.假定出租车的等效渗透率变化不大, 分别取5天内所有微波数据宏观基本图参数与出租车数据宏观基本图参数的比值平均值作为扩展系数, 则ρeqk =2.34%, ρeqq =1.25%.
2) 根据出租车平均密度与平均流量取不同的扩展系数.假定出租车平均密度在一定范围内, 等效渗透率变化不大, 取这一范围内的出租车密度相对于微波数据密度的比值并取平均值作为等效渗透率.平均流量的等效渗透率取法同上.结果如表 1所示.
| 表 1 基于出租车GPS数据的等效渗透率 Table 1 Equivalent penetration rate of taxi GPS data |
方法1分别计算密度和流量的扩展系数, 但思路基本建立在渗透率一致分布的前提上;方法2假设在一定范围内的等效渗透率维持定值, 分段取平均值作为该区间的等效渗透率.
按照同样方法处理剩余4天的出租车GPS数据与微波检测数据, 得到每5分钟的3个宏观基本参数.根据式(14)~(16), 计算观测值和估计值之间的误差, 结果如表 2所示.可以看出, 方法2的各项误差指标均比方法1低, 表现更好.采用方法2的扩展系数对出租车GPS数据进行扩展.
| 表 2 2种方法的均方根误差比较 Table 2 RMSE comparison of two expansion methods |
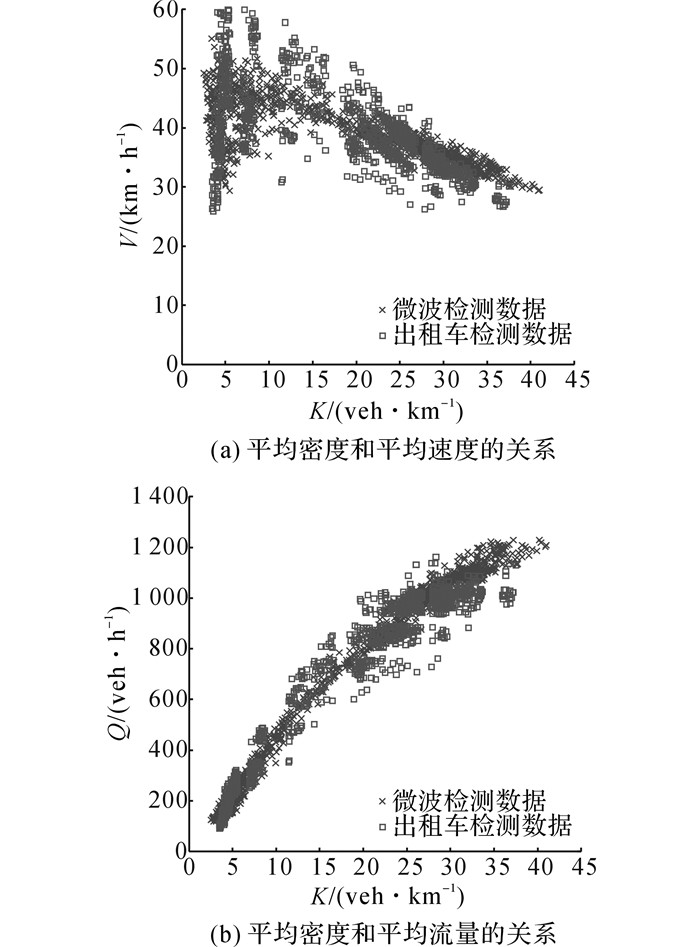
基于第2种扩展系数的计算方法, 对出租车GPS数据进行扩展, 结果如图 5所示.扩展后的宏观基本图与利用微波检测器数据构建的宏观基本图形态上一致, 两者之间的关系可以用二次函数表示.将扩展后的移动检测数据MFD与固定检测数据MFD对比, 两者相差不大, 散点分布较接近.扩展后的MFD显示, 当路网车辆密度达到16 veh/km时, 路网平均流量达到最大, 约为670 veh/h.对比此前连续5天根据微波数据获得的MFD可知, 当车辆密度达到17 veh/km时, 路网内平均流量达到最大, 约为720 veh/h, 扩展后的宏观基本图在车辆密度上相差不多.
|
图 5 扩展后的移动检测数据MFD与固定检测数据MFD对比 Fig. 5 MFD comparison of expanded probe data and remote microwave data |
本文针对基于固定检测数据MFD估计方法的不足, 提出基于移动检测数据并采用密度和流量分段后的均值作为该段等效渗透率的路网MFD计算方法.结果表明, 根据平均密度和平均流量, 在一定范围内考虑不同的扩展系数优于直接采用微波数据对出租车数据渗透率的算术平均值, 计算误差更小.今后, 可以考虑缩小研究范围, 分块分析不同区域的MFD, 从而为研究分区域交通控制方法提供参考.
| [1] |
DAGANZO C F. Urban gridlock:Macroscopic modeling and mitigation approaches[J]. Transportation Research Part B, 2007, 41(1): 49-62. DOI:10.1016/j.trb.2006.03.001 |
| [2] |
GEROLIMINIS N, DAGANZO C F. Existence ofurban-scale macroscopic fundamental diagrams:Some experimental findings[J]. Transportation Research Part B, 2008, 42(9): 759-770. DOI:10.1016/j.trb.2008.02.002 |
| [3] |
GAYAH V, DIXIT V. Using mobile probe data and the macroscopic fundamental diagram to estimate network densities[J]. Journal of the Transportation Research Board, 2013, 2390(-1): 76-86. |
| [4] |
LECLERCQ L, CHIABAUT N, TRINQUIER B. Macroscopic fundamental diagrams:A cross-comparison of estimation methods[J]. Transportation Research Part B, 2014, 62(2): 1-12. |
| [5] |
DU J, RAKHA H, GAYAH V V. Deriving macroscopic fundamental diagrams from probe data:Issues and proposed solutions[J]. Transportation Research Part C, 2015, 66: 136-149. |
| [6] |
AMBVHL L, MENENDEZ M. Data fusion algorithm for macroscopic fundamental diagram estimation[J]. Transportation Research Part C, 2016, 71: 184-197. DOI:10.1016/j.trc.2016.07.013 |
| [7] |
GAYAH V V, DAGANZO C F. Clockwise hysteresis loops in the macroscopic fundamental diagram:an effect of network instability[J]. Transportation Research Part B, 2011, 45(4): 643-655. DOI:10.1016/j.trb.2010.11.006 |
| [8] |
姬杨蓓蓓. 基于仿真实验验证宏观基本图的存在性[J]. 武汉理工大学学报:交通科学与工程版, 2013, 37(5): 929-933. JIYANG Bei-bei. Existence verification of macroscopic fundamental diagram (MFD) based on simulation method[J]. Journal of Wuhan University of Technology:Transportation Science and Engineering, 2013, 37(5): 929-933. |
| [9] |
马万经, 廖大彬. 网络交通流宏观基本图:回顾与前瞻[J]. 武汉理工大学学报:交通科学与工程版, 2014, 38(6): 1266-1233. MA Wan-jing, LIAO da-bin. Progress and prospects of macroscopic fundamental diagram[J]. Journal of Wuhan University of Technology:Transportation Science and Engineering, 2014, 38(6): 1266-1233. |
| [10] |
岳圆圆. 基于多源数据的北京市多层次交通流基本图研究[D]. 北京: 北京交通大学, 2015. YUE Yuan-yuan. Multi-level fundamental diagram of traffic flow for Beijing based on multi-source data[D]. Beijing: Beijing Jiaotong University, 2015. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2917330 |
| [11] |
许菲菲, 何兆成, 沙志仁. 交通管理措施对路网宏观基本图的影响分析[J]. 交通运输系统与信息, 2013, 13(2): 185-190. XU Fei-fei, HE Zhao-cheng, SHA Zhi-ren. Impacts of traffic management measures on urban network macroscopic fundamental diagram[J]. Journal of Transportation System Engineering and Information Technology, 2013, 13(2): 185-190. |
| [12] |
韦薇. 基于宏观基本图的城市路网交通状态判别与监控[D]. 杭州: 浙江大学, 2015. WEI Wei. Study on the macroscopic fundamental diagram based on simulation[D]. Hangzhou: Zhejiang University, 2015. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZJTX201209001008.htm |
| [13] |
朱琳, 于雷, 宋国华. 基于MFD的路网宏观交通状态及影响因素研究[J]. 华南理工大学学报:自然科学版, 2012, 40(11): 138-146. ZHU Lin, YU Lei, SONG Guo-hua. MFD-based investigation into macroscopic traffic status of urban networks and its influencing factors[J]. Journal of South China University of Technology:Natural Science Edition, 2012, 40(11): 138-146. |
| [14] |
贺正冰, 关伟, 樊玲玲, 等. 北京市快速环路宏观基本图特征研究[J]. 交通运输系统工程与信息, 2014, 14(2): 199-205. HE Zheng-bing, GUAN Wei, FAN Ling-ling, et al. Characteristic of macroscopic fundamental diagram for Beijing urban ring freeways[J]. Journal of Transportation System Engineering and Information Technology, 2014, 14(2): 199-205. |
| [15] |
NAGLE A, GAYAH V. The accuracy of network-wide traffic state estimation using mobile probe data[J]. Journal of the Transportation Research Board, 2014, 2421: 1-11. DOI:10.3141/2421-01 |



