颗粒破碎是颗粒之间相互作用的重要行为之一, 是化工、制药、食品和岩土等多个领域的重要研究课题.研究表明, 颗粒的破碎行为主要取决于颗粒的大小、形状、材料性质和接触分布等因素[1-2].目前, 对颗粒破碎的研究主要考虑了颗粒的大小和形状.如McDowell等[3-4]通过径向加载试验和劈裂试验, 提出颗粒的破碎强度服从Weibull分布.该类研究只能反映颗粒在两个接触点情况下的破碎规律, 忽略了接触力对颗粒的限制作用.
Tsoungui等[5-8]针对随机接触力分布下的二维颗粒, 先后提出拉伸失效准则和剪切失效准则.Tsoungui等[5-6]认为二维颗粒的开裂满足拉伸失效准则, 即取决于中心拉应力;同时, 颗粒在各向同性作用下难以破裂, 在不均匀应力作用下容易发生破坏.Ben-nun和Einav在Sukumaran等[7]的研究基础上提出剪切破坏准则, 弥补了拉伸失效准则的不足, 解释了各向同性压缩状态下颗粒的破碎过程[8].该方法将接触力的平均法向分量与破碎阈值进行比较, 判断颗粒是否发生破碎.
近年来, 国内外学者逐渐意识到接触分布对颗粒破碎的重要影响.Salami等[9]在MTS试验机上加装颗粒夹持装置, 通过调整夹具的数量和角度, 开展多点约束下的颗粒破碎试验.试验表明, 配位数与接触点分布对颗粒破碎有重要影响.该试验不易稳定控制夹具, 需要较大的试验机刚度, 目前发表的试验数据较少.Wang等[10]采用离散单元法模拟不同配位数的颗粒的破碎行为, 得到颗粒破碎强度与配位数成线性关系的规律.尽管接触状态对颗粒破碎强度的影响逐渐得到重视, 但已有的研究成果大多只是对配位数进行简单分析;由于颗粒受周边颗粒的约束具有多变和复杂性, 难以用统一标准对约束模式进行量化.
为了研究局部约束对单颗粒破碎的影响, 本文在颗粒周边安置刚性板来模拟周围颗粒对单颗粒的约束, 通过改变刚性板的个数和位置设计一系列颗粒局部约束模式.采用奇异值分解(singular value decomposition, SVD)的方法, 对描述约束状态的矩阵进行分解, 得到量化约束状态的特征值.基于Voronoi图形网格划分法, 在连续-离散耦合分析方法(combined finite-discrete element method, FDEM)的基础上开展颗粒破碎的数值试验, 分析破碎过程中的应力分布和裂缝的发展, 得到二维颗粒破碎阈值与奇异值之间的关系.
1 连续-离散耦合分析方法作为连续介质力学方法和非连续介质力学方法的统一体, 连续-离散耦合分析方法采用有限元法计算单元内部的应力和变形.根据断裂力学理论判断模型是否开裂, 运用离散元方法对离散块体进行接触分析, 定义裂面间的接触本构关系, 充分发挥了有限单元法和离散单元法各自的优势[11-14].运用FDEM能够准确地呈现岩体加载期间裂纹的演化和破坏过程[15], 是一种理想的数值模拟方法.
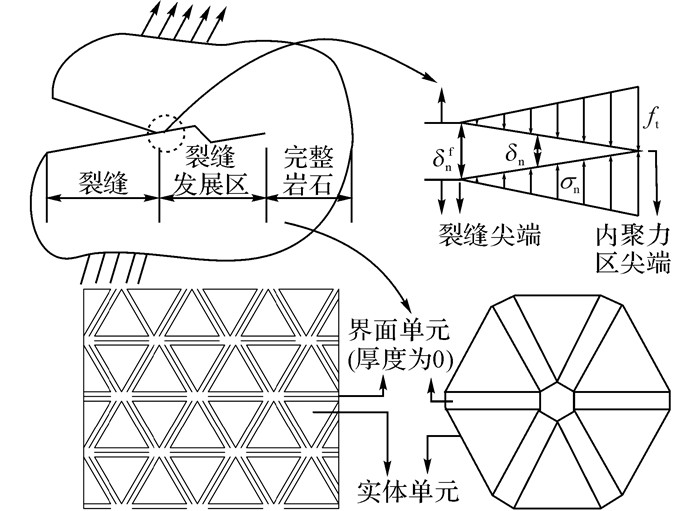
当采用FDEM方法模拟颗粒破碎时, 将二维颗粒看作由弹性实体单元和无厚度界面单元组成的理想系统.使用内聚力模型(cohesive zone model, CZM)[16-19]描述材料的裂纹萌生、发展直至失效的过程.当内聚力区开始承载时, 界面单元的的本构关系满足线弹性规律;当材料达到峰值强度时, 单元应力状态相应地达到裂缝起裂准则, 界面单元刚度开始退化, 材料的承载能力随之减弱, 最终界面单元完全失效, 新的裂纹面产生.张拉状态下的黏聚力模型如图 1所示, 便于展示, 将图中界面单元的厚度进行放大, 内聚力区应力从真实裂纹到内聚力区尖端逐渐提高;界面单元与相邻实体单元采用共节点方式分布, 以实现单元间力和位移的传递.
|
图 1 黏聚力模型与界面单元 Fig. 1 Cohesive zone model and interface element |
为了模拟裂纹的萌生、发展过程, 采用Mohr-Coulomb准则作为裂纹起裂准则, 根据界面单元的应力状态判断界面单元出现何种开裂.当界面单元的正应力σn达到抗拉强度ft时, 发生Ⅰ型开裂;当界面单元的切应力τs超过抗剪强度fs时, 发生Ⅱ型开裂, fs表示为
| $ {f_{\rm{s}}} = c - {\sigma _{\rm{n}}}\tan \varphi ;{\sigma _{\rm{n}}} < {f_{\rm{t}}}. $ | (1) |
式中:c、φ分别为材料的黏聚力和内摩擦角.
通常情况下, 材料的破坏是由拉应力和切应力共同作用导致的.当界面单元的法向应力和切应力满足
| $ {\left\{ {\frac{{\left\langle {{\sigma _{\rm{n}}}} \right\rangle }}{{{f_{\rm{t}}}}}} \right\}^2} + {\left\{ {\frac{{{\tau _{\rm{s}}}}}{{{f_{\rm{s}}}}}} \right\}^2} \ge 1 $ | (2) |
时, 界面单元开始出现复合开裂.式中:〈〉为Macaulay括号.
2 奇异值分解矩阵的奇异值分解(SVD)是专业数学领域中一种性质优良的完全正交分解法, 是现代数值分析和线性代数分析中的重要方法[20-21].自19世纪70年代由Beltrami和Jordan提出至今, SVD已在最优化问题、广义逆矩阵、最小二乘法问题以及控制理论、系统辨识、讯号处理和统计分析等诸多领域得到了广泛的应用[22-23].
与特征值分解原理相似, SVD分解可以得到若干特征向量和相应特征值(奇异值), 即通过特征值的表达形式将原本抽象复杂的数据信息集中并简化, 奇异值的大小代表对应特征所占权重.尽管这两种分解方法有一定的相似性, 相比之下, 奇异值分解突破了待分解矩阵形式的限制, 可以运用于任意矩阵的分解, 是一种性质更优良的矩阵分解法.奇异值分解定理[21]如下:A是秩为r的任意m×n阶矩阵, A∈Crm×n, 存在m阶酉矩阵U和n阶酉矩阵V满足
| $ \mathit{\boldsymbol{A}} = \mathit{\boldsymbol{U}} \mathit{{\boldsymbol{Σ}}}{\mathit{\boldsymbol{V}}^{\rm{T}}}. $ | (3) |
式中:
| $ \mathit{\boldsymbol{ Σ }}=\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{S}}&{\bf{0}}\\ {\bf{0}}&{\bf{0}} \end{array}} \right], $ |
其中S=diag [p1, p2, p3, …, pr], p1≥p2≥…≥pr>0;U满足UTAATU对角矩阵, V满足VTATAV对角矩阵.
二维空间中SVD的几何意义如图 2所示[24].原始域中的一个单位圆经过矩阵变换A旋转拉伸成为一个椭圆, 它的长轴Av1(或p1u1)和短轴Av2(或p2u2)分别对应变换后的2个标准正交向量, 即椭圆范围内最长和最短的2个向量, p1和p2为两个不同的奇异值.定义在单位圆上的函数|Ax|分别在v1和v2方向上取得最大和最小值, 寻找矩阵的奇异值的过程即为优化函数|Ax|的过程;结果表明, 该函数取得最优值的向量为矩阵AAT的特征向量, 奇异值为ATA的特征值.将SVD原理推广至n维原始域, 即矩阵A将n维空间Rn的标准正交基{ν1, ν2, …, νn}映射到m维空间Rm的标准正交基{u1, u2, …, um}上, 即AV=UΣ, 其中V为原始域的标准正交基, U为经过A变换后的标准正交基, Σ为V中的向量与U中相对应向量之间的关系.

|
图 2 奇异值分解的几何意义 Fig. 2 Geometric meaning of SVD |
奇异值在数据统计中常被用于主成分分析(principal components analysis, PCA), 以达到降维的目的[25-26].主成分分析的中心思想是通过剔除次要的特征值, 利用相对较少的特征对样本进行描述, 从而达到降低特征空间维数、保留原数据重要信息的目的.利用SVD获取量化颗粒局部约束模式的最简化指标, 是本文重要的数据处理基础.
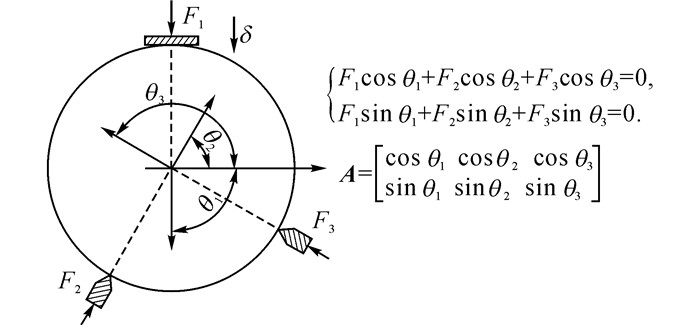
以3接触点颗粒试样为例, 采用位移控制加载方式, 通过顶部加载板对试样施压, 试样顶部与其他接触部位均产生力的作用.根据颗粒的静力平衡方程, 可以得到描述该约束模式的矩阵A, 如图 3所示, 角度θi为接触力Fi与颗粒水平正轴所夹角度.在试样模型、加载方式、加载速率等试验条件保持不变的情况下, 不同的约束状态均可以借助相应的矩阵进行描述.借助Matlab程序对矩阵A进行分解, 得到量化颗粒约束状态的奇异值p1、p2, 如图 2所示.图中, p1、p2表示矩阵对同一单位圆分别关于长、短轴的变形作用程度, 以(p1+p2)/ 2表示约束模式的平均奇异值水平, 以p1-p2表示奇异值的偏状态, 结合二维矩阵SVD分解的几何意义, 可以认为当奇异值偏状态程度p1-p2偏低时, 约束模式对颗粒两个特征维度的“贡献”相当, 即约束模式具备更显著的各向同性性质.奇异值及相关量的获得最大程度地简化了不同约束状态的表达形式, 更有利于试验数据的处理与分析.
|
图 3 3接触力情况下的矩阵奇异值分解过程图 Fig. 3 Process of SVD for grain under certain set of three contact forces |
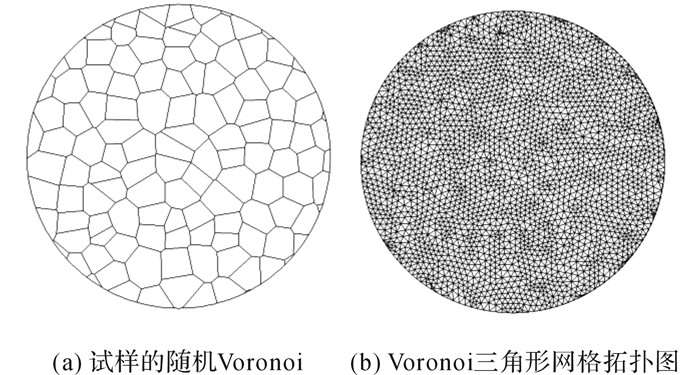
考虑到实际工程中的颗粒材料, 如堆石体粗粒土的粒径一般为0.5~800 mm, 采用直径为70 mm的二维平面应变模型, 并假定试样厚度为1.在二维颗粒圆周安置刚性板来模拟周围颗粒对单颗粒的约束, 通过改变刚性板的个数和角度来改变颗粒的接触模式.刚性板与试样之间定义接触关系且摩擦系数取为0, 采用位移控制式加载施加于顶部加载板, 加载速率为5×10-3 m/s.为了避免常规网格拓扑结构规则、裂纹扩展形态单一的缺陷, 采用以随机均布Voronoi图为基础的三角形划分方式进行网格划分, 平均网格尺寸为1.5 mm, 该划分方法更加真实地模拟了可能的裂纹扩展路径.统计可得:试样共5 077个实体单元、7 529个界面单元、35 714个节点.如图 4所示为二维平面试样的Voronoi图和网格划分图.
|
图 4 二维试样网格示意图 Fig. 4 Voronoi diagram and mesh topology of two-dimensional particle model |
在考虑二维颗粒破碎的细观数值模拟中, 设定以下参数:线弹性实体单元的密度ρ、弹性模量E和泊松比ν;界面单元法向和切向刚度knc、ksc, Ⅰ型和Ⅱ型断裂能GnC、GsC, c, φ和ft;单元间摩擦系数μe, 单元与加载板摩擦系数μr等.
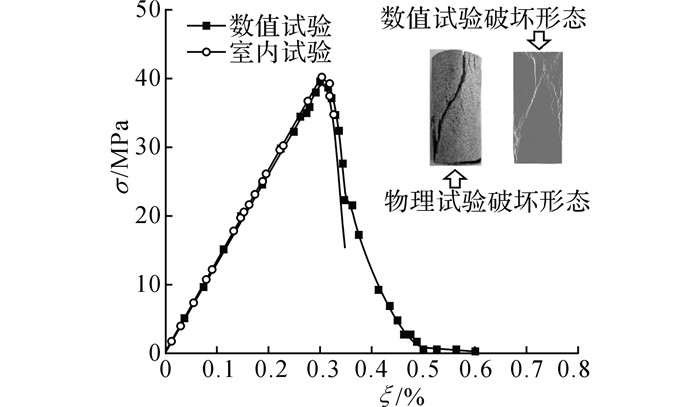
为了使所取的细观参数合理、可行, 并验证FDEM方法对颗粒破碎过程模拟的适用性, 对Kazerani[27]的砂岩单轴压缩试验进行数值重现.单轴压缩试验采用80 mm×160 mm的二维平面应变模型, 通过位移控制式加载施于上、下刚性加载板.将数值模拟结果[28]与室内试验结果进行对比分析, 不断优化参数取值使单轴压缩应力σ-轴向应变ξ曲线、单轴抗压强度及破坏形态与室内试验结果一致, 如图 5所示.采用优化参数对接触点为2的颗粒破碎进行模拟验证, 得到数值试验与室内试验的试样破坏形态对比图, 如图 6所示.两者的破碎形态相似, 破碎强度误差较小, 最终确定各细观参数, 如表 1所示.
|
图 5 单轴压缩应力-轴向应变曲线对比 Fig. 5 Stress-strain response of laboratory uniaxial test compared with response of FDEM |

|
图 6 二维圆盘颗粒破坏形态对比图 Fig. 6 Comparison of laboratory and numerical failure modes |
| 表 1 细观参数取值 Table 1 Values of mesoscopic parameters |
为了考察约束模式对颗粒的破碎强度和破碎形式的影响, 在4种配位数下调整接触角度, 设计不同的约束模式.对于不同的约束模式, 开展奇异值分解和颗粒破碎数值模拟试验.图 7给出各个配位数下的典型约束模式简图.SVD分解结果如表 2~5所示.表中, p1, 2为各接触状态下所得的奇异值.采用同一个试样进行FDEM颗粒破碎模拟, 消除了试样对结果的影响.在加载过程中, 采用相同的加载方式、加载速率, 避免了试验方法可能造成的影响.
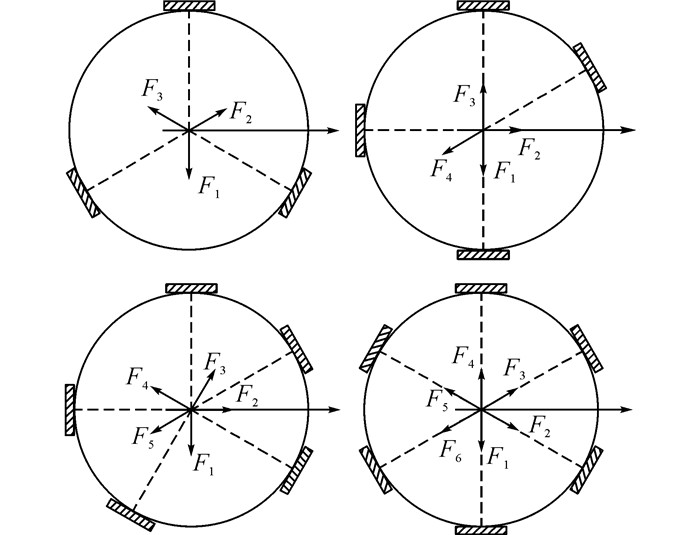
|
图 7 不同配位数下的约束模型简化图 Fig. 7 Loading configurations tested with different coordination number |
| 表 2 3配位数情况下的SVD分解结果 Table 2 Singular values of samples with three contacts |
| 表 3 4配位数情况下的SVD分解结果 Table 3 Singular values of samples with four contacts |
| 表 4 5配位数情况下的SVD分解结果 Table 4 Singular values of samples with five contacts |
| 表 5 6配位数情况下的SVD分解结果 Table 5 Singular values of samples with six contacts |
试样在初始加载过程中, 应力主要集中于约束点附近, 并由约束点至试样内部逐渐降低.随着加载进行, 试样内部出现由各个约束部位逐渐开展的裂纹, 部分裂纹贯通形成宏观裂缝;约束点附近区域出现局部裂纹, 此时应力主要集中于裂缝附近.图 8给出3-M4试样在加载过程中的Mises应力云图.图中, ld为加载点径向位移.当径向位移达到0.20 mm时, 试样内部出现贯穿性裂缝;当径向位移达到0.26 mm时, 侧向约束部位出现向贯穿裂缝端部发展的裂缝.

|
图 8 3-M4试样加载过程应力云图 Fig. 8 Distribution of stress in sample 3-M4 duringcrushing |
当试样达到峰值强度后发生脆性破坏, 部分试样的破碎形态如图 9所示.不同约束模式下试样的破碎形态不同, 接触点个数越多的试样破坏形态越复杂.结合各个试样的破碎过程分析可得, 由于加载位移由顶部加载板传递, 靠近竖直加载轴线的约束部位极易生成初始裂纹, 并发展成为宏观贯穿裂缝, 宏观裂缝附近由于挤压作用形成较多的无规则破碎块体;同时, 圆周侧向约束部位由于剪切作用产生裂纹, 并向顶部或底部约束部位扩展.试样接触点越多或接触点分布越均匀, 试样的初始贯穿裂缝越纤细.破碎规律与Salami等[9]的物理试验规律基本一致.
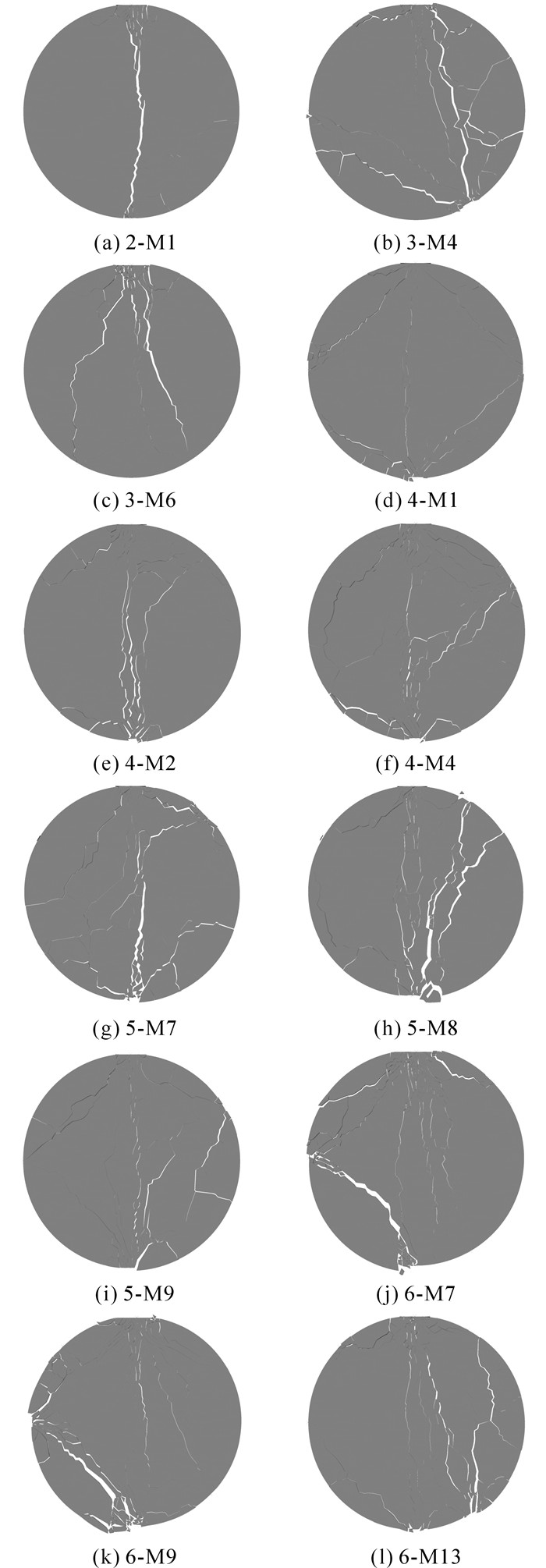
|
图 9 不同约束模式下试样的破坏形态 Fig. 9 Failure modes of samples under different contact forms |
为了研究不同约束模式对颗粒破碎强度的影响, 分别对4种配位数下不同接触角度的试样进行数值加载试验后, 获得峰值荷载Fmax.利用SVD得到量化颗粒不同接触状态的特征值p1、p2、平均奇异值水平值p1+p2/2以及奇异值偏状态值p1-p2, 并寻求约束模式、奇异值与试样破碎强度三者之间的联系.如图 10~13所示分别为3~6个配位数下的颗粒峰值荷载Fmax与p1+p2/2的关系曲线和Fmax与p1-p2的关系曲线.

|
图 10 3配位数情况下峰值荷载与奇异值的关系曲线 Fig. 10 Trend curves of peak force and singular values under three contacts |

|
图 11 4配位数情况下峰值荷载与奇异值的关系曲线 Fig. 11 Trend curves of peak force and singular values under four contacts |
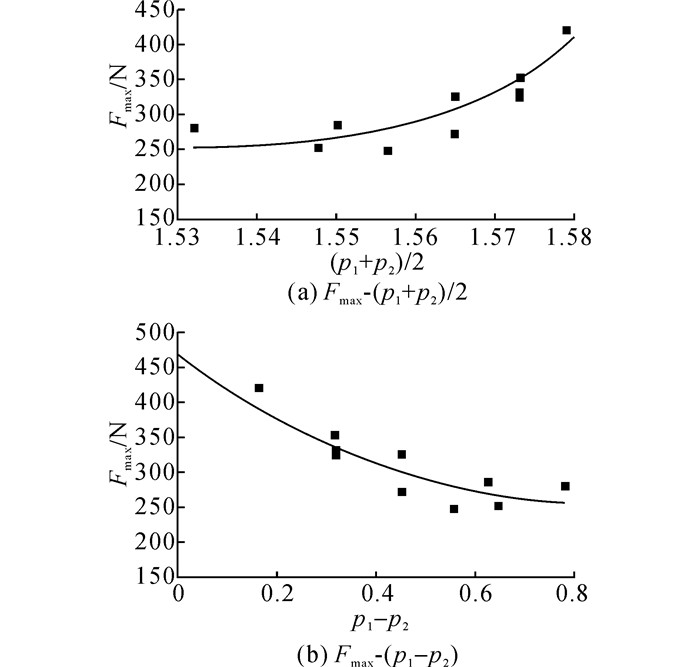
|
图 12 5配位数情况下峰值荷载与奇异值的关系曲线 Fig. 12 Trend curves of peak force and singular values under five contacts |
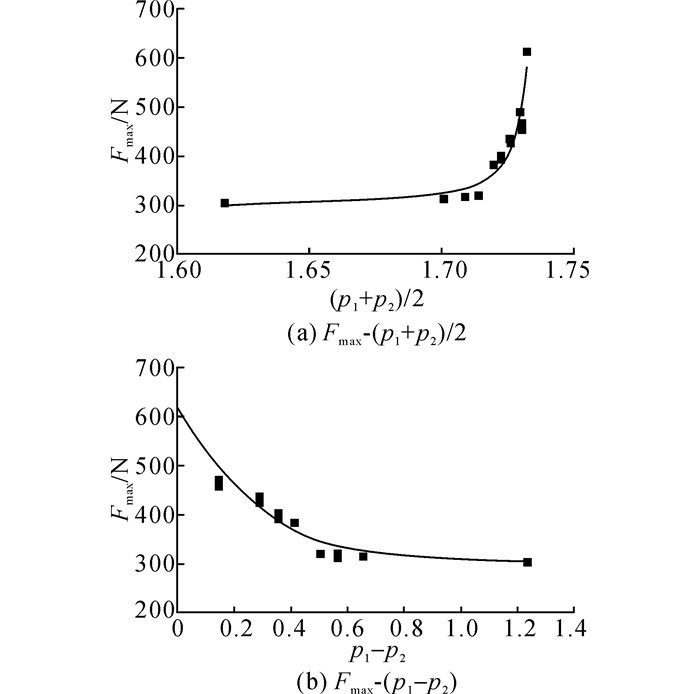
|
图 13 6配位数情况下峰值荷载与奇异值的关系曲线 Fig. 13 Trend curves of peak force and singular values under six contacts |
由图 10~13可以看出, 约束模式或对应奇异值的改变对颗粒的破碎强度有显著影响.当配位数相同时, (p1+p2)/2越大, 试样的峰值荷载越大, 强度越高;p1-p2越大, 试样的峰值荷载越小, 强度越低.表 6给出6配位数颗粒破碎模拟结果.可以看出, 当颗粒接触点个数或配位数相同时, 奇异值偏状态程度随平均奇异值的增大而降低, 抵抗破碎的能力随之增强, 表明颗粒的破碎阈值与平均奇异值呈正相关关系, 其他配位数情况下的结果规律与6配位数所得规律一致.根据二维矩阵SVD分解的几何意义可知, 当奇异值偏状态程度偏低(平均奇异值偏大)时, 分解所得的奇异值较接近, 说明约束模式对颗粒两个特征维度的“贡献”相差无几, 即约束模式的各向同性性质显著, 导致颗粒内部的应力状态趋近于静水压力状态, 颗粒较难破碎.
| 表 6 6配位数情况下不同约束模式的奇异值和峰值强度汇总 Table 6 Summary of singular values and peak forces of different forms under six contacts |
对于不同配位数的情形, 颗粒接触点或配位数越多, 分解得到的平均奇异值越大, 颗粒的破碎荷载阈值越高, Salami等[9]的物理试验验证了这一结论的合理性.
5 结论(1) 配位数越多的颗粒破坏形态越复杂.在颗粒破碎过程中, 靠近竖直加载轴线的约束部位先出现初始裂纹, 并逐渐发展成为宏观贯穿裂缝, 继而圆周侧向约束出现向贯穿裂缝首尾部位扩展的裂纹.
(2) 当配位数相同时, 颗粒的破碎阈值与平均奇异值呈正相关关系, 即平均奇异值(p1+p2)/2越高或偏状态程度p1-p2越低, 试样抵抗破碎的能力越强;当配位数不同时, SVD分解得到的平均奇异值随着颗粒接触点的增多而增大, 且配位数越多, 颗粒破碎阈值越高.
本文在设计颗粒的约束模式时, 仅选用4种配位数和若干典型角度(30°、45°和60°等)对刚性板进行控制, 设计模式的局限性使模拟结果存在许多填充空间.为了建立适用于任意约束状态的颗粒破碎阈值模型, 丰富约束模式、选用更加符合的统计模型、深入研究奇异值在约束模式和破碎阈值间的桥梁作用, 并对规律进行完善是后续研究的重要工作.
| [1] |
AURSUDKIJ B. A laboratory study of railway ballast behaviour under traffic loading and tamping maintenance[D]. Nottingham: University of Nottingham, 2007. https://www.researchgate.net/publication/37245673_A_laboratory_study_of_railway_ballast_behaviour_under_traffic_loading_and_tamping_maintenance
|
| [2] |
CAVARRETTA I, COOP M, O'SULLIVAN C. The influence of particle characteristics on the behaviour of coarse grained soils[J]. Géotechnique, 2010, 60(6): 413-423. DOI:10.1680/geot.2010.60.6.413 |
| [3] |
MCDOWELL G R, HARIRECHE O. Discrete element modelling of soil particle fracture[J]. Géotechnique, 2002, 52(2): 131-136. DOI:10.1680/geot.2002.52.2.131 |
| [4] |
LIM W L, MCDOWELL G R. The importance of coordination number in using agglomerates to simulate crushable particles in the discrete element method[J]. Géotechnique, 2007, 57(8): 701-705. DOI:10.1680/geot.2007.57.8.701 |
| [5] |
TSOUNGUI O, VALLET D, CHARMET J C. Use of contact area trace to study the force distributions inside 2D granular systems[J]. Granular Matter, 1998, 1(2): 65-69. DOI:10.1007/s100350050010 |
| [6] |
TSOUNGUI O, VALLET D, CHARMET J C, et al. Size effects in single grain fragmentation[J]. Granular Matter, 1999, 2(1): 19-27. DOI:10.1007/s100350050030 |
| [7] |
SUKUMARAN B, EINAV I, DYSKIN A. Qualitative assessment of the influence of coordination number on crushing strength using DEM[C]//2006 AIChE Annual Meeting. San Francisco: [s. n. ], 2006. https://www.researchgate.net/publication/290203381_Qualitative_assessment_of_the_influence_of_coordination_number_on_crushing_strength_using_DEM
|
| [8] |
BENNUN O, EINAV I. The role of self-organization during confined comminution of granular materials[J]. Philosophical Transactions of the Royal Society of London A:Mathematical, Physical and Engineering Sciences, 2010, 368(1910): 231-247. DOI:10.1098/rsta.2009.0205 |
| [9] |
SALAMI Y, DANO C, HICHER P Y, et al. The effects of the coordination on the fragmentation of a single grain[C]//Proceedings of ISGG. Warwick: IOP, 2015, 26(1): 012015. http://www.researchgate.net/publication/282511801_The_effects_of_the_coordination_on_the_fragmentation_of_a_single_grain
|
| [10] |
WANG P, ARSON C. Discrete element modeling of shielding and size effects during single particle crushing[J]. Computers and Geotechnics, 2016, 78: 227-236. DOI:10.1016/j.compgeo.2016.04.003 |
| [11] |
常晓林, 胡超, 马刚, 等. 模拟岩体失效全过程的连续-非连续变形体离散元方法及应用[J]. 岩石力学与工程学报, 2011, 30(10): 2004-2011. CHANG Xiao-lin, HU Chao, MA Gang, et al. Continuous-discontinuous deformable discrete element method to simulate the whole failure process of rock masses and application[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(10): 2004-2011. |
| [12] |
焦玉勇, 张秀丽, 刘泉声, 等. 用非连续变形分析方法模拟岩石裂纹扩展[J]. 岩石力学与工程学报, 2007, 26(4): 682-691. JIAO Yu-yong, ZHANG Xiu-li, LIU Quan-sheng, et al. Simulation of rock crack propagation using discontinuous deformation analysis method[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(4): 682-691. |
| [13] |
POTYONDY D O, CUNDALL P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1329-1364. DOI:10.1016/j.ijrmms.2004.09.011 |
| [14] |
MUNJIZA A, BANGASH T, JOHN N W M. The combined finite-discrete element method for structural failure and collapse[J]. Engineering Fracture Mechanics, 2004, 71(4): 469-483. |
| [15] |
MA G, ZHOU W, NG T T, et al. Microscopic modeling of the creep behavior of rockfills with a delayed particle breakage model[J]. Acta Geotechnica, 2015, 10(4): 481-496. DOI:10.1007/s11440-015-0367-y |
| [16] |
MA G, ZHOU W, CHANG X L. Modeling the particle breakage of rockfill materials with the cohesive crack model[J]. Computers and Geotechnics, 2014, 61(61): 132-143. |
| [17] |
MA G, ZHOU W, REGUEIRO R A, et al. Modeling the fragmentation of rock grains using computed tomography and combined FDEM[J]. Powder Technology, 2017, 308: 388-397. DOI:10.1016/j.powtec.2016.11.046 |
| [18] |
SONG S H, PAULINO G H, BUTTLAR W G. A bilinear cohesive zone model tailored for fracture of asphalt concrete considering viscoelastic bulk material[J]. Engineering Fracture Mechanics, 2006, 73(18): 2829-2848. DOI:10.1016/j.engfracmech.2006.04.030 |
| [19] |
ROE K L, SIEGMUND T. An irreversible cohesive zone model for interface fatigue crack growth simulation[J]. Engineering Fracture Mechanics, 2003, 70(2): 209-232. DOI:10.1016/S0013-7944(02)00034-6 |
| [20] |
KLEIBERGEN F, PAAP R. Generalized reduced rank tests using the singular value decomposition[J]. Journal of Econometrics, 2006, 133(1): 97-126. DOI:10.1016/j.jeconom.2005.02.011 |
| [21] |
LANGE K. Numerical analysis for statisticians[M]. New York: Springer, 2010, 129-142.
|
| [22] |
蒋卓芸, 夏雪. 奇异值分解及其简单应用[J]. 成都大学学报:自然科学版, 2015, 34(4): 364-366. JIANG Zhuo-yun, XIA Xue. Singular value decomposition and it's simple application[J]. Journal ofChengdu University:Natural Science Edition, 2015, 34(4): 364-366. |
| [23] |
罗小桂, 何雁. 矩阵奇异值分解在计算技术中的应用[J]. 计算机与现代化, 2006(6): 67-68. LUO Xiao-gui, HE Yan. Application of matrix singular value decomposition (SVD) in computing technologies[J]. Computer and Modernization, 2006(6): 67-68. |
| [24] |
邓勇. 矩阵奇异值分解的几何意义[J]. 喀什师范学院学报, 2012, 33(3): 8-10. DENG Yong. Geometrical significance on singular value decomposition of matrix[J]. Journal of Kashgar Teachers College, 2012, 33(3): 8-10. |
| [25] |
SMITH L I. A tutorial on principal components analysis[J]. Information Fusion, 2002, 51(52): 65. |
| [26] |
WALL M E, RECHTSTEINER A, ROCHA L M. Singular value decomposition and principal component analysis[M]//BERRAR D P, DUBITZKY W, GRANZOW M, et al. A practical approach to microarray data analysis. New York: Kluwer, 2003: 91-109.
|
| [27] |
KAZERANI T. Effect of micromechanical parameters of microstructure on compressive and tensile failure process of rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 64(6): 44-55. |
| [28] |
ZHOU W, YUAN W, MA G, et al. Combined finite-discrete element method modeling of rockslides[J]. Engineering Computations, 2016, 33(5): 1530-1559. DOI:10.1108/EC-04-2015-0082 |



