高维多目标优化问题(many-objective optimization problems, MaOPs)是指目标维数>3的多目标优化问题, 是目前进化算法领域公认的研究难点和热点[1-3].经典的多目标进化算法(multi-objective evolutionary algorithms, MOEAs), 特别是基于Pareto支配的多目标进化算法, 比如NSGA-II[4]、SPEA2[5]、PESA-II[6]等, 无法很好地解决这一类问题[7-8], 原因[9-10]主要如下:1)随着目标维数的增大, 种群中个体几乎都是互不支配的, Pareto支配关系无法产生足够的选择压力去促使种群进化;2)由于Pareto支配关系的失效, 导致后续的分布性维护操作占主导地位, 使得最终得到的解集分布性很好但收敛性很差.
针对上述两方面的问题, 国内外学者分别提出2种不同的解决思路:改进Pareto支配关系和改进分布性维护操作.前者是对Pareto支配关系进行宽松化, 使之更好地区别个体, 增加个体的选择压力, 比如CDAS[11]、grid-dominance[12]、Fuzzy-dominance[13].该类方法尽管求解效果有了很大提升, 但引入了过多的参数且不便于调节.
传统的分布性维护操作, 如小生境[14]、拥挤距离[4]、聚类[5]等, 由于过分地强调分布性, 会偏好于在稀疏区域的极端个体, 在很大程度上阻碍了种群的进化[15].Deb等[16]提出适用于解决高维多目标问题的NSGA-Ⅲ, 但由于基于Pareto的支配关系比较个体, 导致收敛性不足.最近, 学者们通过在分布性维护操作中引入一定程度的收敛信息, 很好地解决了解集收敛性和分布性失衡的问题, 比如基于坐标转换的密度评估(shift-based density estimation, SDE)方法[17]和基于拐点的邻域惩罚密度评估方法[18].这类方法通过在分布性维护操作中引入收敛信息能够取得很好的效果, 这为基于改进分布性维护操作的高维多目标进化算法提供了另外一种思路.
基于上述思路, 结合数学中超平面垂直投影的相关知识, 提出基于超平面投影的高维多目标进化算法(many-objective evolutionary algorithm based on hyperplane projection, HPEA).为了构造单位超平面, 对种群进行极端点归一化处理, 运用超平面投影理论, 将种群个体垂直投影到单位超平面上;结合K最近邻法和小生境技术改进Harmonic平均距离, 对投影点的拥挤密度进行评估;为了在分布性维护操作中引入收敛信息, 结合个体到单位超平面的垂直距离这一收敛信息, 构造λ-distance, 更好地平衡解集的收敛性和分布性.
1 问题描述和相关工作 1.1 高维多目标优化问题的数学描述不失一般性, 一个具有n维决策变量、M维目标函数的多目标优化问题, 以最小化多目标优化问题为例, 可以表述为
| $ \left. \begin{array}{l} \min F\left( \mathit{\boldsymbol{x}} \right) = {f_1}[\mathit{\boldsymbol{x}}), {f_2}\left( \mathit{\boldsymbol{x}} \right), \cdots , {f_M}\left( \mathit{\boldsymbol{x}} \right){]^{\rm{T}}};\\ \mathit{\boldsymbol{x}} = {\left[ {{x_1}, {x_2}, \cdots , {x_n}} \right]^{\rm{T}}} \subset \mathit{\Omega } \subset {{\bf R}^n}. \end{array} \right\} $ | (1) |
式中:x为n维决策变量;Ω为决策空间;目标函数F为需要同时优化的M个目标, 当M>3时, 式(1)为高维多目标优化问题.
给定2个决策变量x、y∈Ω, 称x Pareto支配y(x≻y), 则须满足以下2个条件:
| $ \left. \begin{array}{l} \forall i \in \left\{ {1, 2, \cdots , M} \right\}:{f_i}\left( \mathit{\boldsymbol{x}} \right) \le {f_i}\left( \mathit{\boldsymbol{y}} \right);\\ \exists i \in \left\{ {1, 2, \cdots , M} \right\}:{f_i}\left( \mathit{\boldsymbol{x}} \right) < {f_i}\left( \mathit{\boldsymbol{y}} \right). \end{array} \right\} $ | (2) |
若不存在x∈Ω, 使x≻x*, 则称x*为Pareto非支配解.所有Pareto非支配解构成的集合称为Pareto最优解集(PS), 对应的目标函数构成的解集称为Pareto前沿面(PF),
| $ {\rm{PF}} = \left\{ {F\left( \mathit{\boldsymbol{x}} \right) \in {{\bf R}^m}|\mathit{\boldsymbol{x}} \in {\rm{PS}}} \right\}. $ |
超平面投影是HPEA算法的重要环节, 其中收敛信息由个体到超平面的垂直距离体现, 分布信息由个体在超平面上投影点的位置构成.本文介绍有关超平面投影的相关公式.假设n维超平面H的方程表达式为
| $ \begin{array}{l} \left( {{{\tilde y}_1}, {{\tilde y}_2}, \cdots , {{\tilde y}_n}} \right) = \\ \left. \begin{array}{l} \;\;\;\;\left( {{y_1} - {w_1}t, {y_2} - {w_2}t, \cdots , {y_n} - {w_n}t} \right);\\ t = \sum _{i = 1}^n{w_i}{y_i} + b/\sum _{i = 1}^nw_i^2. \end{array} \right\} \end{array} $ | (3) |
假设d(P, H)为点P(y1, y2, …, yn)到超平面H的垂直距离, 计算公式为
| $ d\left( {P, H} \right) = \frac{{\left| {\sum _{i = 1}^n{w_i}{y_i} + b} \right|}}{{\sqrt {\sum _{i = 1}^nw_i^2} }}. $ | (4) |
由于所需超平面为单位超平面
| $ \left. \begin{array}{l} \left( {{{\tilde y}_1}, {{\tilde y}_2}, \cdots , {{\tilde y}_n}} \right) = \left( {{y_1} - t, {y_2} - t, \cdots , {y_n} - t} \right), \\ t = \left( {\sum _{i = 1}^n{y_i} - 1} \right)/n; \end{array} \right\} $ | (5) |
| $ d\left( {P, H} \right) = \frac{{\left| {\sum _{i = 1}^n{y_i} - 1} \right|}}{{\sqrt d }}. $ | (6) |
对于高维多目标优化问题, Pareto支配关系已无法有效地区分个体的优劣, 导致选择重心落在分布性维护操作上;传统的分布性维护操作(如小生境、拥挤距离、聚类等)在高维情况下的效果不太理想[15].为此, 对传统的分布性维护操作进行改进.首先采用NSGA-Ⅲ中的极端点归一化技术对种群进行归一化处理, 构造出单位超平面;然后采用超平面投影技术, 将高维空间中的点垂直投影到单位超平面上;接着通过改进的Harmonic平均距离, 评估超平面上投影点的拥挤密度, 构造能够同时包含收敛信息和分布信息的λ-distance, 从而达到在分布性维护操作中引入收敛信息的目的.
2.1 超平面投影为了构造单位超平面, 采用文献[16]的极端点归一化技术对合并种群R进行归一化处理.具体步骤如下.
1) 在种群R中寻找出每一维坐标轴所对应的极端点, 第i个极端点的求解公式为
| $ z_i^{{\rm{extreme}}} = \mathop {\arg \min }\limits_{\mathit{\boldsymbol{u}} \in R} \left\{ {\mathop {\max }\limits_{1 \le j \le M} \left\{ {\left( {{f_j}\left( \mathit{\boldsymbol{u}} \right) - z_j^{\min }} \right)/\mathit{\boldsymbol{w}}_j^i} \right\}} \right\}. $ | (7) |
式中:i={1, 2, …, M};zmin为在种群R在每一维目标上的最小值, zmin=[z1min, z2min, …, zMmin];wi=[w1i, w2i, …, wMi], 当j≠i时, wji=10-6, 否则, wii=1.
2) 用zextreme构造超平面H.设超平面H的截距式为
| $ \frac{{{f_1}}}{{{a_1}}} + \frac{{{f_2}}}{{{a_2}}} + \cdots + \frac{{{f_M}}}{{{a_M}}} = 1. $ | (8) |
式中:a1, a2, …, aM为超平面H与每一维坐标轴的截距.将M个极端点代入式(8), 可以根据解线性方程组的方法求出a1, a2, …, aM, 其中当方程组增广矩阵的秩小于M或ai < 0时, a=zmax, zmax=[z1max, z2max, …, zMmax]为在种群R中每一维目标上的最大值.
3) 种群R中的每一个个体可以归一化为
| $ f_i^n\left( \mathit{\boldsymbol{u}} \right) = \frac{{{f_i}\left( \mathit{\boldsymbol{u}} \right) - z_i^{\min }}}{{{a_i} - z_i^{\min }}};\mathit{\boldsymbol{u}} \in R, i = \left\{ {1, 2, \cdots , M} \right\}. $ | (9) |
经过归一化后, 超平面H与每一维坐标轴的截距将会变成1, 从而使本文构造的超平面为单位超平面.基于该单位超平面, 介绍提出的垂直投影技术.
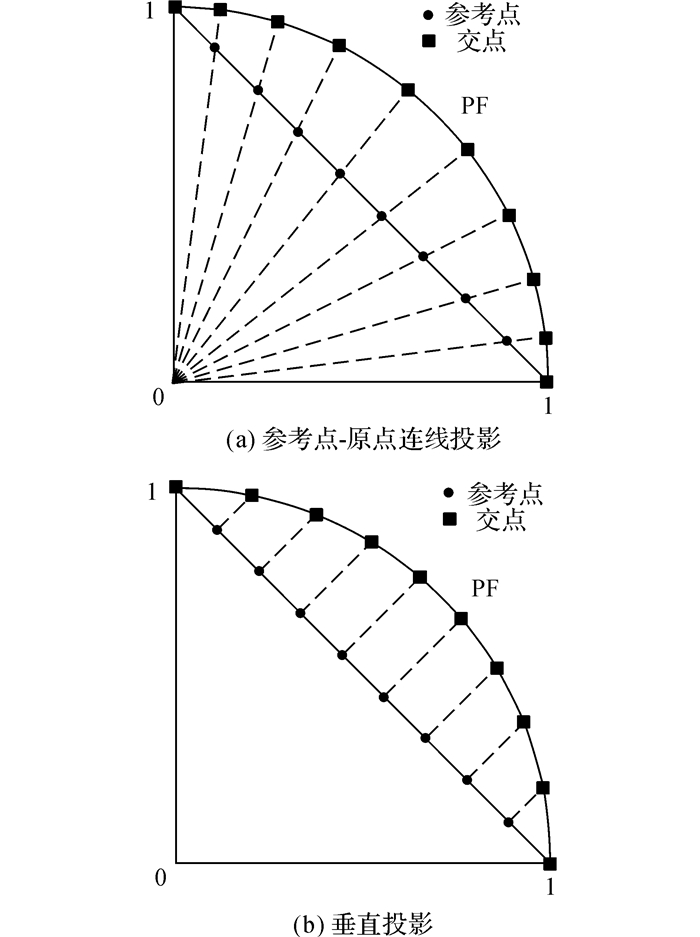
由于大多数问题的最优前沿面是事先未知的, NSGA-Ⅲ采用在单位超平面上预先设置参考点, 会导致即使参考点在单位超平面上是均匀分布的, 解集不一定是均匀分布的.比如图 1(a)所示的最优前沿面为凹面的情况, 很显然在边界处个体较密集, 中间区域个体较稀疏.采用超平面法线方向取代NSGA-Ⅲ中参考点和原点的连线方向, 作为个体分布性的评估依据, 示意图如图 1(b)所示, 优势在于不论最优前沿面凹凸, 均匀分布的参考点总能够对应均匀分布的解集.另外, NSGA-Ⅲ的参考点设置采用单纯形法, 规模受到分段参数H的制约, 不能任意设置, 并且在高维空间中生成均匀分布的参考点很困难.直接采用个体到超平面的垂直投影点来反映个体的分布情况, 一方面避免了在高维空间中设置均匀分布参考点的难题, 另一方面垂直投影比参考点-原点连线投影更能够保证解集的分布性.
|
图 1 投影示意图 Fig. 1 Illustration of hyperplane projection |
基于以上分析, 可以根据式(5)求出fn(u)在单位超平面上的垂直投影点
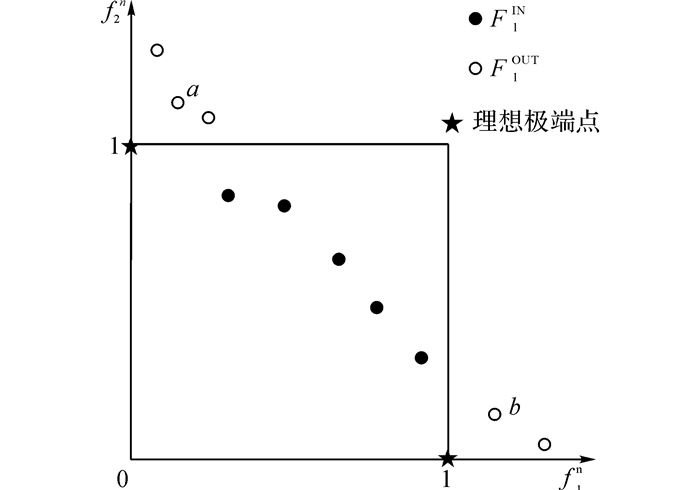
传统的分布性维护操作, 如小生境、拥挤距离、聚类等, 会导致一些收敛性很差的个体获得很好的密度估计值.为了消除这一影响, 基于2.1节的归一化技术, 首先构造一超方形判别并排除临界层Fl中收敛性较差的个体, 判别过程如下.若∀i∈{1, 2, …, M}, fin(u)≤1, 则个体u位于单位超矩形之内, 属于收敛性较好的个体;若∃i∈{1, 2, …, M}, fin(u)>1, 则个体u位于单位超矩形之外, 属于收敛性较差的个体, 用于寻找极端解, 超方形判别的二维示意图如图 2所示.
|
图 2 超方形判别二维示意图 Fig. 2 Two-dimensional illustration of hypercube judgment |
若FlIN少于所需选择的个体数J=N-|P|, 则FlIN直接进入下一代, 剩余个体从FlOUT中选择.由于位于单位超矩形外的个体对种群收敛性没有任何益处, 理想极端点集合用单位矩阵E表示, 选取离对应理想极端点最近的J-|FlIN|个个体用于对Pareto前沿面上的极端点搜索, 如图 1的a、b两点, 提高种群分布性.若FlIN≥J, 则开展基于λ-distance的个体选择.
2.3 基于λ-distance的个体选择基于λ-distance的个体选择可以将收敛信息引入到分布性维护操作中, 平衡解集的收敛性和分布性.对于最小化问题, 规定超平面以下的个体到超平面的距离为负值, 超平面以上的个体到超平面的距离为正值, 使位于超平面以下的个体优于超平面之上的个体.基于式(6), 个体到超平面的垂直距离可以表示为
| $ {d_1}\left( \mathit{\boldsymbol{u}} \right) = \frac{{\sum\limits_{i = 1}^M {{f_i}\left( \mathit{\boldsymbol{u}} \right) - 1} }}{{\sqrt M }}. $ | (10) |
式中:fi(u)为个体u的第i维目标函数值, M为目标维数.d1(u)越小, 个体u的收敛性越好.
投影到单位超平面上的投影点由于分离了个体的收敛信息, 能够反映个体的分布信息.通常来说, 传统的分布性维护操作均可以用来评估投影点的拥挤密度, 采用改进的Harmonic平均距离[19]评估投影点的拥挤密度, 计算公式为
| $ {d_2}\left( \mathit{\boldsymbol{u}} \right) = \frac{K}{{\frac{1}{{d_1^{\mathit{\boldsymbol{\tilde u}}}}} + \frac{1}{{d_2^{\mathit{\boldsymbol{\tilde u}}}}} + \cdots + \frac{1}{{d_K^{\mathit{\boldsymbol{\tilde u}}}}}}}. $ | (11) |
式中:
有以下2种情况须分别讨论:1)当临界层Fl为F1时,
近期, 文献[16]的实验结果表明, 基于分解的多目标进化算法(MOEA/D)中的PBI聚合函数, 通过调节惩罚因子θ能够很好地在解集收敛性与分布性之间保持平衡.对照PBI距离形式, λ-distance的表现形式如下:
| $ D\left( \mathit{\boldsymbol{u}} \right) = {d_1}\left( \mathit{\boldsymbol{u}} \right) - \lambda {d_2}\left( \mathit{\boldsymbol{u}} \right). $ | (12) |
式中:λ为惩罚因子, 用以调节个体收敛性与分布性所占的比重.D(u)越小, 代表个体越优秀.
在FlIN中选择一个D最小的个体加入到P中, 以此重复, 直到使种群P的大小为N, 再进行下一代进化.基于λ-distance的个体选择流程如算法1所示.
算法1 基于λ-distance的个体选择
输入:FlIN, 投影点集
输出:优秀个体q及投影点
1 for each u∈FlIN do
2 计算代表收敛信息的d1(u)
3 if
4 在
5 else
6 K=min(|FlIN|, |P|)
7 在
8 end if
9 计算D(u)=d1(u)-λd2(u)
10 end for
11 q=arg minu∈FlIN(D(u))
2.4 算法总体流程对基于Pareto支配的多目标优化算法的环境选择(environmental selection)进行改进, 通过在分布性维护操作中引入收敛信息, 使算法的综合性能得到进一步的提升.下面给出基于超平面投影的高维多目标进化算法HPEA的算法框架.
算法2 高维多目标进化算法HPEA
输入:种群大小N, 目标维数M.
输出:种群P
随机初始化种群P
1 while termination criterion not met do
2 P'= Mating_selection(P)
3 Q= Genetic_operator (P')
4 U=P∪Q
5 (F1, F2, …)=Non_dominated_sort (U)
6 P=∅, i=1
7 while |P∪Fi| < N do
8 P=P∪Fi, i=i+1
9 end while
10 临界层Fl=Fi
11 if |P∪Fl|=N then
12 P=P∪Fl, break
13 else
14 (
15 J=N-|P|, j=0
16 (FlIN, FlOUT)=Hypercube_ judgment(Fl)
17 if |FlIN| < J
18 D=min(dist(FlOUT, E))
19 Rank=sort(D)
20 P=P∪FlIN∪FlOUT(Rank(1:J-|FlIN|))
21 else
22 while j < J do
23 (q,
24 P=P∪{q},
25 Fl=Fl-{q},
26 end while
27 end if
28 end if
29 end while
2.5 计算复杂度分析HPEA的算法复杂度主要集中在环境选择.设种群规模为N, 目标维数为M, 考虑最坏的情况, 即所有的个体都是互不支配的.环境选择阶段包括5个过程:合并种群的非支配排序, 计算合并种群的投影点, 计算合并种群到单位超平面的垂直距离, 计算个体拥挤密度, 选择个体.前3个过程的复杂度分别为O(MN2)、O(MN)和O(MN).虽然后两个过程每当选择完一个个体都要重复计算个体的K个近邻距离, 但是可以运用数据结构和调用规则将个体之间的距离矩阵存储起来调用减少计算量, 计算复杂度为O(N2log2N);然后用λ-distance选择一个个体, 计算复杂度为O(N).环境选择总的计算复杂度为O(MN2)+O(N2log2N).HPEA总的计算复杂度为O(MN2)+O(N2log2N).
3 仿真实验与结果分析为了检验该算法的性能, 选取目前具有代表性的5种算法SPEA2+SDE[17]、MOEA/D-PBI[20]、NSGA-Ⅲ[16]、GrEA[12]和KnEA[18], 在高维多目标优化领域通用的DTLZ[21]测试函数集上进行对比实验.其中, HPEA采用Matlab R2016b编写;SPEA2+SDE和GrEA的C代码可以在http://www.cs.bham.ac.uk/~limx/publication.html得到;MOEA/D-PBI的Matlab代码可以在http://dces.essex.ac.uk/staff/zhang/webofmoead.htm下载;NSGA-Ⅲ的C++代码可以在http://web.ntnu.edu.tw/~tcchiang/publications/nsga3cpp/nsga3cpp.htm获得;KnEA的Matlab代码可以在http://www.soft-computing.de/jin-pub_year.html获取.所有的算法都是在Intel Pentium、4 GB内存、2.6 GHz主频, win7 64位操作系统的计算机上运行.
3.1 算法性能评价指标反向世代距离(inverted generation distance, IGD)[22]是衡量算法综合性能的评价指标, 能够同时评价解集的收敛性和分布性, 定义为
| $ {\rm{IGD}}(P, {P^*}) = \frac{{{\sum _{v \in {P^*}}}d\left( {\mathit{\boldsymbol{v}}, P} \right)}}{{|{P^*}|}}. $ | (13) |
式中:P为算法在目标空间获得的最终解集;P*为均匀分布的真实Pareto前沿面;d(v, P)为真实Pareto前沿面上的点v∈P*到最终解集的最小欧氏距离;|P*|为P*的势, 即真实Pareto前沿面上点的总数.只有当解集的收敛性和分布性都好时, IGD才小, 即IGD越小, 算法的综合性能越好.为了计算IGD指标, 为每个测试函数生成了10 000个均匀分布的非支配解, 近似表征Pareto前沿面.
3.2 测试函数为了验证该算法的有效性, 选取目前高维多目标优化领域通用的DTLZ[21]测试函数集进行仿真实验.其中, DTLZ1是线性多模态的, 用以测试算法的收敛能力;DTLZ2是凹面的, 用以测试算法在增大目标维数时的运算能力;DTLZ3是凹面多模态的, 用来测试算法收敛到全局最优的能力;DTLZ4是凹面有偏好的, 用来测试算法保持分布性的能力;DTLZ5是凹面退化的, 用来测试算法收敛到一条曲线的能力;DTLZ6是凹面退化且有偏好的, 也是用来测试算法收敛到一条曲线的能力, 但难度加大;DTLZ7是不连续多模态的, 用来测试算法在不同Pareto前沿面保持分布性的能力.为了测试该算法在目标函数具有不同量纲的测试问题上的性能, 选取文献[16]的SDTLZ1和SDTLZ2, 它们分别是DTLZ1和DTLZ2的目标函数值乘以一个比例因子10i, 比如对于3目标的SDTLZ1, 目标函数值f1、f2、f3是分别乘以100、101、102.所有测试函数的决策变量个数V=M+k-1.对于DTLZ1和SDTLZ1, k=5;对于DTLZ2-6和SDTLZ2, k=10;对于DTLZ7, k=20.对于不同的M, SDTLZ1和SDTLZ2的比例因子是不同的, 具体设置如表 1所示.
| 表 1 SDTLZ1和SDTLZ2的比例因子设置 Table 1 Scaling factor for SDTLZ1 and SDTLZ2 |
每种算法在每一个测试函数上独立运行30次, 参照文献[12], 以最大函数评价次数MFE为终止条件, 其中DTLZ1、DTLZ3、DTLZ6和SDTLZ1的MFE=100 000, 其余函数的MFE=30 000.交叉算子采用模拟二进制交叉, ηc=20(其中NSGA-Ⅲ算法ηc=30), 交叉率pc=1.0;变异算子采用多项式变异, ηm=20, pm=1/V(其中V为决策空间的维数).HPEA、SPEA2+SDE、GrEA和KnEA 4种算法的种群大小均设置为100.由于MOEA/D-PBI和NSGA-Ⅲ的种群大小与均匀分布的参考点规模有关, 且由M和每维目标分段数H的组合数决定, 不能随意设置.采用双层分布法[16], 将种群大小设置为与100相近的数, 分别为105、85、128和65, 分别对应的目标维数为3、5、8和10.MOEA/D-PBI:邻域大小T=20, 邻域个体选择概率δ=0.9, 惩罚参数θ=5;SPEA2+SDE归档集大小与种群大小相同;GrEA的网格划分数div和KnEA的拐点比率均依照原始文献设置.
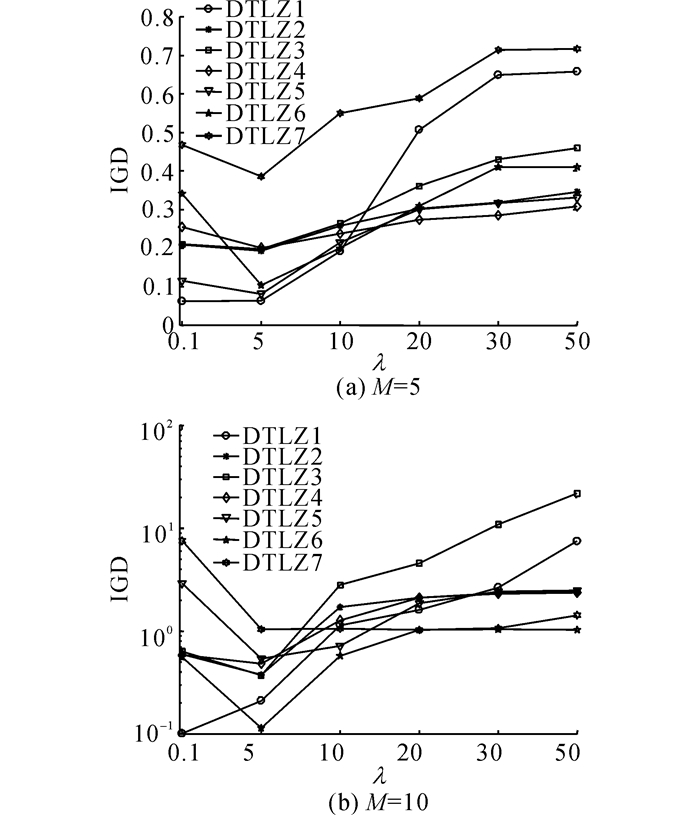
3.4 实验仿真与分析 3.4.1 λ参数分析分析2个参数:改进Harmonic平均距离的邻域大小K和λ-distance中的惩罚因子λ.其中, K借鉴小生境中半径的取值思想, 取种群的平方根10.下面主要对λ进行分析.考虑λ的6个不同取值:0.1、5、10、20、30、50, λ越大表示分布信息越占主导地位.选取5目标和10目标的DTLZ1-7测试函数进行实验, 以统计λ变化对性能影响的规律.通过实验独立重复进行30次, 求取IGD平均值, 最后以折线图的形式表现, 如图 3所示.
|
图 3 在6个不同λ下, HPEA在5目标和10目标的全部DTLZ函数上获得的IGD平均值 Fig. 3 Average IGD values obtained by different changes in value of λ on DTLZ1-7 problems with five-and ten-objective, respectively |
从图 3可得如下结论.1)参数λ在5目标和10目标上的变化规律大致相同, 说明λ对目标维数不是很敏感.2)对于DTLZ2-7测试问题, 均是当λ=5, 即在分布性维护操作中分布性信息所占比重大于收敛性信息所占比重时, 算法的性能最优;对于DTLZ1测试问题, 当λ=0.1时, 算法性能达到最优, 但与λ=5时的结果相差不大.
为了算法的通用性, 统一规定λ=5.
3.4.2 实验结果分析HPEA与SPEA2+SDE、MOEA/D-PBI、NSGA-Ⅲ、GrEA和KnEA在IGD值上的比较统计结果如表 2所示, 分别为30次独立运行结果的平均值, 其中最好的结果用黑色加粗表示.为了比较HPEA与另外5种算法获得的平均IGD值之间差异的显著性, 采用Wilcoxon秩和检验进行两两比较, 显著性水平取0.05.表 2中, “+”、“-”、“≈”分别表示HPEA显著优于、显著劣于和无差别于另外5种算法.
| 表 2 6种算法在不同目标维数的DTLZ测试例子上获得的IGD平均值 Table 2 IGD Average values obtained by six algorithms on DTLZ instances with different number of objectives |
从表 2可以看出:HPEA算法整体表现最好, 能够有效处理所有的测试函数, 尤其是在DTLZ2和DTLZ3的8、10目标, DTLZ4的3、5、10目标, DTLZ7的10目标以及SDTLZ1的5、10目标、SDTLZ2的10目标上取得最好的结果, 且在DTLZ1和DTLZ2的3、5目标、DTLZ3的3目标、DTLZ5的10目标、DTLZ7的5、8目标和SDTLZ2的3目标上取得次好的结果, 只是在DTLZ5和DTLZ6上, 结果不太突出, 说明HPEA收敛到一条曲线的能力一般, 原因在于HPEA需要构建超平面, 当前沿面为曲线时会在算法后期无法找到M个极端点来构造超平面, 也无法很好地收敛到一条曲线.
SPEA2+SDE算法的整体表现与HPEA接近, 在DTLZ1、DTLZ3、DTLZ5、DTLZ6和DTLZ7上都取得了很好的效果, 特别是在DTLZ1的5、8目标、DTLZ5的3目标、DTLZ6的5目标、DTLZ7的8目标以及SDTLZ1的3目标上取得了最好的结果, 在其他测试函数上效果明显, 是一个稳定且性能比较全面的算法.
MOEA/D-PBI在DTLZ2的3目标和DTLZ5的5、8目标取得了最好的结果, 但在DTLZ4和DTLZ6上的测试结果不是很理想, 说明MOEA/D-PBI不太适合解决有偏好的函数问题.另外, 在SDTLZ1和SDTLZ2上的求解效果不佳.
NSGA-Ⅲ在DTLZ1的3、10目标、DTLZ5的10目标和DTLZ7的3目标上取得了最好的结果, 但对DTLZ6的处理效果不是很好.由于NSGA-Ⅲ需要通过极端点来构造超平面, 对曲线的收敛能力不佳.此外, 在处理SDTLZ1和SDTLZ2测试问题上, NSGA-Ⅲ表现出与HPEA相当的效果, 由此说明极端点归一化技术对不同量纲目标函数问题的有效性.
GrEA在DTLZ2和DTLZ4上都能够取得很好的效果, 但在DTLZ6上表现很差, 说明该算法不太适合处理退化函数问题.值得注意的是, GrEA在SDTLZ2的5目标上取得了最好的结果, 并且在SDTLZ1和SDTLZ2的其他目标维数上取得了很好的结果.这主要是因为GrEA将目标空间的每一维划分成相同的段数, 本质上是起到目标值归一化的作用.
KnEA在DTLZ3和DTLZ7的3、5目标、DTLZ6的3、8目标上取得了最好的结果, 在DTLZ4和SDTLZ2上取得了与HPEA相近的结果.相比之下, 在DTLZ1上的表现不太理想.
本文算法与SPEA2+SDE和KnEA同属于在分布性维护操作中引入收敛信息, 在各例测试函数上的效果不错, 由此说明在分布性维护操作中引入收敛信息能够更好地平衡解集收敛性与分布性, 提高解集的综合性能.
从Wilcoxon秩和检验的统计结果中可以看出:在36例DTLZ测试问题中, HPEA显著优于SPEA2+SDE 23次、MOEA/D-PBI 30次、NSGA-Ⅲ 25次、GrEA 26次和KnEA 23次, 由此说明在DTLZ测试函数上, 本文算法相对于其他算法具有较大的优势.
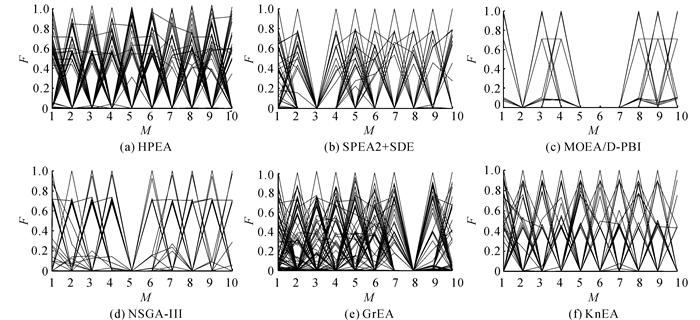
为了直观地反映所有算法得到的最终解集在高维目标空间中的分布情况, 采用平行坐标(parallel coordinates)来可视化高维目标数据, 其中数据来源于30次独立运行中IGD最接近平均值的那一组数据.限于篇幅, 只给出6种算法在10目标DTLZ4上最终解集的平行坐标图, 如图 4所示.图中,F为目标值.
|
图 4 6种算法在10目标DTLZ4测试问题上最终解集的平行坐标图 Fig. 4 Parallel coordinates of final non-dominated solutions obtained by six algorithms on ten-objective DTLZ4 instance |
如图 4所示为各算法在10目标DTLZ4测试问题上最终解集的平行坐标图.DTLZ4测试用来测试算法保持解集分布性的能力, 从图 4可以看出, HPEA在收敛性和分布性上都获得了满意的效果;SPEA2+SDE、NSGA-Ⅲ和GrEA在收敛性上均稍优于HPEA, 但都存在某维目标解丢失的情况, 导致分布性比HPEA差, 其中SPEA2+SDE在第3维目标上的解丢失, NSGA-Ⅲ在第5维目标上的解丢失, GrEA在第9维目标上的解丢失;MOEA/D-PBI分布性严重缺失, 只是收敛到Pareto前沿面的少数边界解而无法找到中间解;KnEA得到的解集性能与HPEA相似, 收敛性比HPEA稍好, 但分布性比HPEA差.
3.4.3 λ-distance的有效性分析为了验证λ-distance的有效性, 在分布性维护操作中只采用改进的Harmonic平均距离来选择个体, 不再引入收敛信息, 其他步骤与HPEA相同, 将该HPEA版本记为v-HPEA.为了消除目标值不同范围的影响, 只选取归一化问题DTLZ1-4.对比结果如表 3所示, 分别为30次独立运行结果的平均值与标准差, 其中最好的结果用黑色加粗表示.表中, “+”表示HPEA显著优于v-HPEA.
| 表 3 HPEA和v-HPEA在DTLZ1-4测试问题上的IGD平均值与标准差 Table 3 Average and standard deviation of IGD values obtained by HPEA and v-HPEA on DTLZ1-4 problems with different number of objectives |
从表 3可以看出:HPEA在所有DTLZ测试问题上的结果都显著优于v-HPEA, v-HPEA在三维目标测试问题上能够获得与HPEA相近的结果, 但随着目标维数的增大, v-HPEA的求解结果明显恶化.这是由于在高维空间中, v-HPEA在分布性维护阶段只以分布信息为主导因素选择个体, 导致过分注重分布性而使种群无法很好地收敛到最优前沿面.由此可以说明λ-distance的有效性, 尤其是在高维目标空间中, 能够更好地在解集收敛性与分布性之间保持平衡.
4 结语针对现有多目标进化算法不能很好地在解集收敛性和分布性之间保持平衡的问题, 本文提出基于超平面投影的高维多目标进化算法HPEA.为了更好地评估个体的拥挤密度, 通过归一化技术构造单位超平面, 将个体投影到单位超平面上;结合K最近邻法和小生境技术改进Harmonic平均距离, 在超平面上评估投影点的拥挤密度;不同于以往多目标进化算法在分布性操作阶段只考虑分布信息, 结合个体到单位超平面的垂直距离这一收敛信息, 构造λ-distance.在标准测试函数集DTLZ上的实验结果表明:本文算法与另外5种算法相比, 能够更好地在解集收敛性和分布性之间取得平衡, 提高解集质量.接下来的工作将会融合约束处理技术, 使HPEA算法能够处理带约束条件的高维多目标优化问题.
| [1] |
PURSHOUSE R C, FLEMING P J. On the evolutionary optimization of many conflicting objectives[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 770-784. DOI:10.1109/TEVC.2007.910138 |
| [2] |
孔维健, 丁进良, 柴天佑. 高维多目标进化算法研究综述[J]. 控制与决策, 2010, 25(3): 321-326. KONG Wei-jian, DING Jin-liang, CHAI Tian-you. Survey on large-dimensional multi-objective evolutionary algorithms[J]. Control and Decision, 2010, 25(3): 321-326. |
| [3] |
巩敦卫, 季新芳, 孙晓燕. 基于集合的高维多目标优化问题的进化算法[J]. 电子学报, 2014, 42(1): 77-83. GONG Dun-wei, JI Xin-fang, SUN Xiao-yan. Solving many-objective optimization problems using set-based evolutionary algorithms[J]. Acta Electronica Sinica, 2014, 42(1): 77-83. |
| [4] |
DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017 |
| [5] |
ZITZLER E, LAUMANNS M, THIELE L. SPEA2: improving the strength Pareto evolutionary algorithm[R]. Swiss: Technical Report Gloriastrass, 2001. http://ci.nii.ac.jp/naid/10017663175
|
| [6] |
CORNE D W, JERRAM N R, KNOWLES J D, et al. PESA-Ⅱ: region-based selection in evolutionary multiobjective optimization[C]//Proceedings of the 3rd Annual Conference on Genetic and Evolutionary Computation. San Francisco: Morgan Kaufmann, 2001: 283-290. http://dl.acm.org/citation.cfm?id=2955289
|
| [7] |
陈小红, 李霞, 王娜. 高维多目标优化中基于稀疏特征选择的目标降维方法[J]. 电子学报, 2015, 43(7): 1300-1307. CHEN Xiao-hong, LI Xia, WANG Na. Objective reduction with sparse feature selection for many objective optimization problem[J]. Acta Electronica Sinica, 2015, 43(7): 1300-1307. |
| [8] |
过晓芳, 王宇平, 代才. 新的混合分解高维多目标进化算法[J]. 浙江大学学报:工学版, 2016, 50(7): 1313-1321. GUO Xiao-fang, WANG Yu-ping, DAI Cai. New hybrid decomposition many-objective evolutionary algorithm[J]. Journal of Zhejiang University:Engineering Science, 2016, 50(7): 1313-1321. |
| [9] |
ISHIBUCHI H, TSUKAMOTO N, NOJIMA Y. Evolutionary many-objective optimization: a short review[C]//IEEE World Congress on Computational Intelligence. Hongkong: IEEE, 2008: 2419-2426.
|
| [10] |
LI K, DEB K, ZHANG Q, et al. An evolutionary many-objective optimization algorithm based on dominance and decomposition[J]. IEEE Transactions on Evolutionary Computation, 2015, 19(5): 694-716. DOI:10.1109/TEVC.2014.2373386 |
| [11] |
SATO H, AGUIRRE H E, TANAKA K. Controlling dominance area of solutions and its impact on the performance of MOEAs[M]//Evolutionary multi-criterion optimization. Berlin: Springer, 2007: 690-702. http://link.springer.com/10.1007/978-3-540-70928-2_5
|
| [12] |
YANG Sheng-xiang. A grid-based evolutionary algorithm for many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2013, 17(5): 721-736. DOI:10.1109/TEVC.2012.2227145 |
| [13] |
HE Zhe-nan, YEN G G, ZHANG Jun. Fuzzy-based Pareto optimality for many-objective evolutionary algorithms[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(2): 269-285. DOI:10.1109/TEVC.2013.2258025 |
| [14] |
HORN J, NAFPLIOTIS N, GOLDBERG D E. A niched Pareto genetic algorithm for multiobjective optimization[C]//IEEE World Congress on Computational Intelligence. Orlando: IEEE, 1994: 82-87. http://www.researchgate.net/publication/2631294_A_Niched_Pareto_Genetic_Algorithm_for_Multiobjective_Optimization?citationList=outgoing
|
| [15] |
郑金华, 申瑞珉, 李密青, 等. 一种基于信息分离的高维多目标进化算法[J]. 软件学报, 2015, 26(5): 1013-1036. ZHENG Jin-hua, SHEN Rui-min, LI Mi-qing, et al. Evolutionary algorithm based on information separation for many-objective optimization[J]. Journal of Software, 2015, 26(5): 1013-1036. |
| [16] |
DEB K, JAIN H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part Ⅰ:solving problems with box constraints[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 577-601. DOI:10.1109/TEVC.2013.2281535 |
| [17] |
LI Mi-qing, YANG Sheng-xiang, LIU Xiao-hui. Shift-based density estimation for Pareto-based algorithms in many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(3): 348-365. DOI:10.1109/TEVC.2013.2262178 |
| [18] |
ZHANG Xing-yi, TIAN Ye, JIN Y C. A knee point-driven evolutionary algorithm for many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2015, 19(6): 761-776. DOI:10.1109/TEVC.2014.2378512 |
| [19] |
毕晓君, 张永建, 陈春雨. 基于模糊支配的高维多目标进化算法MFEA[J]. 电子学报, 2014, 42(8): 1653-1659. BI Xiao-Jun, ZHANG Yong-jian, CHEN Chun-yu. A many-objective evolutionary algorithm based on fuzzy dominance:MFEA[J]. Acta Electronica Sinica, 2014, 42(8): 1653-1659. |
| [20] |
ZHANG Qing-fu, LI Hui. MOEA/D:a multiobjective evolutionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712-731. DOI:10.1109/TEVC.2007.892759 |
| [21] |
DEB K, THIELE L, LAUMANNS M, et al. Scalable test problems for evolutionary multiobjective optimization[M]//Evolutionary multiobjective optimization. London: Springer, 2005: 105-145. http://www.springerlink.com/index/q404757t4q25m64l.pdf
|
| [22] |
ZITZLER E, THIELE L, LAUMANNS M, et al. Performance assessment of multiobjective optimizers:an analysis and review[J]. IEEE Transactions on Evolutionary Computation, 2003, 7(2): 117-132. DOI:10.1109/TEVC.2003.810758 |


