在过去的几十年里,基于对双足动物运动问题的研究,已经积累了很多关于双足机器人步态生成方法的理论与实验结果.考虑双足机器人行走稳定性的步态生成方法,Shin等[1-3]采用Vukobratovic提出的基于零点矩(ZMP)的方法.除了步行稳定性问题,双足机器人的另一个重要问题是能量消耗.考虑能量消耗的双足步行机器人的最优步态规划问题可以等效为一个标准的最优控制问题,可以通过打靶法或者参数优化等方法来解决[4-5].二十多年前,McGeer[6]从节能的角度出发,提出被动行走的概念.在接下来的几年中,Lee等[7-9]对被动行走进行深入的研究.虽然被动行走不需要任何输入,但只能使机器人沿着一个微小的坡度向下行走.Cao等[10-14]提出既能使双足机器人在水平地面行走,又考虑了能量消耗问题的一系列运动控制方法;针对一些模型参数未知的双足步行机器人的情形,Satoh等[15-16]提出基于迭代学习控制的最优步态规划方法.
考虑能量消耗的最优轨迹规划问题已经在很多领域得到了广泛的研究.在机器人领域,经常采用参考步态来使得双足机器人在运动过程中降低能耗[17].另一方面,当机器人在复杂环境下行走时,需要具备避开障碍物的能力,这意味着每一步的初始位置(初始速度)和设计的终端位置(终端速度)以及步行时间段通常都是不同的.从这个观点来看,双足机器人的最优步态规划问题等效为由不同边界条件表征的一系列最优控制问题.有限时间最优控制问题可以转化为计算哈密顿系统状态轨迹的问题.进一步讲,它可以转化为一个由两个常微分方程组成的两点边值问题[18].很多传统方法,如打靶法[19],都可以用来求解这个问题.打靶法的基本原理是通过迭代计算来获得满足边界值的轨迹.若改变边界值,则这些传统方法需要再次求解两点边值问题,这将给实际机器人的在线步态规划计算带来沉重的负担.
最近10年,Park等[20-21]提出基于生成函数的轨迹生成方法.生成函数方法将轨迹生成分为2个部分,即线下和线上部分.线下部分求解哈密顿-雅克比方程得到生成函数,线上部分利用生成函数生成由不同边界条件表征的一系列最优状态轨迹和输入;因此,该方法具有线上计算效率高的优点.针对线下计算部分,Hao等[22]提出递归的数值算法,用于求解非线性系统的哈密顿-雅克比方程来得到生成函数.为了进一步降低在线计算量,Hao等[23]针对有限时间线性二次型最优控制问题,提出双生成函数方法,即通过使用一对生成函数来计算生成最优轨迹.该方法进一步地将线上工作量转移到了线下,是目前生成函数方法中在线计算效率最高的一种.
本文将双生成函数方法应用于在水平地面行走的双足步行机器人的最优步态生成.基于双生成函数方法,最优状态和输入是状态边界条件以及初始和终端时间的函数.针对有限时间线性二次型最优控制问题,线下可以预先计算出生成函数,从而使得调整步长和步伐时间的线上计算量几乎为零.本文首先线性化双足步行机器人的动力学方程,并规划生成参考的最优步态轨迹和输入力矩.在此基础上,设计常规的PD控制器,使得非线性机器人模型的轨迹可以跟踪参考的轨迹.通过将参考变量输入到非线性系统所得到的轨迹与参考轨迹进行比较,可以得到模型线性化后的误差.仿真结果表明,当机器人以合理的步长进行低速行走时,由线性化引起的建模误差非常小.这意味着线性系统的最优状态和输入可以作为实际的非线性机器人系统的最优状态和输入.综上,当控制双足机器人行走时,尤其是在复杂的环境中行走时,双生成函数方法将非常有效.
1 基于双生成函数的线性最优控制介绍有限时间线性最优控制问题的一些预备知识以及如何利用双生成函数方法来求解有限时间的最优控制问题[23].
1.1 线性最优控制问题介绍有限时间线性最优控制问题以及如何将其等效为常微分方程的两点边值问题[24].考虑如下的有限时间线性二次型最优控制问题:
| $ \left. \begin{array}{l} \mathop {\min }\limits_u \frac{1}{2}\smallint _{{t_0}}^{{t_{\rm{f}}}}({\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{Qx}} + {\mathit{\boldsymbol{u}}^{\rm{T}}}\mathit{\boldsymbol{Ru}}){\rm{d}}t;\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{Bu}}, \\ \;\;\;\;\mathit{\boldsymbol{x}}({t_0}) = {\mathit{\boldsymbol{x}}_0}, \mathit{\boldsymbol{x}}({t_{\rm{f}}}) = {\mathit{\boldsymbol{x}}_{\rm{f}}}. \end{array} \right\} $ | (1) |
式中:x和u分别为系统的状态变量和输入变量,x∈Rn,u∈Rm;A和B为常数矩阵,A∈Rn×n,B∈Rn×m;Q为半正定矩阵,Q∈Rn×n;R为正定矩阵,R∈Rm×m;x0和xf分别为状态的初始值和终端值,x0∈Rn,xf∈Rn;t0和tf分别为初始时间和终端时间.目的是找到最优的输入u*(t)来最小化代价函数,同时需要满足边界约束条件.
引入一个列向量λ∈Rn来代表协态,根据庞特里亚金最小值原理[24]可知,式(1)的代价函数取最小值的一个必要条件是
| $ \mathit{\boldsymbol{\dot x}} = {H_\mathit{\boldsymbol{\lambda }}}\left( {\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\lambda }}} \right), \mathit{\boldsymbol{\dot \lambda }} = - {H_\mathit{\boldsymbol{x}}}\left( {\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\lambda }}} \right), $ | (2) |
| $ {\mathit{\boldsymbol{u}}^*} = - {\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }}. $ | (3) |
式中:H(·)表示偏导数∂H/∂(·),H为哈密顿函数,定义为
| $ H\left( {\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\lambda }}} \right) = \frac{1}{2}{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{Qx}} + {\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\mathit{\boldsymbol{Ax}} - \frac{1}{2}{\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{\lambda }}. $ |
由此,求解最优控制问题(1)的状态轨迹等效为求解式(2)中常微分方程所构成的两点边值问题.采用双生成函数方法来求解该两点边值问题.
1.2 双生成函数方法根据变量及时间方向(正向和逆向分别用下标f和b表示)的不同,存在8种类型的生成函数.除去不具有良定性[20]的4种,在剩下的4种中,任意1对都可以求解最优控制问题(1).当使用除了Ff(λ, x0, t)和Fb(λ, xf, t)这1对以外的其他生成函数对时,协态的初始值λ0或终端值λf这2个未知量必须事先求解得到.此外,若使用1对具有相同时间方向的生成函数(即f和f,以及b和b),则会使得求解过程随着时间间隔的增加出现数值不稳定的问题[23].综上所述,Ff(λ, x0, t)和Fb(λ, xf, t)这一对是最好的选择.
基于双生成函数Ff(λ, x0, t)和Fb(λ, xf, t),下面的定理给出问题(1)的最优状态和输入.
定理 假设Xf(t)、Yf(t)、Xb(t)和Yb(t)(t∈[t0, tf]),满足下面的常微分方程[23]:
| $ {{\mathit{\boldsymbol{\dot X}}}_{\rm{f}}}\left( t \right) = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{X}}_{\rm{f}}}\left( t \right) - \mathit{\boldsymbol{X}}_{\rm{f}}^{\rm{T}}\left( t \right){\mathit{\boldsymbol{A}}^{\rm{T}}} - \mathit{\boldsymbol{X}}_{\rm{f}}^{\rm{T}}\left( t \right)\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{X}}_{\rm{f}}}\left( t \right) + \mathit{\boldsymbol{G}}, {\rm{ }} $ | (4) |
| $ {{\mathit{\boldsymbol{\dot Y}}}_{\rm{f}}}\left( t \right) = - {\mathit{\boldsymbol{Y}}_{\rm{f}}}\left( t \right)\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{X}}_{\rm{f}}}\left( t \right) + {\mathit{\boldsymbol{Y}}_{\rm{f}}}\left( t \right){\mathit{\boldsymbol{A}}^{\rm{T}}}, $ | (5) |
| $ {{\mathit{\boldsymbol{\dot X}}}_{\rm{b}}}\left( t \right) = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{X}}_{\rm{b}}}\left( t \right) - \mathit{\boldsymbol{X}}_{\rm{b}}^{\rm{T}}\left( t \right){\mathit{\boldsymbol{A}}^{\rm{T}}} - \mathit{\boldsymbol{X}}_{\rm{b}}^{\rm{T}}\left( t \right)\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{X}}_{\rm{b}}}\left( t \right) + \mathit{\boldsymbol{G}}, $ | (6) |
| $ {{\mathit{\boldsymbol{\dot Y}}}_{\rm{b}}}\left( t \right) = - {\mathit{\boldsymbol{Y}}_{\rm{b}}}\left( t \right)\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{X}}_{\rm{b}}}\left( t \right) + {\mathit{\boldsymbol{Y}}_{\rm{b}}}\left( t \right){\mathit{\boldsymbol{A}}^{\rm{T}}}, $ | (7) |
与边界条件
| $ {\mathit{\boldsymbol{X}}_{\rm{f}}}({t_0}) = \mathit{\boldsymbol{0}}, {\mathit{\boldsymbol{Y}}_{\rm{f}}}({t_0}) = - I, $ | (8) |
则有限时间线性二次型最优控制问题(1)的最优状态x*(t)和输入u*(t)(t∈[t0, tf])由下式给出:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}^*}\left( t \right)}\\ {{\mathit{\boldsymbol{u}}^*}\left( t \right)} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_{\rm{b}}}\left( t \right){{({\mathit{\boldsymbol{X}}_{\rm{f}}}\left( t \right) - {\mathit{\boldsymbol{X}}_{\rm{b}}}\left( t \right))}^{ - 1}}\mathit{\boldsymbol{Y}}_{\rm{f}}^{\rm{T}}\left( t \right), }&{ - {\mathit{\boldsymbol{X}}_{\rm{f}}}\left( t \right){{({\mathit{\boldsymbol{X}}_{\rm{f}}}\left( t \right) - {\mathit{\boldsymbol{X}}_{\rm{b}}}\left( t \right))}^{ - 1}}\mathit{\boldsymbol{Y}}_{\rm{b}}^{\rm{T}}\left( t \right)}\\ {{\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}{{({\mathit{\boldsymbol{X}}_{\rm{f}}}\left( t \right) - {\mathit{\boldsymbol{X}}_{\rm{b}}}\left( t \right))}^{ - 1}}\mathit{\boldsymbol{Y}}_{\rm{f}}^{\rm{T}}\left( t \right), }&{{\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}{{({\mathit{\boldsymbol{X}}_{\rm{f}}}\left( t \right) - {\mathit{\boldsymbol{X}}_{\rm{b}}}\left( t \right))}^{ - 1}}\mathit{\boldsymbol{Y}}_{\rm{b}}^{\rm{T}}\left( t \right)} \end{array}} \right]\\ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}({t_0})}\\ {\mathit{\boldsymbol{x}}({t_{\rm{f}}})} \end{array}} \right]. \end{array} $ | (10) |
式中:x(t0)=x0和x(tf)=xf是给定的边界条件值.
根据上述定理,通过计算式(4)~(7)的数值积分得到Xf(t)、Yf(t)、Xb(t)和Yb(t),由式(10)得到针对不同边界条件的最优状态和最优输入.
2 双足步行机器人最优步态生成 2.1 双足步行机器人双足步行机器人可以在适当的初始条件下在缓坡上向下行走,还可以通过输入关节力矩的方式使双足步行机器人能够在水平面上行走.机器人如图 1所示,物理参数和变量如表 1所示.主要的建模假设如下(其他假设参见文献[4]).
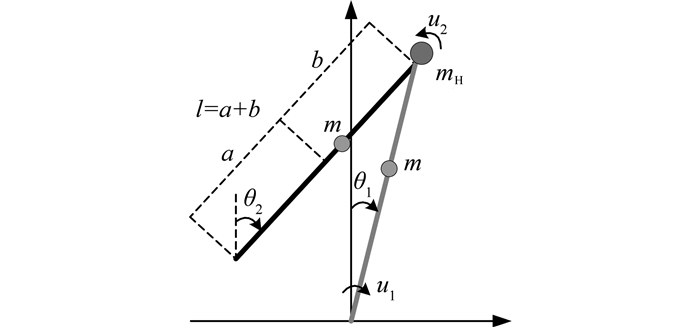
|
图 1 双足步行机器人模型 Fig. 1 Model of biped walking robot |
| 表 1 双足步行机器人的参数和变量 Table 1 Parameters and variables of biped walking robot |
假设1 支撑腿的转换发生在摆动腿接触地面和当前支撑腿离开地面的瞬间.
假设2 摆动腿与地面的碰撞被认为是非弹性且无滑动的.
| $ \mathit{\boldsymbol{M}}\left( \mathit{\boldsymbol{\theta }} \right)\mathit{\boldsymbol{\ddot \theta }} + \mathit{\boldsymbol{N}}\left( {\mathit{\boldsymbol{\theta }}, \mathit{\boldsymbol{\dot \theta }}} \right)\mathit{\boldsymbol{\theta }} + \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{\theta }} \right) = \mathit{\boldsymbol{Cu}}. $ | (11) |
式中:
| $ \begin{array}{l} \mathit{\boldsymbol{M}}\left( \mathit{\boldsymbol{\theta }} \right) = \left[ {\begin{array}{*{20}{c}} {{m_{\rm{H}}}{l^2} + m{a^2} + m{l^2}}&{ - mlb\cos ({\theta _1} - {\theta _2})}\\ { - mlb\cos ({\theta _1} - {\theta _2})}&{m{b^2}} \end{array}} \right], \\ \mathit{\boldsymbol{N}}\left( {\mathit{\boldsymbol{\theta }}, \mathit{\boldsymbol{\dot \theta }}} \right) = \left[ {\begin{array}{*{20}{c}} 0&{ - mlb{{\dot \theta }_2}\sin ({\theta _1} - {\theta _2})}\\ {mlb{{\dot \theta }_1}\sin ({\theta _1} - {\theta _2})}&0 \end{array}} \right], \\ \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{\theta }} \right) = \left[ {\begin{array}{*{20}{c}} { - ({m_{\rm{H}}}l + m\left( {a + l} \right))g\sin {\theta _1}}\\ {mgb\sin {\theta _2}} \end{array}} \right], \\ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} 1&{ - 1}\\ 0&1 \end{array}} \right]. \end{array} $ |
定义状态变量x为
| $ \mathit{\boldsymbol{x}} = {[{\theta _1}, {\theta _2}, {{\dot \theta }_1}, {{\dot \theta }_2}]^{\rm{T}}} = {[{x_1}, {x_2}, {x_3}, {x_4}]^{\rm{T}}}, $ |
则图 1中机器人的线性化动力学方程为
| $ \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{Bu}}. $ |
式中:u=[u1, u2]T,
| $ \begin{array}{l} \mathit{\boldsymbol{A}} = \\ \left[ {\begin{array}{*{20}{c}} 0&0&1&0\\ 0&0&0&1\\ {\frac{{g({m_{\rm{H}}}l + m\left( {a + l} \right))}}{{{m_{\rm{H}}}{l^2} + m{a^2}}}}&{\frac{{ - mgl}}{{{m_{\rm{H}}}{l^2} + m{a^2}}}}&0&0\\ {\frac{{gl({m_{\rm{H}}}l + m\left( {a + l} \right))}}{{b({m_{\rm{H}}}{l^2} + m{a^2})}}}&{\frac{{ - g({m_{\rm{H}}}{l^2} + m{a^2} + m{l^2})}}{{b({m_{\rm{H}}}{l^2} + m{a^2})}}}&0&0 \end{array}} \right], \end{array} $ | (12) |
| $ \begin{array}{l} \mathit{\boldsymbol{B}} = \\ \left[ {\begin{array}{*{20}{c}} 0&0\\ 0&0\\ {\frac{1}{{{m_{\rm{H}}}{l^2} + m{a^2}}}}&{\frac{{l - b}}{{b({m_{\rm{H}}}{l^2} + m{a^2})}}}\\ {\frac{l}{{b({m_{\rm{H}}}{l^2} + m{a^2})}}}&{\frac{{{m_{\rm{H}}}{l^2} + m{a^2} + m{l^2} - mbl}}{{m{b^2}({m_{\rm{H}}}{l^2} + m{a^2})}}} \end{array}} \right], \end{array} $ | (13) |
针对上述线性化的机器人模型,考虑能量消耗,设定最优控制问题(1).目标是找到一系列最优的输入u*(t),使得能耗代价函数取最小值,同时满足相对应的一系列边界条件.在实际中,由于驱动器的限制,踝关节输入和髋关节输入都不应太大,需要合理选择代价函数中的权重矩阵R.给出如下具体的算法,用于生成针对不同边界条件和不同时间间隔的最优状态和输入轨迹.
算法
●线下部分:1)将动力学方程(11)线性化,即根据式(11)、(12)分别得到矩阵A和B;2)设定问题(1)中的矩阵Q和R;3)根据边界条件(8)和(9),数值求解式(4)~(7),得到生成函数的系数Xf(t)、Yf(t)、Xb(t)和Yb(t).
●线上部分:4)根据式(10)生成最优状态x*和最优输入u*;5)若改变边界条件x0和/或xf和/或初始时间t0和/或终端时间tf,则转到步骤4).
在上述算法中,线上只进行简单的代数运算,计算量很小,因此改变机器人每一步的边界条件和/或时间周期是非常方便的.若希望将这些线性系统的轨迹视为非线性系统(11)的最优轨迹,则需要分析由线性化建模所造成的误差,该工作将在2.3节展开.
2.3 基于PD控制的轨迹跟踪大多数工业机器人都采用了经典的PD控制器.使用该控制方法,使得非线性系统的状态和输入可以跟踪机器人的参考状态和参考输入(即线性系统的状态和输入).
针对双足步行机器人的动力学方程(11),设计PD控制律如下:
| $ \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{K}}_\theta }({\mathit{\boldsymbol{\theta }}^{{\rm{ref}}}} - \mathit{\boldsymbol{\theta }}) + {\mathit{\boldsymbol{K}}_{\dot \theta }}({{\mathit{\boldsymbol{\dot \theta }}}^{{\rm{ref}}}} - \mathit{\boldsymbol{\dot \theta }}) + {\mathit{\boldsymbol{u}}^{{\rm{ref}}}}. $ |
式中:Kθ和
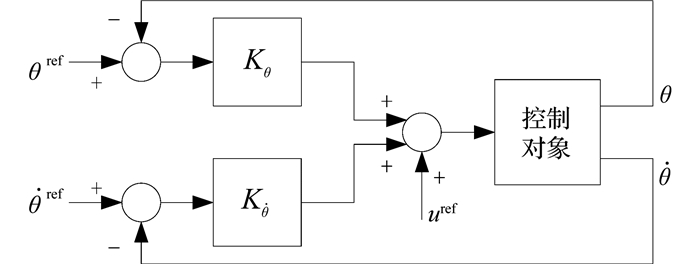
|
图 2 PD控制器框图 Fig. 2 PD controller |
图 1中,双足步行机器人的参数为:a=0.5 m,b=0.5 m,l=1.0 m,m=5 kg,mH=10 kg,g=9.8 m/s2.基于部分试探性仿真,设定参数Q=I,R=diag [10,1].若R=diag [1,1],则踝关节力矩大于髋关节力矩;若R=diag [100,1],则踝关节力矩非常小,髋关节力矩非常大.图 2中,将PD控制器的比例系数和微分系数设定为Kθ=diag [100,50],
双足步行机器人行走一步的时间周期在支撑腿的当前转换瞬间之后开始,并且在支撑腿的下一个转换瞬间之前结束.由此可知,行走一步的状态的初始值和终端值分别是当前冲击后和下一次冲击前的状态值.以双生成函数方法生成的关于线性系统的最优状态和输入作为参考量.
双生成函数方法的特点是针对不同边界条件,可以高效地生成一系列相对应的最优状态和输入.为了展现该优点,考虑设置连续多步仿真实例.首先介绍步态的转换模型.假设2表明机器人的姿态在过渡瞬间保持不变[25],即
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{\theta }}^ + } = \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{\theta }}^ - }, \\ \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} = \left[ {\begin{array}{*{20}{c}} 0&1\\ 1&0 \end{array}} \right]. \end{array} \right\} $ | (14) |
式中:Γ用于交换即将到来的摆动阶段的支撑角和摆动角,冲击前和冲击后变量分别用上标“-”和“+”来标识.由式(14),可以得到
| $ {\mathit{\boldsymbol{\theta }}^ - } = \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{\theta }}^ + }. $ |
假设2表明,机器人关于冲击脚的角动量以及冲击前支撑腿关于髋关节的角动量是守恒的.这些守恒定律引起了机器人速度的突变,即
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ - }({\mathit{\boldsymbol{\theta }}^ - }){\mathit{\boldsymbol{\dot\theta }}^ - } = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ + }({\mathit{\boldsymbol{\theta }}^ + }){{\mathit{\boldsymbol{\dot \theta }}}^ + }. $ | (15) |
式中:
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ - }({\mathit{\boldsymbol{\theta }}^ - }) = \\ \left[ {\begin{array}{*{20}{c}} { - mab + ({m_{\rm{H}}}{l^2} + 2mal)\cos (\theta _2^ - - \theta _1^ - )}&{ - mab}\\ { - mab}&0 \end{array}} \right], \end{array} $ |
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ - }({\mathit{\boldsymbol{\theta }}^ - }) = \\ \left[ {\begin{array}{*{20}{c}} {ml(l - b\cos (\theta _1^ + - \theta _2^ + )) + m{a^2} + {m_{\rm{H}}}{l^2}, }&{mb\left( {b - l\cos \left( {\theta _1^ + - \theta _2^ + } \right)} \right)}\\ { - mbl\cos (\theta _1^ + - \theta _2^ + ), }&{m{b^2}} \end{array}} \right]. \end{array} $ |
由式(14)、(15)可知,机器人腿冲击后的角速度可以从冲击前的角速度推导得到:
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot \theta }}}^ + } = {\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ + }\left( {{\mathit{\boldsymbol{\theta }}^ + }} \right)} \right)^{ - 1}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ - }\left( {{\mathit{\boldsymbol{\theta }}^ - }} \right){{\mathit{\boldsymbol{\dot \theta }}}^ - } = \\ \;\;\;\;\;\;{\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ + }\left( {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{\theta }}^ - }} \right)} \right)^{ - 1}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^ - }\left( {{\mathit{\boldsymbol{\theta }}^ - }} \right){{\mathit{\boldsymbol{\dot \theta }}}^ - }. \end{array} $ | (16) |
根据式(16),设置如下7步连续步态的边界条件:
| $ \left. {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{x}}^1}(t_0^1] = {{\left[ {0, 0, 0, 0} \right]}^{\rm{T}}}, }&{t_0^1 = 0;}\\ {{\mathit{\boldsymbol{x}}^1}\left[ {t_{\rm{f}}^1} \right] = {{\left[ {0.1, - 0.1, 0.4, - 0.4} \right]}^{\rm{T}}}, }&{t_{\rm{f}}^1 = {{1.0}^ - };}\\ {{\mathit{\boldsymbol{x}}^2}\left[ {t_0^2} \right] = {{\left[ { - 0.1, 0.1, 0.47, 0.52} \right]}^{\rm{T}}}, }&{t_0^2 = {{1.0}^ + };}\\ {{\mathit{\boldsymbol{x}}^2}\left[ {t_{\rm{f}}^2} \right] = {{\left[ {0.1, - 0.1, 0.4, - 0.4} \right]}^{\rm{T}}}, }&{t_{\rm{f}}^2 = {{2.0}^ - };}\\ {{\mathit{\boldsymbol{x}}^3}\left[ {t_0^3} \right] = {{\left[ { - 0.1, 0.1, 0.47, 0.52} \right]}^{\rm{T}}}, }&{t_0^3 = {{2.0}^ + };}\\ {{\mathit{\boldsymbol{x}}^3}\left[ {t_{\rm{f}}^3} \right] = {{\left[ {0.1, - 0.1, 0.4, - 0.4} \right]}^{\rm{T}}}, }&{t_{\rm{f}}^3 = {{3.0}^ - };}\\ {{\mathit{\boldsymbol{x}}^4}\left[ {t_0^4} \right] = {{\left[ { - 0.1, 0.1, 0.47, 0.52} \right]}^{\rm{T}}}, }&{t_0^4 = {{3.0}^ + };}\\ {{\mathit{\boldsymbol{x}}^4}\left[ {t_{\rm{f}}^4} \right] = {{\left[ {0.2, - 0.2, 0.8, - 0.8} \right]}^{\rm{T}}}, }&{t_{\rm{f}}^4 = {{3.8}^ - };}\\ {{\mathit{\boldsymbol{x}}^5}\left[ {t_0^5} \right] = {{\left[ { - 0.2, 0.2, 0.85, 0.77} \right]}^{\rm{T}}}, }&{t_0^5 = {{3.8}^ + };}\\ {{\mathit{\boldsymbol{x}}^5}\left[ {t_{\rm{f}}^5} \right] = {{\left[ {0.2, - 0.2, 0.8, - 0.8} \right]}^{\rm{T}}}, }&{t_{\rm{f}}^5 = {{4.6}^ - };}\\ {{\mathit{\boldsymbol{x}}^6}\left[ {t_0^6} \right] = {{\left[ { - 0.2, 0.2, 0.85, 0.77} \right]}^{\rm{T}}}, }&{t_0^6 = {{4.6}^ + };}\\ {{\mathit{\boldsymbol{x}}^6}\left[ {t_{\rm{f}}^6} \right] = {{\left[ {0.2, - 0.2, 0.8, - 0.8} \right]}^{\rm{T}}}, }&{t_{\rm{f}}^6 = {{5.4}^ - };}\\ {{\mathit{\boldsymbol{x}}^7}\left[ {t_0^7} \right] = {{\left[ { - 0.2, 0.2, 0.85, 0.77} \right]}^{\rm{T}}}, }&{t_0^7 = {{5.4}^ + };}\\ {{\mathit{\boldsymbol{x}}^7}\left[ {t_{\rm{f}}^7} \right] = {{\left[ {0, 0, 0, 0} \right]}^{\rm{T}}}, }&{t_{\rm{f}}^7 = 6.2.} \end{array}} \right\} $ |
式中:xi(t)、t0i、tfi分别为在时间t的状态、第i步的初始时间和终端时间,t-(t+)为刚好在时间t前(时间t后)的时刻.机器人从静止状态开始行走,最后终止于静止状态.前3步的时间周期为1.0,后4步为0.8.
仿真结果如图 3~5所示。图中,实线表示参考状态和输入,虚线表示经PD控制器调节后的非线性系统的状态和输入.图 3给出7步连续步态所对应的状态和输入轨迹,其中第i(i=1, 2, …, 7)个时间间隔中的线段表示与第i步相对应的轨迹.图 4给出对应于图 3的跟踪误差.图 5给出第2、3步和第5、6步的
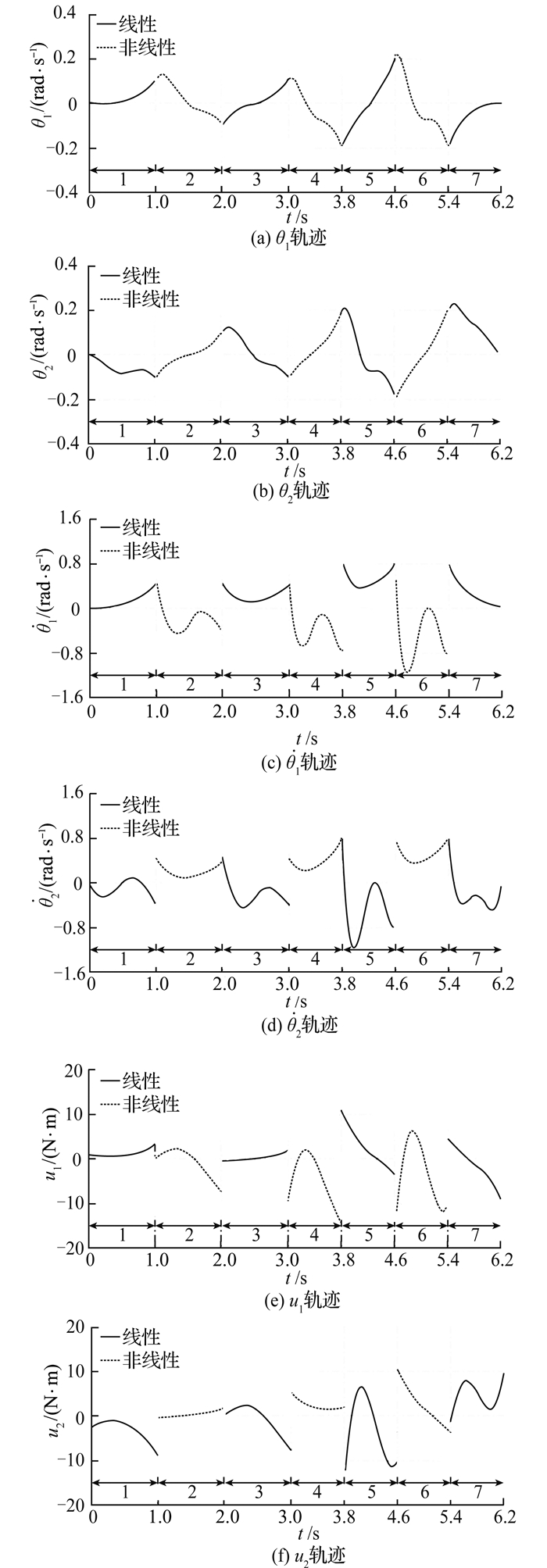
|
图 3 7个步态的状态和输入轨迹 Fig. 3 State and input trajectories for 7 gaits |
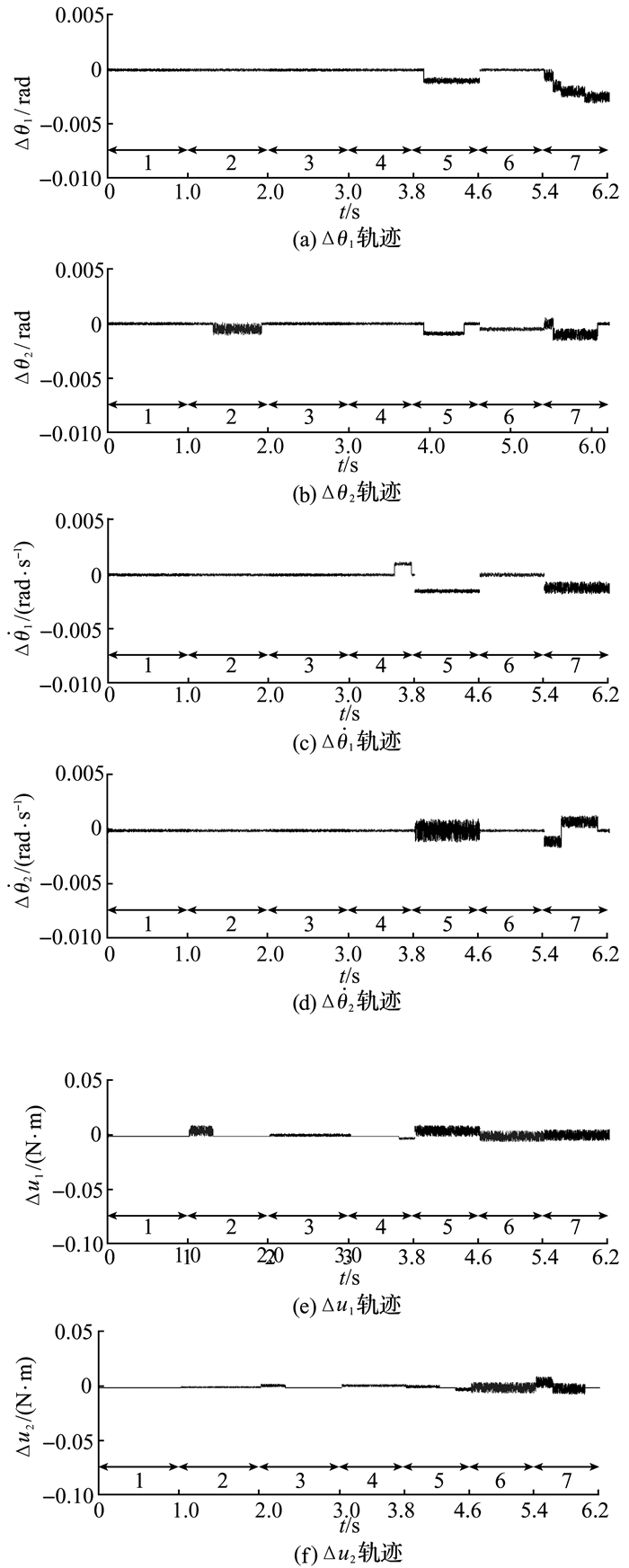
|
图 4 7个步态的状态和输入轨迹跟踪误差 Fig. 4 Tracking error of state and input trajectories for 7 gaits |
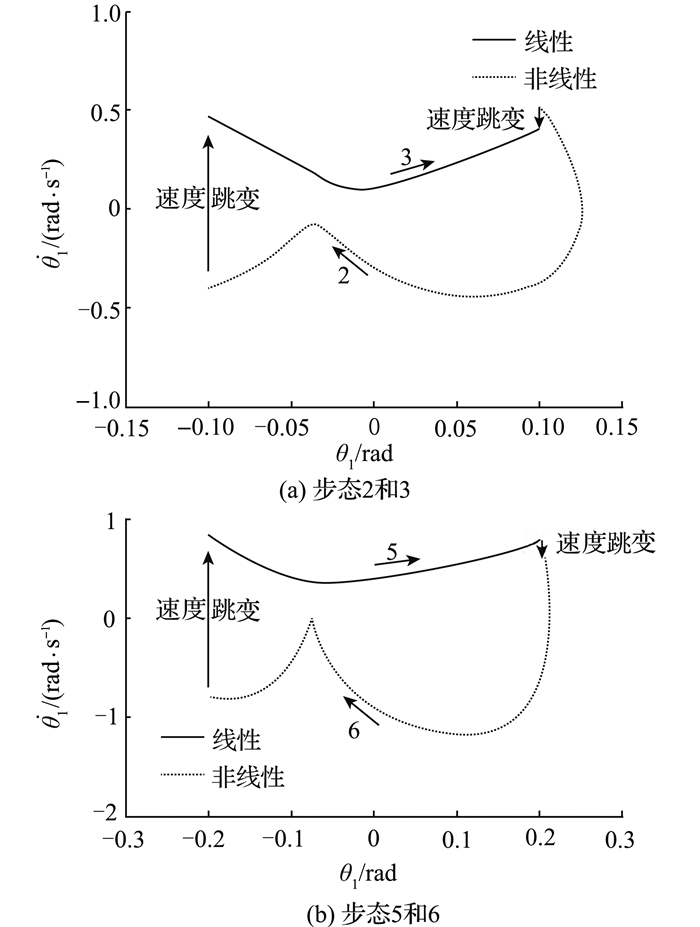
|
图 5
步态2-3和5-6的 |
根据双生成函数方法给出最优解的特殊结构,大部分计算量(即数值积分部分)被转移到线下,线上针对不同的边界条件只进行简单的代数运算.仿真结果表明,利用该方法可以在线、高效地生成机器人的步态.由图 3可以看出,PD控制器所调节产生的非线性系统的状态轨迹和输入轨迹能够很好地跟踪参考轨迹.同时,图 4显示由线性建模所产生的误差可以控制到较小范围内.线性化模型的最优步态和输入可以看作是机器人非线性模型(11)的最优步态和输入.此外,如图 3(e)、(f)所示,生成得到的踝关节输入和髋关节输入都很小(不大于15 N·m),显示了该方法的实用性.如图 4所示,第2、3步和第5、6步的相位图形成闭环,这表明机器人的运动是周期性的,与步态设置相符.
4 结语本文将双生成函数方法应用于双足步行机器人的能量最优稳定步态的规划生成中.该方法具有在线规划高效的优点.此外,由于双生成函数方法是针对线性系统的,在应用时,需要将双足步行机器人的动力学方程线性化.线性化所造成的建模误差可以由所设计的PD控制器来进行调节控制.仿真结果表明,当机器人以合理的步长并在合适的时间段行走时,由线性化引起的建模误差较小.得益于双生成函数方法的优点,在不同的边界条件下,根据需要实时地优化步态和输入是非常方便的,对实际的机器人控制非常有用.本文没有考虑双足机器人与地面接触的情况,这一点将在后续进行研究.
| [1] |
SHIN H K, KIM B K. Energy-efficient gait planning and control for biped robots utilizing the allowable ZMP region[J]. IEEE Transactions on Robotics, 2014, 30(4): 986-993. DOI:10.1109/TRO.2014.2305792 |
| [2] |
张博, 杜志江, 孙立宁, 等. 双足步行机器人步态规划方法研究[J]. 机械与电子, 2008(4): 52-55. ZHANG Bo, DU Zhi-jiang, SUN Li-ning, et al. Research on gait planning of biped walking robot[J]. Machinery and Electronics, 2008(4): 52-55. |
| [3] |
李攀, 魏洪兴. 双足机器人步态规划方法研究[J]. 机械工程与自动化, 2017(4): 22-24. LI Pan, WEI Hong-xing. Method of gait planning for biped robot[J]. Mechanical Engineering and Automation, 2017(4): 22-24. |
| [4] |
ROSTAMI M, BESSONNET G. Sagittal gait of a biped robot during the single support phase.part 2:optimal motion[J]. Robotica, 2001, 19(3): 241-245. |
| [5] |
SAIDOUNI T, BESSONNET G. Generating globally optimised sagittal gait cycles of a biped robot[J]. Robotica, 2003, 21(2): 199-210. |
| [6] |
MCGEER T. Passive dynamic walking[J]. International Journal of Robotics Research, 1990, 9(2): 62-82. DOI:10.1177/027836499000900206 |
| [7] |
LEE J H, OKAMOTO S, KOIKE H, et al. Development and motion control of a biped walking robot based on passive walking theory[J]. Artificial Life and Robotics, 2014, 19(1): 68-75. DOI:10.1007/s10015-013-0132-y |
| [8] |
SAFA A, NARAGHI M. The role of walking surface in enhancing the stability of the simplest passive dynamic biped[J]. Robotica, 2015, 33(1): 195-207. DOI:10.1017/S0263574714000204 |
| [9] |
GRITLI H, BELGHITH H, KHRAIEF N. OGY-based control of chaos in semi-passive dynamic walking of a torso-driven biped robot[J]. Nonlinear Dynamics, 2015, 79(2): 1363-1384. DOI:10.1007/s11071-014-1747-9 |
| [10] |
CAO Y, SUZUKI S, HOSHINO Y. Uphill and level walking of a three-dimensional biped quasi-passive walking robot by torso control[J]. Robotica, 2016, 34(3): 483-496. DOI:10.1017/S0263574714001593 |
| [11] |
ZHU H, LUO H, MEI T, et al. Energy-efficient bio-inspired gait planning and control for biped robot based on human locomotion analysis[J]. Journal of Bionic Engineering, 2016, 13(2): 271-282. DOI:10.1016/S1672-6529(16)60300-1 |
| [12] |
WANG L, LIU Z, CHEN C, et al. Energy-efficient svm learning control system for biped walking robots[J]. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(5): 831-837. DOI:10.1109/TNNLS.2013.2242486 |
| [13] |
ASANO F, YAMAKITA M, KAMAMICHI N, et al. A novel gait generation for biped walking robots based on mechanical energy constraint[J]. IEEE Transactions on Robotics and Automation, 2004, 20(3): 565-573. DOI:10.1109/TRA.2004.824685 |
| [14] |
COLLINS S, RUINA A, TEDRAKE R, et al. Efficient bipedal robots based on passive-dynamic walkers[J]. Science, 2005, 307(5712): 1082-1085. DOI:10.1126/science.1107799 |
| [15] |
SATOH S, FUJIMOTO K, HYON S. A framework for optimal gait generation via learning optimal control using virtual constraint[C]//Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems. Nice: IEEE, 2008: 3426-3432. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4650860
|
| [16] |
FUJIMOTO K, SUGIE T. Iterative learning control of hamiltonian systems:I/O based optimal control approach[J]. IEEE Transactions on Automatic Control, 2003, 48(10): 1756-1761. DOI:10.1109/TAC.2003.817908 |
| [17] |
SHIN H K, KIM B K. Energy-efficient gait planning and control for biped robots utilizing vertical body motion and allowable ZMP region[J]. IEEE Transactions on Industrial Electronics, 2015, 62(4): 2277-2286. DOI:10.1109/TIE.2014.2360152 |
| [18] |
MCENEANEY W, DOWER P. The principle of least action and fundamental solutions of mass-spring and n-body two-point boundary value problems[J]. SIAM Journal on Control and Optimization, 2015, 53(5): 2898-2933. DOI:10.1137/130921908 |
| [19] |
CRISTIANI E, MARTINON P. Initialization of the shooting method via the Hamilton-Jacobi-bellman approach[J]. Journal of Optimization Theory and Applications, 2010, 146(2): 321-346. DOI:10.1007/s10957-010-9649-6 |
| [20] |
GUIBOUT V, SCHEERES D J. Solving relative two point boundary value problems:spacecraft formation flight transfers application[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(4): 693-704. DOI:10.2514/1.11164 |
| [21] |
PARK C, SCHEERES D J. Determination of optimal feedback terminal controllers for general boundary conditions using generating functions[J]. Automatica, 2006, 42(5): 869-875. DOI:10.1016/j.automatica.2006.01.015 |
| [22] |
HAO Z, FUJIMOTO K. Approximate solutions to the Hamilton-Jacobi equations for generating functions with a quadratic cost function with respect to the input[C]//Proceedings of the 4th IFAC Workshop on Lagrangian and Hamiltonian Methods for Nonlinear Control. Bertinoro: Elsevier, 2012: 194-199. http://www.sciencedirect.com/science/article/pii/S1474667015337666
|
| [23] |
HAO Z, FUJIMOTO K, HAYAKAWA Y. Optimal trajectory generation for linear systems based on double generating functions[J]. SICE Journal of Control, Measurement, and System Integration, 2012, 6(3): 194-201. |
| [24] |
GEERING H P. Optimal control with engineering applications[M]. 1st ed. Berlin: Springer, 2007, 24-35.
|
| [25] |
HURMUZLU Y, CHANG T H. Rigid body collisions of a special class of planar kinematic chains[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1992, 22(5): 964-971. DOI:10.1109/21.179836 |



