随着动力锂离子电池在电动汽车、工业储能等领域应用的不断深入, 电池管理系统有着重要的研究意义与应用价值[1].作为保障电池安全可靠工作的重要组成部分, 近年来锂离子电池的故障诊断研究受到了研究者们更多的重视[2-5].对于单电池而言, 很多故障难以直接检测, 但会导致电池内部参数的变化, 如电解液泄漏会改变电池的极化参数, 接触不良会表现为电池欧姆内阻的增加; 此外内部参数可以有效地反映出电池的健康状态(state of health, SOH).给出系统参数的实时估计值, 对于系统故障的精确检测、分离与容错控制具有重要的意义.
目前, 电池内部参数估计通常作为电池的SOC估计的辅助研究出现[6-11].Zhang等[6-7]基于EKF, 给出电池参数的实时估计.Liu等[8]引入Gause-Newton法,对电池参数进行迭代求解.Liu等[9]研究基于粒子滤波(particle filter, PF)的参数估计方法.由于电池参数通常是时变的, Sun等[10-11]通过带有恒定遗忘因子的递推最小二乘法(recursive least square method, RLSM), 进行电池参数辨识.Chen等[12-14]将参数辨识算法应用于电池故障诊断中进行研究.Chen等[12]采用大偏差原理分析诊断可靠性, Zhang等[13-14]针对串并联电池组着重分析电池容量损耗型故障.上述方法大多只适用于参数定常或缓慢变化的情况, 对于故障电池而言, 当出现参数突变或大幅变化的情况时, 上述方法可能会失效.
为了解决上述问题, 周东华等[15-16]在EKF的基础上提出带有时变渐消因子的强跟踪滤波器(strong tracking filter, STF).该方法对模型不确定性的鲁棒性较强, 同时对于时变状态与参数的估计具有较好的跟踪功能; 因此适用于故障发生时系统参数时变且变化幅度较大时进行在线估计.王小旭等[17]将STF的思想引入UKF, 形成了UTSTF算法.该方法不仅继承了STF高鲁棒性的优点, 而且克服了原有方法在非线性问题上的局限性, 省去了计算Jacobian矩阵的繁琐, 适用于高阶问题.该算法在发动机状态估计、INS/GPS组合导航中得到了成功的应用[18-19].
本文首次应用UTSTF算法, 针对动态特性更复杂的锂离子电池参数偏差型故障的精确诊断问题进行研究.由于电池参数在模型中的非线性较强且具有不确定性, 可以将电池参数引入状态变量, 采用UTSTF算法对状态和参数联合估计, 实现电池时变参数的实时跟踪, 根据不同参数的估计值可以达到故障识别与分离的目的.
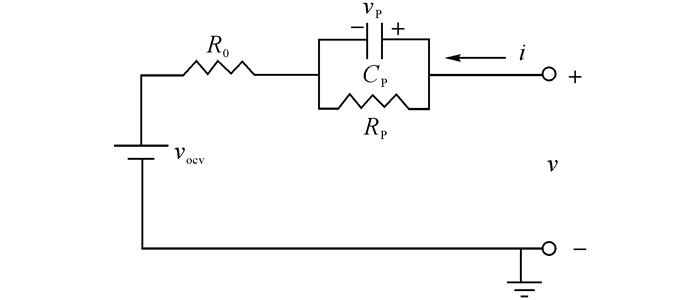
1 电池模型锂离子电池的数学模型可分以为等效电路模型、电化学模型及人工神经元网络模型等.其中一阶等效电路模型能够准确地描述电池的特性, 同时简单易于分析.采用的等效电路模型如图 1所示, 数学关系为
|
图 1 锂离子电池一阶等效电路模型 Fig. 1 One-order equivalent circuit model of li-ion battery |
| $ {{\dot v}_p}\left( t \right) = \frac{{ - 1}}{{{R_{\rm{p}}}{C_{\rm{p}}}}}{v_{\rm{p}}}\left( t \right) + \frac{1}{{{C_{\rm{p}}}}}i\left( t \right), $ | (1) |
| $ v\left( t \right) = {v_{{\rm{ocv}}}} + {v_{\rm{p}}}\left( t \right) + i\left( t \right){R_0}. $ | (2) |
式中:Rp为电池的极化内阻, R0为电池的欧姆内阻, Cp为电池的极化电容, i(t)为电池电流, vocv为开路电压, v(t)为端电压.
电池的SOC由下式给出:
| $ s\left( t \right) = s({t_0}) + \smallint _{{t_0}}^t\frac{1}{{{Q_0}}}i\left( \tau \right){\rm{d}}\tau . $ | (3) |
式中:Q0为电池容量.
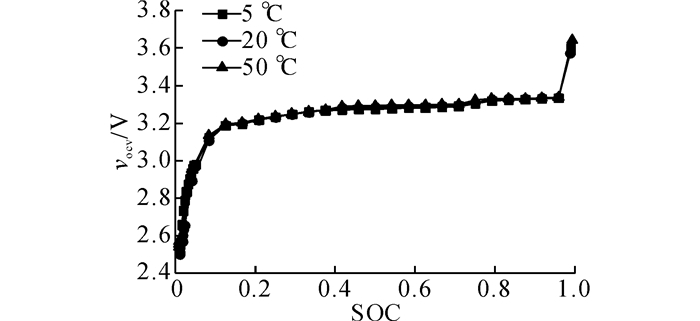
实际中,开路电压vocv为s(t)的非线性函数vocv=g(s).通过实验给出磷酸铁锂电池在5、20、50 ℃下的OCV-SOC特性曲线, 如图 2所示.可见, vocv随温度的变化不明显, 可以视作仅为s(t)的函数.统一采用7次多项式拟合得到
|
图 2 OCV-SOC特性曲线 Fig. 2 OCV-SOC characteristic mapping curve |
| $ \begin{array}{l} {v_{{\rm{ocv}}}} = 397.4{s^7} - 1434{s^6} + 2093{s^5} - 1583{s^4} + \\ \;\;\;\;661.2{s^3} - 150.5{s^2} + 17.38s + 2.417. \end{array} $ | (4) |
动态充放过程中影响锂离子电池性能的主要时变参数为Cp、Rp、R0.定义扩展状态变量xk=[sk, v(p)k, Cp, Rp, R0]T, 由于时变参数的变化规律未知, 取时变参数的定常部分作为状态方程, 结合式(1)~(4),可得离散形式下构成电池的联合状态空间方程:
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{x}}_{k + 1}} = \mathit{\boldsymbol{A}}({\mathit{\boldsymbol{x}}_k}){\mathit{\boldsymbol{x}}_k} + \mathit{\boldsymbol{B}}({\mathit{\boldsymbol{x}}_k}){i_k} + {\mathit{\boldsymbol{r}}_k}, \\ {v_{k + 1}} = h({\mathit{\boldsymbol{x}}_{k + 1}}, {i_{k + 1}}) + {e_{k + 1}}. \end{array} \right\} $ | (5) |
式中:
| $ \left. \begin{array}{l} \mathit{\boldsymbol{A}}({\mathit{\boldsymbol{x}}_k}) = {\rm{diag}}\left[ {1, \exp \left( { - \frac{T}{{{R_{\rm{p}}}{C_{\rm{p}}}}}} \right), 1, 1, 1} \right], \\ \mathit{\boldsymbol{B}}({\mathit{\boldsymbol{x}}_k}) = {\left[ {T/{Q_0}, {R_{\rm{p}}}\left[ {1 - \exp \left( { - \frac{T}{{{R_{\rm{p}}}{C_{\rm{p}}}}}} \right)} \right], 0, 0, 0} \right]^{\rm{T}}}; \end{array} \right\} $ | (6) |
| $ h({\mathit{\boldsymbol{x}}_{k + 1}}, {i_{k + 1}}) = g({s_{k + 1}}) + {v_{\left( p \right)k + 1}} + {i_{k + 1}}{R_0}. $ | (7) |
vk为系统输出, ik为系统激励, rk为系统噪声, ek为测量噪声, T为采样时间.假定系统噪声和测量噪声序列互不相关且分别为零均值, 协方差矩阵为Q和R的高斯白噪声.
2.2 UTSTF联合估计方法传统UKF对非线性问题的适应性较好, 但存在鲁棒性较差的问题, 对突变状态的估计不具有跟踪能力.当系统趋于稳定时, 增益阵Kk+1将趋于0, 此时若系统模型发生突变, 尽管残差εk+1增大, 但Kk+1εk+1较小, 新时刻的状态估计值几乎不发生变化.UTSTF的核心思想是在UKF的基础上, 自适应地调整预测协方差阵, 使得不同时刻的残差序列保持相互正交.通过削弱旧数据对当前估计值的影响, 从而使滤波器对数据具有较强的跟踪性.预测协方差阵通过引入时变渐消因子λk+1来自适应调整.UTSTF可以视为一种自适应无迹卡尔曼滤波器(adaptive unscented Kalman filter, AUKF).当电池发生参数偏差型故障时, 由于式(5)的模型不匹配, 需要引入UTSTF估计时变参数.
UTSTF算法首先要对n维状态变量x进行无迹变换, 获取2n+1个Sigma点ξi与相应的加权系数Wm、Wc.
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{\xi }}_0} = \mathit{\boldsymbol{\hat x}};\\ {\mathit{\boldsymbol{\xi }}_i} = \mathit{\boldsymbol{\hat x}} + {\left( {\sqrt {\left( {n + \kappa } \right)\mathit{\boldsymbol{P}}} } \right)_i}, i = 1, 2, \cdots , n, \\ {\mathit{\boldsymbol{\xi }}_i} = \mathit{\boldsymbol{\hat x}} - {\left( {\sqrt {\left( {n + \kappa } \right)\mathit{\boldsymbol{P}}} } \right)_i}, i = n + 1, n + 2, \cdots , 2n. \end{array} \right\} $ | (8) |
| $ \left. \begin{array}{l} W_0^{\rm{m}} = \kappa /\left( {n + \kappa } \right);\\ W_0^{\rm{c}} = \kappa /\left( {n + \kappa } \right) + (1 - {\alpha ^2} + \beta );\\ W_i^{\rm{m}} = W_i^{\rm{c}} = 1/\left[ {2\left( {n + \kappa } \right)} \right], i = 1, 2, \cdots , 2n. \end{array} \right\} $ | (9) |
式中:κ=α2(n+k)-n, 其中α为比例因子, 可取0.01;β用于提高方差的精度, 对于高斯分布可取2.
算法的具体步骤如下.
1) 初始化.状态估计值
2) 状态与输出预测.将Sigma点ξi, k按式(5)传递为γi, k+1|k, 由γi, k+1|k得到一步状态预测
| $ \left. \begin{array}{l} {\gamma _{i, k + 1|k}} = \mathit{\boldsymbol{A}}({\mathit{\boldsymbol{\xi }}_{i, k}}){\mathit{\boldsymbol{\xi }}_{i, k}} + \mathit{\boldsymbol{B}}({\mathit{\boldsymbol{\xi }}_{i, k}}){i_k}, \\ {{\mathit{\boldsymbol{\hat x}}}_{k + 1|k}} = \sum\limits_{i = 0}^{2n} {\left( {W_i^{\rm{m}}{\gamma _{i, k + 1|k}}} \right)} , \\ {\mathit{\boldsymbol{P}}_{k + 1|k}} = \sum\limits_{i = 0}^{2n} {\{ W_i^{\rm{c}}[{\gamma _{i, k + 1|k}} - {{\hat x}_{k + 1|k}}] \times } \\ \;\;\;\;\;\;\;\;\;\;\;\;{[{\mathit{\boldsymbol{\gamma }}_{i, k + 1|k}} - {{\mathit{\boldsymbol{\hat x}}}_{k + 1|k}}]^{\rm{T}}}. \end{array} \right\} $ | (10) |
利用
| $ \begin{array}{l} \;\;\;{{\mathit{\boldsymbol{\hat v}}}_{k + 1|k}} = \sum\limits_{i = 0}^{2n} [ W_i^{\rm{m}}h({\mathit{\boldsymbol{\xi }}_{i, k + 1|k}}, {i_{k + 1}})], \\ {P_{{{\mathit{\boldsymbol{\hat v}}}_{k + 1}}}} = \sum\limits_{i = 0}^{2n} \{ W_i^{\rm{c}}[h({\mathit{\boldsymbol{\xi }}_{i, k + 1|k}}, {i_{k + 1}}) - {{\hat v}_{k + 1|k}}] \times \\ \;\;\;\;\;\;\;\;\;\;\;[h({\mathit{\boldsymbol{\xi }}_{i, k + 1|k}}, {i_{k + 1}}) - {{\hat v}_{k + 1|k}}]\} , \\ {\mathit{\boldsymbol{P}}_{{{\hat x}_{k + 1}}\hat v}}_{_{k + 1}} = \sum\limits_{i = 0}^{2n} {\rm{\{ }} W_i^{\rm{c}}[{\mathit{\boldsymbol{\xi }}_{i, k + 1{\rm{|}}k}} - {{\mathit{\boldsymbol{\hat x}}}_{k + 1|k}}] \times \\ \;\;\;\;\;\left. \begin{array}{l} {[h({\mathit{\boldsymbol{\xi }}_{i, k + 1|k}}, {i_{k + 1}}) - {{\mathit{\boldsymbol{\hat v}}}_{k + 1|k}}]^{\rm{T}}}, \\ {\varepsilon _{k + 1}} = {v_{k + 1}} - {{\hat v}_{k + 1|k}}. \end{array} \right\} \end{array} $ | (11) |
式中:εk+1为滤波残差.采用文献[17]的次优方法,求取渐消因子:
| $ {\lambda _{k + 1}} = \left\{ \begin{array}{l} {\lambda _0}, \;\;\;{\lambda _0} \ge 1\\ 1, \;\;\;{\lambda _0} < 1 \end{array} \right., {\lambda _0} = \frac{{{\rm{tr}}({N_{k + 1}})}}{{{\rm{tr}}({M_{k + 1}})}}. $ | (12) |
其中:
| $ \left. {\begin{array}{*{20}{c}} {{N_{k + 1}} = {V_{k + 1}} - \eta R - \mathit{\boldsymbol{P}}_{{{\mathit{\boldsymbol{\hat x}}}_{k + 1}}{{\mathit{\boldsymbol{\hat v}}}_{k + 1}}}^{\rm{T}}P_{k + 1|k}^{ - 1} \times }\\ {\mathit{\boldsymbol{QP}}_{k + 1|k}^{ - 1}{P_{{{\mathit{\boldsymbol{\hat x}}}_{k + 1}}{{\mathit{\boldsymbol{\hat v}}}_{k + 1}}}}, }\\ {{M_{k + 1}} = {P_{\hat v}}_{_{k + 1}} - {V_{k + 1}} + {N_{k + 1}}.} \end{array}} \right\} $ | (13) |
| $ {V_{k + 1}} = \left\{ {\begin{array}{*{20}{c}} {\xi _1^2, }\\ {\frac{{\rho {V_k} + \xi _{k + 1}^2}}{{1 + \rho }}, } \end{array}} \right.\begin{array}{*{20}{c}} {k = 0;}\\ {k \ge 1.} \end{array} $ | (14) |
式中:0 < ρ≤1为遗忘因子, 通常取0.95;η≥1为弱化因子.
修正预测协方差阵, 可得
| $ \begin{array}{l} {\mathit{\boldsymbol{P}}_{k + 1|k}} = {\lambda _{k + 1}}\sum\limits_{i = 0}^{2n} \{ W_i^{\rm{c}}[{\mathit{\boldsymbol{\xi }}_{i, k + 1|k}} - {{\mathit{\boldsymbol{\hat x}}}_{k + 1|k}}] \times \\ \;\;\;\;\;\;\;\;\;\;\;\;{[{\xi _{i, k + 1|k}} - {{\mathit{\boldsymbol{\hat x}}}_{k + 1|k}}]^{\rm{T}}}\} . \end{array} $ | (15) |
利用修正后的Pk+1|k与
3) 状态更新.
| $ \left. \begin{array}{l} {{\mathit{\boldsymbol{\hat x}}}_{k + 1|k + 1}} = {{\mathit{\boldsymbol{\hat x}}}_{k + 1|k}} + {\mathit{\boldsymbol{K}}_{k + 1}}{\varepsilon _{k + 1}}, \\ {\mathit{\boldsymbol{K}}_{k + 1}} = {\mathit{\boldsymbol{P}}_{{{\mathit{\boldsymbol{\hat x}}}_{k + 1}}}}_{{{\mathit{\boldsymbol{\hat v}}}_{k + 1}}}{\mathit{\boldsymbol{P}}_{{{\mathit{\boldsymbol{\hat v}}}_{k + 1}}}}^{ - 1}, \\ {\mathit{\boldsymbol{P}}_{k + 1|k + 1}} = {\mathit{\boldsymbol{P}}_{k + 1|k}} - {\mathit{\boldsymbol{K}}_{k + 1}}{P_{{{\mathit{\boldsymbol{\hat v}}}_{k + 1}}}}K_{k + 1}^{\rm{T}}. \end{array} \right\} $ | (16) |
4) 令k=k+1, 返回2)继续迭代.
3 参数偏差型故障的诊断方法根据时变参数的变化方式, 可以将故障分为突变型偏差故障与缓变型偏差故障[15].对于电池系统, 在故障发生时,内部活性物质的扩散能力与接触能力会改变, 分别对应于时间常数τ=RpCp、欧姆内阻R0的变化, 因此考虑τ与R0在2种故障类型下的诊断方法.定义
| $ \mathit{\boldsymbol{\theta }} = \frac{1}{{N + 1}}\sum\limits_{j = 0}^N {\left[ {\begin{array}{*{20}{c}} {{{\hat \tau }_{k - j}}}\\ {{{\hat R}_{0(k - j)}}} \end{array}} \right]} , $ | (17) |
| $ {\mathit{\boldsymbol{S}}^1} = \frac{1}{N}{\sum\limits_{j = 0}^N {\left( {\left[ {\begin{array}{*{20}{c}} {{{\hat \tau }_{k - j}}}\\ {{{\hat R}_{0(k - j)}}} \end{array}} \right] - {\mathit{\boldsymbol{\theta }}^*}} \right)} ^2}. $ | (18) |
| $ {\mathit{\boldsymbol{S}}^2} = \frac{1}{N}{\sum\limits_{j = 0}^N {\left( {\left[ {\begin{array}{*{20}{c}} {{{\hat \tau }_{k - j}}}\\ {{{\hat R}_{0(k - j)}}} \end{array}} \right] - \mathit{\boldsymbol{\theta }}} \right)} ^2}. $ | (19) |
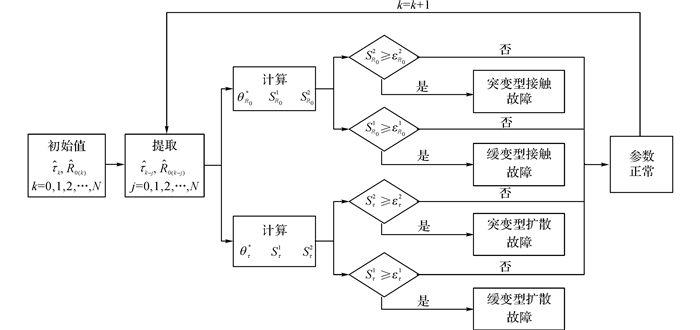
式中:N为数据窗长度, θ*为参数的正常值.定义缓变型故障阈值ε1与突变型故障阈值ε2.阈值根据不同情况由人为经验选取.电池故障诊断流程如图 3所示.
|
图 3 电池参数偏差型故障的诊断流程 Fig. 3 Parameter-biased fault diagnosis process of battery |
通过控制环境温度的突变与缓变,模拟电池的参数偏差型故障, 分别采用UTSTF算法与UKF算法对电池参数进行在线估计.电池测试平台由BTS-4000电池检测设备、BLH-100温控箱、计算机及监控软件组成, 如图 4所示.实验对象为WX-14I3220磷酸铁锂动力电池, 容量为20 AH, 充电截止电压为3.65 V, 放电截止电压为2.5 V, 充电倍率为1 C, 持续放电倍率为3 C.

|
图 4 电池测试平台 Fig. 4 Battery testing bench |
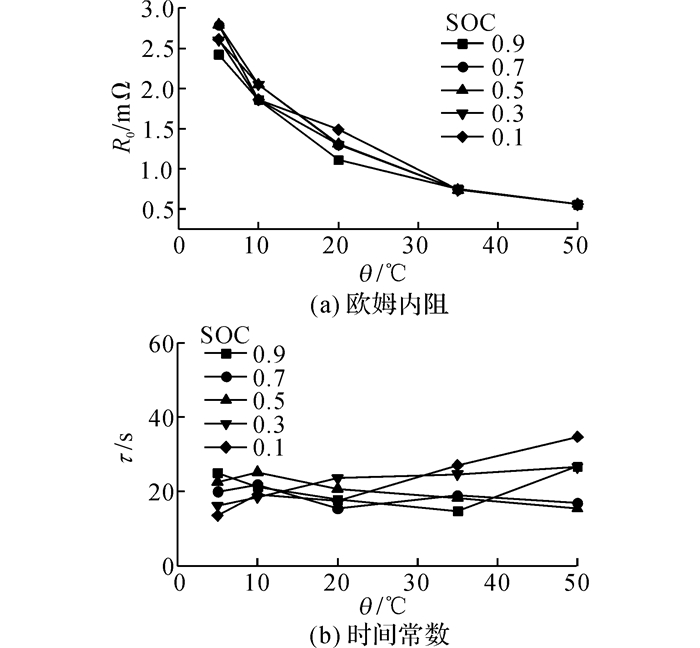
图 5通过脉冲放电测试,给出R0和τ在不同温度与SOC下的离线辨识结果.θ为温度.从图 5可见,R0随θ降低而增加, τ随θ变化较小, 与文献[20]的结论类似.在模拟故障中, 将电池实时温度、SOC对应图 5可以得到参数的真实值, 从而验证UTSTF算法的有效性.采用DST工况对电池进行充放测试, 电流I如图 6所示.采样间隔为1 s, 工况时长为3 600 s.电池状态与参数的初始估计中, SOC根据静置时的开路电压按图 2关系选取:s0=0.75;极化电压在-0.05 V到0.05 V间选取:vp(0)=-0.03 V; 参数均按20 ℃时的离线辨识结果选取:R0=Rp=1 mΩ, Cp=30 kF.
|
图 5 R0和τ的离线辨识结果 Fig. 5 Off-line identification results of R0 andτ |
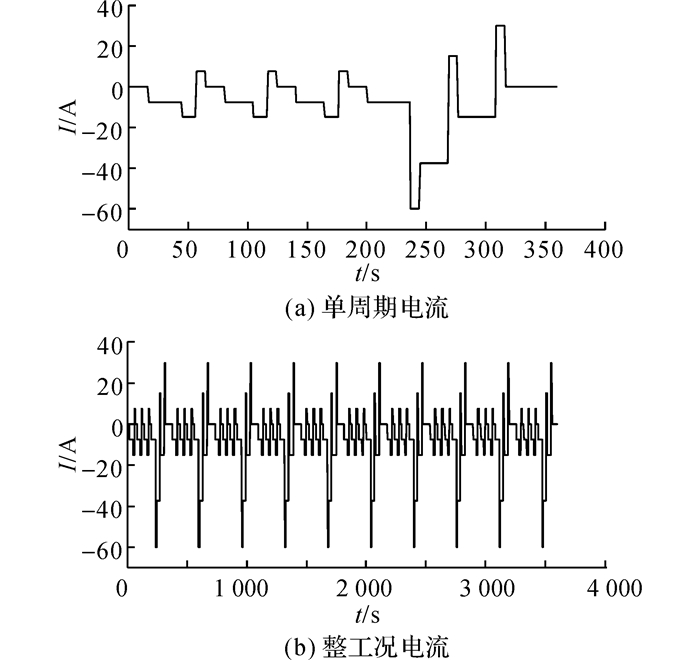
|
图 6 DST工况电池电流 Fig. 6 Battery current for DST profile |
在0~3 600 s内, 控制环境温度从50 ℃逐步降低至5 ℃, 模拟参数缓变型故障.电池端电压U的测量值如图 7所示.图 8(a)给出UTSTF与UKF这2种算法下R0的估计值对比.由图 8(a)可以看出, UTSTF与UKF对R0的估计值均随时间变化快速降低后增加, 这是由于初始值选取的偏大造成的, 同时表明2种算法对初始值选择均不敏感.在1 000 s后, UTSTF算法的估计值变化幅度更大, 在3 600 s时估计值为2.88 mΩ; UKF的估计值为1.62 mΩ, 相对误差分别为15.3 %和43.8 %.当R0变化幅度较大时, UKF不具有跟踪能力, 估计值为有偏的; UTSTF鲁棒性更好, 估计值更接近于真实值.
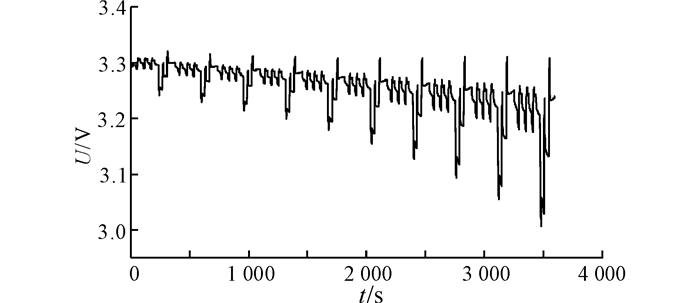
|
图 7 参数缓变型故障电池端电压 Fig. 7 Terminal voltage of battery of parameter-soft fault |
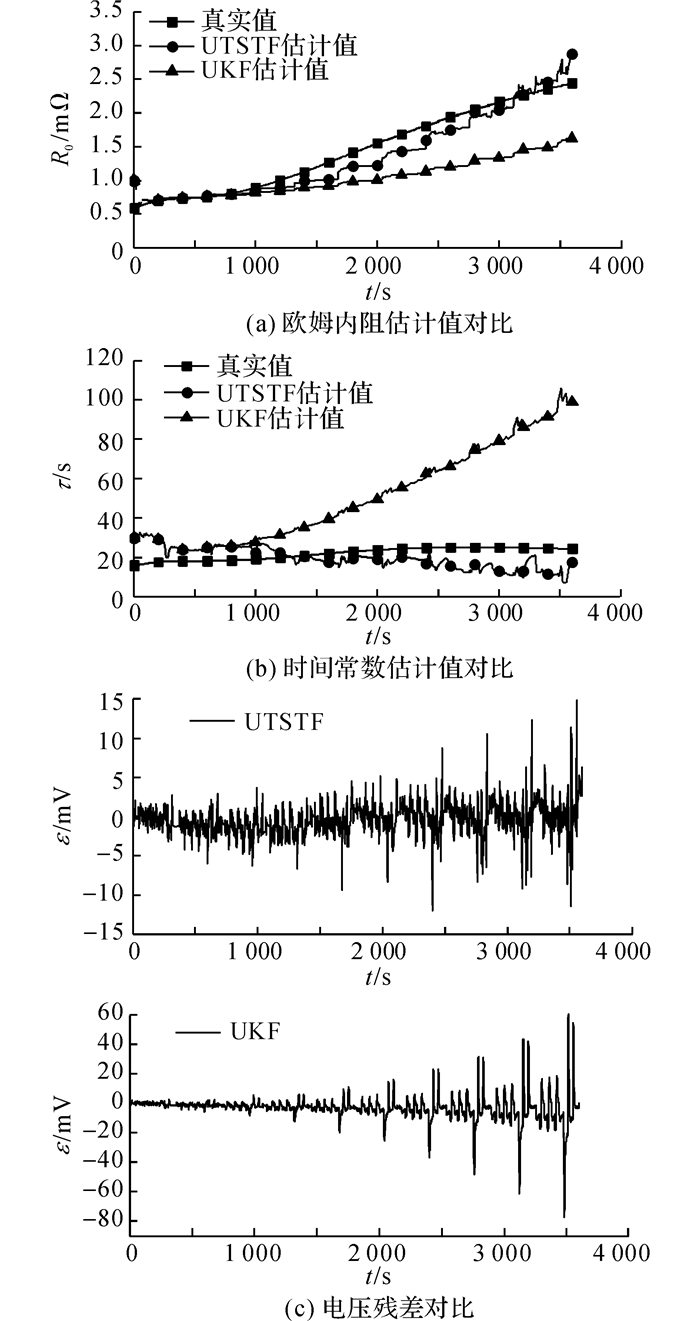
|
图 8 参数缓变型故障的估计结果 Fig. 8 Estimation results of parameter-soft fault |
图 8(b)中, τ的估计值在800 s后2种算法呈不同的变化趋势.UTSTF给出的估计值随时间变化缓慢, 最终时刻的相对误差为30.8 %, 误差较高的原因与模型阶数较低、极化内阻与极化电容的可辨识性差等因素有关; UKF的估计值呈上升趋势, 最终时刻估计值已达到98.7 s, 相对误差为331.7 s, 显然UKF的估计结果是发散的.
为了进一步说明UTSTF的跟踪能力, 图 8(c)给出2种算法下端电压估计残差ε的对比.由于UTSTF中的自适应渐消因子可以调整协方差阵使残差序列尽可能保持正交, ε绝对值基本保持在15 mV以内; UKF下的ε明显发散, 且在2 000 s后具有较大的波动, 最大残差达到80 mV, UKF因此失效.
以数据窗长度N=50, 正常值θ*=[20, 0.5]T, 阈值ε1=[202, 12]T为例, 参数缓变型故障诊断结果如表 1所示.诊断结果显示, UTSTF在2 411 s诊断出接触型故障, 比UKF快70.3 %; UKF在1 648 s误诊出扩散型故障, UTSTF结果为正常.UTSTF的诊断准确性、可靠性均高于UKF.
| 表 1 参数缓变型故障诊断结果 Table 1 Diagnosis result of parameter-soft fault |
在0~1 200 s内, 保持电池在50 ℃恒温环境中, 1 200 s时将电池置于5 ℃的恒温环境中直至3 600 s, 模拟参数突变型故障.端电压变化如图 9所示.图 10(a)中,2种算法R0的估计值在1 300 s前均收敛为0.70 mΩ, 真实值为0.61 mΩ, 相对误差为14.3%.之后UTSTF的估计值快速上升, UKF对突变参数的跟踪效果较差.3 600 s时UTSTF的估计值为2.57 mΩ, UKF的估计值为1.74 mΩ, 相对误差分别为8.4 %和26.6 %.
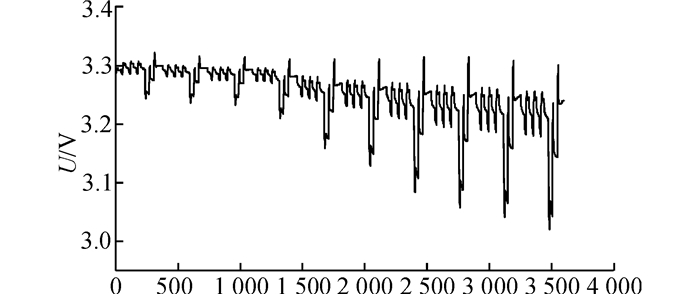
|
图 9 参数突变型故障电池端电压 Fig. 9 Terminal voltage of battery of parameter-abrupt fault |

|
图 10 参数突变型故障的估计结果 Fig. 10 Estimation results of parameter-abrupt fault |
图 10(b)中,2种算法下τ的估计值在1 300 s前收敛到19 s, 相对误差为25%.之后与缓变型故障类似, UTSTF收敛在18 s附近, UKF发散, 最终时刻的相对误差分别为16.9 %和372 %.
对于突变型故障, 图 10(c)中ε对比更明显.当ε在1 300 s后突然增大时, UTSTF可以快速调整使ε保持在15 mV内; UKF在ε突增后将ε继续扩大, 在2 300 s后最大残差达到60 mV, 算法失效.
以N=100, ε2=[52, 0.12]T为例, 突变型故障诊断结果如表 2所示.诊断结果中UTSTF在1 712 s诊断出接触型故障, UKF漏诊为正常; 对于扩散型故障, UTSTF在1 368 s误诊为故障, UKF诊断为正常.UTSTF出现误诊主要是由于单渐消因子无法对每个状态变量独立进行调整, 导致τ估计值受R0估计值的影响在1 400 s左右产生较大幅度的波动, 可以通过引入多重渐消因子[16]解决该问题.UTSTF算法的诊断结果优于UKF.
| 表 2 参数突变型故障诊断结果 Table 2 Diagnosis result of parameter-abrupt fault |
本文针对锂离子电池的参数偏差型故障诊断问题, 将电池系统状态与参数进行联合估计, 提出基于UTSTF算法的时变参数估计与故障诊断方法.实验证实, UTSTF算法对电池故障参数的跟踪能力明显优于UKF算法, 具有较高的诊断可靠性和适中的计算量,因此可以应用于电池管理系统中, 对电池内部行为进行实时监测, 当电池发生故障时,能够快速、准确地给出内部参数的估计值, 从而完成故障的检测与分离.通过后续研究, 本文算法将扩展应用于电池组故障诊断中, 为复杂电池系统故障在线诊断提供了一种全新的思路.
| [1] |
ANDREA D. Battery management systems for large lithium-ion battery packs[M]. Norwood: Artech House, 2010, 4-6.
|
| [2] |
SIDHU A, IZADIAN A, ANWAR S. Adaptive nonlinear model-based fault diagnosis of Li-ion batteries[J]. IEEE Transactions on Industrial Electronics, 2015, 62(2): 1002-1011. DOI:10.1109/TIE.2014.2336599 |
| [3] |
XIA B, SHANG Y, NGUYEN T, et al. A correlation based fault detection method for short circuits in battery packs[J]. Journal of Power Sources, 2017, 337(1): 1-10. |
| [4] |
CHEN W, CHEN W T, SAIF M, et al. Simultaneous fault isolation and estimation of lithium-ion batteries via synthesized design of Luenberger and learning observers[J]. IEEE Transactions on Control Systems Technology, 2014, 22(1): 290-298. DOI:10.1109/TCST.2013.2239296 |
| [5] |
CHEN Z, LIN F, WANG C, et al. Active diagnosability of discrete event systems and its application to battery fault diagnosis[J]. IEEE Transactions on Control Systems Technology, 2014, 22(5): 1892-1898. DOI:10.1109/TCST.2013.2291069 |
| [6] |
ZHANG X, WANG Y, YANG D, et al. An on-lineestimation of battery pack parameters and state-of-charge using dual filters based on pack model[J]. Energy, 2016, 115(11): 219-229. |
| [7] |
HE H, XIONG R, ZHANG X, et al. State-of-charge estimation of the lithium-ion battery using an adaptive extended Kalman filter based on an improved Thevenin model[J]. IEEE Transactions on Vehicular Technology, 2011, 60(4): 1461-1469. DOI:10.1109/TVT.2011.2132812 |
| [8] |
LIU L, WANG L Y, CHEN Z, et al. Integrated system identification and state-of-charge estimation of battery systems[J]. IEEE Transactions on Energy conversion, 2013, 28(1): 12-23. DOI:10.1109/TEC.2012.2223700 |
| [9] |
LIU X, CHEN Z, ZHANG C, et al. A novel temperature-compensated model for power Li-ion batteries with dual-particle-filter state of charge estimation[J]. Applied Energy, 2014, 123(6): 263-272. |
| [10] |
SUN F, XIONG R. A novel dual-scale cell state-of-charge estimation approach for series-connected battery pack used in electric vehicles[J]. Journal of Power Sources, 2015, 274(1): 582-594. |
| [11] |
SUN F, XIONG R, HE H. A systematic state-of-charge estimation framework for multi-cell battery pack in electric vehicles using bias correction technique[J]. Applied Energy, 2016, 162(1): 1399-1409. |
| [12] |
CHEN Z, WANG L Y, YIN G, et al. Accurate probabilistic characterization of battery estimates by using large deviation principles for real-time battery diagnosis[J]. IEEE Transactions on Energy Conversion, 2013, 28(4): 860-870. DOI:10.1109/TEC.2013.2280136 |
| [13] |
ZHANG H, PEI L, SUN J, et al. Online diagnosis for the capacity fade fault of a parallel-connected lithium ion battery group[J]. Energies, 2016, 9(5): 387. DOI:10.3390/en9050387 |
| [14] |
ZHENG Y, HAN X, LU L, et al. Lithium ion battery pack power fade fault identification based on Shannon entropy in electric vehicles[J]. Journal of Power Sources, 2013, 223(2): 136-146. |
| [15] |
周东华. 一类非线性系统故障检测与诊断的滤波器方法[D]. 上海: 上海交通大学, 1990. ZHOU Dong-hua. A class of nonlinear system fault detection and diagnostic filters[D]. Shanghai: Shanghai Jiao Tong University, 1990. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y130465 |
| [16] |
ZHOU D H, SU Y X, XI Y G, et al. Extension of Friedland's separate-bias estimation to randomly time-varying bias of nonlinear systems[J]. IEEE Transactions on Automatic Control, 1993, 38(8): 1270-1273. DOI:10.1109/9.233167 |
| [17] |
王小旭, 赵琳, 夏全喜, 等. 基于Unscented变换的强跟踪滤波器[J]. 控制与决策, 2010, 25(7): 1063-1068. WANG Xiao-xu, ZHAO Lin, XIA Quan-xi, et al. Strong tracking filter based on unscented transformation[J]. Control and Decision, 2010, 25(7): 1063-1068. |
| [18] |
孙国强, 黄蔓云, 卫志农, 等. 基于无迹变换强跟踪滤波的发电机动态状态估计[J]. 中国电机工程学报, 2016, 36(3): 615-623. SUN Guo-qiang, HUANG Man-yun, WEI Zhi-nong, et al. Dynamic stateestimation for synchronous machines based on unscented transformation of strong tracking filter[J]. Proceedings of the CSEE, 2016, 36(3): 615-623. |
| [19] |
胡高歌, 刘逸涵, 高社生, 等. 改进的强跟踪UKF算法及其在INS/GPS组合导航中的应用[J]. 中国惯性技术学报, 2014(5): 634-639. HU Gao-ge, LIU Yi-han, GAO She-sheng, et al. Improved strong tracking UKF and its application in INS/GPS integrated navigation[J]. Journal of Chinese Inertial Technology, 2014(5): 634-639. |
| [20] |
CHIANG C J, YANG J L, CHENG W C. Temperature and state-of-charge estimation in ultracapacitors based on extended Kalman filter[J]. Journal of Power Sources, 2013, 234(6): 234-243. |
| [21] |
DONG G, WEI J, ZHANG C, et al. Online state of charge estimation and open circuit voltage hysteresis modeling of LiFePO4 battery using invariant imbedding method[J]. Applied Energy, 2016, 162(1): 163-171. |
| [22] |
WANG Y, ZHANG C, CHEN Z. On-line battery state-of-charge estimation based on an integrated estimator[J]. Applied Energy, 2017, 185(1): 2026-2032. |
| [23] |
ZHANG C, WANG L Y, LI X. Robust and adaptive estimation of state of charge for lithium-ion batteries[J]. IEEE Transactions on Industrial Electronics, 2015, 62(8): 4948-4957. DOI:10.1109/TIE.2015.2403796 |
| [24] |
RAHIMI-EICHI H, BARONTI F, CHOW M Y. Online adaptive parameter identification and state-of-charge coestimation for lithium-polymer battery cells[J]. IEEE Transactions on Industrial Electronics, 2014, 61(4): 2053-2061. DOI:10.1109/TIE.2013.2263774 |
| [25] |
DEY S, AYALEW B. A diagnostic scheme for detection, isolation and estimation of electrochemical faults in lithium-ion cells[C]//ASME Dynamic Systems and Control Conference. Columbus: ASME, 2015: V001T13A001-V001T13A001. http://www.researchgate.net/publication/280556871_A_Diagnostic_Scheme_for_Detection_Isolation_and_Estimation_of_Electrochemical_Faults_in_Lithium-ion_Cells
|
| [26] |
MARCICKI J, ONORI S, RIZZONI G. Nonlinear fault detection and isolation for a lithium-ion battery management system[C]//ASME Dynamic Systems and Control Conference. Cambridge: ASME, 2010: 607-614. https://www.researchgate.net/publication/267491474_Nonlinear_Fault_Detection_and_Isolation_for_a_Lithium-Ion_Battery_Management_System
|



