2. 青岛科技大学 机电学院, 山东 青岛 266061;
3. 华中科技大学 能源与动力工程学院, 湖北 武汉 430074
2. School of Eletro-Mechanical Engineering Qingdao University of Science and Technology, Qingdao 266061, China;
3. School of energy and power engineering, Huazhong University of Science and Technology, Wuhan 430074, China
强化换热是大多数换热系统设计需要衡量的一个重要因素, 其对于提高能源利用效率节约能源尤为重要.在HVAC & R行业中, 蒸发器和冷凝器作为重要的换热设备, 其换热效率直接影响到整个系统的能源利用率, 因而强化换热管被广泛运用这类换热器中以提高系统效率.强化换热的方式可分为主动(需要外部能量输入)和被动(无外部能量输入).其中被动强化方式可按照其表面修饰的方式分为常规尺度、微小尺度和纳米尺度[1].本研究中所使用的内螺纹管和3种三维强化管(1EHT、2EHT-1和2EHT-2)均采用微小尺度强化技术.传统内螺纹管已有广泛的研究基础, 如Jiang等[2]对4种不同制冷剂在光滑管和内螺纹管内的流动沸腾传热进行了实验研究, 实验结果表明,制冷剂R22、R134a、R407C和R410A在外径为9.52 mm的内螺纹管内相对于在光管内的换热系数强化倍率分别为1.86、1.60、1.69和1.78, 并将实验结果与现存换热关联式进行比较, 发现文献[3]中的关联式对于多工质的预测效果较差, 亟待拟合一个预测精度较高适用于多工质的普适性关联式.
区别于内螺纹管的螺纹齿, 三维强化表面管采用三维强化单元来修饰内外表面.目前对三维强化管内汽液两相强化换热性能的研究还很少, 可查的文献有Aroonrt等[4]对一种三维表面强化管(顶包管)的冷凝强化换热特性进行实验研究, 测试结果表明, 顶包管的换热系数强化倍率可达1.3~1.4, 表面的凹痕能制造更多扰动增强湍动.
本文采取实验方法, 对工质R410A在6种不同强化换热管和1根光滑管内的流动沸腾换热特性进行测量, 根据实验结果对比不同强化管的强化换热性能, 并对内螺纹管和三维强化换热管的强化换热性能和机理进行探讨.
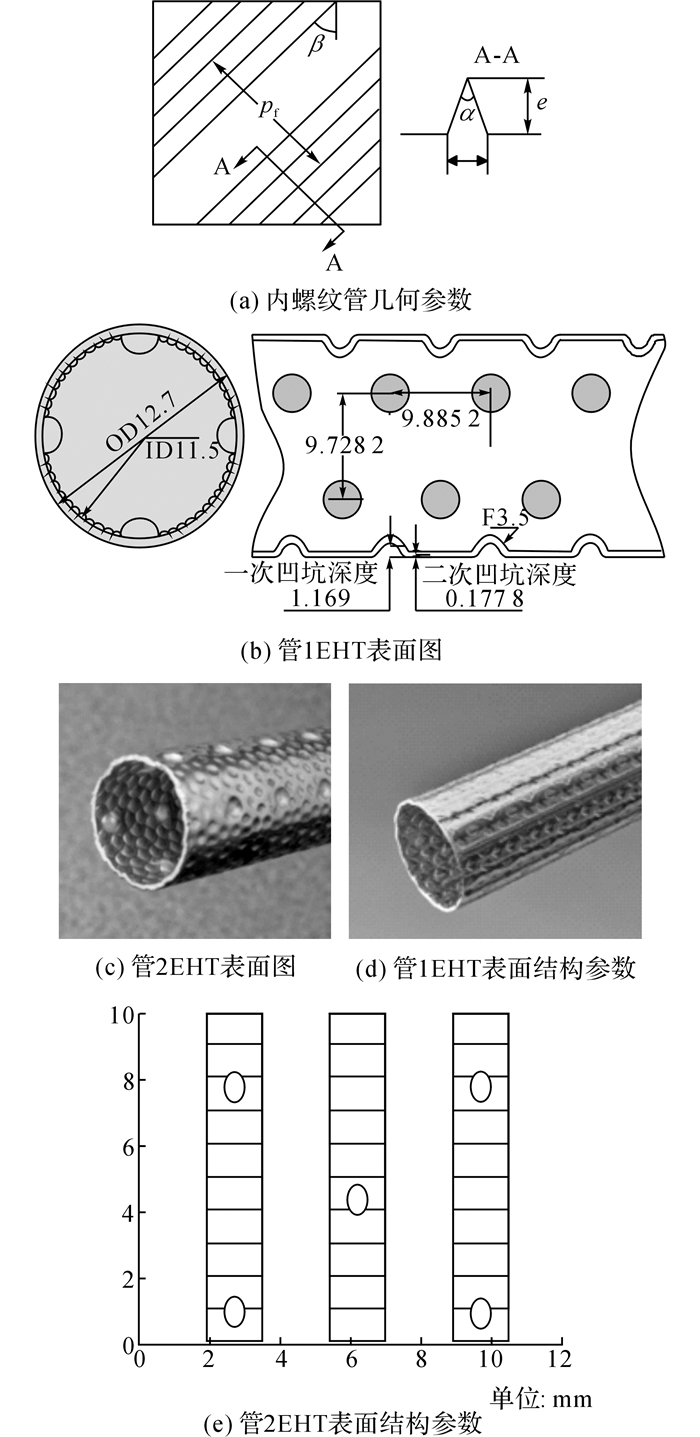
1 实验系统本研究采用的3根内螺纹管的齿形参数如图 1(a)所示.其中β为螺旋角,α为齿顶角,e为齿高,pf为相邻齿间的法向节距.三维强化管1EHT强化表面由2种强化方式复合组成:一种是花瓣形凹痕阵列形成的一次表面粗糙单元, 另一种是较深的球形凹痕阵列单元, 管1EHT内外强化表面的结构特征如图 1(b)和(d)所示.据Guo等[5]的研究, 1EHT管在冷凝和蒸发工况下均有显著的强化换热性能, 特别是在蒸发工况下, 换热性能优于传统的人形齿管, 可见该种强化管适合用于制造蒸发换热器, 改善换热器能源利用效率.2EHT-1和2EHT-2强化换热管则由酒窝型凹痕阵列组成的粗糙单元和沿管长方向的浅凹槽组成, 管表面的结构特征如图 1(c)和(e)所示, 图中横线填充区域即最深处为330 μm的表面凹槽, 2种管的表面结构十分相似, 唯一的区别在于其中管2EHT-1的凹坑顶点相对于圆周平面深度为250 μm, 而管2EHT-2为330 μm.3种三维强化管(1EHT、2EHT-1和2EHT-2)的外径和内径相同, 分别为12.7和11.5 mm, 内表面积分别为同等直径光滑管的1.112、1.02和1.03倍;光滑管的外径和内径分别为12和10 mm;3根内螺纹管的具体几何参数列于表 1中.其中ns为齿数, β为螺旋角, α为齿顶角, e为齿高, do为管型外径, di为齿根直径, Aai/Afr为相对于齿根直径di的内表面积扩展比, dh为水力直径.
|
图 1 内螺纹管和三维强化管的强化表面结构及其参数 Fig. 1 Surface structures and corresponding parameters of micro-fin tubes and three-dimensionalenhanced tubes |
| 表 1 3种内螺纹管的详细几何参数 Table 1 Geometric parameters of three kinds of micro-fin tubes |
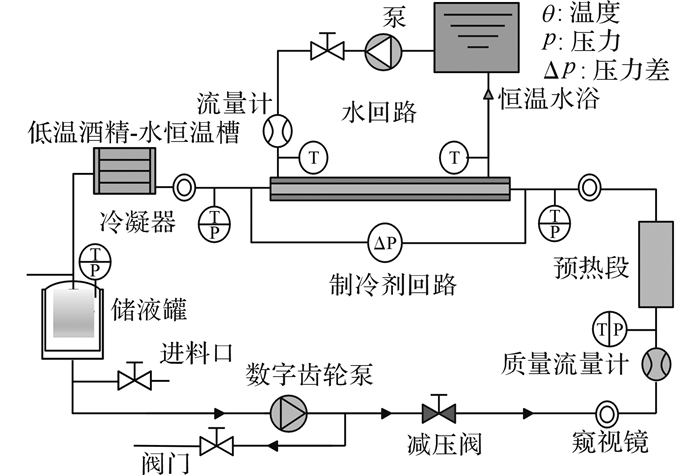
管内蒸发换热实验系统如图 2所示, 由2个循环回路组成:包含测试段的制冷剂R410A回路;与测试段进行换热的水回路.储液罐中的制冷剂R410A经电子齿轮泵带动开始循环, 经过科氏质量流量计后, 进入预热段.预热段采用电加热装置加热, 通过控制输入热量使测试段的进口干度达到目标值.
|
图 2 管内蒸发换热和压降测试装置原理图 Fig. 2 System diagram of test rig for heat transfer and pressure drop during in-tube evaporation |
测试段为一个长度为2 m的水平逆流套管换热器, 其中测试管外侧为水, 内侧为制冷剂.制冷剂的进出口温度采用经校准过误差在±0.1 ℃以内的铂电阻测量;制冷剂进口的饱和压力则由压力传感器来测量.整个测试段的压降由安装在测试段进出口处的差压传感器来测量.本实验中测量得到的换热系数是指整个测试段范围内的平均值而不是局部值, 测得的压降也是测试段总压降.工质最后经过低温恒温槽, 被冷凝、过冷回到储液罐中完成循环.具体的实验系统介绍可见Wu等[6-7]的研究.
2 实验工况和数据推算 2.1 实验工况蒸发的实验工况为:饱和温度为6 ℃, 质量流速在80~320 kg/(m2s)热流密度的变化区间为10~50 kW/m2, 进口和出口干度分别为0.2和0.9.质量流速和热流密度的计算均是基于名义内径di计算的.
2.2 数据演算数据采集系统对采集的温度压力等参数进行演算以获取管内换热系数.测试段的换热量由套管换热器的水侧热量平衡来计算:
| $ {Q_{t, ts}} = {c_{{\rm{pl, w, ts}}}}{m_{{\rm{w, ts}}}}({\theta _{{\rm{w, ts, out}}}} - {\theta _{{\rm{w, ts, in}}}}). $ | (1) |
式中:cpl, w, ts为平均温度下的比热容, mw, ts为水质量流量, θw, ts, out为测试段进口水温, θw, ts, in为出口水温.
对数平均温差(θd)由管外环侧水的进出口温度以及管内的制冷剂饱和温度决定:
| $ {\theta _{\rm{d}}} = \frac{{\left( {{\theta _{{\rm{sat}}}} - {\theta _{{\rm{w, ts, in}}}}} \right) - \left( {{\theta _{{\rm{sat}}}} - {\theta _{{\rm{w, ts, out}}}}} \right)}}{{\ln \left[ {\left( {{\theta _{{\rm{sat}}}} - {\theta _{{\rm{w, ts, in}}}}} \right)/\left( {{\theta _{{\rm{sat}}}} - {\theta _{{\rm{w, ts, out}}}}} \right)} \right]}}. $ | (2) |
假设没有污垢热阻, 制冷剂蒸发换热系数为
| $ {h_{\rm{i}}} = {\left[ {{A_{\rm{i}}}\left( {\frac{{{Q_{{\rm{t, ts}}}}}}{{{\theta _{\rm{d}}}}} - \frac{1}{{{h_{\rm{o}}}{A_{\rm{o}}}}} - \frac{{{d_{\rm{o}}}\ln ({d_{\rm{o}}}/{d_{\rm{i}}})}}{{2k{A_{\rm{o}}}}}} \right)} \right]^{ - 1}}. $ | (3) |
式中:Ai为基于内螺纹管的齿根内径或三维强化管的名义内径di计算的, Ao为测试管的外表面面积, ho为环状水侧换热系数.具体的制冷剂进出口干度计算和环状水侧换热系数的确定细节可见文献[7], 本文采用相同的数据处理方法.
由于测试段水平放置, 重力作用产生的压降为零, 因而测量得到的总压降可表示为加速压降和摩擦压降两部分之和:
| $ \Delta p = \Delta {p_{\rm{a}}} + \Delta {p_{\rm{f}}}. $ | (4) |
密度变化引起的加速压降部分可以利用下式计算:
| $ \Delta {p_{\rm{a}}} = G\left\{ {{{\left[ {\frac{{{x^2}}}{{{\rho _{\rm{v}}}\varepsilon }} + \left( {\frac{{1 - {x^2}}}{{{\rho _{\rm{l}}}\left( {1 - \varepsilon } \right)}}} \right)} \right]}_{{\rm{out}}}} - {{\left[ {\frac{{{x^2}}}{{{\rho _{\rm{v}}}\varepsilon }} + \frac{{{{\left( {1 - x} \right)}^2}}}{{{\rho _{\rm{l}}}\left( {1 - \varepsilon } \right)}}} \right]}_{{\rm{in}}}}} \right\}. $ | (5) |
式中:x为干度,G为质量流速,ρl和ρv分别为制冷剂饱和液态和气态的密度,ε为管内截面孔隙率, 可利用Rouhani和Axelsson飘移流模型[8]计算:
| $ \begin{array}{l} \varepsilon = \frac{x}{{{\rho _{\rm{v}}}}}[\left( {1 + 0.12\left( {1 - x} \right)} \right)\left( {\frac{x}{{{\rho _{\rm{v}}}}} + \frac{x}{{{\rho _{\rm{l}}}}}} \right) + \\ \frac{{1.18\left( {1 - 2} \right){{\left[ {g\sigma 5\left( {{\rho _{\rm{l}}} - {\rho _{\rm{v}}}} \right)} \right]}^{0.25}}}}{{G\rho _{\rm{l}}^{0.5}}}{]^{ - 1}}. \end{array} $ | (6) |
这3种三维强化管外表面均是粗糙不平的, 不能直接使用Gnielinski公式[9]来预测水侧换热系数ho, 因而采用威尔逊图解法来计算强化管外水侧换热系数:
| $ \frac{1}{{U{A_{\rm{o}}}}} = \frac{1}{{{A_{\rm{o}}}{h_{\rm{o}}}}} + \frac{1}{{a{A_{\rm{i}}}{h_{\rm{i}}}}} + \frac{{{d_{\rm{i}}}\ln ({d_{\rm{o}}}/{d_{\rm{i}}})}}{{2k{A_{\rm{i}}}}}. $ | (7) |
其中, U为测试段换热器总的换热系数;Ao和Ai分别为测试管外表面积和内表面积;k为测试管壁导热系数;a是三维强化管水侧换热系数相对于光滑管的倍率.测量结果表明3种强化换热管1EHT, 2EHT-1和2EHT-2的水侧换热强化倍率分别为2.52、1.48和1.52.
2.3 实验结果不确定度数据采集系统中采用的铂电阻温度计、压力传感器、差压传感器、科氏质量流量计和电磁流量计等设备均经过严格校准.实验系统中采用的传感器测量不确定度及由此计算得到的参数不确定度均列于表 2.此外, 为验证预热段和测试段的热平衡性能, 使用光滑管进行单相换热实验, 对比发现测试段热平衡性能良好, 热损失率低于3%.
| 表 2 测量参数及计算参数不确定度 Table 2 Uncertainty for primary measurements and dependent quantities |
流型对管内的传热特性有着重要决定作用, 针对水平光滑管内流动沸腾流型变化规律已有大量的研,如Kattan等[10-12]提出的流型图.其中本文采用Wojtan等[11]提出的流型图来判断测试光滑管内任一工况下的流型.
Liebenberg等[13-14]实验研究后发现内螺纹管内间歇流到环状流的临界线较光滑管会发生在更小的干度, 分层波状流到环状流的转变线较光滑管下移至更小的质量流速区域, 因而在光管流型图[11]基础上采用Liebenberg等[13]提出的间歇流到环状流的临界线和Sharar等[14]提出的分层波状流到环状流的临界线修正以适用于内螺纹管内流型的预测. Liebenberg等[13]提出的间歇流到环状流的临界干度预测公式为
| $ {x_{{\rm{IA}}}} = {\left\{ {\left[ {0.595{{\left( {\frac{{{\rho _{\rm{v}}}}}{{{\rho _{\rm{l}}}}}} \right)}^{ - 4/7}}{{\left( {\frac{{{\mu _{\rm{l}}}}}{{{\mu _{\rm{v}}}}}} \right)}^{1/7}}} \right] + 1} \right\}^{ - 1}}. $ | (8) |
式中:ρl和ρv分别为液相和气相的密度, μl和μv分别为液相和气相的运动黏度.
Sharar等[13]提出的分层波状流到环状流的临界预测公式为
| $ \begin{array}{l} {G_{{\rm{wavy, microfin}}}} = \left\{ {\frac{{16A_{{\rm{VD}}}^3g{d_{\rm{i}}}{\rho _{\rm{l}}}{\rho _{\rm{v}}}}}{{{x^2}{{\rm{ \mathsf{ π} }}^2}{{\left( {1 - {{\left( {2{h_{{\rm{LD}}}} - 1} \right)}^2}} \right)}^{0.5}}}} \times } \right.\\ {\left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\frac{{{{\rm{ \mathsf{ π} }}^2}}}{{25h_{{\rm{LD}}}^2}} \times \left( {\frac{{We}}{{Fr}}} \right)_L^{ - 1}} \right] + 1} \right\}^{0.5}} - 15. \end{array} $ | (9) |
式中:AVD为气相横截面积无量纲常数;g为重力加速度;hLD为液面高度无量纲常数;We是Webb常数;Fr是弗劳德常数.
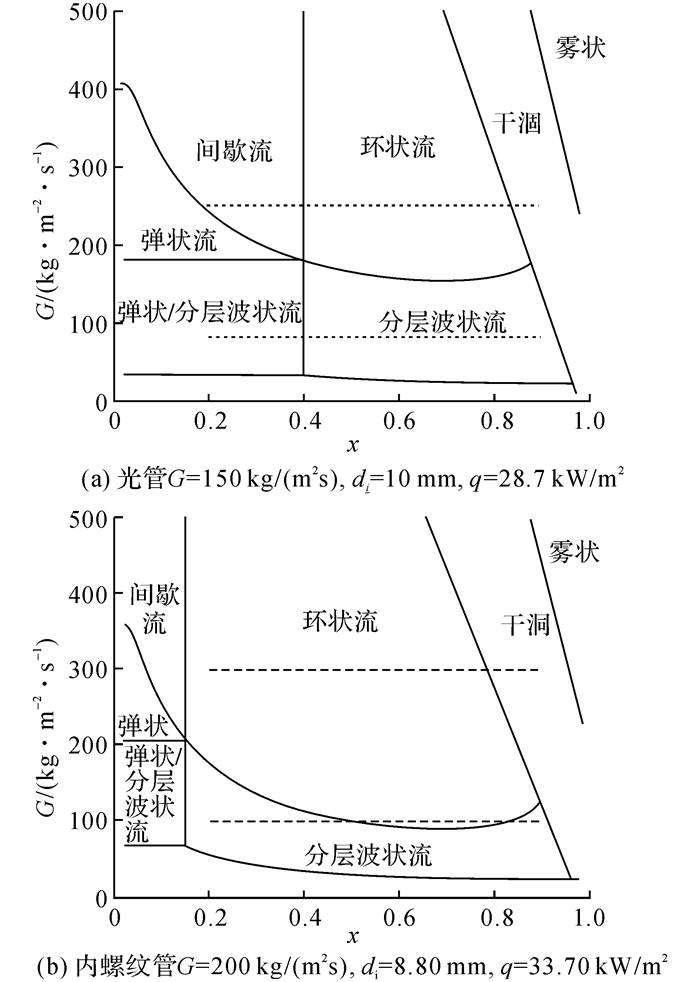
具体的流型图如图 3所示, 图中所示的2种虚线之间的区域即实验研究中测试段所处的流型范围, 在质量流速较高的情况下会出现环状流而在干度较低区域则会有部分区域为弹状流;而内螺纹管内的控制流型为环状流, 波状分层流只存在于质量流速较小的测试区域内.
|
图 3 Wojtan管内蒸发流型图 Fig. 3 Wojtan flow pattern map for in-tube evaporation |
目前文献中还缺乏三维强化表面对于流型变化影响的研究, 可查的报道只有Sarmadian等[15]在对一种螺旋顶包管管内冷凝换热进行实验可视化探究后发现类似于人形齿管, 该强化管将促使从环状流到间歇流的转变临界线推迟至更小的干度值.测试采用的3根三维强化管结构独特, 目前还不存在成熟的流型模型, 还需更多研究来探究表面结构对流型的影响.
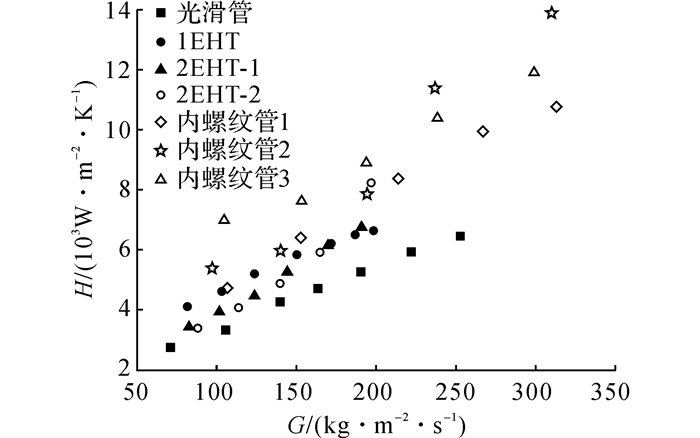
3.2 流动沸腾换热系数如图 4所示为6种强化换热管的蒸发换热系数h和质量流速G的关系.对比3种三维强化管, 管1EHT管在G < 170 kg/(m2s)时性能最好;而2EHT-1和2EHT-2在G>170 kg/(m2s)时换热系数较优, 且两管间的换热性能相似, 这是因为两管的表面特征相近, 只是表面的凹痕深度存在些微差距.
|
图 4 蒸发换热系数随质量流速变化 Fig. 4 Heat transfer coefficient for evaporation versus mass velocities |
这3种三维强化换热管的性能均优于对应的光滑管, 强化后的换热系数可达到光管相应值的1.13~1.53倍, 远大于各自对应的内表面积扩展比.三维强化表面的凹痕能够打断近壁液膜边界层, 增强汽液两相界面的波动进而促进两相热量和质量交换, 同时能制造液膜分离流和二次流, 加快热流从管内壁到液膜的传递速率.此外, 对于蒸发现象三维强化表面的微小凹痕还可以增加核态沸腾的汽化核心数目.因此, 三维强化表面有着显著的蒸发强化换热性能.
内螺纹管内的实验测试结果表明在质量流速G < 220 kg/(m2s)时, 内螺纹管3具有最高的换热系数;质量流速G>220 kg/(m2s)时, 内螺纹管1具有最高的换热系数.Wu等[6]提出管内流型为间歇流或环状流时, 液膜厚度与齿高的比值接近于1, 齿整体浸没在液膜中时, 齿表面的扩展面与液膜充分接触会有较高的换热系数;如果齿高于液膜, 与气体接触的表面换热效率较低, 反之, 若齿低于液膜, 则会存在液膜导热热阻导致整体换热恶化.据内螺纹管内流型图 3(b), 当G>150 kg/(m2s)时, 可认为测试段全为环状流, 使用液膜厚度计算公式:
| $ \delta = \sqrt {{A_{\rm{C}}}/{\rm{ \mathsf{ π} }}} \cdot \left( {1 - \sqrt \varepsilon } \right). $ | (10) |
式中:AC为内螺纹管的真实横截面积, 为式(6)计算得到的截面空隙率.
液膜厚度随着质量流速和干度的提高而降低, 对比3根内螺纹管的液膜厚度与齿高可以发现, 当G < 200 kg/(m2s)时, 内螺纹管3的齿高最接近液膜厚度, 因而其在该质量流速区域内具有最好的换热性能;随着质量流速上升液膜厚度减小, 液膜厚度逐渐接近内螺纹管2的齿高, 内螺纹管2的换热性能迅速提升, 在质量流速较高区域内表现出最好的换热性能.然而, 内螺纹管1在几乎整个测试区域内都表现出最差的换热性能, 这可能是其最小的螺旋角β导致的.由于离心力作用较小, 内螺纹管内的液膜在重力作用下堆积在管底部, 在湿周方向上液膜厚度分布不均, 大部分湿周上液膜厚度与齿高差距较大, 换热效率偏低.
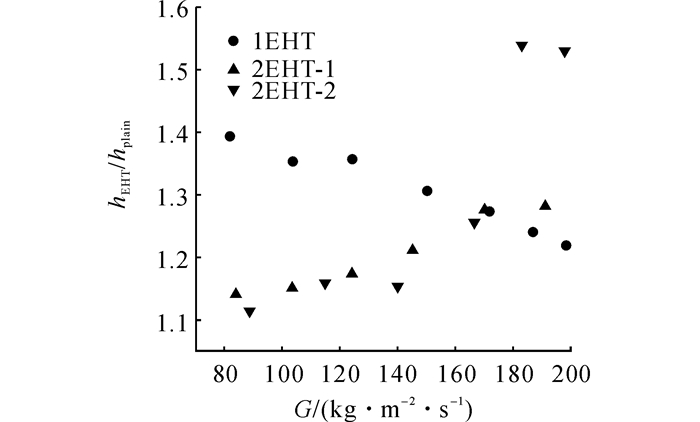
三维强化管与光滑管的换热系数之比(强化倍率)hEHT/hplain随质量流速的变化趋势如图 5所示, 管1EHT的强化倍率随质量流速增加而减小, 2EHT-1和2EHT-2管的强化倍率则逐渐升高而后趋于平缓, 其中2EHT-2的强化倍率在G>140 kg/(m2s)时迅速上升.造成这一差异的原因可能包括管1EHT与管2EHT相比而言, 除了表面较深的凹坑外, 整个管内表面还有花瓣形的凹痕分布, 在质量流速较低的情况下, 这些较深的凹坑能够大大增加管底部堆积液膜内部的湍动, 强化冷热流体混合, 此时强化效率较高, 而随着质量流速增加, 流体内部本身的湍动逐渐增加, 因而强化作用有限, 整体而言, 相对于光管的强化效果会有所减弱, 在内螺纹管中也有类似的现象.2EHT-1和2EHT-2管的强化倍率随着质量流速增大而增大, 这有别于传统的强化换热管, 这可能是因为微小凹坑在质量流速较高时能体现出更高的强化换热效率, 在质量流速较高时对对流换热的影响作用更加显著有效.值得注意的是管2EHT-2在某些质量流速下的蒸发换热系数稍高于内螺纹管, 这说明三维强化结构的换热潜力十分巨大.
|
图 5 三维强化换热管相对于光管的强化倍率 Fig. 5 Enhancement ratio of 3D enhanced heat transfer tubes relative to plain tube |
总体上来说, 3根内螺纹管的性能要优于3根三维强化管(包含管径的影响), 但可以发现三维强化换热管具有以较小的换热面积扩展比实现较优强化换热性能的潜力.针对目前存在的三维强化换热管的参数特征, 可以通过优化凹坑的排布方式、深度和数量来优化三维强化换热管的性能.
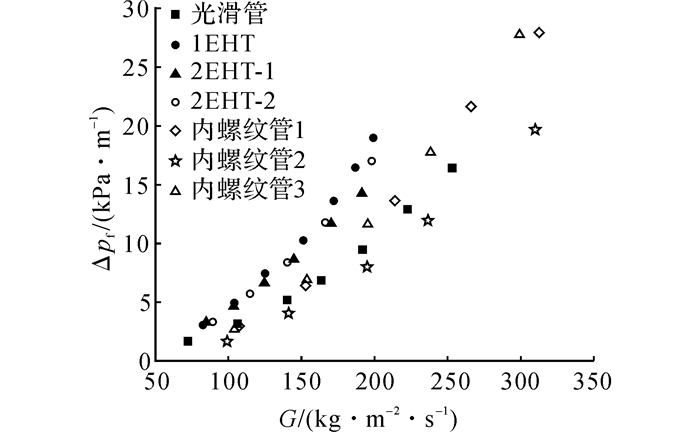
3.3 摩擦压降在压降方面, 6种强化换热管和1种光滑管的总摩擦压降Δpf如图 6所示, 压降均随着质量流速的增加而增加.3种三维强化换热管具有相似的摩擦压降特性, 均大于光滑管的摩擦压降, 其中管1EHT具有最高的摩擦压降, 管2EHT-1的摩擦压降稍小于2EHT-2, 可见管表面的凹痕越深, 管内摩擦压降可能越高.这是因为表面较深凹痕制造的液膜湍流动影响范围广, 会带来更大的流动阻力.综合压降和换热系数考虑, 可以发现管1EHT在质量流速G < 170 kg/(m2s)时有最优的综合性能, 而管2EHT-2在质量流速大于G>170 kg/(m2s)时表现最好.三管间各异的性能表明可以通过优化三维表面结构参数如凹痕深度和排布方式来提高三维强化管的综合性能.
|
图 6 摩擦压降随质量流速变化 Fig. 6 Frictional pressure drop versus mass velocities |
这3种内螺纹管中, 管3和管1的摩擦压降损失明显大于管2, 管2具有最低的摩擦压降损失.这可能是因为管2最低的齿高, 高齿相较低齿会带来更多的近壁液膜湍动, 增加壁面剪切应力从而提高摩擦系数.管3较大的螺旋角β会加速齿间的液体流动, 增加摩擦压降损失, 因而管3的摩擦压降稍大于管1.
4 结论(1) 三维强化换热管具有较好的蒸发强化换热性能, 明显优于对应的测试光管, 在一些质量流速下, 换热性能甚至优于管径更小的内螺纹管.其中三维强化管1EHT在质量流速G < 170 kg/(m2s)时有着较高的换热系数, 而管2EHT-2在G>170 kg/(m2s)时换热性能更加出色.三维强化换热管表面的凹痕在液膜近壁流动时能打断边界层, 并制造分离流增强液膜湍动, 促进冷热流体混合, 使液膜温度分布更加均匀合理.
(2) 3种内螺纹管的换热性能差异较大, 其中管3在质量流速G < 220 kg/(m2s)时换热系数最高, 而管2在质量流速G>220 kg/(m2s)时换热系数最高, 这可能是由前述的内螺纹管的齿高和液膜厚度之比的变化引起的.压降方面, 内螺纹管3始终具有最高的摩擦压降.
(3) 总体上来说, 在相同条件下3根三维强化管的换热性能要略差于内螺纹管, 但三维强化换热管具有以较小的换热面积扩展比实现较优强化换热性能的潜力, 可以通过进一步优化三维强化换热管的结构参数, 如凹坑的排布方式、深度和数量等等.
本文测试的新型EHT三维表面强化换热管具有良好的流动沸腾换热性能, 为蒸发换热强化提供一种新的思路, 区别于传统的内螺纹管、人形齿管和微肋管, 以较小的换热面积获得较高的换热性能.三维强化换热管在蒸发器应用方面拥有较强的竞争力, 接下来将更进一步研究干度、热流量和管径等因素对换热性能的影响.
| [1] |
WU Z, SUNDN B. On further enhancement of single-phase and flow boiling heat transfer in micro/minichannels[J]. Renewable and Sustainable Energy Reviews, 2014, 40: 11-27. DOI:10.1016/j.rser.2014.07.171 |
| [2] |
JIANG G B, TAN J T, NIAN Q X, et al. Experimental study of boiling heat transfer in smooth/micro-fin tubes of four refrigerants[J]. International Journal of Heat and Mass Transfer, 2016, 98: 631-642. DOI:10.1016/j.ijheatmasstransfer.2016.03.024 |
| [3] |
CHIOU C B, LU D C, CHEN C C, et al. Heat transfer correlations of forced convective boiling for pure refrigerants in micro-fin tubes[J]. Applied Thermal Engineering, 2011, 31(5): 820-826. DOI:10.1016/j.applthermaleng.2010.10.031 |
| [4] |
AROONRAT K, WONGWISES S. Experimental study on two-phase condensation heat transfer and pressure drop of R-134a flowing in a dimpled tube[J]. International Journal of Heat and Mass Transfer, 2017, 106: 437-448. DOI:10.1016/j.ijheatmasstransfer.2016.08.046 |
| [5] |
GUO S P, WU Z, LI W, et al. Condensation and evaporation heat transfer characteristics in horizontal smooth, herringbone and enhanced surface EHT tubes[J]. International Journal of Heat and Mass Transfer, 2015, 85: 281-291. DOI:10.1016/j.ijheatmasstransfer.2015.01.115 |
| [6] |
WU Z, SUNDN B, WANG L, et al. Convective condensation inside horizontal smooth and microfin tubes[J]. Journal of Heat Transfer, 2014, 136(5): 051504-11. DOI:10.1115/1.4026370 |
| [7] |
WU Z, WU Y, SUNDEN B, et al. Convective vaporization in micro-fin tubes of different geometries[J]. Experimental Thermal and Fluid Science, 2013, 44: 398-408. DOI:10.1016/j.expthermflusci.2012.07.012 |
| [8] |
ROUHANI S Z, AXELSSON E. Calculation of void volume fraction in the subcooled and quality boiling regions[J]. International Journal of Heat and Mass Transfer, 1968, 13(2): 383-393. |
| [9] |
GNIELINSKI V. New equations for heat and mass transfer in turbulent pipe and channel flows[J]. Nasa Sti/recon Technical Report A, 1976, 75(2): 8-16. |
| [10] |
KATTAN N, THOME J R, FAVRAT D. Flow boiling in horizontal tubes:Part 1-development of a diabatic two-phase flow pattern map[J]. Journal of Heat Transfer, 1998, 120(1): 140-147. DOI:10.1115/1.2830037 |
| [11] |
THOME J R, HAJAL J E. Two-Phase flow pattern map for evaporation in horizontal tubes:latest version[J]. Heat Transfer Engineering, 2003, 24(6): 3-10. DOI:10.1080/714044410 |
| [12] |
WOJTAN L, URSENBACHER T, THOME JR. Investigation of flow boiling in horizontal tubes:Part Ⅰ-a new diabatic two-phase flow pattern map[J]. International Journal of Heat and Mass Transfer, 2005, 48(14): 2955-2969. DOI:10.1016/j.ijheatmasstransfer.2004.12.012 |
| [13] |
LIEBENBERG L, MEYER J P. Refrigerant condensation flow regimes in enhanced tubes and their effect on heat transfer coefficients and pressure drops[J]. Heat Transfer Engineering, 2008, 29(6): 506-520. DOI:10.1080/01457630801891532 |
| [14] |
SHARAR D J, JANKOWSKI N R, BAR-COHEN A. Modified model for improved flow regime prediction in internally-grooved tubes[C]//ASME 2013 International Technical Conference and Exhibition on Packaging and Integration of Electronic and Photonic Microsystems, Burlingame:ASME, 2013:V002T08A042. http://www.researchgate.net/publication/264933943_Modified_Model_for_Improved_Flow_Regime_Prediction_in_Internally-Grooved_Tubes
|
| [15] |
SARMADIAN A., SHAFAEE M., MASHOUF H., et al. Condensation heat transfer and pressure drop characteristics of R-600a in horizontal smooth and helically dimpled tubes[J]. Experimental Thermal and Fluid Science, 2017, 86: 54-62. DOI:10.1016/j.expthermflusci.2017.04.001 |



