在工程和自然界中, 不可压缩自由液面与固体建筑物之间相互作用的现象非常普遍.针对自由液面在复杂计算域的运动过程, 可以采用固定网格法来模拟不可压缩流体在下游存在不同形状的固体障碍物时的运动情况[1].
在自由液面洪水运动过程中往往存在很多复杂的物理现象, 比如自由液面破碎, 水跃等现象.计算流体力学的主要难点之一是如何有效地捕捉洪水自由液面位置和液面破碎现象, 同时精确预测洪水前锋的演进过程.目前有2种有效的方法可以用来捕捉自由液面, 包括流体体积法(volume of fluid, VOF)和水平集法(level set method).在VOF法中, 移动的界面用F函数表示, F函数定义为每个网格内流体的体积分数.已经有很多改进的VOF格式被应用到模拟流体运动过程, 比如piecewise-linear interface construction (PLIC-VOF)[2], tangent of hyperbola for interface capturing (THINC)[3], weighed line interface calculation (WLIC) [4].另一种界面捕捉技术是水平集法, 已经有很多水平集法应用于溃坝洪水的模拟[5-8].在水平集法中, 两相流的交界面用水平集函数的零等位面隐性地给出, 界面的形状和曲率可以很容易地通过水平集函数直接求解得到.水平集法模拟的洪水运动过程是一个非守恒的算法, 随着计算时间的增加, 会出现较严重的质量亏盈现象, 导致模拟的流场失真[9].目前,学者们提出了包括coupled level set and volume of fluid (CLSVOF) method[10-11], interface preserving level set method[12]和particle level set (PLS) method[13]在内的很多方法来解决质量亏盈的问题.另一个难点是如何更高精度地求解水平集函数和重距离方程(redistance equation)中的空间导数项.权重本质无振荡格式(weighted essentially non-oscillatory schemes, WENO)可以用来离散水平集函数.由于水平集函数是连续的且导数是不连续的, 使用这种格式可以避免数值振荡.Merriman等[14-16]对这种方法进行了深入的研究.
对于自由液面水流与固体构筑物之间相互作用的数值模拟, 在准确捕捉自由液面的同时需要解决不规则固壁边界的问题.为了更好地在笛卡尔直角坐标系下描述壁面边界的几何形状, Zhang等[17-18]提出浸入边界法.浸入边界法包括连续力法和离散力法2种经典的方法.第一种方法在微分方程离散之前在连续性方程中添加反馈力, 一般具有解析表达式, 主要用于模拟弹性边界问题, 如生物膜在流场作用下的变形和运动.离散力法则通过离散后的Navier-Stokes方程中求出反馈力[19-20], 但一般无法得到解析表达式.与连续力法相比, 离散力法对形状不变的固体有更清晰的表达, 能够更准确地模拟含刚体的流体运动.
为了更好地捕捉自由液面水流运动并精确地处理流体与固壁边界, 本文提出结合界面保持水平集法和基于离散力的浸入边界法来模拟溃坝洪水遇到下游障碍物的运动过程.采用差分插值浸入边界方程(differential-based interpolation immersed boundary formulation)来处理固体交界面[21], 能够有效提升计算效率.采用界面保持水平集法捕捉自由液面, 相比传统水平集法[22]可以更有效地保持质量守恒.水平集方程的空间项使用6阶迎风紧致差分格式(upwinding combined compact difference scheme, UCCD)离散, 时间项使用6阶辛龙格-库塔(symplectic Runge-Kutta)格式离散.UCCD格式的使用可以减小计算过程中的色散误差, 避免流体体积的亏盈或波动.使用WENO格式离散重距离方程.提出简单的数值算法来处理固体和液体的重叠区域.与文献[32]中下游带固定障碍物的溃坝洪水实验过程进行对比, 验证本文方法的准确性和可靠性.
1 控制方程 1.1 水平集方程水平集法[22]定义水和空气的交界面为零水平集, 即水平集函数ϕ(x, y, t)=0, 由此将该零水平集曲线嵌入到高一维的水平集函数中来计算.当流体移动时, ϕ会随之运动, 其中零水平集的位置是要追踪的自由液面的位置.ϕ(x, y, t)在不同相的符号是相反的, 在本研究中, ϕ(x, y, t)>0代表水, 反之代表气体.当界面随着流体移动时, ϕ的运动必须满足以下的对流运动方程:
| $ \frac{{\partial \phi }}{{\partial t}} + u \cdot \nabla \phi = 0. $ | (1) |
式中:u为流体速度, t为时间.ϕ在开始时被指定为符号距离函数, 表达式如下:
| $ \phi \left( {x, t} \right) = \left\{ \begin{array}{l} d, x \in 水;\\ 0, x \in 交界面;\\ - d, x \in 气体. \end{array} \right. $ | (2) |
式中:d为到自由液面的最短距离.任意时间步长中的ϕ可以通过式(1)计算得到.求解下述重距离方程:
| $ \frac{{\partial \phi }}{{\partial \tau }} = {\mathop{\rm sgn}} ({\phi _0})\left( {1 - |\nabla \phi |} \right) + \lambda \delta \left( {\nabla \phi } \right)|\nabla \phi |, $ | (3) |
可以使得ϕ始终保持为距离函数.式中:τ为人工时间; sgn (ϕ)是平滑符号函数, sgn (ϕ)=2(H(ϕ)-0.5).
Heaviside函数表达如下:
| $ H\left( \phi \right) = \left\{ \begin{array}{l} 0, \phi < - \varepsilon .\\ \frac{1}{2}\left[ {1 + \frac{\phi }{\varepsilon } + \frac{1}{{\rm{ \mathsf{ π} }}}\sin \frac{{{\rm{ \mathsf{ π} }}\phi }}{\varepsilon }} \right], |\phi | \le \varepsilon ;\\ 1, \phi > \varepsilon . \end{array} \right. $ | (4) |
式中:ε为界面的厚度, 其值一般等于Δx, Δx为网格大小.式(3)中λδ(∇ϕ)|∇ϕ|项的使用, 可以保证流体在阶跃层保持体积守恒.Delta函数δ(ϕ)由∂H(ϕ)/∂ϕ得到:
| $ \delta \left( \phi \right) = \left\{ {\left. \begin{array}{l} 0, |\phi | > \varepsilon ;\\ \frac{1}{2}\left( {1 + \cos \;\;\frac{{{\rm{ \mathsf{ π} }}\phi }}{\varepsilon }} \right), |\phi | \le \varepsilon . \end{array} \right)} \right. $ | (5) |
系数λ[12]为
| $ \lambda = - \frac{{{\smallint _\mathit{\Omega }}\delta \left( \phi \right)\left[ {{\mathop{\rm sgn}} ({\phi _{{\rm{new}}}})(1 - |\nabla \phi |} \right]{\rm{d}}\mathit{\Omega }}}{{{\smallint _\mathit{\Omega }}{\delta ^2}\left( \phi \right)|\nabla \phi |{\rm{d}}\mathit{\Omega }}}. $ | (6) |
界面保持水平集法通过求解式(1)、(3),捕捉两相流的交界面.
1.2 Navier-Stokes方程假设水和空气都是不可压缩且无掺混的.无因次形式的动量方程和连续性方程为
| $ \begin{array}{l} \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \left( {\mathit{\boldsymbol{U}}\cdot\nabla } \right)\mathit{\boldsymbol{U}} = - \frac{{\nabla p}}{{\rho \left( \phi \right)}} + \\ \;\;\;\;\frac{1}{{\rho \left( \phi \right)}}\nabla \left[ {\frac{{\mu \left( \phi \right)}}{{Re}}(\nabla \mathit{\boldsymbol{U}} + \nabla {\mathit{\boldsymbol{U}}^{\rm{T}}})} \right] + \frac{1}{{F{r^2}}}{{\rm{e}}^g}, \end{array} $ | (7) |
| $ \nabla \cdot U = 0. $ | (8) |
式中:ρ(ϕ)和μ(ϕ)分别表示密度和黏度, U为速度, p为压力, eg为重力.
式(7)中的无因次系数Re和Fr分别定义为:
| $ Re = \frac{{{\rho _1}VL}}{{{\mu _1}}}, Fr = \frac{V}{{\sqrt {gL} }}. $ | (9) |
式中:V和L分别为特征速度和特征长度.自由液面的曲率可以由水平集方程直接求解得到:
| $ \kappa \left( \phi \right) = \nabla \cdot \frac{{\nabla \phi }}{{|\nabla \phi |}}. $ | (10) |
在本次研究中, 连续表面压力(continuum surface force, CSF)模型[23]被用来表示密度和黏度的阶跃条件, 即用Heaviside方程来描述过渡层的密度和黏度, 以防止出现非物理振荡.Heaviside方程的表达式如下:
| $ \rho \left( \phi \right) = {\rho _{\rm{a}}} + ({\rho _1} - {\rho _{\rm{a}}})H\left( \phi \right), $ | (11) |
| $ \mu \left( \phi \right) = {\mu _{\rm{a}}} + ({\mu _1} - {\mu _{\rm{a}}})H\left( \phi \right). $ | (12) |
式中:下标“a”和“1”分别表示空气和水.
2 数值离散格式 2.1 水平集方程使用迎风紧致差分格式[24-25]来求解水平集方程, 这种高精度有限差分格式能够在使用较少网格的情况下得到更精确的结果.下面给出用迎风紧致差分格式离散的∂ϕ/∂x项, 其中∂2ϕ/∂x2项作为未知解引入方程中:
| $ \begin{array}{l} {b_1}\frac{{\partial \phi }}{{\partial x}}{|_{i - 1}} + \frac{{\partial \phi }}{{\partial x}}{|_i} + {b_3}\frac{{\partial \phi }}{{\partial x}}{|_{i + 1}} = \\ \;\;\;\frac{1}{h}({a_1}{\phi _{i - 2}} + {a_2}{\phi _{i - 1}} + {a_3}{\phi _i}) + \\ \;\;\;h\left( {{c_1}\frac{{{\partial ^2}\phi }}{{\partial {x^2}}}{|_{i - 1}} + {c_2}\frac{{{\partial ^2}\phi }}{{\partial {x^2}}}{|_i} + {c_3}\frac{{{\partial ^2}\phi }}{{\partial {x^2}}}{|_{i + 1}}} \right), \end{array} $ | (13) |
| $ \begin{array}{l} \overline {{c_1}} \frac{{{\partial ^2}\phi }}{{\partial {x^2}}}{|_{i - 1}} + \overline {{c_2}} \frac{{{\partial ^2}\phi }}{{\partial {x^2}}}{|_i} + \overline {{c_3}} \frac{{{\partial ^2}\phi }}{{\partial {x^2}}}{|_{i + 1}} = \\ \;\;\;\frac{1}{{{h^2}}}(\overline {{a_1}} {\phi _{i - 1}} + \overline {{a_2}} {\phi _i} + \overline {{a_3}} {\phi _{i + 1}}) + \\ \;\;\;\frac{1}{h}\left( {\overline {{b_1}} \frac{{\partial \phi }}{{\partial x}}{|_{i - 1}} + \overline {{b_2}} \frac{{\partial \phi }}{{\partial x}}{|_i} + \overline {{b_3}} \frac{{\partial \phi }}{{\partial x}}{|_{i + 1}}} \right). \end{array} $ | (14) |
式(14)的9个未知系数可以通过泰勒展开得到, 令
| $ \frac{{\partial \phi }}{{\partial x}} = \frac{{\partial \phi }}{{\partial x}}{|_{{\rm{excat}}}} + 0.773\;816\;553 \times {10^{ - 6}}\Delta {x^6}\frac{{{\partial ^7}\phi }}{{\partial {x^7}}} + o(\Delta {x^7}). $ | (15) |
使用6阶精度的Runge-Kutta格式[27]来离散式(1)的时间项:
| $ \frac{{{\rm{d}}\phi }}{{{\rm{d}}t}} = F\left( \phi \right). $ | (16) |
任意n时刻的ϕn是已知量, 可以通过下述的过程可以求得下一时刻的ϕ:
| $ \begin{array}{l} {\phi ^{(1)}} = {\phi ^n} + \Delta t[\frac{5}{{36}}{F^{(1)}} + \left( {\frac{2}{9} + \frac{{2\tilde c}}{3}} \right){F^{(2)}} + \\ \;\;\;\;\;\;\;\;\;\;\left( {\frac{5}{{36}} + \frac{{\tilde c}}{3}} \right){F^{(3)}}], \end{array} $ | (17) |
| $ \begin{array}{l} {\phi ^{(2)}} = {\phi ^n} + \Delta t[\left( {\frac{5}{{36}} - \frac{{5\tilde c}}{{12}}} \right){F^{(1)}} + \frac{2}{9}{F^{(2)}} + \\ \;\;\;\;\;\;\;\;\;\left( {\frac{5}{{36}} + \frac{{5\tilde c}}{{12}}} \right){F^{(3)}}], \end{array} $ | (18) |
| $ \begin{array}{l} {\phi ^{(3)}} = {\phi ^n} + \Delta t[\left( {\frac{5}{{36}} - \frac{{\tilde c}}{3}} \right){F^{(1)}} + \\ \;\;\;\;\;\;\;\;\left( {\frac{2}{9} - \frac{{2\tilde c}}{3}} \right){F^{(2)}} + \frac{5}{{36}}{F^{(3)}}]. \end{array} $ | (19) |
式中:
| $ \tilde c = \frac{1}{2}\sqrt {\frac{3}{5}.} $ |
F(i)(i=1, 2, 3)分别表示F(≡-U·∇ϕ)在t=n+(1/2+
| $ {\phi ^{n + 1}} = {\phi ^n} + \frac{{\Delta t}}{9}\left[ {2{F^{(1)}} + 4{F^{(2)}} + \frac{5}{2}{F^3}} \right]. $ | (20) |
对于重距离方程(3), 使用5阶权重本质无振荡格式(WENO)[28]离散空间项.使用3阶TVD Runge-Kutta格式[29]离散时间项:
| $ {\phi ^{(1)}} = {\phi ^{(n)}} + \Delta \tau L({\phi ^{(0)}}), $ | (21) |
| $ {\phi ^{(2)}} = \frac{3}{4}{\phi ^{(n)}} + \frac{1}{4}{\phi ^{(1)}} + \frac{1}{4}\Delta \tau L({\phi ^{(1)}}), $ | (22) |
| $ {\phi ^{(n + 1)}} = \frac{1}{3}{\phi ^{(n)}} + \frac{2}{3}{\phi ^{(2)}} + \frac{2}{3}\Delta \tau L({\phi ^{(2)}}). $ | (23) |
处理下游带障碍物的算例时, 一些数值方法和计算软件的做法是将障碍物作为边界条件进行处理, 需要用特定的网格对边界进行拟合; 浸入边界法是将障碍物的效应用虚拟力的形式反馈到流场中, 而不需要调整网格.在笛卡尔坐标系下求解实际问题时, 由于障碍物的复杂性及其位置的随机性, 网格点不一定位于浸入障碍物的边界处,需要在位于固体-液体的网格细胞处插补速度.若使用常用的多项式代数方法处理边界, 则可能会产生较大的数值振荡[30].为了避开这种不稳定问题, 采用插补方法, 即所谓的浸入边界法(immersed boundary)[21].
如图 1所示, 首先定义点Q为固体内虚拟点A对称于边界点P的镜像点, 因此AP与PQ之间的距离相等, 即AP=PQ.点A的速度可以由点P和点Q的速度通过泰勒公式展开得到:

|
图 1 微分插值示意图 Fig. 1 Schematic of the differential interpolation scheme |
| $ {u_A} = 2{u_P} - {u_Q}. $ | (24) |
式中:uA、uP、uQ分别为点A、P、Q的速度.由于点P位于固体边界上, uP=0, 只需要求解uQ,就可以得到目标的插补速度.
垂直边界的速度需要满足下面的对流方程:
| $ \frac{{\partial u}}{{\partial \tau }} + \mathit{\boldsymbol{\vec n}} \cdot \nabla u = 0. $ | (25) |
式中:τ为人工时间, n为单位法向量.对式(25)使用1阶迎风格式进行离散:
| $ \frac{{u_A^{\tau + 1} - u_A^\tau }}{{\Delta \tau }} + {n_x}\frac{{u_A^\tau - u_B^\tau }}{{\Delta x}} + {n_y}\frac{{u_D^\tau - u_A^\tau }}{{\Delta y}} = 0. $ | (26) |
式中:Δx和Δy分别为x和y方向上的网格间距.假设点Q的速度在人工时间Δτ=APQ=2AP后传输到点A, 即uAτ+1=uQ.由于点A是虚拟点, uAτ是不确定的.uAτ可以通过外推法求解, 外推方程如下:
| $ \frac{{\partial u}}{{\partial {\tau ^*}}} + {n_x}(\Delta xu{'_{xx}}) + {n_y}(\Delta yu{'_{yy}}) = 0. $ | (27) |
式中:u'xx和u'yy的定义为
| $ u{'_{xx}}\left( {i, j} \right) = ({u_{i, j}} - 2{u_{i - 1, j}} + {u_{i + 1, j}})/\Delta {x^2}, $ | (28) |
| $ u{'_{yy}}\left( {i, j} \right) = ({u_{i, j}} - 2{u_{i - 1, j}} + {u_{i + 1, j}})/\Delta {y^2}. $ | (29) |
当nx≥0时, u'xx(i, j)=uxx(i-1, j); 当nx < 0时, u'xx(i, j)=-uxx(i+1, j); 当ny≥0时, u'yy(i, j)=uyy(i, j-1);当ny < 0时, u'yy(i, j)=uyy(i, j+1).通过求解式(26)至稳态, 可以求得uAτ和点A的插补速度.
2.3 Navier-Stokes方程求解不可压缩流体的Navier-Stokes方程的重点在于求解计算域中每个网格点的流速和压力.流速使用如3.1节所描述的高阶精度紧致差分格式求解, 将式(13)、(14)中的ϕ用u(或v)替换.主要目的是在求解Navier-Stokers方程提高对流稳定性的同时, 增加色散精度.
在Navier-Stokes方程中, 当速度项和压力项耦合时, 很难求解.为了解决该问题, 使用投影法[31]分布求解压力项, 具体步骤如下.
1) 设置水中的ϕ=1, 空气中的ϕ=-1.使用式(3)初始化水平集方程, 求解ϕ至稳态.
2) 定义流体属性, 包括根据式(12)、(13)求得的ρ(ϕ)和黏度μ(ϕ).
3) 利用浸入边界法,计算浸入固体边界处的插补速度uA*.
4) 求得下面动量方程的中间速度u*:
| $ \begin{array}{l} \frac{{{\mathit{\boldsymbol{u}}^*} - {\mathit{\boldsymbol{u}}^n}}}{{\Delta t}} = \\ \;\;\; - ({\mathit{\boldsymbol{u}}^n}\cdot\nabla ){\mathit{\boldsymbol{u}}^n} + \frac{1}{{Re}}\frac{{\nabla \cdot (2\mu \left( \phi \right){\mathit{\boldsymbol{D}}^n})}}{{\rho \left( \phi \right)}} + \frac{1}{{F{r^2}}}\mathit{\boldsymbol{e}}. \end{array} $ | (30) |
式中:D=(∇u+∇uT)/2.忽略压力梯度项.
5) 加上连续性约束∇un+1=0, 求解压力泊松方程得到pn+1:
| $ \frac{{{\mathit{\boldsymbol{u}}^{n + 1}} - {\mathit{\boldsymbol{u}}^*}}}{{\Delta t}} = - \frac{{\nabla {p^{n + 1}}}}{{\rho \left( \phi \right)}}. $ | (31) |
6) 从式(19)得到真实时间步的速度un+1.
7) 用UCCD格式离散水平集方程的空间项, 用symplectic Runge-Kutta格式离散时间项, 求解得到ϕn+1.
8) 对ϕn+1进行重距离化, 假如液体与固体障碍物重合, 将空气和固体障碍物中的ϕ设为-1, 将水中的ϕ设为1, 求解式(3)至稳态.
9) 重复2)~8), 为一次循环.
3 数值结果与讨论质量差Merror的定义如下:
| $ {M_{{\rm{error}}}} = \frac{{\smallint \left[ {H\left( {\phi , t} \right) - H\left( {\phi , t = 0} \right)} \right]{\rm{d}}\mathit{\Omega }}}{{\smallint H\left( {\phi , t = 0} \right){\rm{d}}\mathit{\Omega }}}. $ | (32) |
式中:Ω为整个计算域.模拟结果均已无因次化.
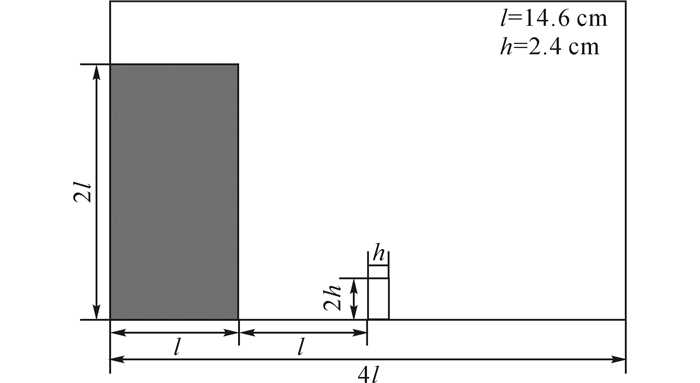
3.1 下游带矩形障碍物的自由液面运动溃坝洪水计算模型及参数如图 2所示.水的密度和黏性系数分别为1 000 kg/m3和0.001 kg/(m·s); 空气的密度和黏性系数分别为1 kg/m3和0.000 01 kg/(m·s), 重力加速度为9.81 m/s2.描述水体运动的2个无因次参数分别为雷诺数Re= 174 000, 弗劳德数Fr=1, 不考虑边界层, 左、右下界均为滑移边界条件.初始状态下, 左侧水体保持静止, 开闸之后在重力条件下向右侧倾泻, 流经障碍物后到达右侧挡板.综合考虑计算效率和准确性, 测试不同计算参数后, 确定计算网格数为320×200.
|
图 2 矩形障碍物溃坝算例示意图 Fig. 2 Sketch of dam break with rectangular obstacle |
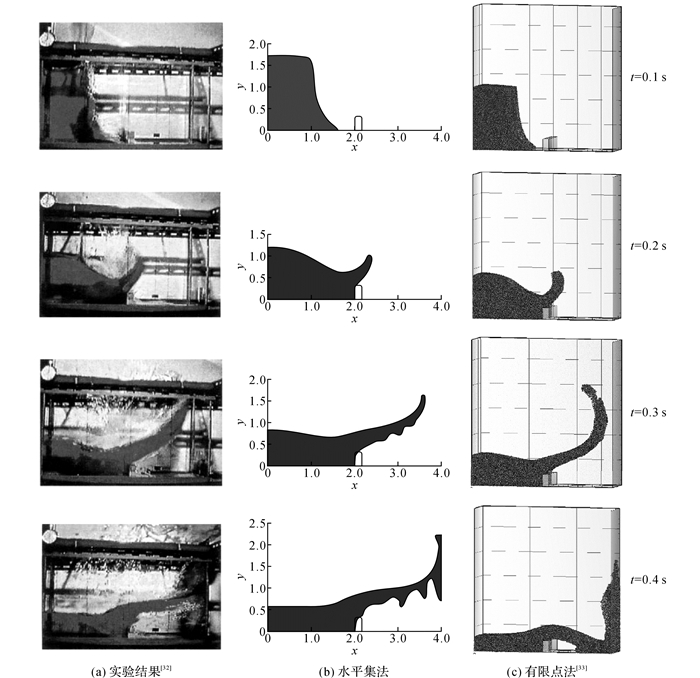
图 3给出不同时刻数值程序的模拟结果和实验现象[32].水体开始泄流0.1 s后, 形成溃坝洪水.当水体运动至1.3 s左右时, 水体前锋形状开始受到垂直障碍物的干扰, 之后与障碍物发生撞击, 在0.2 s时形成水舌继续向右前迸射, 伴随有水花的飞溅.0.3 s时, 水体前锋已经非常接近右边界, 即将发生碰撞.0.4 s时, 水体与右侧壁面碰撞后开始下坠, 伴随有自由液面破碎.给出有限点法的计算结果[33].从图 3可以看出, 采用该算法能够很好地捕捉实验中自由液面的变化情况.
|
图 3 带矩形障碍物溃坝问题在不同时刻下的对比图 Fig. 3 Comparison of snapshot at several time instants for dam break with rectangular obstacle |
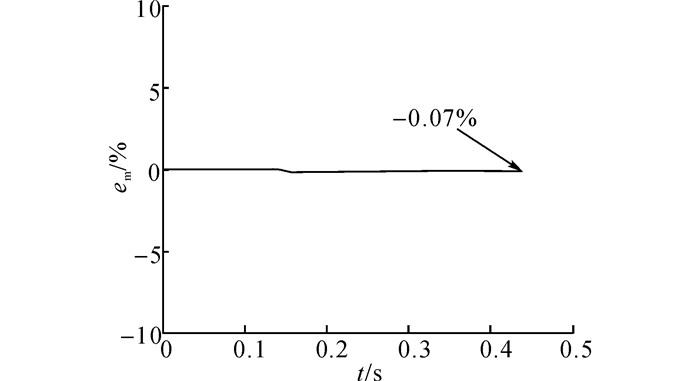
图 4给出数值模拟过程中前0.5 s的质量误差em.通常来说, 经典的水平集法在计算溃坝问题时会出现较大的质量误差.从图 4可以看出, 在整个计算过程中, 模型一直保持很好的质量守恒性, 由此说明该界面保持水平集法在质量守恒方面表现很好.
|
图 4 数值模拟质量差随时间的变化 Fig. 4 Mass error versus time for simulation |
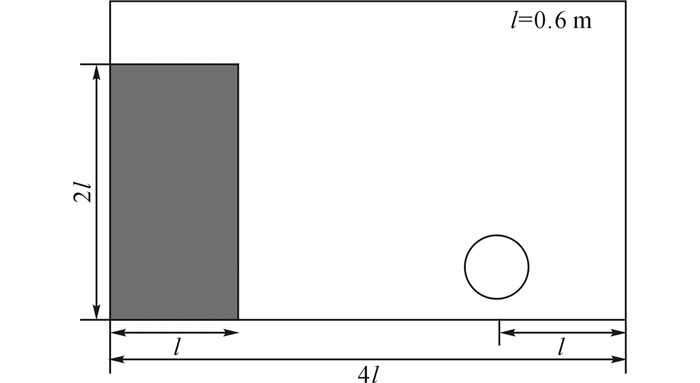
为了进一步测试模型模拟任意障碍物的能力, 模拟下游带悬空圆形障碍物的溃坝洪水算例.圆可以被分解成很多斜率不同的线段, 在直角坐标系下无法与网格对齐, 使问题更复杂.计算域如图 5所示, 半径为0.19 m的障碍物放置在距离右侧边界0.6 m的位置, 离下底高度为0.26 m, Re=1 455 000, 其他参数设置及初始条件与4.1节相同.
|
图 5 带圆型障碍物溃坝算例示意图 Fig. 5 Sketch of dam break with circular obstacle |
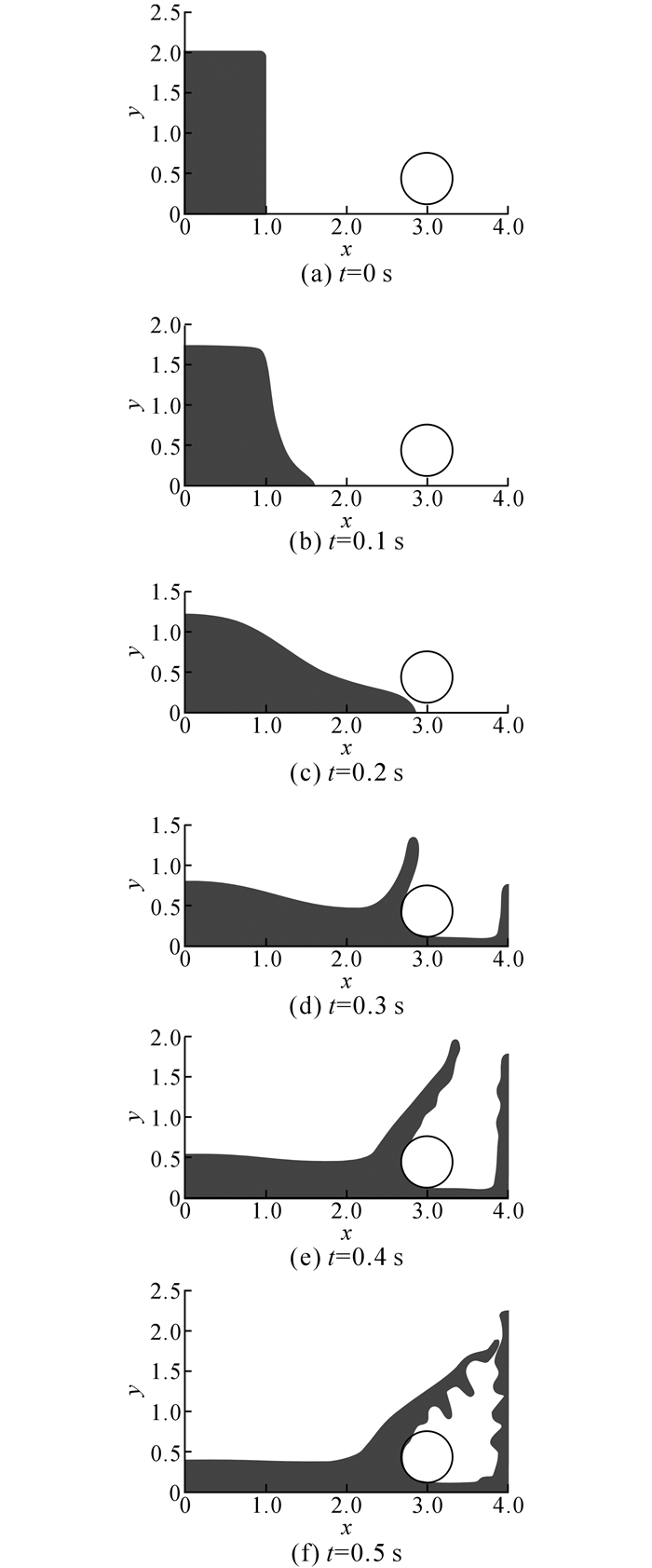
图 6显示了数值模拟的结果, 溃坝洪水受圆形障碍物阻挡之后, 水体前进、撞击、爬升等过程都被很好地再现出来, 说明采用该浸入边界法可以很有效地处理流体经过复杂形状的障碍物的边界问题.
|
图 6 不同时刻带圆型障碍物的溃坝洪水自由液面形状 Fig. 6 Water profiles at several time instants for dam break with circle obstacle |
(1) 改善了传统水平集法在模拟过程中的质量盈亏问题.模拟显示, 该改进可以在模拟流体动态过程中保持很好的质量守恒性.
(2) 提出简单的数值过程, 来处理模拟过程中出现的液体与固体障碍物重叠的问题.利用投影法求解Navier-Stikes方程中的压力项, 有效地提高了计算效率.
(3) 通过与实验结果相比, 本文的数值模拟结果很好地再现了自由液面演进过程中遭遇障碍物后受扰动、撞击、形成水舌、下坠等一系列复杂的物理现象.下游带悬空支撑的圆柱形障碍物算例的模拟显示, 采用浸入边界法能的有效地处理水流流经复杂形状障碍物时的过程.
(4) 本文方法在模拟自由液面大变形、快速变化、与障碍物相互作用的流动问题中体现出了较大的优势.
本文方法具有较高的精度, 使得计算量大大增加, 尤其表现在使用CCD方法离散Navier-Stokes方程时.笔者尝试过使用3阶QUICK(quadratic upwind interpolation for convective kinematics)格式求解动量方程.该格式能够得到较不错的结果, 大大减少了计算时间.在保持水平集法拥有较高计算精度的条件下, 如何提高计算效率, 将该方法应用到实际地形或大尺度溃坝问题的数值模拟, 是今后值得更深入探讨的问题.
| [1] |
YANG J, STERN F. Sharp interface immersed-boundary/level-set method for wave-body interactions[J]. Journal of Computational Physics, 2009, 228(17): 6590-6616. DOI:10.1016/j.jcp.2009.05.047 |
| [2] |
YOUNGS D L. Time-dependent multi-material flow with large fluid distortion[M]//Numerical Methods in Fluid Dynamics. Cambridge: Academic Press, 1982: 273-285. http://ci.nii.ac.jp/naid/10007969491
|
| [3] |
XIAO F, HONMA Y, KONO T. A simple algebraic interface capturing scheme using hyperbolic tangent function[J]. International Journal for Numerical Methods in Fluids, 2005, 48(9): 1023-1040. DOI:10.1002/(ISSN)1097-0363 |
| [4] |
YOKOI K. Efficient implementation of THINC scheme:a simple and practical smoothed VOF algorithm[J]. Journal of Computational Physics, 2007, 226(2): 1985-2002. DOI:10.1016/j.jcp.2007.06.020 |
| [5] |
HOLM E J, LANGTANGEN H P. A method for simulating sharp fluid interfaces in groundwater flow[J]. Advances in Water Resources, 1999, 23(1): 83-95. DOI:10.1016/S0309-1708(99)00003-2 |
| [6] |
GRILLO A, LOGASHENKO D, STICHEL S, et al. Simulation of density-driven flow in fractured porous media[J]. Advances in Water Resources, 2010, 33(12): 1494-1507. DOI:10.1016/j.advwatres.2010.08.004 |
| [7] |
FROLKOVI P. Application of level set method for groundwater flow with moving boundary[J]. Advances in Water Resources, 2012, 47(10): 56-66. |
| [8] |
YUE W, LIN C L, PATEL V C. Numerical simulation of unsteady multidimensional free surface motions by level set method[J]. International Journal for Numerical Methods in Fluids, 2003, 42(8): 853-884. DOI:10.1002/(ISSN)1097-0363 |
| [9] |
李向阳, 王跃发, 禹耕之, 等. 改进水平集法模拟不可压缩两相流动时质量守恒的体积校正法[J]. 中国科学B辑:化学, 2008(7): 636-644. LI Xiang-yang, WANG Yue-fa, YU Geng-zhi, et al. Volume correction for mass conversation in simulation of incompressible two-phase flow by improving the level set method[J]. Science in China (Ser. B:Chemistry), 2008(7): 636-644. |
| [10] |
SUSSMAN M, PUCKETT E G. A coupled level set and volume-of-fluid Method for computing 3D and axisymmetric incompressible two-phase flows[J]. Journal of Computational Physics, 2000, 162(2): 301-337. DOI:10.1006/jcph.2000.6537 |
| [11] |
WANG Z, YANG J, KOO B, et al. A coupled level set and volume-of-fluid method for sharp interface simulation of plunging breaking waves[J]. International Journal of Multiphase Flow, 2009, 35(3): 227-246. DOI:10.1016/j.ijmultiphaseflow.2008.11.004 |
| [12] |
SUSSMAN M, FATEMI E. An efficient interface-preserving level set redistancing algorithm and Its application to interfacial incompressible fluid flow[J]. Siam Journal on Scientific Computing, 1999, 20(4): 1165-1191. DOI:10.1137/S1064827596298245 |
| [13] |
WANG Z, YANG J, STERN F. An improved particle correction procedure for the particle level set method[J]. Journal of Computational Physics, 2009, 228(16): 5819-5837. DOI:10.1016/j.jcp.2009.04.045 |
| [14] |
MERRIMAN B, BENCE J K, OSHER S J. Motion of multiple junctions:a level set approach[J]. Journal of Computational Physics, 1994, 112(2): 334-363. DOI:10.1006/jcph.1994.1105 |
| [15] |
ZHAO H K, CHAN T, MERRIMAN B, et al. A variational level set approach to multiphase motion[J]. Journal of Computational Physics, 1996, 127(1): 179-195. DOI:10.1006/jcph.1996.0167 |
| [16] |
YOKOI K. A variational approach to multi-phasemotion of gas, liquid and solid based on the level set method[J]. Computer Physics Communications, 2009, 180(7): 1145-1149. DOI:10.1016/j.cpc.2009.01.022 |
| [17] |
ZHANG Y. A level set immersed boundary method for water entry and exit[J]. Communications in Computational Physics, 2010, 8(2): 265-288. |
| [18] |
YANG J, STERN F. Sharp interface immersed-boundary/level-set method for wave-body interactions[J]. Journal of Computational Physics, 2009, 228(17): 6590-6616. DOI:10.1016/j.jcp.2009.05.047 |
| [19] |
YANG J, BALARAS E. An embedded-boundary formulation for large-eddy simulation of turbulent flows interacting with moving boundaries[J]. Journal of Computational Physics, 2006, 215(1): 12-40. DOI:10.1016/j.jcp.2005.10.035 |
| [20] |
YANG J, STERN F. A simple and efficient direct forcing immersed boundary framework for fluid-structure interactions[J]. Journal of Computational Physics, 2012, 231(15): 5029-5061. DOI:10.1016/j.jcp.2012.04.012 |
| [21] |
CHIU P H, LIN R K, SHEU T W H. A differentially interpolated direct forcing immersed boundary method for predicting incompressible Navier-Stokes equations in time-varying complex geometries[J]. Journal of Computational Physics, 2010, 229(12): 4476-4500. DOI:10.1016/j.jcp.2010.02.013 |
| [22] |
SUSSMAN M, SMEREKA P, OSHER S. A level set approach for computing solutions to incompressible two-phase flow[J]. Journal of Computational Physics, 1994, 114(1): 146-159. DOI:10.1006/jcph.1994.1155 |
| [23] |
YOKOI K. A practical numerical framework for free surface flows based on CLSVOF method, multi-moment methods and density-scaled CSF model:numerical simulations of droplet splashing[J]. Journal of Computational Physics, 2013, 232(1): 252-271. DOI:10.1016/j.jcp.2012.08.034 |
| [24] |
CHU P C, FAN C. A three-point combined compact difference scheme[J]. Journal of Computational Physics, 1998, 140(2): 370-399. DOI:10.1006/jcph.1998.5899 |
| [25] |
CHIU P H, SHEU T W H. On the development of a dispersion-relation-preserving dual-compact upwind scheme for convection-diffusion equation[J]. Journal of Computational Physics, 2009, 228(10): 3640-3655. DOI:10.1016/j.jcp.2009.02.008 |
| [26] |
YU C H, WANG D, HE Z, et al. An optimized dispersion-ralation-preserving combined compact difference scheme to solve advection equations[J]. Journal of Computational Physics, 2015, 300(C): 92-115. |
| [27] |
MCLACHLAN R I. Area preservation in computational fluid dynamics[J]. Physics Letters A, 1999, 264(1): 36-44. DOI:10.1016/S0375-9601(99)00763-X |
| [28] |
JIANG G S, PENG D. Weighted ENO schemes for Hamilton-Jacobi equations[J]. Siam Journal on Scientific Computing, 1970, 21(6): 2126-2143. |
| [29] |
SHU C W, OSHER S. Efficient implementation of essentially non-oscillatory shock-capturing schemes[J]. Journal of Computational Physics, 1988, 77(2): 439-471. DOI:10.1016/0021-9991(88)90177-5 |
| [30] |
TSENG Y H, FERZIGER J H. A ghost-cell immersed boundary method for flow in complex geometry[J]. Journal of Computational Physics, 2003, 192(2): 593-623. DOI:10.1016/j.jcp.2003.07.024 |
| [31] |
CHORIN A J. Numerical solution of the Navier-Stokes equations[J]. Mathematics of Computation, 1968, 22(104): 17-34. |
| [32] |
KOSHIZUKA S, TAMAKO H, OKA Y. A particle method for incompressible viscous flow with fluid fragmentation[J]. Comput Fluid Dynamics Journal, 1995, 4: 29-46. |
| [33] |
卢雨, 胡安康, 刘亚冲. 基于有限点法的自由面流动的数值模拟[J]. 浙江大学学报:工学版, 2016, 50(1): 55-62. LU Yu, HU An-kang, LIU Ya-chong. Numerical simulation of free surface flow based on finite point method[J]. Journal of Zhejiang University:Engineering Science, 2016, 50(1): 55-62. |



