2. 上海宇航系统工程研究所, 上海 201108
2. Aerospace System Engineering Shanghai, Shanghai 201108, China
形状记忆聚合物(shape memroy polymers, SMPs)在橡胶态具有良好的变形能力, 通过状态变化可实现临时变形的固定及恢复、弹性模量大幅变化等, 近年成为学术研究热点[1-3].在材料热力学本构方程研究方面, Diani等[4-5]提出了两相理论;Bhattacharrya等[6]提出4单元模型并将其推广到非线性分析中;Gu等[7]提出了热诱导SMPs的三维有限变形力学本构, 并编写数值计算程序.吕海宝等[8]解释了形状记忆效应的物理机制, 章巧芳等[9-12]基于Tobushi的理论建立了三维ABAQUS材料函数, 刘猛等[13]用Maxwell模型表示初始相, 非线性弹簧表示激活相, 建立三元件模型来预测形状记忆聚氨酯的力学性能.
从线性黏弹性理论出发, Baghani等[14-17]采用广义Maxwell模型结合时温叠加原理对形状记忆效应进行数值模拟, 该法计算简便、参数易于测定, 但假定SMPs的弹性响应部分为线弹性, 参数测定建立在线性黏弹性范围内.限制于此, 不能考虑结构分析中大应变问题, 而SMPs制成的结构物往往经历较大应变, 因此有必要将文献[15-17]的方法推广到有限应变格式下, 并建立相应的材料参数测定方法.
本文首先建立有限应变格式的黏弹性本构方程, 并推导相应的材料参数的拟合公式.然后以环氧基形状记忆树脂为例(epoxy shape memory polymer, ESMP), 进行拉伸-松弛试验, 并对ESMP的有限应变黏弹性特性进行研究, 总结其黏性、弹性等随温度的变化关系.针对复杂的三维SMPs结构分析问题, 利用高分子聚合物受力时体积不变特性推导需补充的材料参数, 并借助ABAQUS建立数值分析方法.最后对拉伸-松弛试验进行数值模拟, 对比计算结果验证所提本构方程的正确性.
1 有限应变黏弹性本构方程推导SMPs属于高分子聚合物, 经典的遗传积分形式的黏弹性本构方程[18]可写成:
| $ \sigma \left( {\varepsilon , t} \right) = \smallint _0^tg\left( {t - s} \right)\frac{{{\rm{d}}{\sigma _0}\left( s \right)}}{{{\rm{d}}s}}{\rm{d}}s. $ | (1) |
式中:σ0(s)为弹性响应部分, g(t)为衰减函数,可写成Prony级数的形式:
| $ g\left( t \right) = 1 - \sum\limits_{i = 1}^N {\left[ {{g_i}\left( {1 - \exp \left( {\frac{{ - t}}{{{\tau _i}}}} \right)} \right)} \right]} . $ | (2) |
其中,N为Prony级数项数,gi为无量纲系数,τi为松弛时间.
有限应变时, 采用Neo-Hookean超弹性本构方程描述SMPs的弹性响应, 其应变能函数[19]为
| $ U = {C_{10}}\left( {{{\bar I}_1} - 3} \right) + \frac{1}{{{D_1}}}{\left( {{J_{{\rm{el}}}} - 1} \right)^2}. $ | (3) |
式中:I1为应力不变量,
SMPs受力时可假定体积不变[15, 18], 即J=1, 忽略材料热膨胀, 即Jel=J=1, I1=I1.应变能函数式(3)变成:
| $ U = {C_{10}}\left( {{I_1} - 3} \right). $ | (4) |
由式(4)求出超弹性应力与伸长率λ的关系:
| $ {\sigma _0}\left( \lambda \right) = \frac{{\partial U}}{{\partial \lambda }} = 2{C_{10}}\left( {\lambda - \frac{1}{{{\lambda ^2}}}} \right). $ | (5) |
其中, 伸长率与应变(对数应变)均为时间的函数, 且有λ(t)=exp [ε(t)], 将其代入式(5)得到超弹性应力-应变关系:
| $ {\sigma _0}\left( t \right) = 2{C_{10}}\left\{ {\exp \left[ {\varepsilon \left( t \right)} \right] - \exp \left[ { - 2\varepsilon \left( t \right)} \right]} \right\}. $ | (6) |
将式(6)代入式(1)并积分得到有限应变格式的黏弹性本构方程:
| $ \sigma \left( {\varepsilon , t} \right) = 2{C_{10}}\left[ {A - \sum\limits_{i = 1}^N {\int\limits_0^t {{g_i}} } BC\dot \varepsilon \left( s \right){\rm{d}}s} \right]. $ | (7) |
式中:
| $ \begin{array}{l} A = \exp \left[ {\varepsilon \left( t \right)} \right] - \exp \left[ { - 2\varepsilon \left( t \right)} \right], \\ B = 1 - \exp \left( {\frac{{s - t}}{{{\tau _i}}}} \right), \\ C = \exp \left[ {\varepsilon \left( t \right)} \right] + 2\exp \left[ { - 2\varepsilon \left( t \right)} \right]. \end{array} $ |
本构方程式(7)中需确定参数C10、gi、τi, 式中σ(t)、ε(t)是以时间为变量的未知函数, 两者相互耦合且具有强非线性, 随Prony级数项数增多, 材料参数的数量还会增加, 要通过试验测定参数需控制变量, 控制应变历史ε(t)(或应力历史σ(t))为已知量进行试验, 对测出的σ(t)(或ε(t))时间序列进行拟合,求解材料参数.可选择的试验包括蠕变试验、松弛试验等.本文选择松弛试验, 控制应变历史ε(t)为已知量, 测试应力的时间序列, 通过式(7)推导拟合公式, 确定材料参数.
以往的聚合物松弛试验在数据处理时往往忽略加载段的影响.为提高参数测定的准确度, 在参数拟合时将加载段也纳入拟合范围, 考虑应力历史对材料松弛过程的影响.此外, SMPs力学性能与温度密切相关, 尤其在玻璃转换点θg附近, 弹性模量、松弛时间等对温度变化具有较大的敏感性[20].因此针对不同温度分别验证式(7)的适用性, 并探讨SMPs在不同温度下的黏弹性力学特征.
2.2 温度分组与拉伸-松弛试验选用文献[21]中的环氧基形状记忆聚合物(epoxy shape memory polymer, ESMP)进行试验, 首先采用动态热力学分析仪(dynamic mechanical analyzer, DMA)测试材料的θg点, 以1 Hz的频率施加正弦周期荷载, 进行温度扫描得到θg=47.3 ℃.储能模量E'及耗能角正切值tan δ随温度θ变化见图 1.基于此选定拉伸-松弛试验的温度为40、45、50及55 ℃共4组.

|
图 1 储能模量及损耗角正切值曲线 Fig. 1 Curve of storage modulus and loss tangent |
拉伸-松弛试验中为保证试件边缘整齐, 不出现应力集中导致的破坏, 采用铣床将ESMP薄板加工为150 mm×20 mm×2.5 mm的矩形试件(图 2), 试验中夹持长度为25 mm.图 2中LT为试件总长, LC为夹持长度, w0为试件宽度.

|
图 2 环氧基形状记忆树脂试件 Fig. 2 Specimen of epoxy shape memory polymer |
拉伸-松弛试验步骤:测量试件长L0(夹具间距离)、宽w0和厚T0, 宽度和厚度用于计算面积A0;匀速拉伸60 s, 至伸长量为ΔL.ESMP的变形能力随温度升高而增强, 在试验时随温度升高增加拉伸量;保持约束360 s使试件发生应力松弛.各组试验L0、A0、ΔL及拉伸位移速度v、拉伸应变速率v如表 1所示, 试验得到σ-t曲线如图 4所示.
| 表 1 各组试件试验参数 Table 1 Experimental data of specimen in various group |

|
图 3 拉伸-松弛试验 Fig. 3 Tension-relaxation experiment |

|
图 4 各温度下应力-时间曲线及拟合结果 Fig. 4 Curves of stress-time at various temperatures with fitting results |
试验中得到拉力T及位移读数, 采用本构方程式(7)拟合时需转换成Cauchy应力σ和对数应变ε(t).已知Cauchy应力σ和工程应力P的关系[22]为:
| $ \sigma = {J^{ - 1}}F \cdot P. $ | (8) |
式中:J=1, F为变形梯度.于是有
| $ \sigma = \frac{{TL}}{{{A_0}{L_0}}}. $ | (9) |
式中:L为各时刻下试件长度.
将匀速拉伸阶段的应变视为时间的线性函数, 通过ε(t)-t曲线进行线性拟合得到ε(t)的显式表达式ε(t)=vt.也可将应变视作时间二次函数或其他形式函数, 采用相应形式的函数进行拟合求出ε(t)的显式表达式, 处理方法相同.将ε(t)=vt代入式(7)积分得到拉伸段的应力计算公式:
| $ \begin{array}{l} \sigma \left( {\varepsilon , t} \right) = {\sigma _0}\left( t \right) - \sum\limits_{i = 1}^N {\left\{ {{g_i}\left[ {{\sigma _0}\left( t \right) - \exp \left( { - \frac{t}{{{\tau _i}}}} \right) \times } \right.} \right.} \\ \left( {\frac{{2v{C_{10}}{\tau _i}}}{{1 + v{\tau _i}}}\left( {\exp \frac{{1 + v{\tau _i}}}{{{\tau _i}}}t} \right) - 1} \right) + \\ \left. {\left. {\left. {\frac{{4v{C_{10}}{\tau _i}}}{{1 - 2v{\tau _i}}}\left( {\exp \left( {\frac{{1 - 2v{\tau _i}}}{{{\tau _i}}}t} \right) - 1} \right)} \right)} \right]} \right\}. \end{array} $ | (10) |
在松弛段v=0, 设拉伸阶段时间长t1, 得松弛段ε(t)=vt1, 带入式(7)积分得到应力计算公式:
| $ \begin{array}{*{20}{l}} {\sigma \left( {\varepsilon , t} \right) = {\sigma _0}\left( t \right) - \sum\limits_{i = 1}^N {\left\{ {{g_i}\left[ {{\sigma _0}\left( {{t_1}} \right) - \exp \left( { - \frac{t}{{{\tau _i}}}} \right) \times } \right.} \right.} }\\ {\left( {\frac{{2v{C_{10}}{\tau _i}}}{{1 + v\;{\tau _i}}}\left( {\exp \frac{{1 + v{\tau _i}}}{{{\tau _i}}}{t_1}} \right) - 1} \right) + }\\ {\left. {\left. {\left. {\frac{{4v{C_{10}}{\tau _i}}}{{1 - 2v\;{\tau _i}}}\left( {\exp \left( {\frac{{1 - 2v{\tau _i}}}{{{\tau _i}}}{t_1}} \right) - 1} \right)} \right)} \right]} \right\}.} \end{array} $ | (11) |
采用式(10)和(11)对试验测量的σ-t数据进行非线性拟合即可确定材料参数.
3.2 拟合过程及结果参数拟合的步骤如下:
1) 基于式(10)和(11)采用Origin软件编制非线性拟合程序, 拟合算法采用Levenberg Marquardt迭代;
2) 利用式(9)进行数据处理, 对拉伸段的ε(t)-t线性拟合得应变率v值;
3) 调整σ-t数据分布密度, 应力衰减迅速区域采用更密集σ(t)数据增加该区的拟合权重;
4) 利用第(1)步编制的非线性拟合程序对σ-t数据进行拟合.
拟合结果见图 4(a)和(b), 得到的材料参数见表 2.可发现随温度升高初始模量C10变小, 观察松弛模量的表达式:
| 表 2 各组温度下Prony级数参数 Table 2 Prony series parameters at various temperatures |
| $ Y\left( t \right) = 2{C_{10}}\left\{ {1 - \sum\limits_{i = 1}^N {\left\{ {\left. {{g_i}\left( {1 - \exp \left( {\frac{{ - t}}{{{\tau _i}}}} \right)} \right)} \right]} \right.} } \right\}. $ | (12) |
令时间趋于无穷大, 则exp (-t/τi)趋于0, 聚合物模量将达到平衡值, 该平衡值是总模量中弹性部分, 随时间衰减部分是黏性部分[18].求出各组弹性部分
| $ {M_{\rm{E}}} = 2{C_{10}}\left( {1 - \sum\limits_{i = 1}^N {{g_i}} } \right) $ |
和黏性部分
| $ {M_{\rm{V}}} = 2{C_{10}}\sum\limits_{i = 1}^N {{g_i}} $ |
模量值列于表 3, 弹性部分模量值随温度基本不变, 黏性部分模量所占的比例RV随温度升高而减小, 即随温度升高材料黏性减小、流动性增强.
| 表 3 各组温度下模量的弹性及黏性部分 Table 3 Elastic and viscous part of modulus |
针对复杂的结构问题可采用ABAQUS进行数值法求解, 数值求解时先将式(7)在时间域上离散, 构造增量形式的本构方程, 再改写为Jaumann应力率形式的式(13), 详细推导过程参考文献[19].
| $ \begin{array}{l} \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over \tau } }}\left( {t + \Delta t} \right) = \left( {1 - \sum\limits_{i = 1}^n {({\alpha _i}{g_i})} } \right)\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over \tau } }}_0^D\left( {t + \Delta t} \right) + \\ \left( {1 - \sum\limits_{i = 1}^n {({\alpha _i}{k_i})} } \right)\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over \tau } }}_0^H\left( {t + \Delta t} \right) - \\ \sum\limits_i^n {\left\{ {({\beta _i}{g_i}){\rm{dev}}\left[ {\mathit{\boldsymbol{\breve{\hat{\tau}} }}_0^D\left( t \right)} \right]} \right\}} - \sum\limits_i^n {\left\{ {{\gamma _i}{\rm{dev}}\;\left[ {\mathit{\boldsymbol{\breve{\hat{\tau}} }}_i^D\left( t \right)} \right]} \right\}} . \end{array} $ | (13) |
式中:
| $ \begin{array}{l} \;\;\;\;\;\;\;{\alpha _i} = 1 - \frac{{{\tau _i}}}{{\Delta t}}(1 - {\gamma _i}), \\ {\beta _i} = \frac{{{\tau _i}}}{{\Delta t}}(1 - {\gamma _i}) - {\gamma _i}, {\gamma _i} = \exp \left( { - \frac{{\Delta t}}{{{\tau _i}}}} \right); \end{array} $ |
gi、ki、τi为Prony级数参数, 分别对应剪切模量和体积模量;
| $ {\rm{dev}}\left( \cdot \right) = \left( \cdot \right) - \frac{1}{3}\left( \cdot \right):\mathit{\boldsymbol{I}}. $ |
利用ABAQUS的Standard求解器, 采用有限时间增量步法对拉伸-松弛试验进行数值模拟.建立与试件尺寸相同的有限元模型, 两端采用MPC约束, 约束一端控制点全部自由度, 并约束另一端5个自由度, 仅释放拉伸方向(图 5中Z方向).采用尺寸为1 mm×1 mm×1 mm的八结点六面体混合单元(编号C3D8H)对结构进行划分, 共6 060个单元.SMPs在橡胶态时泊松比接近0.5[15], 采用普通单元时刚度矩阵接近奇异阵, 且在数值积分点计算的应力值具有极强的振荡性, 采用混合单元可解决此问题[19].数值模拟时还需补充Neo-Hookean模型中的参数D1及体积模量的Prony级数参数ki.假定SMPs体积模量不随时间衰减[19], 得ki=0;取泊松比ν=0.49[15], 参数D1由下式[22]求解:
|
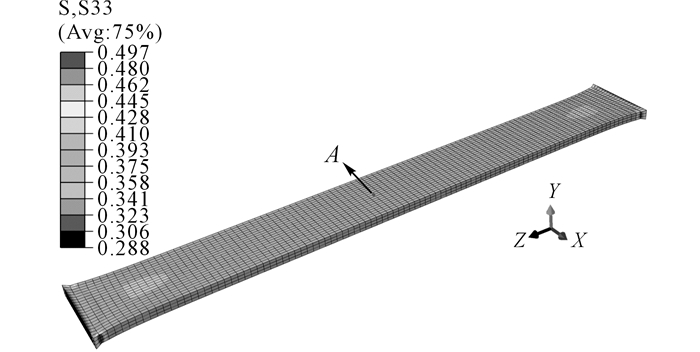
图 5 55 ℃试件拉伸-松弛后拉伸应力分布 Fig. 5 Tension stress distribution of specimen at 55 ℃ after tension-relaxation |
| $ {D_1} = \frac{{3\left( {1 - 2\nu } \right)}}{{4{C_{10}}\left( {1 + \nu } \right)}}. $ | (14) |
计算中建立2个黏弹性分析步并打开几何非线性开关, 收敛准则设置为黏性应变计算容差小于10-5.第一分析步时长为60 s, 用于施加位移荷载;第二分析步时长为360 s, 用于保持位移约束使应力发生松弛.采用自动时间增量步, 初始增量步设为0.001 s.采用牛顿拉普逊迭代法求解, 结果显示单一时间增量步中最多迭代6次即可收敛.计算过程在普通4线程PC上耗时约3 min.将收敛容差改为10-6后耗时约17 min, 效率有一定降低.如图 5所示为第二分析步结束时拉伸应力分布, 试件中间区域拉伸应力为0.401 MPa.
对比试件中间点A(图 5)试验结果和模拟结果的差别.由于ESMP应力响应与应变和时间都相关, 绘制四组温度下σ-t和σ-ε曲线分别见图 6和图 7(a)、(b), 拉力T随时间变化曲线见图 8.结果显示, 各组数据中试验值与模拟值在一范数下最大误差为1.1%.
|
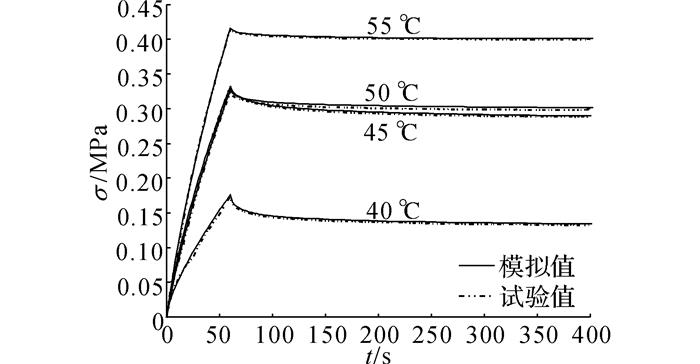
图 6 各温度下数值模拟与试验应力-时间曲线对比 Fig. 6 Comparison of stress-time curve at various temperatures between simulations and experiments |
|
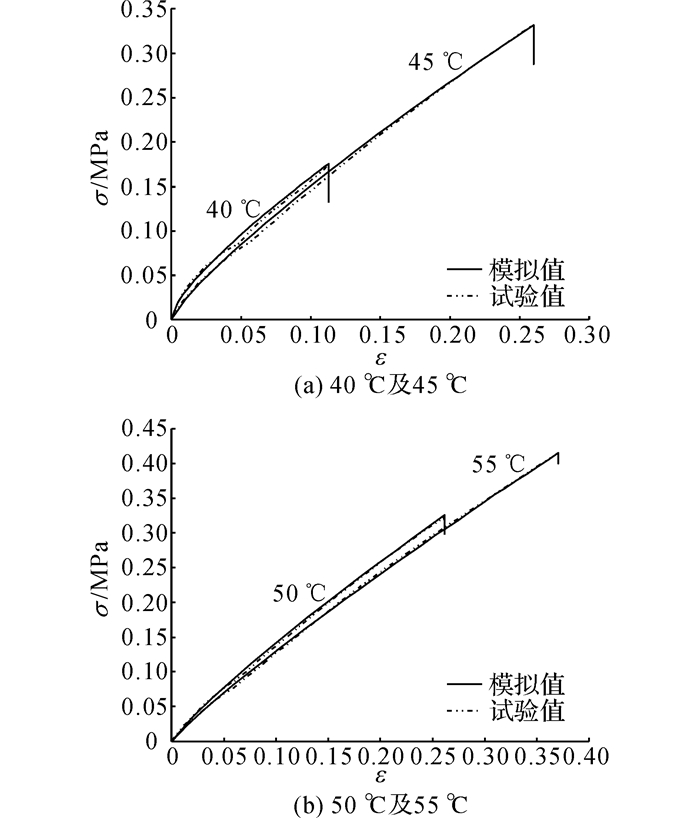
图 7 各温度下数值模拟与试验的应力-应变曲线对比 Fig. 7 Comparison of stress-strain curve at various temperatures between simulations and experiments |
|
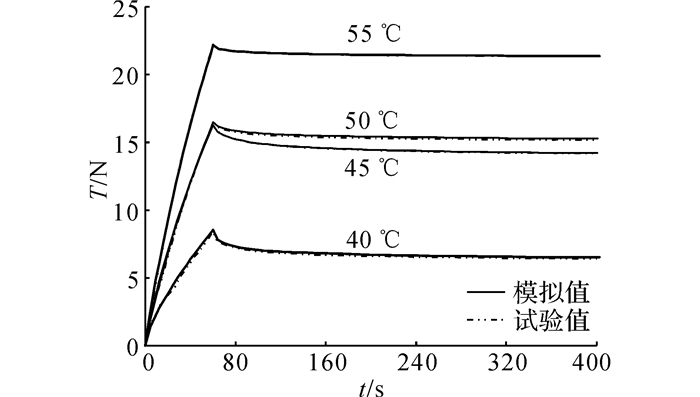
图 8 各温度下数值模拟与试验的拉力对比 Fig. 8 Comparison of tension force at various temperatures between experiment and simulation |
试验与模拟结果对比表明:利用方程式(7)描述材料本构关系, 再利用式(10)、(11)拟合确定材料参数, 并采用有限时间增量步法进行数值计算能较准确的描述SMPs有限应变黏弹性特性.同时, 图 6和图 8显示,在试验温度范围内该环氧基形状记忆树脂均表现黏弹性特点, 且随温度升高, 应力的衰减量更小, 材料黏性减弱.
5 结语本文推导了Prony级数形式的有限应变黏弹性本构方程, 采用ESMP进行拉伸-松弛试验, 利用所提本构方程推出拉伸-松弛试验的参数拟合公式, 拟合确定了材料参数.在不同温度下对ESMP进行试验, 发现在本文试验的温度范围内,ESMP均表现黏弹性特点, 且随温度升高总模量变小, 总模量中黏性部分的比例降低, 但弹性部分的模量大小保持不变.数值模拟时需补充材料参数D1和ki, 根据SMPs体积不变特性给出其计算公式.拉伸-松弛试验数值模拟结果表明,所提本构方程能有效预测SMPs的黏弹性力学特性.在推导本构方程以及参数拟合公式时除引入高聚物的各向同性、体积不变性假设外未引入其他假设, 对于其他具有同样特点的高聚物, 本文推导的有限应变黏弹性本构方程和参数拟合公式也是适用的.
| [1] |
KAROTHU D P, WESTON J, DESTA I T, et al. Shape-memory and self-healing effects in mechanosalient molecular crystals[J]. Journal of the American Chemical Society, 2016, 138(40): 13298-13306. DOI:10.1021/jacs.6b07406 |
| [2] |
JI S, WANG J, OLAH A, et al. Triple-shape-memory polymer films created by forced-assembly multilayer coextrusion[J]. Journal of Applied Polymer Science, 2017, 134(5): 44405-44415. |
| [3] |
GARCIA-HUETE N, AXPE E, CUEVAS J M, et al. In situ measurements of free volume during recovery process of a shape memory polymer[J]. Polymer, 2017, 109: 66-70. DOI:10.1016/j.polymer.2016.12.042 |
| [4] |
DIANI J, LIU Y, GALL K. Finite strain 3D thermoviscoelastic constitutive model for shape memory polymers[J]. Polymer Engineering & Science, 2006, 46(4): 486-492. |
| [5] |
CHEN Y C, LAGOUDAS D C. A constitutive theory for shape memory polymers. Part Ⅱ[J]. Journal of the Mechanics and Physics of Solids, 2008, 56(5): 1766-1778. DOI:10.1016/j.jmps.2007.12.004 |
| [6] |
BHATTACHARYYA A, TOBUSHI H. Analysis of the isothermal mechanical response of a shape memory polymer rheological model[J]. Polymer Engineering and Science, 2000, 40(12): 2498-2510. DOI:10.1002/(ISSN)1548-2634 |
| [7] |
GU J, SUN H, FANG C. A finite deformation constitutive model for thermally activated amorphous shape memory polymers[J]. Journal of Intelligent Material Systems and Structures, 2015, 26(12): 1530-1538. DOI:10.1177/1045389X14544147 |
| [8] |
吕海宝, 冷劲松, 杜善义. 形状记忆聚合物力学行为及其物理机制[J]. 固体力学学报, 2017, 38(1): 1-12. LU Hai-bao, LENG Jing-song, DU Shan-yi. Working mechanism for the mechanical behavior of shape memory polymer[J]. Chinese Journal of Solid Mechanics, 2017, 38(1): 1-12. |
| [9] |
章巧芳, 林文武, 张钦, 等. 热驱动形状记忆聚合物三维力学本构模型[J]. 浙江工业大学学报, 2015, 43(1): 43-46. ZHANG Qiao-fang, LIN Wen-wu, ZHANG Qin, et al. 3D constitutive model of temperature-induced shape memory polymers[J]. Journal of Zhejiang University of Technology, 2015, 43(1): 43-46. |
| [10] |
周博, 刘彦菊, 冷劲松. 形状记忆聚合物的宏观力学本构模型[J]. 中国科学:物理学力学天文学, 2010, 40(7): 896-903. ZHOU Bo, LIU Yan-ju, LENG Jing-song. Macro constitutive model of shape memory polymers[J]. Scientia Sinica Phys, Mech & Astron, 2010, 40(7): 896-903. |
| [11] |
谭巧. 形状记忆环氧聚合物及其复合材料的典型力学行为研究[D]. 哈尔滨: 哈尔滨工业大学, 2015. TAN Qiao. Typical mechanical behavior of epoxy shape memory polymer and its composite[D]. Harbin: Harbin Institute of Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10213-1015957495.htm |
| [12] |
时光辉. 形状记忆聚合物及其智能结构热力学行为研究[D]. 北京: 北京工业大学, 2013. SHI Guang-hui. Thermomechanical properties of shape memory polymer and its smart structures[D]. Beijing: Beijing University of Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10005-1013046981.htm |
| [13] |
刘猛, 付翔, 朱曜峰, 等. 基于相变理论的形状记忆聚氨酯的本构方程的构建[J]. 浙江理工大学学报:自然科学版, 2016, 35(4): 559-564. LIU Meng, FU Xiang, ZHU Yao-feng, et al. Constitutive model of shape memory polyurethanes based on phase transformation theory[J]. Journal of Zhejiang Sci-Tech University:Natural Sciences, 2016, 35(4): 559-564. |
| [14] |
BAGHANI M, NAGHDABADI R, ARGHAVANI J, et al. A thermodynamically-consistent 3D constitutive model for shape memory polymers[J]. International Journal of Plasticity, 2012, 35: 13-30. DOI:10.1016/j.ijplas.2012.01.007 |
| [15] |
DIANI J, GILORMINI P, FREDY C, et al. Predicting thermal shape memory of crosslinked polymer networks from linear viscoelasticity[J]. International Journal of Solids and Structures, 2012, 49(5): 793-799. DOI:10.1016/j.ijsolstr.2011.11.019 |
| [16] |
YU K, GE Q, QI H J. Reduced time as a unified parameter determining fixity and free recovery of shape memory polymers[J]. Nature Communications, 2014, 5: 3066. DOI:10.1038/ncomms4066 |
| [17] |
罗玲. 基于黏弹性理论的树脂及其纤维复合材料的形状记忆数值模拟[D]. 济南: 山东大学, 2013. LUO Ling. Simulation of shape memory properties for resin and their fiber reinforced composites based on viscoelasticity[D]. Jinan: Shandong University, 2013. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2329127 |
| [18] |
GUTIERREZ-LEMINI D. Engineering viscoelasticity[M]. New York: Springer Science & Business Media, 2014, 116-138.
|
| [19] |
DASSUALT S. Abaqus theory guide[J]. Providence:Dassault Systemes Simulia Corporation, 2016, 4821-4826. |
| [20] |
郑宁. 高应变形状记忆聚合物[D]. 杭州: 浙江大学, 2016. ZHENG Ning. High strain shape memory polymers[D]. Hangzhou: Zhejiang University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10335-1016052981.htm |
| [21] |
游晋, 房光强, 陈务军, 等. 形状记忆环氧树脂及其碳纤维织物增强环氧树脂的动态力学性能[J]. 复合材料学报, 2017, 34: 1-7. YOU Jin, FANG Guang-qiang, CHEN Wu-jun, et al. Dynamic mechanical properties of shape memory epoxy polymer and 4-harness satin carbon fiber weave reinforced composites[J]. Acta Materiae Compositae Sinca, 2017, 34(1): 1-7. |
| [22] |
BELYTSCHKO T, LIU W K, MORAN B. Nonlinear finite elements for continua and structures[M]. 2nd edition. Chichester: John Wiley & Sons, Ltd, 2013, 69-81.
|



