2. 宁波职业技术学院 海天学院, 浙江 宁波 315800;
3. 浙江大学 工程力学学系, 浙江 杭州 310027;
4. 浙江大学 浙江省软体机器人与智能器件研究重点实验室, 浙江 杭州 310027;
5. 浙江大学 软物质科学研究中心, 浙江 杭州 310027
2. Haitian School, Ningbo Polytechnic, Ningbo 315800, China;
3. Department of Engineering Mechanics, Zhejiang University, Hangzhou 310027, China;
4. Key Laboratory of Soft Machines and Smart Devices of Zhejiang Province, Zhejiang University, Hangzhou 310027, China;
5. Soft Matter Research Center, Zhejiang University, Hangzhou 310027, China
对于热作用时间较长的稳态传热过程及热传播速度较快的非稳态常规传热过程, 通常采用Fourier定律来描述热流密度与温度梯度之间的关系, 可以满足精度要求.随着超短激光脉冲的出现和制冷水平的提高, 出现了极高(低)温条件下的传热问题和超急速传热问题, 使得Fourier定律中的准平衡条件假设不再成立.经典热弹性理论中的热传导方程是抛物线方程, 意味着热以无穷大速度传播, 这与实验观测明显不符合.Cattaneo等[1-2]推导出描述温度传播过程的双曲线热传导方程, 这种基于非Fourier定律的热传导理论统称为广义热传导理论.20世纪60年代发展出广义热弹性理论,克服了经典热弹性理论的不足, 得到与实验一致的结果.Lord和Shulman[3](L-S)、Green和Lindsay[4](简写为G-L)、Green和Naghdi[5](G-N)分别对经典热弹性理论进行修正, 各自建立了广义热弹性理论.利用这些理论, 可以充分地展示热扰动在介质内的传播和波动效应.Jiang等[6]忽略热弹耦合作用,利用Laplace变换,给出空心球壳在受内、外温度荷载作用下的广义热传导的数值解.Babaei等[7]利用Laplace变换,得到功能梯度空心球壳的广义热传导响应.此外, 分离变量法[8-11]在球体表面受热冲击作用的传热分析中广为应用.Tariq等[12]首先采用差分法求解温度场, 然后将其作为已知项, 利用差分法, 开展各向异性圆柱在外表面受广义热传导下的力电耦合分析.赵伟涛等[13]基于G-L理论,采用Laplace正反变换及热冲击瞬时特征,研究实心球体外表面突然受到均匀热冲击的问题.Shi等[14]基于L-S理论,利用Laplace数值反变换,研究空心球体外表面受各种不同热冲击荷载作用的问题.考虑热传导方程的非线性, Kiani等[15]结合广义微分求积法和纽马克时域搜索法, 分析基于L-S理论的弹性球壳.随着压电材料的广泛应用, 压电材料的广义热弹性问题受到了普遍重视, 但鉴于分析的复杂性, 绝大多数研究局限于一维问题.Chandrasekharaiah[16]推导出压电材料的本构方程, 得到L-S型的热传导方程, 但没有给出具体算例.Aouadi[17]考虑材料参数随温度变化的情况,采用状态空间法,分析一维压电杆一端受热冲击的情况.Babaei等[18]采用混合有限元方法,分析外表面受热冲击的无限长压电圆柱壳.田晓耕等[19-20]采用直接有限元方法,求解广义压电热弹性问题.
对于广义热弹性问题, 通常采用的求解方法为积分变换、差分法及有限元方法.积分变换方法可以将时间域的偏微分方程组变换为频域的偏微分或常微分方程组再进行求解, 然后将频域解进行相应积分反变换, 获得时域响应.求解过程明确, 方法简单, 但是存在若干局限性, 比如采用数值反变换容易引入离散误差和截断误差, 导致热的波动性不明显, 影响了本质特性的展示.Tian等[21]建立广义热弹性过程的有限元控制方程, 避免了数值积分反变换造成的误差, 直接在时间域求解, 相对积分变换方法, 可以获得更多的求解信息.有限差分方法主要是根据实际问题寻找合适的差分方法, 将问题离散化后求解, 其中差分格式决定了解的精度, 且必须满足收敛性和稳定性要求.总之, 尽管人们已对广义热弹性问题发展出很多有效的分析模型和计算方法, 但随着新结构和新材料技术的不断发展以及各类广义热弹性理论的涌现, 寻求计算效率高且编程相对简单的方法一直是力学工作者努力的方向.虽然积分变换法存在局限性, 但通过合理的参数选择, 往往可以得到满足精度要求的数值结果.将源于控制论的状态空间法结合积分变换法用于求解广义热弹性问题, 不失为一个好的选择.事实上, 本文所建立的方法推导过程清晰, 列式统一, 容易推广应用于叠层及功能梯度球壳;其他结构如板、圆柱壳可以采用几乎相同的步骤,建立计算模型进行求解.
本文针对压电球壳的球对称热冲击问题, 基于L-S广义热弹性理论, 采用Laplace变换后, 通过对基本方程的重新整理,建立变换域的6阶变系数齐次状态方程;采用层合近似法, 将变系数系统矩阵转化为常系数矩阵, 建立传递关系, 引入边界条件求得频域响应;开展数值反变换,获得时域结果.数值算例重点考察热冲击作用下压电球壳的温度、应力、位移和电场等随时间的变化以及热弛豫时间对这些物理量演化规律的影响.
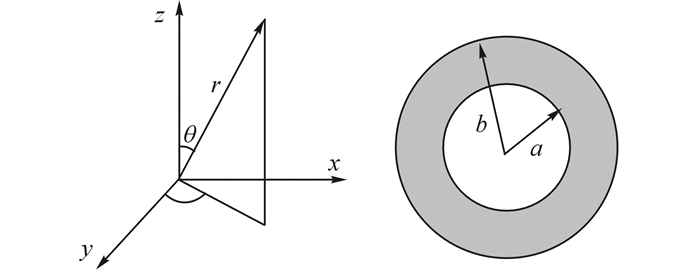
1 状态方程的建立考虑内半径为a、外半径为b的径向极化的压电空心球壳受球对称热冲击作用, 如图 1所示,此时不存在极向和环向位移, 本构方程[22-23]可以写为
|
图 1 球坐标及球壳示意图 Fig. 1 Spherical coordinates and geometry of sphericalshell |
| $ \left. {\begin{array}{*{20}{l}} {{\mathit{\Sigma }_{\theta \theta }} = \left( {{c_{11}} + {c_{12}}} \right)u + {c_{13}}r\frac{{\partial u}}{{\partial r}} + {e_{31}}r\frac{{\partial \mathit{\Phi }}}{{\partial r}} - r{\beta _1}\mathit{\Pi }, }\\ {{\mathit{\Sigma }_{\phi \phi }} = \left( {{c_{11}} + {c_{12}}} \right)u + {c_{13}}r\frac{{\partial u}}{{\partial r}} + {e_{31}}r\frac{{\partial \mathit{\Phi }}}{{\partial r}} - r{\beta _1}\mathit{\Pi }, }\\ {{\mathit{\Sigma }_{rr}} = 2{c_{13}}u + {c_{33}}r\frac{{\partial u}}{{\partial r}} + {e_{33}}r\frac{{\partial \mathit{\Phi }}}{{\partial r}} - r{\beta _3}\mathit{\Pi }, }\\ {{\mathit{\Delta }_\theta } = {\mathit{\Delta }_\phi } = r{D_\theta } = r{D_\phi } = 0, }\\ {{\mathit{\Delta }_r} = 2{e_{31}}u + {e_{33}}r\frac{{\partial u}}{{\partial r}} - {\varepsilon _{33}}r\frac{{\partial \mathit{\Phi }}}{{\partial r}} + r{g_3}\mathit{\Pi }.} \end{array}} \right\} $ | (1) |
式中:Π为温度变化值;Σij=rσij为求解方便所引入的自定义应力分量, r为径向坐标值, σij为应力分量;Δi=rDi, 其中Di为电位移分量;Φ为电势;cij、εij、eij、g3分别为弹性、介电、压电及热释电常数;βi为热模量.
考虑惯性力的影响, 球对称问题运动方程可以写为
| $ {\nabla _2}{\mathit{\Sigma }_{rr}} + {\mathit{\Sigma }_{rr}} - {\mathit{\Sigma }_{\theta \theta }} - {\mathit{\Sigma }_{\phi \phi }} = \rho {r^2}\frac{{{\partial ^2}u}}{{\partial {t^2}}}. $ | (2) |
式中:∇2=r∂/∂r.球对称静电平衡方程可以写为
| $ \frac{1}{{{r^2}}}\frac{\partial }{{\partial r}}\left( {{r^2}{D_r}} \right) = \frac{1}{{{r^2}}}\frac{\partial }{{\partial r}}\left( {r{\Delta _r}} \right) = 0. $ | (3) |
考虑耦合效应的压电球壳L-S型方程[16]为
| $ \begin{array}{l} {\nabla _2}{\mathit{\Theta }_r} + {\mathit{\Theta }_r} + \frac{\partial }{{\partial t}}\\ \left[ {\rho {c_{\rm{v}}}\mathit{\Pi } + {\theta _0}\left( {{\beta _3}\frac{{\partial u}}{{\partial r}} + 2{\beta _1}\frac{u}{r}} \right) - {\theta _0}{g_3}\frac{{\partial \mathit{\Phi }}}{{\partial r}}} \right] = 0. \end{array} $ | (4) |
式中:Θr=rqr, qr为径向热流密度, cv为常应变下的比热容, θ0为环境摄氏温度.
由非Fourier定理可知:
| $ {k_{33}}{\nabla _2}\mathit{\Pi } = - \left( {{\mathit{\Theta }_r} + \tau {{\mathit{\dot \Theta }}_r}} \right). $ | (5) |
式中:k33为径向热传导系数, τ为热松弛时间.
考虑球壳内外表面应力自由, 且内、外表面电势为零, 内表面绝热, 外表面受突加温升作用, 即
| $ \left. {\begin{array}{*{20}{l}} {{\mathit{\Sigma }_{rr}}\left( {r, t} \right){|_{r = a}} = {\mathit{\Sigma }_{rr}}\left( {r, t} \right){|_{r = b}} = 0, }\\ {{k_{33}}\frac{{\partial \theta \left( {r, t} \right)}}{{\partial r}}{|_{r = a}} = 0, }\\ {\mathit{\Pi }\left( {r, t} \right){|_{r = b}} = {\mathit{\Pi }_0}H\left( t \right), }\\ {\mathit{\Phi }\left( {r, t} \right){|_{r = a}} = \mathit{\Phi }\left( {r, t} \right){|_{r = b}} = 0.} \end{array}} \right\} $ | (6) |
对式(1)~(5)进行一定的重新整理, 引入拉普拉斯变换:
| $ \left. {\begin{array}{*{20}{l}} {F\left( s \right) = L\left[ {f\left( t \right)} \right] = \smallint _0^\infty \exp \left( { - st} \right)f\left( t \right){\rm{d}}t;}\\ {{\mathop{\rm Re}\nolimits} \left( s \right) > 0, \;\;\;s = \sigma + {\rm{i}}\omega .} \end{array}} \right\} $ | (7) |
进一步消除对时间的导数, 从而可以得到如下6阶齐次状态方程[24]:
| $ \begin{array}{l} r\frac{{\rm{d}}}{{{\rm{d}}r}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\Sigma }_{rr}}}\\ u\\ \mathit{\Phi }\\ {{\mathit{\Delta }_r}}\\ \mathit{\Pi }\\ {{\mathit{\Theta }_r}} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {2B - 1}&{ - 2{k_1} + \rho {r^2}{s^2}}&0&{2C}&{2{k_6}r}&0\\ {\frac{{{\varepsilon _{33}}}}{A}}&{ - 2B}&0&{\frac{{{e_{33}}}}{A}}&{{k_4}r}&0\\ {\frac{{{e_{33}}}}{A}}&{ - 2C}&0&{\frac{{{c_{33}}}}{A}}&{{k_5}r}&0\\ 0&0&0&{ - 1}&0&0\\ 0&0&0&0&0&{ - \frac{{1 + \tau s}}{{{k_{33}}}}}\\ { - {\theta _0}r{k_4}s}&{ - 2{\theta _0}r{k_7}s}&0&{ - {\theta _0}r{k_5}s}&{ - \left( {\rho {c_v} + {\theta _0}{k_8}} \right){r^2}s}&{ - 1} \end{array}} \right]\\ \left[ {\begin{array}{*{20}{c}} {{\mathit{\Sigma }_{rr}}}\\ u\\ \mathit{\Phi }\\ {{\mathit{\Delta }_r}}\\ \mathit{\Pi }\\ {{\mathit{\Theta }_r}} \end{array}} \right]. \end{array} $ | (8) |
式中:
| $ \left. {\begin{array}{*{20}{l}} {A = {c_{33}}{\varepsilon _{33}} + e_{33}^2, \;\;\;B = ({c_{13}}{\varepsilon _{33}} + {e_{31}}{e_{33}})/A,\\ \;\;C = ({c_{13}}{e_{33}} - {c_{33}}{e_{31}})/A, }\\ {{k_1} = 2({c_{13}}B + {e_{31}}C) - \left( {{c_{11}} + {c_{12}}} \right),\\ {k_2} = {k_1}/2 - {c_{66}}, {k_3} = {\varepsilon _{11}} + e_{15}^2/{c_{44}}, }\\ {{k_4} = ({\varepsilon _{33}}{\beta _3} - {g_{33}}{e_{33}})/A, \;{k_5} = ({e_{33}}{\beta _3} + {c_{33}}{g_{33}})/A, \\\;{k_6} = {e_{31}}{k_5} + {c_{13}}{k_4} - {\beta _1}, }\\ {{k_7} = {\beta _1} - {\beta _3}B - 2{g_{33}}{k_4}, \;{k_8} = {\beta _3}{k_4} - {g_{33}}{k_5}.} \end{array}} \right\} $ | (9) |
频域方程式(8)可以由时域状态方程经Laplace变化而导出, 即Laplace变换和方程重组的次序可以颠倒过来, 但结果是一致的.
2 状态方程的求解为了后续计算方便, 进行如下无量纲化处理:
| $ \left. \begin{array}{l} c = \sqrt {\frac{{{c_{33}}}}{\rho }} , \eta = \frac{{\rho {c_{\rm{v}}}}}{{{k_{33}}}}, {r^*} = c\eta r, {u_r}^* = c\eta {u_r}, {t^*} = {c^2}\eta t, {\tau ^*} = {c^2}\eta \tau , {\mathit{\Pi }^*} = \frac{{{\beta _3}\mathit{\Pi }}}{{{c_{33}}{\theta _0}}}, \\ {\mathit{\Phi }^*} = c\eta \frac{{{\varepsilon _{33}}}}{{{e_{33}}}}\mathit{\Phi }, {\mathit{\Sigma }_{rr}}^* = \frac{{c\eta }}{{{c_{33}}}}{\mathit{\Sigma }_{rr}}, {\mathit{\Delta }_r}^* = \frac{{c\eta }}{{{e_{33}}}}{\mathit{\Delta }_r}, {\mathit{\Theta }_r}^* = \frac{{{\beta _3}}}{{{c_{33}}{k_{33}}{T_0}}}{\mathit{\Theta }_r}. \end{array} \right\} $ | (10) |
式中:c为弹性纵波波速;η为热黏度系数,η=ρcv/k33.为了简便起见, 省略后续公式右上标符号“*”.将式(10)代入式(8), 可得
| $ \frac{{\rm{d}}}{{{\rm{d}}r}}\mathit{\boldsymbol{V}} = \mathit{\boldsymbol{MV}}. $ | (11) |
式中:V=[Σrr, u, Φ, Δr, Π, Θr]T,
| $ \mathit{\boldsymbol{M}} = \frac{1}{r}\left[ {\begin{array}{*{20}{c}} {2B - 1}&{\frac{{ - 2{k_1} + \rho {r^2}{s^2}}}{{{c_{33}}}}}&0&{\frac{{2C{e_{33}}}}{{{c_{33}}}}}&{\frac{{2{k_6}{\theta _0}r}}{{{\beta _3}}}}&0\\ {\frac{{{c_{33}}{\varepsilon _{33}}}}{A}}&{ - 2B}&0&{\frac{{e_{33}^2}}{A}}&{\frac{{{k_4}{c_{33}}{\theta _0}r}}{{{\beta _3}}}}&0\\ {\frac{{{c_{33}}{\varepsilon _{33}}}}{A}}&{ - \frac{{2C{\varepsilon _{33}}}}{{{e_{33}}}}}&0&{ - \frac{{{c_{33}}{\varepsilon _{33}}}}{A}}&{\frac{{{k_5}{c_{33}}{\varepsilon _{33}}{\theta _0}r}}{{{\beta _3}{e_{33}}}}}&0\\ 0&0&0&{ - 1}&0&0\\ 0&0&0&0&0&{ - \left( {1 + \tau s} \right)}\\ { - \frac{{{k_4}{\beta _3}rs}}{{{k_{33}}\eta }}}&{ - \frac{{2{k_8}{\beta _3}rs}}{{{c_{33}}{k_{33}}\eta }}}&0&{ - \frac{{{k_5}{e_{33}}{\beta _3}rs}}{{{c_{33}}{k_{33}}\eta }}}&{ - \frac{{\left( {\rho {c_{\rm{v}}} + {\theta _0}{k_9}} \right){r^2}s}}{{{k_{33}}\eta }}}&{ - 1} \end{array}} \right]. $ |
该系统矩阵是变系数的, 可以采用近似层合模型将其转化为常系数.将球壳沿厚度方向等分为p层, 使得每层的厚度足够小, 矩阵中的r坐标变量取为子层中间厚度, 即r=a+(2i-1)(b-a)/(2p), 由矩阵理论易得式(11)的解为
| $ \left. \begin{array}{l} \mathit{\boldsymbol{V}}\left( r \right) = \exp \left[ {\left( {r - {r_{i - 1}}} \right){\mathit{\boldsymbol{M}}^{(i)}}} \right]\mathit{\boldsymbol{V}}({r_{i - 1}});\\ {r_{i - 1}} \le r \le {r_i}, i = 1, 2, \cdots , p. \end{array} \right\} $ | (12) |
相邻子层间的连续条件要求状态变量连续, 于是从式(12)出发递推可得
| $ \mathit{\boldsymbol{V}}\left( b \right) = \mathit{\boldsymbol{TV}}\left( a \right). $ | (13) |
式中:
| $ \mathit{\boldsymbol{T}} = \prod\limits_{i = 1}^p {\exp \left[ {\frac{{\left( {b - a} \right)}}{p}{\mathit{\boldsymbol{M}}^{(i)}}} \right], } $ |
为6阶方阵.引入式(6), 球壳外表面温升函数经拉普拉斯变换后变为
| $ \mathit{\Pi }{\mathit{|}_{r = b}} = {\mathit{\Pi }_0}/s. $ | (14) |
将式(14)代入式(13), 可得
| $ \begin{array}{l} {\left[ {0, {u_r}\left( b \right), 0, {\mathit{\Delta }_r}\left( b \right), {\mathit{\Pi }_0}/s, {\mathit{\Theta }_r}\left( b \right)} \right]^{\rm{T}}} = \\ \;\;\;\;\mathit{\boldsymbol{T}}{\left[ {0, {u_r}\left( a \right), 0, {\mathit{\Delta }_r}\left( a \right), \mathit{\Pi }\left( a \right), 0} \right]^{\rm{T}}}. \end{array} $ | (15) |
进一步处理后,可得
| $ \left[ {\begin{array}{*{20}{c}} {{T_{12}}}&{{T_{14}}}&{{T_{15}}}\\ {{T_{32}}}&{{T_{34}}}&{{T_{35}}}\\ {{T_{52}}}&{{T_{54}}}&{{T_{55}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {u\left( a \right)}\\ {{\mathit{\Delta }_r}\left( a \right)}\\ {\mathit{\Pi }\left( a \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {{\mathit{\Pi }_0}/s} \end{array}} \right]. $ | (16) |
式中:Tij为矩阵T的元素.由此可以求得球壳内表面的状态量, 利用式(13)可以求得沿径向任意位置的状态量.非零导出变量为
| $ {\mathit{\Sigma }_{\theta \theta }} = {\mathit{\Sigma }_{\phi \phi }} = \left( {{c_{11}} + {c_{12}}} \right){u_r} + {c_{13}}\nabla {u_r} + {e_{31}}\nabla \mathit{\Phi } - r{\beta _1}\mathit{\Pi }\mathit{.} $ | (17) |
当压电球壳的电学边界条件为开路(电位移为零)时, 球壳内部所有电位移为零, 式(11)退化为4阶状态方程.此时, 状态量选取与纯弹性问题一样, 球壳内、外表面电势差求解可以作为导出量得到.
根据电势为零的边界条件所建立的状态方程式(11),可以退化到各向同性弹性球壳外表面受热冲击的情况, 令
| $ {c_{12}} = {c_{13}} = \lambda , \;\;\;{c_{11}} = {c_{33}} = \lambda + 2\mu , \;\;\;{\beta _1} = {\beta _3} = \beta . $ | (18) |
同时移去电势及电位移量, 从而得到如下4阶齐次状态方程:
| $ \frac{{\rm{d}}}{{{\rm{d}}r}}\mathit{\boldsymbol{V}} = \mathit{\boldsymbol{MV}}. $ | (19) |
式中:
| $ \begin{array}{l} \mathit{\boldsymbol{V}} = {[{\mathit{\Sigma }_{rr}}, u, \mathit{\Pi }, {\mathit{\Theta }_r}]^{\rm{T}}}, \mathit{\boldsymbol{M}} = \frac{1}{r}\\ \left[ {\begin{array}{*{20}{c}} {\frac{{\lambda - 2\mu }}{{\lambda + 2\mu }}}&{\frac{{4\mu \left( {3\lambda + 2\mu } \right)}}{{\lambda + 2\mu }} + \rho {r^2}{s^2}}&{ - \frac{{4\mu \beta {T_0}r}}{{\lambda + 2\mu }}}&0\\ {\frac{1}{{\lambda + 2\mu }}}&{ - \frac{{2\lambda }}{{\lambda + 2\mu }}}&{\frac{{\beta {T_0}r}}{{\lambda + 2\mu }}}&0\\ 0&0&0&{ - \frac{{1 + \tau s}}{{{k_{33}}}}}\\ { - \frac{{\beta rs}}{{\left( {\lambda + 2\mu } \right){k_{33}}\eta }}}&{ - \frac{{4\mu {\beta ^2}rs}}{{\left( {\lambda + 2\mu } \right){k_{33}}\eta }}}&{ - \left( {\rho {c_{\rm{v}}} + \frac{{{\beta ^2}{T_0}}}{{\lambda + 2\mu }}} \right)\frac{{{r^2}s}}{{{k_{33}}\eta }}}&{ - 1} \end{array}} \right]. \end{array} $ |
对于绝大多数情形, 无法采用解析公式直接将频域解转换为时域解, 必须采用数值方法进行Laplace反变换.Durbin等[25-29]对不同的数值方法进行比较和分析, 得出适用的范围.本文采用Durbin[25]提出的Fourier级数法:
| $ \begin{array}{l} f\left( t \right) = \frac{{\exp \left( {\alpha t} \right)}}{T}\\ \left\{ { - \frac{1}{2}{\mathop{\rm Re}\nolimits} \left( {\bar f\left( \alpha \right)} \right) + \sum\limits_{k = 0}^{{\rm{NUSM}}}} \right.\\ \left. {\left[ {{\mathop{\rm Re}\nolimits} \left[ {\bar f\left( {\alpha + {\rm{i}}\frac{{k{\rm{ \mathsf{ π} }}}}{T}} \right)} \right]\cos \left( {\frac{{k{\rm{ \mathsf{ π} }}}}{T}t} \right) - {\mathop{\rm Im}\nolimits} \left[ {\bar f\left( {\alpha + {\rm{i}}\frac{{k{\rm{ \mathsf{ π} }}}}{T}} \right)} \right]\sin \left( {\frac{{k{\rm{ \mathsf{ π} }}}}{T}t} \right)} \right]} \right\}. \end{array} $ | (20) |
式中:T为反变换的周期,α为衰减系数.合理的参数取值为5≤αT≤10, 50≤NUSM≤5 000.计算时, 首先可以根据控制误差确定α, 然后根据最大变换时长确定T, 同时确保两者乘积位于上述数值区间.为了减少截断误差, NUSM一般要取500以上.
3 算例分析为了验证本文理论推导和程序编制的正确性, 首先与文献[14]中各向同性弹性球壳受热冲击作用计算结果进行对比.球壳参数为:内半径a=0.01 m, 外半径b=0.1 m, λ=49.6 GPa, μ=25.56 GPa, β=4.938×106 Ν/(m2·K), ρ=2 700 k/m3, τ=0.026 ×10-12 s, k33=121 W·m/K, Π0=400 ℃, θ0=20 ℃.对应式(6)所采用的边界条件为
| $ \left. \begin{array}{l} {\sigma _{rr}}\left( {r, t} \right){|_{r = a}} = {\sigma _{rr}}\left( {r, t} \right){|_{r = b}} = 0, \\ r\frac{{\partial \mathit{\Pi }\left( {r, t} \right)}}{{\partial r}}{|_{r = a}} = 0, \mathit{\Pi }\left( {r, t} \right){|_{r = b}} = {\mathit{\Pi }_0}H\left( t \right). \end{array} \right\} $ | (21) |
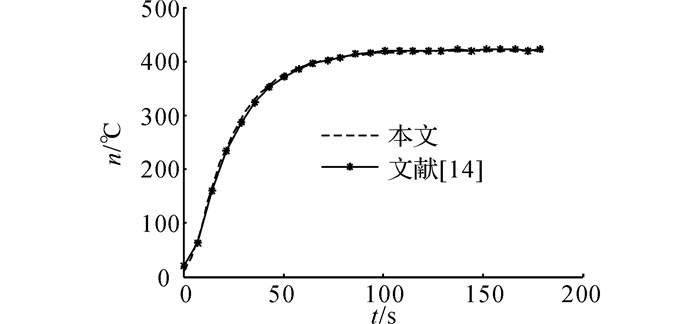
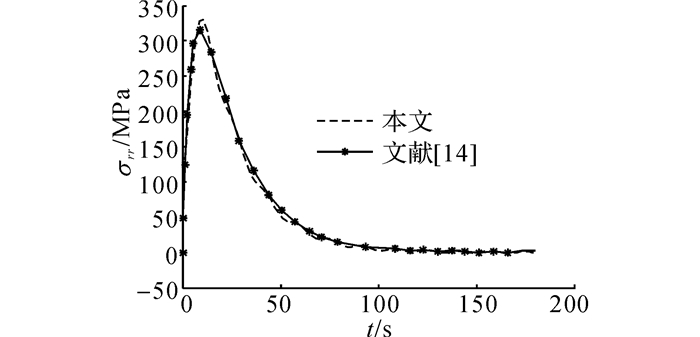
采用层合近似法将球壳沿径向细分90等分和文献[14]方法得到的球壳内部一点处温度与径向应力随时间变化的结果吻合得非常好(见图 2、3), 表明本文理论推导和数值计算的正确性.图 3中,t'为无量纲时间.
|
图 2 球壳内r=0.05 m处温度随时间的变化 Fig. 2 Variation of temperature change with time(r=0.05 m) |
|
图 3 球壳内r=0.05 m处径向应力随时间的变化 Fig. 3 Variation of radial stress with time (r=0.05 m) |
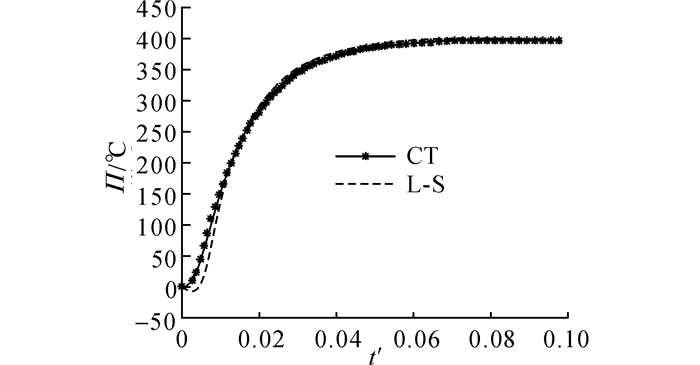
下面考虑无量纲内径为0.8、外径为1.0的压电空心球壳, 内表面绝热, 外表面施加温度荷载Π0Η(t), 温差Π0=400 ℃, θ0=20 ℃, 内、外表面电势为零, 计算采用硒化镉, 材料参数见表 1.首先取无量纲热弛豫时间τ=0.001.图 4~8给出球壳内沿着厚度方向各状态变量随时间的变化.从图 4可以看出, L-S理论考虑了热弛豫效应之后, 内表面温度的升高过程相比经典耦合热弹性理论表现出一定的滞后性, 温度升高之前的小幅波动主要由计算过程中的虚假数值振荡所致[30].
| 表 1 硒化镉材料参数表 Table 1 Material parameters of Cadmium selenide |
|
图 4 球壳内表面温度随时间的变化(τ=0.001) Fig. 4 Variation of temperature change with time at the inner surface (τ=0.001) |
|
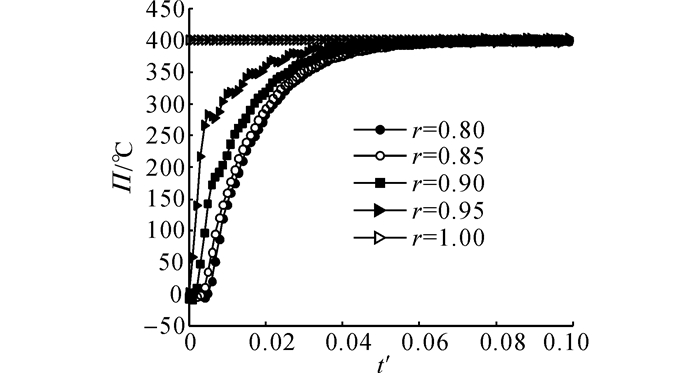
图 5 球壳内不同位置处温度随时间的变化(τ=0.001) Fig. 5 Variations of temperature change with time along at different locations (τ=0.001) |
|
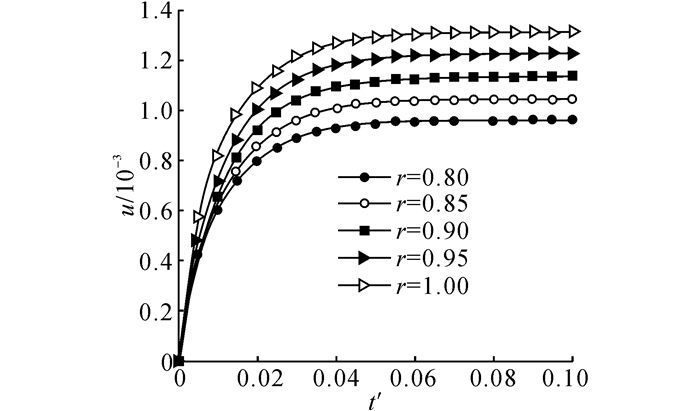
图 6 球壳内不同位置处无量纲径向位移随时间的变化(τ=0.001) Fig. 6 Variations of nondimensional radial displacement with time at different locations (τ=0.001) |
|
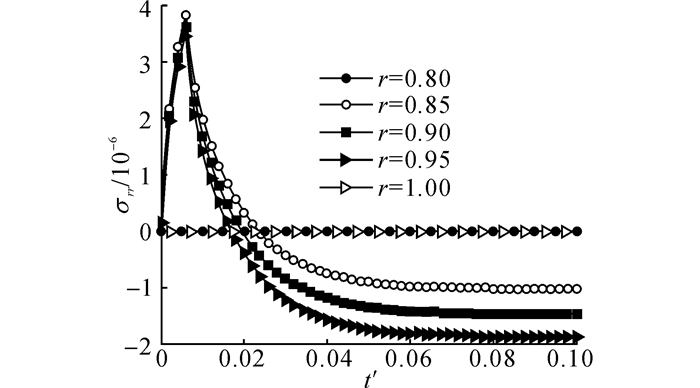
图 7 球壳内不同位置处无量纲径向应力随时间的变化(τ=0.001) Fig. 7 Variations of nondimensional radial stress with time at different locations (τ=0.001) |
|
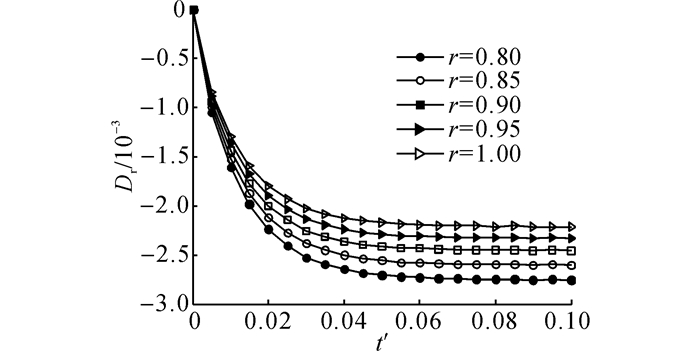
图 8 球壳内不同位置处无量纲径向电位移随时间的变化(τ=0.001) Fig. 8 Variations of nondimensional radial electric displacement with time at different locations (τ=0.001) |
图 5给出球体不同位置处温度随时间的变化, 温度从外表面到内表面逐渐升高, 最后趋于稳定.图 6表明整个压电空心球壳从外表面至内表面不断向外膨胀, 反映了热弹性波的传播.图 7表明球壳内部存在急速的拉、压应力转换, 最终趋于压应力.可以发现, 在t'=0.006时达到峰值拉应力, 此时热波以无量纲速度
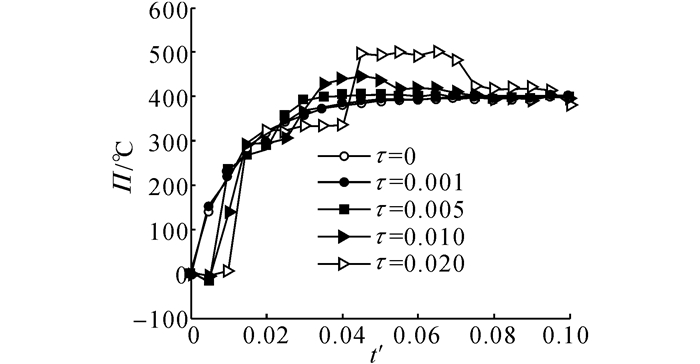
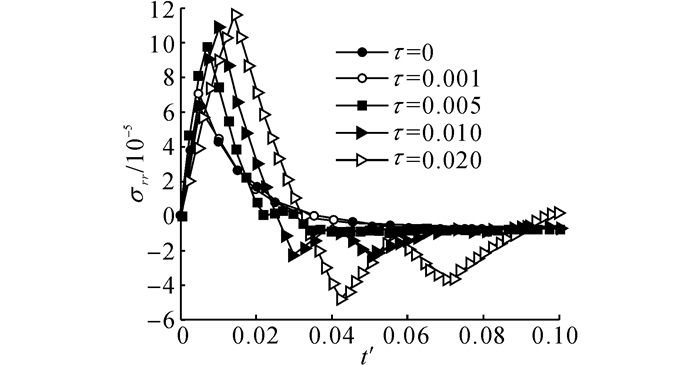
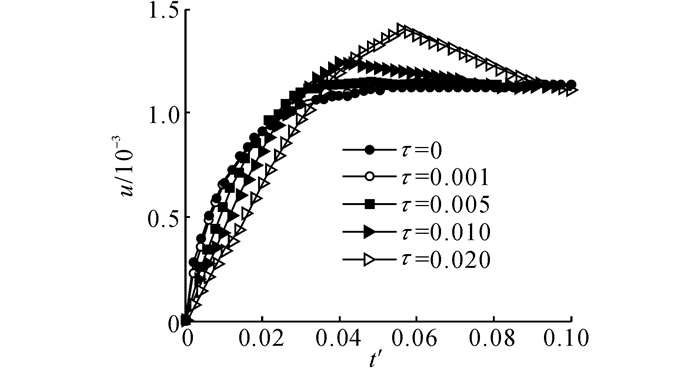
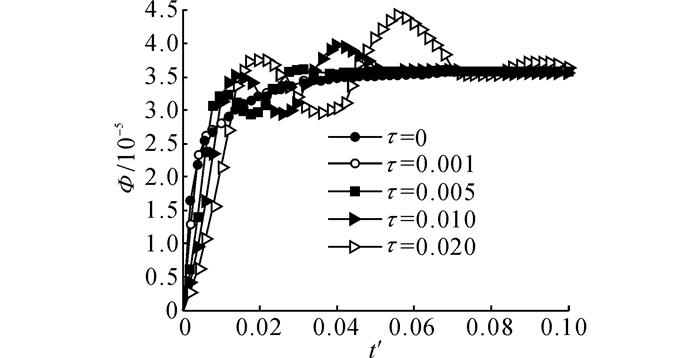
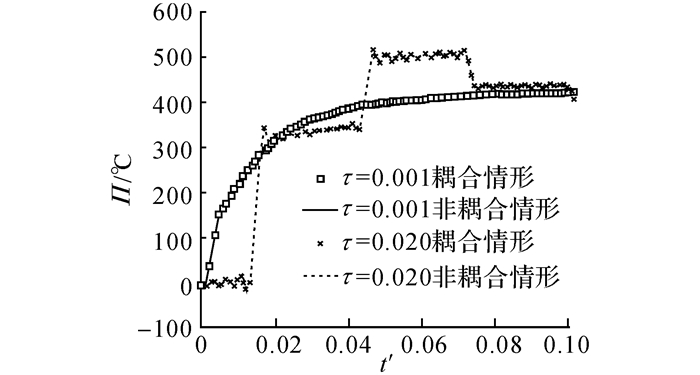
分别取τ=0.001、0.005、0.01、0.02, 对球壳中部的各物理量进行计算.从图 9~12可以看出, 随着热弛豫时间的增大, 各物理量传播速度下降, 但峰值增加, 最后趋向于稳定, 这是由于随着时间的推移, 热波波前的阶跃变小所造成的.峰值增加这个现象应归于热滞后所产生的效果:随着τ的增大, 热扰动速度迅速减小, 此时热流与温度分布之间的延迟效果越来越明显, 这将导致球体内的温度分布呈现阶跃性分布, 从而形成幅值很大的温度梯度, 受其影响球体内各点在周围热膨胀作用下相互挤压, 进而形成较大的物理量峰值.图 13分别对比广义热传导方程中τ取0.001和0.02时考虑耦合和非耦合的情况.可以看出,热传导方程中的耦合项对温度传播的影响较小, 在求解温度分布时可以忽略;当热弛豫时间较大时, 球壳内部的温度升高可以超过边界上施加的温度.这种现象在经典Fourier热传导中不会出现, 只有在超急速传热情形下, 当热传导时间与材料的热弛豫时间相当时, 材料的局部热平衡结构已不能维持, 从而出现局部温度超过热平衡温度的现象[31], 这时的温度场特性不能用一般的热力学观点来解释.热量的传递应作为一种波来考虑, 此时球体内的温度场分布不再连续, 在热波波前尚未到达的区域内, 温度保持初始温度不变;当内表面反射的热波与外表面入射的热波交汇后, 导致球体内部温度会超过边界处设定的温度.这种急速传热情形下温度传播的特有现象在工程实际中具有重要意义.图 13表明, 当τ较小时, 波动现象不明显, 与经典Fourier热传导一致;当τ越来越大时, 表现出明显的波动特征(如波前间断点).
|
图 9 对应不同τ的球壳中间厚度处温度随时间的变化(r=0.90) Fig. 9 Variations of temperature change at middle point with time for different thermal relaxation times (r=0.90) |
|
图 10 对应不同τ的球壳中间厚度处无量纲径向应力随时间的变化(r=0.90) Fig. 10 Variations of nondimensional radial stress at middle point with time for different thermal relaxation times (r=0.90) |
|
图 11 对应不同τ的球壳中间厚度处无量纲径向位移随时间的变化(r=0.90) Fig. 11 Variations of nondimensional radial displacement at middle point with time for different thermal relaxation times (r=0.90) |
|
图 12 对应不同τ的球壳中间厚度处无量纲电势值随时间的变化(r=0.90) Fig. 12 Variations of nondimensional electric potential at middle point with time for different thermal relaxation times (r=0.90) |
|
图 13 对应不同τ的球壳中间厚度处温度随时间的变化:耦合与非耦合情形(r=0.90) Fig. 13 Variations of temperature change at middle point with time: coupling and uncouplingcases (r=0.90) |
(1) 分析压电球壳中间厚度处各状态量的数值发现,随着τ的增大, 各状态变量的峰值增加.
(2) 在广义热传导方程中,耦合项对于本文算例中的温度影响不大, 可以忽略.
(3) 本文方法可以避免较复杂的有限元编程计算, 可以推广应用于叠层或功能梯度压电球壳表面受任意类型热冲击荷载作用的响应分析.
| [1] |
CATTANEO C. Sulla conduzionedelcalore[J]. Attisem Mat Fis Univ Modena, 1948, 3: 83-101. |
| [2] |
VERNOTTE P. Les paradoxes de la theorie continue de I'equation de la chaleur[J]. Compute Rendus, 1958, 246(22): 3154-3155. |
| [3] |
LORD H W, SHULMAN Y. A generalized dynamical theory of thermoelasticity[J]. Journal of the Mechanics and Physics of Solids, 1967, 15(5): 299-309. DOI:10.1016/0022-5096(67)90024-5 |
| [4] |
GREEN A E, LINDSAY K A. Thermoelasticity[J]. Journal of Elasticity, 1972, 2(1): 1-7. DOI:10.1007/BF00045689 |
| [5] |
GREEN A E, NAGHDI P M. Thermoelasticity without energy dissipation[J]. Journal of Elasticity, 1993, 31(3): 189-208. DOI:10.1007/BF00044969 |
| [6] |
JIANG F M, SOUSA A C M. Analytical solution for hyperbolic heat conduction in a hollow sphere[J]. Journal of Thermophysics and Heat Transfer, 2005, 19(4): 595-598. DOI:10.2514/1.13472 |
| [7] |
BABAEI B H, CHEN Z T. Hyperbolic heat conduction in a functionally graded hollow sphere[J]. International Journal of Thermophysics, 2008, 29(4): 1457-1469. DOI:10.1007/s10765-008-0502-1 |
| [8] |
赵伟涛, 吴九汇. 球体表面受任意周期热扰动时非傅里叶导热的求解与分析[J]. 西安交通大学学报, 2014, 4(1): 13-18. ZHAO Wei-tao, WU Jiu-hui. Solution and analysis of non-Fourier heat conduction in a solid sphere under arbitrary periodic surface thermal disturbance[J]. Journal of Xi'an Jiaotong University, 2014, 4(1): 13-18. DOI:10.7652/xjtuxb201401003 |
| [9] |
ZHAO W T, WU J H, CHEN Z. Analysis of non-Fourier heat conduction in a solid sphere under arbitrary surface temperature change[J]. Archive of Applied Mechanics, 2014, 84(4): z505-518. DOI:10.1007/s00419-013-0814-x |
| [10] |
SHIRMOHAMMADI R. Temperature transients in spherical medium irradiated by laser pulse[J]. International Communications in Heat and Mass Transfer, 2008, 35(8): 1017-1023. DOI:10.1016/j.icheatmasstransfer.2008.04.015 |
| [11] |
TSAI C S, HUNG C I. Thermal wave propagation in a bi-layered composite sphere due to a sudden temperature change on the outer surface[J]. International Journal of Heat and Mass Transfer, 2003, 46(26): 5137-5144. DOI:10.1016/S0017-9310(03)00369-7 |
| [12] |
TARIQ T D, MALAK N, MOH'D AIN. Transient thermal stresses in an orthotropic cylinder under the hyperbolic heat conduction model[J]. Heat Transfer Engineering, 2008, 29(7): 632-642. DOI:10.1080/01457630801922501 |
| [13] |
赵伟涛, 吴九汇, 白宇, 等. 受热冲击时球体的广义热弹性分析[J]. 西安交通大学学报, 2013, 47(7): 108-113. ZHAO Wei-tao, WU Jiu-hui, BAI Yu, et al. Generalized thermoelastic analysis for sphere under thermal shock[J]. Journal of Xi'an Jiaotong University, 2013, 47(7): 108-113. DOI:10.7652/xjtuxb201307020 |
| [14] |
SHI X Y, SHANG X C. Transient response of thermoelastic hollow sphere under thermal shocks[J]. Journal of Thermal Stresses, 2014, 37: 707-726. DOI:10.1080/01495739.2014.885334 |
| [15] |
KIANI Y, ESLAMI M R. The GDQ approach to thermally nonlinear generalized thermoelasticity of a hollow sphere[J]. International Journal of Mechanical Sciences, 2016, 118: 195-204. DOI:10.1016/j.ijmecsci.2016.09.019 |
| [16] |
CHANDRASEKHARAIAH D S. A general linear thermoelasticity theory for piezoelectric media[J]. ActaMechanica, 1988, 71(1-4): 39-49. |
| [17] |
AOUADI M. Generalized thermo-piezoelectric problems with temperature dependent properties[J]. International Journal of Solids and Structures, 2006, 43: 6347-6358. DOI:10.1016/j.ijsolstr.2005.09.003 |
| [18] |
BABAEI M H, CHEN Z T. The transient coupled thermo-piezoelectric response of a functionally graded piezoelectric hollow cylinder to dynamic loadings[C]//Proceedings of the Royal Society A. London: [s. n. ], 2009: 1-15. http://www.jstor.org/stable/25661483
|
| [19] |
田晓耕, 张婕, 沈亚鹏. 不同理论下广义压电热弹性问题的有限元求解[J]. 力学学报, 2006, 38(4): 553-558. TIAN Xiao-geng, ZHANG Jie, SHEN Ya-peng. Sloving generalized piezothermoelastic problem by FEM with different theories[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(4): 553-558. |
| [20] |
田晓耕, 沈亚鹏. 广义热弹性问题研究进展[J]. 力学进展, 2012, 42(1): 18-28. TIAN Xiao-geng, SHEN Ya-peng. Research progress in generalized thermoelasticproblems[J]. Advances in Mechanics, 2012, 42(1): 18-28. DOI:10.6052/1000-0992-2012-1-lxjzJ2011-115 |
| [21] |
TIAN X G, ZHANG J, SHEN Y P, et al. Finite element method for generalized piezothermoelastic problems[J]. International Journal of Solids and Structures, 2007, 44: 6330-6339. DOI:10.1016/j.ijsolstr.2007.02.035 |
| [22] |
CHEN W Q, SHIOYA T. Piezothermoelastic behavior of a pyroelectric spherical shell[J]. Journal of Thermal Stresses, 2001, 24(2): 105-120. DOI:10.1080/01495730150500424 |
| [23] |
DING H J, CHEN W Q. Three dimensional problems of piezoelasticity[M]. New York: Nova Science Publishers, 2001.
|
| [24] |
刘承斌. 压电球壳的若干多场耦合问题研究[D]. 杭州: 浙江大学, 2016. LIU Cheng-bin. Multifield coupling analysis of piezoelectric spherical shell[D]. Hangzhou: Zhejiang University, 2016. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y3111703 |
| [25] |
DURBIN F. Numerical inversion of Laplace transformation:an efficient improvement to Durbin and Abate's method[J]. Computer Journal, 1974, 17(4): 371-376. DOI:10.1093/comjnl/17.4.371 |
| [26] |
HONG G, HIRDES U. A method for the numerical inversion of Laplace transform[J]. Journal of Computational and Applied Mathematics, 1984, 10(1): 113-132. DOI:10.1016/0377-0427(84)90075-X |
| [27] |
DAVIES B, MARTIN B. Numerical inversion of the Laplace transform:a survey and comparison of methods[J]. Journal of Computational Physics, 1979, 33(1): 1-32. DOI:10.1016/0021-9991(79)90025-1 |
| [28] |
CRUMP K S. Numerical inversion of Laplace transforms using a Fourier series approximation[J]. Journal of the Association for Computing Machinery, 1976, 23(1): 89-96. DOI:10.1145/321921.321931 |
| [29] |
韩光松, 余志勇. Laplace变换数值反演的参数选择[J]. 兰州大学学报:自然科学版, 2009, 45(增1): 116-119. HAN Guang-song, YU Zhi-yong. Parameters determination in numerical inversion of Laplace transforms[J]. Journal of Lanzhou University:Natural Science, 2009, 45(supple.1): 116-119. |
| [30] |
郭攀, 吴文华, 吴志刚. 非傅里叶热弹性的时域间断迦辽金有限元方法[J]. 力学学报, 2013, 45(3): 447-450. GUO Pan, WU Wen-hua, WU Zhi-gang. Time discontinuous Galerkin finite element method for generalized thermo-elastic wave of non-Fourier effects[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(3): 447-450. DOI:10.6052/0459-1879-12-217 |
| [31] |
张浙, 刘登瀛. 超急速传热时球体内非稳态热传导的非傅里叶效应[J]. 工程热物理学报, 1998, 19(5): 601-605. ZHANG Zhe, LIU Deng-ying. Non-Fourier effects in rapid transient heat conduction in a spherical medium[J]. Journal of Engineering Thermo-physics, 1998, 19(5): 601-605. |



