20世纪90年代, De Doncker等^[1]提出双有源桥式(dual active bridge, DAB)DC-DC变换器拓扑^[1].该拓扑具有电气隔离、双向功率传输等优点, 在分布式新能源发电领域中受到越来越多的关注；双有源桥式DC-DC变换器容易实现模块级联且具有功率双向流动的特点, 在固态变压器中有较多的应用；此外, 该变换器功率密度高且可零电压软开关(zero voltage switching, ZVS), 能够有效减小变换器的体积和质量, 在电动汽车、不间断电源UPS等领域应用广泛^[2-7].

双有源桥目前较多采用单移相控制方式^[8](single phase shift, SPS).该方法主要通过变压器漏感(含少量串联电感)传递能量, 但存在回流功率较大和软开关实现范围受限等问题, 进而导致开关管的电流应力和开关损耗增大, 同时使得电感、变压器等磁性元件损耗增加, 这些问题已经成为提升双有源桥变换器效率的一大瓶颈^[9-12].

为了克服单移相控制的缺点, 学者们提出在电路拓扑上的改进方法.Chung等^[13-14]提出在全桥上增加辅助电路的方法, 虽然提升了系统的功率特性, 但存在硬件电路设计复杂和新增器件增加损耗等问题.不改变原有硬件电路、只改变控制方式来优化系统性能成为当前研究的主要方向.Zhao等^[15]提出电感电流最小峰值控制策略, 降低了系统回流功率；赵彪等^[12]提出“第一类”双重移相控制(first dual phase shift, FDPS)方法.利用该控制方法可以同时调节原边H桥内移相角和原、副边H桥间的外移相角, 扩大传输功率的可调范围, 控制方式更加灵活；张勋等^[16]在文献[12]的研究基础上, 采用数学方法分析了回流功率最小时的内、外移相角选取方法, 但是因双有源桥原、副边控制方式的不对称导致最优回流功率控制的结果分段太多, 使得实际变换器的控制系统难以设计；Wu等^[17-18]提出三重移相控制(triple phase shift, TPS)方法, 该控制方法通过原边全桥内的移相角、副边全桥内的移相角和原、副边全桥之间移相角等3个变量来控制.尽管TPS性能较SPS和FDPS有一定改善, 但是由于控制量较多, 工作模态和工况种类繁多, 变量选取考虑的因素较多, 系统整体控制比较复杂；Zhao等^[19-20]基于DAB移相控制建立统一模型, 提出提高电路效率的控制策略；Hou等^[21]提出基于统一相移控制的简单电流应力控制方法, 它可以克服传统电流应力优化的缺点来获得较低的电流应力；Myoungho等^[22]提出“第二类”双重移相控制(second dual phase shift, SDPS)方法, 该控制方法采用原副边对称控制的形式, 同时调节2个移相角, 即全桥间移相角和2个全桥内的移相角, 但文献[22]只是进行了理论与模态分析, 没有通过数学公式进行定量分析计算, 缺乏实际应用的条件.

在文献[22]的研究基础上, 本文对“第二类”双重移相控制的回流功率进行定量优化分析, 并将最优回流控制下的电流应力与“第一类”双重移相控制进行比较.通过建立数学模型, 以罗列的形式呈现不同移相控制方式的功率特性, 寻得最佳的控制方式.通过实验验证该控制方式的可行性.

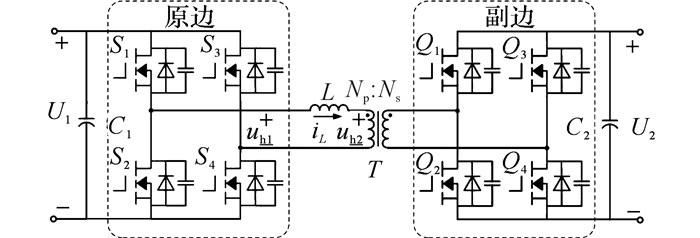
1 “第二类”双重移相控制工作原理

典型的DAB拓扑结构如图 1所示, 由2个全桥和1个高频变压器T组成.假设功率由DAB原边流向副边.其中, U₁、U₂分别为DAB输入、输出电压, C₁、C₂为输入、输出电容, u_h1为原边桥臂中点电压, u_h2为副边桥臂中点电压折合到原边后的电压, L为变压器漏感(包含少量串联电感), n=N_p/N_s是高频变压器的匝比, 设电压调节比k=U₁/(nU₂)≥1, T_hs为半开关周期.

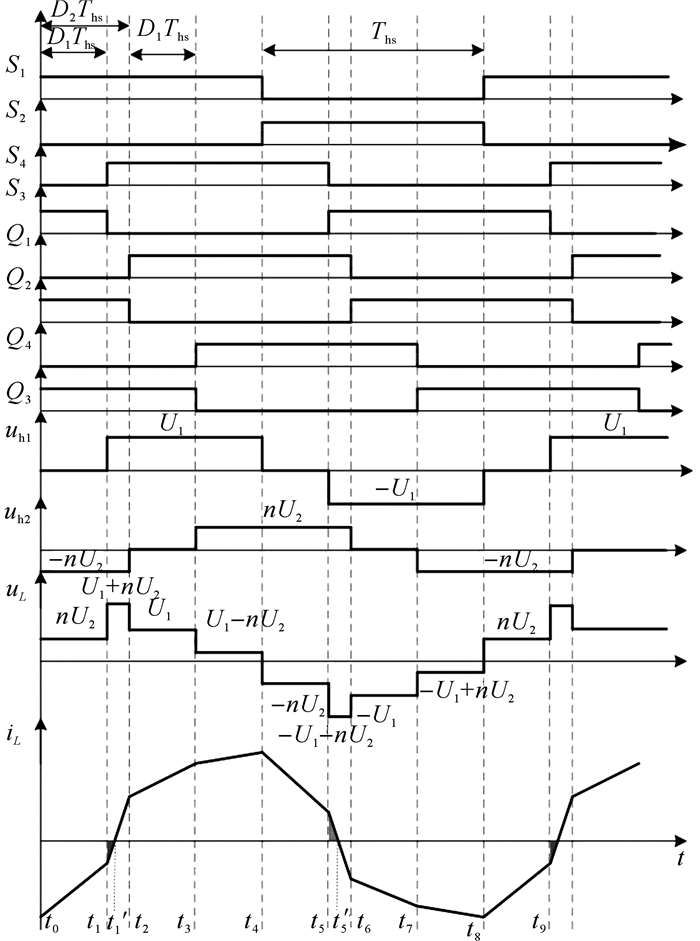
“第二类”双重移相控制(SDPS)的工作原理如下：变压器原、副边全桥的同一桥臂上、下开关管分别采用50%占空比交替导通, 采用2个移相角(自由度)来控制DAB传输功率的大小和方向.其中原边和副边全桥内部对角开关管驱动之间的移相角相等, 定义为等效内移相比D₁；原边全桥与副边全桥之间的移相角定义为等效外移相比D₂.工作原理波形如图 2所示(D₁≤D₂), 以功率从变压器原边流向副边为例.

图 2中, t₁~t₁'阶段和t₅~t₅'阶段, 桥臂中点电压u_h1与电感电流i_L方向相反, 即传输功率为负, 该阶段内电感内储存的能量回传到电源侧, 该功率定义为回流功率(即图中阴影部分).当负载功率一定时, DAB的回流功率越大, 则需要正向传输越多的功率, 即输入电流变大, 使得开关管的电流应力增大, 同时增加了导通损耗和变压器的磁损, 降低了变换器的工作效率^[12].

若D₁仅调节原边全桥内对角开关管的移相且副边全桥内不移相, 即为‘第一类’双重移相控制.工作原理如图 3所示(D₁≤D₂).

若D₁=0, 则简化为传统单移相控制, 即原、副边全桥内部均无移相, DAB功率传输的大小和方向仅仅通过D₂来调节.

2 功率与电流应力特性分析 2.1 功率的数学模型

“第二类”双重移相控制的工作原理如图 2所示, 开关频率f_s=1/(2T_hs), 考虑电感电流的对称性i_L(t₀)=-i_L(t₄), 可得主要转折点电流：

$ {i_L}({t_0}) = \frac{{n{U_2}{T_{{\rm{hs}}}}}}{{2L}}[({D_1} - 1)k + 1 - {D_1} - 2{D_2}], $

(1)

$ {i_L}({t_1}) = \frac{{n{U_2}{T_{{\rm{hs}}}}}}{{2L}}[({D_1} - 1)k + 1 + {D_1} - 2{D_2}], $

(2)

$ {i_L}({t_2}) = \frac{{n{U_2}{T_{{\rm{hs}}}}}}{{2L}}[(2{D_2} - {D_1} - 1)k + 1 - {D_1}], $

(3)

$ {i_L}({t_3}) = \frac{{n{U_2}{T_{{\rm{hs}}}}}}{{2L}}[(2{D_2} + {D_1} - 1)k + 1 - {D_1}]. $

(4)

式中:0≤D₁≤D₂≤1, k为电压调节比, 传输功率为

$ \begin{array}{l} {P_{{\rm{SDPS}}}} = \frac{1}{{{T_{{\rm{hs}}}}}}\int_0^{{T_{{\rm{hs}}}}} {{u_{h1}}{i_L}} \left( t \right){\rm{d}}t = \\ \;\;\;\;\;\;\;\;\;\frac{{n{U_1}{U_2}}}{{4{f_{\rm{s}}}L}}[ - D_1^2 + 2{D_2}(1 - {D_2})]. \end{array} $

(5)

回流功率为

$ {Q_{{\rm{SDPS}}}} = \frac{{n{U_1}{U_2}}}{{16\left( {k + 1} \right){f_{\rm{s}}}L}}{[(1 - {D_1})k + 2{D_2} - {D_1} - 1]^2}. $

(6)

“第一类”双重移相控制的驱动波形和电感电流波形如图 3所示.工作原理在1章中已有分析, 由文献[12]可得P_FDPS与回流功率Q_FDPS：

$ {P_{{\rm{FDPS}}}} = \frac{{n{U_1}{U_2}}}{{4{f_{\rm{s}}}L}}[{D_1}(2{D_2} - {D_1} - 1) + 2{D_2}(1 - {D_2})]. $

(7)

$ {Q_{{\rm{FDPS}}}} = \frac{{n{U_1}{U_2}}}{{16\left( {k + 1} \right){f_{\rm{s}}}L}}[(1 - {D_1})k + 2{D_2} - 2{D_1} - 1){]^2}. $

(8)

令D₁=0, 即为单移相控制, 则

$ {P_{{\rm{SPS}}}} = \frac{{n{U_1}{U_2}}}{{2{f_{\rm{s}}}L}}{D_2}(1 - {D_2}), $

(9)

$ {Q_{{\rm{SPS}}}} = \frac{{n{U_1}{U_2}}}{{16\left( {k + 1} \right){f_{\rm{s}}}L}}{[k + 2{D_2} - 1]^2}. $

(10)

为了简化计算, 以单移相控制最大传输功率为基准值, 各功率取其标幺值进行分析, 基准值为

$ {P_{\rm{N}}} = \frac{{n{U_1}{U_2}}}{{8{f_{\rm{s}}}L}}. $

(11)

不同移相控制下传输功率的标幺值p与回流功率的标幺值q如下：

1) SDPS：

$ \begin{array}{l} \;\;\;\;p = - 2D_1^2 + 4{D_2}(1 - {D_2}), \\ q = \frac{{{{[(1 - {D_1})k + 2{D_2} - {D_1} - 1]}^2}}}{{2\left( {k + 1} \right)}}. \end{array} $

2) FDPS：

$ \begin{array}{l} p = 2{D_1}(2{D_2} - {D_1} - 1) + 4{D_2}(1 - {D_2}), \\ \;\;q = \frac{{[(1 - {D_1})k + 2{D_2} - 2{D_1} - 1){]^2}}}{{2\left( {k + 1} \right)}}. \end{array} $

3) SPS：

$ p = 4{D_2}(1 - {D_2}), q = {\frac{{(k + 2{D_2} - 1)}}{{2\left( {k + 1} \right)}}^2}. $

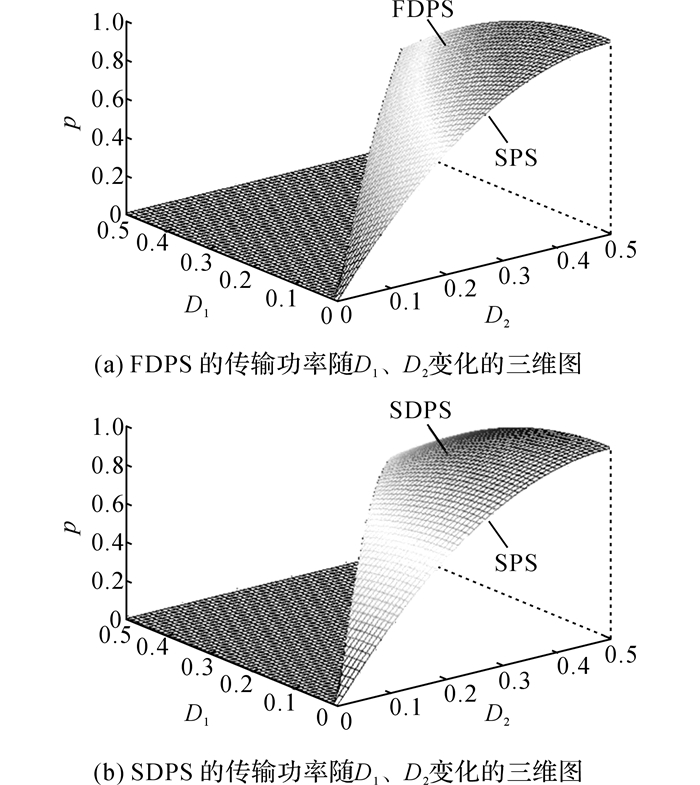
其中, 0≤D₁≤D₂≤1, k≥1.可以得到如图 4所示的SPS、FDPS、SDPS控制下的p与D₁、D₂的关系曲线图.在实际工程中, 一般要求0≤D₁≤D₂≤0.5.当D₁=0时, FDPS或SDPS为SPS控制, 即图中的曲线为SPS的p与D₂的关系图.针对任一传输功率p, FDPS和SDPS都有较多(D₁、D₂)组合满足功率要求, 只是不同(D₁、D₂)组合下回流功率不同, 变换器的电流应力也不同.从图 4中颜色冷暖色调的深浅可以看出：在相同参数D₁与D₂下, SDPS的传输功率p比FDPS更大, 即相同传输功率下, SDPS的组合(D₁、D₂)选取数比FDPS更多, 控制也更加灵活.

2.2 回流功率的优化控制算法

回流功率影响着变换器的效率.为了减小开关管电流应力、提升功率传输效率, 需要对DPS的回流功率进行优化控制.“第一类”双重移相控制在某一固定传输功率下获得最小回流功率控制的方法已在文献[16]中分析, 探讨如何选取最优的D₁、D₂来使“第二类”双重移相控制的回流功率达到最小.

设传输功率为p, 则有

$ - 2D_1^2 + 4{D_2}(1 - {D_2}) = p. $

(12)

以D₁为常量, 可得

$ {D_2} = \frac{1}{2} - \frac{1}{2}\sqrt {1 - p - 2D_1^2} . $

(13)

事实上, 若t₁和t₅时刻前电感电流已经降为0, 即电感电流处于断续状态, 则回流功率q=0；因此有i_L(t₁)≤0, 即

$ ({D_1} - 1)k + 1 + {D_1} - 2{D_2} \le 0. $

(14)

“第二类”双重移相控制回流功率直接由式(1-D₁)k+2D₂-D₁-1决定.

设$g({D_1}) = (1 - {D_1})k - \sqrt {1 - p - 2D_1^2} - {D_1} $，则导数

$ g'({D_1}) = - k - 1 + \frac{{2{D_1}}}{{\sqrt {1 - p - 2D_1^2} }}. $

(15)

令g'(D₁)=0，可得

$ {D_{_1*}} = \left( {k + 1} \right)\sqrt {\frac{{1 - p}}{{2{{\left( {k + 1} \right)}^2} + 4}}} , $

(16)

因此g(D₁)在[0, D_1*]单调递减, 在[D_1*, D₂]单调递增.

结合条件0≤D₁≤D₂≤1, 可以得出：在不同传输功率下, 变换器获得最小回流功率时的等效内、外占空比及最小回流功率如下(推导过程见附录A).

1) $ 0 \le p < \frac{1}{2}$：

$ \begin{array}{l} {D_1} = \frac{1}{3} - \frac{1}{6}\sqrt {4 - 6p} , {D_2} = \frac{1}{3} - \frac{1}{6}\sqrt {4 - 6p} , \\ {q_{\min }} = \frac{2}{{k + 1}}{\left( {\frac{2}{3} + \frac{1}{6}\sqrt {4 - 6p} } \right)^2}{\left( {k - 1} \right)^2}. \end{array} $

2) $\frac{1}{2} \le p < \frac{2}{3} $：

当$ k \ge \sqrt {\frac{{18\left( {1 - p} \right)}}{{{{\left( {\sqrt {4 - 6p} - 1} \right)}^2}}} - 2} - 1$时,

$ \begin{array}{l} {D_1} = \frac{1}{3} + \frac{1}{6}\sqrt {4 - 6p} , {D_2} = \frac{1}{3} + \frac{1}{6}\sqrt {4 - 6p} , \\ {q_{\min }} = \frac{2}{{k + 1}}{\left( {\frac{2}{3} - \frac{1}{6}\sqrt {4 - 6p} } \right)^2}{\left( {k - 1} \right)^2}. \end{array} $

当$ k < \sqrt {\frac{{18\left( {1 - p} \right)}}{{{{\left( {\sqrt {4 - 6p} - 1} \right)}^2}}} - 2} - 1$时,

$ \begin{array}{l} {D_1} = \left( {k + 1} \right)\sqrt {\frac{{1 - p}}{{2{{\left( {k + 1} \right)}^2} + 4}}} , {D_2} = \frac{1}{2} - \sqrt {\frac{{1 - p}}{{2{{\left( {k + 1} \right)}^2} + 4}}} , \\ {q_{\min }} = \frac{1}{{2\left( {k + 1} \right)}}{\left[ {k - ({k^2} + 2k + 3)\sqrt {\frac{{1 - p}}{{2{{\left( {k + 1} \right)}^2} + 4}}} } \right]^2}. \end{array} $

3) $ \frac{2}{3} \le p \le 1$：

$ \begin{array}{l} {D_1} = \left( {k + 1} \right)\sqrt {\frac{{1 - p}}{{2{{\left( {k + 1} \right)}^2} + 4}}} , {D_2} = \frac{1}{2} - \sqrt {\frac{{1 - p}}{{2{{\left( {k + 1} \right)}^2} + 4}}} , \\ {q_{\min }} = \frac{1}{{2\left( {k + 1} \right)}}{\left[ {k - ({k^2} + 2k + 3)\sqrt {\frac{{1 - p}}{{2{{\left( {k + 1} \right)}^2} + 4}}} } \right]^2}. \end{array} $

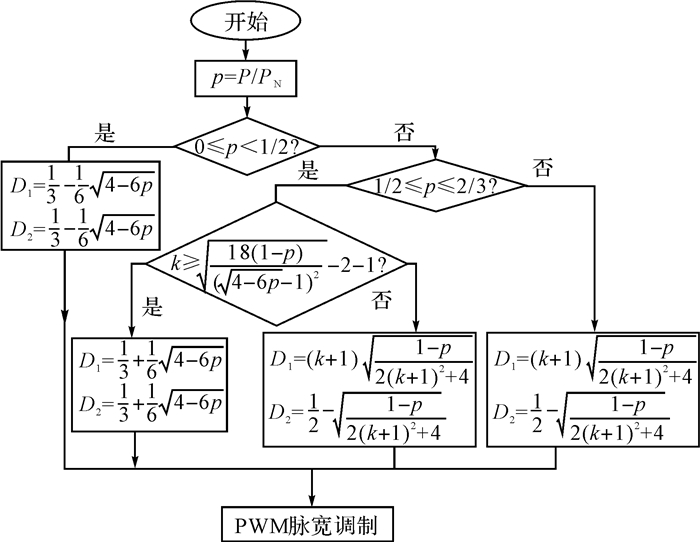
“第二类”双重移相控制比第一类(见附录B)简略很多^[16].它在获得q_min结果时有较简单的D₁、D₂选取方式, 有较高的应用价值和实际意义.如图 5所示为“第二类”双重移相控制的最优回流功率控制的流程图.

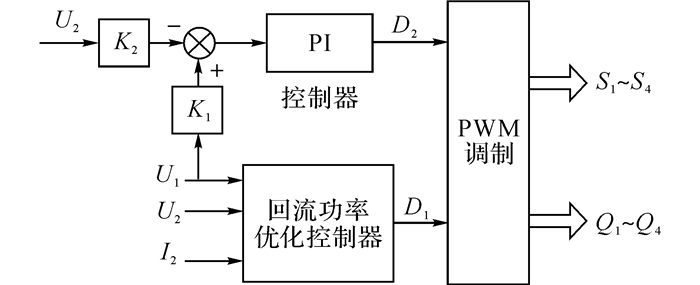
如图 6所示为回流功率优化的DAB移相角控制框图.图中, U₁、U₂、I₂分别为输入电压、输出电压和输出电流, K₁、K₂分别为U₁、U₂的采样系数.回流功率优化控制器通过采样U₁、U₂、I₂得出k和p, 根据表2可得实时的D₁；输入输出电压通过闭环控制实时调节D₂, 稳定输出电压, 同时控制变换器始终处于回流功率最小的工作状态, 保证了变换器具有较高的工作效率.

2.3 电流应力比较分析

当传输相同功率时, 两类双重移相控制较传统单移相控制都有更小的电流应力，且有更多对(D₁, D₂)组合可供选择^[16], 因此对两类双重移相控制的最优控制时的电流应力进行比较分析.

假设两类DPS的传输功率均为p, 根据(5)、(7)、(11), 可得，FDPS和SDPS控制的D₂表达式分别为

$ D_2^{{\rm{FDPS}}} = \frac{1}{2} + \frac{{{D_1}}}{2} - \frac{1}{2}\sqrt {1 - p - D_1^2} , $

(17)

$ D_2^{{\rm{SDPS}}} = \frac{1}{2} - \frac{1}{2}\sqrt {1 - p - 2D_1^2} . $

(18)

由文献[16]和2.1节可知：FDPS和SDPS在一个工作周期内的电感电流最大取值分别为

$ {i_{L\max 1}} = k + \left( {1 - k} \right){D_1} - \sqrt {1 - p - D_1^2} , $

(19)

$ {i_{L\max 2}} = k - \left( {1 - k} \right){D_1} - \sqrt {1 - p - 2D_1^2} . $

(20)

当采用最优回流功率控制时, 即i_Lmax1与i_Lmax2最小值分别在

$ {D_1} = \left( {k + 1} \right)\sqrt {\frac{{1 - p}}{{{{\left( {k + 1} \right)}^2} + 1}}} 、{D_1} = \left( {k + 1} \right)\sqrt {\frac{{1 - p}}{{2{{\left( {k + 1} \right)}^2} + 4}}} $

处取得, 将之分别代入式(19)、(20)，可得

$ {i_{L\max 1}} = k - {k^2}\sqrt {\frac{{1 - p}}{{{{\left( {k + 1} \right)}^2} + 1}}} , $

(21)

$ {i_{L\max 2}} = k - ({k^2} + 1)\sqrt {\frac{{1 - p}}{{2{{\left( {k + 1} \right)}^2} + 4}}} . $

(22)

FDPS与SDPS电流峰值之差为

$ \begin{array}{l} \Delta {i_{L\max }} = {i_{L\max 1}} - {i_{L\max 2}} = {\rm{ }}\\ \;\;\;\;\sqrt {1 - p} \left[ {\frac{{{k^2} + 1}}{{\sqrt {2{{\left( {k + 1} \right)}^2} + 4} }} - \frac{{{k^2}}}{{\sqrt {{{\left( {k + 1} \right)}^2} + 1} }}} \right]. \end{array} $

(23)

由文献[23]可知：在移相控制下, 双有源桥软开关的可实现范围随着k的增大而先增大后减小, 并在k=1时取得最大值.在实际应用中, 通常将DAB变换器的电压调节比设为1.由图 7可知：当k=1时, Δi_Lmax>0, 即SDPS的电流应力比FDPS小.由文献[24]可知：在传输相同功率的情况下, FDPS控制下的变换器电流应力比SPS小很多, 且这种差异在p或k较大时更加明显.TPS控制由于控制自由度较多, 控制方法复杂, 且电流应力的有更优的结果^[18], 所以相较于DAB其他的移相控制方式, SDPS是一种兼得功率效率与控制器设计可靠性的控制方式.

3 实验验证

为了验证“第二类”双重移相控制回流功率优化的实际效果及可行性, 搭建如图 8所示的DAB实验平台.控制芯片采用TI公司的TMS28335 DSP芯片, 主要参数如下：输入电容C₁=1 000 μF, 输出电容C₂=2 000 μF, 漏感(含串联电感)L_s=41 μH, 开关频率f_s=50 kHz, 变压器匝比n=N_p/N_s=1/3, 输入电压U₁=50 V, 输出电压U₂=150 V.

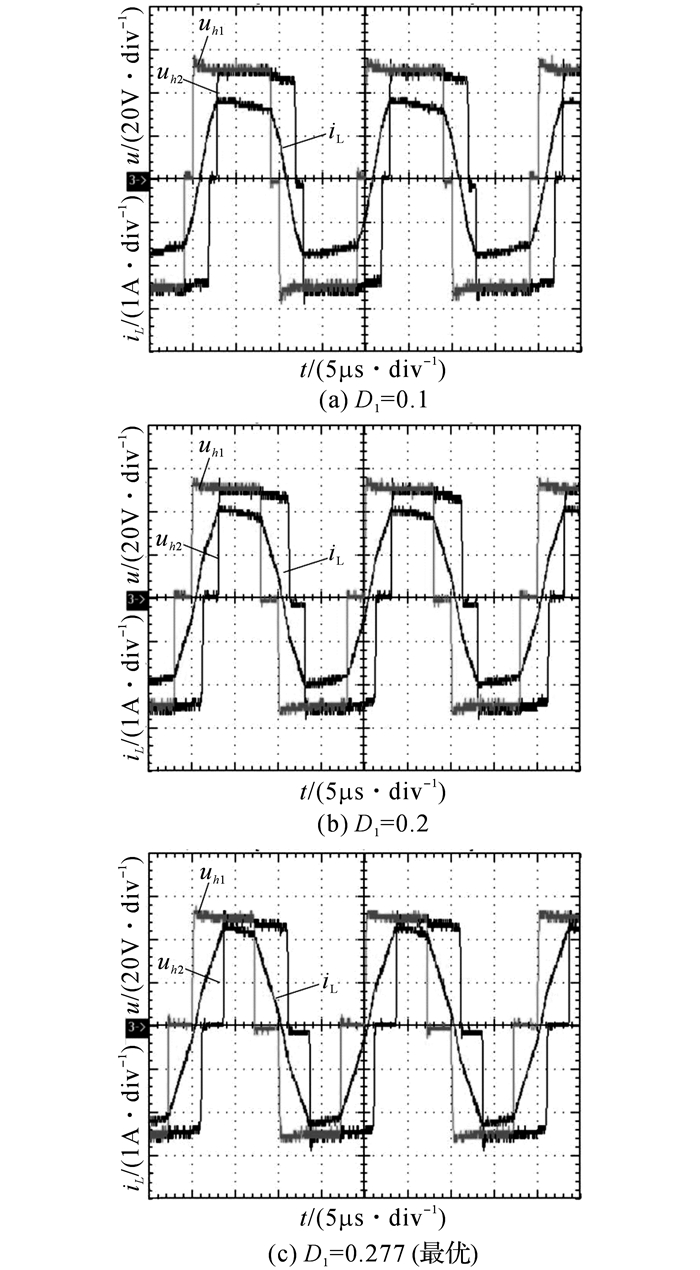
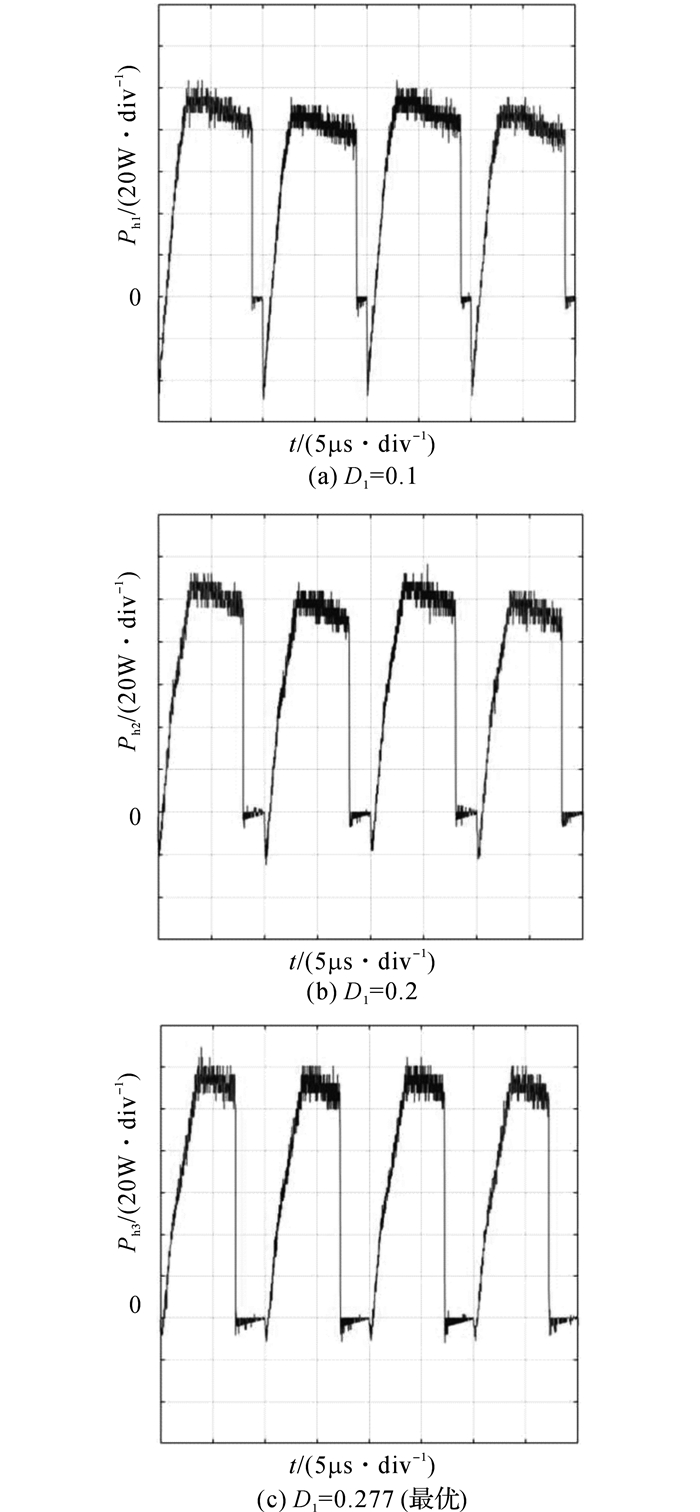
如图 9所示为采用“第二类”双重移相控制在恒定负载下内移相角D₁取不同值时的u_h1、u_h2和电感电流i_L的波形, 对应的DAB原边全桥瞬时功率输出如图 10所示.图中, 传输功率P=118.4 W.可以看出：在相同的传输功率下, 不同内移相角时变换器的回流功率和造成的电感电流应力不同.从图 10可以得出：在最优内移相比D₁=0.277时, 回流功率达到最小, 此时电路中几乎不存在回流功率.开关管损耗和磁芯损耗都减小, 变换器的效率提高.

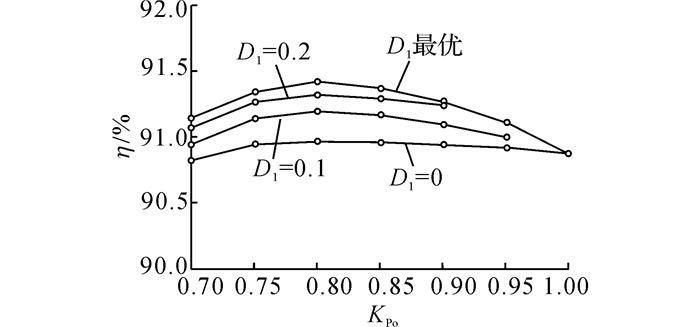
如表 1所示为图 9(c)控制下的主要损耗理论计算值, 可以得出，理论计算总损耗为9.87W.如图 11所示为采用SDPS控制不同D₁下的效率η曲线图.图中，k_P0为载重比.可以看出：采用最优SDPS控制的效率始终比D₁取其他值高, 且在0.8满载时效率达到最大, 为91.41%.实验总损耗为11.13 W, 与理论计算值基本一致.

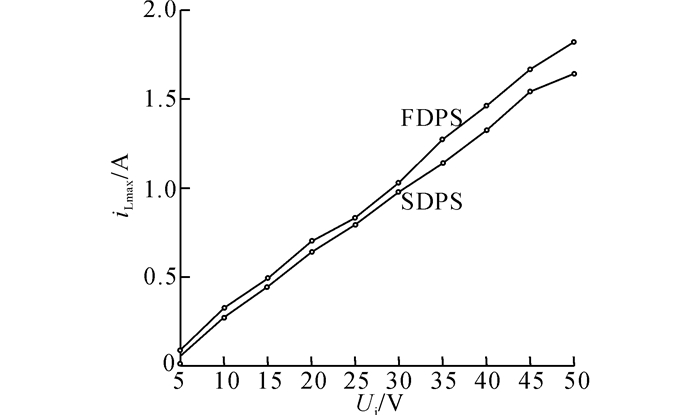
如图 12所示为均采用最优回流功率控制下的FDPS和SDPS的电感电流峰值随输入电压变化关系的曲线图.在一个开关周期内, 电感电流峰值表征开关管的电流应力.可以看出，SDPS与FDPS的电感电流峰值随着输入电压的增加而增加, 采用最优回流功率控制的SDPS的电流峰值始终比FDPS低, 且两者的差值随着输入电压的增大而增大.

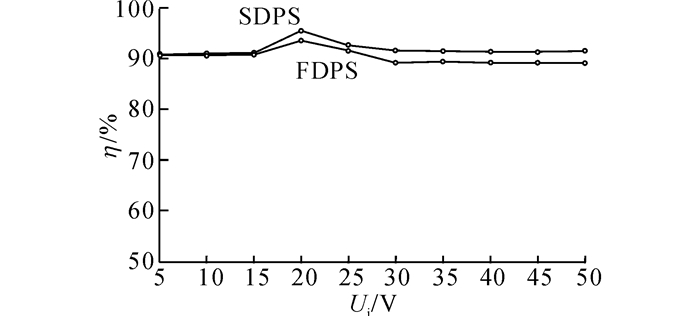
如图 13所示为分别采用FDPS与SDPS最优控制时变换器效率随输入电压变化的关系曲线.可以看出：采用SDPS最优控制的效率始终比FDPS高.

4 结论

(1) 相比于“第一类”双重移相控制的最优回流功率控制策略, 提出的的控制策略控制方式简单, 有更好的可操作性和可实践性.

(2) 在相同的传输功率下, “第二类”双重移相控制在最优回流功率控制下的电流应力比第一类更小, 基本达到了DAB的所有移相控制中电流应力最小的状态.

(3) 通过电流应力的减少, 降低了开关管器件的电流要求, 减少了磁性元件的损耗.

附录A

由2.2节可知：g(D₁)在$[0, \left( {k + 1} \right) \times \sqrt {\left( {1 - p} \right)/(2{{\left( {k + 1} \right)}^2} + 4)} ] $单调递减, 在$ [\left( {k + 1} \right) \times \sqrt {1 - p/(2{{\left( {k + 1} \right)}^2} + 4)} , {D_2}]$单调递增, ${D_2} = (1 - \sqrt {1 - p - 2D_1^2} )/2 $.

考虑占空比条件D₁≤D₂, 可得：$ {D_1} \le 1/2, {D_1} \le \sqrt {\left( {1 - p} \right)/2} $且6D₁²-4D₁≥-p.可以推出

$ 6{({D_1} - 1)^2} \ge \frac{2}{3} - p. $

(A-1)

当2/3≤p≤1时, 式(A-1)恒成立, 故取

$ {D_1} = \left( {k + 1} \right)\sqrt {\left( {1 - p} \right)/(2{{\left( {k + 1} \right)}^2} + 4)} . $

(A-2)

当1/2≤p < 2/3时,

$ \begin{array}{l} {D_1} \in \left[ {0, \frac{1}{3} - \frac{1}{6}\sqrt {4 - 6p} } \right] \cup \\ \;\;\;\;\;\;\;\left[ {\frac{1}{3} + \frac{1}{6}\sqrt {4 - 6p} , \sqrt {\left( {1 - p} \right)/2} } \right]. \end{array} $

(A-3)

当0≤p < 1/2时,

$ {D_1} \in \left[ {0, \frac{1}{3} - \frac{1}{6}\sqrt {4 - 6p} } \right]. $

(A-4)

考虑到g(D₁)在$ [0, \left( {k + 1} \right) \times \sqrt {\left( {1 - p} \right)/(2{{\left( {k + 1} \right)}^2} + 4)} ]$单调递减, 在$[\left( {k + 1} \right) \times \sqrt {\left( {1 - p} \right)/[2{{\left( {k + 1} \right)}^2} + 4]} , {D_2}] $单调递增.当1/2≤p < 2/3时, 只需对$ \left( {k + 1} \right) \times \sqrt {\left( {1 - p} \right)/(2{{\left( {k + 1} \right)}^2} + 4)} $与$1/3 - \sqrt {4 - 6p} /6 $、$ 1/3 + \sqrt {4 - 6p} /6$、$ \sqrt {\left( {1 - p} \right)/2} $进行比较, 以使D₁取得最佳值.

当0≤p < 1/2时, 只需对$ \left( {k + 1} \right) \times \sqrt {\left( {1 - p} \right)/(2{{\left( {k + 1} \right)}^2} + 4)} $与$ 1/3 - \sqrt {4 - 6p} /6$进行比较，以使D₁取得最佳值.

当1/2≤p < 2/3时,

假设

$ \begin{array}{l} 1/3 + \sqrt {4 - 6p} /6 \le \left( {k + 1} \right)\sqrt {\left( {1 - p} \right)/(2{{\left( {k + 1} \right)}^2} + 4)} \Leftrightarrow \\ \;\;\;{\left( {k + 1} \right)^2} \ge \frac{{18\left( {1 - p} \right)}}{{{{\left( {\sqrt {4 - 6p} - 1} \right)}^2}}} - 2. \end{array} $

(A-5)

定义$f\left( p \right) = \left[ {18\left( {1 - p} \right)} \right]/{\left( {\sqrt {4 - 6p} - 1} \right)^2} - 2 $,

易得f(p)在[1/2, 2/3)递减, $ f\left( {\frac{1}{2} + } \right) = + \infty , f\left( {\frac{2}{3}} \right) = 4$.

所以当

$ k \ge \sqrt {\left[ {18\left( {1 - p} \right)} \right]/{{\left( {\sqrt {4 - 6p} - 1} \right)}^2} - 2} - 1 $

时, 式(A-5)成立, 假设成立.又

$ \left( {k + 1} \right)\sqrt {\left( {1 - p} \right)/[2{{\left( {k + 1} \right)}^2} + 4]} \le \sqrt {\left( {1 - p} \right)/2} $

显然成立.当

$ 1 \le k \le \sqrt {\left[ {18\left( {1 - p} \right)} \right]/{{\left( {\sqrt {4 - 6p} - 1} \right)}^2} - 2} - 1 $

时, 需要进一步讨论函数

$g\left( {\frac{1}{3} - \frac{1}{6}\sqrt {4 - 6p} } \right) $与$ g\left( {\frac{1}{3} + \frac{1}{6}\sqrt {4 - 6p} } \right)$的大小.

$ g\left( {\frac{1}{3} + \frac{1}{6}\sqrt {4 - 6p} } \right) \le g\left( {\frac{1}{3} - \frac{1}{6}\sqrt {4 - 6p} } \right), $

故${D_1} = \frac{1}{3} + \frac{1}{6}\sqrt {4 - 6p} $.

当0≤p < 1/2时,

假设

$ \begin{array}{l} \frac{1}{3} - \frac{1}{6}\sqrt {4 - 6p} \le \left( {k + 1} \right)\sqrt {\left( {1 - p} \right)/[2{{\left( {k + 1} \right)}^2} + 4]} \Leftrightarrow \\ \;\;{\left( {k + 1} \right)^2} \ge \left[ {18\left( {1 - p} \right)} \right]/\sqrt {4 - 6p} + 1{)^2} - 2, \end{array} $

(A-6)

定义

$ h\left( p \right) = \left[ {18\left( {1 - p} \right)} \right]/{\left( {\sqrt {4 - 6p} + 1} \right)^2} - 2], $

则h(p)在[0, 1/2)的最大值

$ h{\left( p \right)_{\max }} \le h\left( {1/2} \right) = 2.5; $

k≥1, 则假设成立, 故

$ {D_1} = \frac{1}{3} - \frac{1}{6}\sqrt {4 - 6p} . $

(A-7)

综上所述, 可得表2的结论.

附录B