随着电力系统中分布式电源与非线性负荷的增加, 电网信号中谐波所占比例越来越大.在谐波和噪声的干扰下, 如何快速准确地分析电网信号具有重大意义.目前, 电网信号测量方法可以分为频域和时域两大类.
时域方法可以分为Prony方法[1-2]、加权最小二乘法[3-4]以及Klaman方法[5-7]等.Prony方法和加权最小二乘法均需构造一个离散线性预测模型(LPM), 该模型的特征多项式的根包含信号的阻尼系数和频率.Kalman方法从另一个角度解决问题, 它利用谐波的幅值和相位生成信号的状态空间描述, 利用新测量值来更新状态变量的估计.这些时域方法的主要问题在于计算量较大, 导致不适合应用于嵌入式系统中进行实时运算.
频域方法一般基于快速傅里叶变换(FFT), 其主要的误差来自于频谱泄漏和栅栏效应, 两者分别可以用加窗和插值消除.因此, 通常的算法流程包含时域加窗、FFT, 频域插值3个步骤[8-9].Belege等[10]讨论最大旁瓣衰减窗的性质, 提供了窗函数的DTFT的近似.该近似函数可以将窗函数的DTFT从累加的形式转化为连乘的形式, 从而通过连续两个DFT的比值来消去幅值、相位以及难以处理的三角函数, 得到关于频率的简单关系.汉宁窗作为最大旁瓣衰减窗的一种, 同样具有这个性质, 并且因为较小的主瓣宽度而更适合多频率信号的估计.采用时域加汉宁窗的操作之后, 频域上相距较远的谐波在DFT峰值附近的频谱泄漏可以忽略, 因此峰值附近的插值点可以认为只受到单一分量的影响.这是众多文献的算法适用的前提条件, 即各分量在频谱上的距离较远.
随着电力电子装置的广泛应用, 信号的间谐波成分不可忽视.间谐波是基波的非整数次谐波, 它插入两个整数次谐波之间, 减小了分量之间的频谱距离, 此时众多文献算法的适用条件将不再得到满足.事实上, 如果分析窗口较短, 同时信号内含有频率接近谐波的间谐波, 那么信号在频域上将会出现重叠的双分量.在重叠区域取插值点进行谐波分量的参数估计, 则文献中的算法将会失效.这种情况如此难以处理, 即使是讨论间谐波的文献, 通常也只能假设采样时长足够长, 从而使相邻两个分量不会重叠.比如刘昊等[11]讨论了间谐波, 利用分量的能量集中在主瓣内的特点, 提出不同的插值公式;贾清泉等[12]将加窗信号在频域上平移, 把非同步采样信号转化成同步采样信号, 以此估计分量的频率、幅值和相位;刘亚梅等[13]提前补偿线性相位偏移, 对加余弦窗后的DFT值进行多层求和, 提出基于余弦组合窗的多层插值频域校正法;蒋春芳等[14]采用多项式逼近的方法,算出频率的小数部分;惠锦等[15]引入相位补偿, 提出奇数频点插值算法;马晓春等[16]列出大量需要非同步采样的场合, 在所有谐波和间谐波的频率均已知并且固定的情况下估计各谐波间谐波的幅值和相位;曹健等[17]在时域上用最小二乘法扫描出带噪声信号的谐波和间谐波的个数和大致频率, 利用时频原子变换分析每个分量.这些文献都对间谐波的检测进行了深入研究, 但算法的输出是单个分量的频率、幅值和相位, 不能同时估计插值点上重叠的两个分量.在少量明确提出估计重叠双分量问题的文献中, 问题通常采用搜索的办法解决[18-19].采用搜索的方法估计重叠双分量需要较大的计算量, 在实时性较高的场合不适用.
本文提出频域Prony方法以估计信号的重叠双分量.重叠分量的频率估计问题在应用汉宁窗的性质之后可以转化为复指数函数的线性组合, 采用Prony方法可将其进一步转化为对差分方程系数的估计.在将差分方程写成矩阵形式之后, 差分方程的系数对应于近似矩阵的零空间, 因此可以通过原矩阵的奇异值分解获得.利用估计得到的差分方程系数,可以解出2个重叠分量的频率.
1 信号模型研究的多分量信号的离散时域表达式为
| $ \begin{array}{l} s\left[ n \right] = \sum\limits_{m = 1}^M {\left\{ {{A_m}\exp \left( {{\alpha _m}\frac{n}{N}} \right)\exp \left( {2{\rm{ \mathsf{ π} j}}{f_m}\frac{n}{N} + j{\phi _m}} \right)} \right\}} ;\\ \;\;\;n = 0,1, \cdots ,N - 1. \end{array} $ | (1) |
式中:M为信号的谐波数, {αm, fm, Am, ϕm}分别为第m个谐波的阻尼系数、频率、幅值和相位, N为分析窗口的长度.fm表示分析窗口中包含的分量的周期数(cycles in record), 它的单位是bin.设实际的采样频率和分量频率分别为Fs和Fm, 则
| $ \frac{{{f_m}}}{N} = \frac{{{F_m}}}{{{F_{\rm{s}}}}}. $ | (2) |
式中:任意的fi和fj(i≠j)之间可以不具有整数倍数关系.
采用的汉宁窗的时域表达式为
| $ {w_{\rm{H}}}\left[ n \right] = \frac{1}{2} - \frac{1}{2}\cos \left( {2{\rm{ \mathsf{ π} }}\frac{n}{N}} \right);n = 0,1, \cdots ,N - 1. $ | (3) |
对应的DTFT为
| $ \begin{array}{l} {w_{\rm{H}}}\left( v \right) = \sum\limits_{n = 0}^{N - 1} {\left\{ {{w_{\rm{H}}}\left[ n \right]\exp \left( { - 2{\rm{ \mathsf{ π} j}}v\frac{n}{N}} \right)} \right\}} \buildrel\textstyle.\over= \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{N}{{2{\rm{ \mathsf{ π} }}}}\frac{{\sin \left( {\pi v} \right)}}{{v\left( {1 - {v^2}} \right)}}\exp \left( { - {\rm{ \mathsf{ π} j}}v} \right). \end{array} $ | (4) |
式(4)的近似在
对s[n]加汉宁窗后得到的加窗信号时域表达式为
| $ x\left[ n \right] = s\left[ n \right]{w_{\rm{H}}}\left[ n \right], $ | (5) |
对应的DTFT为
| $ \begin{array}{l} X\left( v \right) = \sum\limits_{n = 0}^{N - 1} {\left\{ {x\left[ n \right]\exp \left( { - 2{\rm{ \mathsf{ π} j}}v\frac{n}{N}} \right)} \right\}} = \\ \;\;\;\;\;\;\;\sum\limits_{n = 0}^{N - 1} {\sum\limits_{m = 1}^M {\left\{ {{w_{\rm{H}}}\left[ n \right]{A_m}\exp \left[ {2{\rm{ \mathsf{ π} j}}\left( {{f_m} + {\alpha _m}/2{\rm{ \mathsf{ π} j}}} \right)\frac{n}{N} + } \right.} \right.} } \\ \;\;\;\;\;\;\;\left. {\left. {{\rm{j}}{\phi _m}} \right]\exp \left( { - 2{\rm{ \mathsf{ π} j}}v\frac{n}{N}} \right)} \right\} = \\ \;\;\;\;\;\;\;\sum\limits_{m = 1}^M {\left\{ {{A_m}\exp \left( {{\rm{j}}{\phi _m}} \right){W_{\rm{H}}}\left( {v - {f_m} - \frac{{{\alpha _m}}}{{2{\rm{ \mathsf{ π} j}}}}} \right)} \right\}} . \end{array} $ | (6) |
式(4)中的变量v可以是复数, 因此可以用复频率来统一表示谐波分量的阻尼系数和频率, 即设第m个谐波的复频率为
| $ {v_m} = {f_m} + \frac{{{\alpha _m}}}{{2{\rm{ \mathsf{ π} j}}}}. $ | (7) |
式中:vm的实数部分对应分量的频率, 虚数部分包含分量的阻尼系数.式(6)可以简写为
| $ X\left( v \right) = \sum\limits_{m = 1}^M {\left[ {{A_m}\exp \left( {{\rm{j}}{\phi _m}} \right){W_{\rm{H}}}\left( {v - {v_m}} \right)} \right]} . $ | (8) |
式(8)为x[n]的DTFT公式.DFT是对DTFT的频域采样, 对x[n]进行FFT处理, 则可得X[k],
| $ X\left[ k \right] = X\left( k \right);\;\;\;k = 0,1, \cdots ,N - 1. $ | (9) |
式中:等式左边表示FFT的结果, 等式右边表示DTFT在f=k时的取值.
该算法需要解决的问题可以描述为:给定FFT结果{X[k]|k=0, 1, …, N-1}的峰顶X[kf]附近的p个点X[k], 其中k=[kb, kb+1, …, kb+p-1]T且kb≤kf≤kb+p-1, 设计插值算法以估计X[k]上的重叠分量.
如果区间[kb, kb+p-1]上只有一个分量, 其他谐波的频谱泄露被汉宁窗有效抑制, 那么利用式(8)、(9),可得
| $ X\left[ \mathit{\boldsymbol{k}} \right] = {A_1}\exp \left( {{\rm{j}}{\phi _1}} \right){W_{\rm{H}}}\left( {\mathit{\boldsymbol{k}} - {v_1}{\bf{1}}} \right). $ | (10) |
式中:k=[kb, kb+1, …, kb+p-1]T为p×1向量;1为元素全为1的向量,维数由参与计算的矩阵或向量确定.对于该类插值点仅受单一分量影响的种情况,文献已经有了深入的研究, 比如Belega等[20-21]给出2种不同的估计{v1, A1, ϕ1}的方法, 它们分别要求p=3和p=2.当区间[kb, kb+p-1]上包含2个重叠分量时, 式(10)改写成
| $ \begin{array}{l} X\left[ \mathit{\boldsymbol{k}} \right] = {A_1}\exp \left( {{\rm{j}}{\phi _1}} \right){W_{\rm{H}}}\left( {\mathit{\boldsymbol{k}} - {v_1}{\bf{1}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;{A_2}\exp \left( {{\rm{j}}{\phi _2}} \right){W_{\rm{H}}}\left( {\mathit{\boldsymbol{k}} - {v_2}{\bf{1}}} \right). \end{array} $ | (11) |
此时Belega等[20-21]的算法将会失效.利用提出的算法可以处理这种情况.因为式(11)中有8个实数未知数(其中vx为复数), 算法至少需要4个FFT值, 即p≥4.为了降噪考虑, 取p=5.需要说明的是, 本文算法能够很容易推广到n个重叠分量, p≥2n+1个插值点的一般的情况.
2 复频率估计首先利用变量替换简化推导, 设
| $ {z_1} = {k_{\rm{b}}} - {v_1},\;\;\;{z_2} = {k_{\rm{b}}} - {v_2}, $ | (12) |
则式(11)转化为
| $ \begin{array}{l} X\left[ \mathit{\boldsymbol{k}} \right] = X\left[ {{k_{\rm{b}}}\;{\bf{1}} + \mathit{\boldsymbol{q}}} \right] = \\ {A_1}\exp \left( {{\rm{j}}{\phi _1}} \right){W_{\rm{H}}}\left( {{z_{\rm{1}}}\;{\bf{1}} + \mathit{\boldsymbol{q}}} \right) + {A_2}\exp \left( {{\rm{j}}{\phi _2}} \right){W_{\rm{H}}}\left( {{z_{\rm{2}}}\;{\bf{1}} + \mathit{\boldsymbol{q}}} \right). \end{array} $ | (13) |
式中:q=[0, 1, …, 4]T.对式(13)不断变形, 直到得出X[k]和{z1, z2}之间的简单关系.
根据WH(v)的近似公式(4), 容易得到
| $ \frac{{{{\hat W}_{\rm{H}}}\left( {z + 1} \right)}}{{{{\hat W}_{\rm{H}}}\left( z \right)}} = \frac{{z - 1}}{{z + 2}}. $ | (14) |
多次利用式(14)的结论,可以将
| $ \left[ {\begin{array}{*{20}{c}} {{{\hat W}_{\rm{H}}}\left( z \right)}\\ {{{\hat W}_{\rm{H}}}\left( {z + 1} \right)}\\ {{{\hat W}_{\rm{H}}}\left( {z + 2} \right)}\\ {{{\hat W}_{\rm{H}}}\left( {z + 3} \right)}\\ {{{\hat W}_{\rm{H}}}\left( {z + 4} \right)} \end{array}} \right] = {{\hat W}_{\rm{H}}}\left( z \right)\left[ {\begin{array}{*{20}{c}} 1\\ {\frac{{z - 1}}{{z + 2}}}\\ {\frac{{z - 1}}{{z + 2}}\frac{z}{{z + 3}}}\\ {\frac{{z - 1}}{{z + 2}}\frac{z}{{z + 3}}\frac{{z + 1}}{{z + 4}}}\\ {\frac{{z - 1}}{{z + 2}}\frac{z}{{z + 3}}\frac{{z + 1}}{{z + 4}}\frac{{z + 2}}{{z + 5}}} \end{array}} \right]. $ | (15) |
式(15)可以简写为
| $ {{\hat W}_{\rm{H}}}\left( {z{\bf{1}} + \mathit{\boldsymbol{q}}} \right) = V\left( z \right)\mathit{\boldsymbol{g}}\left( z \right), $ | (16) |
式中:
| $ V\left( z \right) \buildrel \Delta \over = \frac{{\hat W\left( z \right)}}{{\left( {z + 2} \right)\left( {z + 3} \right)\left( {z + 4} \right)\left( {z + 5} \right)}}, $ | (17) |
| $ \mathit{\boldsymbol{g}}\left( z \right) \buildrel \Delta \over = \left[ {\begin{array}{*{20}{c}} {\left( {z + 2} \right)\left( {z + 3} \right)\left( {z + 4} \right)\left( {z + 5} \right)}\\ {\left( {z - 1} \right)\left( {z + 3} \right)\left( {z + 4} \right)\left( {z + 5} \right)}\\ {\left( {z - 1} \right)z\left( {z + 4} \right)\left( {z + 5} \right)}\\ {\left( {z - 1} \right)z\left( {z + 1} \right)\left( {z + 5} \right)}\\ {\left( {z - 1} \right)z\left( {z + 1} \right)\left( {z + 2} \right)} \end{array}} \right], $ | (18) |
分别为标量和5×1的向量;
将式(16)代入式(13), 可得
| $ \begin{array}{l} X\left[ \mathit{\boldsymbol{k}} \right] = {A_1}\exp \left( {{\rm{j}}{\phi _1}} \right)V\left( {{z_1}} \right)\mathit{\boldsymbol{g}}\left( {{z_1}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;{A_2}\exp \left( {{\rm{j}}{\phi _2}} \right)V\left( {{z_2}} \right)\mathit{\boldsymbol{g}}\left( {{z_2}} \right). \end{array} $ | (19) |
式(19)中A1exp (jϕ1)V(z1)和A2exp (jϕ2)V(z2)都是未知标量, 可以简单地用k1和k2表示, 即
| $ {k_1} = {A_1}\exp \left( {{\rm{j}}{\phi _1}} \right)V\left( {{z_1}} \right),\;\;\;{k_2} = {A_2}\exp \left( {{\rm{j}}{\phi _2}} \right)V\left( {{z_2}} \right), $ | (20) |
则式(19)变成一个二元高次方程组:
| $ X\left[ \mathit{\boldsymbol{k}} \right] = {k_1}\mathit{\boldsymbol{g}}\left( {{z_1}} \right) + {k_2}\mathit{\boldsymbol{g}}\left( {{z_2}} \right). $ | (21) |
式中:k=[kb, kb+1, …, kb+4]T;g(zx)为5×1的向量, 其每一个元素都是zx的4次多项式, 如式(18)所示.
式(21)需要进一步化简.设
| $ \mathit{\boldsymbol{h}}\left( z \right) \buildrel \Delta \over = {\left[ {1,z,{z^2},{z^3},{z^4}} \right]^{\rm{T}}}, $ | (22) |
则将g(z)的每个元素展开成z的4次多项式, 可得g(z)和h(z)之间的线性关系,
| $ \mathit{\boldsymbol{g}}\left( z \right) = \mathit{\boldsymbol{Mh}}\left( z \right). $ | (23) |
系数矩阵M的逆M-1为
| $ {\mathit{\boldsymbol{M}}^{ - 1}} = \frac{1}{{360}}\left[ {\begin{array}{*{20}{c}} 1&{ - 4}&6&{ - 4}&1\\ 1&2&{ - 12}&{14}&{ - 5}\\ 1&2&{18}&{ - 46}&{25}\\ 1&2&{ - 12}&{134}&{ - 125}\\ 1&2&{18}&{ - 286}&{625} \end{array}} \right]. $ | (24) |
式(21)可以进一步变化为
| $ {\mathit{\boldsymbol{M}}^{ - 1}}X\left[ \mathit{\boldsymbol{k}} \right] = {k_1}\mathit{\boldsymbol{h}}\left( {{z_1}} \right) + {k_2}\mathit{\boldsymbol{h}}\left( {{z_2}} \right). $ | (25) |
采用Prony方法和矩阵奇异值分解法,求得式(25)的解z1和z2.
设y=M-1X[k]=[y0, y1, y2, y3, y4]T, 将式(25)按每一项展开可得
| $ {k_1}z_1^n + {k_2}z_2^n = {y_n};\;\;\;\;n = 0,1,2,3,4. $ | (26) |
式中:[y0, y1, y2, y3, y4]是FFT值左乘M-1得到的已知值, 通常含有噪声;[k1, k2]为未知系数, [z1, z2]为待求量.
式(26)具有差分方程的通解的形式, 和Prony方法的模型一致.如果将z1, 2看成特征多项式
| $ {a_2}{z^2} + {a_1}z + {a_0} = 0 $ | (27) |
的根, 那么k1z1n+k2z2n是差分方程
| $ {a_2}{y_{n + 2}} + {a_1}{y_{n + 1}} + {a_0}{y_n} = 0 $ | (28) |
的通解.
由式(27)可知, 求解z1, 2即求解系数{a2, a1, a0};由式(28)可知, {a2, a1, a0}可以通过已知值{y0, y1, y2, y3, y4}的内在联系获得.
将式(28)写成矩阵形式:
| $ \mathit{\boldsymbol{B\xi }} \buildrel\textstyle.\over= {\bf{0}}, $ | (29) |
式中:
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{y_2}}&{{y_1}}&{{y_0}}\\ {{y_3}}&{{y_2}}&{{y_1}}\\ {{y_4}}&{{y_3}}&{{y_2}} \end{array}} \right],\mathit{\boldsymbol{\xi }} = \left[ {\begin{array}{*{20}{c}} {{a_2}}\\ {{a_1}}\\ {{a_0}} \end{array}} \right], $ | (30) |
式(29)中取
| $ \left( {\mathit{\boldsymbol{B}} - \mathit{\boldsymbol{D}}} \right)\mathit{\boldsymbol{\xi }} = {\bf{0}}, $ | (31) |
式中:D为矫正矩阵, 它消除B中噪声的影响.本节的目标是找到范数较小的矫正矩阵D,使B-D非列满秩.
B-D可以通过奇异值分解法得到.类似的算法称为总体最小二乘法[22].设B的奇异值分解为
| $ \mathit{\boldsymbol{B}} = \mathit{\boldsymbol{U \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{V}}^{\rm{H}}} = \sum\limits_{i = 1}^3 {\left( {{\sigma _i}{\mathit{\boldsymbol{u}}_i}\mathit{\boldsymbol{v}}_i^{\rm{H}}} \right)} , $ | (32) |
奇异值按照顺序σ1≥σ2≥σ3排列, 则B的秩r最佳逼近
| $ {{\mathit{\boldsymbol{\hat B}}}_r} = \sum\limits_{i = 1}^r {{\sigma _i}{\mathit{\boldsymbol{u}}_i}\left( {\mathit{\boldsymbol{v}}_i^{\rm{H}}} \right)} , $ | (33) |
式中:1≤r≤3, 设
| $ \mu \left( r \right) = \frac{{{{\left\| {\mathit{\boldsymbol{\hat B}}} \right\|}_F}}}{{{{\left\| \mathit{\boldsymbol{B}} \right\|}_F}}} = \frac{{\sqrt {\sigma _1^2 + \cdots + \sigma _r^2} }}{{\sqrt {\sigma _1^2 + \sigma _2^2 + \sigma _3^2} }}, $ | (34) |
算法取r为满足μ(r)>1-∈的最小整数, 其中∈是接近于0的正数, 在本文仿真中取∈=10-5.
讨论算法对r的不同取值的处理.
当r=2时,
当r=3时, B没有相对较小的奇异值, 因此不存在范数较小的D使B-D非列满秩.这说明系统模型的阶设置得过小, 插值点X[k]上的重叠分量不只有两个.此时可能的处理手段有以下2种:
1) 引入更多的插值点, 设置更高的系统的阶.
2) 使分量之间的距离增大, 将重叠分量的数目限制到2个及2个以下.
该算法能够很容易扩展到更多插值点和更高系统阶数的情形.比如当插值点数为7, 系统阶数为3时, 只需重新推导矩阵M, 把特征多项式(27)扩展成3次多项式, 将式(30)中的B变成4×4矩阵, ξ变成4×1向量, 那么能够求得3个分量的复频率.电网信号的谐波频率通常是基波的整数倍数, 这意味着相邻谐波之间的距离基本固定并且相差不大, 如果算法引入更多的插值点, 那么插值点上重叠分量的数目很可能同步增加, 问题没有解决, 因此上面的第1个方案是不合适的.如果采用第2个方案, 那么算法只需要增加分析窗口的长度, 使分析窗口中含有的信号周期数变大, 即谐波分量之间的距离增大, 重叠分量的数目降低, 从而转化为r=2的情况.
当r=1时, 插值点上只有一个分量, 或者说两个重叠分量完全重合, 此时式(28)退化为
| $ {a_1}{y_{n + 1}} + {a_0}{y_n} = 0. $ | (35) |
只需3个插值点{y0, y1, y2},即可得到{a1, a0}的估计.设
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {{y_1}}&{{y_0}}\\ {{y_2}}&{{y_1}} \end{array}} \right],\mathit{\boldsymbol{\zeta }} = \left[ {\begin{array}{*{20}{c}} {{a_1}}\\ {{a_0}} \end{array}} \right], $ | (36) |
则退化的差分方程(35)可以写成矩阵形式:
| $ \mathit{\boldsymbol{C\xi }} \buildrel\textstyle.\over= {\bf{0}}, $ | (37) |
采用奇异值分解法求解.此时, z1=z2, 且均为a1z+a0=0的根.仅仅采用3个插值点而不是5个插值点的原因在于汉宁窗的主瓣宽度只有4 bin, 即使考虑到非同步采样, 分量频率附近的3个插值点就已经包含了DFT频域上关于该分量的几乎全部信息, 剩下的2个插值点不但不能提供充分的信息, 而且会给估计带来其他谐波和噪声的影响.算法需要减少插值点, 只取5个插值点里最中心的3个值, 并求这些插值点上的1个分量.
综合上面3种情况可知, 式(30)给出的矩阵B的有效秩r对应X[k]中分量的个数, 并且
1) 当r=2时, 算法可以直接用奇异值分解法获得2个分量的复频率估计.
2) 当r=3时, 信号的模型不再准确, 算法需要增加分析窗口的长度, 使重叠分量的数目变少.
3) 当r=1时, 插值点上只有1个分量, 算法只需留下最中心的3个插值点, 利用和r=2时相似的方法求得该分量的复频率估计.
该算法的框架如图 1所示.
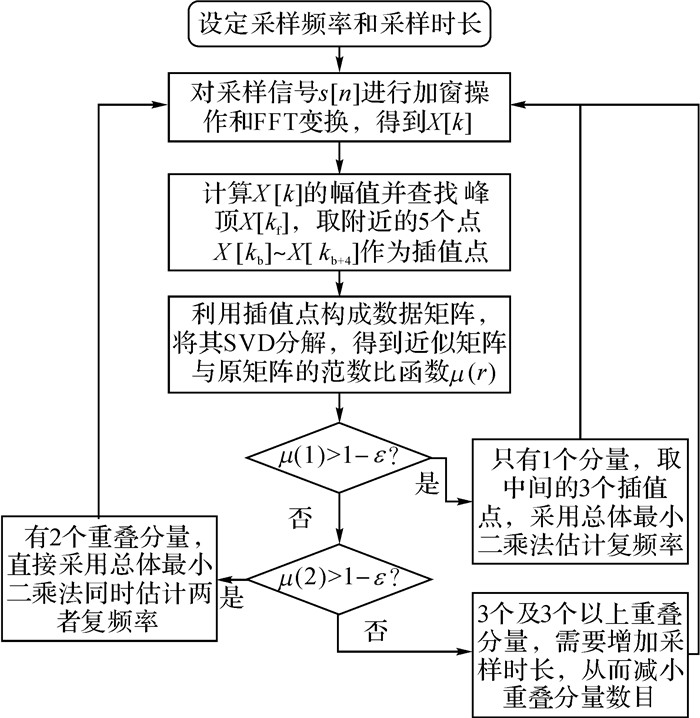
|
图 1 频域Prony算法流程图 Fig. 1 Flow chart of frequency-domain based Prony's algorithm |
假设原信号s[n]中包含了白色高斯噪声(WGN), 则s[n]的DFT
| $ S\left[ k \right] = \sum\limits_{n = 0}^{N - 1} {\left[ {s\left[ n \right]\exp \left( { - 2{\rm{ \mathsf{ π} j}}k\frac{n}{N}} \right)} \right]} . $ | (38) |
将包含复数的白色高斯噪声.因为经过汉宁窗加窗操作后, X[k]和S[k]之间具有以下联系[21]:
| $ X\left[ k \right] = \frac{1}{2}S\left[ k \right] - \frac{1}{4}S\left[ {k - 1} \right] - \frac{1}{4}S\left[ {k + 1} \right], $ | (39) |
X[k]包含了零均值、同方差, 但是不相互独立的复数噪声.因为算法利用公式y=M-1X[k]计算y时左乘了矩阵M-1, y包含了零均值、不同方差并且不相互独立的复数噪声.
设
| $ {{y'}_q} = {y_q}/{3^q},\;\;\;\;q = 0,1, \cdots ,4, $ | (40) |
则y′q包含的噪声方差比较接近, 对y′q应用总体最小二乘法的效果将优于yq.y′q代入式(26)计算得到z′1, 2, z1, 2可以根据
| $ {z_{1,2}} = 3{{z'}_{1,2}} $ | (41) |
求得.
3 幅值相位估计在复频率v1, 2已知的情况下, 分量的幅值和相位可以通过最小二乘法获得.
如果X[k]含有2个分量且复频率的估计为
| $ \begin{array}{l} X\left[ \mathit{\boldsymbol{k}} \right] = {A_1}\exp \left( {{\rm{j}}{\phi _1}} \right){W_{\rm{H}}}\left( {\mathit{\boldsymbol{k}} - {{\hat v}_1}{\bf{1}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;{A_2}\exp \left( {{\rm{j}}{\phi _2}} \right){W_{\rm{H}}}\left( {\mathit{\boldsymbol{k}} - {{\hat v}_2}{\bf{1}}} \right), \end{array} $ | (42) |
写成矩阵形式, 可得
| $ \left[ {{W_{\rm{H}}}\left( {\mathit{\boldsymbol{k}} - {{\hat v}_1}{\bf{1}}} \right){W_{\rm{H}}}\left( {\mathit{\boldsymbol{k}} - {{\hat v}_2}{\bf{1}}} \right)} \right]\left[ \begin{array}{l} {A_1}\exp \left( {{\rm{j}}{\phi _1}} \right)\\ {A_2}\exp \left( {{\rm{j}}{\phi _2}} \right) \end{array} \right] = X\left[ \mathit{\boldsymbol{k}} \right]. $ | (43) |
式(43)具有Pζ=q的形式, 可以采用最小二乘法求得ζ的估计为
| $ \mathit{\boldsymbol{\hat \zeta }} = {\left( {{\mathit{\boldsymbol{P}}^{\rm{H}}}\mathit{\boldsymbol{P}}} \right)^{ - 1}}{\mathit{\boldsymbol{P}}^{\rm{H}}}\mathit{\boldsymbol{q}}. $ | (44) |
此时,
如果X[k]只含有一个分量, 那么用类似的方法可以求得幅值和相位.
4 仿真验证将本文算法与文献[20]、[21]算法进行比较.三者的差别体现在频率和阻尼系数的估计上, 当这两者的估计值已知时, 幅值和相位可以用最小二乘法求得.只比较3种算法对信号的频率和阻尼系数的估计误差.
在Belega等[20]提出的算法中, 复频率v=f+α/2πj的估计为
| $ \hat v = {k_{\rm{f}}} + \frac{{2X\left[ {{k_{\rm{f}}} + 1} \right] - 2X\left[ {{k_{\rm{f}}} - 1} \right]}}{{X\left[ {{k_{\rm{f}}} + 1} \right] + X\left[ {{k_{\rm{f}}} - 1} \right] - 2X\left[ {{k_{\rm{f}}}} \right]}}, $ | (45) |
式中:X[kf]为DFT的峰值.将该方法称为比例法.
在Diao等[21]提出的算法中, 定义
| $ \rho = \frac{{X\left[ {{k_{\rm{f}}} + \lambda } \right]}}{{X\left[ {{k_{\rm{f}}}} \right]}},E = \exp \left( {2{\rm{ \mathsf{ π} j}}\frac{1}{N}} \right). $ | (46) |
式中:X[kf]为DFT的峰值, λ=sgn(|X[kf+1]|-|X[kf-1]|).z=exp (α/N+2πj(f-kf)/N)满足
| $ \left( {1 - \rho {E^{ - \lambda }}} \right){z^2} + \left( {{E^\lambda } - {E^{ - \lambda }}} \right)\left( {1 + \rho } \right)z + \rho {E^\lambda } - 1 = 0, $ | (47) |
即求解式(47)的根,可以得到频率和阻尼系数的估计.本节将该方法称为求根法.
3种算法具有相同的加窗和FFT操作以及不同的对X[k]的插值处理.其中加窗操作需要的计算量均为O(N), FFT操作需要的计算量均为O(Nlog(N)).因为N取值较大(比如1 024), 与加窗和FFT操作相比, 3种算法插值处理的计算量可以忽略.具体而言, 比例法的插值处理式(45)所需计算量最小, 求根法的插值处理式(47)所需计算量其次, 本文的插值处理式(25)、(32)所需计算量最大.本文算法中, 式(25)需要5×5的矩阵和5×1的向量相乘, 共25次乘法和20次加法, 远小于O(Nlog(N)), 可以忽略;式(32)需要3×3矩阵的奇异值分解, 由于任意方阵Aq的奇异值分解计算量为O(q3), 式(32)的计算量可以忽略.3种算法都具有较高的计算效率.
4.1 单分量信号的估计在单分量信号的估计中, 设信号表达式为
| $ \begin{array}{*{20}{c}} {s\left[ n \right] = A\exp \left( {\alpha \frac{n}{N}} \right)\exp \left( {2{\rm{ \mathsf{ π} j}}f\frac{n}{N} + {\rm{j}}\phi } \right) + u\left[ n \right];}\\ {n = 0,1, \cdots ,N - 1,} \end{array} $ | (48) |
式中:A=1, ϕ在[0, 2π]中均匀分布, α和f在不同的仿真中设置不同, u[n]为标准差为σ的白色高斯噪声.
参数θ∈{α, f}的估计误差使用均方根误差(RMSE)来描述:
| $ {\rm{RMSE}}\left( {\hat \theta } \right) = \sqrt {\frac{1}{R}\sum\limits_{r = 1}^R {{{\left( {\hat \theta - \theta } \right)}^2}} } , $ | (49) |
式中:R为仿真的次数.
先后比较在不同的频率f、不同的阻尼系数α和不同的信噪比A2/(2σ2)下3种算法的性能.其中, 本文算法取3个插值点分析对应的1个分量.
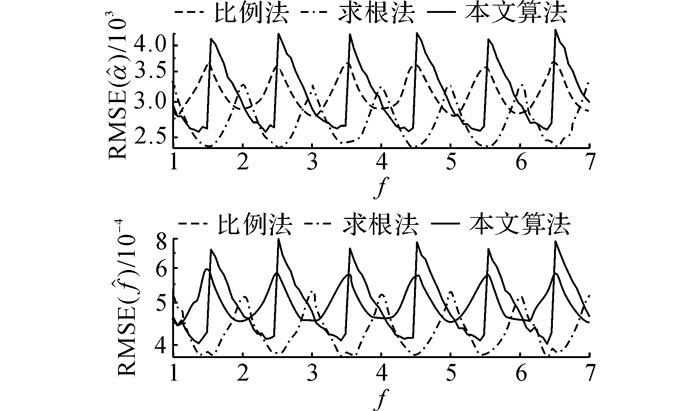
在第1个仿真中, 设α在[-2, 2]内均匀分布, 噪声标准差为σ=0.01, 对固定的f∈[1, 7], 执行R=104次估计, 得到的结果如图 2所示.
|
图 2 不同频率下阻尼系数和频率的估计误差 Fig. 2 Estimation errors of damping factors andfrequencies for signals with different frequencies |
由图 2可知, 3种算法的估计精度十分相近, 它们对阻尼系数和频率的估计误差均随频率呈现周期变化.
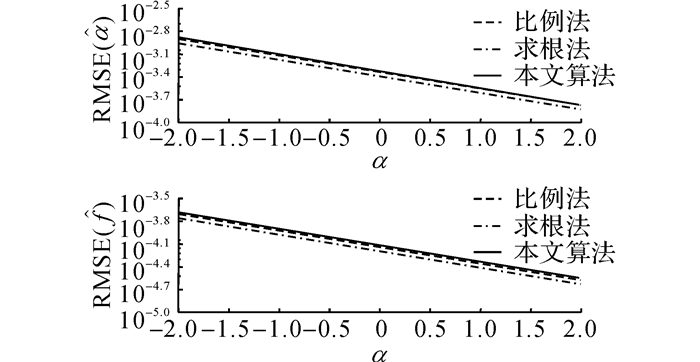
在第2个仿真中, 设f在[2, 3]内均匀分布, 噪声标准差为σ=0.01, 对固定的α∈[-2, 2], 执行R=104次估计, 得到的结果如图 3所示.
|
图 3 不同阻尼系数下阻尼系数和频率的估计误差 Fig. 3 Estimation errors of damping factors and frequencies for signals with different damping factors |
由图 3可知, 3种算法的估计精度十分相近, 它们对阻尼系数和频率的估计误差均随阻尼系数的增大而减小.这是因为阻尼系数越大, 信号的能量越大, 在噪声的能量不变的情况下, 算法的估计更准确.
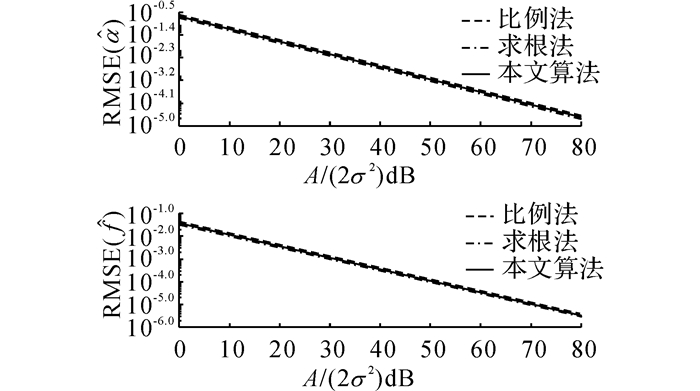
在第3个仿真中, 设α在[-2, 2]内均匀分布, f在[2, 3]内均匀分布, 对固定的A2/2σ2∈[0, 80] dB, 执行R=104次估计, 得到的结果如图 4所示.
|
图 4 不同信噪比下阻尼系数和频率的估计误差 Fig. 4 Estimation errors of damping factors and frequencies for signals with different SNR |
由图 9可知, 3种算法的估计精度十分相近, 它们对阻尼系数和频率的估计误差均随A2/(2σ2)的增大而减小, 这是因为A2/(2σ2)越大,信号的信噪比越大, 算法的估计更准确.
在上述3个仿真实验中可以发现,3种算法对单一分量的估计误差十分接近.文献[21]的算法估计精度略高, 这是因为它没有使用汉宁窗的近似公式(4), 而文献[20]和本文算法中均使用了这个近似公式.
4.2 双分量信号的估计在双分量信号的估计中, 设信号表达式为
| $ \begin{array}{l} s\left[ n \right] = A\exp \left( {\alpha \frac{n}{N}} \right)\exp \left( {2{\rm{ \mathsf{ π} j}}f\frac{n}{N} + {\rm{j}}\phi } \right) + \\ \;\;\;\;\;\;\;\;\;\;{A_{\rm{h}}}\exp \left( {{\alpha _h}\frac{n}{N}} \right)\exp \left( {2{\rm{ \mathsf{ π} j}}{f_{\rm{h}}}\frac{n}{N} + {\rm{j}}{\phi _{\rm{h}}}} \right) + u\left[ n \right];\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;n = 0,1, \cdots ,N - 1. \end{array} $ | (50) |
式中:A=1, ϕ和ϕh相互独立并在[0, 2π]中均匀分布, α和αh相互独立并在[-2, 2]中均匀分布, f在[2, 3]中均匀分布, {Ah, fh}在不同的仿真中设置不同, u[n]为标准差为σ的白色高斯噪声.
本文称{A, ϕ, α, f}为主要分量的参数, 称{Ah, ϕh, αh, fh}为次要分量的参数.因为文献[20-21]的算法只能测量单分量, 先后比较在不同的频率差fh-f、不同的幅值比Ah/A和不同的信噪比A2/(2σ2)下, 3种算法对主要分量的估计, 给出本文算法对次要分量的估计.仿真取kf为最接近f的整数.
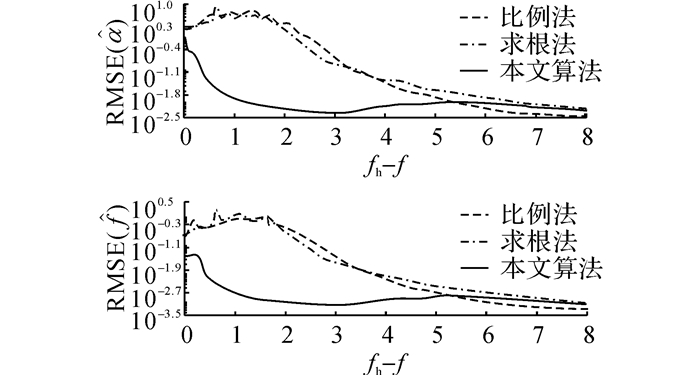
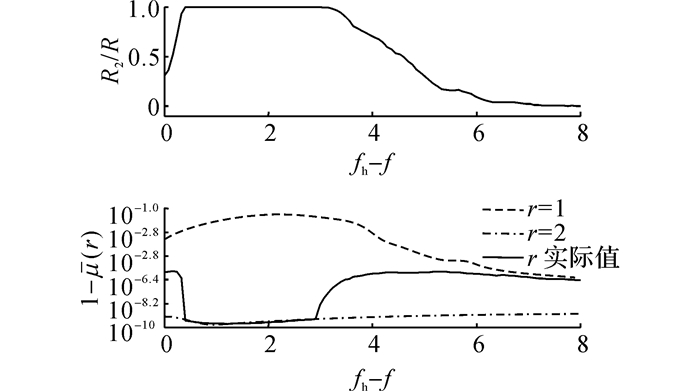
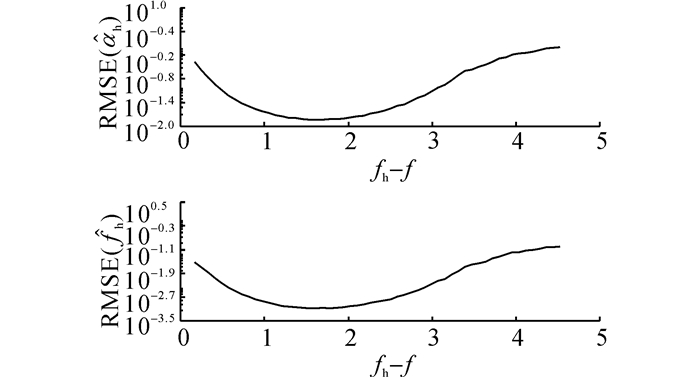
在第一个仿真中, 设Ah=0.5, 噪声标准差σ=0.01, 对固定的fh-f∈[0, 8], 执行R=104次估计, 得到的结果如图 5~7所示.如图 5所示为在不同频率差下, 3种算法对主要分量的估计误差;在R次仿真中, 定义R1和R2分别为本文算法检测到单分量和双分量的次数(显然R=R1+R2), 如图 6所示为双分量的检测比例R2/R以及有效秩为1、2或按阈值取值时的Frobenius范数比;如图 7所示为当R2/R>0.5时, 次要分量的估计误差.
|
图 5 不同频率差下主要分量的估计误差 Fig. 5 Estimation errors of primary component for various frequency differences of two components |
|
图 6 不同频率差下双分量检测比例以及Frobenius范数比相关曲线 Fig. 6 Dual-component detection ratios and Frobenius norm ratios for various frequency differences of two components |
|
图 7 不同频率差下次要分量的估计误差 Fig. 7 Estimation errors of secondary component for various frequency differences of two components |
1) 当fh-f>5时, 3种算法对主要分量的估计误差趋于一致, 并且本文算法的双分量检测比例逐渐下降, 这是因为汉宁窗的主瓣宽度为4 bin; 再考虑到非同步采样, 当2个分量在频域上的距离超出5 bin时, 分量之间的影响可以忽略, 此时对双分量信号的估计事实上退化成对单分量信号的估计.
2) 当fh-f∈(0.5, 3)时, 利用该算法始终检测出双分量, 并且主要分量和次要分量的估计误差极小, 其他2种算法失效.
3) 当fh-h接近于0时, 该算法有较高的概率将信号检测为单分量, 这是因为2个分量在频域上相互重叠, 此时本文的算法估计误差最小.
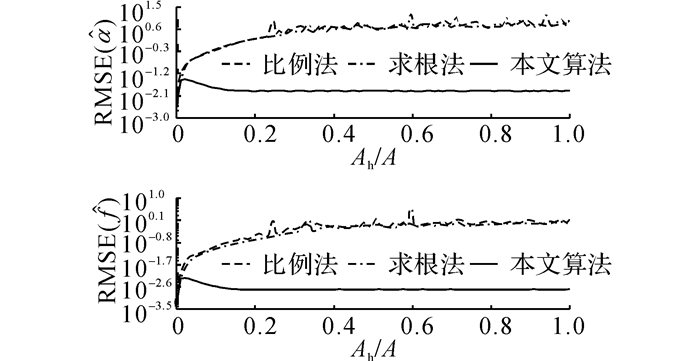
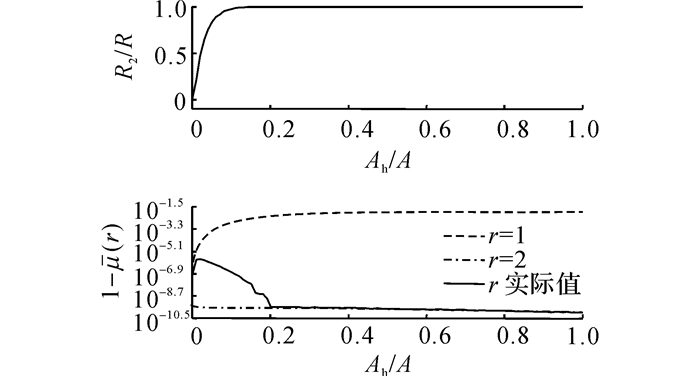
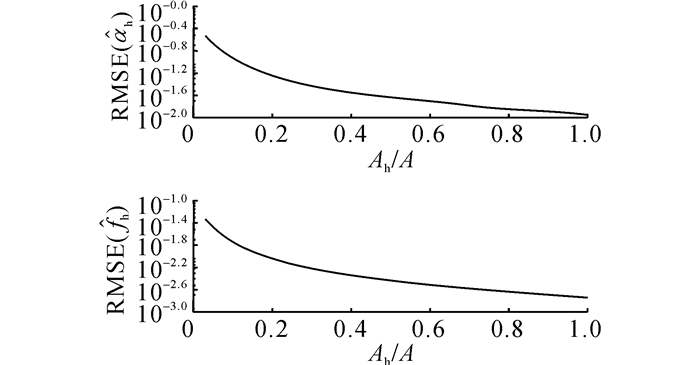
在第2个仿真中, 设fh-f=1, 噪声标准差σ=0.01, 对固定的Ah/A∈[0, 1], 执行R=104次估计, 得到的结果如图 8~10所示, 图 8~10的含义与不同频率差下的仿真相同.比较图 8~10可得如下结论.
|
图 8 不同幅值比下主要分量的估计误差 Fig. 8 Estimation errors of primary component fordifferent amplitude ratios of two components |
|
图 9 不同幅值比下双分量检测比例及Frobenius范数比相关曲线 Fig. 9 Dual-component detection ratios and Frobenius norm ratios for different amplitude ratios of two components |
|
图 10 不同幅值比下次要分量的估计误差 Fig. 10 Estimation errors of secondary component for different amplitude ratios of two components |
1) 当Ah/A < 0.01时, 3种算法对主要分量的估计误差基本一致, 并且本文算法有较高的概率检测为单一分量, 这是因为次要分量的幅值较小, 被噪声掩盖了;
2) 当Ah/A>0.2时, 本文算法始终检测出双分量, 并且主要分量和次要分量的估计误差极小, 其他2种算法失效.
3) 当有效秩取2时, 1-μ(r)与Ah/A在对数坐标系下成负线性关系(斜率接近于0), 这是因为此时1-μ(r)可以用来衡量噪声占总体信号的比例, 当Ah增大时, 噪声占总体信号的比例变小.
4) 有效秩取1时, 1-μ(r)随着Ah/A的增大而增大(逐渐接近饱和), 这是因为此时1-μ(r)可以用来衡量次要分量和噪声共同占据总体信号的比例, 随着次要分量的比例变大, 1-μ(r)逐渐变大.
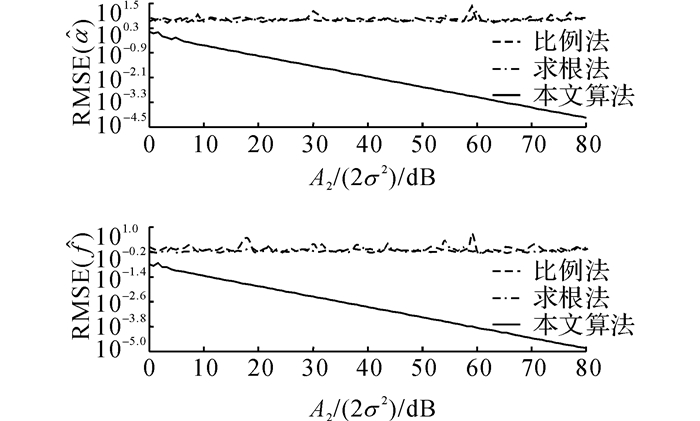
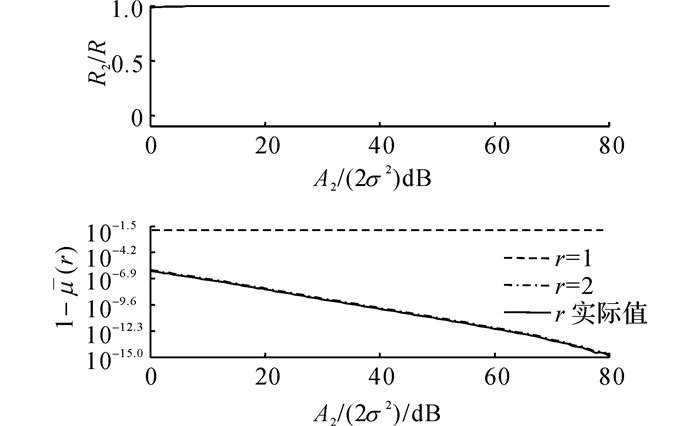
在第3个仿真中, 设Ah=0.5, fh-f=1, 对固定的A2/(2σ2)∈[0, 80]dB, 执行R=104次估计, 得到的结果如图 11~13所示.图 11~13的含义与不同频率差下的仿真相同.比较图 11~13可得如下结论.
|
图 11 不同信噪比下主要分量的估计误差 Fig. 11 Estimation errors of primary component fordifferent |
|
图 12 不同信噪比下双分量检测比例及Frobenius范数比相关曲线 Fig. 12 Dual-component detection ratios and Frobenius norm ratios for different SNRs |
|
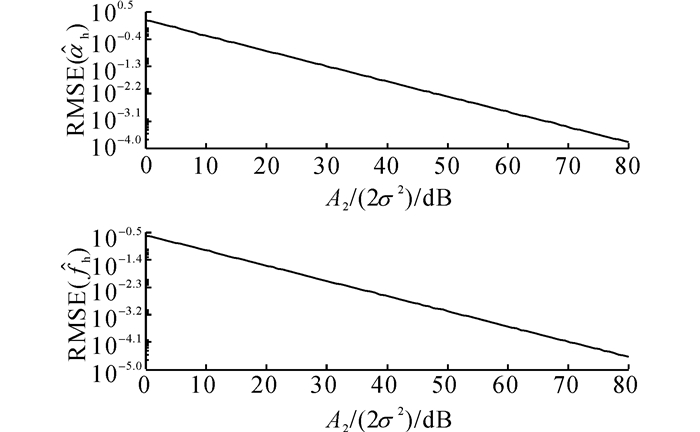
图 13 不同信噪比下次要分量的估计误差 Fig. 13 Estimation errors of secondary component for different SNRs |
1) 本文算法在A2/(2σ2)∈[0, 80]dB变化的过程中, 始终检测出双分量, 并且主要分量和次要分量的估计误差随着A2/2σ2的增大而减小, 其他2种算法失效.
2) 有效秩取2时, 1-μ(r)与A2/2σ2在对数坐标系下成负线性关系, 这是因为此时1-μ(r)可以用来衡量噪声占总体信号的比例, 当信噪比变大时, 噪声占总体信号的比例变小;
3) 当有效秩取1时, 1-μ(r)基本保持不变, 这是因为此时1-μ(r)可以用来衡量次要分量和噪声共同占据信号的比例, 次要分量的能量固定并且远远高于噪声, 曲线可以近似为次要分量占信号的比例, 并且该比例是一个常量.
由上述3个仿真实验可知,本文算法对重叠双分量十分有效, 这里的重叠指2个分量在频谱上的距离小于4 bin.文献[20]、[21]的算法均不能处理这种情况.
5 结语利用提出的频域Prony算法可以解决衰减多谐波信号中存在重叠双分量时的估计问题.当双分量在频域上的距离小于4 bin时, 常规的算法不再适用, 本文的算法能够处理这一情况.
给定DFT峰值附近的5个点, 该算法可以利用汉宁窗的性质将复频率估计问题转化为二元高次方程组.通过Prony方法, 这个方程组的求解可以转化为差分方程的参数估计.将差分方程写成矩阵形式之后, 差分方程的参数估计可以通过矩阵的奇异值分解得到.本文利用近似矩阵和原矩阵的Frobenius范数比估计出矩阵的有效秩, 确定插值点上含有的分量数目, 针对3种情况分别给出解决方案.此外, 在已知复频率估计值的情况下, 谐波分量的幅值相位估计可以通过最小二乘法获得.
本文的仿真部分比较了本文与文献[20]、[21]中2种典型算法的估计误差.当信号的插值点仅包含单分量时, 三者的估计误差十分接近;当信号的插值点上含有重叠双分量时, 本文算法能够准确估计出2个分量的复频率, 文献[20]、[21]中的算法失效.
本文算法可以扩展到插值点同时包含3个及3个以上分量的情况, 此时插值点的数量需要增加, 常系数矩阵M需要重新计算.
| [1] |
CHEN C I, CHANG G W. An efficient Prony-based solution procedure for tracking of power system voltage variations[J]. IEEE Transactions on Industrial Electronics, 2013, 60(7): 2681-2688. DOI:10.1109/TIE.2012.2196896 |
| [2] |
ZYGARLICKI J, MROCZKA J. Variable-frequency Prony method in the analysis of electrical power quality[J]. Metrology and Measurement Systems, 2012, 19(1): 39-48. |
| [3] |
ZHOU Z, SO H C. Linear prediction approach to oversampling parameter estimation for multiple complex sinusoids[J]. Signal Processing, 2012, 92(6): 1458-1466. DOI:10.1016/j.sigpro.2011.12.003 |
| [4] |
ZHOU Z, SO H C, CHRISTENSEN M G. Parametric modeling for damped sinusoids from multiple channels[J]. IEEE Transactions on Signal Processing, 2013, 61(15): 3895-3907. DOI:10.1109/TSP.2013.2260334 |
| [5] |
CHAKIR M, KAMWA I, LE HUY H. Extended C37. 118.1 PMU algorithms for joint tracking of fundamental and harmonic phasors in stressed power systems and microgrids[J]. IEEE Transactions on Power Delivery, 2014, 29(3): 1465-1480. DOI:10.1109/TPWRD.2014.2318024 |
| [6] |
RAY P K, SUBUDHI B. Ensemble-Kalman-filter-based power system harmonic estimation[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(12): 3216-3224. DOI:10.1109/TIM.2012.2205515 |
| [7] |
BAGHERI A, MARDANEH M, RAJAEI A, et al. Detection of grid voltage fundamental and harmonic components using Kalman filter and generalized averaging method[J]. IEEE Transactions on Power Electronics, 2016, 31(2): 1064-1073. DOI:10.1109/TPEL.2015.2418271 |
| [8] |
BORKOWSKI J, KANIA D, MROCZKA J. Interpolated-DFT-based fast and accurate frequency estimation for the control of power[J]. IEEE Transactions on industrial Electronics, 2014, 61(12): 7026-7034. DOI:10.1109/TIE.2014.2316225 |
| [9] |
CANDAN Ç. Fine resolution frequency estimation from three DFT samples:case of windowed data[J]. Signal Processing, 2015, 114: 245-250. DOI:10.1016/j.sigpro.2015.03.009 |
| [10] |
BELEGA D, DALLET D. Estimation of the multifrequency signal parameters by interpolated DFT method with maximum sidelobe decay[C]//4th IEEE Workshop on. Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications. Dortmund: IEEE, 2007: 294-299. https://ieeexplore.ieee.org/document/4488425/
|
| [11] |
刘昊, 王猛, 王昌吉, 等. 一种实时精确估计电力谐波和间谐波参数的方法[J]. 电力系统自动化, 2014, 38(20): 90-95. LIU Hao, WANG Meng, WANG Chang-ji, et al. A real-time accurate estimating method for electric power harmonics and inter-harmonics[J]. Automation of Electric Power Systems, 2014, 38(20): 90-95. DOI:10.7500/AEPS20140130003 |
| [12] |
贾清泉, 杨晓雯, 宋知用. 一种电力系统谐波信号的加窗频移算法[J]. 中国电机工程学报, 2014, 34(10): 1631-1640. JIA Qing-quan, YANG Xiao-wen, SONG Zhi-yong. A window frequency shift algorithm for power system harmonic analysis[J]. Proceedings of the CSEE, 2014, 34(10): 1631-1640. |
| [13] |
刘亚梅, 惠锦, 杨洪耕. 电力系统谐波分析的多层DFT插值校正法[J]. 中国电机工程学报, 2012, 32(25): 182-188. LIU Ya-mei, HUI Jin, YANG Hong-geng. Multilayer DFT interpolation correction approach for power system harmonic analysis[C]//Proceedings of the CSEE. 2012, 32(25): 182-188. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgdjgcxb201225023 |
| [14] |
蒋春芳, 刘敏. 基于双插值FFT算法的间谐波分析[J]. 电力系统保护与控制, 2010(3): 11-14. JIANG Chun-fang, LIU Min. Inter-harmonics analysis based on double interpolation FFT algorithm[J]. Power System Protection and Control, 2010(3): 11-14. DOI:10.7667/j.issn.1674-3415.2010.03.003 |
| [15] |
惠锦, 杨洪耕. 用于谐波/间谐波分析的奇数频点插值修正法[J]. 中国电机工程学报, 2010, 30(16): 67-72. HUI Jin, YANG Hong-geng. An approach for harmonic/inter-harmonic analysis based on the odd points interpolation correction[J]. Proceedings of the CSEE, 2010, 30(16): 67-72. |
| [16] |
马晓春, 刘旭东. 一种电力谐波分析新算法[J]. 中国电机工程学报, 2013, 33(18): 6-8. MA Xiao-chun, LIU Xu-dong. A novel algorithm for electric power system harmonic analysis[J]. Proceedings of the CSEE, 2013, 33(18): 6-8. |
| [17] |
曹健, 林涛, 徐遐龄, 等. 基于最小二乘法和时频原子变换的谐波/间谐波测量算法[J]. 电工技术学报, 2011, 26(10): 1-7. CAO Jian, LIN Tao, XU Xia-ling, et al. Monitoring of power system harmonic/inter-harmonics based on least squares algorithm and time frequency transform[J]. Transactions of China Electrotechnical Society, 2011, 26(10): 1-7. |
| [18] |
贾清泉, 姚蕊, 王宁, 等. 一种应用原子分解和加窗频移算法分析频率相近谐波/间谐波的方法[J]. 中国电机工程学报, 2014, 34(27): 4605-4612. JIA Qing-quan, YAO Rui, WANG Ning, et al. An approach to detect harmonics/inter-harmonics with closing frequencies using atomic decomposition and windowed frequency shifting algorithm[J]. Proceedings of the CSEE, 2014, 34(27): 4605-4612. |
| [19] |
周菁菁, 王彭, 赵春宇, 等. 基于频率搜索的间谐波闪变检测方法[J]. 电力系统自动化, 2014, 38(7): 60-65. ZHOU Jing-jing, WANG Peng, ZHAO Chun-yu, et al. A detection method of interharmonics-caused flicker based on frequency-searching[J]. Automation of Electric Power Systems, 2014, 38(7): 60-65. DOI:10.7500/AEPS20130816001 |
| [20] |
BELEGA D, PETRI D. Frequency estimation by two-or three-point interpolated Fourier algorithms based on cosine windows[J]. Signal Processing, 2015, 117: 115-125. DOI:10.1016/j.sigpro.2015.05.005 |
| [21] |
DIAO R, MENG Q. An interpolation algorithm for discrete Fourier transforms of weighted damped sinusoidal signals[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(6): 1505-1513. DOI:10.1109/TIM.2013.2289585 |
| [22] |
张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004, 17.
|



