2. 山东理工大学 交通与汽车工程学院, 山东 淄博 255000;
3. 大连理工大学 交通运输工程学院, 辽宁 大连 116024
2. College of Transportation and Automotive Engineering, Shandong University of Technology, Zibo 255000, China;
3. College of Communication and Transportation Engineering, Dalian University of Technology, Dalian 116024, China
信号控制是保障交叉口安全性、提升交通流运行效率的重要手段.现有交通信号控制系统多具备自适应功能, 依靠环形线圈检测器统计交通流的时变特性, 进而以车辆延误、排队长度等指标最优为目标确定信号控制策略及信号控制方案[1-3].在实际应用中, 线圈检测器的损坏率及故障率很高[4-5], 且其他类型的检测器数据, 包括视频、微波、地磁等均很难直接接入现有信号控制系统, 致使很多信号控制器只能采用固定式配时方案.作为自适应控制的一种降级策略, 信号控制器通常须配置多套固定式多时段备用方案, 在数据感应、传输、接收故障等现象发生时, 依据实际情况合理选择备用方案[6].
目前, 时段划分的相关研究成果很少.在实际应用中, 交通工程师多根据交叉口总流量的大致变化规律, 将一天划分为若干时段, 典型的如高峰时段、平峰时段、低峰时段等[7].这种经验式的划分方法很难得到最优解[8];不同工程师有着个性化经验, 针对同一对象,划分结果往往表现出很大的差异性, 且不利于协调控制整体效益的提升.在理论探索方面, 一些学者建立基于数据聚类的时段划分算法.如Smith等[7]以交叉口交通流量和时间占有率为指标, 利用K-means算法划分控制时段, 采用分类回归树评估划分结果;Wang等[9]引入非层次聚类, 针对离群点从平滑处理的角度梳理了人工调整原则;针对K-means方法需要事先输入分类个数的缺陷, Ratrout[10]引入减法聚类, 利用Synochro仿真获取最佳聚类数.此外, Park等[8, 11-14]基于人工智能算法构建了一类时段划分方法, 包括遗传算法[11-13]、非支配排序遗传算法(non-dominated sorting genetic algorithm-II, NSGAII)[8]、加强学习算法等[14].
以上方法对单点定时控制有很大的参考价值, 但存在如下问题:1)多数方法不能自动优化合理的聚类数目, 需要多次对比实验数据才能得到最佳结果;2)具备自动输出聚类数目的方法多通过全枚举的方式, 计算时间复杂度较大;3)得到最佳聚类个数之后,需后续人工调整才能确定时段划分结果, 属于半智能型的方法.针对以上不足, 本文利用动态递归有序聚类对流量序列进行聚类分割, 在降低算法时间复杂度的同时,自动输出最优方案.
1 模型建立有序聚类又称最优分割, 最早由Fisher提出, 主要是针对有序序列, 在不改变样本前后顺序的前提下寻求最优分割方法, 分割之后的每条子序列称为一类.该方法的基本原则为:最优解使得同类之间的相似度最大, 类间的相似度最小[15].有序聚类可以极大地减少离散点, 得到全局最优解, 同时不需要任何人工调整.通常情况下, 有序聚类包含类内离差计算(一般用类直径表示)、类间离差值测算(又称类间损失函数或目标函数)和最佳聚类数优化(又称分割数)3步.
1.1 类直径时段划分通常以天为基本时间单元, 即一天的流量数据为一条时间序列.设被选用时段划分的流量序列为A, 若A包含T个数据样本, 则时间序列可以表示为A={X1, X2, …, XT}.定义类G包含的数据样本有{Xi, Xi+1, …, Xj}(1≤i<j≤T), 则利用序号代表数据, 可以将类G记为
| $ G = \left\{ {i, i + 1, \cdots, j} \right\}. $ | (1) |
对于交通流量序列, 每一类均对应一个控制时段.在有序聚类中, 类内数据的差异程度即类内离差, 一般用类内直径来衡量.针对类G, G={i, i+1, …, j}, 类内离差即类内直径为
| $ D\left( {i, j} \right) = \left| {{X_t}-E_G^*} \right|t = \left( {i, i + 1, \cdots, j} \right). $ | (2) |
式中:D(i, j)为类G的类内离差, 即第i~j个数据样本之间所有样本的离散度;Xt为第t个序列样本所对应的流量;EG*为类G中所有流量的均值.
1.2 目标函数类内离差定义了类中方差的变化量, 进而可以利用所有类的离差累积和作为类间误差, 一个最优的分割方案必然确保类间误差最小.有序聚类中,将类间误差(又称损失函数)最小作为寻求最优方案的判别准则.
假设将某个时间序列的T个数据样本进行K次划分, it表示类间分割点, 记为it={i1, i2, …, iK}, 其中1=i1 < i2 < … < iK < T, 则分割情况可以表示为
| $ \begin{array}{l} \underbrace {\left[{{i_1}, {i_1} + 1, \cdots, {i_2}-1} \right]}_{{G_1}}\underbrace {\left[{{i_2}, {i_2} + 1, \cdots, {i_3}-1} \right]}_{{G_2}} \cdots \\ \underbrace {\left[{{i_K}, {i_K} + 1, \cdots, T} \right]}_{{G_K}}. \end{array} $ | (3) |
由式(3)可知, K次分割之后的时段个数为K.令b(T, K)表示上述分割方法, L[b(T, K)]表示这种分割方法的损失函数, 即类间离差, 则有
| $ L\left[{b\left( {T, K} \right)} \right] = \sum\limits_{t = 1}^K {D\left( {{i_t}, {i_{t + 1}} -1} \right)} . $ | (4) |
若p(T, K)代表一种最优的划分方案, 则有
| $ \begin{array}{l} p\left( {T, K} \right) = \arg \mathop {\min }\limits_{i \in \left\{ {1, 2, \cdots, T} \right\}} L\left[{b\left( {T, K} \right)} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{t = 1}^K {D\left( {{i_t}, {i_{t + 1}} -1} \right)} . \end{array} $ | (5) |
基础的有序分类算法是限定一个最大K, 在枚举并对比所有K全部分类方法损失值的基础上筛选最优方案, 算法复杂度为
| $ g\left( {T, K} \right) = O\left( {{T^2}K} \right). $ | (6) |
为了降低模型的时间复杂度, 有必要引入递归优化的思想, 即针对任何一种最优分割方式p(T, K), 该时间序列K次分隔最优的前提是(K-1)类分割最优, 也即在(K-1)次分割最优的基础上, 只需对比(K-1)个K次分割方法便可得到最优K次分隔.在基础的有序聚类方法中, 针对分割方式b(T, K), 共有CT-1K-1种具体分法, 损失函数的递推公式为
| $ \left. \begin{array}{l} L\left[{b\left( {T, 2} \right)} \right] = \mathop {\min }\limits_{2 \le j \le T} \left\{ {D\left( {1, j - 1} \right) + D\left( {j, T} \right)} \right\}, \\ L\left[{b\left( {T, K} \right)} \right] = \mathop {\min }\limits_{K \le j \le T} \left\{ {L\left[{p\left( {j-1, K-1} \right)} \right] + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {D\left( {j, T} \right)} \right\}. \end{array} \right\} $ | (7) |
以式(7)为基础, 采用动态递推有序聚类的控制时间划分过程可以分解为如下步骤.
1) 针对特定划分方案b(T, K), 即固定T和K, 首先界定分段点iK, 使得L[b(iK-1, K-1)]+D(iK, T)达到最小, 即
| $ \begin{array}{l} L\left[{b\left( {{i_K}-1, K-1} \right)} \right] + D\left( {{i_K}, t} \right) = \\ \;\;\;\;\;\;\mathop {\min }\limits_{K \le {j_K} \le T} \left\{ {L\left[{b\left( {{j_K}-1, K-1} \right)} \right] + D\left( {{j_K}, T} \right)} \right\}. \end{array} $ | (8) |
2) 搜索倒数第2个分段点iK-1, 满足
| $ \begin{array}{l} L\left[{b\left( {{i_{K-1}}-1, K-2} \right)} \right] + D\left( {{i_{K - 1}}, t} \right) = \\ \;\;\;\;\;\;\mathop {\min }\limits_{K - 1 \le {j_{K - 1}} \le {i_k}} \left\{ {L\left[{b\left( {{j_{K-1}}-1, K-2} \right)} \right] + D\left( {{j_{K -1}}, {i_k}} \right)} \right\}. \end{array} $ | (9) |
3) 依次类推, 重复2), 得到分割数为K的最优解, 即当L[b(T, K)]最小时所对应的方案.
在采用递归动态规划后, 算法复杂度为
| $ g\left( {T, K} \right) = O\left( K \right). $ | (10) |
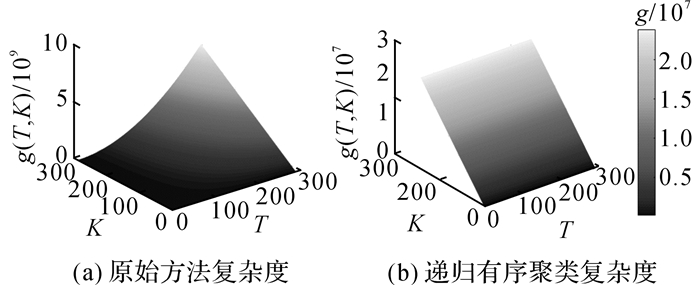
全枚举方法和动态递推下的方法的算法复杂度对比如图 1所示.
|
图 1 原始方法与递归有序聚类的时间复杂度 Fig. 1 Time complexity of original method and dynamic recurrence order clustering |
已知不同K下的最小L[b(T, K)], 如何选择最优的K是进行有序分割的另一关键问题.
1.3 最佳聚类数在理想情况下, 如果目标函数与K之间存在非单调关系, 获取最佳的K异常简单.在多数情况下, 目标函数值会随着K的增大而单调递减, 此时需要明确的判别准则才能提取最优的K.具体方法可以分为2类:1)经验法, 依靠工程师的实践经验, 结果具有很强的主观性, 更不具有一般性;2)阈值法, 满足L[p(T, K-1)]+L[p(T, K)] < δ(δ>0)的K为最佳分割数, 但对于如何确定阈值δ是一大难题, 不合适的δ会对聚类结果产生很大的影响.
为了克服上述方法所存在的缺陷, 参考常用聚类数目选择中的“拐点方法”, 将目标函数趋势图中“拐点”所对应的K界定为最佳分割数.现有算法须人工识别“拐点”, 缺乏智能性并存在一定的随机性.由于损失函数是一典型的凹函数, 斜率与K单调负相关, 变化率在拐点处最显著.为此,将上述问题转化为优化问题, 即计算任意2个相邻K下的最优分割损失值离差斜率, 斜率突变位置的K为最佳分割数Kop.令K次分割和(K+1)次分割所对应的离差斜率为tan K, 则有
| $ \tan K = L\left[{p\left( {T, K + 1} \right)} \right] - L\left[{p\left( {T, K} \right)} \right]. $ | (11) |
令前、后2个连续斜率的变化率为diff, 则有
| $ {\rm{diff}}\left( {{K^*}} \right) = \left| {\frac{{\tan K-\tan \left( {K-1} \right)}}{{\tan K-\tan \left( {K + 1} \right)}}} \right|. $ | (12) |
最佳分割数Kop为
| $ {K_{{\rm{op}}}} = {K^*};{\rm{s}}{\rm{.t}}{\rm{.diff}}\left( {{K^*}} \right) = \max \left\{ {{\rm{diff}}\left( K \right)} \right\}. $ | (13) |
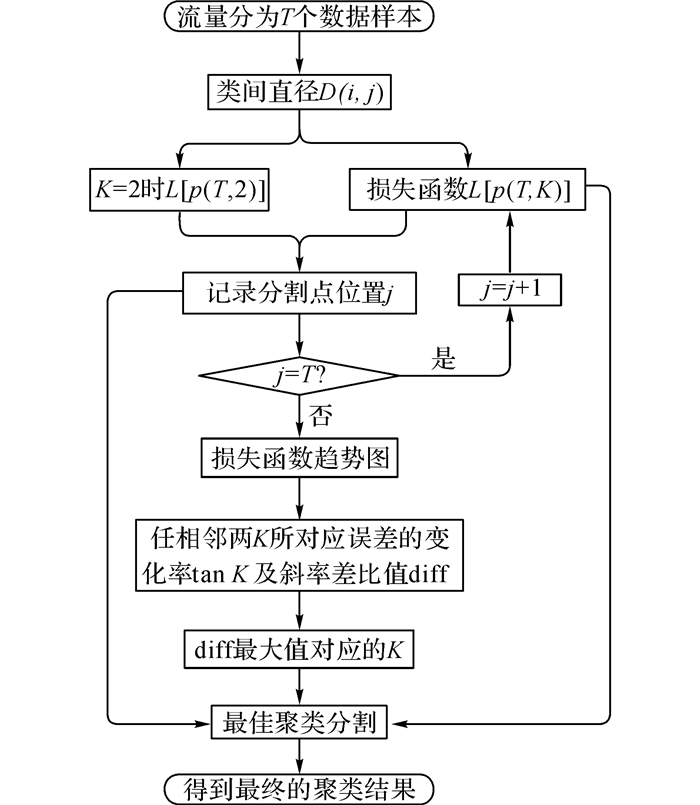
综上所述, 递归有序聚类时段划分流程如图 2所示.
|
图 2 递归有序聚类时段划分流程图 Fig. 2 Flow chart of dynamic recurrenceorder clustering |
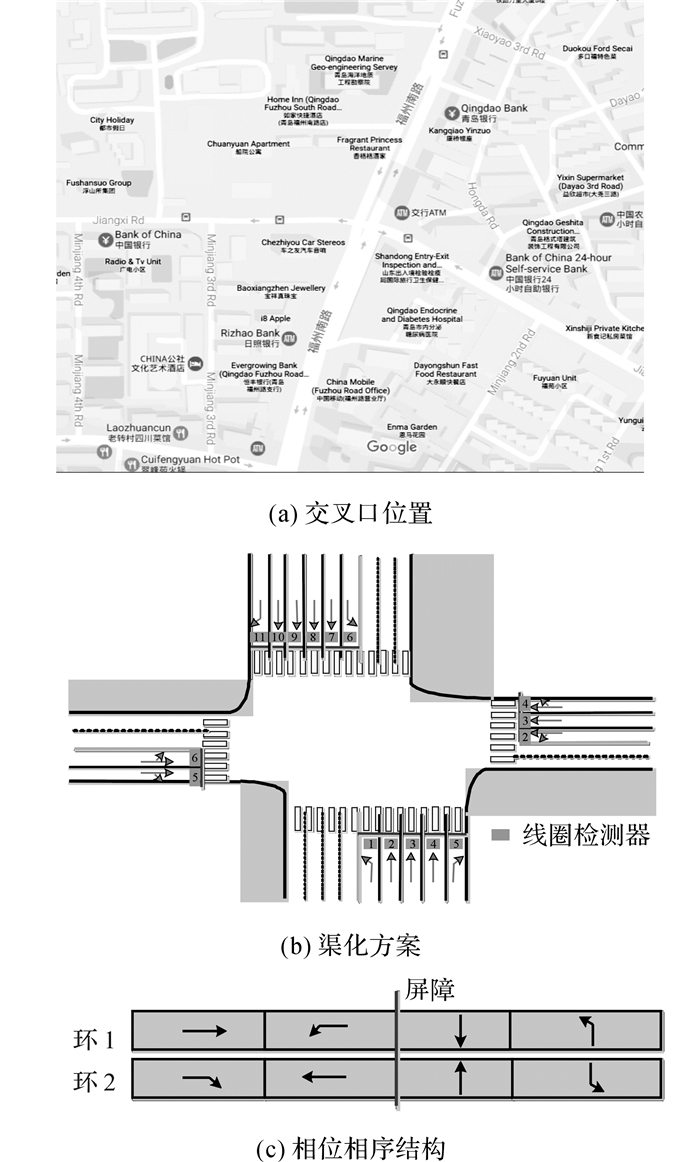
为了验证该算法的有效性, 以青岛市江西路-福州南路交叉口为研究对象(见图 3), 具体的几何布局属性如下:1)东西进口两车道, 北进口6车道, 南进口5车道;2)北、南、西、东4个进口道的长度分别为562、426、413和443 m;3)交叉口采用固定式的信号配时方案;4)路段进出口流量很低, 对干线交通流的影响很小;5) 4条进口道均不允许路侧停车.
|
图 3 算法验证实验测试区域 Fig. 3 Algorithm verification of intersection |
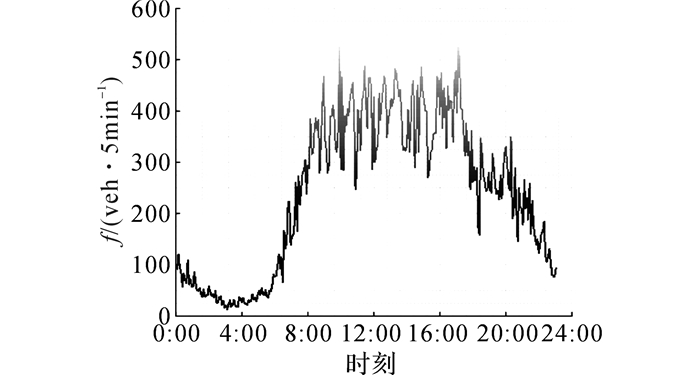
该路口布设有闯红灯自动记录系统, 可以统计每条车道的交通流量、时间占有率等信息.由于右转车辆不受信号控制, 取所有进口的直行和左转车辆总和表征交叉口的总交通需求.通过青岛市交通管控平台,以5 min为时间间隔,调取2016年7月9号的流量数据, 分布规律如图 4所示.
|
图 4 交叉口7月9日流量分布 Fig. 4 Flow distribution of Jul.9 |
由于常规K-means聚类方法仅考虑交通流量的数值属性, 同一类内的数据点由于时间上的不连续性, 须将同一类的时间序列划分为不同部分, 即需要后续人工调整;时段数通常多于聚类数.由于任何一类样本都可能被划分为很多时段, 人工调整后通常会出现一些很短的时段, 即离散点, 致使信号方案频繁切换.在信号控制中, 频繁切换方案会干扰驾驶员的驾驶行为, 带来一定的安全隐患.为了避免这一问题, 原始划分方案需要二次调整, 一个通常被遵循的原则是单个时段的时间长度不小于45 min[13].这一原则的合理性有待商榷, 且同一原则下会有不同的调整方案, 最终结果具有一定的随机性, 更难以保证全局最优性.
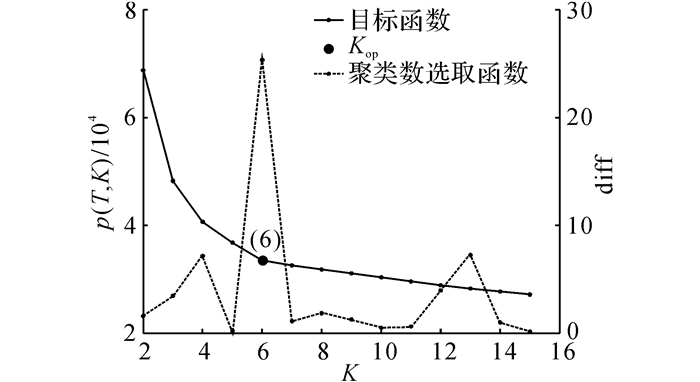
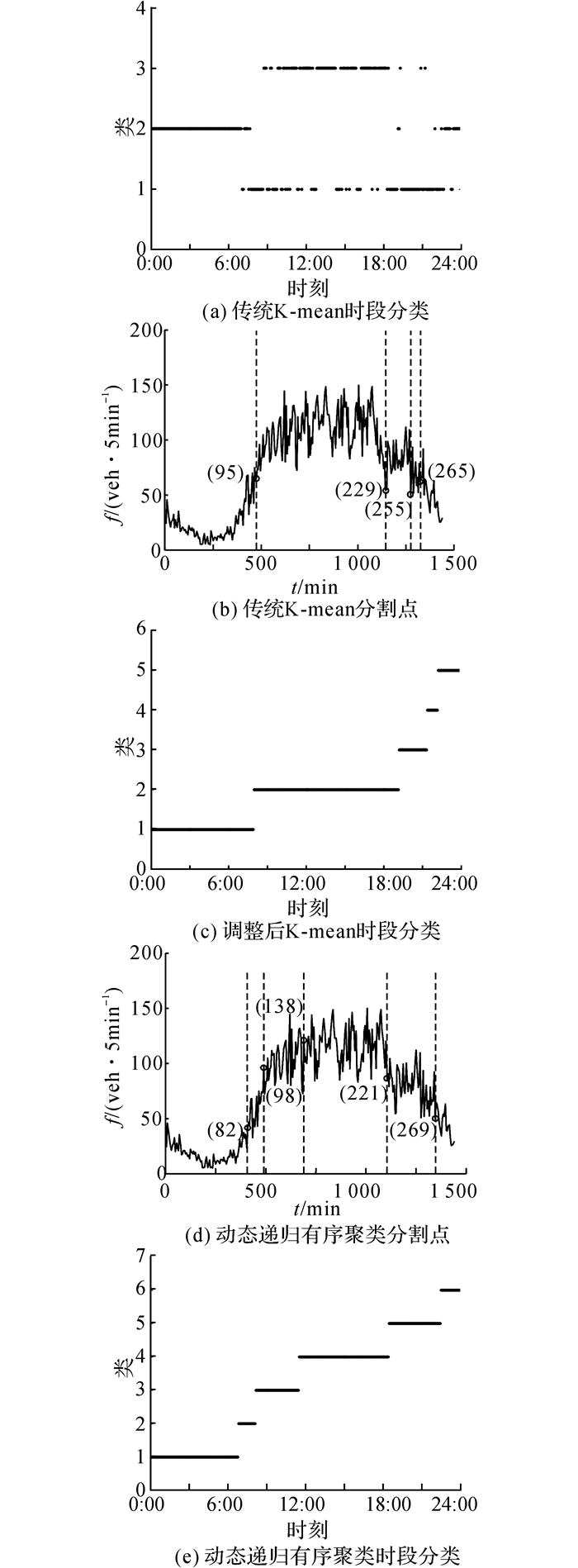
以图 3的交叉口、图 4的流量数据为例, p(T, K)和离差斜率的趋势如图 5所示, 拐点所对应的K为6, 故新方法的最佳分割个数为6, 即一天24 h应被分为6个时段.原始K-means、人工调整后的K-means以及本文方法的优化结果如图 6所示.图中,f为流量.从直观上看, 原始K-means方法的时段过密, 不能直接用于信号控制, 对其人工调整后合并为5个时段, 且分布相对集中.新方法的时段总数适中, 分布相对均匀, 很好地适应了交通流的变化模式.
|
图 5 分割数分析图 Fig. 5 Analysis chart of clustering number |
|
图 6 调整前、后K-mean方法与动态递归有序聚类的分割点和时段分类 Fig. 6 TOD breakpoints and TOD interval classifications of K-means before and after adjustment and dynamic recurrence order clustering |
一个直接有效的评价方法应该是将不同方案应用于实际控制, 通过收集、整理、对比不同方案下交通流运行数据完成方法验证.该方式存在如下问题:交通流具有很强的不可再现性, 任意两天之间的流量模式均会有所差异, 不同流量模式下很难比较方案间的实施效果.借助VISSIM仿真确保在完全相同的流量情况下验证方法优劣性[16-18].
为了展示时段调整对交通流运行效率的影响, 所有信号方案均保持相位相序结构不变, 方案如图 3(c)所示.针对某一时段, 可以用该时段内各个车道组的平均交通流量优化信号周期和相位绿信比, 具体的优化方法有很多.采用经典的Webster算法计算周期时长并基于等饱和度原则分配相位绿信比,
| $ {C_0} = \frac{{1.5L + 5}}{{1-\sum\nolimits_{p = 1}^Z {\frac{{{q_p}}}{{{s_p}}}} }}, $ | (14) |
| $ {g_p} = \max \left\{ {{g_{p, \min }}, \frac{{{q_p}/{s_p}}}{{\sum\nolimits_{p = 1}^Z {{q_p}/{s_p}} }}} \right\}. $ | (15) |
式中:C0为信号周期时长;L为所有相位的总损失时间, 一般取为所有相位总绿灯间隔时间之和, 本文取为20 s;qp为相位p的关键车道组流量;sp为相位p所对应的关键车道组饱和流量;Z为相位数;qp为相位p的绿灯时长;gp, min为确保行人过街安全性的相位最小绿灯时长, 本文取为15 s.K-means人工调整后和新方法优化得到的TOD方案与相应的信号控制方案如表 1所示.表中,ge、gw、gsns、gsnl分别为东进口、西进口、南北直行和南北左转绿灯时间.
| 表 1 时段划分及信号控制方案 Table 1 Time division and signal control plan |
在VISSIM仿真中,有很多驾驶行为和路径选择行为的模型参数, 均采用默认值, 不影响方案优劣性对比分析结果.借助VISSIM软件中的VAP模块,将多时段控制方案嵌入至仿真模型.为了考虑方案的随机性, 每种方案下仿真10次, 仿真种子数从42变化至51.
在评价过程中, 若评价时间间隔设置过短, 则交通流的运行效率指标会存在较大波动.例如针对某相位, 若评价时间间隔等于绿灯时长且相位绿信比为0.5, 则每一个红灯和绿灯时长均可以视为一个评价时段, 而绿灯期间的排队长度和车均延误必然较红灯期间大幅降低, 运行效率指标呈现出周期性的突变.为了避免这一现象, 通常将评价时间间隔设置为15 min.
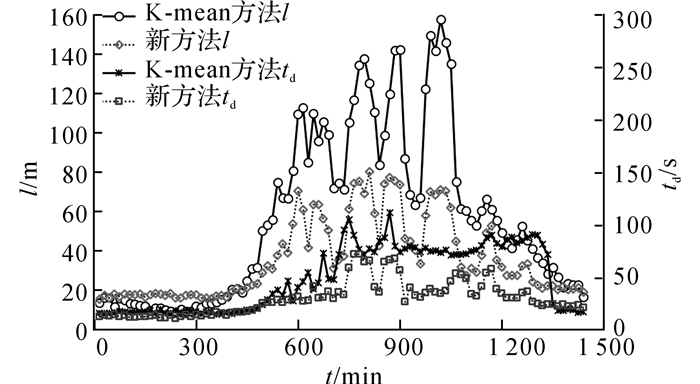
基于优秀时段划分方案的信号控制方案必然可以提升交通流的运行效率, 降低高峰时段的排队长度l和车均延误td;针对平峰尤其是低峰时段, 不同时段下的信号控制方案往往差异不大, 相应的运行效率指标相对接近, 如图 7所示.
|
图 7 不同方案下评价间隔内的运行效率 Fig. 7 Operation efficiency of different schemes in various time intervals |
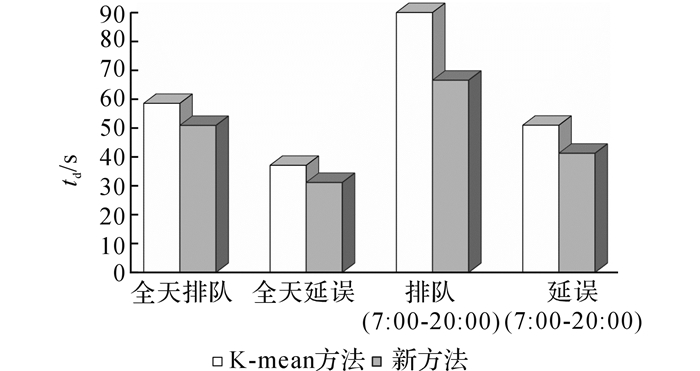
以全天24 h为评价范围, 新方案相对于传统方案(K-means聚类优化方案)的车均延误和平均排队长度降低了16.02%和13.05%;若以7:00-20:00为评价范围, 则新方法相对于传统方法2个指标的下降幅度分别是19.05%和26.04%, 如图 8所示.采用新方法显著提升了交通流的整体运行效率, 尤其是高流量时段的运行效率.
|
图 8 不同方案下全天平均运行效率 Fig. 8 Average operation efficiency of different schemes for the whole day |
以算法复杂度来评价, 直接采用传统的有序聚类方法所需的运算时间为4.25 h, 动态规划递归下的有序聚类方法所需的运算时间仅为0.25 s, 极大地降低了模型复杂度和运算时间, 适合于大规模数据的应用.
4 结语本文基于有序聚类提出信号控制时段划分方法, 引入动态递归,建立最佳分割数和最优划分方案的搜索方法.该方法可以直接输出划分结果, 无需任何人工调整;相对于传统的有序聚类方法, 时间复杂度极大降低.基于青岛市实际路网及实测数据进行仿真验证.结果表明, 高峰时段内新方法相对于传统K-means方法, 路口车均延误和排队长度分别降低了19.05%和26.04%;从全天的情况来看, 2项指标分别降低了16.02%和13.05%.采用新方法确保了交通流的运行效率, 被证明是一种科学的、有潜在应用价值的划分方式.
| [1] |
赵伟明, 王殿海, 朱文韬, 等. 基于改进NJW算法的交通控制时段划分[J]. 浙江大学学报:工学版, 2014, 48(12): 2259-2265. ZHAO Wei-ming, WANG Dian-hai, ZHU Wen-tao, et al. Optimization of time-of-day breakpoints based on improved NJW algorithm[J]. Journal of Zhejiang University:Engineering Science, 2014, 48(12): 2259-2265. |
| [2] |
林培群, 卓福庆, 姚凯斌, 等. 车联网环境下交叉口交通流微观控制模型及其求解与仿真[J]. 中国公路学报, 2015, 28(8): 82-90. LIN Pei-qun, ZHUO Fu-qing, YAO Kai-bin, et al. Solving and simulation of microcosmic control model of intersection traffic flow in connected-vehicle network environment[J]. China Journal of Highway and Transport, 2015, 28(8): 82-90. |
| [3] |
SCHMÖCKER J D, AHUJA S, BELL M G H. Multi-objective signal control of urban junctions Framework and a London case study[J]. Transportation Research Part C:Emerging Technologies, 2008, 16(4): 454-470. DOI:10.1016/j.trc.2007.09.004 |
| [4] |
JEFF B X, HAO P, SUN Z. Real time queue length estimation for signalized intersections using travel times from mobile sensors[J]. Transportation Research Part C:Emerging Technologies, 2011, 19(6): 1133-1156. DOI:10.1016/j.trc.2011.01.002 |
| [5] |
AHMED M M, ABDEL-ATY M A. The viability ofusing automatic vehicle identification data for real-time crash prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(2): 459-468. DOI:10.1109/TITS.2011.2171052 |
| [6] |
CEYLAN H, BELL M G H. Traffic signal timing optimization based on genetic algorithm approach, including drivers' routing[J]. Transportation Research Part B:Methodological, 2004, 38(4): 329-342. DOI:10.1016/S0191-2615(03)00015-8 |
| [7] |
SMITH B L, SCHERER W T, HAUSER T A, et al. Data-driven methodology for signal timing plan development:a computational approach[J]. Computer-Aided Civil and Infrastructure Engineering, 2002, 17(6): 387-395. DOI:10.1111/mice.2002.17.issue-6 |
| [8] |
ABBASM, SHARMAA, JUNGY. Optimization of time of day plan scheduling using a multi-objective evolutionary algorithm[C]//Proceeding of Transportation Research Board Annual Meeting. Washington D. C: Transportation Research Board, 2005. https://works.bepress.com/anuj_sharma/6/
|
| [9] |
WANG X, COTTRELL W, MU S. Using K-means clustering to identify time-of-day break points for traffic signal timing plans[C]//2005 IEEE Intelligent Transportation Systems. Vienna: IEEE, 2005: 586-591. https://ieeexplore.ieee.org/document/1520102/
|
| [10] |
RATROUT N T. Subtractive clustering-based k-means technique for determining optimum time-of-day breakpoints[J]. Journal of Computing in Civil Engineering, 2010, 25(5): 380-387. |
| [11] |
PARK B B, SANTRA P, YUN I, et al. Optimization of time-of-day breakpoints for better traffic signal control[J]. Transportation Research Record:Journal of the Transportation Research Board, 2004(1867): 217-223. |
| [12] |
PARK B B, LEE D H, YUN I. Enhancement of time of day based traffic signal control[C]//IEEE International Conference on Systems, Man and Cybernetics, 2003. Washington DC: IEEE, 2003: 3619-3624. https://ieeexplore.ieee.org/document/1244451/?reload=true&arnumber=1244451
|
| [13] |
LEE J, KIM J, PARK B B. A genetic algorithm-based procedure for determining optimal time-of-day break points for coordinated actuated traffic signal systems[J]. KSCE Journal of Civil Engineering, 2011, 15(1): 197-203. DOI:10.1007/s12205-011-1093-0 |
| [14] |
MANNION P, DUGGAN J, HOWLEY E. An experimental review of reinforcement learning algorithms for adaptive traffic signal control[M]//Autonomic road transport support systems. Switzerland: Springer, 2016: 47-66.
|
| [15] |
NIELSEN F, NOCK R. Optimal interval clustering:application to Bregman clustering and statistical mixture learning[J]. IEEE Signal Processing Letters, 2014, 21(10): 1289-1292. DOI:10.1109/LSP.2014.2333001 |
| [16] |
金盛, 徐程, 王殿海. 城市路网交叉口检测器均衡布设优化方法[J]. 浙江大学学报:工学版, 2013, 47(03): 515-521. JIN Sheng, XU Cheng, WANG Dian-hai. Optimal traffic detector locations for equal distribution at urban network intersections[J]. Journal of Zhejiang University:Engineering Science, 2013, 47(03): 515-521. |
| [17] |
杨晓光, 蒲文静, 龙亮. 基于交通冲突分析的交叉口机动车信号灯设置[J]. 同济大学学报:自然科学版, 2005, 33(12): 1596-1599. YANG Xiao-guang, PU Wen-jing, LONG Liang. Traffic signal warrant study based on traffic conflict analysis for uncontrolled intersections[J]. Journal of Tongji University:Natural Science, 2005, 33(12): 1596-1599. |
| [18] |
MA D F, LUO X, LI W J, et al. Traffic demand estimation for lane groups at signal-controlled intersectionsusing travel times from video-imaging detectors[J]. IET Intelligent Transport Systems, 2017, 11(4): 222-229. DOI:10.1049/iet-its.2016.0233 |



