2. 中铁十一局集团第五工程有限公司, 重庆 400037;
3. 招商局重庆交通科研 设计院有限公司, 重庆 400067;
4. 重庆工商大学 管理学院, 重庆 400067;
5. 中建隧道建设有限公司, 重庆 401320
2. The Fifth Engineering Co. Ltd of China Railway 11 Bureau Group Co. Ltd, Chongqing 400037, China;
3. China Merchants Chongqing Communications Research and Design Institute Co. Ltd, Chongqing 400067, China;
4. School of Management, Chongqing Technology and Business University, Chongqing 400067;
5. China Construction Tunnel Engineering Co. Ltd, Chongqing 401320, China
随着我国公路、铁路、城市地铁的快速发展, 受地形的限制, 不可避免地利用连拱隧道通过特殊场地.在黄土地区, 连拱隧道在线路和洞口位置的选择上较分离式隧道有较大的优势, 且路基土石方及防护工程少, 投资较少, 同时对环境影响较小.黄土连拱隧道围岩较为特殊, 且跨度大, 设计和施工都较复杂.目前对连拱隧道的理论分析还不完善[1], 因此, 模型试验和数值仿真分析连拱隧道的动态开挖是较为可靠的研究手段.模型试验方面, 刘涛等[2]采用压力盒、数码摄像、沉降板等仪器分析了云南省元磨高速公路的一座连拱隧道, 但试验的应力监测只对隧道的径向应力进行了分析.肖林萍等[3]利用模型试验研究了三导坑法、双导坑法和中导坑拓展法的开挖过程位移和应力的变化.李树忱等[4]利用相关监测元件研究了极浅埋连拱隧道的开挖, 监测了围岩的应力应变.吴梦军[5]对大跨连拱隧道展开三维数值分析, 得到了围岩应力、位移随开挖步的变化规律.白浪峰等[6]利用应力分析法分析了连拱隧道围岩松动区的发展过程及范围.Chu等[7]分析了均质、双层以及三层围岩的连拱隧道的应力及位移规律.数值模拟方面.季毛伟等[8-9]对连拱隧道不同开挖方案及不同隧洞位置进行了分析, 选出了最优的方案及位置.Do等[10-12]分别模拟盾构、输电塔下的双连拱隧道施工及中隔墙优化分析, 为连拱施工开挖提供了很好的参考建议.此外, 钟祖良等[13-14]利用理论分析了连拱隧道损伤分布规律、围岩稳定性及松动圈荷载.
从目前国内外的研究成果来看, 对于黄土连拱隧道的研究相对较少[15-17].以往对黄土连拱隧道也主要从开挖方案、中隔墙结构分析以及两导洞开挖面合理间距等展开研究, 但对黄土连拱隧道每个断面的整个开挖过程研究很少, 特别是对不同开挖步下黄土连拱隧道的压力拱范围变化的研究几乎没有, 而如果能分析得到黄土连拱隧道压力拱范围, 将对连拱隧道的设计和施工都有较大的裨益.因此, 本文通过大型室内模型试验的方法模拟连拱隧道中导洞开挖, 利用相关测试元件, 对隧道轮廓位移时程曲线、围岩应力分布规律进行分析, 并利用FLAC3D软件进一步分析黄土连拱隧道不同开挖步的位移及压力拱范围.
1 黄土连拱隧道相似模型试验 1.1 依托工程概况山西省汾阳某隧道为双连拱二车道公路隧道, 隧道围岩由第四系中更新统离石组(Q21)黄土组成, 为Ⅳ级围岩.地质调查及钻探揭示, 隧道围岩范围内无地下水分布.隧道起讫桩号为K71+785~K71+965, 全长180 m, 洞顶最大埋深约39.0 m, 隧道总体走向为230°.单个隧道内轮廓净宽10.70 m, 净高7.05 m.隧道左右线轴线距离13.70 m.隧道为直线隧道, 隧道纵坡为-2.647%.
1.2 模型试验系统本次试验采用“公路隧道结构与围岩综合试验系统”进行模拟.系统由三大子系统组成[5], 模型试验台架如图 1所示.

|
图 1 公路隧道试验平台 Fig. 1 Experimental platform of highway tunnel |
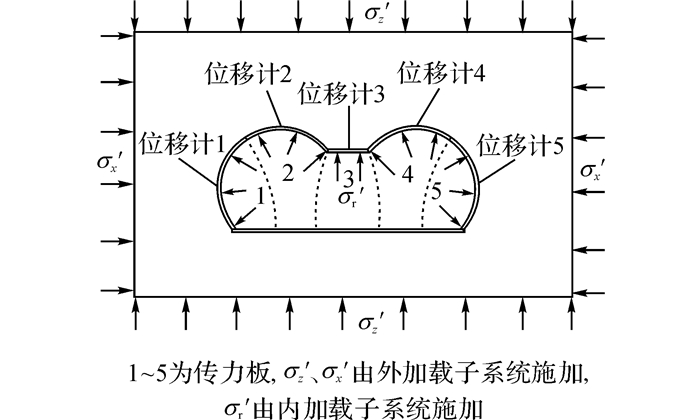
加载系统基于“先加载、后挖洞”的原理, 采用液压千斤顶在模型试件外轮廓加载约束反力用以模拟隧道围岩的边界条件[1];内加载系统通过内部向模型施加荷载并逐级释放来分别模拟围岩的初始应力状态以及隧道的不同开挖步的开挖, 从而使模型试验应力状态与原型完全一致, 其原理如图 2所示.
|
图 2 黄土连拱隧道模型试验原理图 Fig. 2 Schematic diagram of model test for loess double arch tunnel |
该系统的内加载隧道内轮廓尺寸为300~600 mm, 其几何相似比Cl=40:1~80:1, 其模型试件外轮廓尺寸为2.4 m×1.6 m×1.6 m, 一次试验材料用量达10 t左右.以几何相似比和容重相似比为基础, 确定的相似比如下:
| $ {{C}_{\text{l}}}=45:1, $ | (1) |
| $ {C_{\rm{ \mathsf{ γ} }}} = 1:1, $ | (2) |
| $ C{_{\rm{ \mathsf{ μ} }}} = {C_{\rm{ \mathsf{ φ} }}} = 1:1, $ | (3) |
| $ {C_{\rm{ \mathsf{ σ} }}} = {C_{\rm{E}}} = {C_{\rm{c}}} = 45:1. $ | (4) |
式中:Cγ为容重相似比, Cl为几何相似比, Cμ为泊松比的相似比, Cφ为内摩擦角的相似比, Cσ为应力相似比, CE为弹性模量的相似比, Cc表示黏聚力相似比.
1.4 模型试验材料本次相似材料选取河砂、石膏、膨润土、页岩土作为配比材料进行5组不同配比的试验, 确定满足试验所需的相似材料, 页岩土、砂、膨润土、石膏、水的配合比为40:30:10:6:14, 围岩模型与原型的力学参数如表 1所示.表中, γ为重度, E为弹性模量, μ为泊松比, φ为摩擦角, c为黏聚力.
| 表 1 Ⅳ级围岩物理力学参数 Table 1 Physico-mechanical parameters of grade Ⅳsurrounding rock |
试验过程中, 模型材料按配比试验时的击实度控制, 严格控制每层材料的厚度, 当试件下半部分模型材料填筑完成后, 安装内加载系统, 如图 3(a)所示, 然后对模型材料上半部分进行制作;模型材料填筑完成后3 d撤除外模板, 将试件置于通风干燥处, 如图 3(b)所示;当符合试验要求时, 将试件放入外加载系统, 并就位于大型试验平台上, 如图 3(c)所示.

|
图 3 模型试验的试件制作过程 Fig. 3 Specimen preparation process of model test |
根据黄土连拱隧道的工程地质条件, 对公路隧道结构与围岩综合试验系统进行应力边界条件的模拟, 模型的竖直应力σ′z按下式计算:
| $ {\sigma '_z} = \frac{{{\sigma _z}}}{{{C_\sigma }}} = \frac{{\gamma H}}{{{C_\sigma }}} = \gamma H'. $ | (5) |
式中:σz、H、H′分别为原型隧道的竖直应力、原型隧道埋置深度、模型隧道埋置深度.
设σ′x=σ′y, ε′x=ε′y=0, 根据广义胡克定律, 有
| $ \left. \begin{array}{l} {{\varepsilon '}_x} = \frac{1}{E}\left[{{{\sigma '}_x}-\mu \left( {{{\sigma '}_y} + {{\sigma '}_z}} \right)} \right], \\ {{\varepsilon '}_y} = \frac{1}{E}\left[{{{\sigma '}_y}-\mu \left( {{{\sigma '}_x} + {{\sigma '}_z}} \right)} \right]. \end{array} \right\} $ | (6) |
则模型的水平应力:
| $ {\sigma '_x} = \frac{\mu }{{1-\mu }}{\sigma '_z} = \lambda \gamma H'. $ | (7) |
式中:σ′x(σ′y)、ε′x(ε′y)、λ、分别为模型的x(y)向水平应力、模型x(y)向水平应变、模型的侧压力系数.
将式(5)、(7)代入模型参数, 计算可得外边界应力:σ′z=17.3 kPa, σ′x=7.4 kPa;而内边界应力, 限于试验的约束, 本试验中内轮廓由5块传力板组成, 每一块传力板区域只能加载同一应力, 由于隧道轮廓为不规则形状, 且为了试验中围岩初始受力及变形的协调, 5块传力板取相同值, 考虑到原型(施工现场)隧道围岩受一定构造应力的影响, 初始应力本身分布复杂, 此处对内加载应力做简化处理, 其值取外加载竖直方向和水平方向应力的平均值, 即
| $ {\sigma '_{\rm{r}}} = \left( {{{\sigma '}_z} + {{\sigma '}_x}} \right)/2 = 12.35\;{\rm{kPa}}{\rm{.}} $ |
此时, 模型隧道的围岩会在内外加载应力的作用下进行应力调整,进而模拟初始应力状态.然后根据油压系统尺寸计算出内外加载系统油压, 均等分6级逐步加载, 每次加载后稳压0.5 h, 最后一级荷载稳定1 h.
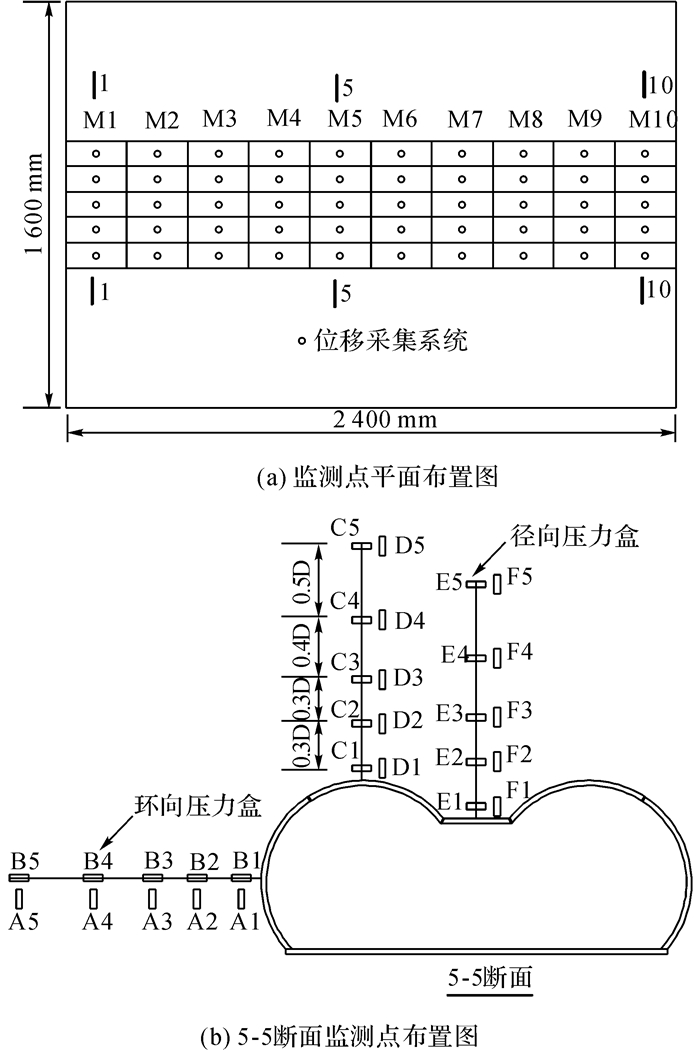
1.7 模型试验的监测布置及开挖方案试验中监测的主要内容是隧道轮廓的位移以及围岩内部的应力场.监测布置图如图 4, 模型纵向共分为10个断面, 每个断面设位移测点5个(如图 2所示), 其中1、5号测点位于拱腰, 2、4号测点位于拱顶, 3号测点位于中隔墙, 所采集位移为径向位移.压力盒布置于M1、M5、M10三个断面, 布置原则如下:
|
图 4 黄土连拱隧道模型试验的监测布置图 Fig. 4 Monitoring plan of model test for loess double arch tunnel |
1) 围岩内压力盒埋设点到隧道轮廓的距离分别为:0.0D、0.3D、0.6D、1D、1.5D(D为隧道的洞高), 且每一个布置点布置测试径向和环向2个方向的压力盒.
2) 压力盒布置在左右隧洞的拱腰、拱顶以及中隔墙围岩范围(右侧压力盒布置与左侧相同, 限于篇幅未示意).
此次试验中, 模型试验开挖采用中导洞法.模型纵向开挖顺序如表 2所示(表中每次中导洞开挖完1 h后进行支护, 但在开挖次序中未示意), 其中, Mx-y的x表示断面编号;y表示每个断面的5个独立模拟开挖传力板编号(如图 2所示), 卸载每一块传力板处的油压模拟相应位置隧道围岩的开挖.简化的平面开挖顺序如下:卸载传力板3(中导洞开挖)→加载传力板3(中隔墙浇筑)→卸载传力板1(左洞左导洞开挖)→卸载传力板2(左洞右导洞开挖)→卸载传力板5(右洞右导洞开挖)→卸载传力板4(右洞左导洞开挖).
| 表 2 模型试验纵向开挖顺序 Table 2 Longitudinal excavation sequence of the model test |
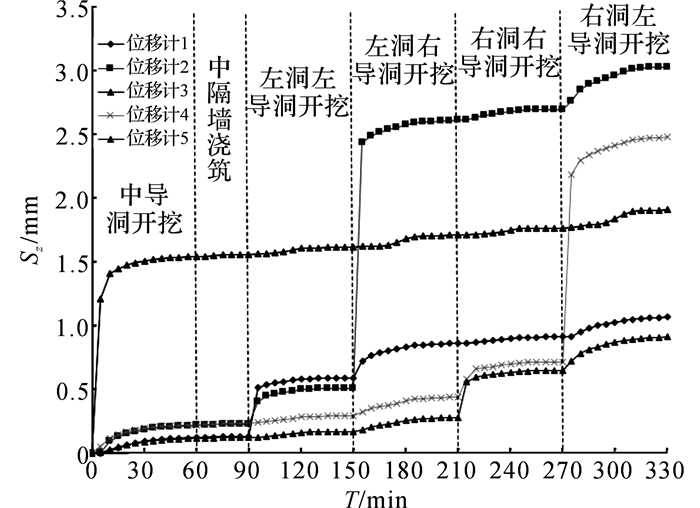
如图 5所示为模型试验隧道轮廓(典型断面M5, 其他断面曲线类似)各位移计的位移随时间变化的曲线图, 图中Sz为竖向位移, T为时间.
|
图 5 隧道轮廓位移-时间变化规律 Fig. 5 Displacement-time variation law of tunneloutline |
(1) 利用中导洞法开挖黄土连拱隧道时, 隧道轮廓发生位移最大为位移计2处, 沉降量为3.03 mm, 其次为位移计4处, 沉降量为2.48 mm, 即两隧道拱顶处的沉降量最大.位移计3处, 即中隔墙处的位移, 为1.91 mm.最小的沉降量发生在位移计1、5处, 即隧道两边拱腰处位移, 分别为1.07 mm和0.91 mm.
(2) 从位移时程曲线的发展形状可知, 随着黄土连拱隧道不同导洞的开挖, 其总体形状呈台阶形增长, 且各台阶的增长对应各导洞初期开挖的位移突变.因此, 在施工阶段, 各个导洞开挖初期应注意及时支护及封闭, 减少黄土连拱隧道的整体变形.此外, 在黄土连拱隧道左右两洞开挖过程中, 任一单洞隧道的顶点位移都会在开挖本隧道靠近中隔墙侧导洞时有一个急剧增加的阶段.例如, 在位移计2处的位移, 在开挖左洞右导洞时的位移增量最大, 占其总沉降量的69.24%, 其原因可能是左洞右导洞未开挖时, 该区域黄土体对大跨度的连拱隧道能起到较好的支撑作用, 类似单洞隧道核心土的作用, 开挖后形成了较大跨度的隧道断面, 该区域应力释放较快;同时, 经过多次的应力重分布, 该区域围岩损伤也较大.因此, 在施工时应特别重视靠近中隔墙导洞的开挖和支护, 避免发生坍塌.同样地, 位移计4处也有类似的情况.
(3) 位移计3处的位移主要集中在中导洞的开挖, 占其总沉降量的80.66%, 中隔墙砌筑后的位移呈非常小的趋势增加, 说明中隔墙的砌筑较好的阻碍了位移的增加.位移计1处的位移总体较小, 在进行左洞左导洞开挖时变形量最大, 占总变形量的42.89%, 而在进行右洞开挖时, 对此处的位移影响已经很小;同样, 位移计5处的变化类似.各处位移计位移量在各个开挖过程沉降量的比例如表 3所示.
| 表 3 不同开挖阶段各位移计处变形量占总变形量的百分比 Table 3 Percentage of deformation in total of displacement meters at different excavation stages |
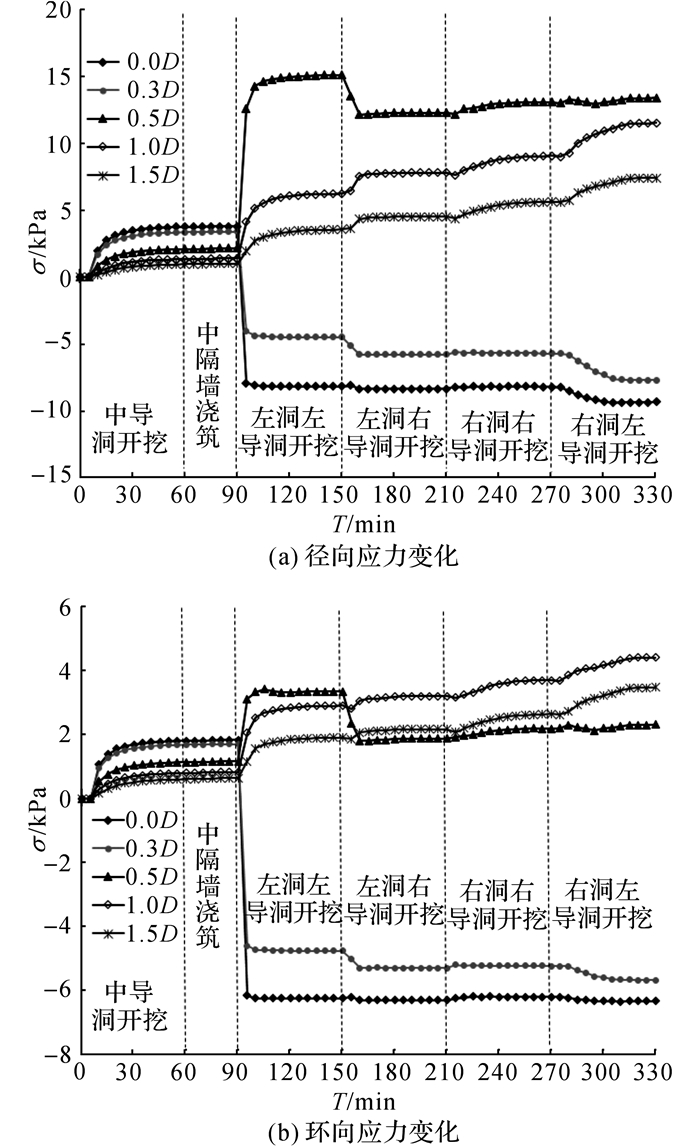
本次试验分析围岩压力采用相对压力值, 即各点的压力是相对于隧道开挖前的改变值[6].正值表示压力增大, 负值表示压力减小.黄土连拱隧道开挖全过程中左拱腰处围岩各测点的应力变化情况如图 6所示, 图中σ为应力.可以看出, 中导洞的开挖, 使得左拱腰处的径向应力和环向应力都有不同程度的增加, 说明虽然开挖导洞较小, 但对围岩的影响范围是较大的.当中隔墙的浇筑后, 较好的阻止了围岩应力的变化, 应力变化较为平稳.当左洞左导洞开挖时, 径向应力和环向应力变化都较剧烈, 靠近隧道轮廓(0.0D、0.3D)的应力都急剧减小, 说明隧道的开挖, 使得靠近隧道轮廓的围岩应力释放较大;离隧道轮廓0.5D~1.5D的径向应力和环向应力却是增大的, 其中离隧道轮廓0.5D的径向应力增加值最大, 说明此区域形成了压力拱.当左洞右导洞开挖时, 0.0D、0.3D的应力仍在减小, 此时, 0.5D的应力也开始减小, 说明随着开挖洞室的增大, 围岩松动圈的范围也扩大了;而1D、1.5D的应力却在增加, 说明压力拱转移到了此区域.当右洞右导洞开挖时, 左拱腰的应力变化较小, 可能是因为开挖距离较远, 且有中隔墙及核心土在两导洞之间起了支撑作用.当右洞左导洞开挖时, 可以很明显地看到各点的应力值在此开挖步的初期几乎没发生改变, 10 min左右后才开始发生变化, 说明对于黄土连拱隧道, 由于开挖跨度大, 黄土抗剪强度小, 致使较大范围土体参与承受围岩压力, 通过与文献[6]对比发现, 黄土连拱隧道的开挖对隧道周边围岩的应力分布影响较同等级围岩的连拱隧道范围更大.
|
图 6 左拱腰各测点应力变化曲线 Fig. 6 Stress change curve of each monitoring point in left tunnel hance |
黄土连拱隧道开挖全过程中左拱顶围岩各测点的应力变化情况如图 7所示.可以看出, 中导洞的开挖样使周边围岩应力重分布较为复杂, 而中隔墙的浇筑较好地阻止了应力的变化.当左洞左导洞开挖时, 径向应力有较大幅度的减小, 但0.5D、1.0D、1.5D的环向应力却有较大幅度的增加, 说明此处形成了围岩压力承载拱.当左洞右导洞开挖时, 径向应力进一步减小, 0.0D、0.3D、0.5D的环向应力也减小, 说明松动区范围在增大.当右洞右导洞开挖时, 径向应力几乎无变化, 环向应力除0.0D处应力无变化外, 其他处都经历先减小再缓慢增加的过程, 同样说明黄土连拱隧道的开挖影响范围较大.当右洞左导洞开挖时, 径向应力较小幅度的减小, 可能是应力已经释放完的原因;0.5D、1.0D、1.5D环向应力有较大幅度的增加, 说明此范围形成了围岩动态压力拱.

|
图 7 左拱顶各测点应力变化曲线 Fig. 7 Stress change curve of each monitoring point in left tunnel vault |
黄土连拱隧道开挖全过程中隔墙围岩各测点的应力变化情况如图 8所示, 当左洞先后开挖, 中隔墙处各点的径向应力和环向应力都有不同程度的增加, 说明中隔墙的浇筑, 较好地起到了支撑作用, 也使得此处的围岩成为开挖左洞时的动态压力拱的一部分.当右洞右导洞开挖时, 0.0D、0.3D、0.5D的应力增加, 而1.0D、1.5D的应力变化较小, 可知, 0.0D~0.5D处于动态压力拱区域, 而0.5D~1.0D为压力拱与原岩应力状态分界区域.反映隧道围岩由隧道轮廓面往外分别处于松动圈→压力拱→原岩应力状态.当右洞左导洞开挖时, 由于左右洞都已开挖, 使得此处的应力重分布较为复杂, 靠近轮廓范围的应力经历减小→增大→减小→平稳的阶段.因此, 对于黄土连拱隧道中隔墙上部的围岩, 应及时注浆或打入锚杆, 防止因应力的多次变化造成围岩损伤而出现垮塌(由于左、右洞开挖后的围岩压力变化情况相似, 此处只给出左导洞各监测点及中隔墙应力变化曲线来说明围岩压力变化情况).

|
图 8 中隔墙各测点应力变化曲线 Fig. 8 Stress change curve of each monitoring point in the middle wall |
为了验证模型试验的结果, 对黄土连拱隧道进行了FLAC3D的数值模拟.数值模型尺寸如图 2所示, 数值模型的参数取模型试验参数, 如表 1.本构模型采用Mohr-Coulomb准则, 初始荷载取自重荷载.水平方向边界以中隔墙为中心, 沿x正负向各取4倍洞径, 边界施加水平位移约束;竖直方向, 上边界取至地表, 下边界取隧道洞高的三倍, 施加竖向位移约束[18].开挖方案与模型试验完全一致, 即双侧导洞的开挖为预留核心土的CD法, 具体开挖顺序如下:中导洞开挖(K1)→中隔墙浇筑(K2)→左洞左导洞开挖(K3)→左洞右导洞开挖(K4)→右洞右导洞开挖(K5)→右洞左导洞开挖(K6).
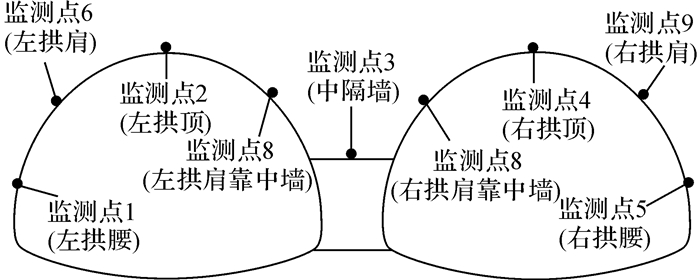
3.2 隧道轮廓位移对比分析由于模型试验的条件限制, 试验中每个断面只有5个点监测位移变化, 不能较全面反应黄土连拱隧道开挖过程中各部位的变形情况, 在数值模拟中布置了如图 9的监测点, 其中监测点1~5与试验中位移监测点一一对应, 监测点6~9为数值模拟中增加的监测点(各个监测点所处位置如图中括号所示).
|
图 9 数值模拟监测点示意图 Fig. 9 Monitoring point diagram of numerical simulation |
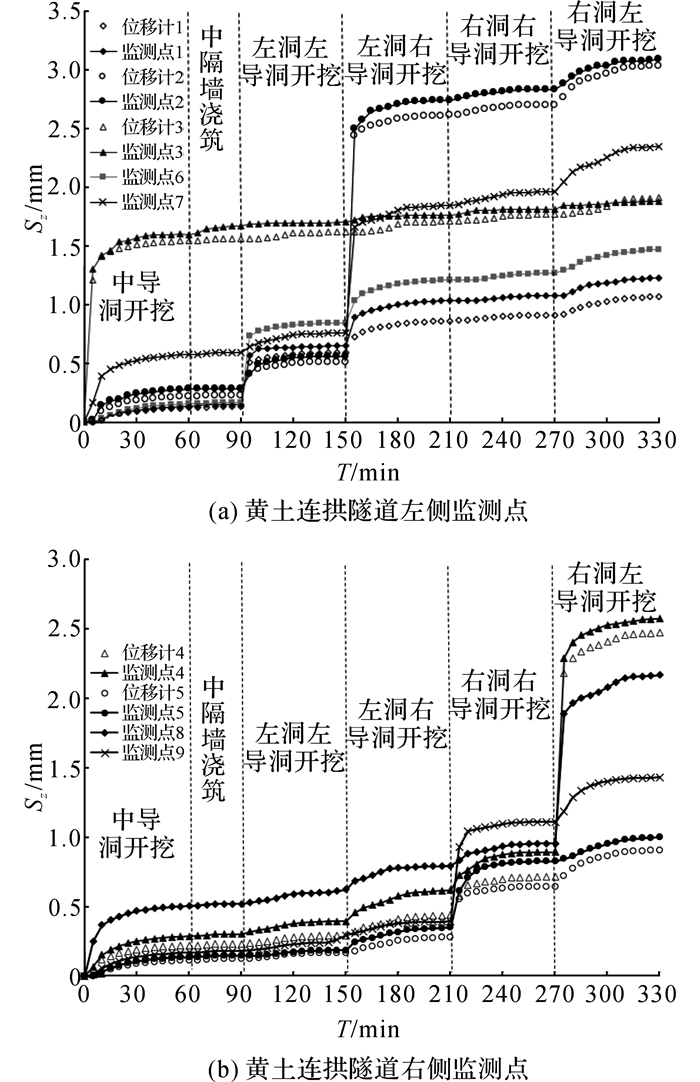
通过对数值模型的计算, 将得到的位移时程曲线与模型试验的结果进行对比, 如图 10所示.通过分析图 10, 可知:
|
图 10 模型与数值条件下隧道轮廓位移-时间对比图 Fig. 10 Displacement-time comparison curve of tunnel outline under model and numerical conditions |
1) 数值模型监测点1~5与模型试验的位移计1~5的位移时程曲线都呈台阶形发展, 说明模型试验的位移的发展趋势是正确的, 同时, 数值模拟的位移时程结果整体比模型试验的要大, 这可能是模型试验中相似材料物理力学性质的细微差异造成的.此外, 数值模拟中两隧道的拱顶处位移也为最大, 且在开挖本隧道靠近中隔墙侧导洞时, 拱顶位移出现了较大突变, 印证了在施工中应特别重视靠近中隔墙的导洞的开挖和支护.
2) 监测点6~9的位移时程曲线同样呈台阶形发展, 其中监测点6、监测点9的位移值仅比各侧拱腰大0.2~0.5 mm, 说明在远离中隔墙的两侧(小)导洞, 拱肩与拱腰处的位移差别不大;而监测点7、8(两洞拱肩靠近中墙侧)的最终位移值分别比监测点6、9大1.60、1.47倍, 其位移值仅比拱顶位移小, 说明黄土连拱隧道靠近中隔墙的两侧拱肩范围在经过多次的应力重分布后变形更大.各个部位的位移大小关系如下:左拱顶>右拱顶>左拱肩(靠中隔墙侧)>中隔墙>右拱肩(靠中隔墙侧)>左拱肩>右拱肩>左拱腰>右拱腰.
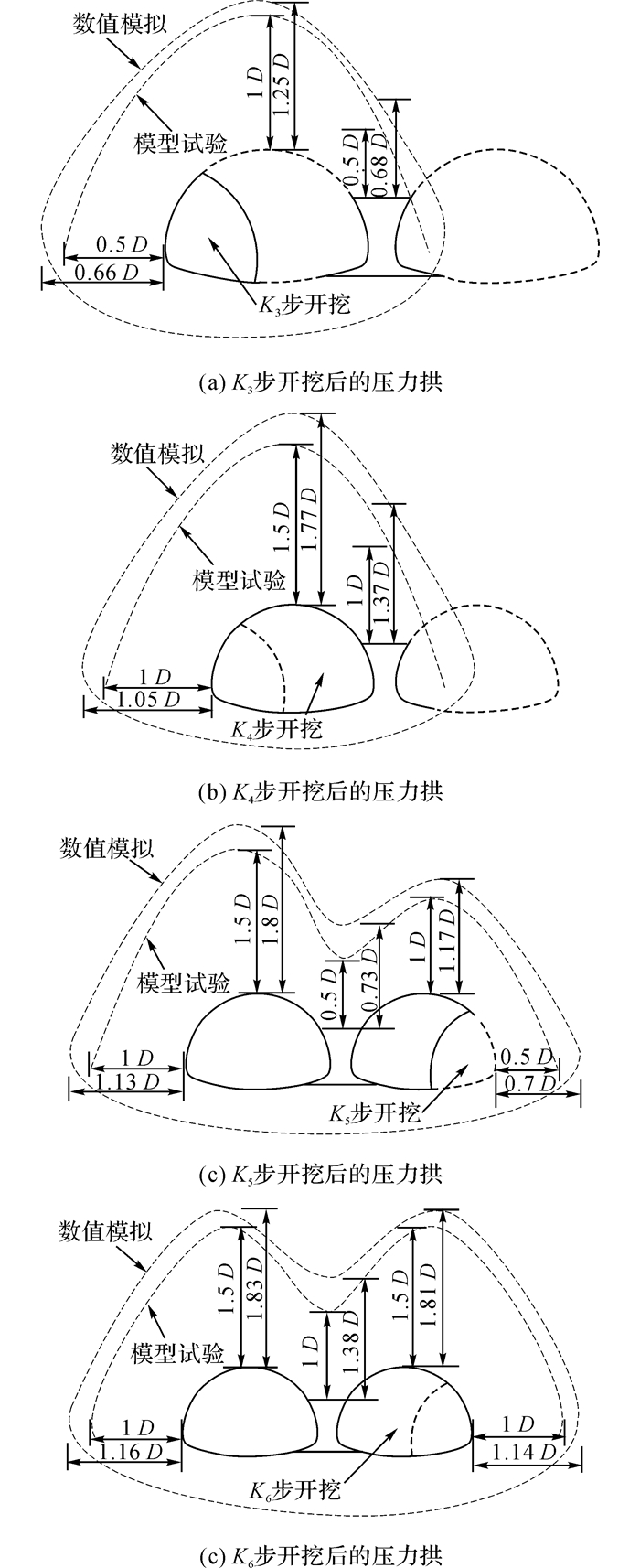
3.3 隧道开挖压力拱对比分析目前对连拱隧道压力拱发生、形成机制的研究并不成熟.参考单洞隧道开挖, 围岩分别处于松动圈→压力拱→原岩应力状态的原理[18-20], 连拱隧道也同样存在类似的规律.所谓压力拱是隧道开挖后围岩自我调节形成的具有拱力学特性的结构, 在压力拱区域的应力是增加的[19].文献[6]、[19]都得到了环向应力对压力拱起决定作用, 径向应力影响相对较小的结论.因此, 本文通过监测环向应力增加区域, 并结合压力拱内的松动圈径向应力减小的特点, 确定黄土连拱隧道的压力拱.由于模型试验不能对黄土连拱隧道的仰拱进行监测, 不同开挖步下模型试验与数值模拟的压力拱如图 11(K1、K1开挖步的压力拱与开挖单洞隧道类似, 此处不作分析)所示.通过分析图 11, 可知:
|
图 11 不同开挖步的压力拱 Fig. 11 Pressure arch of different step excavations |
1) 数值模拟所得到的围岩压力拱范围比模型试验稍大, 但两者的发展趋势较为相同.从各开挖步压力拱形状可知, 两洞拱顶的松动区域最大, 其次为中隔墙及拱腰区域.
2) 当K3、K5步开挖时, 先行导洞拱顶的压力拱大约为1D范围;当K4、K6步开挖时, 单洞隧道拱顶的压力拱大约为1.5D范围, 通过对比文献[6]所得到的松动圈大致为1D范围, 可知黄土连拱隧道的松动圈范围大1.5倍.因此, 对黄土连拱隧道所采取的支护参数应比同等级围岩的连拱隧道更高.
3) 从各开挖步压力拱范围可知, 中隔墙处的压力拱经历了从0.5D→1D→0.5D→1D的变化, 也印证了中隔墙上部的应力重分布较为复杂, 为防止该部分围岩损伤太大而发生坍塌, 在结构设计中应对该部分进行重点关注, 在施工中对此范围的围岩应注浆或打入锚杆, 加强支护.
4 结论本文根据相似原理配置了相似模型材料, 模拟了黄土连拱隧道中导洞开挖法的动态开挖过程, 综合室内模型试验和数值模拟的结果, 得出了以下结论:
1) 随着黄土连拱隧道不同导洞的开挖, 各监测点的位移时程曲线形状呈台阶形增长, 且各台阶的增长对应各导洞初期开挖的位移突变, 特别是任一单洞隧道的顶点位移都会在开挖本隧道靠近中隔墙侧导洞时有一个急剧增加的过程.因此, 在施工阶段, 各个导洞开挖初期应注意及时支护及封闭, 特别应注意靠近中隔墙导洞的开挖和支护, 并在施工中加强监测, 避免发生坍塌.
2) 黄土连拱隧道的压力拱范围比同等级围岩的连拱隧道更大, 当K3、K5步开挖时, 先行导洞拱顶的压力拱大约为1D;当K4、K6步开挖时, 单洞隧道拱顶的压力拱大约为1.5D.因此, 对于黄土连拱隧道,在结构设计时应提高整体支护参数.
3) 从K3~K6开挖步, 黄土连拱隧道中隔墙上部围岩压力拱经历了从0.5D→1D→0.5D→1D的变化, 形成了多次的应力重分布, 因此, 在结构设计与施工中应对这些部位重点关注, 在施工中对此范围的围岩应注浆或打入锚杆, 加强支护.
| [1] |
邱长林, 刘彬, 何林生, 等. 整体式中隔墙连拱隧道模型试验及现场监测[J]. 岩土力学, 2012, 33(9): 2625-2631. QIU Chang-lin, LIU Bin, HE Lin-sheng, et al. Model test and in-situ monitoring of double-arch tunnel with integrated middle wall[J]. Rock and Soil Mechanics, 2012, 33(9): 2625-2631. |
| [2] |
刘涛, 沈明荣, 陶履彬, 等. 连拱隧道动态施工模型试验与三维数值仿真模拟研究[J]. 岩石力学与工程学报, 2006, 25(9): 1802-1808. LIU Tao, SHEN Ming-rong, TAO Lv-bin, et al. Model test and 3d numerical simulation study on excavation of double-arch tunnel[J]. Chinese Journal of RockMechanics and Engineering, 2006, 25(9): 1802-1808. |
| [3] |
肖林萍, 赵玉光, 申玉生, 等. 双连拱隧道结构内力样式及围岩稳定性模型试验研究[J]. 岩石力学与工程学报, 2005, 24(23): 4346-4351. XIAO Lin-pin, ZHAO Yu-guang, SHEN Yu-sheng, et al. Model experimental study on style of structural internal force and stability of surrounding rock in double-arch tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(23): 4346-4351. DOI:10.3321/j.issn:1000-6915.2005.23.023 |
| [4] |
李树忱, 袁超, 李术才, 等. 极浅埋连拱隧道施工过程围岩力学行为的模型试验研究[J]. 煤炭学报, 2012, 37(5): 713-718. LI Shu-chen, YUAN Chao, LI Shu-cai, et al. Model test dtudy on mechanical behavior of extremely shallow double-arch tunnel during excavation[J]. Journal of China Coal of Society, 2012, 37(5): 713-718. |
| [5] |
吴梦军. 大跨扁平连拱隧道施工时空效应与二次衬砌最佳支护时机研究[D]. 重庆: 重庆大学, 2011. WU Meng-jun. Study on construction space-time effect and optimal supporting time of large span and flat multi-arch tunnel[D]. Chongqing: Chongqing University, 2011. |
| [6] |
白浪峰, 徐前卫, 田龙岗, 等. 软弱破碎连拱隧道松动区模型试验与分析[J]. 岩石力学与工程学报, 2013, 32(增2): 3610-3618. BAI Lang-feng, XU Qian-wei, TIAN Long-gang, et al. Model test and analysis of loose zone in soft and cracked surrounding rock of multi-arch tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(Suppl. 2): 3610-3618. |
| [7] |
CHU B L, HSU S C, CHANG Y L, et al. Mechanical behavior of a twin-tunnel in multi-layered formations[J]. Tunnelling and Underground Space Technology, 2007, 22(3): 351-362. DOI:10.1016/j.tust.2006.06.003 |
| [8] |
季毛伟, 吴顺川, 高永涛, 等. 双连拱隧道施工监测及数值模拟研究[J]. 岩土力学, 2011, 32(12): 3787-3795. JI Mao-wei, WU Shun-chuan, GAO Yong-tao, et al. Construction monitoring and numerical simulation of multi-arch tunnel[J]. Rock and Soil Mechanics, 2011, 32(12): 3787-3795. DOI:10.3969/j.issn.1000-7598.2011.12.041 |
| [9] |
CHEHADE F H, SHAHROUR I. Numerical analysis of the interaction between twin-tunnels:influence of the relative position and construction procedure[J]. Tunnelling and Underground Space Technology, 2008, 23(2): 210-214. DOI:10.1016/j.tust.2007.03.004 |
| [10] |
DO N A, DIAS D, ORESTE P, et al. Three-dimensional numerical simulation of a mechanized twin tunnels in soft ground[J]. Tunnelling and Underground Space Technology, 2014, 42: 40-51. DOI:10.1016/j.tust.2014.02.001 |
| [11] |
AFIFIPOUR M, HARIFZADEH M, SHAHRIAR K, et al. Interaction of twin tunnels and shallow foundation at Zand underpass, Shiraz metro, Iran[J]. Tunnelling and Underground Space Technology, 2011, 26(2): 356-363. DOI:10.1016/j.tust.2010.11.006 |
| [12] |
WANG S Y, YANG J S, YANG Y H, et al. Construction of large-span twin tunnels below a high-rise transmission tower:a case study[J]. Geotechnical and Geological Engineering, 2014, 32(2): 453-467. DOI:10.1007/s10706-013-9726-3 |
| [13] |
钟祖良, 刘新荣, 刘元雪, 等. 黄土连拱隧道动态施工围岩损伤局部化研究[J]. 岩土力学, 2012, 33(2): 611-616. ZHONG Zu-liang, LIU Xin-rong, LIU Yuan-xue, et al. Study of damage localization of loess multi-arch tunnel's surrounding rock under dynamic construction[J]. Rock and Soil Mechanics, 2012, 33(2): 611-616. |
| [14] |
申玉生, 赵玉光. 双连拱隧道围岩稳定性的模糊概率分析研究[J]. 岩土工程学报, 2005, 27(11): 1358-1361. SHEN Yu-sheng, ZHAO Yu-guang. Research on fuzzy probability analysis of stability of surrounding rock in double-arch tunneling[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(11): 1358-1361. DOI:10.3321/j.issn:1000-4548.2005.11.026 |
| [15] |
钟祖良, 刘新荣, 袁飞, 等. 仰拱一次性开挖长度对黄土连拱隧道稳定性影响研究[J]. 岩土工程学报, 2008, 30(3): 462-466. ZHONG Zu-liang, LIU Xin-rong, YUAN Fei, et al. Effect of excavation length of inverted arch in one step on stability of multi-arch tunnels in loess[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(3): 462-466. |
| [16] |
来弘鹏, 刘苗, 谢永利. 黄土地区浅埋暗挖三连拱地铁隧道围岩压力特征研究[J]. 岩石力学与工程学报, 2011(增1): 3103-3111. LAI Hong-peng, LIU Miao, XIE Yong-li. Study of surrounding rock pressure characteristics of shallow excavation threee-arch metro tunnel in loess region[J]. Chinese Journal of Rock Mechanics and Engineering, 2011(Suppl.1): 3103-3111. |
| [17] |
赖金星, 余德强, 冯志华, 等. 黄土连拱隧道支护结构力学特性现场试验[J]. 现代隧道技术, 2017(5): 180-191. LAI Jin-xing, YU De-qiang, FENG Zhi-hua, et al. Mechanical characteristics of a multi-arch tunnel support structure in loess[J]. Modern Tunnelling Technology, 2017(5): 180-191. |
| [18] |
刘俊, 刘新荣, 赖勇, 等. 不同覆跨比下浅埋软弱隧道的破坏模式[J]. 中南大学学报:自然科学版, 2016, 47(5): 1744-1751. LIU Jun, LIU Xin-rong, LAI Yong, et al. Failure mode of shallow-buried weak tunnel under different thickness-span ratios[J]. Journal of Central South University:Science and Technology, 2016, 47(5): 1744-1751. |
| [19] |
朱合华, 黄锋, 徐前卫. 变埋深下软弱破碎隧道围岩渐进性破坏试验与数值模拟[J]. 岩石力学与工程学报, 2010, 29(6): 1113-1122. ZHU He-hua, HUANG Feng, XU Qian-wei. Model test and numerical simulation for progressive failure of weak and fractured tunnel surrounding rock under different overburden depths[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(6): 1113-1122. |
| [20] |
郑颖人, 徐浩, 王成, 等. 隧洞破坏机理及深浅埋分界标准[J]. 浙江大学学报:工学版, 2010, 44(10): 1851-1856. ZHENG Ying-ren, XU Hao, WANG Cheng, et al. Failure mechanism of tunnel and dividing line standard between shallow and deep bury[J]. Journal of Zhejiang University:Engineering Science, 2010, 44(10): 1851-1856. |



