2. 北京建筑大学 北京未来城市设计高精尖创新中心, 北京 100044;
3. 兰州理工大学 防震减灾研究所, 甘肃 兰州 730050
2. Beijing Advanced Innovation Center for Future Urban Design, Beijing University of Civil Engineering and Architecture, Beijing 100044, China;
3. Institution of Earthquake Protection and Disaster Mitigation, Lanzhou University of Technology, Lanzhou 730050, China
随着计算力学技术的发展, 多尺度有限元建模技术逐渐成为土木工程研究领域关注的焦点.该技术指在有限元建模时将重要的部位用相对精细的单元建模, 而次要的部位用相对粗糙的单元建模, 不同单元的边界采用恰当的连接方式以达到力的平衡和变形的协调, 从而花费较少计算资源和时间并得到较为精确的结果.多尺度建模技术已经被成功应用于大型结构的动力学计算、计算流体力学(computational fluid dynamics, CFD)模拟以及复合材料的微观模拟等领域[1-5], 然而目前依旧存在以下问题:1)对于多尺度模拟合理性的验证研究相对偏少.该验证研究一般可采用试验法或数值模拟法这2种方法.试验法指通过相应试件的试验结果对多尺度数值模拟结果进行对比, 如程小卫等[6]通过建立经典钢筋混凝土梁落锤试验相关的多尺度模型, 与试验结果进行比较, 验证了多尺度的合理性, 然而该方法由于相关试验数据较为匮乏, 成本较高, 并且适应性差, 极少被采用;数值模拟法指针对多尺度模型建立相应的单一尺度模型, 并将计算结果进行对比以进行验证, 由于目前数值模拟技术已发展得颇为成熟, 这种方法更为通用, 如陆新征等[7]提出了有限元微观模型与宏观模型的界面连接方法, 针对某正八边形筒模型压弯加载算例进行验证, 并将其应用于工程中;2)目前大部分研究只采用单一的多尺度建模方法进行大型结构的建模并进行计算, 但很少有对于不同多尺度建模实现方法进行对比的研究, 为数不多的尝试如Panasenko[8]也只是着重于多尺度衔接方程的数理推导, 并没有论述实际应用效果的异同.3)大多研究局限于结构静力或动力分析, 而涉及构件局部疲劳分析的多尺度有限元建模技术的研究几乎没有, 仅有的涉及裂纹扩展的研究也过于偏重于微观材料特性的研究, 如Rafiitabar等[9]对某宏观板建立多尺度模型, 并且确保了微观原子的连续性的基础上从微观角度分析了材料的断裂问题.因此基于上述三点存在的问题, 这一课题亟需进一步研究.
高层高耸钢结构的焊接结点易产生局部应力集中, 在风的作用下易萌生疲劳裂纹, 针对这一课题, 已有部分学者进行了相关研究, 如Repetto等[10-11]对高耸结构的风致疲劳问题进行了大量研究, 分别从频域和时域角度进行了结构顺风向、横风向的疲劳分析, 取得了大量的研究成果;Jia[12]以海上钻井平台的火炬臂为工程背景, 建立了以概率为基础的风致疲劳分析程序, 通过非线性时域分析, 研究了不同拽力系数对分析结果的影响;不过以上研究由于采用名义应力法进行疲劳寿命评估, 并没有建立多尺度有限元模型, 对于结构局部应力状态和疲劳裂纹萌生的研究不够深入.Dong等[13-15]对挪威海岸线附近的风电塔进行了长期的监测, 并且考虑海浪对结构的影响, 综合分析了结构结点的长期风致疲劳破坏, 该研究主要采用理论推导的方式进行热点应力以及应力集中系数的计算, 并没有涉及多尺度有限元分析;笔者也对该课题进行了一定研究[16-17], 已就某高层钢框架结构建立了由梁单元到壳单元再到实体单元过渡的多尺度有限元模型, 在此基础上针对局部焊接结点进行了风致疲劳分析, 然而并未就多尺度有限元模型应用于疲劳分析的合理性进行验证.因此针对此问题, 亟需建立一种可靠的能用于钢结构风致疲劳分析的多尺度有限元模型, 并对其合理性进行验证.
本文采用数值模拟法进行多尺度的验证, 对结构分别采用实体单元和梁单元建立2种单一尺度模型以便进行对比, 然而高层钢结构尺寸较大、较为复杂, 如对整个结构采用实体单元建立体尺度模型则显得单元数过多, 较为困难, 因此本文对此进行简化, 选择某结构形式较简单的二层框架结构为算例, 分别在大型通用有限元软件ANSYS中采用约束方程法和子模型法建立多尺度有限元模型, 在此基础上分别进行风荷载静力分析、时程分析及风致疲劳分析, 通过与实体单元及梁单元建立的单一尺度模型进行对比以验证其合理性,并在此基础上研究局部模型大小的选择.
1 多尺度模型连接原理多尺度有限元模型涉及梁单元与壳单元的连接、壳单元与实体单元的连接以及梁单元与实体单元的连接.由于这些单元的自由度不完全相同, 欲实现共用节点的刚接, 需要建立约束方程.
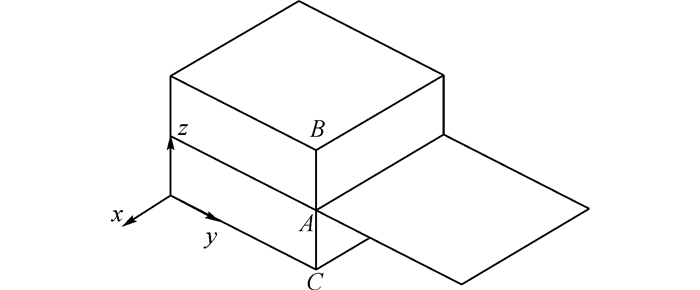
约束方程是一种联系自由度的线性方程.以三维实体单元与壳单元连接进行说明, 如图 1所示, 由于实体单元每个节点有沿着x、y、z三个方向的平动自由度, 而壳单元每个节点除了这3个自由度还具有绕x、y、z三个轴的转动自由度, 如仅共用节点, 节点的连接情况默认为铰接, 这显然与实际情况不相符, 因此需对壳单元上的各节点与相应实体单元的节点建立约束方程.在有限元建模中有多种可供选择的方法建立约束方程, 其中通过设置刚性区以自动建立约束方程的方法较为简单.
|
图 1 约束方程法原理示意图 Fig. 1 Principle demonstration constraint equation method |
对图 1中模型建立约束方程时, 以B、A、C三点为例, 规定A为主节点, B、C为从节点, 通过以下约束方程生成主节点和从节点之间的刚性线, 完成约束方程的建立[18]:
| $ {{C}_{1}}\cdot {{u}_{yB}}+{{C}_{2}}\cdot {{r}_{xA}}+{{C}_{3}}\cdot {{u}_{yC}}={{C}_{0}}, $ | (1) |
| $ {{{C}'}_{1}}\cdot {{u}_{xB}}+{{{C}'}_{2}}\cdot {{r}_{yA}}+{{{C}'}_{3}}\cdot {{u}_{xC}}={{{C}'}_{0}}. $ | (2) |
式中:uxC、uyC、uxB和uyB分别为C、B两点沿x、y方向的平移;rxA和ryA分别为点A绕和y轴的转动自由度;C′i及Ci’(i=0, 1, 2, 3)为与几何尺寸有关的系数.由此可见约束方程法的核心过程是“约束方程的建立”.
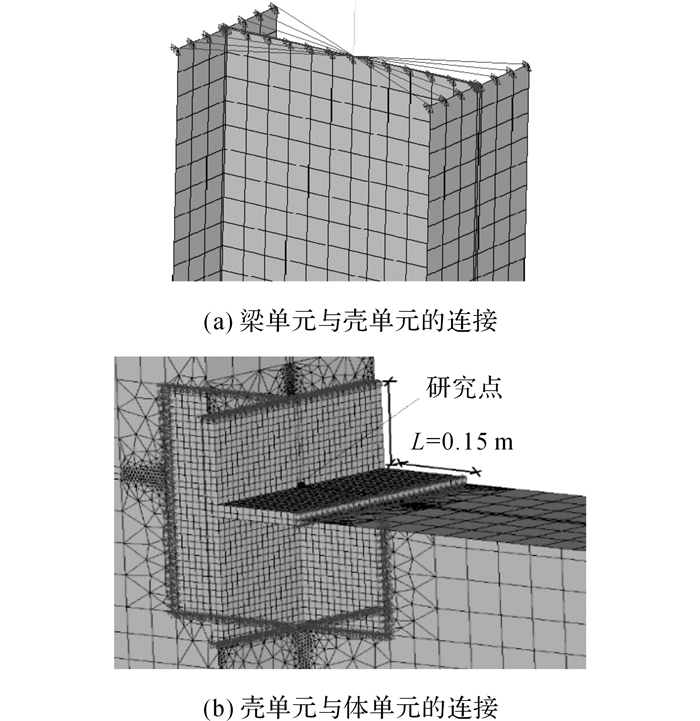
如图 2所示, 采用上述过程分别建立梁单元与壳单元的连接以及壳单元与实体单元的连接, 从而实现构件从梁单元到壳单元再到实体单元的过渡.梁单元与实体单元的连接与此类似.
|
图 2 约束方程法的连接 Fig. 2 Connection by constraint equation method |
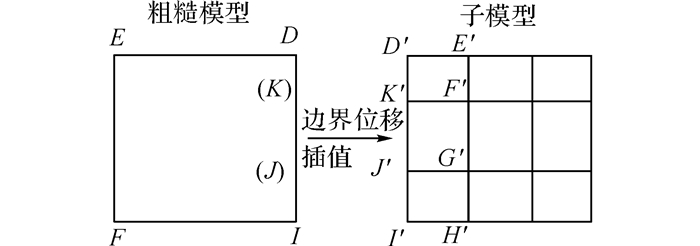
子模型法是另一种实现多尺度计算的方法, 又称为切割边界位移法.子模型法基于圣维南原理[19], 因此当切割位置远离应力集中区域时即可获得较精确的结果.子模型法的有限元模型主要包括粗糙模型和子模型两部分, 其核心思想为通过对粗糙模型进行边界切割, 并将该边界上节点的计算位移值作为子模型的边界条件, 进而对子模型进行分析, 以某二维平板单元的子模型计算进行说明, 如图 3所示.
|
图 3 子模型法的原理示意 Fig. 3 Principle demonstration of the sub-model method |
首先在粗糙模型中进行分析并求得结果, 设粗糙模型单元ADEF, 其形函数矩阵为N, 单元结点位移列阵为a, 因此单元内任意一点的位移列阵u[20]可表示如下:
| $ \mathit{\boldsymbol{u}}=\left( \begin{align} &u \\ &v \\ \end{align} \right)=\mathit{\boldsymbol{Na}}. $ | (3) |
由此可插值得粗糙模型D、K、J、I四点的位移列阵uD、uK、uJ和uI, 这4点分别对应子模型中的点D′、K′、J′、I′, 随后将uD、uK、uJ和uI作为子模型的边界条件即可进一步对子模型进行求解.由于子模型法的切割边界必须位于壳单元或实体单元上, 梁单元不能利用上述方法进行插值, 本文讨论的子模型法只限于切割壳单元或实体单元.由此可见子模型法的核心过程是“边界切割及位移插值”.
如图 4所示, 采用上述方法对壳单元进行切割, 并将切割边界的位移值赋予作为实体模型的子模型.

|
图 4 子模型的边界切割 Fig. 4 Boundary cutting of sub-model |
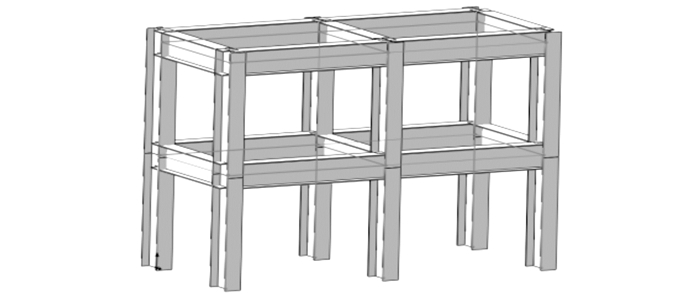
某二层单跨钢框架结构平面形状为矩形, 长为6 m, 宽为2.5 m, 层高均为2.5 m, 如图 5所示, 钢柱和钢梁均选用截面为550 mm×300 mm×12 mm×18 mm的H型钢, 并且采用焊接连接, 钢材材料为Q345B, 弹性模量E=206 GPa, 泊松比υ=0.3, 模型底部与地面固接, 忽略土与结构的相互作用.由于目前对于风致疲劳的研究大多数局限于日常风作用下的动力和疲劳问题, 不考虑如台风或龙卷风等极端天气的影响, 本文只考虑日常风的作用, 可采用弹性分析进行简化, 忽略结构的非线性问题, 并且假设风向仅沿着结构的横向, 并与结构表面垂直.
|
图 5 某二层钢架结构三维图 Fig. 5 3D figure one two-layer steel frame structure |
由此可沿结构横向取一榀框架作为研究对象, 分别在大型通用有限元软件ANSYS中建立以下多种模型.
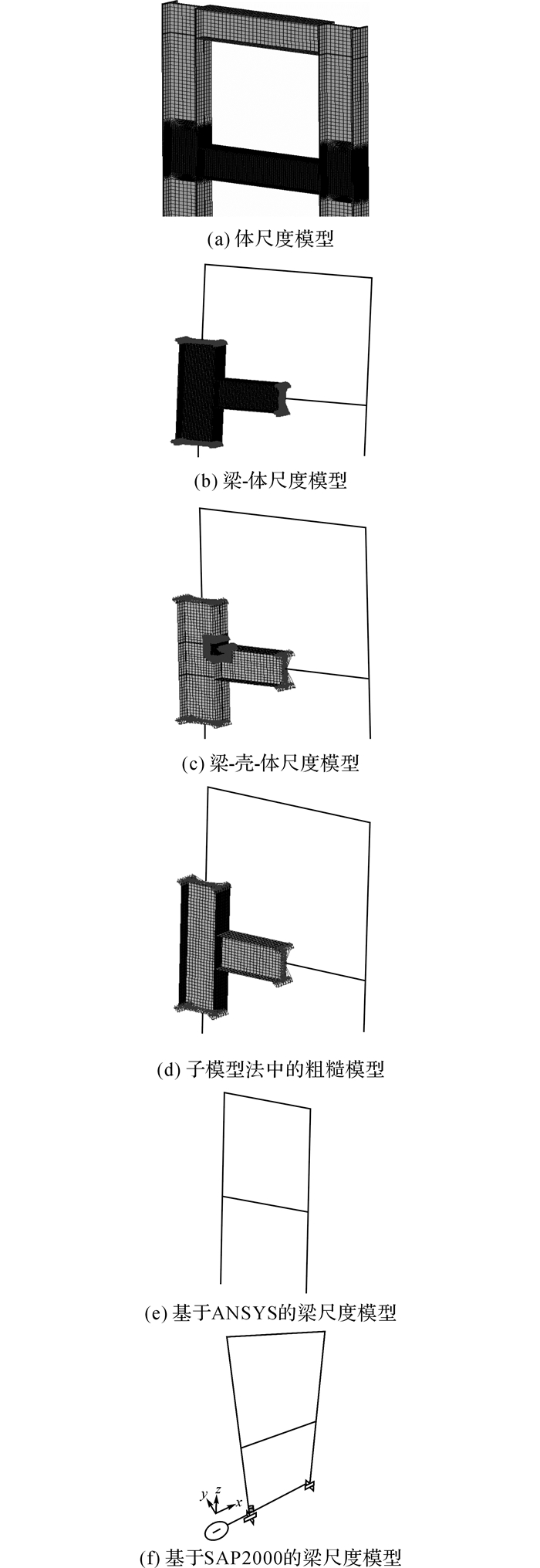
1) 体尺度模型, 即该榀框架全部采用实体单元进行建模和网格划分, 其中梁柱结点处的实体单元采用尺寸为0.01 m的映射网格划分, 其余部位采用0.05 m的映射网格进行划分;
2) 梁-体尺度模型, 即该榀框架的梁柱结点处用实体单元进行建模, 其余部分用梁单元建模, 并利用约束方程法连接边界, 其中梁柱结点处采用0.01 m的映射网格进行划分;
3) 梁-壳-体尺度模型, 即该榀框架的梁柱结点用壳单元模拟, 并将该梁的上翼缘与柱的连接焊缝处用实体单元进行模拟, 其余部分依旧用梁单元模拟, 采用约束方程法形成梁单元-壳单元-实体单元的多尺度过渡, 其中焊缝附近的实体单元采用网格尺寸为0.01 m的映射网格进行划分, 而壳单元采用0.05 m的映射网格划分, 两者连接处采用自由网格划分进行过渡;
4) 子模型法模型, 该榀框架的梁柱结点用壳单元模拟, 其余部位用梁单元模拟, 形成子模型法的粗糙模型, 并进一步对该梁柱结点梁的上翼缘与柱的连接焊缝处建立子模型进行边界切割, 并保证子模型的切割部位与模型3)中建立约束方程的边界部位相同, 其中粗糙模型采用0.05 m的映射网格进行划分, 而子模型采用0.01 m的映射网格进行划分;
5) 梁尺度模型, 即模型中所有的单元均由梁单元组成, 为了便于对上述单一尺度模型进行验证和对比, 额外采用有限元软件SAP2000建立同样的梁尺度模型.
上述各模型如图 6所示, 其中在ANSYS里梁单元采用BEAM188单元, 壳单元采用SHELL63单元, 而实体单元采用SOLID45单元.表 1对前4种模型分别从有限元模型的节点数及单元数进行了概括, 可以发现, 尽管体尺度模型和梁-体尺度模型可通过不同尺寸网格的过渡进一步缩减网格尺寸, 但采用多尺度建模方法依旧可大幅度减少节点数和单元数, 其中梁-壳-体尺度模型和子模型法模型可最大限度地节省计算资源, 因此本文重点研究这2种模型.
|
图 6 各有限元模型示意图 Fig. 6 Demonstration graph of finite element models |
| 表 1 各模型单元数及节点数 Table 1 Element and node number of models |
首先研究在静力荷载作用下多尺度模型的合理性, 对上述模型进行风荷载的静力分析, 风荷载按《建筑结构荷载规范》[21]的规定选取, 计算公式如下:
| $ {{\omega }_{\text{k}}}={{\beta }_{z}}{{\mu }_{\text{s}}}{{\mu }_{z}}{{\omega }_{0}}. $ | (4) |
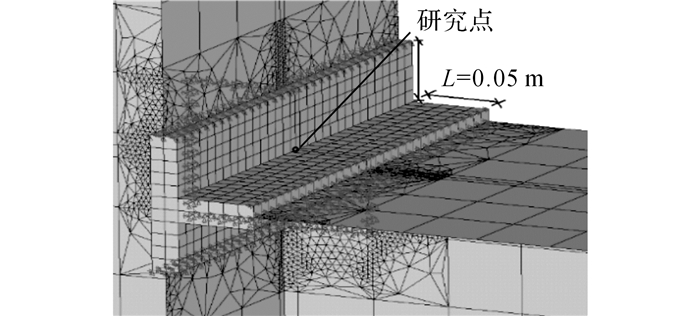
式中:wk为风荷载标准值;βz为高度z处的风振系数, 此处可取1;μs为风荷载体型系数, 由于本结构表面为封闭式房屋矩形平面, 因此在迎风面取+0.8, 背风面取-0.5;μz为风压高度变化系数, 此处近似取0.65;w0为基本风压, 当地50年重现期的w0=0.4 kN/m2, 由此可计算得风荷载标准值wk=0.338 kN/m2.将此榀框架所受的风荷载等效为集中力施加在梁柱结点上并进行分析, 选择结构自振周期T、顶部位移d及梁柱结点梁上翼缘与柱连接焊缝中心研究点处的Mises应力σM以及各模型与体尺度模型这3个量之间的差距D作为对比指标, 该研究点位置见图 2(b)及图 10, 计算结果如表 2所示.
|
图 10 L=0.05 m时的局部模型图 Fig. 10 Local model figure when L=0.05 m |
| 表 2 各模型在静力荷载作用下的计算结果 Table 2 Calculation results of each model under static loading |
由表 2可见, 由于梁尺度模型不能提取局部研究点位置的应力值, 不便于进行应力比较, 但从自振周期及顶部位移这两方面看, 全部采用精细单元建模的体尺度模型与全部采用宏观单元建模的梁尺度模型吻合良好, 这说明体尺度模型足以作为多尺度模型计算结果对比的参照物.这3种多尺度模型的自振周期、位移及应力计算结果与体尺度模型相比也较为相近, 偏差率均低于15%, 这说明多尺度模型与体尺度模型在自振周期及位移值这2项的偏差率甚至低于5%,这可能是由于针对有限结构细部构造进行的精细化建模对位移这类结构整体宏观指标产生的影响相对较小的缘故, 而相对而言,应力等结构微观指标受到的影响较大, 造成应力差距稍大, 因此下文不再以位移值及自振周期作为指标进行对比, 仅针对研究点的应力进行比较.从表中还能看出, 子模型法相对于另外2种多尺度模型来说, 与体尺度模型的计算结果差距最小, 即子模型法的精度最高;而梁-壳-体尺度模型和梁-体尺度模型的精度基本相同.造成这种现象的原因可能是采用约束方程法进行多尺度连接时, 不同的单元交界面的直接连接造成了精准度的下降, 而对于子模型法而言, 由于采用边界切割和位移插值, 回避了不同单元交界面的直接连接, 因此精准度略高.
4 风荷载动力时程分析及疲劳分析对上述4种模型进行风荷载作用下的动力时程分析, 由于还需对结构进行风致疲劳分析, 基本风速的选取应当参考疲劳分析中基本风速的选择方法, 可取当地的10 m高处的年平均风速v0=18.66 m/s.随机脉动风场的模拟采用谐波叠加法, 时间间隔为0.5 s, 总时间为100 s, 风速谱采用Davenport风速谱[22]:
| $ \frac{n{{S}_{v}}\left( n \right)}{v_{0}^{2}}=\frac{4k{{x}^{2}}}{n{{\left( 1+{{x}^{2}} \right)}^{\frac{3}{4}}}}, $ | (5) |
| $ x=1\ 200\frac{n}{{{v}_{0}}}. $ | (6) |
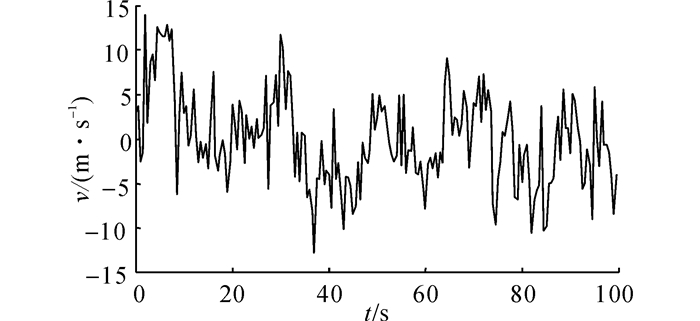
式中:n为脉动风频率;k为地面粗糙系数, 取0.03;Sv(n)为脉动风功率谱.生成的脉动风如图 7所示, v为脉动风速, t为时间.通过逆傅里叶变换将模拟的风速时程转换成功率谱密度曲线, 与目标Davenport谱进行对比, 如图 8所示,发现模拟谱与目标谱的功率谱密度函数大部分频段吻合较好.
|
图 7 脉动风速时程图 Fig. 7 Time-history figure of fluctuating wind |

|
图 8 功率谱对比图 Fig. 8 Comparison of power spectrum |
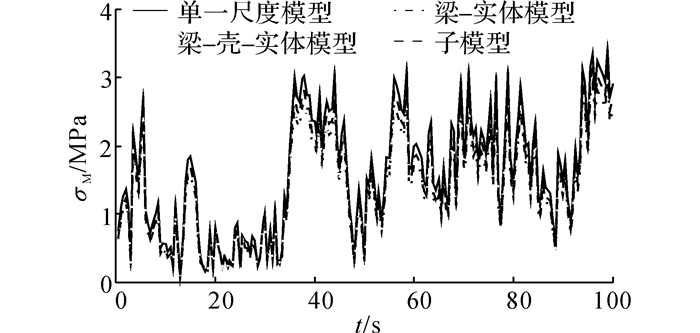
将上述风速时程转化为风压时程并将此榀框架所受的风荷载等效为集中力施加在梁柱结点上, 选取前文所述的研究点位置的Mises应力σM作为指标进行比较, 其时程分析结果如图 9所示, 该时间段内的最大Mises应力σMmax如表 3所示.
|
图 9 动力荷载下各模型Mises应力时程图 Fig. 9 Mises stress time-history figure of models under dynamic load |
| 表 3 该时间段内最大Mises应力 Table 3 Largest Mises stress during this time |
从图 9及表 3中可以看出, 4种模型的Mises应力时程吻合较好, 并且在动力荷载作用下, 子模型法的精度依旧最高, 而另外2种多尺度模型的精度相当.
采用热点应力外推法对4种模型的梁上翼缘与柱连接焊缝处(研究点附近)在上述风荷载作用下的疲劳寿命进行分析, 具体过程及相关的疲劳破坏规律分析可参考文献[17], 此处不再赘述.国际焊接学会(IW)推荐的热点应力外推法规定, 应根据距焊缝焊趾处x1=0.4t和x2=1.0t两点处的应力σ0.4t及σ1.0t外推焊趾处的热点应力σhs, 外推公式[23]如下:
| $ {{\sigma }_{\text{hs}}}=1.67{{\sigma }_{0.4t}}-0.67{{\sigma }_{1.0t}}. $ | (7) |
采用最大主应力作为疲劳应力参数, 根据式(7)计算4种模型在100 s风荷载作用下的热点主应力时程, 疲劳分析的S-N(应力幅-寿命)曲线可选取FAT100曲线, 如下式所示:
| $ \Delta {{\sigma }^{m}}N=\text{C}\text{.} $ | (8) |
式中:Δσ为应力幅;m=5;N为应力幅Δσ作用下的失效循环数;C为常数, 取6.851×1015[24].采用雨流计数法及Palmgren-Miner线性累积损伤准则将该100 s风荷载作用下的变幅热点主应力幅时程转化为造成相同疲劳损伤的等效常幅应力幅Δσe, 计算公式[23, 25]如下:
| $ \Delta {{\sigma }_{\text{e}}}={{\left[\frac{\sum\nolimits_{i=1}^{k}{{{n}_{i}}{{\left( \Delta {{\sigma }_{i}} \right)}^{m}}}}{{{N}_{\text{e}}}} \right]}^{\frac{1}{m}}}. $ | (9) |
式中:Δσi为变幅主应力时程中第i个造成疲劳损伤的应力幅;ni为应力幅Δσi作用下的作用次数;Ne为等效应力幅Δσe的作用次数.由于相同的等效常幅应力幅在同一S-N曲线中对应相同的疲劳损伤和疲劳寿命, 如式(8)所示, 可选取等效常幅应力幅Δσe作为指标进行疲劳损伤的比较, 结果如表 4所示.
| 表 4 各模型等效常幅应力幅 Table 4 Effective constant stress amplitude of models |
由表 4可见, 3种多尺度模型与体尺度模型相比, 等效常幅应力幅Δσe吻合较好, 偏差均低于15%.其中, 子模型法的计算结果与体尺度模型的差距最小, 这说明在结构风致疲劳的分析中, 子模型法依旧精度最高, 而另外2多尺度模型的精度相近.
由式(8)可见, 随着应力幅的减小, 对应的失效循环次数将会增加, 即该焊缝将拥有更久的疲劳寿命, 这说明应力幅是造成构件疲劳破坏的重要指标.通过对比表 4中各模型的等效常幅应力幅Δσe可以发现,多尺度建模将会略微降低该焊缝处的应力幅, 即进行疲劳分析时, 计算出的疲劳寿命比实际疲劳寿命偏大, 计算结果将略微偏于危险, 这点在工程应用中值得注意, 因此推荐采用某大于1的修正系数β乘以多尺度模拟得到的应力幅结果, 以便考虑该因素的影响.针对与该结构类似的工程, 推荐β>1.15, 以便能更加保守和安全地进行疲劳损伤分析及寿命评估.
经过以上对比发现, 尽管约束方程法的精度不如子模型法, 但建模时通过刚性区建立多点约束方程的过程相对简单, 且概念清晰, 因此也能较好地满足工程需要.
5 局部模型区域大小研究在实际大型结构的多尺度建模中, 应当在满足准确度要求的前提下尽可能减小局部细观尺度模型区域的大小以减少计算资源消耗, 以下对局部细观尺度模型区域大小的选择进行讨论.
本文采用局部模型边界离研究点横向轴线的距离L作为衡量局部细观尺度模型区域大小的具体参数, 如图 2(b)及图 10所示.选取该榀框架的梁-壳-体尺度模型和子模型法模型, 分别建L为0.025、0.05、0.075、0.100、0.125和0.15 m的6种模型, 施加上文所述的静力风荷载和动力风荷载时程, 研究其对静力荷载、动力荷载及疲劳分析计算结果的影响.
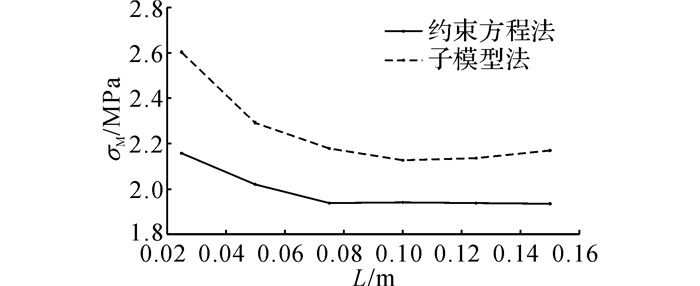
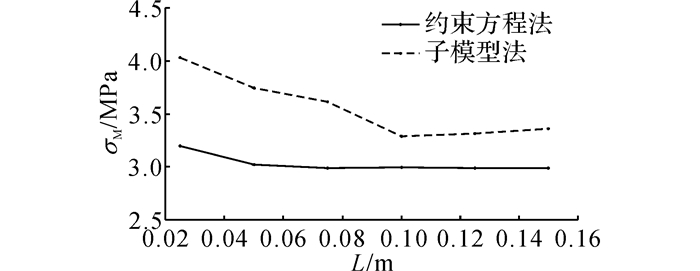
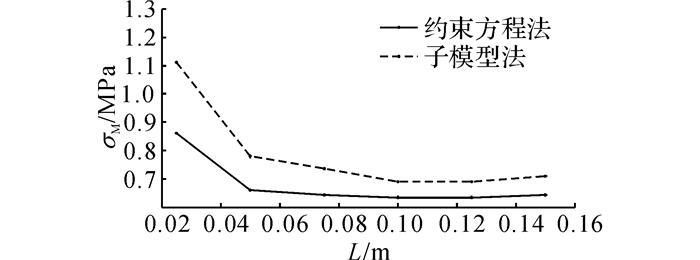
选取梁上翼缘与柱连接焊缝处(研究点位置)的Mises应力、时间段内的最大Mise应力及等效常幅应力幅Δσe作为指标进行对比, 结果如图 11~13所示.可以发现, 随着局部模型边界离研究点横向轴线的距离L的增大, 即局部模型的增大, 焊趾处Mises应力及等效常幅应力幅Δσe总体均呈现减小的趋势, 即疲劳损伤减小, 疲劳寿命增大.其中, 子模型法的计算结果对于L的减小表现得更为敏感, 计算结果受影响更大, 变化也更快, 而约束方程法对于距离的敏感度相对较小, 也表现得更为滞后.
|
图 11 静力荷载下Mises应力随距离变化图 Fig. 11 Change of Mises stress with distance under static load |
|
图 12 动力荷载下最大Mises应力随距离变化图 Fig. 12 Change of largest Mises stress with distanceunder dynamic load |
|
图 13 动力荷载下等效常幅应力幅随距离变化图 Fig. 13 Change of effective constant stress amplitude with distance under dynamic load |
由此可见,局部细观尺度模型区域大小对于多尺度建模的准确度来说至关重要, 当位置过于接近要提取应力结果的区域时, 易造成应力结果失真, 这点在子模型法中表现得更为明显, 这是由于子模型法的位移插值实质上相当于基于圣维南原理对边界的位移荷载进行了等效, 如图 3所示, 相当于将粗糙模型I两点的位移列阵等效为I’、J’、K’、D’四点的位移列阵施加在子模型上, 而圣维南原理指出, 如果实际载荷被等效载荷代替以后, 应力和应变在载荷施加的位置附近将会有改变, 而在远离荷载施加位置处无改变.随着上述边界离研究部位横向轴线距离的减小, 即局部模型区域的减小, 切割边界越来越接近提取应力的点, 这使得该处的应力越来越受到荷载等效的影响;而约束方程法的计算结果则受边界位置选取的影响相对较小, 这是因为约束方程法直接采用约束方程对边界节点的自由度进行相应的约束, 不涉及边界位移的插值计算及相应的荷载等效.
由以上对比发现, 约束方程法和子模型法各有优劣, 相对而言子模型法结果更为精准, 但是受局部模型区域大小的影响较大;与之相反, 尽管约束方程法的精度不如子模型法, 但是受局部模型区域大小的影响较小.在结构较为复杂、局部模型单元数较多的情况下, 推荐使用约束方程法建立多尺度模型, 以便尽可能缩小局部模型, 减少单元数;而在结构略微简单些、局部模型单元数能够保证不影响计算效率的情况下, 推荐采用子模型法, 从而获得更高的精度.
6 结论(1) 采用约束方程法或子模型法建立的多尺度有限元模型在静力荷载、动力荷载及疲劳分析中均能取得较好的精度.这说明多尺度建模方法在大型结构的疲劳分析中有着较好的应用前景.
(2) 子模型法相对于约束方程法的精度更高, 但是更易受局部细观尺度模型区域大小的影响.针对与本工程梁柱尺寸类似的钢框架结构, 建议当采用约束方程法时, 边界离研究部位横向轴线的距离选为0.05 m, 而当采用子模型法时, 上述数值应适当增加, 取0.10 m.
(3) 多尺度建模时, 在结构较复杂、局部模型单元数过多时, 推荐使用约束方程法建立多尺度模型;而当结构略简单、局部模型单元数相对较少时, 推荐采用子模型法.
(4) 基于多尺度有限元建模的疲劳寿命分析将会得到略偏危险的计算结果, 因此推荐对该分析得到的应力幅乘以略大于1的修正系数进行修正, 以便使结果更加偏于保守和安全.
| [1] |
COLELLA F, REIN G, CARVEL R, et al. Analysis of the ventilation systems in the Dartford tunnels using a multi-scale modelling approach[J]. Tunnelling and Underground Space Technology, 2010, 25(4): 423-432. DOI:10.1016/j.tust.2010.02.007 |
| [2] |
LI Z X, ZHOU T Q, CHAN T H T, et al. Multi-scale numerical analysis on dynamic response and local damage in long-span bridges[J]. Engineering Structures, 2007, 29(7): 1507-1524. DOI:10.1016/j.engstruct.2006.08.004 |
| [3] |
KADOWAKI H, LIU W K. Bridging multi-scale method for localization problems[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(30): 3267-3302. |
| [4] |
CAO Y, WANG P, JIN X, et al. Tunnel structureanalysis using the multi-scale modeling method[J]. Tunnelling and Underground Space Technology, 2012, 28: 124-134. DOI:10.1016/j.tust.2011.10.004 |
| [5] |
丁幼亮, 李爱群, 缪长青, 等. 大跨桥梁结构损伤诊断与安全评估的多尺度有限元模拟研究[J]. 地震工程与工程振动, 2006, 26(2): 66-72. DING You-liang, LI A-iqun, MIAO Chang-qing, et al. Multi-level finite element modeling of long-span bridges for structural damage diagnosis and safety evaluation[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(2): 66-72. |
| [6] |
程小卫, 李易, 陆新征, 等. 基于多尺度模型的RC框架撞击倒塌响应数值分析[J]. 振动与冲击, 2016, 35(5): 82-88. CHENG Xiao-wei, LI Yi, LU Xin-zheng, et al. Numerical analysis for collapse response of a RC frame subjected to impact loading based on multi-scale model[J]. Journal of Vibration and Shock, 2016, 35(5): 82-88. |
| [7] |
陆新征, 林旭川, 叶列平. 多尺度有限元建模方法及其应用[J]. 土木工程与管理学报, 2008, 25(4): 76-80. LU xin-zheng, LIN Xu-chuan, YE lie-ping. Multi-scale finite element modeling method and its application[J]. Journal of Civil Engineering and Management, 2008, 25(4): 76-80. |
| [8] |
PANASENKO G P. Multi-scale modelling for structures and composites[M]. Dordrecht: Springer, 2005, 1-19.
|
| [9] |
RAFⅡTABAR H, HUA L, CROSS M. A multi-scale atomistic-continuum modelling of crack propagation in a two-dimensional macroscopic plate[J]. Journal of Physics Condensed Matter, 1998, 40(10): 2375. |
| [10] |
REPETTO M P, SOLARI G. Wind-induced fatigue collapse of real slender structures[J]. Engineering Structures, 2010, 32(12): 3888-3898. DOI:10.1016/j.engstruct.2010.09.002 |
| [11] |
REPETTO M P, SOLARI G. Wind-induced fatigue of structures under neutral and non-neutral atmospheric conditions[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2007, 95(9): 1364-1383. |
| [12] |
JIA J. Investigations of a practical wind-induced fatigue calculation based on nonlinear time domain dynamicanalysis and a full wind-directional scatter diagram[J]. Ships & Offshore Structures, 2014, 9(3): 272-296. |
| [13] |
DONG W, MOAN T, GAO Z. Fatigue reliability analysis of the jacket support structure for offshore wind turbine considering the effect of corrosion and inspection[J]. Reliability Engineering & System Safety, 2012, 106(106): 11-27. |
| [14] |
DONG W, MOAN T, GAO Z. Long-term fatigueanalysis of multi-planar tubular joints for jacket-type offshore wind turbine in time domain[J]. Engineering Structures, 2011, 33(6): 2002-2014. DOI:10.1016/j.engstruct.2011.02.037 |
| [15] |
DONG W, XING Y, MOAN T, et al. Time domain-based gear contact fatigue analysis of a wind turbine drivetrain under dynamic conditions[J]. International Journal of Fatigue, 2013, 48(1): 133-146. |
| [16] |
FANG Z, LI A, LI W, et al. Wind-induced fatigueanalysis of high-rise steel structures using equivalent structural stress method[J]. Applied Sciences, 2017, 7(1): 71. DOI:10.3390/app7010071 |
| [17] |
方钊, 李爱群, 李万润, 等. 高层钢框架支撑结构多尺度风致疲劳分析方法[J]. 东南大学学报:自然科学版, 2017, 47(1): 137-141. FANG Zhao, LI Ai-qun, LI Wan-run, et al. Multi-scale wind-induced fatigue analysis method of high-rise steel braced frame structure[J]. Journal of SoutheastUniversity:Natural Science Edition, 2017, 47(1): 137-142. |
| [18] |
王新敏. ANSYS工程结构数值分析[M]. 北京: 人民交通出版社, 2013, 394-399.
|
| [19] |
徐芝纶. 弹性力学(上册)[M]. 北京: 高等教育出版社, 2006, 23-25.
|
| [20] |
王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003, 56-61.
|
| [21] |
中华人民共和国建设部. 中华人民共和国国家标准. 建筑结构荷载规范GB50009-2001), 2002. http://www.cnki.com.cn/Article/CJFDTotal-GJBZ200605011.htm
|
| [22] |
武岳, 孙瑛, 郑朝荣, 孙晓颖. 风工程与结构抗风设计[M]. 哈尔滨: 哈尔滨工业大学出版社, 2014.
|
| [23] |
HOBBACHER A. Recommendations for Fatigue Design of Welded Joints and Components[M]. Basel: Springer International Publishing, 2016.
|
| [24] |
张彦华. 焊接结构疲劳分析[M]. 北京: 化学工业出版社, 2013, 107-117.
|
| [25] |
崔闯, 卜一之, 张清华, 等. 基于热点应力法的正交异性钢桥面板疲劳寿命评估[J]. 桥梁建设, 2014, 44(4): 62-67. CUI Chuang, BU Yi-zhi, ZHANG Qing-hua, et al. Fatigue life assessment of orthotropic steel deck plate based on hot spot stress method[J]. Bridge Construction, 2014, 44(4): 62-67. |



