桩基础在道路工程、桥梁工程以及离岸工程中得到越来越广泛的应用, 其服役期间不仅承受上部结构自重产生的静力荷载作用, 还承受车辆、波浪、风等产生的循环荷载作用:如竖向交通循环荷载下的单桩以及水平向波浪和风荷载下的群桩.循环荷载作用下桩-土界面弱化机制的研究有助于深入揭示桩-土界面力学特性和荷载传递机理, 对于深入研究桩基的长期承载性能具有重要意义.

国内外诸多学者针对土与结构界面的循环弱化机制开展了一些研究工作.Chan等^[1]进行了循环荷载作用下干砂中的小比例尺模型桩试验, 发现循环荷载下桩基的弱化特性.Poulos^[2]指出循环荷载下桩-土界面的弱化特性是与普通静载作用下桩基相比值得关注的基本问题.此后, Tabucanon等^[3]通过循环剪切试验研究桩-土界面的力学特性和弱化机制, 发现剪切位移幅值越大, 剪切应力与法向应力弱化速率越大.张嘎等^[4]发现常法向边界条件下结构物-土界面循环剪切抗剪强度包络线接近于直线.冯大阔等^[5]发现单向往返剪切路径下接触面在初始剪切时均未达到强度包线, 随着循环剪切次数的增加逐渐接近并达到强度包线.徐肖峰等^[6]利用刚性剪切盒研究了剪切速率对粗粒土强度和变形的影响.刘俊伟等^[7]研究了桩-土界面弱化机制与循环剪切次数的关系.章敏等^[8]进行了不同循环加载频率和剪切位移幅值下桩-土界面力学特性的研究, 研究发现桩-土界面循环弱化与加载频率和剪切位移幅值密切相关.Lam等^[9]采用界面剪切试验研究了聚合物和膨润土护壁泥浆对混凝土-砂界面剪切特性的影响.除此之外, 许多学者对循环荷载下桩-土界面土颗粒的破碎进行了相应的研究^[10-11].

综上所述, 现有研究成果已揭示了土与结构界面(尤其桩-土界面)循环弱化的部分机理, 但目前有关不同剪切位移幅值和初始法向应力对土与结构界面循环弱化影响规律的研究相对较少, 对界面循环弱化机制的研究仍不够完善.本文通过自主研发的大尺度恒刚度(constant normal stiffness, CNS)界面循环剪切仪, 系统研究不同剪切位移幅值和初始法向应力下钢板-标准砂界面循环剪切机理, 以期更为全面地揭示桩-土界面循环弱化机制.

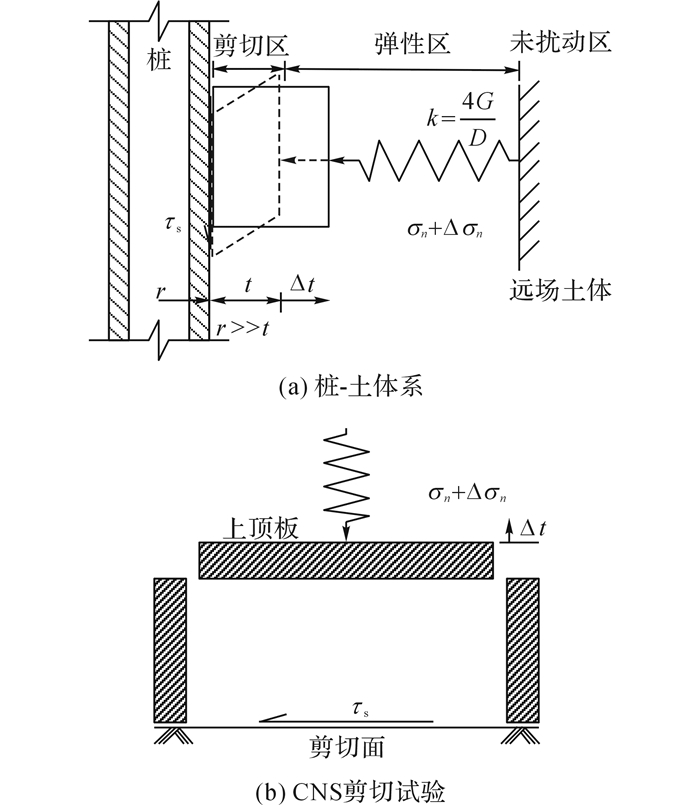
根据扰动程度可将桩侧土体划分为3个区域：剪切区、弹性区以及未扰动区.剪切区土体紧邻桩身, 存在某一特定的薄层剪切带, 剪切过程中发生较大变形；未扰动区为远场土体不发生任何变形；弹性区土体位于剪切区与未扰动区之间, 以水平向弹性变形为主^[12-13], 如图 1(a)所示.其中，τ_s为切应力，r为桩半径，t为剪切带厚度.

图 1

图 1 桩-土体系和CNS剪切试验对比图 Fig. 1 Analogy between pile-soil interaction and CNS test

基于此, 利用CNS剪切试验类比桩-土界面的剪切特性及桩侧土体的变形特征, 能够更加真实的再现桩-土体系, 如图 1(b)所示.其中, 下剪切盒内部钢板试块模拟现有工程中广泛应用的钢管桩；上剪切盒内部砂土模拟桩侧剪切区土体.理想化弹簧组(上端固定)通过上顶板施加弹性区土体对剪切区土体的法向作用, 弹簧变形量Δt表示剪切带厚度的变化量.

剪切带厚度的变化Δt会导致桩侧法向应力σ_n的变化^[14], 两者之间的关系如下：

式中：Δσ_n为桩侧法向应力增量, G为桩周土体的剪切模量, D为桩径, Δt为剪切带厚度的变化量, k为CNS剪切仪弹簧刚度.

根据CNS剪切仪研制机理, 制成室内大型恒刚度桩-土界面剪切仪, 如图 2所示.剪切仪上剪切盒内部尺寸为700 mm×300 mm×300 mm(长×宽×高), 下剪切盒外部尺寸为900 mm×320 mm×120 mm(长×宽×高), 内部(放置钢板)尺寸为500 mm×300 mm×100 mm(长×宽×高).剪切过程中, 钢板在剪切方向上始终位于上剪切盒对应的范围内, 保证了剪切面积的恒定.采用弹簧提供法向恒刚度, 其劲度系数k=50 kPa/mm.可实现的剪切速率范围为0.15 ~15.00 mm/min.下剪切盒试块表面预埋光纤光栅应变传感器测量桩-土界面的剪应力.

图 2

1-竖向螺杆；2-弹簧组件；3-可拆卸弹簧固定板；4-上剪切盒；5-水平螺杆；6-标准砂；7-钢板；8-下剪切盒；9-变频电机；10-1: 100减速机 图 2 恒刚度桩-土界面剪切仪 Fig. 2 Constant normal stiffness shear apparatus of soil-pile interface

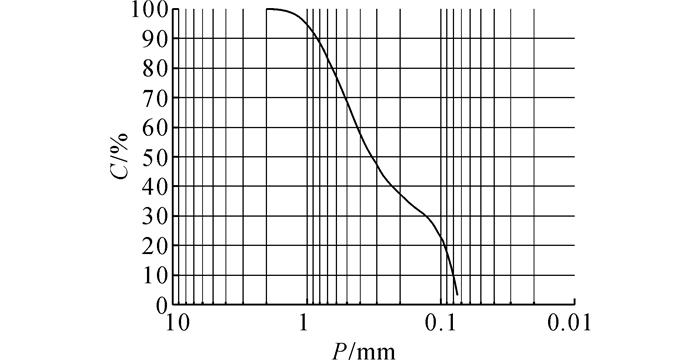
试验采用干燥的ISO标准砂, 砂土粒径在0.075~2.000 mm, 平均粒径d₅₀=0.34 mm.砂土的内摩擦角φ=40.4°, 相对密度G_s=2.71, 最大、最小孔隙比分别为0.856、0.402.标准砂颗粒级配曲线如图 3所示, 其中, C为小于某粒径的土重含量；P为土粒粒径.

图 3

图 3 中国ISO标准砂颗粒级配曲线 Fig. 3 Sand grading curve of China ISO standard

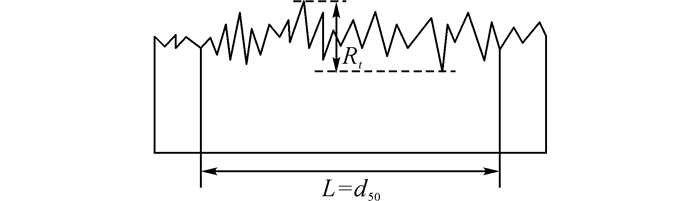
Kishida等^[15]根据颗粒级配曲线得到土样平均粒径d₅₀, 提出一种标准化粗糙度R_n表示方法, 示意图如图 4所示, 计算方法如下：

图 4

图 4 结构物表面粗糙度表示方法 Fig. 4 Representation method of surface roughness of structure

式中：R_t为结构物表面粗糙度.

该方法综合考虑了结构物表面粗糙度、土样粒径尺度对剪切的影响.本试验所用钢板表面粗糙度R_t=12 μm, 代入公式算出其标准化粗糙度R_n=0.035.

为便于分析钢板-标准砂界面循环剪切试验结果, 定义循环剪切路径如图 5所示.x轴表示钢板-标准砂界面相对剪切位移, 由原点0出发, 沿x轴方向①→②→③→④为一完整剪切循环, 并规定①、④阶段为正向剪切, ②、③阶段为负向剪切.

图 5

图 5 循环剪切路径图 Fig. 5 Schematic view of cyclic shear paths

为研究剪切速率v=5 mm/min时不同剪切位移幅值s和不同初始法向应力σ对钢板-标准砂界面循环弱化的影响规律, 先后进行4组恒刚度循环剪切试验, 标准砂密实度D_r均为90%, 前2组试验循环剪切数N=20, 后2组试验循环剪切数N=15.具体剪切试验方案如表 1所示.

表 1

表 1 循环剪切试验方案 Table 1 Cyclic shear test schemes 试验编号 v/(mm·min-1) σ/kPa s/mm SS-1 5 90 10 SS-2 5 110 10 SS-3 5 90 5 SS-4 5 110 5

表 1 循环剪切试验方案 Table 1 Cyclic shear test schemes

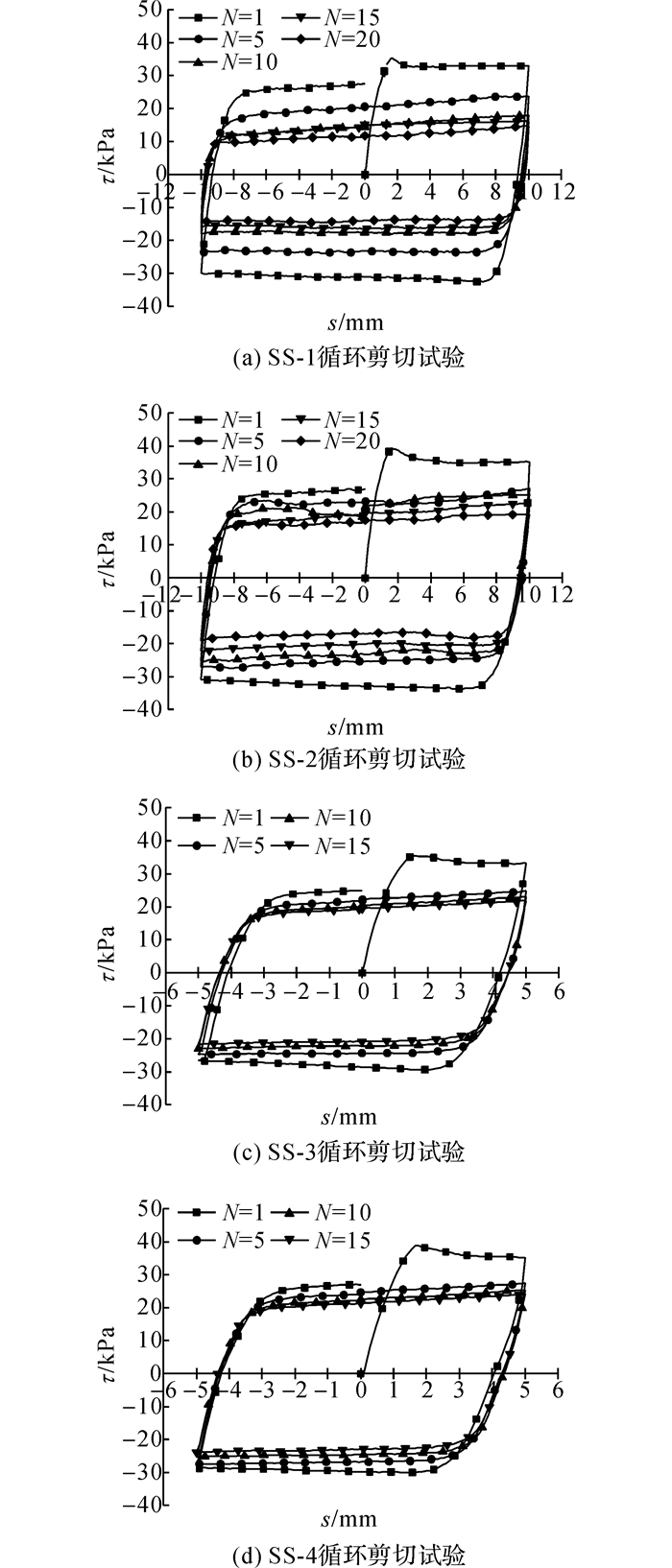
本研究4组恒刚度剪切试验剪切应力-剪切位移关系曲线如图 6所示, 横坐标为剪切位移s, 纵坐标为剪切应力τ.由图 6可知, 钢板-标准砂界面剪切应力-剪切位移关系曲线均成“滞回环”状发展, 滞回环趋于“扁平”, 循环剪切的初始阶段, 相邻滞回环相差较大, 随着循环次数的增加趋于重合.说明, 界面剪切应力随循环次数的增加不断弱化, 且弱化主要集中在初始阶段.第5、10、15、20循环最大正位移处剪切应力较其前5次循环结果衰减幅度如表 2所示.可以发现, 剪切应力的弱化速率随着初始法向应力和剪切位移幅值的增加而增加.剪切位移方向由正向变为负向(①→②阶段)时, 剪切应力由正值迅速降低至最大负值, 所经历的剪切位移较小, 且随着循环次数的增加, 此剪切位移不断变小并趋于稳定；在③→④阶段, 剪切应力变化规律与①→②阶段相似, 两者变化近似以原点为中心呈对称性分布.这与文献[16-17]的研究规律一致.

图 6

图 6 不同循环次数下剪切应力-剪切位移关系曲线 Fig. 6 Curves of shear stress-displacement behaviorunder different cycles

表 2

表 2 第5、10、15、20次循环剪切应力较其前5次循环衰减幅度 Table 2 Attenuation amplitude of shear stress compared with its five cycles before at cycle 5, 10, 15, 20 % 试验编号 第5循环 第10循环 第15循环 第20循环 SS-1 27.93 24.46 11.69 7.69 SS-2 22.52 6.72 11.88 14.11 SS-3 25.04 7.93 5.37 - SS-4 21.98 7.81 5.01 -

表 2 第5、10、15、20次循环剪切应力较其前5次循环衰减幅度 Table 2 Attenuation amplitude of shear stress compared with its five cycles before at cycle 5, 10, 15, 20

4组恒刚度剪切试验界面法向应力-剪切位移关系如图 7所示, 其中σ为法向应力.由图 7可知, 钢板-标准砂界面法向

图 7

图 7 不同循环次数下法向应力-剪切位移关系曲线 Fig. 7 Curves of normal stress and shear displacement behavior with different cycles

应力-剪切位移关系曲线呈“阶梯”状发展, “阶梯”呈现由上向下的发展趋势并趋于“扁平”, 循环剪切的初始阶段, 相邻“阶梯”相差较大, 随着循环次数的增加趋于重合.说明界面法向应力随循环次数的增加不断弱化, 弱化主要集中在初始阶段.第5、10、15、20循环在最大正位移处法向应力较其前5次循环结果衰减幅度如表 3所示.可以发现, 法向应力的弱化速率时随着初始法向应力和剪切位移幅值的增加而增加.Mortara等^[16-17]同样进行了此类研究, 其研究所得结论与本文相似.

表 3

表 3 第5、10、15、20次循环法向应力较其前5次循环衰减幅度 Table 3 Attenuation amplitude of normal stress compared with its five cycles before at cycle 5, 10, 15, 20 % 试验编号 第5循环 第10循环 第15循环 第20循环 SS-1 38.38 26.14 23.75 17.37 SS-2 32.68 17.05 5.39 25.01 SS-3 21.62 8.05 4.83 - SS-4 20.72 8.17 2.88 -

表 3 第5、10、15、20次循环法向应力较其前5次循环衰减幅度 Table 3 Attenuation amplitude of normal stress compared with its five cycles before at cycle 5, 10, 15, 20

将本文4组试验、文献[17]以及文献[14]试验中不同循环次数下的最大剪切应力归一化绘制于图 8中, 拟合的对数函数曲线如图 8所示.其中, N为试验循环次数, 纵坐标为剪切应力τ与最大剪切应力τ_max的比值, 拟合公式如下：

图 8

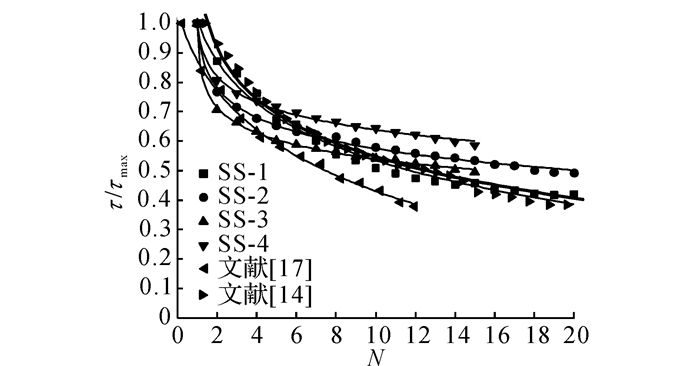
图 8 剪切应力随循环次数变化曲线 Fig. 8 Variations of shear stress with cycle history

式中：τ_max为剪切应力峰值, a、b、c均为常数；N为循环剪切次数.

由图 8可以发现, 试验所得数据与拟合的对数函数相关性较大, 本试验与文献[17]和文献[14]所得曲线的趋势大体相同.随着循环剪切次数N的增加, 界面剪切应力不断弱化, 弱化主要发生在初始阶段, 随着循环次数的增加弱化速率不断降低并趋于平缓.这主要是因为剪切过程中土体发生了减缩.分析认为土体减缩主要归因于颗粒的重新排列和破碎.未开始试验时颗粒长轴和短轴排列杂乱无章, 循环试验过程中, 颗粒长、短轴重新排列, 颗粒长轴方向趋近于剪切方向；处于高位势的土颗粒降低到较低位势的状态；小颗粒进入到大颗粒间的孔隙, 以上原因均减小了土体颗粒占用的体积空间.颗粒破碎是发生土体减缩的另一重要原因, 部分大颗粒破碎为小颗粒, 新形成的小颗粒进入大颗粒构成骨架的孔隙.无论是颗粒的重新排列, 还是大颗粒的破碎均在剪切初始时较为显著, 因此剪切应力的弱化主要发生在初始阶段.

拟合系数如表 4所示.b值表征剪切应力弱化速率, 其值随剪切位移幅值增加而增大, 本次试验中b值范围为0.08~0.22.文献[17]试验中采用的为粗粒土, 剪切过程中颗粒的重新排列和破碎更为显著, 所以剪切应力弱化速率较大.文中第一组试验与文献[14]试验归一化所得曲线相似程度较高.

表 4

表 4 拟合方程系数表 Table 4 Coefficient of fitting equation 试验 a b c 相关系数 SS-1 1.03 0.22 0.11 0.98 SS-2 0.79 0.10 -0.88 0.99 SS-3 0.72 0.08 -0.97 0.99 SS-4 0.83 0.09 -0.85 0.99 文献[17] 1.08 0.27 1.16 0.99 文献[14] 0.98 0.19 -0.65 0.99

表 4 拟合方程系数表 Table 4 Coefficient of fitting equation

图 9表示钢板-标准砂界面应力路径图及其强度包络线, 其中(a)、(b)、(c)、(d)分别表示SS-1、SS-2、SS-3、SS-4循环剪切试验, 横坐标为法向应力σ, 纵坐标为剪切应力τ.图 9(a)、(b)中实线为初始强度包络线, 虚线为峰值强度包络线.由图 9(a)、(b)可得, 剪切位移幅值较大时, 钢板-标准砂界面在初始剪切时剪切强度包络线斜率较小, 界面摩擦角较小, 随着剪切的进行、法向应力的不断降低, 界面摩擦角增加, 应力路径达到峰值强度包络线.图 9(c)、(d)中实线为峰值强度包络线, 虚线为残余强度包络线.由图 9(c)、(d)可知, 剪切位移幅值较小时钢板-标准砂界面在初始剪切时便已达到峰值强度包络线, 随着剪切的进行抗剪强度逐渐降低, 界面摩擦角逐渐变小并趋于稳定.

图 9

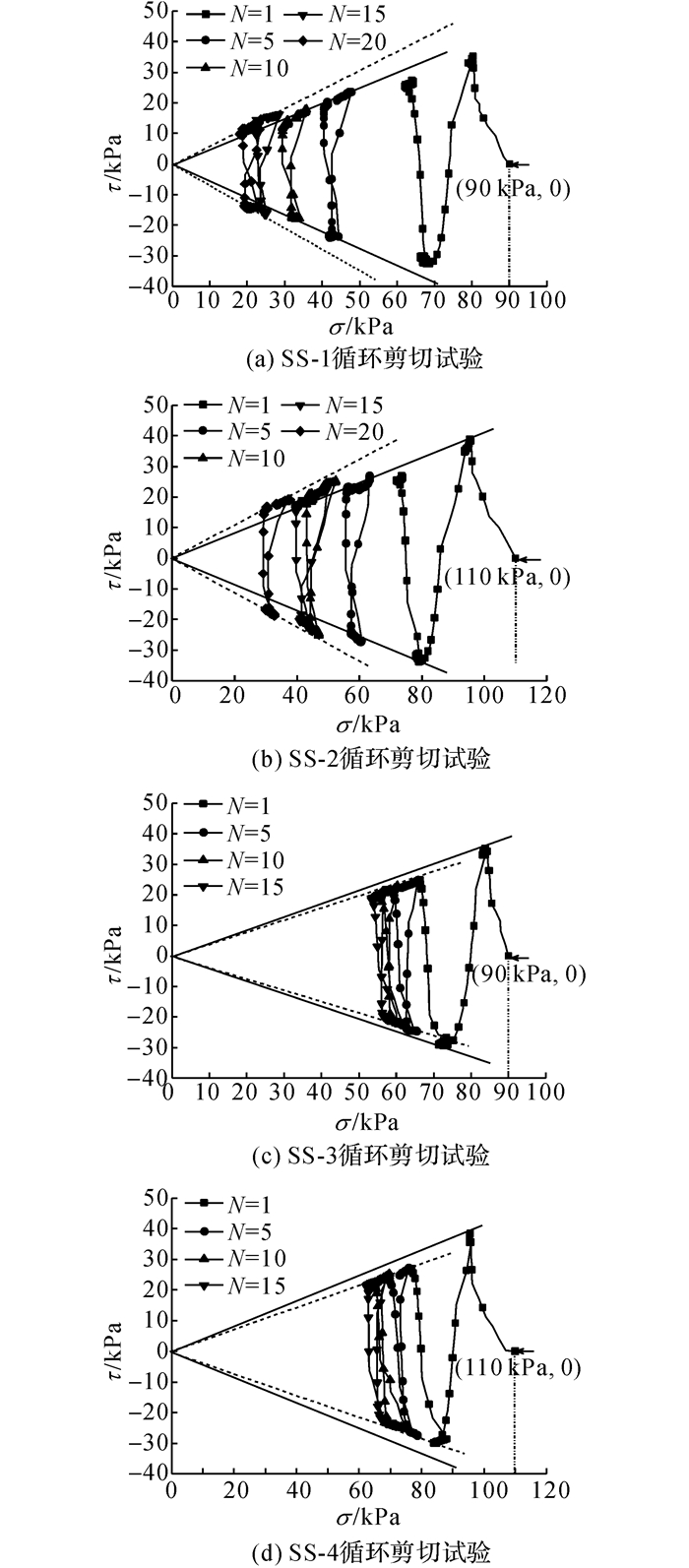
图 9 循环剪切下界面应力路径曲线 Fig. 9 Stress paths of interface under cyclic loading

桩-土体系发生相对运动时, 剪切带范围内的土颗粒发生剪切破坏, 大颗粒破碎成小颗粒, 颗粒平均粒径变小, 剪切带变薄, 如图 10所示.试验结束后在距离界面高度5 cm范围内每隔1 cm取样150 g测得砂样的颗粒级配曲线, 如图 11所示.其中C为小于某粒径的土重含量，P为土粒粒径.由图可知, 距界面0~1 cm范围内砂样颗粒级配曲线发生了明显变化, 距界面1~2 cm、2~3 cm、3~4 cm、4~5 cm范围内砂样颗粒级配曲线未发生太大变化, 说明本试验仅使毗邻桩-土界面1 cm范围内的土颗粒发生一定结构性破坏, 剪切带在距界面1 cm范围内.归纳每组循环剪切试验不同高度范围内砂样的平均粒径d₅₀, 如图 12所示, 其中D表示距桩-土界面的距离.SS-1、SS-2、SS-3、SS-4试验0~1 cm范围内砂样平均粒径分别为：0.20 mm、0.19 mm、0.21 mm、0.20 mm, 较原样砂平均粒径0.34 mm相差较大, 其余位置颗粒平均粒径变化不大.

图 10

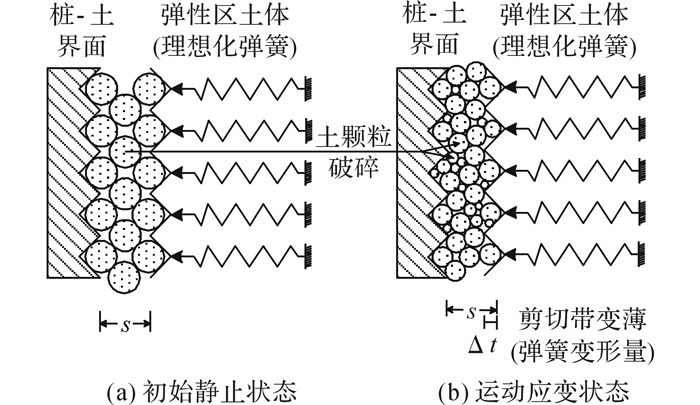
图 10 桩-土界面剪切带变薄 Fig. 10 Thickness decays of shear band in pile-soilinterface

图 11

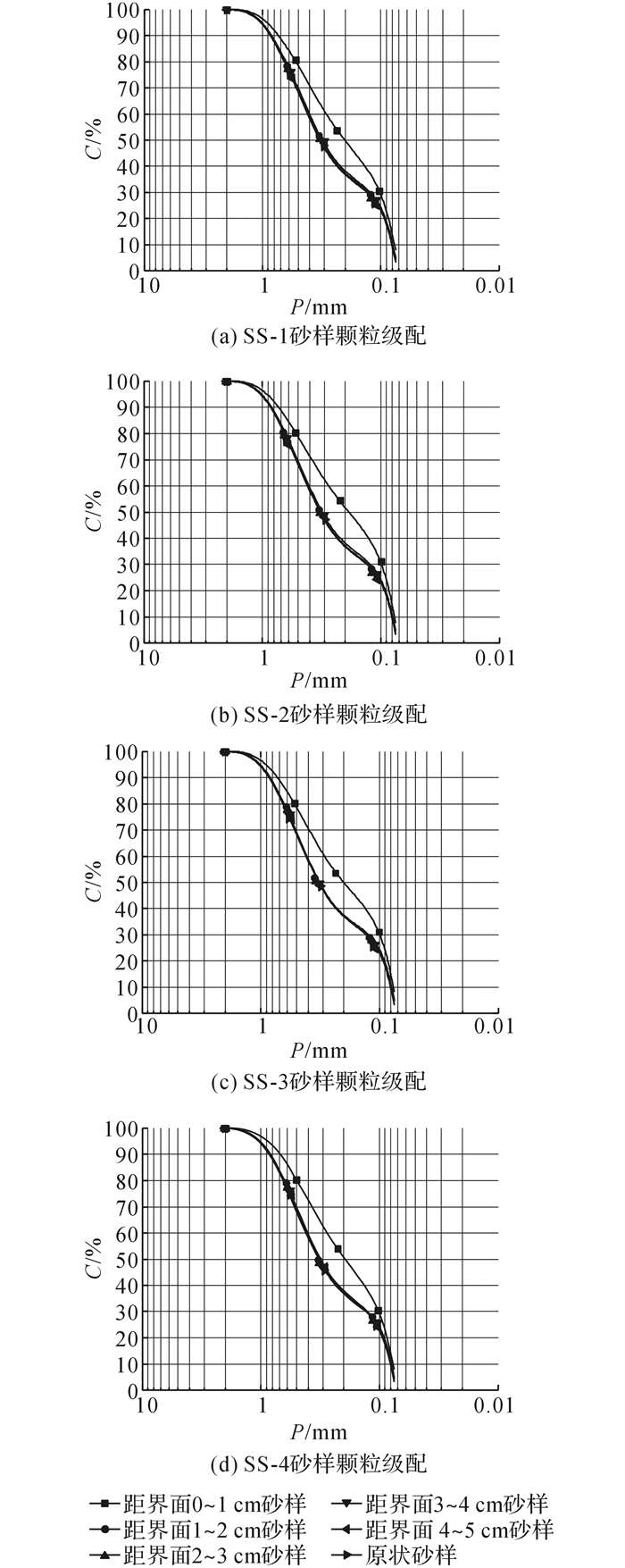
图 11 距砂-钢板界面不同高度处砂样颗粒级配曲线 Fig. 11 Sand grading curves at different heights from sand-steel interface

图 12

图 12 平均粒径d50随砂-钢板界面距离变化曲线 Fig. 12 Variations of median diameter d50 with distance from sand-steel interface

砂颗粒的破碎程度由颗粒破碎率B_t表示, B_t的大小为原状砂样颗粒级配曲线与剪切后砂样颗粒级配曲线下侧的面积差值和原状砂样颗粒级配曲线下侧面积的比值^[18], 如图 13所示, 其计算公式如下：

图 13

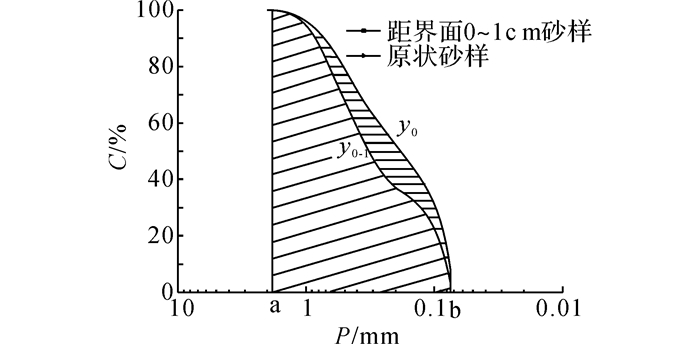
图 13 颗粒破碎的定义 Fig. 13 Definition of particle breakage

式中：B_t为颗粒破碎率；y₀为原状砂样颗粒级配曲线；y_0-1为剪切后距界面0~1 cm的砂样颗粒级配曲线.

颗粒破碎主要发生在距界面0~1 cm的颗粒中, 根据公式求出4组试验破碎率分别为5.2%、5.4%、5.0%、5.2%, 颗粒的破碎率大约为5%.可以发现, 剪切位移幅值相同时, 初始法向应力越大, 剪切带区域砂样平均粒径越小, 颗粒破碎越严重；初始法向应力相同时, 剪切位移幅值越大, 剪切带区域砂样平均粒径越小, 颗粒破碎越严重.

(1) 界面剪切应力-剪切位移关系曲线呈“滞回环”状发展, 界面法向应力-剪切位移关系曲线呈“阶梯”状发展, 剪切的初始阶段相邻“滞回环”、“阶梯”相差较大, 随着循环次数的增加趋于重合；剪切应力和法向应力的弱化速率随初始法向应力和剪切位移幅值的增加而增加.

(2) 随循环剪切次数N的增加, 界面剪切应力呈对数型弱化, 弱化速率逐渐变小并趋于平缓, 弱化的根本原因是界面处砂土颗粒的剪切破碎以及剪切过程中颗粒的重排列.剪切位移幅值较大时, 随着循环次数的增加, 界面摩擦角逐渐增加；剪切位移幅值较小时, 界面摩擦角逐渐变小并趋于稳定.

(3) 距离界面0~1 cm的颗粒平均粒径发生了明显变化, 剪切带在距界面1 cm范围内；剪切带内颗粒破碎率达5%以上, 且初始法向应力越大、剪切位移幅值越大, 颗粒破碎越严重.