在可持续发展战略对地下水资源保护提出明确要求的背景下,对修建于富水地层的深埋隧道,地下水处治原则逐渐由过去的“以排为主”转变为“以堵为主,限量排放”,一方面采取地下水封堵措施,另一方面对地下水进行限量排放,从而实现隧道渗流量和衬砌外水压力之间的平衡[1-4].设计“堵水限排”方案的关键在于计算隧道渗流量和衬砌外水压力,目前隧道渗流场的主要计算方法有实测经验分析法、解析法和数值法等.虽然解析解的推导必须基于大量的假设,但与数值模拟等方法相比,解析解可较为经济、便捷地求出隧道渗流量和衬砌外水压力,并便于对各项参数进行敏感性分析,具有简洁、概念清晰等优点,从理论上把握隧道渗流场的分布规律,为设计、施工提供必要的参考.
由于实际隧道渗流场求解的复杂性,现有的解析计算研究多把地质模型简化为在均质饱和、各向同性的半无限多孔介质内开挖圆形隧道,并于地表作用初始水平水位的计算模型,针对该简化模型,目前主要存在2种求解方法[5].
第一种方法是由王建宇[1]提出的基于达西定律和无限含水层竖井理论的近似解法,该方法将圆形隧道渗流场求解简化为轴对称问题,并推导出相应的水压力和涌水量公式.王秀英等[2-3]在文献[1]的基础上,针对山区高水位隧道建立了隧道渗流场简化模型,推导了隧道排水量及衬砌、注浆圈水压力的解析公式.李鹏飞等[6-7]根据王建宇简化方法,对考虑衬砌和注浆圈的海底隧道渗流场进行了研究,给出了相应的解析解.第一种方法能便捷地对含衬砌和注浆圈的隧道渗流场进行求解,但该方法在求解过程中采用了无限渗流边界,这一假设不能完全合理地反映实际中的围岩区域,使得该方法得到的解析解存在一定误差.对此,应宏伟等[5]采用镜像法将半无限实际渗流场转化为两个无限虚拟渗流场的叠加,推导出考虑注浆圈作用的水下隧道渗流场解析解,该解析解相较于第一种方法得到的解析解更为精确.
第二种方法则是采用复变函数保角变换对计算模型中的半无限平面孔口问题进行转化和求解,包括了多种不同的变换形式和解答方式.Verruijt[8]通过保角变换将半无限空间映射为圆环域,求解了半无限空间中孔洞的应力场与位移场问题.基于文献[8]的求解思路,el Tani[9]对单层半无限介质中的无压圆形孔洞渗流问题进行了研究,并给出了该问题的解析解.Kolymbas等[10]则采用复变函数得到了适用于地表面与隧道圆周为变水头的渗流场解析解.Park等[11]对Tani和Kolymbas的研究进行了比较,并在此基础上得到了隧道圆周分别为变水头和常水头时的渗流解析解.童磊等[12]基于文献[11],利用Fourier解法和流量连续条件,解答了半无限含水层带衬砌隧洞的渗流问题.皇甫明等[13-14]根据模型对称性,对半无限平面取一半结构进行分析,将多连通域问题转变为单连通域问题,完成了隧道渗流场的求解.
与第一种方法相比,第二种方法难以求解含衬砌和注浆圈的隧道渗流场,但对于围岩区域渗流场的求解,第二种方法更加精确、有效.目前对于含注浆圈隧道渗流场的求解绝大多数都直接采用了第一种方法,而采用第二种方法推导的隧道渗流场解析解皆未考虑注浆圈的影响.
本文针对含注浆圈深埋隧道的渗流场解析问题展开研究,建立简化计算模型,将半无限平面分为围岩、衬砌和注浆圈3个区域,对不同区域采用合适的方法进行求解.首先,采用复变函数保角变换将围岩区域渗流场解析问题转化为二维圆环域的Laplace方程求解问题.其次,根据边界条件和层间流量连续条件对围岩、衬砌和注浆圈等3个区域的渗流场进行联立求解,推导出半无限平面含注浆圈深埋隧道渗流场解析解,并与镜像法解析解和数值解进行对比验证.最后,通过算例分析隧道渗流场对注浆参数变化的敏感性.
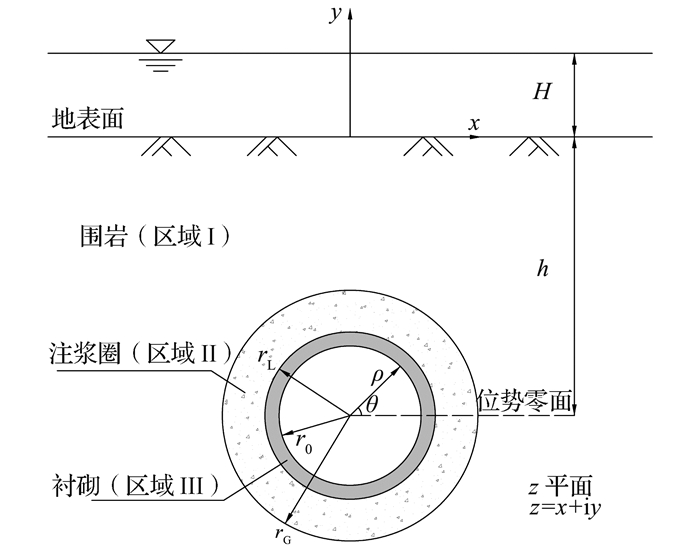
1 模型的建立 1.1 计算模型与基本假设隧道渗流场简化计算模型如图 1所示.研究对象为饱和、均质连续、各向同性的半无限岩体介质,地层表面作用高度为H的水头.岩体内部开挖一个外半径为rL的隧道,隧道中心到地层表面距离为h,围岩渗透系数为kS;衬砌内半径为r0,渗透系数为kL;注浆圈半径为rG,渗透系数为kG;区域Ⅰ、Ⅱ和Ⅲ分别代表围岩、注浆圈及衬砌.
|
图 1 隧道渗流场简化计算模型 Fig. 1 Simplified calculation model for seepage field of tunnel |
基于以上条件,进行如下假设:1)围岩、注浆圈、衬砌均质连续、各向同性;2)岩体与水不可压缩,地下水补给充足;3)渗流为稳定流,运动规律服从Darcy定律;4)隧道埋深远大于半径,即
由于介质的各向同性,根据质量守恒和Darcy定律,隧道周围的二维稳态地下水渗流场满足Laplace方程,在z平面中,区域Ⅰ内的渗流微分方程在直角坐标系中表示如下:
| $ \frac{{{\partial ^2}{\varphi _{\rm{S}}}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{\varphi _{\rm{S}}}}}{{\partial {y^2}}} = 0, $ | (1) |
| $ {\varphi _{\rm{S}}} = \frac{p}{{{\gamma _{\rm{w}}}}} + Y. $ | (2) |
式中:φS为围岩总水头,为压力水头与位置水头之和,p为孔隙水压力,γw为水的单位重度,Y为位置水头,在本文坐标系中Y=y+h.
区域Ⅱ、Ⅲ内的渗流微分方程在极坐标系中可分别表示如下:
| $ \frac{{{\partial ^2}{\varphi _{\rm{G}}}}}{{\partial {\rho ^2}}} + \frac{1}{\rho }\frac{{\partial {\varphi _{\rm{G}}}}}{{\partial \rho }} + \frac{1}{{{\rho ^2}}}\frac{{\partial {\varphi _{\rm{G}}}}}{{\partial {\theta ^2}}} = 0, $ | (3) |
| $ \frac{{{\partial ^2}{\varphi _{\rm{L}}}}}{{\partial {\rho ^2}}} + \frac{1}{\rho }\frac{{\partial {\varphi _{\rm{L}}}}}{{\partial \rho }} + \frac{1}{{{\rho ^2}}}\frac{{\partial {\varphi _{\rm{L}}}}}{{\partial {\theta ^2}}} = 0. $ | (4) |
式中:φG为注浆圈总水头,φL为衬砌总水头,ρ为极径,θ为极角.
当隧道埋深远远大于半径时,水位边界对隧道周边渗流场影响较小,可将渗流路径简化为轴对称形式,并近似认为隧道周边半径相同之处水头相等[15-16],则有初始边界条件如下:
| $ {\varphi _{{\rm{S}}\left( {y = 0} \right)}} = H + h, $ | (5) |
| $ {\varphi _{{\rm{L}}\left( {\rho = {r_0}} \right)}} = {h_0}, $ | (6) |
| $ {\varphi _{{\rm{L}}\left( {\rho = {r_{\rm{L}}}} \right)}} = {\varphi _{{\rm{G}}\left( {\rho = {r_{\rm{L}}}} \right)}} = {h_{\rm{L}}}, $ | (7) |
| $ {\varphi _{{\rm{G}}\left( {\rho = {r_{\rm{G}}}} \right)}} = {h_{\rm{G}}}. $ | (8) |
式中:h0为衬砌内部水头,hL为衬砌与注浆圈交界处水头,hG为注浆圈与围岩交界处水头.
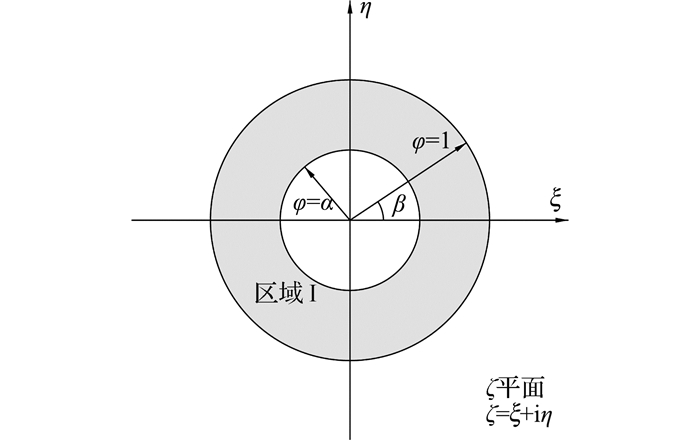
2 模型的求解 2.1 围岩渗流场解析计算计算模型中的围岩区域渗流场解析问题属于半无限平面孔口问题,利用复变函数保角变换能有效地对该问题进行转化和求解.将z平面中的区域Ⅰ按照投影变换公式(9)映射至ζ平面内,得到外径为1,内径为α的圆环域,如图 2所示,φ和β分别为ζ平面中极坐标系的极径与极角.
|
图 2 保角变换区域 Fig. 2 Plane of conformal transformation |
| $ z = \omega \left( \zeta \right) = - {\rm{i}}A\frac{{1 + \zeta }}{{1 - \zeta }}. $ | (9) |
式中:A=h(1-α2)/(1+α2),α采用如下公式计算:
| $ \alpha = \left( {h - \sqrt {{h^2} - r_{\rm{G}}^2} } \right)/{r_{\rm{G}}}. $ | (10) |
根据复变函数中的保角变换原理[17],变换后的势函数同样满足Laplace方程,式(1)在ξ-η坐标系中可改写为
| $ \frac{{{\partial ^2}{\varphi _{\rm{S}}}}}{{\partial {\xi ^2}}} + \frac{{{\partial ^2}{\varphi _{\rm{S}}}}}{{\partial {\eta ^2}}} = 0. $ | (11) |
根据边界条件进行求解,在ζ平面内作用于半径为φ的圆上的总水头可表示为如下的Fourier形式[11]:
| $ {\varphi _{\rm{S}}} = {C_1} + {C_2}\ln \varphi + \sum\limits_{n = 1}^\infty {\left[ {\left( {{C_3}{\varphi ^n} + {C_4}{\varphi ^{ - n}}} \right)\cos n\beta } \right]} . $ | (12) |
式中:C1、C2、C3和C4为待定常数,由边界条件决定.
对于ζ平面中的极坐标系,式(5)和(8)可分别改写为
| $ {\varphi _{{\rm{S}}\left( {\varphi = 1} \right)}} = H + h, $ | (13) |
| $ {\varphi _{{\rm{S}}\left( {\varphi = \alpha } \right)}} = {h_{\rm{G}}}. $ | (14) |
将式(13)代入式(12)可得
| $ {\varphi _{{\rm{S}}\left( {\varphi = 1} \right)}} = {C_1} + \sum\limits_{n = 1}^\infty {\left[ {\left( {{C_3} + {C_4}} \right)\cos n\beta } \right]} = H + h. $ | (15) |
比较等式左、右两边可得
| $ {C_1} = H + h,{C_3} = - {C_4}. $ | (16) |
再将式(14)代入式(12),结合式(16)可得
| $ \begin{array}{l} {\varphi _{{\rm{S}}\left( {\varphi = \alpha } \right)}} = H + h + {C_2}\ln \alpha + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{n = 1}^\infty {\left[ {{C_3}\left( {{\alpha ^n} - {\alpha ^{ - n}}} \right)\cos n\beta } \right]} = {h_{\rm{G}}}. \end{array} $ | (17) |
由于隧道埋深远大于半径,即
| $ {C_2} = \frac{{{h_{\rm{G}}} - H - h}}{{\ln \alpha }},{C_3} = 0. $ | (18) |
则式(12)可改写为
| $ {\varphi _{\rm{S}}} = H + h + \frac{{\ln \varphi }}{{\ln \alpha }}\left( {{h_{\rm{G}}} - H - h} \right). $ | (19) |
由式(19)积分可得区域Ⅰ和区域Ⅱ交界面的渗流量如下:
| $ {Q_{\rm{S}}} = {k_{\rm{S}}}\int_0^{2{\rm{ \mathsf{ π} }}} {\frac{{\partial {\varphi _{\rm{S}}}}}{{\partial \varphi }}\varphi {\rm{d}}\beta } = \frac{{2{\rm{ \mathsf{ π} }}{k_{\rm{S}}}}}{{\ln \alpha }}\left( {{h_{\rm{G}}} - H - h} \right). $ | (20) |
因注浆圈与衬砌内渗流方向以径向为主,则注浆圈与衬砌内渗流可简化为轴对称恒定渗流问题[18],两者的渗流连续微分方程由式(3)、(4)分别简化为
| $ \frac{{{\partial ^2}{\varphi _{\rm{G}}}}}{{\partial {\rho ^2}}} + \frac{1}{\rho }\frac{{\partial {\varphi _{\rm{G}}}}}{{\partial \rho }} = 0, $ | (21) |
| $ \frac{{{\partial ^2}{\varphi _{\rm{L}}}}}{{\partial {\rho ^2}}} + \frac{1}{\rho }\frac{{\partial {\varphi _{\rm{L}}}}}{{\partial \rho }} = 0. $ | (22) |
结合边界条件式(6)~(8),可得方程(21)和(22)的解如下:
| $ {\varphi _{\rm{G}}} = \frac{{{h_{\rm{L}}}\ln {r_{\rm{G}}} - {h_{\rm{G}}}\ln {r_{\rm{L}}}}}{{\ln \left( {{r_{\rm{G}}}/{r_{\rm{L}}}} \right)}} + \frac{{{h_{\rm{G}}} - {h_{\rm{L}}}}}{{\ln \left( {{r_{\rm{G}}}/{r_{\rm{L}}}} \right)}}\ln \rho , $ | (23) |
| $ {\varphi _{\rm{L}}} = \frac{{{h_{\rm{0}}}\ln {r_{\rm{L}}} - {h_{\rm{L}}}\ln {r_{\rm{0}}}}}{{\ln \left( {{r_{\rm{L}}}/{r_{\rm{0}}}} \right)}} + \frac{{{h_{\rm{L}}} - {h_{\rm{0}}}}}{{\ln \left( {{r_{\rm{L}}}/{r_{\rm{0}}}} \right)}}\ln \rho . $ | (24) |
则区域Ⅱ和区域Ⅲ交界面的渗流量为
| $ {Q_{\rm{G}}} = {k_{\rm{G}}}\int_0^{2{\rm{ \mathsf{ π} }}} {\frac{{\partial {\varphi _{\rm{G}}}}}{{\partial \rho }}\rho {\rm{d}}\theta } = \frac{{2{\rm{ \mathsf{ π} }}{k_{\rm{G}}}}}{{\ln \left( {{r_{\rm{G}}}/{r_{\rm{L}}}} \right)}}\left( {{h_{\rm{G}}} - {h_{\rm{L}}}} \right). $ | (25) |
衬砌内侧的渗流量为
| $ {Q_{\rm{L}}} = {k_{\rm{L}}}\int_0^{2{\rm{ \mathsf{ π} }}} {\frac{{\partial {\varphi _{\rm{L}}}}}{{\partial \rho }}\rho {\rm{d}}\theta } = \frac{{2{\rm{ \mathsf{ π} }}{k_{\rm{L}}}}}{{\ln \left( {{r_{\rm{L}}}/{r_{\rm{0}}}} \right)}}\left( {{h_{\rm{L}}} - {h_{\rm{0}}}} \right). $ | (26) |
根据层间渗流量连续条件,各层间渗流量相等,即
| $ Q = {Q_{\rm{S}}} = {Q_{\rm{G}}} = {Q_{\rm{L}}}. $ | (27) |
将式(20)、(25)、(26)代入式(27)解得注浆圈与围岩交界处水头为
| $ {h_{\rm{G}}} = \frac{{B\left( {H + h} \right) - {h_0}\ln \alpha }}{{B - \ln \alpha }} = \frac{{B\left( {H + h} \right) - {h_0}E}}{{B + E}}. $ | (28) |
式中:
| $ B = \left( {{k_{\rm{S}}}/{k_{\rm{G}}}} \right)\ln \left( {{r_{\rm{G}}}/{r_{\rm{L}}}} \right) + \left( {{k_{\rm{S}}}/{k_{\rm{L}}}} \right)\ln \left( {{r_{\rm{L}}}/{r_{\rm{0}}}} \right); $ |
| $ E = \ln \left[ {\left( {h + \sqrt {{h^2} - r_{\rm{G}}^2} } \right)/{r_{\rm{G}}}} \right]; $ |
记C=(kS/kG)ln (rG/rL),D=(kS/kL)ln (rL/r0),则衬砌外水头为
| $ \begin{array}{*{20}{c}} {{h_{\rm{L}}} = \frac{{D\left( {H + h} \right) - {h_0}\left( {\ln \alpha - C} \right)}}{{B - \ln \alpha }} = }\\ {\frac{{D\left( {H + h} \right) - {h_0}\left( {C + E} \right)}}{{B + E}}.} \end{array} $ | (29) |
将式(28)代入式(20)得隧道渗流量为
| $ Q = \frac{{2{\rm{ \mathsf{ π} }}{k_{\rm{S}}}\left( {H + h - {h_0}} \right)}}{{B - \ln \alpha }} = \frac{{2{\rm{ \mathsf{ π} }}{k_{\rm{S}}}\left( {H + h - {h_0}} \right)}}{{B + E}}. $ | (30) |
式(30)即为半无限平面含注浆圈深埋隧道的渗流量解析解,流量以流入隧道为正值,流出隧道为负值.联立式(2)、(28)和(29)可得注浆圈与衬砌外水压力分别为
| $ {p_{\rm{G}}} = {\gamma _{\rm{w}}}\left[ {\frac{{B\left( {H + h} \right) + {h_0}E}}{{B + E}} - y - h} \right], $ | (31) |
| $ {p_{\rm{L}}} = {\gamma _{\rm{w}}}\left[ {\frac{{D\left( {H + h} \right) + {h_0}\left( {C + E} \right)}}{{B + E}} - y - h} \right]. $ | (32) |
应宏伟等[5]基于渗流力学理论,采用镜像法对含注浆圈的水下深埋隧道渗流场进行了求解,求得隧道渗流量、注浆圈外水压力及衬砌外水压力的解析解分别如下:
| $ Q = \frac{{2{\rm{ \mathsf{ π} }}{k_{\rm{S}}}\left( {H + h} \right)}}{{\ln \frac{{2h}}{{{r_{\rm{G}}}}} + \frac{{{k_{\rm{S}}}}}{{{k_{\rm{G}}}}}\ln \frac{{{r_{\rm{G}}}}}{{{r_{\rm{L}}}}} + \frac{{{k_{\rm{S}}}}}{{{k_{\rm{L}}}}}\ln \frac{{{r_{\rm{L}}}}}{{{r_{\rm{0}}}}}}}, $ | (33) |
| $ {p_{\rm{G}}} = {\gamma _{\rm{w}}}\left[ {\frac{{\left( {\frac{{{k_{\rm{S}}}}}{{{k_{\rm{G}}}}}\ln \frac{{{r_{\rm{G}}}}}{{{r_{\rm{L}}}}} + \frac{{{k_{\rm{S}}}}}{{{k_{\rm{L}}}}}\ln \frac{{{r_{\rm{L}}}}}{{{r_{\rm{0}}}}}} \right)\left( {H + h} \right)}}{{\frac{{{k_{\rm{S}}}}}{{{k_{\rm{G}}}}}\ln \frac{{{r_{\rm{G}}}}}{{{r_{\rm{L}}}}} + \frac{{{k_{\rm{S}}}}}{{{k_{\rm{L}}}}}\ln \frac{{{r_{\rm{L}}}}}{{{r_{\rm{0}}}}} + \ln \frac{{2h}}{{{r_{\rm{G}}}}}}} - y - h} \right], $ | (34) |
| $ {p_{\rm{L}}} = {\gamma _{\rm{w}}}\left[ {\frac{{\frac{{{k_{\rm{S}}}}}{{{k_{\rm{L}}}}}\ln \frac{{{r_{\rm{L}}}}}{{{r_{\rm{0}}}}}\left( {H + h} \right)}}{{\frac{{{k_{\rm{S}}}}}{{{k_{\rm{G}}}}}\ln \frac{{{r_{\rm{G}}}}}{{{r_{\rm{L}}}}} + \frac{{{k_{\rm{S}}}}}{{{k_{\rm{L}}}}}\ln \frac{{{r_{\rm{L}}}}}{{{r_{\rm{0}}}}} + \ln \frac{{2h}}{{{r_{\rm{G}}}}}}} - y - h} \right]. $ | (35) |
对于深埋隧道(
为了进一步验证本文解析解的正确性,采用Abaqus有限元数值模拟软件进行建模和求解,并将解析解与数值解计算结果进行对比验证.隧道几何参数与材料渗透系数如表 1所示,采用以下2种方式进行验证分析:1)令衬砌渗透系数为定值,对不同隧道埋深下的渗流场解析解与数值解计算结果进行对比,并分析埋深变化对计算结果的影响;2)令隧道埋深为定值,对不同衬砌渗透系数下的渗流场解析解与数值解计算结果进行对比,并分析衬砌渗透系数变化对计算结果的影响.
| 表 1 隧道几何参数与模型材料渗透系数 Table 1 Geometric parameters of tunnels and permeability coefficients of model materials |
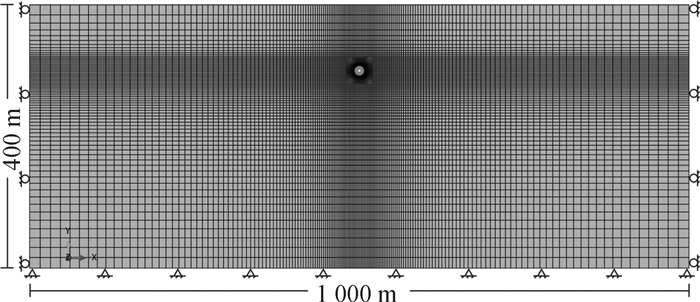
根据隧道渗流场简化解析计算模型(图 1),建立隧道渗流场数值模型如图 3所示,模型横向宽度取10倍最大埋深,共1 000 m,纵向深度取4倍最大埋深,共400 m.模型包括3种材料:围岩、注浆圈和衬砌,其中围岩与注浆圈采用Mohr-Coulomb本构模型,衬砌采用弹性本构模型,材料物理力学参数如表 2所示,表中,ρ为密度,c为黏聚力,φ为摩擦角,E为弹性模量,μ为泊松比.网格划分时采用四节点平面应变孔压实体单元(CPE4P).分析步包含地应力平衡、应力释放与隧道开挖、施作注浆圈与衬砌等,其中隧道开挖与施加衬砌通过生死单元模拟实现,而注浆则通过场变量控制不同分析步的材料属性进行模拟.为了与解析法的稳定流假设一致,分析步类型采用稳态分析.模型力学边界条件为:约束左右两侧边界水平位移,约束底部边界位移.模型渗流边界条件为:左右两侧边界孔隙水压力固定,为定水头边界,底部为不透水边界.隧道开挖后,毛洞边界为自由排水边界,施作衬砌支护后,衬砌内边界为自由排水边界.对于具有一定排水能力的深埋隧道,洞内渗流边界条件可分为等水头和等水压2种条件[10, 13],结合本文模型假设,数值模型的洞内渗流边界条件采用等水头边界条件.
|
图 3 隧道渗流场数值模型 Fig. 3 Numerical model for seepage field of tunnel |
| 表 2 模型材料物理力学参数 Table 2 Physical and mechanical parameters of model materials |
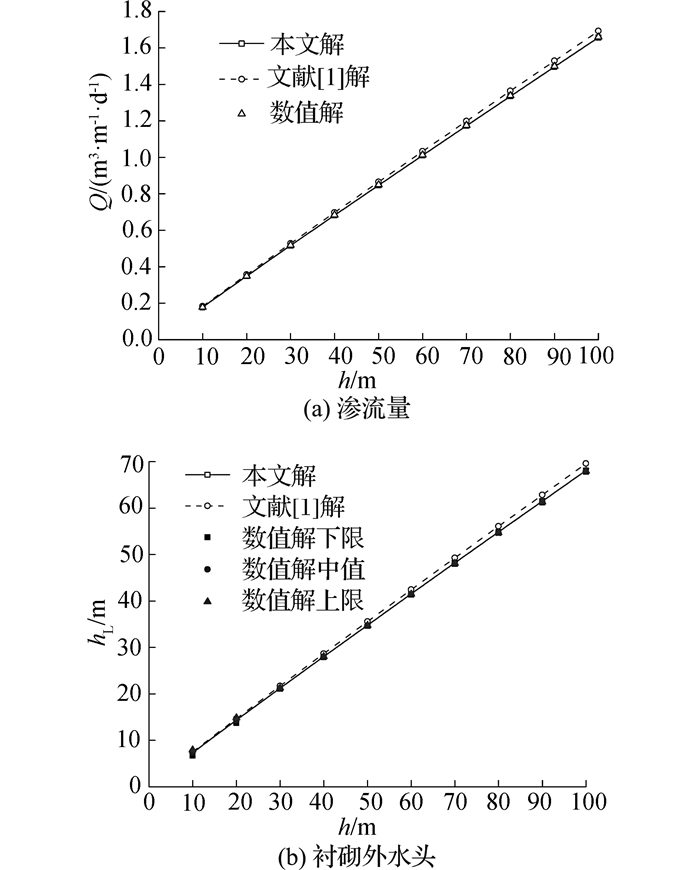
如图 4所示为不同埋深下的隧道渗流场解析解与数值解计算结果对比图.如图 5所示为不同衬砌渗透系数下的隧道渗流场解析解与数值解计算结果对比图.图 4(b)和5(b)中的数值解上限、中值和下限分别指的是衬砌顶部、中部及底部的外水头值,根据图中三者的分布情况可知,对于本文算例,当隧道埋深大于30 m时,水位边界对隧道周边渗流场影响已经很小,可近似认为隧道周边半径相同之处的水头相等,与本文推导解析解时的假设一致.同时,由图 4(b)可知,随着隧道埋深的减小,数值解上限、中值和下限之间的差异逐渐增大.对于浅埋隧道,水位边界对其周边渗流场的影响已不可忽略,以隧道埋深h=10 m为例,由本文解得到的衬砌外水头值为7.33 m,与数值解中值(7.31 m)较为吻合,而与数值解上、下限(7.93 m、6.68 m)则存在较明显的差异,因此浅埋隧道周边的水头分布还需采取其他方法进行研究确定.
|
图 4 不同埋深下隧道渗流场解析解与数值解结果对比 Fig. 4 Comparison between analytical and numericalresults of seepage fields of tunnels under different depths |
|
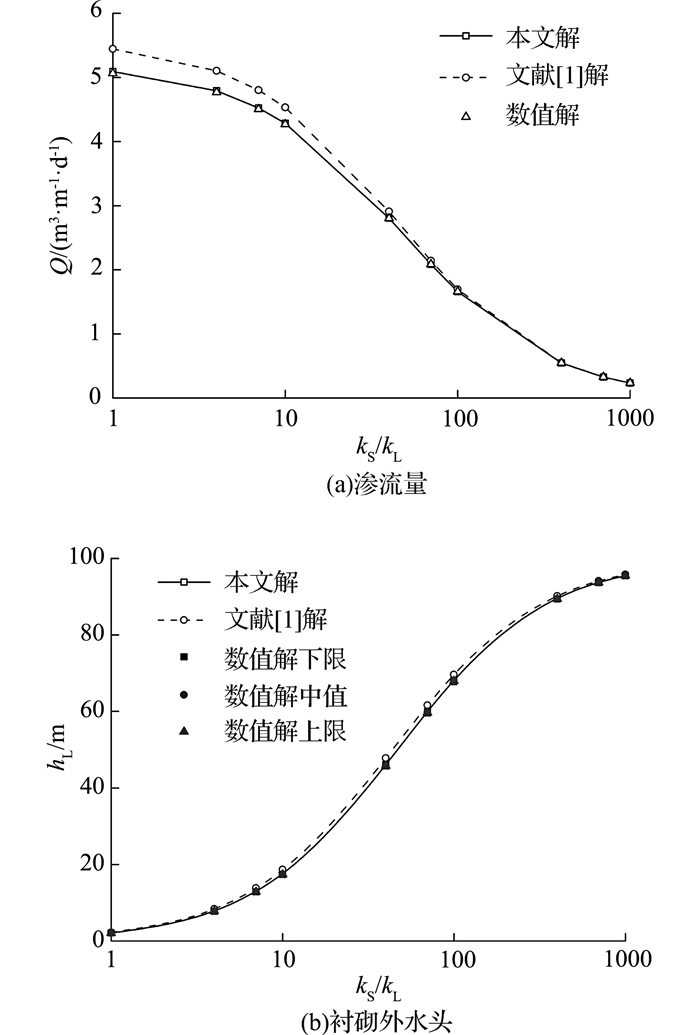
图 5 不同衬砌渗透系数下隧道渗流场解析解与数值解结果对比 Fig. 5 Comparison between analytical and numerical results of seepage fields of tunnels under different permeability coefficients of lining |
由图 4、5可知,隧道渗流量与衬砌外水头随隧道埋深增大近似呈线性增大趋势,而随着衬砌渗透系数的减小,隧道渗流量呈减小趋势,衬砌外水头呈增大趋势.对于深埋隧道,本文解析解与数值解计算结果能很好地吻合,而文献[1]解析解计算结果则略大于本文解和数值解计算结果.对于渗流量,随着埋深和衬砌渗透系数增大,文献[1]解与数值解的差异逐渐增大,而对于衬砌外水头,文献[1]解与数值解的差异随着埋深增大而增大,随着衬砌渗透系数减小则呈现先增大后减小的趋势.这是由于文献[1]在求解时采用了无限渗流边界,这与实际的半无限边界存在一定差异,进而导致高估了隧道渗流量和衬砌外水头.
通过以上对比分析可知,对于半无限平面含注浆圈深埋隧道而言,本文解析解比由无限含水层竖井理论推导的解析解更接近数值解计算结果,进一步验证了本文解析解的可靠性.此外,相较于数值方法建模复杂、计算耗时长等缺点,本文解析解简便实用,便于进行深埋隧道渗流场预测与参数分析.
4 隧道渗流场对注浆参数变化的敏感性分析 4.1 注浆参数影响因子目前,综合考虑环境保护和衬砌结构强度等因素,对于水头大于60 m的富水地层深埋隧道,对地下水多采用“堵水限排”的排导方式,如我国的圆梁山隧道和日本的青函海底隧道[19].地层注浆加固是“堵水限排”防排水系统中广泛采用的堵水方式[20],因此明确注浆参数变化对隧道渗流场的影响规律对富水地层深埋隧道防排水方案的设计具有十分重要的意义.为此,提出注浆参数影响因子,并基于本文解析解与该影响因子分析含注浆圈深埋隧道渗流场对注浆参数变化的敏感性,进而为合理确定注浆参数提供参考.
以采用“堵水限排”防排水系统的含注浆圈深埋隧道为工程背景,为简化分析,假设水位位于地表面(H=0),衬砌内部水头为0,则式(29)和(30)可简化为
| $ {h_{\rm{L}}} = \frac{{\left( {\frac{{{k_{\rm{S}}}}}{{{k_{\rm{L}}}}}\ln \frac{{{r_{\rm{L}}}}}{{{r_{\rm{0}}}}}} \right)h}}{{{F_{\rm{G}}} + \left( {\frac{{{k_{\rm{S}}}}}{{{k_{\rm{L}}}}} - 1} \right)\ln \frac{{{r_{\rm{L}}}}}{{{r_{\rm{0}}}}} + G}}, $ | (36) |
| $ Q = \frac{{2{\rm{ \mathsf{ π} }}{k_{\rm{S}}}h}}{{{F_{\rm{G}}} + \left( {\frac{{{k_{\rm{S}}}}}{{{k_{\rm{L}}}}} - 1} \right)\ln \frac{{{r_{\rm{L}}}}}{{{r_{\rm{0}}}}} + G}}. $ | (37) |
式中:
| $ \begin{array}{*{20}{c}} {G = \ln \left[ {\left( {h + \sqrt {{h^2} - r_{\rm{G}}^2} } \right)/{r_0}} \right];}\\ {{F_{\rm{G}}} = \left( {a - 1} \right)\ln b,} \end{array} $ |
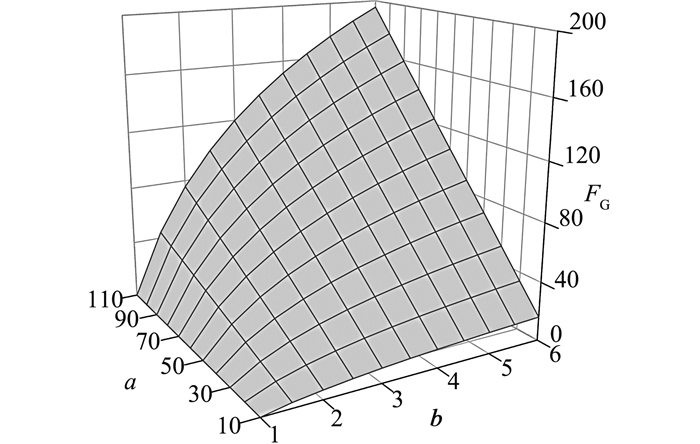
定义其为注浆参数影响因子,其中a=kS/kG,为围岩与注浆圈渗透系数之比,反映了注浆圈的抗渗性;b=rG/rL,为注浆圈半径与隧道外半径之比,反映了注浆圈的厚度.FG随参数a和b的变化规律如图 6所示,FG随a增大呈线性增长趋势,随b增大呈对数增长趋势.在实际工程中,考虑到经济性原则,注浆圈渗透系数的可调整范围要远大于注浆圈厚度,因此参数a,即注浆圈抗渗性是影响FG大小的主要控制因素,而注浆圈厚度为次要控制因素,其意义更多体现在地层加固作用上.综上所述,在确定合理注浆圈参数时,若只考虑注浆圈的堵水作用,应首先确定注浆圈渗透系数的最小值,即参数a的最大值,在此基础上再确定相应的参数b,即注浆圈厚度.
|
图 6 注浆参数影响因子FG随参数a和b的变化 Fig. 6 Variation ofimpact factor FG with parameters a and b |
根据式(36)和(37)可知,含注浆圈深埋隧道渗流场的影响因素包括注浆参数(注浆圈渗透系数和厚度)、衬砌参数(衬砌渗透系数和厚度)、隧道断面尺寸与位置参数(隧道内半径及埋深),且隧道渗流量与衬砌外水头随着注浆参数影响因子FG的增大而减小.为了探讨不同条件下隧道渗流场对注浆参数变化的敏感性,基于本文解析解,分别对不同衬砌渗透系数、隧道埋深和断面尺寸条件下隧道渗流量和衬砌外水头随注浆参数影响因子的变化规律进行算例分析,隧道渗流场计算参数与初始值如表 3所示.
| 表 3 隧道渗流场计算参数与初始值 Table 3 Calculation parameters and initial values for seepage fields of tunnels |
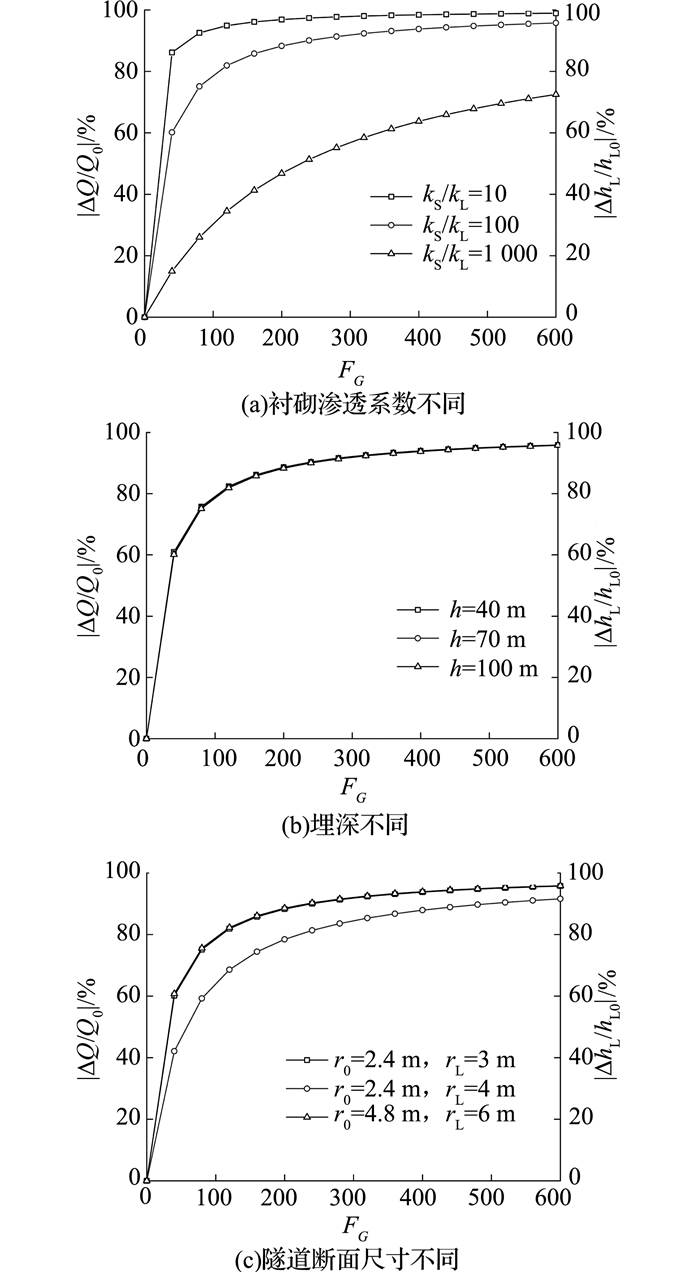
如图 7所示分别为在不同衬砌渗透系数、隧道埋深和断面尺寸条件下,注浆参数影响因子FG对隧道渗流场的影响曲线,曲线横坐标为FG,纵坐标则分别为隧道渗流量、衬砌外水头变化值与初始渗流量Q0、初始衬砌外水头hL0之比的绝对值,其中Q0与hL0为FG=0时隧道的渗流量与衬砌外水头.由图 7中的曲线斜率变化可知,隧道渗流场对注浆参数变化的敏感性随着FG的增大而减弱,可大致分为敏感阶段、过渡阶段和不敏感阶段.对于本文算例,当FG由0增大至100时,隧道渗流量和衬砌外水头均大幅度减小,隧道渗流场呈现出较强的敏感性,但随着FG的继续增大,隧道渗流场的变化逐渐趋于平缓.在实际工程应用中,可根据隧道渗流量和衬砌外水头的设计限值,运用本文解析解求出相应的注浆参数影响因子FG-1和FG-2,两者取大值后再根据4.1中的方法确定合理的注浆圈渗透系数与厚度.
|
图 7 不同衬砌渗透系数、埋深、隧道断面尺寸下注浆参数影响因子FG对隧道渗流场的影响 Fig. 7 Effect of grouting parameters' impact factor FG on seepage fields of tunnels under different permeability coefficients of lining, depths, and tunnel section sizes |
如图 7(a)所示,隧道渗流场对注浆参数变化的敏感性随着衬砌渗透系数减小而减弱,结合表 2中的初始渗流量和衬砌外水头可得,随着衬砌抗渗性的增强,注浆圈的主要作用逐渐由降低渗流量转变为降低衬砌外水头.由图 7(b)可以看出,深埋隧道渗流场对注浆参数变化的敏感性受埋深变化的影响很小,但对于埋深越大的隧道,由于其初始渗流量和衬砌外水头也越大,注浆圈对隧道渗流场的改善作用也越明显.如图 7(c)所示,对于r0=2.4 m、rL=3 m和r0=4.8 m、rL=6 m的隧道,两者渗流场对注浆参数变化的敏感性基本一致,而对于r0=2.4 m、rL=4 m的隧道,其渗流场对注浆参数变化的敏感性则相对减弱.由此可知,深埋隧道渗流场对注浆参数变化的敏感性受隧道断面尺寸变化的影响很小,而衬砌厚度(rL/r0)的变化则会对其产生较明显的影响,隧道渗流场对注浆参数变化的敏感性随着rL/r0的增大而减弱.
5 结论(1) 在隧道衬砌内部水头为0和隧道埋深较大(
(2) 注浆参数变量可由无量纲的注浆参数影响因子FG统一表示,该因子与注浆圈渗透系数负相关,与注浆圈厚度正相关,其中注浆圈渗透系数为主要控制因素,而注浆圈厚度为次要控制因素.
(3) 隧道渗流量、衬砌外水头以及渗流场对注浆参数变化的敏感性随着注浆参数影响因子的增大而减小.隧道渗流场随注浆参数变化可大致分为敏感阶段、过渡阶段和不敏感阶段.在实际工程中,可基于隧道渗流量和衬砌外水头的设计限值,运用解析解求出对应的注浆参数影响因子FG-1和FG-2,两者取大值并根据FG表达式确定合理的注浆圈渗透系数与厚度.
(4) 隧道渗流场对注浆参数变化的敏感性随着衬砌渗透系数的减小和厚度的增大而减弱,而隧道埋深与断面尺寸的变化则对敏感性影响很小.对于埋深越大的隧道,虽然渗流场敏感性变化很小,但由于其初始渗流量和衬砌外水头也越大,注浆圈对隧道渗流场的改善作用也越明显.
| [1] |
王建宇. 再谈隧道衬砌水压力[J]. 现代隧道技术, 2003, 40(3): 5-10. WANG Jian-yu. Once more on hydraulic pressure upon lining[J]. Modern Tunnelling Technology, 2003, 40(3): 5-10. |
| [2] |
王秀英, 王梦恕, 张弥. 计算隧道排水量及衬砌外水压力的一种简化方法[J]. 北方交通大学学报, 2004, 28(1): 8-10. WANG Xiu-ying, WANG Meng-shu, ZHANG Mi. A simple method to calculate tunnel discharge and external water pressure on lining[J]. Journal of Northern Jiaotong University, 2004, 28(1): 8-10. |
| [3] |
王秀英, 王梦恕, 张弥. 山岭隧道堵水限排衬砌外水压力研究[J]. 岩土工程学报, 2005, 27(1): 125-127. WANG Xiu-ying, WANG Meng-shu, ZHANG Mi. Research on regulating water pressure acting on mountain tunnels by blocking ground water and limiting discharge[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(1): 125-127. |
| [4] |
杜朝伟, 王梦恕, 谭忠盛. 水下隧道渗流场解析解及其应用[J]. 岩石力学与工程学报, 2011, 30(增2): 3568-3573. DU Chao-wei, WANG Meng-shu, TAN Zhong-sheng. Analytic solution for seepage field of subsea tunnel and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(Suppl. 2): 3568-3573. |
| [5] |
应宏伟, 朱成伟, 龚晓南. 考虑注浆圈作用水下隧道渗流场解析解[J]. 浙江大学学报:工学版, 2016, 50(6): 1018-1023. YING Hong-wei, ZHU Cheng-wei, GONG Xiao-nan. Analytic solution on seepage field of underwater tunnel considering grounting circle[J]. Journal of Zhejiang University:Engineering Science, 2016, 50(6): 1018-1023. |
| [6] |
李鹏飞, 张顶立, 赵勇, 等. 海底隧道复合衬砌水压力分布规律及合理注浆加固圈参数研究[J]. 岩石力学与工程学报, 2012, 31(2): 280-288. LI Peng-fei, ZHANG Ding-li, ZHAO Yong, et al. Study of distribution of water pressure acting on composite lining and reasonable parameters of grouting circle for subsea tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 280-288. |
| [7] |
YANG G C, WANG X H, WANG X G, et al. Analyses of seepage problems in a subsea tunnel considering effects of grouting and lining structure[J]. Marine Georesources & Geothenology, 2016, 34(1): 65-70. |
| [8] |
VERRUIJT A. A complex variable solution for a deforming circular tunnel in an elastic half plane[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1997, 21(2): 77-89. DOI:10.1002/(ISSN)1096-9853 |
| [9] |
EL TANI M. Circular tunnel in a semi-infinite aquifer[J]. Tunnelling and Underground Space Technology, 2003, 18(1): 49-55. DOI:10.1016/S0886-7798(02)00102-5 |
| [10] |
KOLYMBAS D, WAGNER P. Groundwater ingress to tunnels-the exact analytical solution[J]. Tunnelling and Underground Space Technology, 2007, 22(1): 23-27. DOI:10.1016/j.tust.2006.02.001 |
| [11] |
PARK K H, ADISOM O, LEE J G. Analytical solution for steady-state groundwater inflow into a drained circular tunnel in a semi-infinite aquifer:a revisit[J]. Tunnelling and Underground Space Technology, 2007, 23(2): 206-209. |
| [12] |
童磊, 谢康和, 卢萌盟, 等. 半无限含水层中带衬砌隧洞渗流解析研究[J]. 岩土力学, 2011, 32(1): 305-309. TONG Lei, XIE Kang-he, LU Meng-meng, et al. Analytical study of seepage flow into a lined tunnel in a semi-infinite aquifer[J]. Rock and Soil Mechanics, 2011, 32(1): 305-309. |
| [13] |
皇甫明, 谭忠盛, 王梦恕, 等. 暗挖海底隧道渗流量解析解及其应用[J]. 中国工程科学, 2009, 11(7): 66-70. HUANG FU-ming, TAN Zhong-sheng, WANG Meng-shu, et al. An analytical solution for water inflow into a subsea tunnel and its application[J]. Journal of China Engineering Science, 2009, 11(7): 66-70. |
| [14] |
HUANG F M, WANG M S, TAN Z S, et al. Analytical solutions for steady seepage into an underwater circular tunnel[J]. Tunnelling and Underground Space Technology, 2010, 25(4): 391-396. DOI:10.1016/j.tust.2010.02.002 |
| [15] |
ATKINSON J H, MAIR R J. Loads on leaking and watertight tunnel linings, sewers and buried pipes due to groundwater[J]. Geotechnique, 1983, 33(3): 341-344. DOI:10.1680/geot.1983.33.3.341 |
| [16] |
张冬梅, 刘印, 黄宏伟. 软土盾构隧道渗流场引起的地层和隧道沉降[J]. 同济大学学报:自然科学版, 2013, 41(8): 1185-1190. ZHANG Dong-mei, LIU Yin, HUANG Hong-wei. Leakage-induced settlement of ground and shield tunnel in soft clay[J]. Journal of Tongji University:Natural Science, 2013, 41(8): 1185-1190. |
| [17] |
潘永亮. 复变函数[M]. 北京: 科学出版社, 2004, 170-171.
|
| [18] |
翟云芳. 渗流力学[M]. 北京: 石油工业出版社, 2003, 17.
|
| [19] |
张成平, 张顶立, 王梦恕, 等. 高水压富水区隧道限排衬砌注浆圈合理参数研究[J]. 岩石力学与工程学报, 2007, 26(11): 2270-2276. ZHANG Cheng-ping, ZHANG Ding-li, WANG Meng-shu, et al. Study on appropriate parameters of grounting circle for tunnels with limiting discharge lining in high water pressure and water-enriched region[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(11): 2270-2276. DOI:10.3321/j.issn:1000-6915.2007.11.013 |
| [20] |
刘志春, 万良勇. 地层注浆加固对隧道与地下水相互作用过程中的"双赢"影响效应分析[J]. 现代隧道技术, 2015, 52(2): 87-96. LIU Zhi-chun, WAN Liang-yong. Win-win effect of ground consolidation grounting on the interaction between tunnel and groundwater[J]. Modern Tunnelling Technology, 2015, 52(2): 87-96. |



