改革开放以来, 钢管混凝土结构在土木工程的各个领域得到广泛应用.进入21世纪, 我国高层建筑以及地下建筑发展迅速.钢管混凝土柱的优良特性以及特殊的构造, 极大地促进了学者对梁-柱连接方面的研究.目前, 工程中应用的梁-柱连接形式超过20种, 各种节点形式连接形式不一, 然而都围绕着梁-柱连接的抗滑移以及抗震性能进行研究.
现有研究主要关注钢管与内部混凝土界面黏结滑移问题[1-2]或者组合钢梁桥[3]力学性能研究, 虽然对于外部钢管与混凝土连接问题,我国规范、欧洲规范以及美国规范都有规定, 但是这些规程主要集中在外部连接件的强度或单纯研究一类连接件的抗剪性能, 外部混凝土力学性能以及各部分连接件与混凝土之间的组合效应研究较少.本文开展模型试验研究与数值分析, 在获取钢管荷载-位移曲线以及外部混凝土的破坏模式的基础上, 针对该种连接方式分别进行数值模拟分析, 得到各类连接件在钢管抗滑移过程中的所占比重, 为实际工程设计提供参考.
1 试验概况 1.1 试验材料与试件设计试件参数定义:钢管直径D, 厚度t, 长度L, 焊钉柱底直径ds, 焊钉长度ls, 焊钉率ρ, 具体参数见表 1, 试件共2个, 参数一致.试件所用钢管为普通焊管, 实测钢管钢材屈服强度fy=330 MPa, 极限抗拉强度fu=385 MPa, 弹性模量Es=2.01×105 MPa;抗剪连接件为圆柱形焊钉, 材料参数如下:fy=365 MPa, 极限抗拉强度fu=480 MPa, 弹性模量Es=2.06×105 MPa, 符合《电弧螺柱焊用圆柱头焊钉(GB10433)》规范[4]要求, 采用梅花形布置方式.
| 表 1 试件参数 Table 1 Parameters of the specimens |
混凝土立方体抗压强度实测值fcu, t:外围混凝土为35.0 MPa, 钢管内灌混凝土为40.4 MPa;钢筋抗拉强度实测值fy, t=474 MPa.
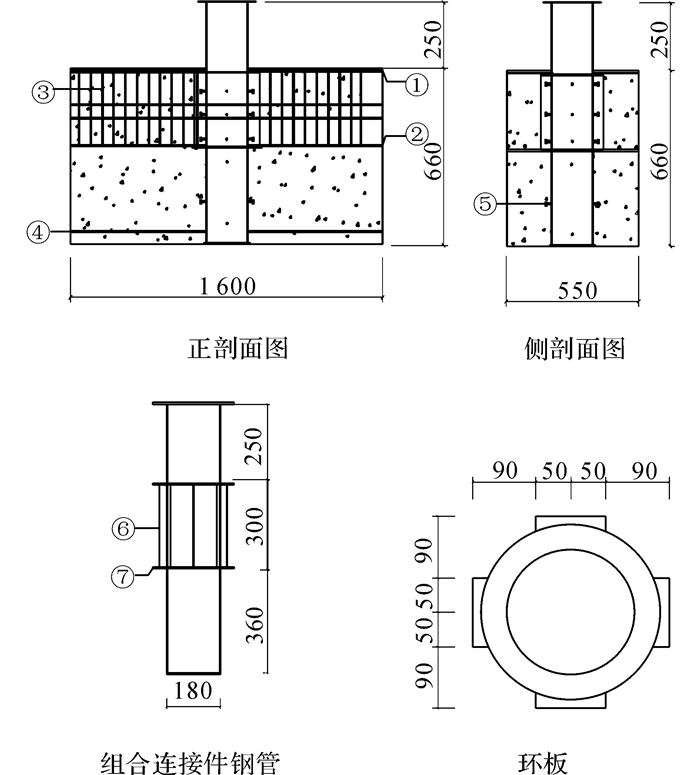
1.2 试件制作混凝土立方体试块强度fcu按《普通混凝土力学性能试验方法标准(GB/T 50081-2002)》规范[5]确定, 试块与试件均为自然养护, 试件尺寸信息如图 1所示, 试件部件信息如表 2所示.
|
图 1 试件配筋及钢管示意图 Fig. 1 Reinforcement and pipe schematic diagram of specimens |
| 表 2 试件部件信息 Table 2 Part massage in specimens |
试件为钢管-混凝土滑移试验节点, 研究采用YAW-10000F型电液伺服多功能试验机对试件进行加载, 位移测量采用百分表, 测试位置如图 2所示, 将试件放置于钢垫块上, 仅保持钢管自由端未约束.位移与应变数据采集使用DH3816静态应变测试系统, 裂缝宽度采用裂缝测宽仪测读.

|
图 2 钢管抗剪试验加载示意图 Fig. 2 Loading sketch of pipe shear test |
正式加载前, 先进行预加载, 集中荷载F=200 kN, 检测各测量装置的可靠性, 卸载后采用荷载-位移双控制模式进行分级加载.荷载控制加载时, 加载速率v=20 kN/min;当荷载-位移曲线到达第一峰值荷载时, 改位移控制加载, v=0.25 mm/min, 直到试件破坏为止.
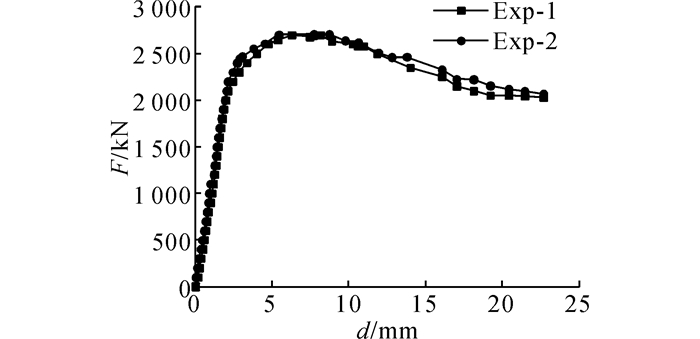
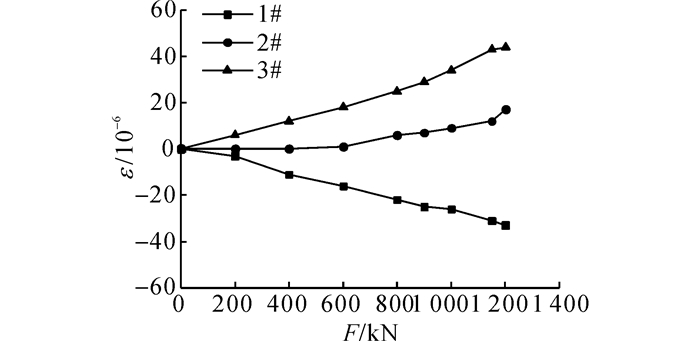
2 试验结果及分析 2.1 承载力与裂缝分析Exp-1、Exp-2钢管底部百分表直接测得的荷载-位移θd曲线见图 3, Exp-2混凝土表面应变-荷载曲线见图 4(1#, 2#, 3#为粘贴的应变片编号, 测量混凝土表面正应变).由图 3可知, 当加载至500 kN时, 荷载-位移成线性关系, 混凝土表面应变较小, 钢管表面与外部混凝土之间协调变形, 试件处于弹性阶段, 钢管与外部混凝土间基本无滑移;当加载至2 700 kN时, 试件处于塑性发展期, 混凝土裂缝随荷载逐渐扩展, 钢管发生稳定滑移;继续加载, 试件进入破坏期, 试件裂缝快速发展, 钢管滑移量急剧增大, 最后试件进入残余状态;钢管推出试验混凝土主要经历3个阶段, 即弹性期、塑性发展期、破坏期.由图 4可知, 在试件加载至1 200 kN的过程中, 混凝土表面应变发展较为稳定, 与荷载基本成线性关系.试件极限承载力均到达2 700 kN, 最终破坏形态为钢管滑移混凝土劈裂破坏.
|
图 3 自由端荷载-位移曲线 Fig. 3 Load-displacement curves of the free end |
|
图 4 Exp-2应变-荷载曲线 Fig. 4 Strain-load curve of Exp-2 |
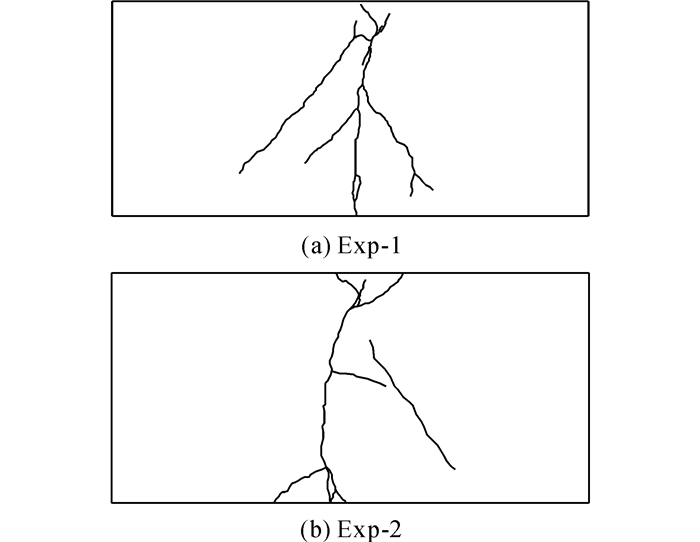
裂缝分布状况详见图 5, Exp-1、Exp-2主裂缝为混凝土纵向裂缝, 伴随若干条斜裂缝.试件Exp-1、Exp-2分别加载至1 600、1 500 kN时出现第1条裂缝, 随着荷载增大, 纵向裂缝迅速向上扩展, 斜裂缝相继出现贯通;当试验加载至2 700 kN时, 裂缝分布为纵向裂缝劈裂破坏, 此时Exp-1、Exp-2最大裂缝宽度均大于2 mm.
|
图 5 混凝土裂缝分布 Fig. 5 Concrete crack distribution |
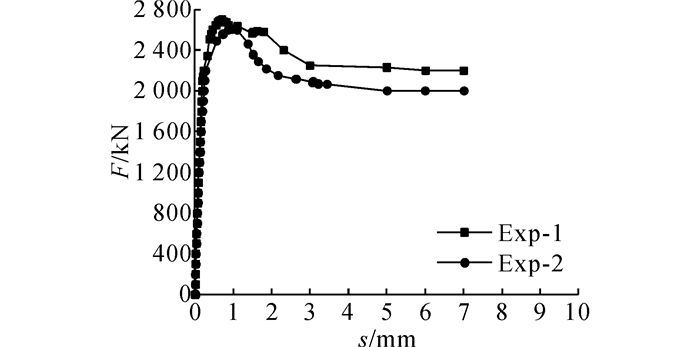
钢管底部架设百分表与钢管相邻混凝土底部架设百分表各测得的为试件底部位移曲线, 两者差值为自由端全过程荷载-滑移(F-s)曲线, 如图 6所示.依据Eurocode-4规定[6], 对延性连接件的特征滑移量(荷载下降至极限承载力的85%时对应的滑移量)超过6 mm时, 可视为该连接件为延性连接件, 因此Exp-1满足规范要求, Exp-2特征滑移量到达6 mm时, 极限承载力为2 000 kN, 为极限承载力2 700 kN的74%, 全过程荷载-滑移曲线基本一致, 因不排除试件制作或者加载过程存在离散差异, 认为两者之间的误差是合理的.
|
图 6 试验自由端荷载-滑移曲线 Fig. 6 Experimental load-slide curve at freedom end |
加载过程中Exp-1与Exp-2混凝土底部出现纵向贯通裂缝, 裂缝宽度随荷载增长较快, 卸载后钢管底部混凝土全部破坏, 部分混凝土呈块状剥离状态脱落, 加载至结束, 主裂缝宽度大于10 mm.
3 数值分析应用有限元软件ABAQUS建立试件的有限元模型, 控制变量分析得到环板、加劲板、焊钉的作用下钢管与混凝土界面的荷载-滑移曲线, 并与我国钢结构设计规范、欧洲Euro code-4、美国AASHTDLRFD规范进行对比.
3.1 有限元模型建立混凝土模拟采用三维实体单元, 本构模型采用《混凝土结构设计规范(GB50010-2010)》推荐的单轴拉压模型[7].分析中混凝土计算参数取值为:钢管外围混凝土弹性模量取31.5×103 MPa, 钢管内部混凝土弹性模量取32.5×103 MPa, 计算中泊松比取0.2, 双轴受压与单轴受压的极限强度比取1.16, 拉伸子午面和压缩子午面的第二应力不变量之比为0.667, 膨胀角取30°, 流动势偏移值为0.1, 黏性系数取0.000 4[8];
钢管模拟采用三维实体单元, 钢管弹性模量取2.01×105 MPa, 屈服强度取330 MPa;钢筋采用三维桁架单元, 钢筋弹性模量取2.06×105 MPa, 屈服强度取500 MPa;钢管与钢筋的计算泊松比取0.3, 本构模型取常用的理想弹塑性模型.
焊钉计算时本构模型采用二折线弹塑性强化模型, 关键点取值如下:屈服强度为365 MPa, 极限抗拉强度为480 MPa, 弹性模量为2.06×105 MPa.
3.1.1 接触方式混凝土边界约束方式与试验相同, 控制顶端竖向位移进行加载.数值分析模型见图 7, 钢管内表面与混凝土法向采用绑定连接[9], 焊钉与钢管为几何一体, 忽略焊接点强度的影响, 采用精细网格划分技术使网格均匀对称化, 更好地克服接触分析中主从面网格穿透以及受力的不均匀性的缺点,以增加分析的精确性, 环板、加劲板与钢管采用绑定连接, 焊钉、环板、钢筋使用嵌入方法与混凝土连接, 钢管与外围混凝土采用面面硬接触, 摩擦系数为0.2[10].

|
图 7 有限元分析(FEA)模型 Fig. 7 Model of finite element analysis (FEA) |
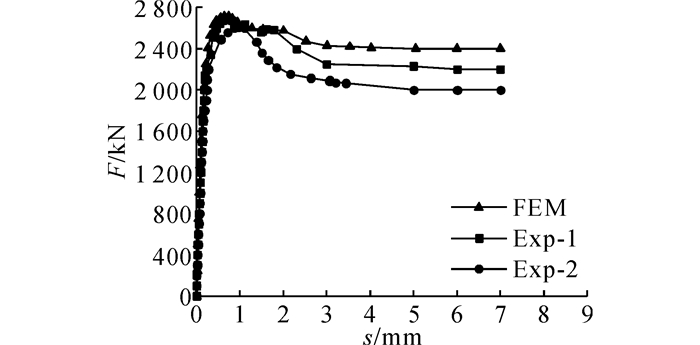
通过对如图 8所示模型的有限元分析, 得出钢管自由端的F-s曲线, 并与试验结果进行对比.由图 9可知:加载初期, FEM曲线与试验曲线Exp-1、Exp-2吻合较好, 钢管与混凝土之间的黏结力与焊钉、环板共同产生的机械咬合力相比较小, 因此前期刚度基本吻合;加载至极限荷载后, 焊钉与环板已发生变形, 部分混凝土压碎开裂甚至脱落导致试件刚度下降较快, 而在数值模拟过程中, 采用的是塑性损伤模型, 在全过程加载中假设混凝土材料为连续体[11], 屈服面的发展由2个硬化参数来控制, 因此刚度退化较试验缓慢, 劈裂段荷载较大, 而进入残余段后, 两者规律基本一致, 荷载趋于稳定.
|
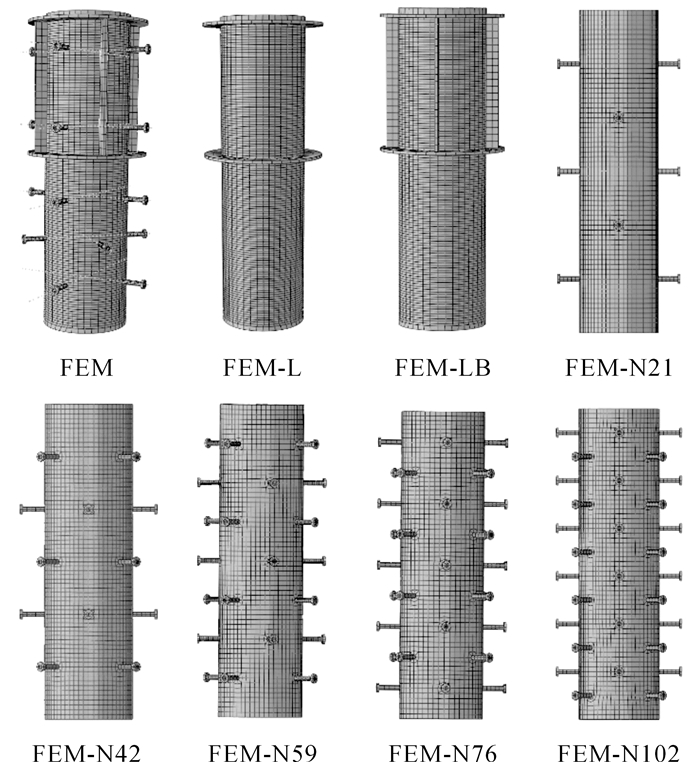
图 8 不同连接件组合钢管试验模型 Fig. 8 Pipe models with different composite connectors |
|
图 9 试验与数值分析钢管自由端荷载-滑移曲线 Fig. 9 Experimental and numerical load-slide curves of steel pipe at freedom end |
由图 9可知,本文采用的计算参数与数值模型合理可行, 因此本节利用数值方法对不同连接件组合钢管模型(如图 8所示)进行深入的模拟与分析.分析内容包括:1)焊钉作用效应;2)环板作用效应(FEM-L);3)环板与加劲板的组合效应(FEM-LB).对比分析不同焊钉率对钢管抗滑移的影响规律, 主要分析的焊钉率有0.21%(FEM-N21)、0.42%(FEM-N4), 0.59%(FEM-N59), 0.76%(FEM-N76), 1.02%(FEM-N102).
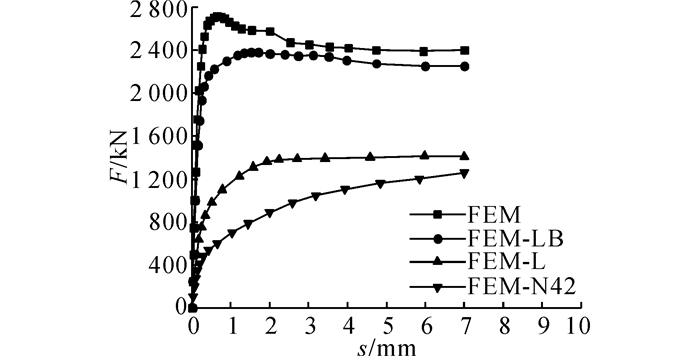
如图 10所示为数值分析得到的不同组合连接件钢管自由端荷载-滑移曲线, 可以发现:FEM、FEM-LB、FEM-L、FEM-N42极限滑移荷载分别为2 700、2 400、1 400、1 200 kN, FEM比仅配置焊钉的FEM-N42极限承载力大125%, FEM-LB比FEM-L极限承载力大71%, 故加劲板能有效提升试件的极限承载力.设计时如能保证环板的抗变形能力, 则能充分利用环板间混凝土的抗压性能, 间接加宽混凝土的受剪面积, 这样从单纯利用连接件抗剪转变为连接件与混凝土协同抗剪, 可以保持连接件良好的延性.
|
图 10 不同组合连接件钢管自由端荷载-滑移曲线 Fig. 10 Load-shide curve of pipe with different compositeconnectors |
我国《钢结构设计规范(GB50017-2003)》给出的单个焊钉抗剪承载力Fu的计算公式[12]如下:
| $ {{F}_{\text{u}}}=0.43{{A}_{\text{s}}}\sqrt{{{f}_{\text{c}}}{{E}_{\text{c}}}}\le 0.7{{A}_{\text{s}}}{{f}_{\text{u}}}. $ | (1) |
式中:As为圆柱头焊钉截面面积;fc为混凝土立方体抗压强度;Ec为混凝土弹性模量;fu为焊钉材料的极限抗拉强度.
欧洲规范Eurecode-4给出的单个焊钉抗剪承载力的计算表达式[6]如下:
| $ {{F}_{\text{u}}}=\min \left\{ 0.8{{f}_{\text{u}}}{{A}_{\text{sv}}}, 0.29{{d}^{2}}\sqrt{{{f}_{\text{ck}}}{{E}_{\text{cm}}}} \right\}. $ | (2) |
式中:fu≤500 MPa;Asv为焊钉截面面积;d为焊钉直径;fck为混凝土圆柱体抗压强度;Ecm为混凝土弹性模量.
美国公路桥梁设计规范AASHTOLRFD给出的单个焊钉抗剪承载力Fu的计算表达式[13]如下:
| $ {{F}_{\text{u}}}=0.5{{A}_{\text{sc}}}\sqrt{{{f}_{\text{ck}}}{{E}_{\text{c}}}}\le {{A}_{\text{sc}}}{{f}_{\text{u}}}. $ | (3) |
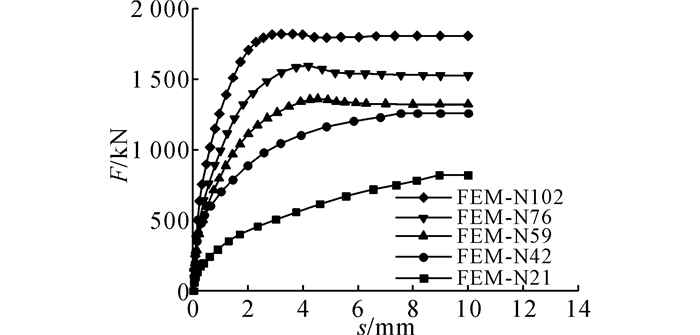
荷载-滑移曲线如图 11所示, 可见焊钉率对钢管弹性抗滑移刚度的影响不大.虽然增大焊钉率, 对钢管塑性抗滑移刚度、极限强度提升明显, 但是高焊钉率的多排焊钉并未改变焊钉作为延性连接件的性质, 各模型的特征滑移量均到达6 mm以上, 符合欧洲规范Eurecode-4要求.
|
图 11 焊钉率影响的钢管自由端荷载-滑移曲线 Fig. 11 Load-slide curve with different ratios of welding nails |
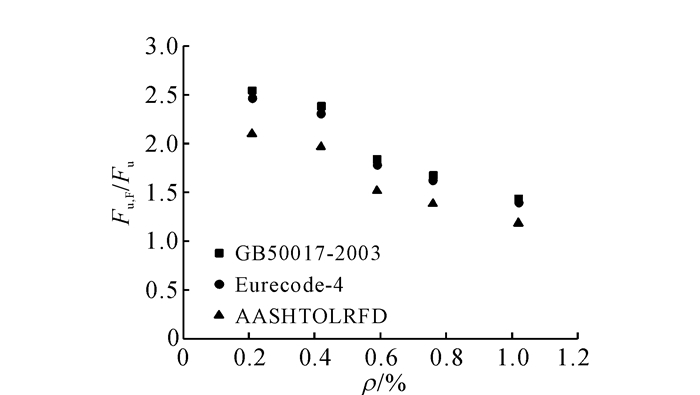
极限荷载下单个焊钉平均抗剪强度模拟值和不同规范计算的结果对比如表 3所示, 随焊钉率的变化规律则如图 12所示.可以看出:美国规范的单钉计算值最大, 欧洲规范次之, 我国规范最小, 各规范的计算值皆小于数值模拟值;且随着焊钉率的增加,单钉平均抗剪强度模拟值与规范计算值逐渐接近并趋于稳定.其原因主要是低焊钉率时破坏模式为焊钉剪断或者拉断产生滑移破坏;高焊钉率工况下, 随着焊钉率的增加, 钢管极限抗滑移强度增大, 钢管的径向变形急剧增加, 外围混凝土在钢管径向力的作用下达到极限抗拉强度开裂致使混凝土对钢管的约束力下降而产生滑移, 破坏模式发生了改变.
| 表 3 极限荷载下单个焊钉模拟结果和规范计算结果 Table 3 Test results and calculated values on basis of different codes |
|
图 12 单钉平均抗剪强度模拟值与规范计算值比值随焊钉率变化规律图 Fig. 12 Average shear strength of single nail and ratio of calculated value of standard nail with different ratios of welding nails |
图 13给出了试件模拟过程中F-s曲线达到峰值时单个焊钉最大抗剪应力模拟值与规范计算值比值随焊钉率的变化规律.由此可见:单个焊钉实际受力大小与规范计算值接近, 加载前期构件剪力主要由焊钉承担, 当焊钉屈服并进入强化阶段后, 焊钉间的混凝土逐渐被压碎, 焊钉应变明显增大, 因此由极限荷载得到的平均焊钉抗剪强度较大.

|
图 13 单个焊钉最大抗剪强度模拟值与规范计算值比值随焊钉率变化规律图 Fig. 13 Maximum shear strength of single nail and ratios of calculated value of standard nail with different ratios of welding nails |
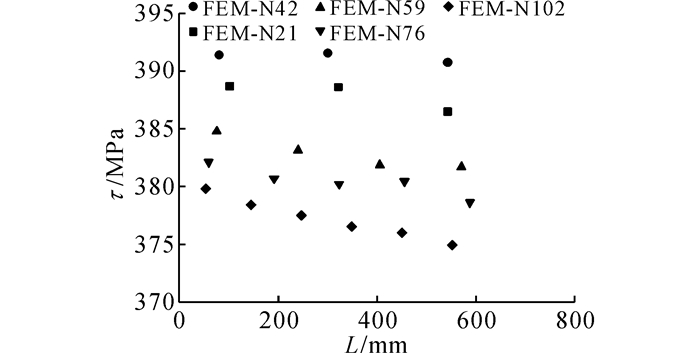
图 14给出了沿钢管长度L方向单个焊钉的应力τ分布, 由图可见:离加载端越远, 焊钉所承受的应力越小, 应力值之差较小
|
图 14 沿长度方向单个焊钉剪切应力分布 Fig. 14 Shear stress distribution of single welding nail in length direction |
(1) 钢管推出试验研究表明, 环板与加劲板的组合能有效利用混凝土的抗压性能, 提升界面的抗滑移性能, 带组合连接件钢管特征滑移量大于6 mm, 符合欧洲规范Eurocode-4对连接件的延性要求.
(2) 设置一定比率的焊钉可在保证界面抗滑承载力的同时有效增大其抗滑移刚度;随着焊钉率的增大, 界面破坏模式由焊钉剪断或者拉断破坏向外围混凝土劈裂引起的钢管滑移破坏转变;焊钉率的增大对界面塑性抗滑移刚度、极限强度提升明显, 但是高焊钉率并未改变焊钉作为延性连接件的性质.
(3) 有限元模拟结果表明:极限荷载下单个焊钉平均抗剪强度模拟值较规范计算值稍大, 因此通过规范计算得到的单个焊钉承载力设计构件有足够的安全系数.沿钢管长度方向单个焊钉的受力离加载端越远, 焊钉承受的荷载越小, 因此实际工程设计时宜考虑群钉强度的折减效应.随着焊钉率的增大, 单钉平均抗剪强度模拟值与规范计算值接近, 且趋于稳定.
| [1] |
许开成, 毕丽萍, 陈梦成. 钢管混凝土界面黏结应力-滑移本构关系试验研究[J]. 建筑结构学报, 2015, 36(增1): 407-412. XU Kai-cheng, BI Li-ping, CHEN Meng-cheng. Experimental study on bond stress-slip constitutive relationship for CFST[J]. Journal of Building Structures, 2015, 36(Suppl.1): 407-412. |
| [2] |
康希良, 赵鸿铁, 薛建阳. 钢管混凝土黏结滑移问题综述分析[J]. 西安建筑科技大学学报:自然科学版, 2006, 38(3): 322-324. KANG Xi-liang, ZHAO Hong-tie, XUE Jian-yang. Summarized review of the bond-slip problems of concrete filled steel tubes (CFST)[J]. Journal of Xi'an University of Architecture & Technology:Natural Science Edition, 2006, 38(3): 322-324. |
| [3] |
林建平, 汪劲丰, 陈春雷, 等. 槽形组合钢梁桥顶推施工线形控制[J]. 桥梁建设, 2014, 44(4): 102-105. LIN Jian-ping, WANG Jin-fen, CHEN Chun-lei, et al. Geometric shape control of trough steel girder composite bridge constructed by incremental launching method[J]. Bridge Construction, 2014, 44(4): 102-105. |
| [4] |
中华人民共和国国家质量监督检验检疫总局. GB/T 10433-2002电弧螺柱焊用圆柱头焊钉[S]. 北京: 中国建筑工业出版社, 2003: 2-7. http://www.doc88.com/p-2015378772232.html
|
| [5] |
中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局. GB/T 50081-2002普通混凝土力学性能试验方法标准[S]. 北京: 中国建筑工业出版社, 2003: 12-14. https://baike.baidu.com/item/GB%C2%B7T50081-2002%E6%99%AE%E9%80%9A%E6%B7%B7%E5%87%9D%E5%9C%9F%E5%8A%9B%E5%AD%A6%E6%80%A7%E8%83%BD%E8%AF%95%E9%AA%8C%E6%96%B9%E6%B3%95%E6%A0%87%E5%87%86
|
| [6] |
Eurocode-4 EN 1994 Design of composite steel and concrete structures. Part 1-1 general rules for buildings[S]. Brussels: CEN-European Committee for Standardization, 2004. http://www.academia.edu/10073042/Eurocode_4_Design_of_composite_steel_and_concrete_structures_Part_1-1_General_rules_and_rules_for_buildings
|
| [7] |
张劲, 王庆扬, 胡守营, 等. ABAQUS混凝土损伤塑性模型参数验证[J]. 建筑结构, 2008, 38(8): 127-130. ZHANG Jin, WANG Qin-yang, HU Shou-ying, et al. Parameters verification of concrete damaged plastic model of ABAQUS[J]. Building Structures, 2008, 38(8): 127-130. |
| [8] |
GENIKOMSOU A S, POLAK M A. Finite elementanalysis of punching shear of concrete slabs using damaged plasticity model in ABAQUS[J]. Engineering Structures, 2015, 98: 38-48. DOI:10.1016/j.engstruct.2015.04.016 |
| [9] |
庄茁. ABAQUS非线性有限元分析与实例[M]. 北京: 科学出版社, 2005, 67-78.
|
| [10] |
徐有邻. 变形钢筋-混凝土粘结锚固性能的试验研究[D]. 北京: 清华大学, 1990: 13-14. XU You-ling. Experimental study of anchorage properties for deformed bars in concrete[D]. Beijing: Tsinghua University, 1990: 13-14. |
| [11] |
彭小婕, 于安林, 方有珍. 混凝土损伤塑性模型的参数分析[J]. 苏州科技学院学报:工程技术版, 2010, 23(3): 41-43. PENG Xiao-jie, YU An-lin, FANG You-zhen. Ananalysis on parameters for concrete damage plasticity model[J]. Journal of Suzhou University of Science and Technology:Engineering and Technology, 2010, 23(3): 41-43. |
| [12] |
中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局. GB50017-2003钢结构设计规范[S]. 北京: 中国建筑工业出版社, 2003: 121-122. http://coyis.com/guifantuji/guifan/201510107852.html
|
| [13] |
American Associate of state Highway and Transportation Officials. AASHTO LRFD bridge design specifications[S]. 8rd ed. Washington D C: American Association of State Highway and Transportation Officials, 2017: 6-176. https://bookstore.transportation.org/item_details.aspx?id=3731
|



