2. 装备发展部驻北京军代室, 北京 100191
2. Military Representative Office in Beijing, Beijing 100191, China
随着通信技术的飞速发展, 世界各国军队都在发展野战环境下的战场无线通信网络体系, 无线通信网络在数字化战场上扮演着越来越重要的角色[1-4].因此研究野战环境下无线通信网络的侦测具有重要的军事对抗意义, 其中一个重要领域就是对无线通信网络真实覆盖范围探测[5].目前民用领域无线通信网络真实覆盖范围探测的主流方案是利用测试终端和扫频仪等工具加载到汽车上进行路测, 该方案在移动通信网络覆盖范围探测方面应用较为广泛[6-7].在军事领域及野战环境中, 通过这种路测方案获得敌方无线通信网络的真实覆盖范围则不可行.
为突破以上传统路测方案在野战环境下的局限性, 通过基于自组网技术的无线感知网络实现对无线通信网络覆盖范围的探测进而生成电磁态势成为一个可行的技术方案.该方案的原理是通过部署于无线通信网络目标区域内的分布式感知节点对无线通信网络的信号强度进行感知, 然后联合所有感知节点的感知数据生成电磁态势.该方案不仅可以通过飞机抛洒、炮弹发射等方法将感知节点投放到敌方战场环境中去, 而且能够实现全方位的自动化感知[8-9], 相比于路测方案能够快速、不间断地探测无线通信网络覆盖情况.赫阳[10]基于感知节点的确定性全覆盖部署方案, 提出了一种无线通信网络电磁态势感知算法.但是该算法对感知节点的部署要求较高, 而在敌方野战环境难实现全覆盖部署.通常只能采取随机投放的方法, 这就不可避免产生感知盲区, 导致无法完整地获取区域电磁态势.
如何在存在感知盲区的限制下完成目标区域的电磁态势生成是一个亟待解决的问题.当前可以采用的方法主要有信号传播模型估计法和插值估计[11].其中信号传播模型估计法主要是根据感知节点接收的信号强度(received signal strength indication, RSSI)选用合适的信号传播衰减模型来估计无线通信网络中心节点的有效通信覆盖范围.该算法复杂度较低, 但是直接使用现有模型不能够精确匹配目标区域的实际地理环境, 精度较低.根据邻域范围内感知节点的特征属性来进行插值点属性估计的方法精度较高[12].常用的插值估计方法有:分型插值法、反距离权重插值法(inverse distance weighted, IDW)和Kriging插值法等.Mrinmoy等[13]根据感知节点接收RSSI值采用反距离权重插值法对插值点RSSI值进行插值估计, 较前述算法一定程度上提高了算法的精度.但是只考虑了插值点与感知节点之间的距离关系, 导致插值精度有待提高.Evangelos等[14]所采用的Kriging插值法是基于感知节点采集RSSI间变异函数值所拟合出的球形模型来对盲区插值点RSSI值估计的一种无偏估计方法.但是在选取变异函数模型时带有一定的人为主观性, 在某些情况下缺乏可信性.
针对以上算法应用在电磁态势生成中的不足, 本文提出一种改进的Kriging插值算法.该算法通过支持向量回归(support vector regression, SVR)从感知节点采集的RSSI之间的变异函数值中拟合出变异函数曲线, 克服传统方法中模型选择的人为主观性因素, 提高算法的可信度和电磁态势生成的精度.
1 Kriging插值法原理Kriging插值法是一种用于地质测量领域的格网化统计方法[15], 在数学上被证明为一种线性无偏估计方法[16], 其原理是通过插值点邻域范围内感知节点的特征属性来对插值点的属性进行最优无偏估计.在本文背景下, 即为利用感知节点采集的RSSI值来估计插值点的RSSI值.
设插值点的RSSI值为R(x0), 其邻域范围内m个经过预处理之后的感知节点采集的RSSI值为R(xi)(i=1, 2, …, m).则对感知节点采集的R(xi)值加权求和可以估计出R(x0).
| $ R\left( {{x_0}} \right) = \sum\limits_{i = 1}^m {\left[ {{\lambda _i}R\left( {{x_i}} \right)} \right]} . $ | (1) |
其中, λi是插值点邻域范围内m个参与插值估计的R(xi)的权重, 从本征假设的条件可得
由感知节点采集的RSSI值R(xi)满足二阶平稳可得:
| $ \left. \begin{array}{l} E\left[ {R\left( {{x_i}} \right) - R\left( {{x_j}} \right)} \right] = 0,\\ {\rm{Var}}\left[ {R\left( {{x_i}} \right) - R\left( {{x_j}} \right)} \right] = E\left\{ {{{\left[ {R\left( {{x_i}} \right) - R\left( {{x_j}} \right)} \right]}^2}} \right\}. \end{array} \right\} $ | (2) |
假设R*(x0)为R(x0)的无偏估计, 此时插值点x0估计方差最小:
| $ \begin{array}{l} {\rm{Va}}{{\rm{r}}_{\min }}\left( {{x_0}} \right) = {\rm{Var}}\left[ {R\left( {{x_0}} \right) - {R^ * }\left( {{x_0}} \right)} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;E\left\{ {{{\left[ {R\left( {{x_0}} \right) - {R^ * }\left( {{x_0}} \right)} \right]}^2}} \right\}. \end{array} $ | (3) |
通过引入拉格朗日乘子μ求条件极值, 可表示为
| $ \frac{\partial }{{\partial {\lambda _i}}}E\left\{ {{{\left[ {R\left( {{x_0}} \right) - {R^ * }\left( {{x_0}} \right)} \right]}^2} - 2\mu \sum\limits_{i = 1}^m {{\lambda _i}} } \right\} = 0 $ | (4) |
式(4)进行计算和化简可得到如下方程组:
| $ \left. \begin{array}{l} \sum\limits_{i = 1}^m {\left[ {{\lambda _i}\gamma \left( {{x_i} - {x_j}} \right)} \right]} + \mu = \gamma \left( {{x_0} - {x_j}} \right);\\ \sum\limits_{i = 1}^m {{\lambda _i}} = 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;j = 1,2, \cdots ,m. \end{array} \right\} $ | (5) |
其中,
作为Kriging插值法的核心部分, 变异函数是为了求解插值点的空间特征而提出的.通过变异函数能够利用感知节点的特征属性值随分离距离变化的规律推断出插值点的特征属性值.空间变异函数值可以通过下式进行计算:
| $ \gamma \left( {{h_j}} \right) = \frac{1}{{2{N_{hj}}}}\sum\limits_{i = 1}^{{N_{hj}}} {{{\left[ {R\left( {{x_i} + {h_j}} \right) - R\left( {{x_i}} \right)} \right]}^2}} . $ | (6) |
其中, hj表示目标区域中一对感知节点的分离距离, Nh j表示所有感知节点对中相距hj的点对数.通过式(6)可以计算出不同分离距离的变异函数值, 这些变异函数值可以拟合出一条变异函数曲线γ(h).根据该曲线可以得出插值点属性与邻域内参与估计的感知节点属性之间的变异函数值, 将其代入式(5)即可得出权重λi和拉格朗日乘子μ.
在进行变异函数曲线拟合时, 通常是利用现有的变异函数模型, 然后通过最小二乘法进行拟合[14].常见的经典变异函数模型有线性模型、高斯模型、球形模型、指数模型等.球形模型的公式可以表示如下:
| $ \gamma \left( h \right) = \left\{ \begin{array}{l} {C_0} + {C_1}\left( {\frac{{3h}}{{2a}} - \frac{{{h^3}}}{{2{a^2}}}} \right),\;\;\;\;0 < \left| h \right| < a;\\ {C_0} + {C_1},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| h \right| > a,\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| h \right| = 0. \end{array} \right. $ | (7) |
其中, a表示变程, C0表示短距离内的变异函数值, C1表示空间中的变异函数值系数, 可以通过已有样本拟合得到.如式(7)所示的球形模型在变异函数拟合中使用较为广泛, 但是在实际应用中也不唯一.
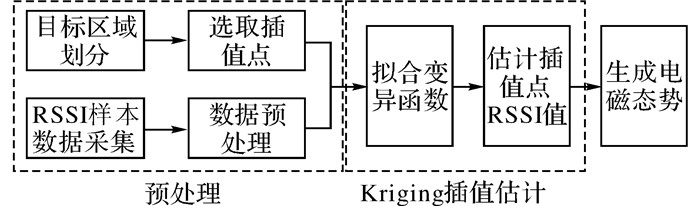
2 无线通信网络电磁态势生成算法如前所述, 随机投放的感知节点存在一定量的感知盲区.为保证无线通信网络电磁态势生成的完备性, 本文所提出的基于无线感知网络的无线通信网络电磁态势生成技术利用Kriging插值实现了对感知盲区的电磁态势感知, 其算法架构如图 1所示.
|
图 1 电磁态势生成算法架构 Fig. 1 Architecture of electromagnetic situation generation algorithm |
算法主要由3个模块组成:预处理、Kriging插值估计和电磁态势生成.其中, 预处理主要完成目标区域划分、插值点选取、RSSI样本数据采集和数据预处理;Kriging插值估计主要包括样本数据集变异函数值计算、变异函数曲线拟合和插值点RSSI值插值估计;电磁态势生成主要是融合插值估计的结果和感知节点采集的数据生成无线通信网络目标区域的电磁等强线.后续将对图 1所示的各算法模块进行详细阐述.
2.1 预处理 2.1.1 目标区域划分和选取插值点为了方便Kriging插值估计中插值点及其邻域的选取, 需要对目标区域进行划分.其中, 基于Voronoi图和Delaunay三角形划分的方案能够将区域划分为若干封闭的三角网格, 且划分后感知节点位置位于三角形顶点处[17].所选取的插值点均位于三角网格之中, 其邻域范围内的感知节点即为所处三角形的3个顶点处的感知节点.限于文章篇幅, 此处仅作简要说明.
2.1.2 RSSI样本数据采集与数据预处理为确保感知节点所采集的接收信号强度的准确性, 需要对数据进行多次采集.由于感知节点每次采集的数据之间相互独立, 则多次采集的RSSI值服从高斯分布[18].因此可以通过高斯滤波滤除小概率干扰项, 得到精确稳定的感知节点RSSI值.
对于每个感知节点多次采集的RSSI值(用RSSIm表示第m次采集的结果), 其采集结果x的密度函数如式(8)所示, 其中n为采集次数, μ为数据集的均值, σ2为方差.
| $ f\left( x \right) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}}~ \sigma }}\exp \left[ { - \frac{{{{\left( {x - \mu } \right)}^2}}}{{2{\sigma ^2}}}} \right], $ | (8) |
| $ {\sigma ^2} = \frac{1}{{n - 1}}\sum\limits_{m = 1}^n {{{\left( {{\rm{RSS}}{{\rm{I}}_m} - \mu } \right)}^2}} , $ | (9) |
| $ \mu = \frac{1}{n}\sum\limits_{m = 1}^n {{\rm{RSS}}{{\rm{I}}_m}} . $ | (10) |
根据式(8)计算出的概率密度函数, 选取高概率发生区f(x)≥0.6 (经验值)范围内对应的RSSI值, 求其几何平均值作为预处理之后的感知节点所采集的RSSI值.
2.2 改进的Kriging插值算法根据前述可知插值点估计的关键在于感知节点RSSI值的变异函数曲线拟合.在解决实际问题时, 模型匹配法需要具体问题具体分析, 通常只能根据经验选取模型或者选取多个变异函数模型进行比对.因此, 模型匹配法缺乏可靠的依据, 无法排除人为主观随意性.而且, 已有模型可能不能完全匹配需拟合的数据集.为了突破模型代入法的局限性, 本文从SVR入手对变异函数曲线进行拟合.理论分析表明, SVR拟合的算法复杂度较模型匹配法会有所增加, 可能会导致计算开销的增加.但是鉴于应用于战场环境的感知节点性能较好, 数据处理能力较强, 且战场环境下对态势感知精度的要求较高, 本文重点研究基于SVR的变异函数拟合.
2.2.1 SVR原理众所周知, 在解决分类问题上支持向量机(SVM)具有较好的泛化能力, 可以在样本数据量有限的情况下获得较优的分类结果[19].在支持向量机中引入ε不敏感损失函数可以得到用于数据拟合的SVR.其基本思想是寻找一个最优分类面使训练样本离该分类面的误差最小[20].
在进行拟合时, 函数曲线多为非线性拟合情况.而在进行SVR拟合时, 大都是进行线性回归拟合.为此, 需要通过非线性映射函数将样本数据映射到高维特征空间进行线性回归.
对于含有k个样本的训练集T={(x1, y1), (x2, y2), …, (xk, yk)}∈(Rn×R).xl(l∈(1, k))表示第l个训练样本的输入向量, yl为其对应的输出值.假设在高维特征空间中的线性回归函数为
| $ f\left( \mathit{\boldsymbol{x}} \right) = w\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( \mathit{\boldsymbol{x}} \right) + b. $ | (11) |
其中, Φ(x)为非线性映射函数, ω、b的求解见式(20).引入ε线性不敏感损失函数:
| $ L\left( {f\left( \mathit{\boldsymbol{x}} \right),y,\varepsilon } \right) = \max \left( {0,\left| {y - f\left( \mathit{\boldsymbol{x}} \right)} \right| - \varepsilon } \right). $ | (12) |
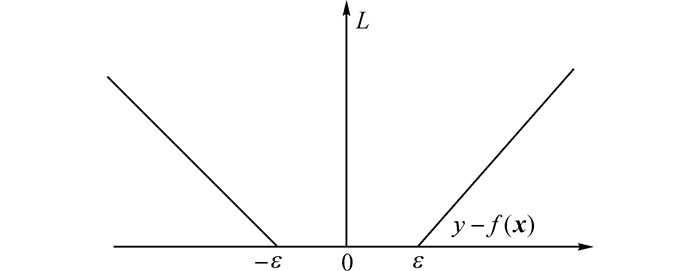
其中, f(x)为式(11)函数输出的预测值, y为样本的真实值.如图 2所示为ε线性不敏感损失函数, 当f(x)与y差值≤ε时, 损失值为0, 否则随差值增大呈线性增长.ε决定了线性回归函数的误差要求, ε越大表示线性回归函数误差越大.
|
图 2 ε线性不敏感损失函数 Fig. 2 ε linear insensitive loss function |
通过引入松弛变量ξl∈(ξ1, ξ2, …, ξk)T、ξl*∈(ξ1*, ξ2*, …, ξk*)T可将线性SVR问题表示为
| $ \mathop {\min }\limits_{w,b,\xi ,{\xi ^ * }} \;\;\;\left\{ {\frac{1}{2}{{\left\| w \right\|}^2} + C\sum\limits_{l = 1}^k {\left( {{\xi _l} + \xi _l^ * } \right)} } \right\}. $ | (13) |
| $ {\rm{s}}.\;{\rm{t}}.\;\;{y_l} - \left[ {w\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( \mathit{\boldsymbol{x}} \right) + b} \right] \le \varepsilon + {\xi _l},l = 1,2, \cdots ,k; $ | (14) |
| $ w\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( \mathit{\boldsymbol{x}} \right) + b - {y_l} \le \varepsilon + \xi _l^ * ,l = 1,2, \cdots ,k; $ | (15) |
| $ {\xi _l} \ge 0,\xi _l^ * \ge 0. $ | (16) |
其中C为惩罚参数, C越大意味着对训练误差大于ε的样本的惩罚力度越大.将求解式(13)~(16)得到的w、b代入式(11)可以构建出高维特征空间中的线性回归函数.
为方便求解, 可以引入拉格朗日乘子αl、αl*得到原问题式(13)~(16)的对偶形式:
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{\alpha ,{\alpha ^ * }} \left\{ {\frac{1}{2}\sum\limits_{l = 1}^k {\sum\limits_{j = 1}^k {\left( {\alpha _l^ * - {\alpha _l}} \right)\left( {\alpha _j^ * - {\alpha _j}} \right)K\left( {{\mathit{\boldsymbol{x}}_l},{\mathit{\boldsymbol{x}}_j}} \right)} } + } \right.}\\ {\left. {\varepsilon \sum\limits_{l = 1}^k {\left( {\alpha _l^ * + {\alpha _l}} \right)} - \sum\limits_{l = 1}^k {\left( {{\alpha _l} - \alpha _l^ * } \right){y_l}} } \right\},} \end{array} $ | (17) |
| $ {\rm{s}}.\;{\rm{t}}.\;\;\sum\limits_{l = 1}^k {\left( {\alpha _l^ * - {\alpha _l}} \right)} = 0, $ | (18) |
| $ 0 \le {\alpha _l} \le {\rm{C}},0 \le \alpha _l^ * \le {\rm{C}}{\rm{.}} $ | (19) |
其中, K(xl, xj)=Φ(xl)Φ(xj)称为SVR的核函数.式(17)~(19)的求解是一个凸二次优化问题[21], 假设
| $ w = \sum\limits_{l = 1}^k {\left[ {\left( {\bar \alpha _l^ * - {{\bar \alpha }_l}} \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{x}}_l}} \right)} \right]} . $ | (20) |
| $ \begin{array}{*{20}{c}} {b = \frac{1}{{{N_{{\rm{NSV}}}}}}\left\{ {\sum\limits_{{{\bar \alpha }_l} \in \left( {0,C} \right)} {\left[ {{y_l} - \sum\limits_{{x_i} \in {\rm{SV}}} {\left( {\left( {{{\bar \alpha }_i} - \bar \alpha _i^ * } \right)K\left( {{\mathit{\boldsymbol{x}}_i},{\mathit{\boldsymbol{x}}_l}} \right)} \right)} - \varepsilon } \right]} + } \right.}\\ {\left. {\sum\limits_{\bar \alpha _l^ * \in \left( {0,C} \right)} {\left[ {{y_l} - \sum\limits_{{x_j} \in {\rm{SV}}} {\left( {\left( {{{\bar \alpha }_i} - \bar \alpha _i^ * } \right)K\left( {{\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{x}}_l}} \right)} \right)} - \varepsilon } \right]} } \right\}.} \end{array} $ | (21) |
其中, N为支持向量(SV)的数目.对于感知节点xi, 若其对应的αi-αi*不为0, 则该感知节点为支持向量.将式(20)、(21)代入式(11)得出线性回归函数:
| $ \begin{array}{l} f\left( \mathit{\boldsymbol{x}} \right) = w\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( \mathit{\boldsymbol{x}} \right) + b = \\ \;\;\;\;\;\;\;\;\;\;\;\sum\limits_{l = 1}^k {\left[ {\left( {\bar \alpha _l^ * - {{\bar \alpha }_l}} \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{x}}_l}} \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( \mathit{\boldsymbol{x}} \right)} \right]} + b = \\ \;\;\;\;\;\;\;\;\;\;\;\sum\limits_{l = 1}^k {\left[ {\left( {\bar \alpha _l^ * - {{\bar \alpha }_l}} \right)K\left( {{\mathit{\boldsymbol{x}}_l},\mathit{\boldsymbol{x}}} \right)} \right]} + b. \end{array} $ | (22) |
由式(21)、(22)可知, 线性回归函数中主要需要确定的是核函数K(xl, x)和惩罚参数C.常用的核函数主要有Sigmod核函数、多项式核函数和RBF径向基核函数等.其中, 在进行Kriging插值的变异函数曲线拟合时, 式(23)所示的RBF核函数效果较优[22].
| $ K\left( {{x_i},{x_j}} \right) = \exp \left( { - \sigma {{\left\| {{x_i} - {x_j}} \right\|}^2}} \right),\;\;\;\;\sigma > 0. $ | (23) |
其中, σ为平滑核函数的核参数.因此, 在进行变异函数曲线的SVR拟合时主要需要确定参数σ和C.本文在进行参数选择时采用李明山等[23]提出的RBF核函数模型参数选择方法, 该方法通过均匀试验设计提出了一种精度较高的快速求取参数的方法, 限于文章篇幅, 不再赘述.
2.2.2 改进的Kriging插值算法步骤前述提到与传统的函数模型匹配法相比, 利用2.2.1节阐述的SVR对Kriging插值算法变异函数曲线进行拟合具有较高的精度和可信度, 能够有效抑制人为主观因素对插值估计产生的影响.其具体的算法步骤如下.
1) 根据式(9)计算所有样本数据对的距离hj以及对应的变异函数值γ(hj), 并生成数据集[hj, γ(hj)];
2) 随机选取数据集中大部分的数据生成训练集T={[h1, γ(h1)], [h2, γ(h2)], …, [hk, γ(hk)]}, 其余数据则为测试集;
3) 利用SVR训练T, 根据训练结果拟合出变异函数曲线γ(h);
4) 使用步骤2)中的测试集对变异函数曲线γ(h)进行性能评估, 若达到预期要求则输出γ(h), 否则修改参数并返回步骤3)重新拟合;
5) 根据符合预期要求的γ(h)得出插值点与其邻域范围内感知节点RSSI之间的变异函数值, 将所求变异函数值代入式(5), 得出λi;
6) 将步骤5)求得的权重λi代入式(1)求得所估计出的插值点RSSI值.
2.3 无线通信网络目标区域电磁态势生成电磁态势生成涉及到数据采集、数据汇聚、数据融合、目标显示、态势标绘和地图支持等关键技术, 鉴于本文研究重点为数据采集、数据插值估计和电磁等强线生成等内容, 此处不再赘述其他关键技术[24].
利用前述2.2节详细介绍的对无线感知网络感知盲区中的电磁态势感知方法生成插值估计的数据;将感知节点采集数据与插值点估计数据进行综合处理, 可以将目标区域中的各位置的信号强度表示出来;生成无线通信网络目标区域的电磁等强线.根据所生成的电磁等强线, 可以比较直观地反映出敌方目标区域中的无线通信网络真实覆盖情况.
3 仿真实验分析 3.1 仿真环境构建为验证本文所提无线通信网络电磁态势生成算法的性能, 不失一般性, 选取8 000 m×8 000 m某丘陵地带作为敌方野战环境, 以基于中心节点的无线通信网络为探测目标进行仿真实验.假设该区域中存在5个无线通信网络中心节点, 采用ATOLL仿真得出其信号覆盖范围如图 3(a)所示.在进行仿真实验验证时假设中心节点个数、位置与信号覆盖范围均为未知.采用随机投放的方式在该区域投放了36个感知节点, 如图 3(b)所示.

|
图 3 信号覆盖范围仿真环境 Fig. 3 Simulation environment of signal coverage |
随机选取30个感知节点作为采样点, 其余6个点作为验证点, 以便对插值精度进行对比分析.为验证本文算法的性能, 本文从变异函数拟合性能分析、改进的Kriging插值估计性能分析2个方面仿真了2个实验, 并在此基础上生成目标区域电磁等强线.
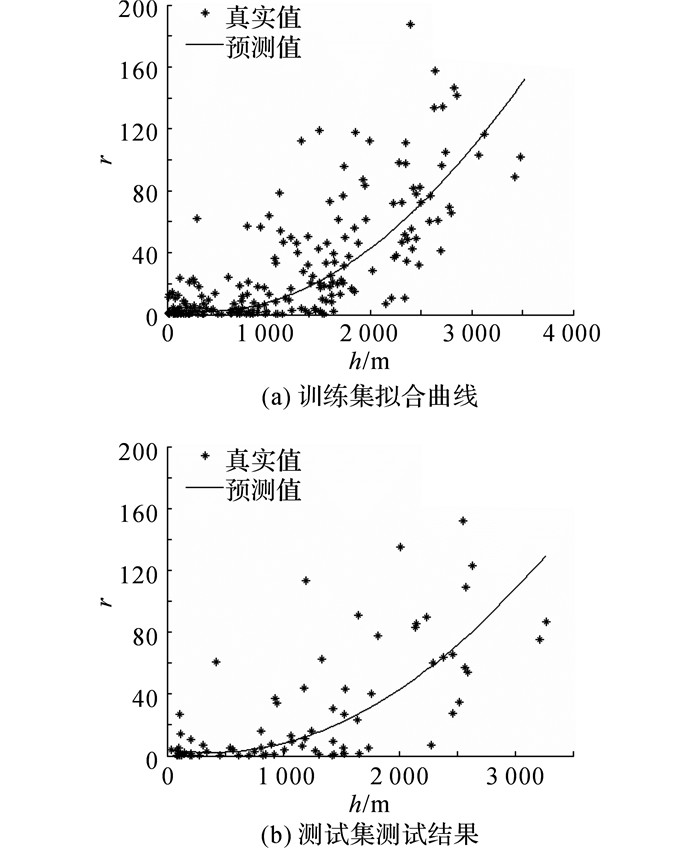
3.2 变异函数拟合性能分析 3.2.1 变异函数拟合精度对比作为本文算法核心步骤, 变异函数拟合的精度决定着Kriging插值的精度.以选取的30个感知节点的接收信号强度为依据生成变异函数数据集.随机抽取80%作为训练集.利用Matlab进行SVR拟合, 结果如图 4所示.
|
图 4 变异函数SVR拟合 Fig. 4 Variation function fitting through SVR |
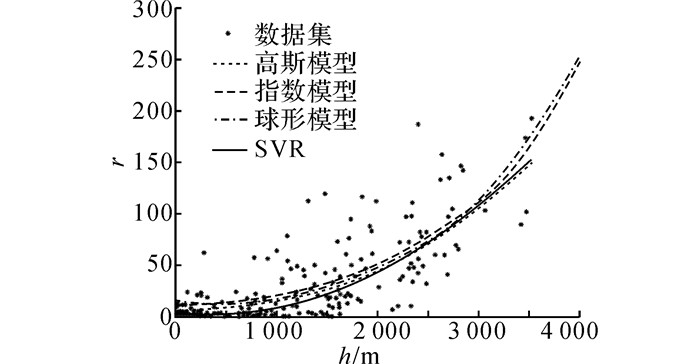
其中图 4(a)为训练集拟合结果, 图 4(b)为测试集测试结果.为了对比算法性能, 分别采用球形模型、高斯模型与指数模型对训练集进行Kriging变异函数拟合, 对比结果如图 5所示.
|
图 5 不同模型变异函数拟合对比 Fig. 5 Variation function fitting comparison through different models |
分别计算各模型的均方根误差RMSE.高斯模型为26.280, 指数模型为30.661, 球形模型为27.785, SVR为25.940.经比较可知, SVR拟合方法RMSE最低, 精度最高.
为了更加有效的衡量各模型的拟合精度, 对30个感知节点进行了5 000次独立随机抽取, 并对其进行拟合实验.多次实验中各模型拟合的平均RMSE和平均决定系数R2如表 1所示.从表 1中可得,本文算法拟合的曲线RMSE较其他模型低且R2较高, 因此本文算法拟合的变异函数曲线吻合度较高.
| 表 1 不同模型拟合性能对比 Table 1 Comparison of fitting performance about different models |
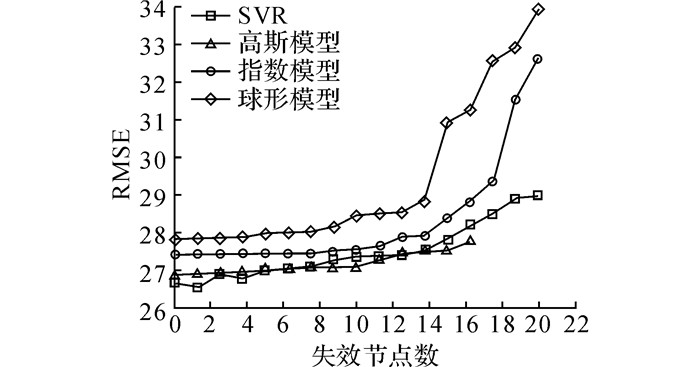
基于对算法的鲁棒性和复杂度的分析, 验证算法的适用性.首先对利用模型拟合的最小二乘法和SVR拟合进行鲁棒性分析.考虑到感知节点在部署至敌方目标区域之后, 可能会受到敌方对抗设备的干扰或者节点消耗殆尽等突发状况, 导致有效的感知节点数量和采集数据量的减少.数据的减少势必对拟合算法的鲁棒性提出了一定的要求.因此通过逐次增加失效的感知节点数, 利用前述3种模型和SVR分别进行拟合, 将拟合的预测值对比原始数据分别计算RMSE, 各模型对比结果如图 6所示.
|
图 6 不同模型RMSE与失效节点数关系 Fig. 6 Relation between RMSE of different models and number of failed nodes |
由图 6可得, 当失效节点数较少时, 各模型的RMSE变化不大, 尤其是SVR与高斯模型更为平稳.当失效节点数较多时, 高斯模型失效, 其他模型RMSE均有所增长, 其中球形模型与指数模型的RMSE呈现快速增长的趋势.因此, 通过以上的对比分析可得, SVR拟合的方法更稳定, 鲁棒性更好.
其次分析算法的计算复杂度.最小二乘法的时间复杂度为O(n2)[25], 而SVR的时间复杂度为O(n3)[26].可以看出, 利用现有的变异函数模型, 然后通过最小二乘法拟合具有较低的计算复杂度, 而本文所采用的机器学习的方法增加了计算复杂度.但是由于模型类型较多, 在实际应用时利用模型拟合的方法存在如何选取模型的问题.通常是选取多个模型进行拟合对比, 选取拟合效果较好的模型.多次进行各个模型的拟合, 会导致计算开销的增加且不一定能选取到最优的变异函数模型.
综上所述, SVR拟合方法具备鲁棒性好、拟合精度高的优点, 利用模型拟合的最小二乘法具备计算复杂度低的优点.因此, 综合考虑鲁棒性、拟合精度和计算复杂度3个因素, 当计算能力较高时, 可以采用SVR进行拟合.而当计算能力较差且要求一定的时效性时, 可以采用传统的最小二乘法.各拟合方法的适用性对比如表 2所示.
| 表 2 不同拟合方法适用性对比 Table 2 Applicability comparison of different fitting methods |
鉴于应用于战场环境的感知节点性能较好, 具备较快的数据处理能力, 能够适应SVR的计算需求.且战场环境下对精度的要求较高, 因此本文采用基于SVR的变异函数拟合.
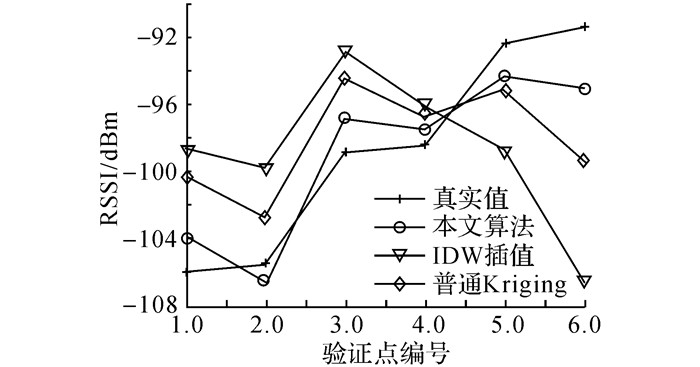
3.3 改进的Kriging插值估计算法性能分析为验证本文所提改进Kriging插值法的估计精度, 以3.1节所选出的6个验证点为例, 将本文算法、普通kriging插值法和IDW插值法针对该6点分别进行插值估计.其插值结果与真实值对比结果如图 7所示.
|
图 7 不同插值算法插值结果 Fig. 7 Interpolation results of different interpolation algorithms |
分别计算3个算法的RMSE, 其中普通Kriging插值法为8.862 2, IDW插值法为19.887 1, 本文算法为5.212 2.经比较可得, 本文算法的RMSE最小, 插值估计精度最高, 性能较好.
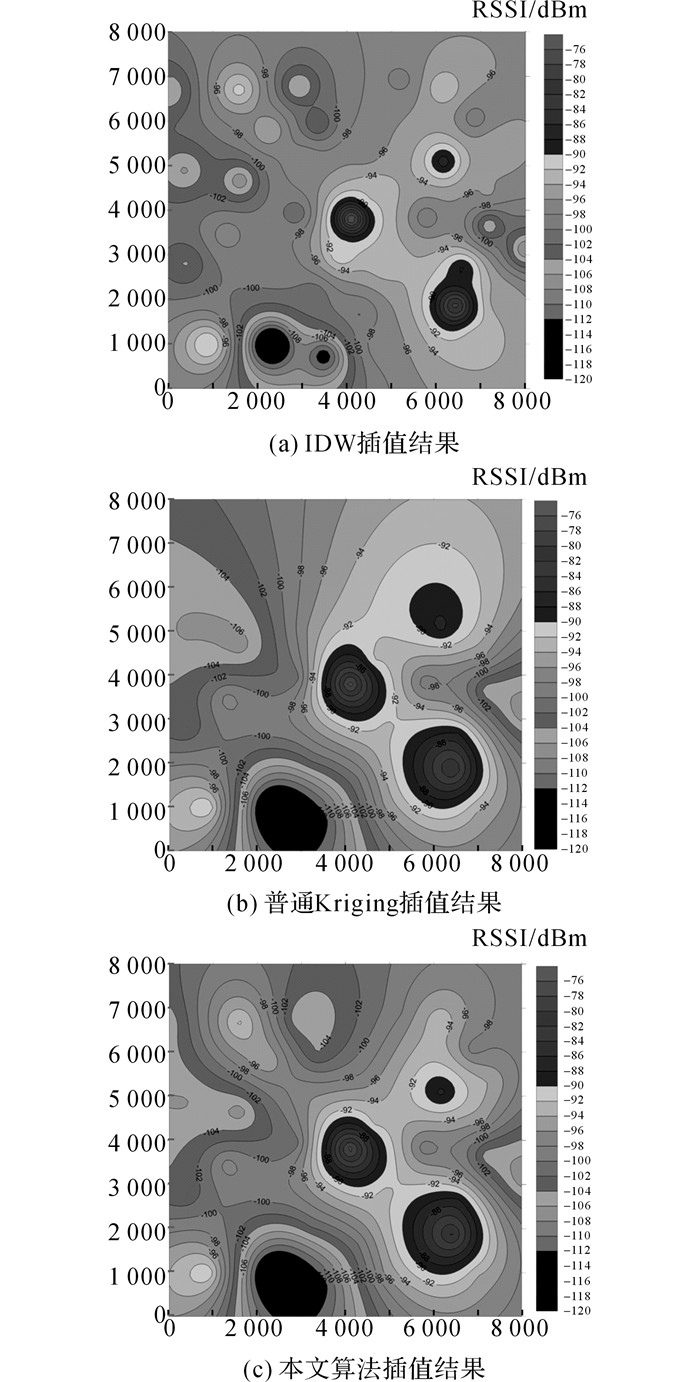
3.4 目标区域电磁态势生成利用3.3节所对比的3种算法对目标区域分别进行插值估计, 将所得的插值点数据结合感知节点采集数据可以生成基于以上3种算法的区域电磁等强线, 如图 8所示.
|
图 8 由3种不同算法估算出的区域电磁等强线 Fig. 8 Electromagnetic isoelectric line of target areaestimated by three different algorithms |
从目标区域中随机选取100个位置点, 分别计算以上3种算法在该100个位置插值结果的RMSE.同时为了保证精度对比的可信度, 以3.2节随机抽取的5 000组实验为例, 对该100个位置点进行3种算法的插值并计算了平均RMSE.其中, IDW插值的平均RMSE为27.3567, 普通Kriging插值为12.5289, 本文算法为9.8756.不难发现本文所提出的改进Kriging插值算法精度更高, 得出的区域电磁等强线最接近于实际情况, 能够更好地反映出无线通信网络的真实覆盖情况.
4 结论本研究从无线感知网络入手, 提出了一种无线通信网络信号覆盖探测算法, 攻克了野战环境下对敌信号探测的技术难题.通过改进的Kriging插值法, 实现了在无线感知网络存在感知盲区的情况下对目标区域的电磁态势生成.所生成的电磁等强线能够直观的显示野战环境中的无线通信网络信号覆盖情况, 对军事战略决策部署具有重要的参考价值.最后, 通过仿真实验验证了论文所生成的区域电磁态势的有效性.论文算法能够在无线感知网络存在感知盲区的情况下完成电磁态势生成, 对无线感知网络节点的部署要求较低, 能够很好地适应敌野战环境, 具有一定可行性和军事应用前景.
| [1] |
OKA D S, MOHAMMAD I, NADEA N P, et al. UAV-based localization for distributed tactical wireless networks using archimedean spiral[C]//2015 International Symposium on Intelligent Signal Processing and Communication Systems (ISPACS), Nusa Dua: IEEE, 2015: 392-396. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=7432802
|
| [2] |
YOUNGSUNG K, AIEXIS K, ANDRES K. Coordinated energy management in resilient microgrids for wireless communication networks[J]. IEEE Journal ofEmerging and Selected Topics in Power Electronics, 2016, 4(4): 1158-1173. DOI:10.1109/JESTPE.2016.2614425 |
| [3] |
YALIN E S, YI S, KARTAVYA N. Search in combined social and wireless communication networks:delay and success analysis[J]. IEEE Transactions on Wireless Communications, 2015, 14(9): 4972-4980. DOI:10.1109/TWC.2015.2430857 |
| [4] |
GAO D P, YU H, CHU Q, et al. Research on tactical internet battlefield environment modeling based on OPNET[C]//20152nd International Conference on Information Science and Control Engineering. Shanghai: IEEE, 2015: 896-900. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7120744
|
| [5] |
GE X H, HUANG M D, CHEN J Q. Wireless single cellular coverage boundary models[J]. IEEE Access, 2016, 4: 3569-3577. DOI:10.1109/ACCESS.2016.2582960 |
| [6] |
MOHAMMAD N A, WALID M D, TAPAN K S. Further validation of an electromagnetic macro model foranalysis of propagation path loss in cellular networksusing measured driving-test data[J]. IEEE Antennas and Propagation Magazine, 2014, 56(4): 108-129. DOI:10.1109/MAP.2014.6931661 |
| [7] |
孙斌, 冯庆坤, 金心宇, 等. 高铁环境中满意通信概率模型及切换算法研究[J]. 浙江大学学报:工学版, 2012, 46(9): 1553-1559. SUN Bin, FENG Qing-lun, JIN Xin-yu, et al. Handoff algorithm and PoSC model under high-speed railway environment[J]. Journal of Zhejiang University:Engineering Science, 2012, 46(9): 1553-1559. |
| [8] |
范时平, 罗丹, 刘艳林. 基于跳距与改进粒子群算法的DV-Hop定位算法[J]. 传感技术学报, 2016, 29(9): 1410-1415. FAN Shi-ping, LUO Dan, LIU Yan-lin. DV-Hop localization algorithm based on Hop-Size and improvement particle swarm optimization[J]. Chinese Journal of Sensors and Actuators, 2016, 29(9): 1410-1415. |
| [9] |
陈战胜, 沈鸿. 能量高效的无线传感器网络路由协议[J]. 计算机科学, 2015, 42(8): 90-94. CHEN Zhan-sheng, SHEN Hong. Energy-efficient multi-hop routing protocol for wireless sensor networks[J]. Computer Science, 2015, 42(8): 90-94. |
| [10] |
赫阳. 基于无线传感器的电磁频谱监测网络研究与仿真[D]. 西安: 西安电子科技大学, 2012. HE Yang. Research and simulation of electromagnetic spectrum monitoring network based on wireless sensor[D]. Xi'an: Xidian University, 2012. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2068484 |
| [11] |
VINCENT S, ALEXANDRE S, YVES L. Theoretical bit error floor analysis of 16-QAM OFDM signal with channel estimation using polynomial interpolation[J]. IET Signal Processing, 2016, 10(3): 254-265. DOI:10.1049/iet-spr.2015.0099 |
| [12] |
ARSHAD A, AUGUSTINE I, BAMIDELE A, et al. Location prediction optimisation in WSNs using kriging interpolation[J]. IET Wireless Sensor Systems, 2016, 6(3): 74-81. DOI:10.1049/iet-wss.2015.0079 |
| [13] |
MRINMOY S, INDRAJIT B, MAINAK C, et al. A node deployment mechanism accounting into received signal strength and frequency diversity for a wireless sensor network[C]//2016 IEEE SENSORS. Orlando: IEEE Press, 2016: 1-3. http://ieeexplore.ieee.org/abstract/document/7808923/
|
| [14] |
EVANGELOS Z, DIMITRIS T, ADRIAN M, et al. Multiterminal source coding with copula regression for wireless sensor networks gathering diverse data[J]. IEEE Sensors Journal, 2017, 17(1): 139-150. |
| [15] |
KOYA S, TAKEO F. Kriging-based interference power constraint:Integrated design of the radio environment map and transmission power[J]. IEEE Trans. on Cognitive Communications and Networking, 2017, 3(1): 13-25. DOI:10.1109/TCCN.2017.2653189 |
| [16] |
SONG X, MIHAI R, JAN K S. Adaptive weighted expected improvement with rewards approach in kriging assisted electromagnetic design[J]. IEEE Trans. on Magnetics, 2013, 49(5): 2057-2060. DOI:10.1109/TMAG.2013.2240662 |
| [17] |
KURT D, MILOS M. Wireless sensor networks:node localization for various industry problems[J]. IEEE Trans. on Industrial Informatics, 2015, 11(3): 752-762. DOI:10.1109/TII.2015.2396007 |
| [18] |
JIANG Q, MA Y, LIU K, et al. A probabilistic radio map construction scheme for crowdsourcing-based fingerprinting localization[J]. IEEE Sensors Journal, 2016, 16(10): 3764-3774. DOI:10.1109/JSEN.2016.2535250 |
| [19] |
WU Q, ZHOU D X. SVM soft margin classifiers:linear programming versus quadratic programming[J]. Neural Computation, 2005, 17(5): 1160-1187. DOI:10.1162/0899766053491896 |
| [20] |
刘扬, 鲁乃唯, 蒋友宝. 结构体系可靠度分析的改进支持向量回归[J]. 浙江大学学报:工学版, 2015, 49(9): 1692-1699. LIU Yang, LU Nai-wei, JIANG You-bao. Adaptive support vector regression method for structural system reliability analysis[J]. Journal of Zhejiang University:Engineering Science, 2015, 49(9): 1692-1699. |
| [21] |
NORIKAZU T, JUN G, TETSUO N. Global convergence of SMO algorithm for support vector regression[J]. IEEE Trans. on Neural Networks, 2008, 19(6): 971-982. DOI:10.1109/TNN.2007.915116 |
| [22] |
SHAHABODDIN S, DALIBOR P, HOSSEIN J, et al. Sensor data fusion by support vector regression methodology:a comparative study[J]. IEEE Sensors Journal, 2015, 15(2): 850-854. DOI:10.1109/JSEN.2014.2356501 |
| [23] |
李明山, 王正明, 张仪. 基于均匀试验设计的支持向量回归参数选择方法[J]. 系统仿真学报, 2008, 20(8): 2195-2199. LI Ming-shan, WANG Zheng-ming, ZHANG Yi. New method for selecting parameters of support vector machine regression based on uniform design[J]. Journal of System Simulation, 2008, 20(8): 2195-2199. |
| [24] |
周倜. 海战场电磁态势生成若干关键技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2013. ZHOU Ti. Research on several key techniques of electromagnetic situation generation in sea battlefield[D]. Harbin: Harbin Engineering University, 2013. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D429694 |
| [25] |
曹诗卉, 亓迎川. 基于最小二乘法平面拟合的点云法矢算法[J]. 空军预警学院学报, 2016, 30(1): 41-43. CAO Shi-hui, QI Ying-chuan. Point cloud normal vector algorithm using least squares planar fitting[J]. Journal of Air Force Early Warning Academy, 2016, 30(1): 41-43. |
| [26] |
陈丽, 陈静, 高清涛, 等. 基于支持向量机与反K近邻的分类算法研究[J]. 计算机工程与应用, 2010, 46(24): 135-137. CHEN Li, CHEN Jing, GAO Qing-tao, et al. Classification algorithm research based on support vector machine and reverse K-nearest neighbor[J]. Computer Engineering and Applications, 2010, 46(24): 135-137. DOI:10.3778/j.issn.1002-8331.2010.24.041 |



