轮式倒立摆是典型的欠驱动系统[1], 因其非线性、多耦合、多变量、本征不稳定等特性备受学术界关注, 研究核心在于机器人直立平衡控制问题.学者们从不同角度进行了深入研究, 并给出了各自解决方法.Pathak等[2]证明轮式倒立摆的强可达性, 采用局部线性反馈方法, 设计出控制直立和转向的双层控制器.Ren等[3]对简化的两轮机器人模型进行分析, 在传统PID的基础上, 借鉴神经网络的级联思想, 设计NN型自适应PID算法, 来减弱干扰和参数多变的影响.Brisilla等[4]通过对轮式倒立摆的非线性模型分析, 建立含有4个未知参量的非线性控制策略.Xu等[5]在不建立模型的情况下, 以模糊逻辑为控制器结构, 模糊控制规则由人工根据经验设计, 该方法能抵制坡度干扰.Raffo等[6]针对鲁棒性, 从博弈角度出发建立算法, 能够在极端情况下实现自平衡控制.Kim等[7]建立了一种非线性的自适应算法, 用于自平衡的控制.常规控制器大都依赖于设计者经验, 控制器的鲁棒性与自适应性受到限制.针对此问题, 构建使机器人自主学习的控制器是一种新思路.目前, 以心理学具身性[8-9]效应为基本原理的人工智能算法能够使机器人和环境交互后自主获取控制规则, 拥有自主学习认知能力.
反应式控制是一种具有涌现能力的机器人控制方法[10-11].Kroemer等[12]将强化学习与反应式控制结合, 使机器臂学会抓取物品.Baklouti等[13]建立了一种多层反应式控制结构, 能使轮椅学会跟踪等活动.Ruan等[14-15]将反应式控制用于自平衡机器人控制.学习自动机组[16]由多个学习自动机[17]单元组成, 可作为知识表达方式[18], Hashemi[19]将其用于优化PID参数, 用于自动电压调节系统的控制.甘晓琴等[20]将其用于仿人智能的研究.
不确定性动机(uncertainty motivation, UM)[21-22]是描述趋向于探索新颖性的一种内在动机(intrinsic motivation, IM), 是心理学概念.具体来讲, 人们的先验知识越少, 行为不确定性越大, 越不会循规蹈矩, 更加愿意自发地探索新的行为, 从而创造出新方法与新思路. Baldassarre等[23-24]对大量内在动机学习应用实例进行分析, 指出内在动机能使学习系统获取所需技能.Salgado等[25]将内在动机驱动认知模型用于机器人目标识别技能的学习, 实验表明该方法能使机器人自主学习.
本文从认知机器人领域出发, 把连续动作自动机组作为知识结构, 引入不确定性动机, 建立内在动机驱动的学习机制, 使机器人与环境多次交互后, 自主学习涌现出直线运动平衡控制规则.
1 轮式倒立摆的组成与模型 1.1 轮式倒立摆的组成实验涉及的轮式倒立摆以课题组自主设计的平衡车为参考, 设计转配图如图 1所示, 由2个车轮、底盘构架、上部配重、2个带有减速器的电机(简称电机)、电池和控制电路等组成.

|
图 1 轮式倒立摆(WIP)装配图 Fig. 1 Assembly drawing of wheel inverted pendulum (WIP) |
电机、电池和控制电路构成轮式倒立摆的电气系统, 其余部分构成机械系统.电气系统通过算法控制2个车轮运动, 使机械系统处于平衡状态.所述控制算法是直线运动自平衡控制关键, 是本文讨论的重点.
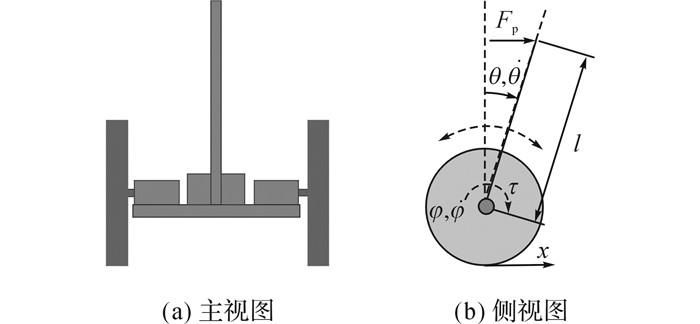
1.2 轮式倒立摆直线运动数学模型为降低直线运动数学模型方程复杂度, 需在保持运动和控制特性的情况下进行简化处理.针对实际轮式倒立摆质量分布不均匀引出的问题, 进行如下简化:假定其各个部分的质量成均匀(左右, 前后)对称分布, 且2个电机的参数相同, 如图 2(a)所示.以电机的转轴为分界点, 可将其分为2个部分, 左、右2个车轮组成一个部分, 剩余的部分可以简化为一个倒立摆.可对倒立摆进一步理想化为质量均匀分布的细杆, 其侧视图如图 2(b)所示.
|
图 2 轮式倒立摆的简化模型 Fig. 2 Simplified model of WIP |
采用拉格朗日方法建立轮式倒立摆直线运动模型.化简后的系统动能方程为
| $ \begin{array}{l} T = \left( {{M_{\rm{w}}} + \frac{1}{2}m} \right){{\dot x}^2} + {I_{\rm{w}}}{{\dot \varphi }^2} + \\ \;\;\;\;\;\;\frac{1}{2}ml\dot x\dot \theta \cos \theta + \frac{1}{6}m{l^2}{{\dot \theta }^2}; \end{array} $ | (1) |
系统的势能方程为
| $ U = \frac{1}{2}m\mathit{l}g\cos \theta . $ | (2) |
式中:x为轮式倒立摆直线运动的位移;φ为电机转子转动的角位移,
令L=T-U, f是轮子与地面的摩擦力, 可建立拉格朗日方程组:
| $ \left. \begin{array}{l} \frac{{\rm{d}}}{{{\rm{d}}t}}\frac{{\partial L}}{{\partial \dot \varphi }} - \frac{{\partial L}}{{\partial \varphi }} = 2\left( {\frac{1}{2}\tau - fr} \right),\\ \frac{{\rm{d}}}{{{\rm{d}}t}}\frac{{\partial L}}{{\partial \dot \theta }} - \frac{{\partial L}}{{\partial \theta }} = - \tau ,\\ \frac{{\rm{d}}}{{{\rm{d}}t}}\frac{{\partial L}}{{\partial x}} - \frac{{\partial L}}{{\partial x}} = 2f. \end{array} \right\} $ | (3) |
将式(1)和(2)代入式(3)后, 结合式x=rφ, 可得轮式倒立摆的直线运动的数学模型:
| $ \left. \begin{array}{l} \frac{1}{2}mrl\ddot \varphi \cos \theta + \frac{1}{3}m{l^2}\ddot \theta - \frac{1}{2}mgl\sin \theta = - \tau ,\\ \;\;\;\;\;\;\left( {2{M_{\rm{w}}}{{\rm{r}}^2} + m{r^2} + 2{I_{\rm{w}}}} \right)\ddot \varphi + \\ \;\;\;\;\;\;\frac{1}{2}mrl\ddot \theta \cos \theta - \frac{1}{2}mrl{{\dot \theta }^2}\sin \theta = \tau . \end{array} \right\} $ | (4) |
其中, r为车轮的半径, 取值为0.15 m.上述模型的参数是参考课题组研制的平衡车获得.
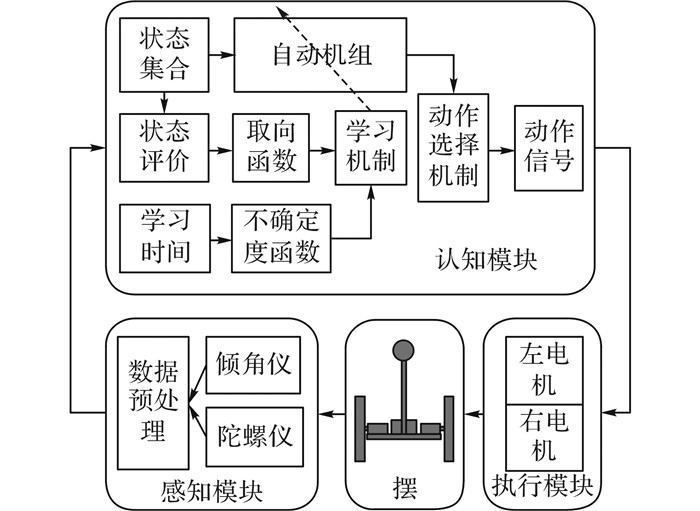
2 WIP-RCS结构所述轮式倒立摆反应式认知系统(wheeled inverted pendulum reactive cognitive system, WIP-RCS).WIP-RCS主要由感知模块、认知模块和执行模块3个模块组成, 此外还包括轮式倒立摆机械结构, 相互关系如图 3所示.
|
图 3 轮式倒立摆反应式认知系统结构简图 Fig. 3 Structure of wheeled inverted pendulum reactive cognitive system (WIP-RCS) |
感知模块获取轮式倒立摆传感器数据, 处理得到摆的状态信息并传递给认知模块;认知模块依据自动机组的映射得到动作信号, 传递给执行模块;执行模块控制电机转动使摆获取新状态, 再将新状态传递给认知模块;此时, 取向函数综合前、后2次的状态评价值, 得到取向值, 取向值与不确定度函数结合经过学习机制对自动机组中的映射关系进行调节, 使有利于摆自平衡的映射点被强化, 反之被减弱;依次往复, 逐渐使自动机组获取控制规则.
2.1 感知模块感知模块是WIP-RCS的输入层, 输入端连接外部环境, 输出端连接认知模块, 主要任务是对传感器的信号进行加工、融合、转换等处理, 获得系统的内部或外部状态, 并将其传递给认知模块.就所述轮式倒立摆而言, 此感知模块主要采用倾角仪和陀螺仪获取倾角和角速度的测量值, 用Kalman融合等算法对信号进行预处理后, 再经过单位换算, 得到轮式倒立摆的详细姿态信息.
2.2 认知模块认知模块是WIP-RCS的核心, 主要任务是获取和实施控制规则.以连续动作学习自动机组为模型, 可由8个单元组成:〈S, O, P, A, V, VS, UM, L〉.规定WIP-RCS从感知模块经过认知模块再到执行模块, 这一完整操作对应一个时刻t具体描述如下.
S:系统状态集合, 令si代表系统的第i状态, 则S={si, s2, …, si, …, sn}, n是状态数目, 由感知模块输出姿态信息离散化后获得.每个状态对应一个连续动作学习自动机, 构成有n单元的学习自动机组.定义s(t)∈S是在t时刻的状态.
O:系统的动作集合, O={o|o∈[omin, omax]}, 其中omin、omax分别输出的最小值和最大值, 定义o(t)为t时刻的动作输出.
P:系统分布函数集合, 令pi(a|ui, σi2)表示状态si对应自动机的分布函数, ui、σi2分别是期望和方差, 则P={pi(a|ui, σi2)|i=1, 2, 3, …, n}, a(t)是t时刻自动机依据概率分布pi(a|ui, σi2)随机选择的输出, 概率分布函数具体形式如下:
| $ {p_i}\left( {a\left| {{u_i},\sigma _i^2} \right.} \right) = \frac{1}{{{\sigma _i}\sqrt {2{\rm{ \mathsf{ π} }}} }}\int_{ - \infty }^a {\exp \left( { - \frac{{{{\left( {a - {u_i}} \right)}^2}}}{{2\sigma _i^2}}} \right){\rm{d}}a} . $ | (5) |
A:动作选择机制, 主要用来将自动机组的输出转换为可执行的动作信号o(t), 本系统主要采用线性化选择方式具体如下:
| $ o\left( t \right) = \left\{ \begin{array}{l} {o_{\min }},\;\;\;\;\;\;u\left( t \right) - a\left( t \right) > 3\sigma \left( t \right);\\ a\left( t \right),\;\;\;\;\;其他;\\ {o_{\max }},\;\;\;\;\;\;a\left( t \right) - u\left( t \right) > 3\sigma \left( t \right). \end{array} \right. $ | (6) |
其中, a(t)表示t时刻自动机的输出, u(t)、σ(t)分别是s(t)所对应自动机分布的期望和标准差.
V:系统状态的评价值, 由感知模块输出的姿态信息决定, 用来计算不确定度的值和取向函数的值, V(t)=vi(t)|i=1, 2, …, n}, vi(t)是t时刻状态si的评价值.设x(t)∈Rr是在t时刻感知模块输出的r维状态信息, 采用二次型进行评价值计算, 进而引入正定矩阵Qr×r, 称为状态评价矩阵, 则t时刻状态评价值为
| $ {v_i}\left( t \right) = \mathit{\boldsymbol{x}}{\left( t \right)^{\rm{T}}}\mathit{\boldsymbol{Qx}}\left( t \right). $ |
VS:取向函数, 由状态评价值决定, 用于评价动作的优劣, 指导P单元中的分布函数参数学习.假定t时刻所处的状态为si, 可得到该状态下的评价值vi(t), 系统操作o(t)后, 执行模块输出动作后, 在t+1时刻到状态sj, 新状态评价值vj(t+1), 取向函数为
| $ {V_{\rm{S}}}\left( {t + 1} \right) = {v_i}\left( t \right) - {v_j}\left( {t + 1} \right). $ |
该值大于0时说明动作有利, 反之亦然.
UM:为不确定度函数, 由系统的学习时间决定, 用来决定P单元中的标准差学习方向.随着时间增加, 系统的不确定动机总体下降, 本系统采用一种幅值随时间递减的波动函数来描述.设r(t)为第t时刻的不确定性值, 则动机可描述为:
| $ r\left( t \right) = \frac{{{\rm{rand}}\left( t \right)}}{{1 + {{\rm{e}}^{0.001 \times t}}}}, $ | (7) |
其中rand (t)∈(0, rm), 是均匀随机数发生器, rm是不确定系数的幅值, 代表不确定性的强度.
L:学习机制, 是更新自动机阵列中分布函数pi(a|ui, σi2)期望和方差的一套策略.在t时刻处于状态si, 以概率pi(a|ui, σi2)选择并执行的动作为o(t), 执行动作后在t+1时刻到达状态sj, 并计算得到取向值VS(t+1)和不确定性值r(t+1).定义ui(t)和σi(t)是第i状态在t时刻期望和标准差, 则期望采用以下公式进行学习:
| $ {u_i}\left( {t + 1} \right) = \left\{ \begin{array}{l} {u_i}\left( t \right) + \alpha \left( {o\left( t \right) - {u_i}\left( t \right)} \right),\;\;\;\;\;{V_{\rm{S}}}\left( {t + 1} \right) > 0;\\ {u_i}\left( t \right) + \alpha \left( { - o\left( t \right) + {u_i}\left( t \right)} \right),\;\;{V_{\rm{S}}}\left( {t + 1} \right) < 0. \end{array} \right. $ | (8) |
标准差以下公式进行学习:
| $ {\sigma _i}\left( {t + 1} \right) = {\sigma _i}\left( t \right) + \beta \left( {r\left( t \right) \times {\sigma _i}\left( t \right) - {\sigma _i}\left( t \right)} \right), $ | (9) |
| $ \alpha = \frac{1}{{1 + {{\rm{e}}^{ - \eta \times \left| {{V_{\rm{S}}}\left( {t + 1} \right)} \right|}}}} \in \left( {0,1} \right), $ | (10) |
其中η∈(0, 1)、β∈(0, 1)是学习系数, 值越大学习的越快, 但学习精度越低;反之亦然.
2.3 执行模块执行模块由2个直流电机、电机的驱动电路以及与直流电机相连接的车轮组成, 接收并执行认知模块的动作选择信号o(t), 再施加给环境, 系统通过控制电机的转速来驱动车轮运动, 进而使轮式倒立摆实现直线运动自平衡.
2.4 WIP-RCS的工作流程设t-1时刻状态s(t-1)=sj, x(t-1)为姿态信息, sj评价值为vj(t-1), o(t-1)是执行的操作.
1) 在时刻t, 感知模块得到轮式倒立摆姿态信息x(t)∈Rr, r是状态信息维度;
2) 认知模块引入感知模块的姿态信息x(t), 并进行离散化处理, 判定系统所处的离散状态s(t)∈S, 令s(t)=si;
3) 根据x(t)对当前状态进行评价, 得到状态的评价值vi(t), 进而计算出操作o(t-1)对应的取向函数值VS(t)和不确定度函数的值r(t);
4) 利用不确定度和取向值, 根据学习机制L, 更新t-1时刻所处状态s(t-1)=sj对应自动机单元pj(a|uj, σj2)中的参数uj和σj;
5) 状态si所对应自动机依照分布函数pi(a|ui, σi2)选中操作a(t), 并通过动作选择机制A输出动作信号o(t);
6) 将动作信号输出给执行模块, 与环境交互后进入到t+1时刻, 此时就完成了一个完整的操作流程, 以此周而往复, 直到学习得到满足要求的概率分布集合P, 并控制轮式倒立摆达到自平衡.
3 学习算法收敛性证明定理1:根据WIP-RCS的工作原理, 不确定度与系统的信息量成反比, 随着学习次数的增加不确定动机值应收敛到极小, 即满足关系:
| $ \mathop {\lim }\limits_{t \to \infty } r\left( t \right) \to 0. $ | (11) |
证明:
因为rand (t)∈(0, rm)是有界函数, 并且
| $ \mathop {\lim }\limits_{t \to \infty } \frac{1}{{1 + {{\rm{e}}^{0.001 \times t}}}} = 0, $ |
所以,
随着学习时间的增长, 不确定性逐渐趋近于零, 定理1证毕.
定理2:要使得该系统具有学习能力, 在学习算法的作用下, 每个状态si对应的自动机单元能够输出最优动作o′i(t)发生概率应趋近于1, 即
| $ \mathop {\lim }\limits_{t \to \infty } {p_i}\left( {{{o'}_i}\left( t \right)\left| {{s_i}} \right.} \right) \to 1. $ | (12) |
证明:结合标准差学习公式(11)和定理1可得
| $ \mathop {\lim }\limits_{t \to \infty } \frac{{{\sigma _i}\left( {t + 1} \right)}}{{{\sigma _i}\left( t \right)}} = \left( {1 - \beta } \right) + \mathop {\lim }\limits_{t \to \infty } r\left( t \right) = 1 - \beta \in \left( {0,1} \right), $ | (13) |
| $ \mathop {\lim }\limits_{t \to \infty } {\sigma _i}\left( t \right) = 0. $ | (14) |
根据自动机组期望学习算法及式(10)和(12), 得
当VS(t+1)>0, 且o(t)>ui(t)时, 此时动作o(t)有利于状态的改进, 可列出不等式:
| $ \left. \begin{array}{l} {u_i}\left( {t + 1} \right) > {u_i}\left( t \right) + 0 \times \left( {o\left( t \right) - {u_i}\left( t \right)} \right),\\ {u_i}\left( {t + 1} \right) < {u_i}\left( t \right) + 1 \times \left( {o\left( t \right) - {u_i}\left( t \right)} \right). \end{array} \right\} $ | (15) |
整理得
| $ {u_i}\left( t \right) < {u_i}\left( {t + 1} \right) < o\left( t \right), $ | (16) |
同理, 当VS(t+1)>0, 且o(t) < ui(t)时, 可以得到不等关系:
| $ {u_i}\left( t \right) > {u_i}\left( {t + 1} \right) > o\left( t \right). $ | (17) |
结论1:当VS(t+1)>0, 更新后的均值ui(t+1)趋向于有利于状态改进的o(t);
当VS(t+1) < 0且o(t) < ui(t)时, 此时动作o(t)不利于状态的改进, 可列出下列不等式组:
| $ \left. \begin{array}{l} {u_i}\left( {t + 1} \right) > {u_i}\left( t \right) + 1 \times \left( { - o\left( t \right) + {u_i}\left( t \right)} \right),\\ {u_i}\left( {t + 1} \right) < {u_i}\left( t \right) + 0 \times \left( { - o\left( t \right) + {u_i}\left( t \right)} \right). \end{array} \right\} $ | (18) |
整理可得
| $ 2 \times {u_i}\left( t \right) - o\left( t \right) < {u_i}\left( {t + 1} \right) < {u_i}\left( t \right), $ | (19) |
同理, 当VS(t+1) < 0, 且o(t)>ui(t)时,
| $ 2 \times {u_i}\left( t \right) - o\left( t \right) > {u_i}\left( {t + 1} \right) > {u_i}\left( t \right). $ | (20) |
结论2:当VS(t+1)>0, 更新后的均值ui(t+1)趋向于远离不利于状态改进的o(t).
综合结论1、2和定理1, 可知自动机以分布函数能够选择的动作趋近于一个确定的点, 即状态si自动机单元满足
WIP-RCS的输入量是倾角及其变化率, 即θ和
| 表 1 WIP-RCS状态划分 Table 1 State division of WIP-RCS |
此时, 状态信息的维度r=2, 实验参数设定如下:状态评价矩阵为Q2×2=[250, 0;0, 0.21], 不确定系数幅值rm=5, 学习系数η=0.9、β=0.000 1, 采样周期为5 ms;初始状态评价值和取向函数值都为0, 初始的电压值为0;每个自动机单元的均值为0, 标准差为5.令两电机电压同步.
4.1 学习能力验证为体现系统学习能力, 实验设定2种实验条件值.条件1:倾角和倾角变化率得初始值分别为θ=-0.2 rad、
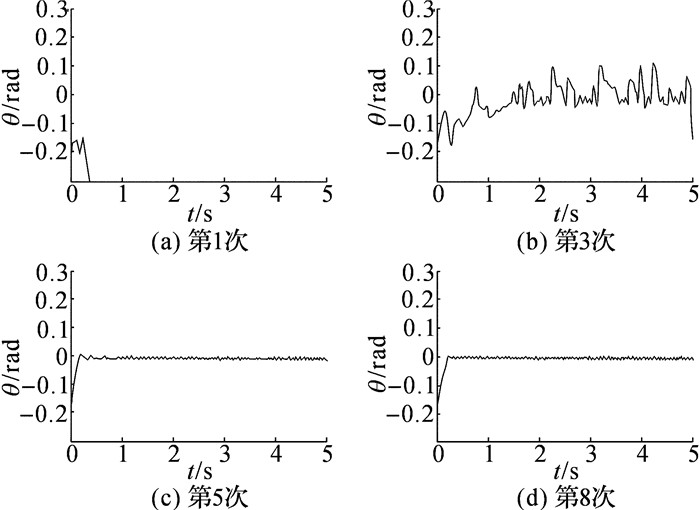
对于条件1, 轮式倒立摆第1次学习不足1 s时间, 发生倾倒;在第3次学习过程中, 倾角在附近大幅度摆动, 且有倾倒趋势;在第5次学习时, 经过0.5 s调节后, 倾角在小范围的保持稳定, 但在前0.5 s的执行过程中出现较小超调振荡;到第8次学习时, 在一定程度上减少了调节时间和超调幅度, 第1、3、5、8次学习的倾角变化如图 4所示.
|
图 4 条件1的倾角变化 Fig. 4 Inclination of case one |
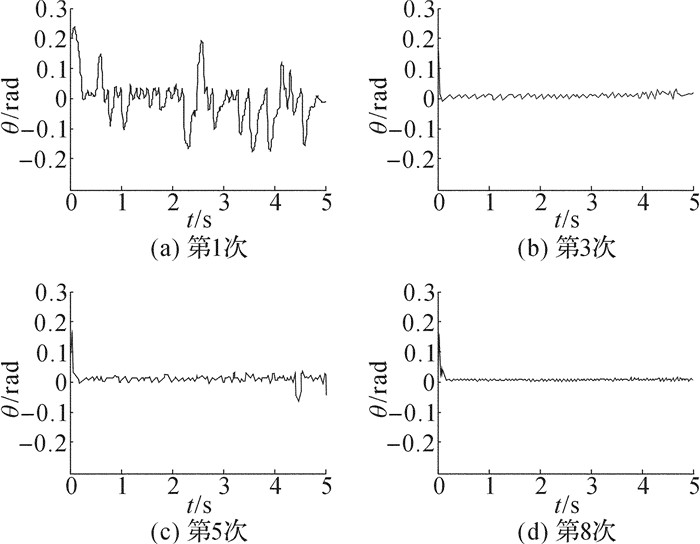
对于条件2情况下, 第1次学习过程中轮式倒立摆没有倾倒, 倾角在0附近大幅度震荡;第3、5次学习过程中能够在稍大的倾角范围保持稳定, 但偶尔出现震荡, 如第5次学习过程中4 s~5 s出现震荡;第8次学习时, 摆角在较小倾角变化范围内保持稳定, 且没有出现超调, 第1、3、5、8次学习过程倾角变化如图 5所示.
|
图 5 条件2的倾角变化 Fig. 5 Inclination of case two |
在这2种条件情况下, 随着学习次数的增加, 轮式倒立摆逐渐由倾倒变为直立平衡, 调节时间和超调量逐渐变小, 且稳定时控制精度精度逐渐提高可达0.01 rad.结果说明, 随着学习时间的增加, 系统通过与环境的多次交互, 获得足够的先验知识, 自主涌现出控制规则, 且控制效果越来越好.自动机组通过采用反应式结构与环境多次的交互, 在均值学习算法的支持下, 使得每个自动机单元获得一个最优值, 综合后自主涌现出控制规则;不确定性系数随时间的减少逐渐趋于0, 并引导自动机单元中的标准差逐渐趋近于0, 使实验中的倾角震荡逐渐减小, 对涌现出的控制规则进一步优化, 进而使调节时间、超调量和控制精度等控制指标得到优化.
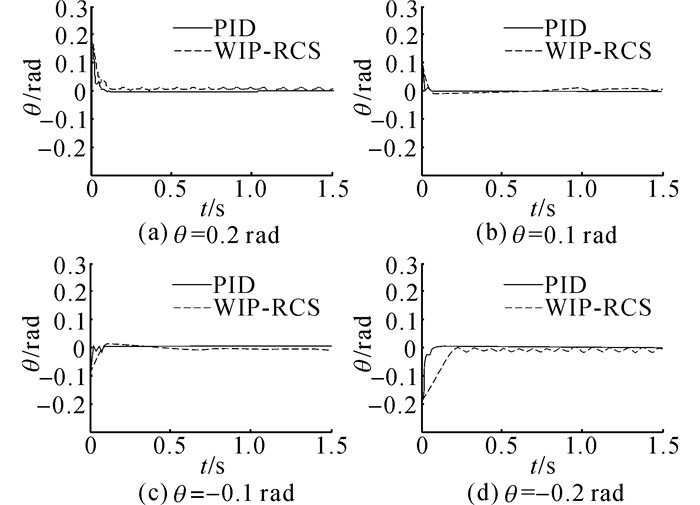
4.2 控制规则的控制能力验证为了验证WIP-RCS方法所获取的控制规律的控制能力, 将本文系统与常规的PID算法在不同偏离角的控制效果进行对比.首先, 让轮式倒立摆偏离角θ=0.2rad和-0.2rad的情况下, 采用WIP-RCS方法反复进行自主学习操作, 直到获得合理的控制规则;然后, 将规则分别在偏离角θ=0.2、0.1、-0.1、-0.2 rad的情况下进行自平衡控制实验, 并与PID对比.
实验过程中倾角变化如图 6所示, WIP-RCS获取的控制规则能够使轮式倒立摆在不同的偏离角下达到自平衡;与PID相比控制效果相当, 故WIP-RCS获取的控制规则具有较好的控制能力.
|
图 6 PID与WIP_PCS控制效果对比 Fig. 6 Comparison of control effect between PID and WIP_PCS |
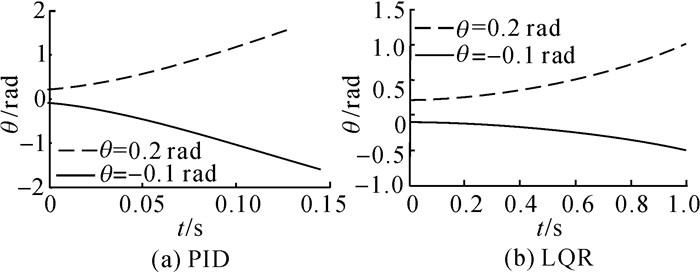
在现实轮式倒立摆的装配过程中, 往往会出现传感器安装不当等问题;在系统的运行过程中, 传感器结构或是电气电压的不稳定, 都会导致数据失真.文中就倾角仪安装错误的情况进行实验, 假设是倾角仪在前后方向反向安装的情况下, 将WIP-RCS与PID和LQR进行对比.首先在倾角仪前后正向安装的情况下设置好PID、LQR和WIP-RCS的参数, 这里WIP-RCS和PID的参数与4.2节中的设定值一致;然后, 模拟反向安装倾角仪, 即让传感器实际传递给控制器的倾角为θ′=-θ, 分别在偏离角为, θ=0.2rad和-0.1rad的偏离角下进行实验, 查看控制效果.
倾角仪反向后, 倾角仪检测的角度变化如图 7, 将PID和LQR分别实验15次, 在这15次中获得了相同的控制效果, 且都导致系统失控, 无法达到自平衡.主要原因在于PID和LQR的参数是基于具体模型设置的, 一旦被控对象结构发生巨大变化, 例如传感器反向安装, 原来的参数将不能维持控制器的控制能力.
|
图 7 倾角仪反向安装PID和LQR效果 Fig. 7 Control effect of PID and LQR for reverse inclinometer |
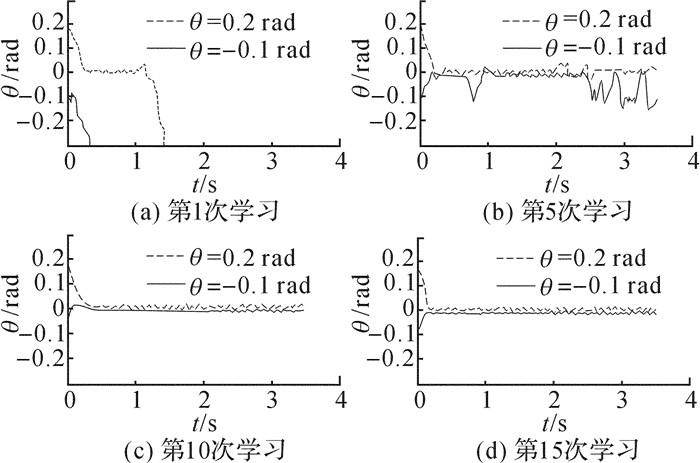
在WIP-RCS方法下, 倒立摆先是倾倒, 经过15次学习后, 倾角控制效果逐渐回复到反装前, 图 8记录了反装后第1、5、10、15次学习的倾角变化.其主要原因在于WIP-RCS方法是在学习理论的指导下建立的方法, 在具体的实施过程中对模型的依赖性低, 能够针对不同的“环境”自主涌现出新规则, 故WIP-RCS有较好的自适应性和鲁棒性.
|
图 8 倾角仪反向安装WIP-RCS方法 Fig. 8 Control effect WIP-RCS for reverse inclinometer |
本文提出了一种轮式倒立摆反应式认知系统WIP-RCS, 与环境交互后, 能够自主涌现出合理的控制规则.该系统的核心部件是自动机组和学习算法, 连续自动机组是WIP-RCS以知识的描述形式, 用以保证控制规则描述的简洁性;采用基于内在动机理论的不确定动机原理, 构建不确定动机驱动的学习算法, 并从理论上证明了该算法的收敛性.针对轮式倒立摆直立平衡控制问题, 通过仿真实验验证了轮式倒立摆系统的自主学习能力;并结合PID控制算法来验证所学习的控制规则的控制能力;在轮式倒立摆结构变化的情况下, 通过与PID和LQR的对比验证WIP-RCS对“环境”自适应能力和鲁棒性.对于该轮式倒立摆认知系统, 下一步的研究应实施到实际轮式倒立摆上, 并尝试完成不同的控制任务;理论研究应关注提高系统新规则涌现速度、控制精度、知识描述结构的简化和提高评价机制的合理性等方面.
| [1] |
GUO Z Q, XU J X, LEE T H. Design and implementation of a new sliding mode controller on an underactuated wheeled inverted pendulum[J]. Journal of the Franklin Institute, 2014, 351(4): 2261-2282. DOI:10.1016/j.jfranklin.2013.02.002 |
| [2] |
PATHAK K, FRANCH J, AGRAWAL S K. Velocity and position control of a wheeled inverted pendulum by partial feedback linearization[J]. IEEE Transactions on robotics, 2005, 21(3): 505-513. DOI:10.1109/TRO.2004.840905 |
| [3] |
REN T J, CHEN T C, CHEN C J. Motion control for a two-wheeled vehicle using a self-tuning PID controller[J]. Control Engineering Practice, 2008, 16(3): 365-375. DOI:10.1016/j.conengprac.2007.05.007 |
| [4] |
BRISILLA R M, ANKARANARAYANAN V. Nonlinear control of mobile inverted pendulum[J]. Robotics and Autonomous Systems, 2015, 70(C): 145-155. |
| [5] |
XU J X, GUO Z Q, LEE T H. Design and implementation of a Takagi-Sugeno-type fuzzy logic controller on a two-wheeled mobile robot[J]. IEEE Transactions on Industrial Electronics, 2013, 60(12): 5717-5728. DOI:10.1109/TIE.2012.2230600 |
| [6] |
RAFFO G V, ORTEGA M G, MADERO V, et al. Two-wheeled self-balanced pendulum workspace improvement via underactuated robust nonlinear control[J]. Control Engineering Practice, 2015, 44: 231-242. DOI:10.1016/j.conengprac.2015.07.009 |
| [7] |
KIM S, KWON S. Nonlinear optimal control design for underactuated two-wheeled inverted pendulum mobile platform[J]. IEEE/ASME Transactions on Mechatronics, 2017, PP(99): 1-1. |
| [8] |
BREAZEAL C, GRAY J, BERLIN M. An embodied cognition approach to mindreading skills for socially intelligent robots[J]. The International Journal of Robotics Research, 2009, 28(5): 656-680. DOI:10.1177/0278364909102796 |
| [9] |
PFEIFER R, LUNGARELLA M, ⅡDA F. Self-organization, embodiment, and biologically inspired robotics[J]. Science, 2007, 318(5853): 1088-1093. DOI:10.1126/science.1145803 |
| [10] |
TOPS M, BOKSEM M A S, QUIRIN M, et al. Internally directed cognition and mindfulness:An integrative perspective derived from predictive and reactive control systems theory[J]. Frontiers in Psychology, 2014, 5: s429. |
| [11] |
罗素, 诺维格. 人工智能: 一种现代方法: 第3版[M]. 殷建平, 祝恩, 刘越, 等译. 1版. 北京: 清华大学出版社, 2013: 831-832.
|
| [12] |
KROEMER O B, DETRY R, PIATER J, et al. Combining active learning and reactive control for robot grasping[J]. Robotics and Autonomous Systems, 2010, 58(9): 1105-1116. DOI:10.1016/j.robot.2010.06.001 |
| [13] |
BAKLOUTI E, AMOR N B, JALLOULI M. Reactive control architecture for mobile robot autonomous navigation[J]. Robotics and Autonomous Systems, 2017, 89: 9-14. DOI:10.1016/j.robot.2016.09.001 |
| [14] |
RUAN X G, CAI J X. Stochastic Fuzzy controller based on OCPFA and applied on two-wheeled self-balanced robot[M]. Berlin Heidelberg: Springer, 2009, 141-151.
|
| [15] |
任红格, 史涛, 张瑞成. 基于操作条件反射机制的感觉运动系统认知模型的建立[J]. 机器人, 2012, 34(3): 292-298. REN Hong-ge, SHI Tao, ZHANG Rui-cheng. Foundation of the sensorimotor system cognitive model with operant conditioning mechanism[J]. Robot, 2012, 34(3): 292-298. |
| [16] |
THATHACHAR M A L, SASTRY P S. Varieties of learning automata:an overview[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2002, 32(6): 711-722. DOI:10.1109/TSMCB.2002.1049606 |
| [17] |
GUO Y, GE H, LI S. A set of novel continuous action-set reinforcement learning automata models to optimize continuous functions[J]. Applied Intelligence, 2017, 46(4): 845-864. DOI:10.1007/s10489-016-0853-4 |
| [18] |
刘晓. 基于连续动作学习自动机的联想强化学习[J]. 山西大学学报:自然科学版, 2015, 38(3): 426-431. LIU Xiao. Associative reinforcement learning based on contiuous-action learning automata[J]. Journal of Shanxi University:Natural Science Edition, 2015, 38(3): 426-431. |
| [19] |
HASHEMI F, MOHAMMADI M. Combination continuous action reinforcement learning automata & pso for design of pid controller for avr system[J]. International Journal of Engineering-Transactions A:Basics, 2014, 28(1): 52. |
| [20] |
甘晓琴. 基于强化学习的仿人智能控制器参数在线学习与优化[D]. 重庆: 重庆大学, 2010: 26-61. GAN Xiao-qin. On-line human simulated intelligent control tuning using reinforcement learning[D]. Chongqing: Chongqing University, 2010: 26-61. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D179462 |
| [21] |
OUDEYER P Y, KAPLAN F. What is intrinsic motivation? A typology of computational approaches[J]. Frontiers in Neurorobotics, 2007, 1(6): 6. |
| [22] |
SIDDIQUE N, DHAKAN P, RANO I, et al. A review of the relationship between novelty, intrinsic motivation and reinforcement learning[J]. Paladyn Journal of Behavioral Robotics, 2017, 8(1). |
| [23] |
BALDASSARRE G, MIROLLI M, et al. Intrinsic motivations and open-ended development in animals, humans, and robots:an overview[J]. Frontiers in Psychology, 2014, 5(3): 985. |
| [24] |
HESTER T, STONE P. Intrinsically motivated model learning for developing curious robots[J]. Artificial Intelligence, 2017, 247: 170-186. DOI:10.1016/j.artint.2015.05.002 |
| [25] |
SALAGADO R, PRIETO A, BELLAS F, et al. Motivational engine with autonomous sub-goal identification for the multilevel darwinist brain[J]. Biologically Inspired Cognitive Architectures, 2016, 17: 1-11. DOI:10.1016/j.bica.2016.07.003 |



