2. 西南交通大学 综合交通运输智能化国家地方联合工程实验室, 四川 成都 610031
2. National United Engineering Laboratory of Integrated and Intelligent Transportation, Southwest Jiaotong University, Chengdu 610031, China
故障模式和影响分析(failure mode and effects analysis, FMEA)方法最初由美国航空航天局所提出, 旨在通过系统分析以实数1~10的形式评估潜在故障模式在频度(occurrence, O)、严重度(severity, S)和不易探测度(detection, D)3个风险因子下的实际表现情况, 三者相乘得到故障模式的风险优先值(risk priority number, RPN), 进而依据各个故障模式的RPN大小采取相应程度的安全控制措施.目前, FMEA方法作为最为有效的事故前预防方法之一, 已在航空航天业、核工业以及机械工业等领域的风险评估研究中发挥巨大效用[1-3], 确保其安全稳定的运作和发展, 但也逐渐显露出一些不足[4]:故障模式评估信息通常具有一定的不确定性, 难以由实数表征;将3种风险因子视为同等重要, 与实际情况不符;RPN计算模型缺乏理论依据, 信息融合过程不合理且易出现相同RPN以致故障模式风险顺序难以判断.
为了克服传统FMEA方法的不足, 众多理论与方法被广泛运用到改进研究之中.在故障模式评估信息方面, 国内外学者先后提出了基于三角模糊数[5]、直觉模糊数[6]、语义变量[7-8]以及置信结构[9]等信息形式的FMEA方法.此外, 粗糙集[3]、模糊粗糙集[10]、三角模糊软集[11]和犹豫模糊集[12]等信息载体也被用于表征FMEA中专家评估信息.然而, 目前尚未出现基于直觉模糊偏好信息的FMEA相关研究, 传统模糊偏好信息使用互补型0.1~0.9标度进行赋值[13], 并认为等级之间分布均匀, 这与部分实际情况(如:经济学中的边际效用递减率)相违背.Xia等[14]利用互反型1~9标度对偏好信息进行赋值, 提出直觉乘法集和直觉乘法偏好关系的概念, 其可同时表征专家对于不同方案间的偏好信息的隶属度、非隶属度和犹豫度.
在风险因子权重方面, 现有的风险因子权重确定方法主要有主观赋权法、客观赋权法和综合赋权法.其中, 主观赋权法一般是通过经验判断法[15]、改进层次分析法[16]或专家评估信息法[5]获取风险因子权重信息, 其简单实用, 但过于依赖专家本身知识经验, 未考虑故障模式评估信息在权重确定中的作用;客观赋权法充分利用故障模式评估信息, 结合其连续熵测度[6]、灰色关联改进熵测度[17]或通过信息集结算子自动生成[18]确定风险因子权重;而综合赋权法结合了主客观赋权法的特点, 较仅考虑单方面因素的赋权法更为准确, 且可根据专家对于评估信息的确定程度调整主客观权重比例, 灵活性和可操作性更强[19].在RPN模型改进方面, 由于FMEA本质是一种多属性决策问题, 层次分析法(analytic hierarchy process, AHP)[20]、TOPSIS[15]、折衷排序法[5]、决策试验和评价实验室(decision making trial and evaluation laboratory, DEMATEL)[19]和全乘比例分析多目标优化[6]等多属性决策方法被广泛用于FMEA研究以改进传统RPN的排序方法.其中, TOPSIS方法计算简便且应用灵活, 但传统TOPSIS方法中采用Euclidean距离度量备选方案与正、负理想解之间的距离将会导致最终排序结果出现偏差[21].为解决此问题, 刘小弟等[22]提出了备选方案和正、负理想解所形成向量的双向投影测度以对传统TOPSIS方法进行改进.
虽然, 当前FMEA研究在故障模式评估信息、风险因子权重和故障模式排序方法等3个方面均作出了一定改进.然而, 现有研究仍存在一些问题亟待解决:专家基本采用决策矩阵形式对不同故障模式在各风险因子下的具体表现进行评估, 忽视专家针对复杂对象直接量化评估时的盲目性和不准确性;所运用TOPSIS排序方法多为传统形式, 未对方法本身局限性进行改进;已有FMEA研究中未考虑专家评估信息和集结后的群体评估信息之间是否达成共识, 而在实际决策过程中, 难免出现部分偏离群体评估信息的极端信息, 若不进行修正将影响决策结果准确性[23].
综上所述, 本文提出一种考虑专家共识的改进FMEA风险评估方法:运用直觉乘法数同时表征专家对于故障模式在风险因子下的实际表现和风险因子重要程度的偏好信息;结合AHP法确定专家权重, 并运用直觉乘法加权平均(intuitionistic multiplicative weighted averaging, IMWA)算子对专家个体评估信息进行集结;分别提出直觉乘法数和直觉乘法偏好矩阵间的兼容测度, 检验群体偏好矩阵是否达到可接受共识条件以进行后续决策;充分考虑主客观因素, 构建专家评估信息法和理想解法相结合的综合赋权法获取风险因子权重信息;引入标准Manhattan距离, 克服传统TOPSIS方法的不足, 提出直觉乘法偏好关系背景下基于双向投影距离的TOPSIS方法对故障模式进行风险排序.最后, 以数控加工中心伺服系统FMEA为例, 验证方法的可行性和有效性.
1 直觉乘法偏好关系 1.1 直觉乘法数定义1[14] 设X是1个有限集合, 称D={〈x, ρD(x), σD(x)〉|x∈X}为直觉乘法集, 其中ρD(x)和σD(x)分别为元素x的隶属度和非隶属度信息, 且1/9≤ρD(x), σD(x)≤9, ρD(x)σD(x)≤1, ∀x∈X.此外, τD(x)=(ρD(x)σD(x))-1为元素x的犹豫度信息, 且1≤τD(x)≤92, ∀x∈X.为后续研究方便, 将直觉乘法数α简写为ρ, σ.
定义2[14] 设α1=(ρ1, σ1)和α2=(ρ2, σ2)为2个直觉乘法数, 且λ为任意大于0的实数, 则关于α1、α2和λ之间的运算规则为
| $ \begin{array}{l} {\alpha _1} \oplus {\alpha _2} = \\ \left( {\frac{{\left( {1 + 2{\rho _1}} \right)\left( {1 + 2{\rho _2}} \right) - 1}}{2},\frac{{2{\sigma _1}{\sigma _2}}}{{\left( {2 + {\sigma _1}} \right)\left( {2 + {\sigma _2}} \right) - {\sigma _1}{\sigma _2}}}} \right); \end{array} $ |
| $ \begin{array}{l} {\alpha _1} \otimes {\alpha _2} = \\ \left( {\frac{{2{\rho _1}{\rho _2}}}{{\left( {2 + {\rho _1}} \right)\left( {2 + {\rho _2}} \right) - {\rho _1}{\rho _2}}},\frac{{\left( {1 + 2{\sigma _1}} \right)\left( {1 + 2{\sigma _2}} \right) - 1}}{2}} \right); \end{array} $ |
| $ \lambda {\alpha _1} = \left( {\frac{{{{\left( {1 + 2{\rho _1}} \right)}^\lambda } - 1}}{2},\frac{{2{{\left( {{\sigma _1}} \right)}^\lambda }}}{{{{\left( {2 + {\sigma _1}} \right)}^\lambda } - {{\left( {{\sigma _1}} \right)}^\lambda }}}} \right); $ |
| $ \alpha _1^\lambda = \left( {\frac{{2{{\left( {{\rho _1}} \right)}^\lambda }}}{{{{\left( {2 + {\rho _1}} \right)}^\lambda } - {{\left( {{\rho _1}} \right)}^\lambda }}},\frac{{{{\left( {1 + 2{\sigma _1}} \right)}^\lambda } - 1}}{2}} \right). $ |
定义3[24] 设α1=(ρ1, σ1)和α2=(ρ2, σ2)为2个直觉乘法数, 且τ1和τ2分别为直觉乘法数α1和α2的犹豫度信息, 则2个直觉乘法数α1和α2之间的标准Manhattan距离为
| $ \begin{array}{l} d\left( {{\alpha _1},{\alpha _2}} \right) = \\ \;\;\;\;\frac{1}{4}\left( {\left| {{{\log }_9}\frac{{{\rho _1}}}{{{\rho _2}}}} \right| + \left| {{{\log }_9}\frac{{{\sigma _1}}}{{{\sigma _2}}}} \right| + \left| {{{\log }_9}\frac{{{\tau _1}}}{{{\tau _2}}}} \right|} \right). \end{array} $ | (1) |
基于直觉乘法数的标准Manhattan距离, 文献[24]提出了直觉乘法数的距离函数和精确函数, 以及直觉乘法数的比较方法.
定义4 设α=(ρ, σ)为1个直觉乘法数, 且τ为直觉乘法数α的犹豫度信息, 则其距离函数和精确函数分别为
| $ p\left( \alpha \right) = \frac{{1 - {{\log }_9}\sigma }}{{2 - {{\log }_9}\rho - {{\log }_9}\sigma }}; $ | (2) |
| $ q\left( \alpha \right) = 1 - \frac{1}{2}{\log _9}\tau . $ | (3) |
定义5 若α1和α2为2个直觉乘法数, 则
1) 若p(α1)>p(α2), 则α1>α2;
2) 若p(α1)=p(α2), 则当q(α1)>q(α2)时, α1>α2;当q(α1)=q(α2)时, α1=α2.
1.2 直觉乘法集成算子定义6[14] 设αi=(ρi, σi), i=1, 2, …, n为1组直觉乘法数, 且IMWA:[1/9, 9]n→[1/9, 9], 若
| $ {\rm{IMWA}}\left( {{\alpha _1},{\alpha _2}, \cdots ,{\alpha _n}} \right) = \mathop \oplus \limits_{i = 1}^n \left( {{w_i}{\alpha _i}} \right), $ | (4) |
则称IMWA为直觉乘法加权平均算子, 其中w=(w1, w2, …, wn)T为αi(i=1, 2, …, n)的权重向量, wi∈[0, 1]且
| $ {\rm{IMA}}\left( {{\alpha _1},{\alpha _2}, \cdots ,{\alpha _n}} \right) = \frac{1}{n}\mathop \oplus \limits_{i = 1}^n {\alpha _i}. $ | (5) |
定理1[14] 设αi=(ρi, σi), i=1, 2, …, n为1组直觉乘法数, w=(w1, w2, …, wn)T为αi(i=1, 2, …, n)的权重向量, wi∈[0, 1]且
| $ \begin{array}{l} {\rm{IMWA}}\left( {{\alpha _1},{\alpha _2}, \cdots ,{\alpha _n}} \right) = \\ \left( {\frac{{\prod\nolimits_{i = 1}^n {{{\left( {1 + 2{\rho _i}} \right)}^{{w_i}}} - 1} }}{2},\frac{{2\prod\nolimits_{i = 1}^n {{\sigma _i}^{{w_i}}} }}{{\prod\nolimits_{i = 1}^n {{{\left( {2 + {\sigma _i}} \right)}^{{w_i}}}} - \prod\nolimits_{i = 1}^n {{\sigma _i}^{{w_i}}} }}} \right). \end{array} $ | (6) |
假设存在由l位知识结构和领域经验不同的专家Dk(k=1, 2, …, l)组成的FMEA团队, Dk根据其经验学识在信息集结过程中被赋予相应权重λk>0, k=1, 2, …, l, 且满足
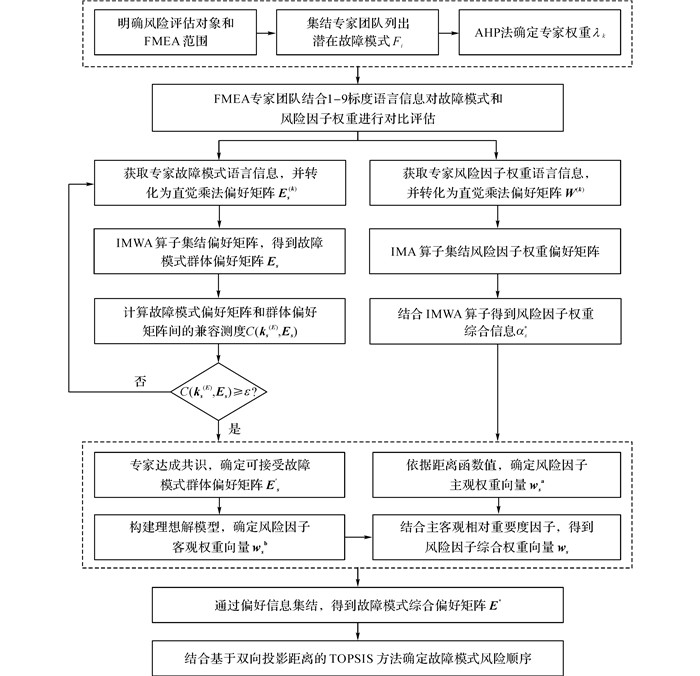
|
图 1 改进的故障模式和影响分析(FMEA)方法流程 Fig. 1 Flowchart of proposed failure mode and effects analysis (FMEA) approach |
FMEA团队针对故障模式和风险因子(频度、严重度和不易探测度)分别进行评估, 得到故障模式和风险因子权重偏好矩阵Es(k)和W(k).其中, αijs(k)和αst(k)的隶属度和非隶属度信息由D的判断依据互反型1-9标度确定, 如表 1所示, 介于表中语言信息之间的偏好信息可依据专家判断由对应标度之间任意量值表示, 而与表中语言信息相反描述的偏好信息所对应量值则为相对量值的倒数形式.
| 表 1 1-9标度语言信息 Table 1 Linguistic information of 1-9 scale |
依据专家知识结构和领域经验的不同由AHP法确定专家权重信息λk, 进而利用IMWA算子集结偏好矩阵Es(k), 由此得到故障模式群体偏好矩阵Es=(αijs)m×m, 其中αijs=(ρijs, σijs).
然而, 在实际决策问题中, FMEA团队成员通常具备不同的知识背景和工作经验, 其对于故障模式的认识各有不同, 极有可能出现部分专家偏好信息与群体偏好信息偏差过大的情况.此时, 若利用上述方法所集结的专家评估信息进行后续研究, 将影响最终故障模式风险排序的准确性.因此, 本文分别提出直觉乘法数和直觉乘法偏好矩阵之间的兼容测度, 以对各专家给出的故障模式偏好矩阵Es(k)和故障模式群体偏好矩阵Es分别进行兼容测度检验, 修正专家极端偏好信息, 以达到专家共识.
定义7 设α1=(ρ1, σ1)和α2=(ρ2, σ2)为2个直觉乘法数, 则α1和α2之间的兼容测度为
| $ C\left( {{\alpha _1},{\alpha _2}} \right) = 1 - d\left( {{\alpha _1},{\alpha _2}} \right). $ | (7) |
其中, d(α1, α2)为标准Manhattan距离, 则C(α1, α2)满足下列性质:
1) 0≤C(α1, α2)≤1;
2) C(α1, α2)=1, 当且仅当α1=α2时;
3) C(α1, α2)=C(α2, α1).
在直觉乘法偏好关系背景下的群体决策问题中, 专家通过对比方案xi和xj获取直觉乘法偏好矩阵A=(αij)m×m, 因此, 可根据偏好矩阵的上三角直觉乘法数之间的距离确定2个矩阵之间的兼容测度.
定义8 设A1=(αij1)m×m和A2=(αij2)m×m为2个直觉乘法偏好矩阵, 则A1和A2之间的兼容测度为
| $ C\left( {{\mathit{\boldsymbol{A}}^1},{\mathit{\boldsymbol{A}}^2}} \right) = 1 - \frac{2}{{n\left( {n - 1} \right)}}\sum\nolimits_{i = 1}^{m - 1} {\sum\nolimits_{j > i}^m {d\left( {\alpha _{ij}^1,\alpha _{ij}^2} \right)} } . $ | (8) |
其中, d(αij1, αij2)为标准Manhattan距离.
由此可知, 兼容测度可以表征2个不同直觉乘法偏好矩阵之间的差异, 定义直觉乘法偏好矩阵之间的可接受兼容测度, 若群体直觉乘法偏好矩阵和不同专家直觉乘法偏好矩阵之间的兼容测度均达到一定阀值, 则判定此时不同专家之间的偏好信息达到一定相近程度, 可继续进行后续决策.
定义9 设A1=(αij1)m×m和A2=(αij2)m×m为2个直觉乘法偏好矩阵, 若C(A1, A2)≥ε, 则判定A1和A2的兼容测度达到可接受条件.其中, ε∈(0, 1]为兼容测度的阀值.
综上所述, 按照下述步骤确定与Es(k)兼容测度可接受的故障模式群体偏好矩阵:
1) 考虑专家权重信息, 利用IMWA算子集结偏好矩阵Es(k), 得到故障模式群体偏好矩阵Es;
2) 分别计算故障模式群体偏好矩阵Es和偏好矩阵Es(k)之间的兼容测度C(Es(k), Es)(k=1, 2, …,l);
3) 依据决策本身重要程度确定兼容测度阀值ε, 若C(Es(k), Es)≥ε, 则判定偏好矩阵之间的兼容测度为可接受的, 可运用故障模式群体偏好矩阵Es进行后续决策;若至少存在k0∈{1, 2, …, l}使得C(Es(k0), Es) < ε, 则需对偏好矩阵Es(k0)中直觉乘法数进行修正, 即通过计算αijs(k0)∈Es(k0)和αijs∈Es之间的兼容测度C(αijs(k0), αijs), 确定兼容测度较小的直觉乘法数αijs(k0), 专家Dk0对其重新评估后返回第一步, 直至兼容测度满足C(Es(k), E′s)≥ε, 可运用故障模式群体偏好矩阵E′s=(α′ijs)m×m进行后续决策.
2.3 风险因子权重的确定综合考虑主客观因素, 通过专家评估信息法和理想解模型法相结合的综合赋权法确定风险因子权重.
首先, 利用IMA算子对风险因子权重偏好矩阵W(k)进行集结, 再考虑专家权重信息结合IMWA算子得到风险因子权重综合信息αs*, 依据其距离函数值的大小确定风险因子主观权重:风险因子权重综合信息距离函数值越大, 风险因子对风险排序影响越大, 权重越大;反之, 风险因子对风险排序影响越小, 权重越小.由式(2)求得风险因子权重综合信息距离函数值p(αs*), 确定风险因子主观权重:
| $ w_s^a = p\left( {\alpha _s^ * } \right)/\sum\nolimits_{s = 1}^n {p\left( {\alpha _s^ * } \right)} . $ | (9) |
其次, 当多属性决策问题中属性权重完全未知时, 若某一备选方案评估信息与理想解距离越小, 则该方案越好, 据此原则可确定使备选方案和理想解总距离最小的属性权重向量[25].因此, 令Fi关于Rs的偏好信息与理想解之间的距离为
| $ \begin{array}{*{20}{c}} {\min \bar f\left( w \right) = \sum\nolimits_{s = 1}^n {\sum\nolimits_{i = 1}^{m - 1} {\sum\nolimits_{j > i}^m {{{\left( {w_s^b} \right)}^2}{d^2}\left( {{{\alpha '}_{ij}},\beta } \right)} } } ,}\\ {{\rm{s}}.\;{\rm{t}}.\;\sum\limits_{j = 1}^n {w_s^b = 1} ,w_s^b \ge 0,s = 1,2, \cdots ,n.} \end{array} $ | (10) |
结合Lagrange方法求解该模型, 得出风险因子客观权重最优解并做归一化处理, 即
| $ \begin{array}{l} w_s^b = {\left( {\sum\nolimits_{s = 1}^n {{{\left( {\sum\nolimits_{i = 1}^{m - 1} {\sum\nolimits_{j > i}^m {{d^2}\left( {{{\alpha '}_{ij}},\beta } \right)} } } \right)}^{ - 1}}} } \right)^{ - 1}} \times \\ \;\;\;\;\;\;\;\;{\left( {\sum\nolimits_{i = 1}^{m - 1} {\sum\nolimits_{j > i}^m {{d^2}\left( {{{\alpha '}_{ij}},\beta } \right)} } } \right)^{ - 1}},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;s = 1,2, \cdots ,n. \end{array} $ | (11) |
最后, 集结风险因子主客观权重wsa={w1a, w2a, …, wna}和wsb={w1b, w2b, …, wnb}, 确定风险因子的综合权重ws={w1, w2, …, wn}, 即
| $ {w_s} = {\varphi _1}w_s^a + {\varphi _2}w_s^b. $ | (12) |
其中, φ1和φ2分别为主观和客观权重的相对重要度, 0≤φ1, φ2≤1, φ1+φ2=1, s=1, 2, …, n.进而, 结合达成专家共识后的故障模式群体偏好矩阵E′s, 利用IMWA算子进行信息融合, 由此得到故障模式综合偏好矩阵E*=(αij*)m×m, 其中αij*=(ρij*, σij*).
2.4 基于改进TOPSIS方法的故障模式风险排序传统TOPSIS方法通过计算备选方案和正、负理想评估值的Euclidean距离, 以与正理想值距离越近同时与负理想值距离越远的原则确定最优备选方案.然而, 与正理想值Euclidean距离更近的方案可能同时与负理想值的Euclidean距离也更近, 则不能全面反映备选方案的优劣性, 影响决策结果的准确性[21].文献[22]充分考虑正、负理想评估值与备选方案之间的关系, 提出了基于备选方案和正负理想值形成向量的双向投影TOPSIS方法.因此, 本文结合此思想构建一种改进TOPSIS方法以对故障模式进行风险排序.
根据故障模式综合偏好矩阵E*, 确定故障模式的正理想偏好值F+={αj+|j=1, 2, …, n}和负理想偏好值F-={αj-|j=1, 2, …, n}, 其中,
| $ \alpha _j^ + = \left( {\min \left( {\rho _{ij}^ * } \right),\max \left( {\sigma _{ij}^ * } \right)} \right),i = 1,2, \cdots ,n; $ | (13) |
| $ \alpha _j^ - = \left( {\max \left( {\rho _{ij}^ * } \right),\min \left( {\sigma _{ij}^ * } \right)} \right),i = 1,2, \cdots ,n. $ | (14) |
然后, 运用标准Manhattan距离确定正、负理想偏好值形成的向量F-F+, 负理想偏好值与Fi偏好值形成的向量F-Fi和Fi偏好值与正理想偏好值形成的向量FiF+, 分别为
| $ {\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}^ + } = \left\{ {d\left( {\alpha _1^ + ,\alpha _1^ - } \right),d\left( {\alpha _2^ + ,\alpha _2^ - } \right), \cdots ,d\left( {\alpha _j^ + ,\alpha _j^ - } \right)} \right\}; $ | (15) |
| $ {\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}_i} = \left\{ {d\left( {\alpha _1^ - ,\alpha _{i1}^ * } \right),d\left( {\alpha _2^ - ,\alpha _{i2}^ * } \right), \cdots ,d\left( {\alpha _j^ - ,\alpha _{ij}^ * } \right)} \right\}; $ | (16) |
| $ {\mathit{\boldsymbol{F}}_i}{\mathit{\boldsymbol{F}}^ + } = \left\{ {d\left( {\alpha _{i1}^ * ,\alpha _1^ + } \right),d\left( {\alpha _{i2}^ * ,\alpha _2^ + } \right), \cdots ,d\left( {\alpha _{ij}^ * ,\alpha _j^ + } \right)} \right\}. $ | (17) |
相应的模分别为
| $ \left| {{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}^ + }} \right| = \sqrt {\sum\nolimits_{j = 1}^n {{{\left( {d\left( {\alpha _j^ + ,\alpha _j^ - } \right)} \right)}^2}} } ; $ | (18) |
| $ \left| {{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}_i}} \right| = \sqrt {\sum\nolimits_{j = 1}^n {{{\left( {d\left( {\alpha _j^ - ,\alpha _{ij}^ * } \right)} \right)}^2}} } ; $ | (19) |
| $ \left| {{\mathit{\boldsymbol{F}}_i}{\mathit{\boldsymbol{F}}^ + }} \right| = \sqrt {\sum\nolimits_{j = 1}^n {{{\left( {d\left( {\alpha _{ij}^ * ,\alpha _j^ + } \right)} \right)}^2}} } , $ | (20) |
进而分别求得F-F+与F-Fi夹角的余弦和F-F+与FiF+夹角的余弦, 即
| $ \begin{array}{l} cos\left( {{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}^ + },{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}_i}} \right) = \\ \;\;\;\;\;\;\frac{{\sum\nolimits_{j = 1}^n {\left[ {d\left( {\alpha _j^ + ,\alpha _j^ - } \right)d\left( {\alpha _j^ - ,\alpha _{ij}^ * } \right)} \right]} }}{{\left| {{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}^ + }} \right|\left| {{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}_i}} \right|}}; \end{array} $ | (21) |
| $ \begin{array}{l} \cos\left( {{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}^ + },{\mathit{\boldsymbol{F}}_i}{\mathit{\boldsymbol{F}}^ + }} \right) = \\ \;\;\;\;\;\;\frac{{\sum\nolimits_{j = 1}^n {\left[ {d\left( {\alpha _j^ + ,\alpha _j^ - } \right)d\left( {\alpha _{ij}^ * ,\alpha _j^ + } \right)} \right]} }}{{\left| {{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}^ + }} \right|\left| {{\mathit{\boldsymbol{F}}_i}{\mathit{\boldsymbol{F}}^ + }} \right|}}. \end{array} $ | (22) |
确定负理想偏好值与Fi形成的向量在正负理想偏好值所形成的向量上的投影PF-F+(F-Fi), 以及正理想偏好值与Fi形成的向量在正负理想偏好值所形成的向量上的投影PF-F+(FiF+), 分别为
| $ \begin{array}{l} {P_{{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}^ + }}}\left( {{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}_i}} \right) = \left| {{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}_i}} \right|\cos \left( {{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}^ + },{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}_i}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\sum\nolimits_{j = 1}^n {d\left( {\alpha _j^ + ,\alpha _j^ - } \right)d\left( {\alpha _j^ - ,\alpha _{ij}^ * } \right)} }}{{\left| {{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}^ + }} \right|}}; \end{array} $ | (23) |
| $ \begin{array}{l} {P_{{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}^ + }}}\left( {{\mathit{\boldsymbol{F}}_i}{\mathit{\boldsymbol{F}}^ + }} \right) = \left| {{\mathit{\boldsymbol{F}}_i}{\mathit{\boldsymbol{F}}^ + }} \right|\cos \left( {{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}^ + },{\mathit{\boldsymbol{F}}_i}{\mathit{\boldsymbol{F}}^ + }} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\sum\nolimits_{j = 1}^n {d\left( {\alpha _j^ + ,\alpha _j^ - } \right)d\left( {\alpha _{ij}^ * ,\alpha _j^ + } \right)} }}{{\left| {{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}^ + }} \right|}}. \end{array} $ | (24) |
由此, 为确定故障模式风险排序, 构建如下贴近度公式:
| $ {C_{{F_i}}} = \frac{{{{\rm{P}}_{{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}^ + }}}\left( {{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}_i}} \right)}}{{{{\rm{P}}_{{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}^ + }}}\left( {{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}_i}} \right) + {{\rm{P}}_{{\mathit{\boldsymbol{F}}^ - }{\mathit{\boldsymbol{F}}^ + }}}\left( {{\mathit{\boldsymbol{F}}_i}{\mathit{\boldsymbol{F}}^ + }} \right)}},i = 1,2, \cdots ,n. $ | (25) |
贴近度CFi越大, 表明Fi实际表现越良好, 风险排序越低;反之, 表明Fi实际表现越差, 风险排序越高.
3 案例分析数控加工中心是由机械设备与数控系统组成的适用于加工复杂零件的高效率自动化机床, 是目前世界上产量最高、应用最广泛的数控机床之一, 其主要由数控装置、伺服系统、机床本体和刀库等4个部分组成.其中, 伺服系统起到精确地复现某个加工过程的反馈控制作用, 对于稳定性和精确度要求极高, Wang等[19]运用改进FMEA方法对数控加工中心的伺服系统进行风险评估, 确定了6个潜在故障模式, 即运动部件卡顿(F1)、复位不准确(F2)、紧固部件松动(F3)、运动部件间隙过大(F4)、机械振动(F5)、运动部件输出故障(F6).本节将在该研究基础之上, 运用考虑专家共识的改进FMEA风险评估方法对数控加工中心伺服系统的6个潜在故障模式进行风险排序.首先, 由4位知识结构和领域经验不同的专家(D1、D2、D3、D4)组成的FMEA团队, 其专家权重由AHP法确定, 即{0.260, 0.519, 0.140, 0.081}, 针对6个故障模式在频度、严重度和不易探测度下的实际表现运用直觉乘法数进行评估, 得到故障模式偏好矩阵Esk(原始矩阵在此省略).依据故障模式偏好矩阵EO(1)、EO(2)、EO(4)和EO(4), 利用IMWA算子对信息进行集结, 求得频度下故障模式群体偏好矩阵EO.进而利用定义8分别计算频度下故障模式偏好矩阵和群体偏好矩阵之间的兼容测度为C(EO(1), EO)=0.918 9, C(EO(2), EO)=0.967 9, C(EO(3), EO)=0.867 3, C(EO(4), EO)=0.942 2.由此可见, EO(4)和EO的兼容测度未达到可接受条件(本文案例中取ε值为0.9), 则计算EO(4)和EO中对应偏好值之间的兼容测度, 确定其中兼容测度较低的偏好值为C(α26O(4), α26O)=0.200 1, C(α34O(4), α34O)=0.207 7, C(α36O(4), α36O)=0.225 2, C(α45O(4), α45O)=0.220 0.因此, 通过专家D3的重新评估, 修正对应偏好值, 故障模式偏好矩阵由EO(4)变为E′O(3), 再次集结偏好矩阵EO(1)、EO(2)、E′O(3)和EO(4), 得到频度下故障模式群体偏好矩阵E′O.此时其与偏好矩阵EO(1)、EO(2)、E′O(3)和EO(4)之间的兼容测度分别为C(EO(1), E′O)=0.925 7, C(EO(2), E′O)=0.971 9, C(E′O(3), E′O)=0.902 0, C(EO(4), E′O)=0.945 2, 达到可接受条件, FMEA团队专家达成共识.按照类似步骤, 确定严重度和不易探测度下兼容测度可接受的故障模式群体偏好矩阵ES和ED.
其次, 4位专家针对频度、严重度和不易探测度对风险排序的重要程度运用直觉乘法数进行评估, 如表 2所示.利用IMA算子对偏好信息进行集结, 再得到风险因子权重综合信息αs*, 利用式(9)求得风险因子主观权重向量为wsa={0.339, 0.375, 0.286};根据故障模式群体偏好矩阵E′O、ES和ED, 构建理想解模型式(10), 求解模型得到风险因子客观权重向量为wsb={0.286, 0.433, 0.281}.本文将风险因子主客观权重视为同等重要, 即φ1=φ2=0.5, 确定风险因子综合权重向量为ws={0.312, 0.404, 0.284}.
| 表 2 风险因子权重直觉乘法偏好矩阵 Table 2 Intuitionistic multiplicative preference matrices of risk factor weights |
再次, 根据故障模式群体偏好矩阵E′O、ES和ED以及风险因子权重向量ws={0.312, 0.404, 0.284}, 利用IMWA算子集结偏好信息得到故障模式综合偏好矩阵E*为
| $ \begin{array}{l} {\mathit{\boldsymbol{E}}^ * } = \\ \left( {\begin{array}{*{20}{c}} {\left( {1,1} \right)}&{\left( {0.8461,0.8830} \right)}&{\left( {1.3432,0.6272} \right)}&{\left( {1.4168,0.5600} \right)}&{\left( {0.1836,4.3000} \right)}&{\left( {0.4551,2.0966} \right)}\\ {\left( {0.8830,0.8461} \right)}&{\left( {1,1} \right)}&{\left( {2.2481,0.4092} \right)}&{\left( {2.0480,0.4656} \right)}&{\left( {0.4054,2.2603} \right)}&{\left( {0.7540,1.1306} \right)}\\ {\left( {0.6272,1.3432} \right)}&{\left( {0.4092,2.2481} \right)}&{\left( {1,1} \right)}&{\left( {1.5109,0.5499} \right)}&{\left( {0.2461,3.8900} \right)}&{\left( {0.5428,1.7680} \right)}\\ {\left( {0.5600,1.4168} \right)}&{\left( {0.4656,2.0480} \right)}&{\left( {0.5499,1.5109} \right)}&{\left( {1,1} \right)}&{\left( {0.1704,4.8880} \right)}&{\left( {0.4806,1.8338} \right)}\\ {\left( {4.3000,0.1836} \right)}&{\left( {2.2603,0.4054} \right)}&{\left( {3.8900,0.2461} \right)}&{\left( {4.8880,0.1704} \right)}&{\left( {1,1} \right)}&{\left( {2.6768,0.3418} \right)}\\ {\left( {2.0966,0.4551} \right)}&{\left( {1.1306,0.7540} \right)}&{\left( {1.7680,0,5196} \right)}&{\left( {1.8338,0.4806} \right)}&{\left( {0.3418,2.6768} \right)}&{\left( {1,1} \right)} \end{array}} \right). \end{array} $ |
最后, 运用基于双向投影距离的TOPSIS方法对故障模式进行风险排序.根据故障模式综合偏好矩阵E*, 结合式(13)和(14)确定故障模式的正理想偏好值F+={αj+|j=1, 2, …, 6}和负理想偏好值F-={αj-|j=1, 2, …, 6}, 利用标准Manhattan距离求得正负理想偏好值形成的向量为F-F+={0.465 0, 0.389 8, 0.445 2, 0.402 7, 0.402 7, 0.412 8}, 其模为1.030 1.进而求得向量F-Fi和FiF+及其相应的模, 并结合式(21)~(24)求得投影PF-F+(F-Fi)和PF-F+(FiF+), i=1, 2, …, 6, 如表 3所示.结合式(25)求得故障模式偏好值与理想偏好值的贴近度分别为CF1=0.730 8, CF2=0.552 3, CF3=0.834 4, CF4=0.977 5, CF5=0, CF6=0.487 2, 确定故障模式风险排序为F5>F6>F2>F1>F3>F4.
| 表 3 改进TOPSIS中向量及其投影 Table 3 Vector and its projection in improved TOPSIS |
根据表 4中风险因子权重的变化信息, 对本文提出的基于直觉乘法偏好关系的FMEA风险评估结果进行灵敏度分析, 其中, Exp.1为综合赋权法求得的原始权重, Exp.2-Exp.4为其他可能出现的风险因子权重, 得到灵敏度分析结果如图 2所示.可以看出, 风险因子权重的变化对于故障模式最终风险排序有一定影响, 除了F5和F1风险顺序分别保持为第1和第4, 其余故障模式风险顺序均发生两次变化.例如当风险因子不易探测度的权重较高, 而风险因子频度和严重度的权重较低时, F4风险顺序由第6位上升至第5位, 这是由于F4在数控加工中心的伺服系统中检测率较低, 若侧重考虑不易探测度风险因子将导致其风险顺序上升.因此, 选取合适的方法确定风险因子权重信息显得尤为重要, 而本文提出的综合赋权法充分考虑专家意见和评估信息本身在权重确定中的作用, 使得风险顺序更为贴近实际.此外, 在本文提出的综合赋权法中, 假设主客观权重同等重要, 即φ1=φ2=0.5.在实际情况中, φ1和φ2的取值可由决策者确定, 当FMEA团队对于风险因子权重信息不太确定或者难以评估时, 应假设φ1<φ2;当FMEA团队对于风险因子权重的评估信息较为确定时, 应假设φ1>φ2.
| 表 4 主客观权重相对重要度灵敏度分析中的风险因子权重 Table 4 Risk factor weights in sensitivity analysis of relative importance factor for subjective and objective weights |
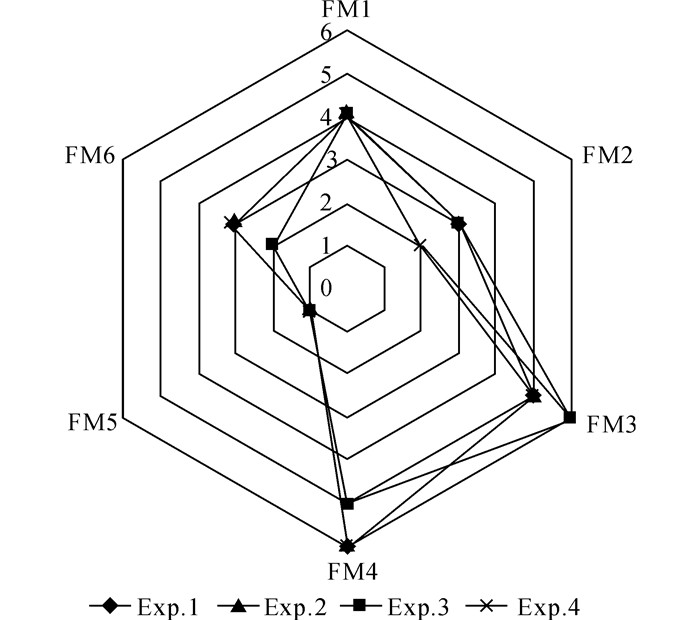
|
图 2 主客观权重相对重要度灵敏度分析结果 Fig. 2 Sensitivity analysis results of relative importance factor for subjective and objective weights |
为验证本文所提FMEA方法的可行性和有效性, 将本文案例故障模式风险排序结果与文献[24]提出的距离函数方法、文献[19]提出的DEMATEL方法计算得出的故障模式风险排序进行对比, 如表 5所示.其中, 距离函数方法沿用本文专家直觉乘法评估信息与风险因子权重;DEMATEL方法则采用文献[19]中的实数型评估信息, 运用熵权法和专家评估法综合确定风险因子权重.
| 表 5 不同方法的故障模式排序结果对比 Table 5 Comparison results of failure modes by different ranking methods |
由表中数据可以看出, 基于双向投影距离的改进TOPSIS方法的故障模式风险顺序与距离函数方法和DEMATEL方法结果一致, 表明该方法是可行的.与改进TOPSIS方法相比, 文献[24]中距离函数方法的故障模式风险排序是在运用IMA算子对故障模式综合偏好矩阵E*进行集结的基础上结合式(2)所得, 将会造成集结过程中偏好矩阵E*原始信息丢失, 且运用不同集结算子可能获得不同排序结果;文献[19]中DEMATEL方法中运用实数型故障模式评估信息, 并未充分考虑实际故障信息的不确定性与不完整性, 且在专家信息集结中未考虑专家共识是否达成, 在出现专家极端评估信息时会造成集结后的综合信息与实际情况出现出入, 影响故障模式排序准确性.同时, 改进TOPSIS方法的故障模式综合评估值较距离函数方法和DEMATEL方法区分度更为显著, 且在信息集结过程中能够修正专家极端评估信息对于决策结果的影响, 在风险因子权重确定时充分考虑主客观因素, 运用本文所提方法可有效地对故障模式进行风险排序.
4 结论(1) 为了将偏好信息拓展至FMEA方法研究之中, 利用直觉乘法数表征专家对于不同故障模式在风险因子下实际表现之间的偏好信息, 较已有FMEA研究中信息载体更为灵活, 且同时表达了偏好信息的隶属度和非隶属度, 有效刻画了专家评估信息的不确定性.
(2) 引入兼容测度对由IMWA算子集结的故障模式群体偏好矩阵进行兼容性检验, 并有针对性地修正偏好矩阵以达到兼容测度可接受条件, 专家达成共识, 有效避免了个别极端评估信息对决策结果的影响;提出了由专家评估法和理想解模型法组成的综合赋权法确定风险因子权重, 较仅考虑单方面因素的赋权法更为准确.
(3) 结合标准Manhattan距离构建了直觉乘法偏好关系背景下的基于双向投影距离的TOPSIS方法, 克服了传统TOPSIS方法的不足, 对故障模式综合偏好矩阵进行信息处理, 确定故障模式风险顺序.数控加工中心的伺服系统FMEA风险评估案例, 表明了本文方法的可行性和有效性.
目前, 企业风险评估专家团队规模日益扩大, 且知识结构和领域经验各有不同, 在未来FMEA研究中, 如何在存在专家评估信息缺失、评估信息形式繁杂或专家意见多极分化等情况下进行风险评估, 得到更为准确的故障模式风险排序需要进一步关注和拓展.
| [1] |
KUTLU A C, EKMEKÇIOLU M. Fuzzy failure modes and effects analysis by using fuzzy TOPSIS-based fuzzy AHP[J]. Expert Systems with Applications, 2012, 39(1): 61-67. |
| [2] |
LIU H C, LIU L, LI P. Failure mode and effects analysis using intuitionistic fuzzy hybrid weighted Euclidean distance operator[J]. International Journal of Systems Science, 2014, 45(10): 2012-2030. DOI:10.1080/00207721.2012.760669 |
| [3] |
SONG W, MING X, WU Z, et al. A rough TOPSIS approach for failure mode and effects analysis in uncertain environments[J]. Quality & Reliability Engineering International, 2014, 30(4): 473-486. |
| [4] |
LIU H C, LIU L, LIU N. Risk evaluation approaches in failure mode and effects analysis:a literature review[J]. Expert Systems with Applications, 2013, 40(2): 828-838. |
| [5] |
SAFARI H, FARAJI Z, MAJIDIAN S. Identifying and evaluating enterprise architecture risks using FMEA and fuzzy VIKOR[J]. Journal of Intelligent Manufacturing, 2016, 27(2): 475-486. DOI:10.1007/s10845-014-0880-0 |
| [6] |
ZHAO H, YOU J X, LIU H C. Failure mode and effect analysis using MULTIMOORA method with continuous weighted entropy under interval-valued intuitionistic fuzzy environment[J]. Soft Computing, 2016, 1-13. |
| [7] |
王晓暾, 熊伟. 基于DLOWG算子的FMEA风险评估方法[J]. 浙江大学学报:工学版, 2012, 46(1): 182-188. WANG Xiao-tun, XIONG Wei. Risk evaluation method in FMEA based on dependent linguistic ordered weighted geometric operator[J]. Journal of Zhejiang Univer-sity:Engineering Science, 2012, 46(1): 182-188. |
| [8] |
CHANG K H. Generalized multi-attribute failure mode analysis[J]. Neurocomputing, 2015, 175: 90-100. |
| [9] |
LIU H C, LIU L, BIAN Q H, et al. Failure mode and effects analysis using fuzzy evidential reasoning approach and grey theory[J]. Expert Systems with Applications, 2011, 38(4): 4403-4415. DOI:10.1016/j.eswa.2010.09.110 |
| [10] |
安相华, 于靖博, 蔡卫国. 基于混合多属性决策和关联分析的模糊粗糙FMEA评估方法[J]. 计算机集成制造系统, 2016, 22(11): 2613-2621. AN Xiang-hua, YU Jing-bo, CAI Wei-guo. Fuzzy rough FMEA evaluation method based on hybrid multi-attribute decision and correlative analysis[J]. Computer Integrated Manufacturing Systems, 2016, 22(11): 2613-2621. |
| [11] |
王浩伦, 徐翔斌, 甘卫华. 基于三角模糊软集的FMEA风险评估方法[J]. 计算机集成制造系统, 2015, 21(11): 3054-3062. WANG Hao-lun, XU Xiang-bin, GAN Wei-hua. Risk evaluation method in FMEA based on triangular fuzzy soft set[J]. Computer Integrated Manufacturing Systems, 2015, 21(11): 3054-3062. |
| [12] |
耿秀丽, 张永政. 基于犹豫模糊集的改进FMEA风险评估方法[J]. 计算机集成制造系统, 2017, 23(2): 340-348. GENG Xiu-li, ZHANG Yong-zheng. Improved FMEA approach for risk evaluation based on hesitant fuzzy set[J]. Computer Integrated Manufacturing Systems, 2017, 23(2): 340-348. |
| [13] |
徐泽水. AHP中两类标度法的关系研究[J]. 系统工程理论与实践, 1999, 19(7): 97-101. XU Ze-shui. Research on the relationship between the two kinds of scaling method in AHP[J]. System Engineering Theory and Practice, 1999, 19(7): 97-101. |
| [14] |
XIA M M, XU Z S, LIAO H C. Preference relations based on intuitionistic multiplicative information[J]. IEEE Transactions on Fuzzy Systems, 2013, 21(1): 113-133. DOI:10.1109/TFUZZ.2012.2202907 |
| [15] |
VAHDANI B, SALIMI M, CHARKHCHIAN M. A new FMEA method by integrating fuzzy belief structure and TOPSIS to improve risk evaluation process[J]. International Journal of Advanced Manufacturing Technology, 2015, 77(1-4): 357-368. DOI:10.1007/s00170-014-6466-3 |
| [16] |
BRAGLIA M. MAFMA:multi-attribute failure mode analysis[J]. International Journal of Quality & Reliability Management, 2000, 17(9): 1017-1033. |
| [17] |
TSAI T N, YEH J H. Identification and risk assessment of soldering failure sources using a hybrid failure mode and effect analysis model and a fuzzy inference system[J]. Journal of Intelligent & Fuzzy Systems, 2015, 28(6): 2771-2784. |
| [18] |
CHANG K H, CHENG C H. Evaluating the risk of failure using the fuzzy OWA and DEMATEL method[J]. Journal of Intelligent Manufacturing, 2011, 22(2): 113-129. DOI:10.1007/s10845-009-0266-x |
| [19] |
WANG X F, ZHANG Y Z, SHEN G X. An improved FMECA for feed system of CNC machining center based on ICR and DEMATEL method[J]. International Journal of Advanced Manufacturing Technology, 2016, 83(1-4): 43-54. DOI:10.1007/s00170-015-7551-y |
| [20] |
EKMEKÇIOLU M, KUTLU A C. A fuzzy hybrid approach for fuzzy process FMEA:an application to a spindle manufacturing process[J]. International Journal of Computational Intelligence Systems, 2012, 5(4): 611-626. DOI:10.1080/18756891.2012.718104 |
| [21] |
华小义, 谭景信. 基于"垂面"距离的TOPSIS法——正交投影法[J]. 系统工程理论与实践, 2004, 24(1): 114-119. HUA Xiao-yi, TAN Jing-xin. Revised TOPSIS method based on vertical projection distance-vertical projection method[J]. System Engineering Theory and Practice, 2004, 24(1): 114-119. |
| [22] |
刘小弟, 朱建军, 刘思峰. 犹豫模糊信息下的双向投影决策方法[J]. 系统工程理论与实践, 2014(10): 2637-2644. LIU Xiao-di, ZHU Jian-jun, LIU Si-feng. Bidirectional projection method with hesitant fuzzy information[J]. System Engineering Theory and Practice, 2014(10): 2637-2644. |
| [23] |
张世涛, 朱建军, 刘小弟. 基于重要度引导偏好识别修正的多粒度语言共识模型[J]. 控制与决策, 2015(9): 1609-1616. ZHANG Shi-tao, ZHU Jian-jun, LIU Xiao-di. Multi-granularity linguistic consensus model based on preferences identification and correction guided by importance degree[J]. Control and Decision, 2015(9): 1609-1616. |
| [24] |
JIANG Y, XU Z S, GAO M. Methods for ranking intuitionistic multiplicative numbers by distance measures in decision making[J]. Computers & Industrial Engineering, 2015, 88(C): 100-109. |
| [25] |
XU Z S. Models for multiple attribute decision making with intuitionistic fuzzy information[J]. International Journal of Uncertainty Fuzziness and Knowledge-Based Systems, 2011, 15(3): 285-297. |



