2. University of Southern California Biological Sciences Department, Los Angeles, CA 90089, USA
2. Biological Sciences Department, University of Southern California, Los Angeles, CA 90089, USA
自养生物在生长与繁殖过程中所合成与存贮的有机物质, 被称为初级生产力.在海洋中, 表层自养生物通过光合作用制造有机物质, 以满足自身新陈代谢和生态系统中异养生物的需求.这部分有机物质, 即初级生产力, 是维持海洋生态系统的基础, 也是构成大洋中生物地球化学循环及全球碳元素循环的重要组成部分.同时, 初级生产力量值受到海洋中各类物理过程(如涡旋、上升流以及混合作用)的影响[1], 并与光合作用中所涉及的叶绿素、溶解氧及其他生态要素浓度密切相关, 对海洋研究有重要意义.
受限于认知与技术手段, 海洋中初级生产力在时间与空间上的测量范围有限, 因此采用数值模拟手段可以对初级生产力的时空变化特征进行有效模拟与预测.Riley[2]最早提出关于海洋生态系统模型的概念;Dugdale等[3]以细分海洋中初级生产力来源推动模拟从简单箱式模型向复杂维度模型转变;Oschlies等[1]用耦合不同动力模型模拟北大西洋初级生产力量值, 证实了以不规则涡旋为代表的动力条件对水表初级生产力影响明显.此后初级生产力的研究重点逐渐向两极海域转移.Slagstad等[4]、Popova等[5]通过模拟北冰洋初级生产力, 指出水体混合作用、光照条件和营养盐分布是决定该海域初级生产力模拟结果的关键因素.
国内早期关于海洋初级生产力的研究仍以通过实测资料分析为主[6-7], 模拟应用起步较晚, 但近年也涌现了一批相关研究:于庆云[8]就切萨比克湾浮游植物动力学特征进行了数值分析;郭琳[9]通过POM-CoSiNE耦合模型对分析了加利福尼亚流独特的流场动力对生物要素的影响等.
尽管数值模拟是研究海洋初级生产力的常用手段, 但现有初级生产力模拟侧重于探索不同海域初级生产总量和长期可能的变化趋势, 缺乏对初级生产力季节性变化特征及生态模型本身特性的研究;同时较难解释初级生产力模拟结果难以匹配14C实际测量值[10-12]的原因.鉴此, 本文逐步优化生态模型, 以测试叶绿素浓度、浮游植物生长速率等生态因素对初级生产力模拟准确度的影响;对大洋站初级生产力季节性变化特征进行分析与归纳, 并探索模拟与实测数据出现差异的可能原因.
1 生态模型的构建与改进本文所用S海洋生态系统模型以Schmittner等[13]创建的生态模型(即原S模型)为基础加以改进而成, 共包含7个要素, 分别为:溶解氧(模型中以DO表示)、溶解无机氮(DIN)、溶解磷酸盐(PO4)、普通浮游植物(P)、固氮类浮游植物(Diazo)、浮游动物(Z), 以及颗粒有机碎屑(D).
为使S模型适应局部海域初级生产力模拟研究, 同时测试不同要素改变对初级生产力模拟可能产生的影响, 本文针对模型主要缺陷进行了逐步优化.
优化一:S模型不使用理想Redfield元素比值计算磷元素浓度.根据Monteiro等[14-15]研究结果, 在中低纬度附近表层以下区域磷元素的再矿化效率一般高于氮元素, 故氮元素为限制水表层初级生产的主要元素, 两者间元素比值也相应浮动.S模型通过对氮磷采用不同再矿化速率的方式, 分离2种限制性营养盐的循环, 有别于原模型以氮元素为踪素的循环体系, 提高水表附近氮与磷元素比, 以更接近实际分布.
优化二:修改浮游植物生长速率公式.原S模型所用浮游植物生长速率方程更重视营养盐浓度的变化, 忽略水温与光照强度的影响;根据Doney等[16-18]的模型说明, 这三者对浮游植物生长速率的影响基本一致.因此S模型通过修改浮游植物生产速率方程, 将光照强度、水温和营养盐浓度同时作为主要影响因子, 更符合实际生物过程.
优化三:增加叶绿素浓度的计算.Kiefer等[19]、Doney等[16]及Lee等[20]研究学者均在文中指出, 生态模型中主要光合作用过程应与叶绿素浓度直接相关, 而原S模型采用浮游植物浓度代替叶绿素浓度参与光合作用过程的方式, 容易忽略其他因素(例如营养盐浓度)对整个光合作用过程的影响, 并可能对模拟结果产生影响.针对这一缺陷, S模型引入与光强和营养盐浓度相关的浮游植物细胞内叶绿素浓度的计算, 更好还原了光合作用所涉及的生物过程.
优化后S模型中的普通浮游植物、固氮类浮游植物、浮游动物和碎屑要素,当以氮元素为示踪素时分别表示为PN、DiazoN、ZN和DN, 以氮浓度计算;而当磷为示踪素时分别表示为PP、DiazoP、ZP和DP,并以磷浓度计算,单位均为mmol·m-3.
预报变量的浓度变化如下:
| $ \frac{{\partial {c_x}}}{{\partial t}} = {R_x} + {S_x}. $ | (1) |
式中:cx为不同要素浓度(x为PN、DiazoN、DIN等);t为时间;Rx为包括对流、扩散在内的要素输移项, 是耦合时物理模块介入的关键点之一;Sx为各要素参与生物地球化学过程源汇项, 具体关系如图 1所示.
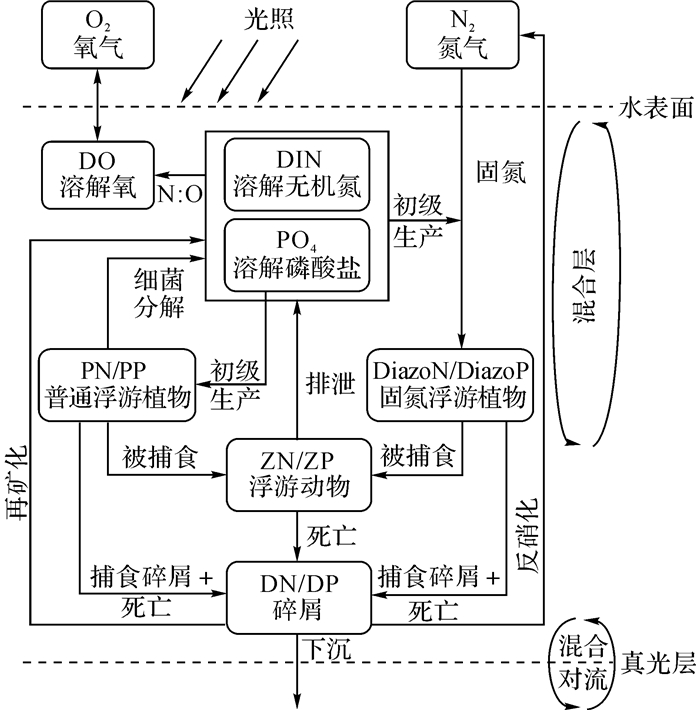
|
图 1 一维生态系统模型生物要素间关系 Fig. 1 1-D ocean ecosystem model schematic diagram |
以氮为示踪素的普通浮游植物源汇项可写为
| $ {S_{{\rm{PN}}}} = {J_{{\rm{PN}}}}{c_{{\rm{PN}}}} - {G_{{\rm{PN}}}}{c_{{\rm{ZN}}}} - {\mu _{{\rm{PN}}}}{\left( {{c_{{\rm{PN}}}}} \right)^2} - {\mu ^ * }{c_{{\rm{PN}}}}. $ | (2) |
式中:JPN为普通浮游植物的生长速率控制方程,GPN为浮游动物对普通浮游植物的捕食速率,μPN为普通浮游植物死亡率, 具体值见表 1;μ*为普通浮游植物通过微生物作用快速回归水体的分解速率.
| 表 1 生态系统模型常量 Table 1 Ecosystem model parameters |
作为模型的主要优化部分, 现生态模型中浮游植物生长速率取决于浮游植物的最大生长速率和水温、营养盐浓度及光照这3大限制因素, 其表达式为
| $ {J_{{\rm{PN}}}} = {J_{\rm{m}}}{\theta _{{\rm{PN}}}}{N_{{\rm{PN}}}}{L_{{\rm{PN}}}}. $ | (3) |
式中:Jm为浮游植物最大生长速率;θPN、NPN和LPN分别代表水温、营养盐浓度及光照强度对普通浮游植物的限制作用:
| $ {\theta _{{\rm{PN}}}} = \frac{1}{{1 + \exp \left( { - {\theta _{{\rm{aP}}}}\left( {\theta - {\theta _{{\rm{bP}}}}} \right)} \right)}}. $ | (4) |
| $ {N_{{\rm{PN}}}} = {\rm{Min}}\left[ {\frac{{{c_{{\rm{DIN}}}}}}{{{c_{{\rm{DIN}}}} + {k_{{\rm{DIN}}}}}},\frac{{{c_{{\rm{PO4}}}}}}{{{c_{{\rm{PO4}}}} + {k_{{\rm{PO4}}}}}}} \right]. $ | (5) |
| $ {L_{{\rm{PN}}}} = \frac{{{\theta _{{\rm{PN}}}}{N_{{\rm{PN}}}}{I_z}}}{{{k_{\rm{I}}}{\theta _{{\rm{PN}}}}{N_{{\rm{PN}}}}{I_z} + {I_z}}}. $ | (6) |
式中:θ为水温;θaP和θbP为分别表示普通浮游植物水温限制斜率与半饱和常数;kDIN和kPO4分别为营养盐半饱和常数;kI为光照半饱和常数;Iz为不同深度水体的光照强度, 随水深z衰退的指数变化式可写为
| $ {I_z} = {I_t}{P_0}\exp \left( { - {k_{\rm{w}}}z - {k_{{\rm{Chl}}}}\int\limits_0^z {{c_{{\rm{Chl}}}}{\rm{d}}z} } \right). $ | (7) |
式中:It为时刻t水表光照强度;P0为光合作用在可吸收光谱范围(350~700 nm)内光强占太阳入射水表光强的比例系数;kw和kChl分别为纯净海水与叶绿素存在导致的光强衰减系数;cChl为水体中叶绿素浓度.本模型参考Kiefer等[19]和Doney等[16]研究思路, 令叶绿素浓度与无机氮浓度、浮游植物浓度及光照强度均相关:
| $ {c_{{\rm{Chl}}}} = {R_{{\rm{Chl}}:{\rm{N}}}}\frac{{{c_{{\rm{DIN}}}}}}{{{c_{{\rm{DIN}}}} + {k_{{\rm{DIN}}}}}}\left( {{c_{{\rm{PN}}}} + {c_{{\rm{DiazoN}}}}} \right). $ | (8) |
式中:RChl:N为水体中叶绿素浓度和溶解无机氮浓度比, 即
| $ {R_{{\rm{Chl}}:{\rm{N}}}} = \left\{ {\begin{array}{*{20}{c}} {R_{{\rm{Chl}}:{\rm{N}}}^{{\rm{Max}}} - \frac{{{I_z}}}{{{I^ * }}}\left( {R_{{\rm{Chl}}:{\rm{N}}}^{{\rm{Max}}} - R_{{\rm{Chl}}:{\rm{N}}}^ * } \right),\;\;\;\;\;{I_z} < {I^ * };}\\ {R_{{\rm{Chl}}:{\rm{N}}}^ * ,\;\;\;\;\;\;{I_z} < {I^ * }.} \end{array}} \right. $ | (9) |
式中:RChl:NMax为在饱和营养盐浓度条件下随光照强度变化可能达到的细胞内叶绿素与氮浓度最大比, 取2.5;RChl:N*为在饱和光强与饱和营养盐浓度条件下细胞内叶绿素与氮浓度比值, 取1;I*为参照光强, 取90 W·m-2.
公式(2)中, 浮游动物对普通浮游植物捕食速率GPN和普通浮游植物快速分解速率可分别为
| $ {G_{{\rm{PN}}}} = {g_{\rm{m}}}\lambda \left( {1 - \exp \left( { - \lambda \left( {{c_{{\rm{PN}}}} + {c_{{\rm{DiazoN}}}}} \right)} \right)} \right){c_{{\rm{PN}}}}. $ | (10) |
| $ {\mu ^ * } = {\mu _0}\exp \left( {\frac{\theta }{{{\theta _{\rm{b}}}}}} \right). $ | (11) |
式中:gm为浮游动物最大捕食速率,λ为Ivlev捕食参数,μ0为营养盐快速回归速率,θb为水温控制常数, 具体数值见表 1.
以磷为示踪素的普通浮游植物源汇项可写为
| $ {S_{{\rm{PP}}}} = {R_{{\rm{P}}:{\rm{N}}}}{S_{{\rm{PN}}}}. $ | (12) |
式中:RP:N为磷氮元素比, 取值见表 1.
1.2 固氮类浮游植物以氮为示踪素的固氮类浮游植物源汇项写为
| $ {S_{{\rm{DiazoN}}}} = {J_{{\rm{DiazoN}}}}{c_{{\rm{DiazoN}}}} - {G_{{\rm{DiazoN}}}}{c_{{\rm{ZN}}}} - {\mu _{{\rm{DiazoN}}}}{c_{{\rm{DiazoN}}}}. $ | (13) |
式中:JDiazoN为固氮类浮游植物生长速率控制方程;GDiazoN为浮游动物对固氮类浮游植物的捕食速率;μDiazoN为固氮类浮游植物死亡率.
| $ {J_{{\rm{DiazoN}}}} = {f_{\rm{D}}}{J_{\rm{m}}}{\theta _{{\rm{DiazoN}}}}{N_{{\rm{DiazoN}}}}{L_{{\rm{DiazoN}}}}. $ | (14) |
式中:fD为固氮浮游植物阻碍生长系数;θDiazoN、NDiazoN与LDiazoN分别为水温、营养盐浓度及光照强度对固氮浮游植物的限制作用:
| $ {\theta _{{\rm{DiazoN}}}} = \frac{{{f_{\rm{D}}}}}{{1 + \exp \left( { - {\theta _{{\rm{aDiazo}}}}\left( {\theta - {\theta _{{\rm{bDiazo}}}}} \right)} \right)}}. $ | (15) |
| $ {N_{{\rm{DiazoN}}}} = \frac{{{c_{{\rm{PO4}}}}}}{{{c_{{\rm{PO4}}}} + {k_{{\rm{PO4}}}}}}. $ | (16) |
| $ {L_{{\rm{DiazoN}}}} = \frac{{{\theta _{{\rm{DiazoN}}}}{N_{{\rm{DiazoN}}}}{I_z}}}{{{k_1}{\theta _{{\rm{DiazoN}}}}{N_{{\rm{DiazoN}}}}{I_z} + {I_z}}}. $ | (17) |
式中:θaDiazo和θbDiazo分别表示固氮类浮游植物水温限制斜率与半饱和常数.
浮游动物对固氮类浮游植物的捕食速率GDiazoN可写为
| $ {G_{{\rm{DiazoN}}}} = {g_{\rm{m}}}\lambda \left( {1 - \exp \left( { - \lambda \left( {{c_{{\rm{PN}}}} + {c_{{\rm{DiazoN}}}}} \right)} \right)} \right){c_{{\rm{DiazoN}}}}. $ | (18) |
以磷为示踪素的固氮类浮游植物源汇项写为
| $ {S_{{\rm{DiazoP}}}} = {R_{{\rm{P}}:{\rm{N}}}}{S_{{\rm{DiazoN}}}}. $ | (19) |
以氮为示踪素的浮游动物源汇项可写为
| $ {S_{{\rm{ZN}}}} = {\gamma _1}\left( {{G_{{\rm{PN}}}} + {G_{{\rm{DiazoN}}}}} \right){c_{{\rm{ZN}}}} - {\gamma _2}{c_{{\rm{ZN}}}} - {\mu _{{\rm{ZN}}}}{\left( {{c_{{\rm{ZN}}}}} \right)^2}. $ | (20) |
式中:γ1为浮游动物捕食吸收效率;γ2为浮游动物排泄速率,μZN为浮游动物死亡率, 数值见表 1.
以磷为示踪素的浮游动物源汇项可写为
| $ {S_{{\rm{ZP}}}} = {R_{{\rm{P}}:{\rm{N}}}}{S_{{\rm{ZN}}}}. $ | (21) |
以氮为示踪素的颗粒有机碎屑源汇项可写为
| $ \begin{array}{*{20}{c}} {{S_{{\rm{DN}}}} = \left( {1 - {\gamma _1}} \right)\left( {{G_{{\rm{PN}}}} + {G_{{\rm{DiazoN}}}}} \right){c_{{\rm{ZN}}}} + {\mu _{{\rm{PN}}}}{{\left( {{c_{{\rm{PN}}}}} \right)}^2} + }\\ {{\mu _{{\rm{DiazoN}}}}{c_{{\rm{DiazoN}}}} + {\mu _{{\rm{ZN}}}}{{\left( {{c_{{\rm{ZN}}}}} \right)}^2} - {\mu _{{\rm{DN}}}}{c_{{\rm{DN}}}} - {\omega _{{\rm{DN}}}}\frac{{\partial {c_{{\rm{DN}}}}}}{{\partial z}}.} \end{array} $ | (22) |
式中:ωDN为沉降速率;μDN为氮元素的再矿化速率, 该速率一般与水体温度相关, 即
| $ {\mu _{{\rm{DN}}}} = {R_{{\rm{CN}}}}\exp \left( {\theta /{\theta _{\rm{b}}}} \right). $ | (23) |
式中:RCN为氮元素再矿化作用的基础速率, 数值见表 1.
以磷为示踪素的颗粒有机碎屑源汇项可写为
| $ \begin{array}{l} {S_{{\rm{DP}}}} = {R_{{\rm{P:N}}}}\left( {\left( {1 - {\gamma _1}} \right)\left( {{G_{{\rm{PN}}}} + {G_{{\rm{DiazoN}}}}} \right){c_{{\rm{ZN}}}} + {\mu _{{\rm{PN}}}}{{\left( {{c_{{\rm{PN}}}}} \right)}^2} + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {{\mu _{{\rm{ZN}}}}{{\left( {{c_{{\rm{ZN}}}}} \right)}^2} + {\mu _{{\rm{DiazoN}}}}{c_{{\rm{DiazoN}}}}} \right) - {\mu _{{\rm{DP}}}}{c_{{\rm{DP}}}}. \end{array} $ | (24) |
式中:μDP为磷元素的再矿化速率, 即
| $ {\mu _{{\rm{DP}}}} = {R_{{\rm{CP}}}}\exp \left( {\theta /{\theta _{\rm{b}}}} \right). $ | (25) |
式中:RCP为磷元素再矿化作用的基础速率.
1.5 溶解无机氮溶解无机氮的源汇项可写为
| $ \begin{array}{l} {S_{{\rm{DIN}}}} = {\mu _{{\rm{DN}}}}{c_{{\rm{DN}}}} + {\mu ^ * }{c_{{\rm{PN}}}} + {\gamma _2}{c_{{\rm{ZN}}}} - {J_{{\rm{PN}}}}{c_{{\rm{PN}}}} - \\ \;\;\;\;\;\;\;\;\;\frac{{{c_{{\rm{DIN}}}}}}{{{c_{{\rm{DIN}}}} + {k_{{\rm{DIN}}}}}}{J_{{\rm{DiazoN}}}}{c_{{\rm{DiazoN}}}}. \end{array} $ | (26) |
溶解氧的源汇项可写为
| $ \begin{array}{l} {S_{{\rm{DO}}}} = - {R_{{\rm{O}}:{\rm{P}}}}\left( {{\mu ^ * }{c_{{\rm{PN}}}} + {\gamma _2}{c_{{\rm{ZN}}}} - {J_{{\rm{PN}}}}{c_{{\rm{PN}}}} - } \right.\\ \;\;\;\;\;\;\;\;\;\left. {{J_{{\rm{DiazoN}}}}{c_{{\rm{DiazoN}}}} + {\mu _{{\rm{DN}}}}{c_{{\rm{DN}}}}} \right). \end{array} $ | (27) |
式中:RO:P为氧磷元素比.
1.7 溶解磷酸盐溶解磷酸盐的源汇项可写为
| $ \begin{array}{l} {S_{{\rm{PO4}}}} = {R_{{\rm{P}}:{\rm{N}}}}\left( {{\mu ^ * }{c_{{\rm{PN}}}} + {\gamma _2}{c_{{\rm{ZN}}}} - {J_{{\rm{PN}}}}{c_{{\rm{PN}}}} - } \right.\\ \;\;\;\;\;\;\;\;\;\left. {{J_{{\rm{DiazoN}}}}{c_{{\rm{DiazoN}}}}} \right) + {\mu _{{\rm{DP}}}}{c_{{\rm{DP}}}}. \end{array} $ | (28) |
上述公式中所涉及常量的符号、取值和单位如表 1所示.
2 物理-生态耦合模型 2.1 物理模块鉴于海洋初级生产力主要发生在真光层附近, 耦合模型采用增加了对流-扩散方程的Gill-Turner(GT)混合层模型[21]作为驱动初级生产力的物理模块, 以准确构建混合层分布.该模型将混合层视为从上至下混合良好的水层, 其深度由水表热能输入导致的水体温度势能变化与水表动能输入导致的水体温度势能变化的平衡位置所决定[21-22].
GT模型的建立遵循3个主要假设[21]:1)所有水体混合能量均从水表进入;2)只有水温能决定水体密度变化;3)混合层搅动能量来源于风应力,并以温度势能形式存储于水体中.
鉴于GT模型视混合层内水体混合均匀, 其垂向水温分布θ可以表述为
| $ \theta = \left\{ \begin{array}{l} {\theta _{\rm{s}}},z \le h;\\ {\theta _{\rm{z}}},z > h. \end{array} \right. $ | (29) |
式中:θz为随水深z变化的垂线温度变化方程, θs为混合层范围内的一致水温, h为混合层深度.同理, 垂向单位水体内热容量H与温度势能P的定义如下:
| $ H = \int\limits_0^D {\theta {\rm{d}}z} . $ | (30) |
| $ P = \int\limits_0^D {z\theta {\rm{d}}z} . $ | (31) |
由水表热辐射及风力变化等导致的单位时间内热容量与温度势能的变化量可简化为与时间相关的函数:
| $ \frac{{{\rm{d}}H}}{{{\rm{d}}t}} = R\sin \omega t. $ | (32) |
| $ \frac{{{\rm{d}}P}}{{{\rm{d}}t}} = \left\{ {\begin{array}{*{20}{c}} {M,}&{\frac{{{\rm{d}}H}}{{{\rm{d}}t}} > 0\left( {热容上升阶段} \right);}\\ {M + \frac{1}{2}h\frac{{{\rm{d}}H}}{{{\rm{d}}t}},}&{\frac{{{\rm{d}}H}}{{{\rm{d}}t}} < 0\left( {热容下降阶段} \right).} \end{array}} \right. $ | (33) |
式中:t取值范围须包含一个完整热循环过程;ω为角速度;R为热能输入振幅;M为单位时间内水体由表面风应力输入的用于混合的动能.依照公式(32)与(33)可估算出不同海域模拟所需R和M值, 如表 2所示.
| 表 2 验证站点R和M值分布 Table 2 R and M values at BATS and HOT |
水温对流扩散方程可表示为
| $ \frac{{\partial \theta }}{{\partial t}} = - {\omega _{\rm{E}}}\frac{{\partial \theta }}{{\partial z}} + \frac{\partial }{{\partial z}}\left( {{k_{\rm{z}}}\frac{{\partial \theta }}{{\partial z}}} \right). $ | (34) |
式中:ωE为垂向上水体对流速度;kz为扩散系数.为简便计算, 不考虑由涡旋等流场变化导致的紊动, 水体垂向流速和扩散系数被设为固定值, 不随深度变化.
2.2 耦合模型的构建基于耦合模型建立的基本假设, 即各生物要素的物理混合过程要远快于生物反应过程, 耦合模型设定实施顺序为物理模块在前, 生态模块在后.在单位时刻, 首先将初始、边界及动力条件分别输入物理与生态模块;其次运行物理模型以计算水温和混合层分布;随后通过混合层深度计算结果将各生物要素在垂直方向上进行混合和重分布;最后将水温等其他相关计算条件输入生态系统模型, 从而模拟出各生物要素的分布变化.如此往复循环, 就构成物理-生态耦合模型, 如图 2所示.

|
图 2 耦合模型基本结构框图 Fig. 2 Basic structure of physical-biological coupled model |
参考混合层深度的变化范围, 本模型选择模拟深度为500 m, 保证模型边界不受混合层变动的影响.模型上下均为开边界, 允许能量及物质通过对流、扩散或下沉等动力作用进行交换.同时为在物质守恒和方向性上满足数值模拟要求, 采用二阶迎风差分显格式以提高计算速度.
包括物理及生物模块在内的整个耦合模型通过Mathematica二次开发平台(版本号10.0)自行编程加以实现.
源程序编写中统一采用i代表时间节点, Δt代表时间步长(4 h);垂直方向上采用两套空间网格以适应物理和生物过程的不同发生速率, 其节点记作j与jj, 分别将垂直深度500 m分为250层(即Δz1为2 m)和50层(Δz2为10 m), 通过满足Courant数条件(
一维物理模型中对流扩散方程的迎风差分格式为
| $ \begin{array}{l} \theta _j^{i + 1} = \theta _j^i - \frac{{\Delta t{\omega _{\rm{E}}}}}{{\Delta z}}\left( {\theta _j^i - \theta _{j - 1}^i} \right) + \\ \;\;\;\;\;\;\;\;\;\frac{{\Delta t{k_{\rm{z}}}}}{{\Delta {z^2}}}\left( {\theta _{j + 1}^i - 2\theta _j^i + \theta _{j - 1}^i} \right),{\omega _{\rm{E}}} \ge 0. \end{array} $ | (35) |
| $ \begin{array}{l} \theta _j^{i + 1} = \theta _j^i - \frac{{\Delta t{\omega _{\rm{E}}}}}{{\Delta z}}\left( {\theta _{j + 1}^i - \theta _j^i} \right) + \\ \;\;\;\;\;\;\;\;\;\frac{{\Delta t{k_{\rm{z}}}}}{{\Delta {z^2}}}\left( {\theta _{j + 1}^i - 2\theta _j^i + \theta _{j - 1}^i} \right),{\omega _{\rm{E}}} < 0. \end{array} $ | (36) |
生态系统模型的差分格式为
| $ c_{xj}^{i + 1} = c_{xj}^i + \Delta t\left( {R_{xj}^i + S_{xj}^i} \right). $ | (37) |
式(22)中沉积项
为对比要素改变对初级生产力最终模拟结果的影响, 本文根据生态模型的不同优化步骤设计了6个耦合模型, 如表 3所示.
| 表 3 根据优化步骤设计的不同耦合模型示意 Table 3 Different coupled models based on optimizationsteps |
模拟过程中涉及的初始条件所用数据来源为百慕大站与夏威夷大洋站通过CTD和Bottle实际测量结果, 边界条件所用数据来源为相应海域卫星数据, 具体如表 4所示, 表中Vwind为海表面10米处风速, HSSH为水表面高度.
| 表 4 耦合模型所用数据来源 Table 4 Field data source of initial and boundary conditions in coupled model |
耦合模型中通过物理模块获得的包括混合层深度与水温在内的物理动力分布, 对于耦合模型的正确建立有着重要影响.如图 3和4所示分别对比了百慕大站与夏威夷站多年平均水温剖面、水表温度及混合层深度h的实测值与模拟结果.
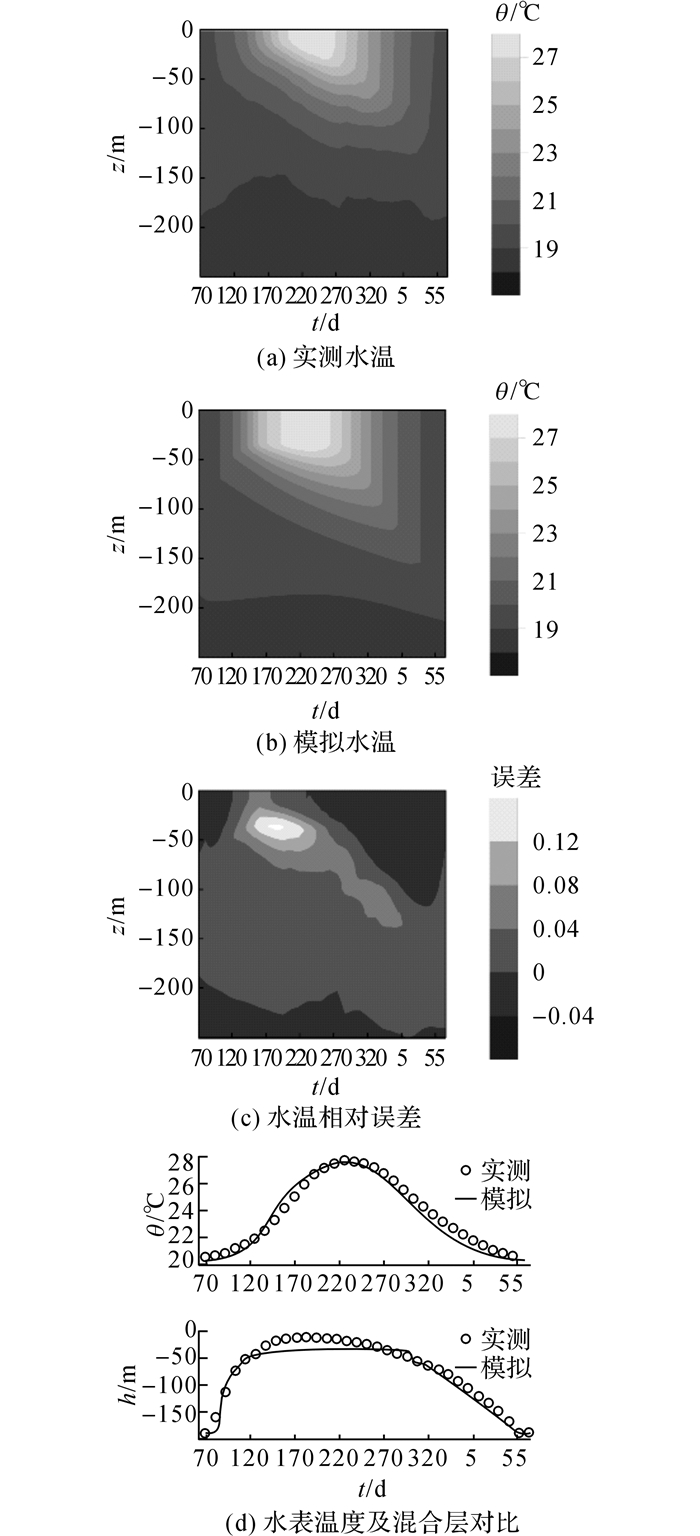
|
图 3 百慕大站多年平均水温剖面实测值与模拟结果对比 Fig. 3 Comparison of climatological field and simulated temperature profile at BATS |

|
图 4 夏威夷站多年平均水温剖面实测值与模拟结果对比 Fig. 4 Comparison of climatological field and simulated temperature profile at HOT |
如图 3(a)所示, 百慕大站多年平均实测水温剖面有显著的季节性变化特征:水表温度从春季19 ℃迅速上升至夏末27 ℃, 再以基本一致的速率于冬季下降至19 ℃.水表层下, 滞后于水表区域的水体升温速率, 和与水表保持一致的降温速率形成了图 3(a)由等温线构成的非对称V状分布.该等温线形状揭示了百慕大站混合层深度的季节性分布规律:冬季和初春深度大, 夏季基本接近表层水域, 季节间变化显著.
图 3(b)模拟结果把握了百慕大站多年平均水温与混合层主要分布特征, 包括水表温度和混合层深度的大规模季节性变化、一致的水表升降温速率及表层下水体升温的滞后效应等.而图 3(c)、(d)量化了实测与模拟之间存在的差异:在水表区域, 春、秋和冬季两者的水温分布差异百分比接近0;而在夏季, 两者的混合层深度与水温分布上存在的差异百分比约介于4%~12%范围内, 最大值接近16%, 仍在可接受范围之内.
如图 4(a)所示, 夏威夷站多年平均水温剖面分布季节性变化特征较弱:春初最低水表温度为23.5℃, 夏末最高水表温度26.5℃, 两者仅相差3 ℃.由于水表温度变化缓慢, 下层水体混合时间充足, 削弱了水体在升温期间发生的滞后效应.该站通过等温线呈现的混合层深度季节性变化同样较弱:春初最大值近100 m, 夏末最小值近50 m, 变化幅度较为有限.
图 4(b)模拟结果与实测水温剖面分布规律保持一致, 包括水表温度和混合层深度相应的季节性变化范围和表层下水体微弱的升温滞后效应.图 4(c)实测与模拟水温分布之间的差异百分比证实两者的吻合度高:在水表区域两者差异百分比基本为0, 表层以下水体差异百分比介于0%~4%之间.
总之, GT混合层模型对百慕大与夏威夷站水表温度与混合层深度变化的模型结果与实际分布吻合度较高, 说明该模型较准确地复制了大洋站水温分布的时空特征.
3.2 耦合模型验证与分析 3.2.1 百慕大站为直观表现生态模型采用不同优化步骤后对初级生产力模拟的准确程度, 本文采用泰勒图[23]对表 3中6个耦合模型所模拟百慕大站2002~2006年初级生产力垂直剖面分布与实测数据进行对比, 如图 5所示.
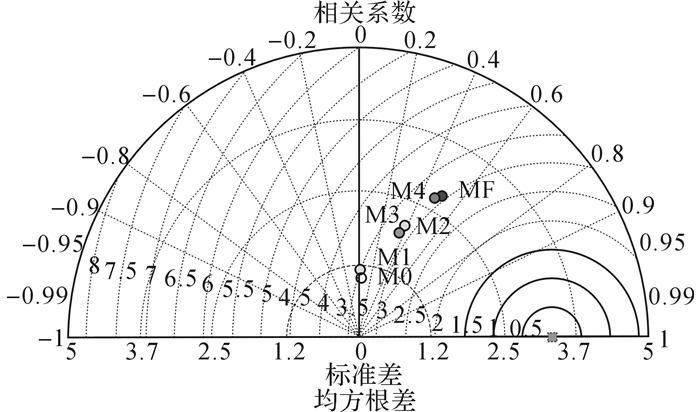
|
图 5 泰勒图对比百慕大站耦合模型优化结果 Fig. 5 Taylor Diagram of optimized coupled models' performance for 2002~2006 primary production distribution with respect to observations at BATS |
泰勒图采用3个标准衡量模型准确度, 分别为:模拟与实测数据的相关系数、标准差及均方根差.当泰勒图中相关系数越大、标准差越接近、均方根差越小, 模型的模拟准确度越高.
图 5显示了耦合模型MF所模拟2002~2006年初级生产力垂直剖面分布与14C实测数据分布的吻合度最高,即相关系数高于0.5、标准差与实测数据最接近、均方根差最小,证实了优化生态模型的可行性.耦合模型M0(以原始S生态模型为基础)和M1(只区分了氮磷循环)模拟初级生产力与实测数据的厢关关系均小于0.1, 吻合度很低.同时, 参考M2、M3及M4在泰勒图中的位置分布(相关系数介于0.4~0.5之间), 可断定修改浮游植物生长速率方程是最有效的优化手段, 而叶绿素浓度计算的介入对最终模拟准确度影响不大.
通过最终优化耦合模型MF模拟所得的百慕大站年平均初级生产力总量为11.3 mol·m-2, 与Doney等[16]和Oschlies等[1]提出的数据基本吻合, 证实了模型对初级生产力的量化较为准确.
如图 6所示为2002~2006年百慕大站海域水深0~140 m单位面积水体内每天初级生产力积分(
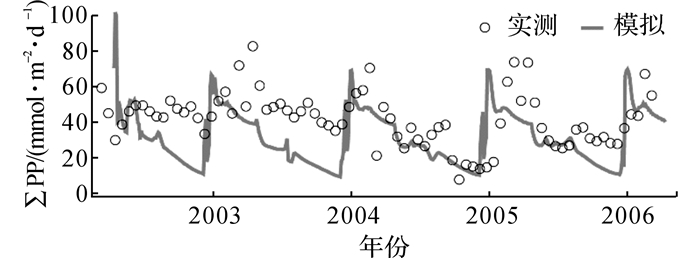
|
图 6 百慕大站上层水域单位面积水体初级生产力实测与模拟值对比 Fig. 6 Comparison of integrated primary production at BATS |
如图 6实线所示, 模拟单位面积水体初级生产力分布与营养盐及浮游植物的季节性变化基本同步, 具有显著且合理的变化特征.在冬末春初, 水体强烈混合作用导致混合层内营养盐浓度迅速上升、浮游植物大规模爆发, 单位面积初级生产力出现明显峰值, 最高平均可达70 mmol·m-2·d-1;后随着营养盐被吸收、浮游植物浓度降低, 单位面积初级生产力下降至10 mmol m-2 d-1.如图 6空心圈所示, 该站通过14C实测所得单位面积水体初级生产力与模拟结果具有相似的分布规律和最值范围, 主要差异为实测初级生产力冬季峰值发生时间落后模拟峰值约20 d, 且夏季实测值略高, 这一现象在2002和2003年度尤为明显.
如图 7所示分别展示了2002~2006年百慕大站实测与模拟初级生产力分布.

|
图 7 百慕大站表层水域实测与模拟初级生产力分布 Fig. 7 Field and simulated distributions of primary production at BATS |
图 7(a)和(b)显示百慕大站实测与模拟初级生产力均发生于表层0~140 m范围内, 证明耦合模型对于真光层深度的模拟较为准确.水表初级生产力PP模拟结果与实测数据的极值范围均介于0~12 mg·m-3·d-1;但分布时间略有区别:模拟水表初级生产力最大值发生时间略早于实测最大值.这一差异与图 6分布重复, 最大可能是GT模型模拟混合层上浮时间提前所致.此外, 实测数据显示2002和2003年百慕大站夏季水表初级生产力基本维持在4~7 mg·m-3·d-1;而模拟值随着营养盐和浮游植物浓度的下降而迅速回落至1~3 mg·m-3·d-1, 两者间存有一定差异.
鉴于模型已经囊括了喜好暖水的固氮类浮游植物, 模拟结果证实了在不改变现有浮游植物生长速率的前提下, 固氮类植物在夏季高温水体下大量生长难以解释实测数据中出现的夏季生产力偏高现象.因此, 猜测夏季间歇出现的生产力高值可能是由测量过程中物理动力过程变化引起的:譬如测量时流场方向改变导致毗邻水域浮游植物进入、不规律涡旋途经所致表层营养盐浓度上升, 及测量区域水体内碳氮元素比例失衡等.
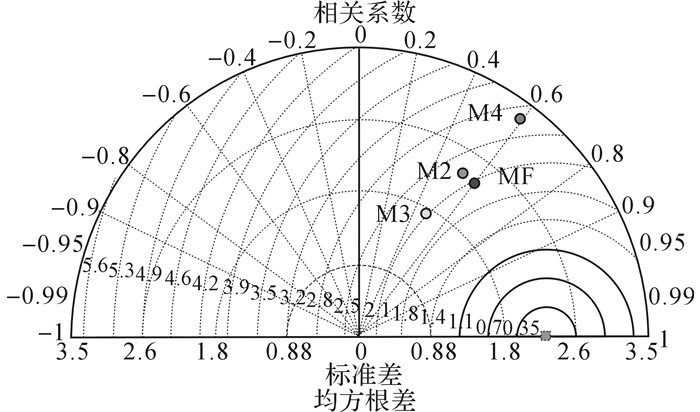
3.2.2 夏威夷站为了对比不同优化举措下耦合模型对多年初级生产力垂直剖面分布的模拟准确度, 本文在夏威夷站同样采用泰勒图对6个耦合模型模拟结果与14C实测数据进行比较, 如图 8所示.
|
图 8 泰勒图对比夏威夷站耦合模型优化结果 Fig. 8 Taylor diagram of optimized coupled models' performance for 2002~2006 primary production distribution with respect to observations at HOT |
模型M0由原始S生态模型构成和M1(仅分离氮磷循环), 由于模拟初级生产力和实测数据间标准差值超出泰勒图范围, 故无法在图中显示.修改了浮游植物生长速率的耦合模型M2、M3和M4的模拟结果与实测数据的相关系数介于0.4和0.6之间, 证实了生长速率方程的修改对耦合模型的模拟准确度有着重要影响.而高于0.6的相关系数,与实测数据基本一致的标准差和接近2.1的均方根差显示耦合模型MF的模拟结果与实测数据的吻合度最高,说明模型改进均有一定合理性.
通过耦合模型MF模拟所得的夏威夷站年平均初级生产力总量为14.2 mol·m-2, 与根据1989~1999年初级生产力测量数据统计得到的夏威夷站附近海域年平均初级生产力总值14.1 mol·m-2保持一致[24].
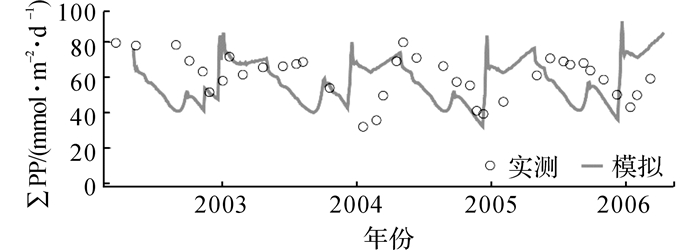
如图 9所示, 比较了2002~2006年间夏威夷站海域0~120 m单位面积水体内初级生产力模拟与实测数据间的差异.
|
图 9 夏威夷站上层水域单位面积水体初级生产力对比 Fig. 9 Comparison of integrated primary production at HOT |
图 9实线显示夏威夷站沿水深积分后模拟得到的单位面积水体初级生产力在冬末出现了明显增长, 但增长幅度仅为同时期百慕大站的1/2, 证实了该站冬季水体混合作用较弱的结论.该峰值在维持了2~3个月后随着浮游植物和营养盐浓度的下降而逐渐回落, 直至夏季末期因固氮类浮游植物短暂爆发性生长而出现少许回升.
图 9空心圈显示该站通过14C实际测得单位面积水体初级生产力的极值范围与模拟结果相似, 但实测单位面积初级生产力的增长与回落过程近乎对称, 受混合作用限制少, 与模拟结果差异明显.同时, 实测最大值发生时间较模拟分布滞后了约2~3个月, 其夏季初级生产力也因回落过程的推迟而明显偏高, 差异可达10~20 mmol·m-2·d-1.
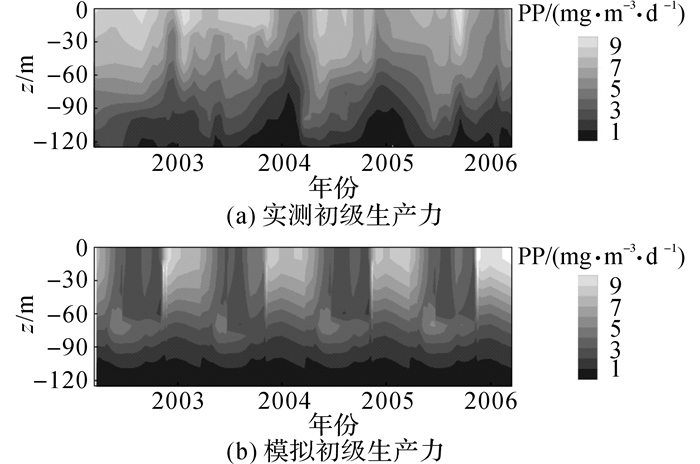
如图 10所示, 夏威夷站实测与模拟初级生产力在极值分布上极具共性;但在季节性分布上存在差异.
|
图 10 夏威夷站表层水域实测与模拟初级生产力分布 Fig. 10 Field and simulated distributions of primary production at HOT |
在图 10中, 模拟水表初级生产力垂直剖面分布具有规律的年际间变化特征:由混合作用引起的冬季峰值维持在8 mg·m-3·d-1约3个月;由夏季固氮类浮游植物大规模增长引起的小峰值在4~5 mg·m-3·d-1区间持续1~2个月.可能受到夏威夷站复杂流场影响, 实测初级生产力的水表分布缺乏规律.例如仅在2003年初, 实测与模拟分布同时达到初级生产力峰值, 其余年间两者均在不同时段达到峰值.实测数据较明显特征是夏季在水表出现持续时间长短不一的初级生产力高值, 最大程度体现了实测与模拟间的差异.
对于夏威夷站出人意料的夏季初级生产力高值, Karl等[24]认为是固氮类浮游植物在夏季大规模生长所致.根据表 1, 固氮类浮游植物最大生长速率为0.3 d-1, 远低于普通浮游植物3 d-1的最大生长速率值.在不改变生长速率的前提下, 固氮植物夏季爆发性生长对初级生产力的贡献量有限, 难以成为实测数据中夏季初级生产力大幅度增加的主因.
3.3 结果与讨论将模拟与实测数据相结合,不难发现百慕大与夏威夷站初级生产力具有基本一致的季节性变化特征,主要表现为:1)受混合作用影响,两站均在冬季出现初级生产力高值,而在其余季节初级生产力则有所下降,这与混合层上浮、浮游植物繁殖后营养盐浓度下降等因素均有关联;2)由于喜好高温水体的固氮类浮游植物存在,两站初级生产力在夏季末均略有上升,但随着水温下降,这一峰值也迅速回落.
两站类似的分布特征说明混合作用和浮游植物浓度均对初级生产力有着重要影响.前者通过物理动力决定混合程度;而后者通过生物浓度决定生产量值.泰勒图对比结果(图 5与8)也证实了这一结果.6个对比模型中, 包含了修改“浮游植物生长速率”耦合模型的模型结果无论是与实测数据的相关系数、标准差还是均方根差值的分布都明显优于不包含该优化内容的耦合模型.
耦合模型在夏季水表初级生产力的模拟上与实测结果之间存在的差异基本可由2部分组成:1)耦合模型与实际结构上的偏差;2)由于14C测量方法自身限制和缺陷造成的偏差.前者可通过采取精度更高的物理模型和涉及生物要素更多、结构更复杂的生态模型的方式减小偏差, 但效果有限.根据Saba等[11]、Laufktter等[18]与Doney等[26]的模拟结果分析, 多数高精度三维耦合模型模拟结果与实测初级生产力的相关系数基本介于0.3~0.6之间, 低于模拟动力参数或模拟营养盐浓度与实测数据间的相关系数, 说明存在于模型初级生产力与实测数据间的差异是一个较普遍的问题.而对于后者即14C测量方法的缺陷可能造成差异的原因, 却难以通过现有手段进行改进.该缺陷主要来源于:1)过小的水体培养空间范围存在着改变生物群落结构、踪素浓度以及在生物捕食过程中缺乏动力作用的潜在可能性[10, 12];2)缺乏对在实际海洋环境对初级生产力影响巨大的动态光照条件的考虑[27];3)14C作为踪素不仅能以非光合作用的途径进入浮游植物细胞, 还会通过呼吸作用被排泄到细胞之外, 这都会在最终放射性测定中低估或高估初级生产力[12];4)14C测量的时空范围有限、数据离散, 难以用于代表整片控制海域长时间连续的初级生产力分布[11, 12, 26].
结合差异产生的主要组成部分, 猜测造成模拟结果与实测数据在夏季期间出现一定差异的主要原因有:1)由小尺度动力过程变化引起的误差.百慕大与夏威夷站在夏季均受到上升流或小尺度涡旋影响, 难以在模型中如实表现, 但在初级生产力定点测量过程中流场的剧烈改变可能影响初级生产力最终测量结果.2)夏季期间由于较高的水体温度和较强的光照条件, 促使培养瓶中生物活动频繁, 在极小空间内群落结构、踪素浓度均可能发生变化, 从而导致实测初级生产力浓度的误差产生.3)表层水体内固氮类浮游植物的大量繁殖会引发生态系统的变化, 不仅使整个系统从“受无机氮限制”向“受磷酸盐限制”转移, 同时还有可能改变细胞或颗粒物质中的元素比值及元素半饱和常数等系数.由于缺乏相应实验数据, 耦合模型所采用参数仍基于“受无机氮限制”生态系统, 在不同海域的模拟中保持一致, 故限制了初级生产力的模拟准确度.
想要证实以上猜测, 还需要精度更高的物理模型和实测数据及对初级生产发生过程的更深入研究, 这些都将在未来研究中逐一进行.
4 结论本文针对GT混合层模型与S生态模型的不足, 逐步加以改进:1)在GT模型中增加对流与扩散模块, 提高模拟精度;2)依靠氮磷元素不同的再矿化速率将S模型中2种元素的循环分离;3)修正浮游植物生长速率方程, 使模型对光合作用的模拟更准确;4)添加浮游植物细胞内叶绿素浓度的计算.
在此基础上将优化后的物理与生态模块以一定的顺序进行耦合, 形成新的物理-生态耦合模型, 并进一步通过泰勒图比较采用不同优化步骤的耦合模型对多年初级生产力垂直剖面分布模拟的准确程度, 确认采用全部优化步骤的耦合模型对于生产力时空变化的模拟与实测数据相似度最高.在所有生态模型优化步骤中, 浮游植物生长速率方程的修正对最终模拟准确度的影响最大, 叶绿素浓度计算的介入则影响最小.
对比模拟与实测数据分布, 最终优化耦合模型较好把握了百慕大和夏威夷站初级生产力的基本季节性变化特征, 包括由混合作用造成的冬季初级生产力迅速增大、夏季初级生产力由于普通浮游植物浓度的下降而降低、夏季末期低纬度海域固氮植物浓度爆发引起的短期初级生产力“逆跌”现象等, 及两大局部海域平均全年生产力量值, 进一步说明耦合模型对于两大站点多年初级生产力模拟的合理性.
而实测与模拟结果中夏季较高初级生产力偏差, 推测其产生原因不局限于耦合模型在精度与维度上的不足, 可能与初级生产力14C测量方法的缺陷、大洋站复杂的小尺度流场运动及固氮浮游植物对生态系统的影响相关, 需要更深入的研究.
| [1] |
OSCHLIES A, GARCON V. Eddy-induced enhancement of primary production in a model of the North Atlantic Ocean[J]. Nature, 1998, 394(6690): 266-269. DOI:10.1038/28373 |
| [2] |
RILEY G A. Factors controlling phytoplankton populations on Georges Bank[J]. Journal of Marine Research, 1946, 6: 54-73. |
| [3] |
DUGDALE R C, GOERING J J. Uptake of new and regenerated forms of nitrogen in primary productivity[J]. Limnology and Oceanography, 1967, 12(2): 196-206. DOI:10.4319/lo.1967.12.2.0196 |
| [4] |
SLAGSTAD D, ELLINGSEN I H, WASSMANN P. Evaluating primary and secondary production in an Arctic Ocean void of summer sea ice:An experimental simulation approach[J]. Progress in Oceanography, 2011, 90(1): 117-131. |
| [5] |
POPOVA E E, YOOL A, COWARD A C, et al. What controls primary production in the Arctic Ocean? Results from an intercomparison of five general circulation models with biogeochemistry[J]. Journal of Geophysical Research, 2012, 117(1): 1-16. |
| [6] |
刘桂梅, 孙松, 王辉. 海洋生态系统动力学模型及其研究进展[J]. 地球科学进展, 2003, 18(3): 427-432. LIU Gui-mei, SUN Song, WANG Hui. Review on the marine ecosystem dynamics model[J]. Advances in Earth Science, 2003, 18(3): 427-432. |
| [7] |
周伟华, 袁翔城, 霍文毅, 等. 长江口领域叶绿素a和初级生产力的分布[J]. 海洋学报, 2004, 26(3): 143-150. ZHOU Wei-hua, YUAN Xiang-cheng, HUO Wen-yi, et al. Distribution of chlorophyll a and primary productivity in the adjacent sea area of Changjiang River Estuary[J]. Acta Oceanologica Sinica, 2004, 26(3): 143-150. |
| [8] |
于庆云. 切萨比克湾(Chesapeake Bay)浮游植物动力学特征的数值模拟研究[D]. 青岛: 中国海洋大学, 2012: 69-73. YU Qing-yun. The study on characters and numerical simulation of phytoplankton dynamics in Chesapeake Bay[D]. Qingdao: Ocean University of China, 2012: 69-73. http://cdmd.cnki.com.cn/Article/CDMD-10423-1012505732.htm |
| [9] |
郭琳. 加利福尼亚流系物理-生态过程的时空演变特征及其动力学机制研究[D]. 青岛: 中国海洋大学, 2015: 63-70. GUO Lin. Analysis of the characteristics and the mechanisms of physical and biological processes in the California Current System[D]. Qingdao: Ocean University of China, 2015: 63-70. http://cdmd.cnki.com.cn/Article/CDMD-10423-1015712732.htm |
| [10] |
WILLIAMS P J B, THOMAS D N, REYNOLDS C S. Phytoplankton productivity:carbon assimilation in marine and freshwater ecosystems[M]. xford: Blackwell Science, 2002, 78-108.
|
| [11] |
SABA V S, FRIEDRICHS M A M, CARR M E, et al. Challenges of modeling depth-integrated marine primary productivity over multiple decades:A case study at BATS and HOT[J]. Global Biogeochemical Cycles, 2010, 24(3): 811-829. |
| [12] |
NICHOLSON D P, STANLEY R H R, BARKAN E, et al. Evaluating triple oxygen isotope estimates of gross primary production at the Hawaii ocean time-series and bermuda atlantic time-series study sites[J]. Journal of Geophysical Research, 2012, 117(5): 1-18. |
| [13] |
SCHMITTNER A, OSCHLIES A, MATTHEWS H D, et al. Future changes in climate, ocean circulation, ecosystems, and biogeochemical cycling simulated for a business-as-usual CO2 emission scenario until year 4000 AD[J]. Global Biogeochemical Cycles, 2008, 22(1): 1-21. |
| [14] |
MONTEIRO F M, FOLLOWS M J. On nitrogen fixation and preferential remineralization of phosphorus[J]. Geophysical Research Letters, 2012, 39(6): L06607. |
| [15] |
MOORE C M, MILLS M M, ARRIGO K R, et al. Processes and patterns of oceanic nutrient limitation[J]. Nature Geoscience, 2013, 6(9): 701-710. DOI:10.1038/ngeo1765 |
| [16] |
DONEY S C, GLOVER D M, NAJJAR R G. A new coupled, one-dimensional biological-physical model for the upper ocean:applications to the JGOFS Bermuda Atlantic Time-Series Study (BATS) site[J]. Deep-Sea Research Π, 1996, 43(2): 591-624. |
| [17] |
LI Q P, FRANKS P J S, LANDRY M R, et al. Modeling phytoplankton growth rates and chlorophyll to carbon ratios in California coastal and pelagic ecosystems[J]. Journal of Geophysical Research, 2010, 115(4): 1-12. |
| [18] |
LAUFKTTER C, VOGT M, GRUBER N, et al. Drivers and uncertainties of future global marine primary production in marine ecosystem models[J]. Biogeosciences, 2015, 12(23): 6955-6984. DOI:10.5194/bg-12-6955-2015 |
| [19] |
KIEFER D A, KREMER J N. Origins of vertical patterns of phytoplankton and nutrients in the temperate, open ocean:a stratigraphic hypothesis[J]. Deep-Sea Research, 1981, 28(10): 1087-1105. DOI:10.1016/0198-0149(81)90049-2 |
| [20] |
LEE Z P, WEIDEMANN A, KINDLE J, et al. Euphotic zone depth:its derivation and implication to ocean-color remote sensing[J]. Journal of Geophysical Research, 2007, 112(3): 9-19. |
| [21] |
GILL A E, TURNER J S. A comparison of seasonal thermocline models with observation[J]. Deep-Sea Research, 1976, 23(5): 391-401. |
| [22] |
TURNER J S, KRAUS E B. A one-dimensional model of the seasonal thermocline. Ⅰ. A laboratory experiment and its interpretation[J]. Tellus, 2010, 19(1): 88-97. |
| [23] |
TAYLOR K E. Summarizing multiple aspects of model performance in a single diagram[J]. Journal of Geophysical Research, 2001, 106(7): 7183-7192. |
| [24] |
WILLIAMS P J B, THOMAS D N, REYNOLDS C S. Phytoplankton productivity: carbon assimilation in marine and freshwater ecosystems[M]//Oxford: Blackwell Science, 2002: 222-264. http://onlinelibrary.wiley.com/doi/10.1046/j.1467-2979.2003.t01-3-00114.x/citedby
|
| [25] |
FENNEL K, SPITZ Y H, LETELIER R M, et al. A deterministic model for N2 fixation at stn. ALOHA in the subtropical North Pacific Ocean[J]. Deep-Sea Research Ⅱ, 2001, 49(1): 149-174. |
| [26] |
DONEY S C, LIMA I, MOORE J K, et al. Skill metrics for confronting global upper ocean ecosystem-biogeochemistry models against field and remote sensing data[J]. Journal of Marine Systems, 2009, 76(1): 95-112. |
| [27] |
CARR M E, FRIEDRICHS M A M, SCHMELTZ M, et al. A comparison of global estimates of marine primary production from ocean color[J]. Deep-Sea Research Ⅱ, 2006, 53(5): 741-770. |



