异重流是由2种流体之间的密度差引起的流体之间互相掺混的现象[1], 这种掺混现象广泛存在于自然界中, 如:河水入海、冷暖空气交汇和沙尘暴等.过去的研究主要集中于密度均匀相同的环境水体, 而未考虑密度分层环境水体对异重流运动的影响[2].通常情况下, 由于海洋盐度、温度等分布不均, 环境流体密度随着水深的增加而逐渐增大, 并且分层环境对异重流运动有重要影响[3].
Cenedese等[4-5]采用实验和数值模拟方法研究了异重流沿坡运动过程中弗劳德数Fr和雷诺数Re数对卷吸系数的影响.Hallworth等[6]开展了开闸式异重流在斜坡上运动时, 斜坡角度对卷吸系数的影响.Ottolenghi等[7]通过实验和数值模拟相结合的方式, 分析了模型的高度和长度之比对异重流卷吸速度的影响.异重流与分层环境水体卷吸过程包含着复杂的多相流相互作用问题, 如:时间短、强非线性、泥沙沉降影响掺混等, 并伴随着内波产生与能量耗散等复杂问题.现有实验手段和数值方法通常是研究线性分层环境下异重流悬浮状态运动过程, 如羽流实验[8]、异重流沿斜坡运动[9], 但不能直观地观察到分层环境流体被卷吸时的运动过程和泥沙运动规律.因此开展三维分层环境中异重流运动的高精度数值模拟, 观察异重流卷吸分层环境水体的演变过程在科学研究和实际工程应用中有重要意义.该问题数值模拟的难点在于物质输运方程和流体控制方程同步求解以及初始状态的泥沙浓度大梯度变化造成的非物理震荡(Gibbs effect)[10]的有效处理方法.
本文拟通过引入精度更高的迎风紧致差分格式(up-winding Combined compact difference, UCCD)改进原模型, 开展线性分层环境下泥沙异重流掺混的数值模拟, 通过悬浮入侵的重力流算例验证该模型, 检验该数学模型用于模拟线性分层环境水体下开闸式泥沙异重流从模型底部入侵的运动问题的能力.
1 数学模型的建立 1.1 控制方程无量纲的黏性不可压流体运动控制方程, 包括连续方程和动量方程.
| $ \nabla \cdot u = 0. $ | (1) |
| $ \frac{{\partial u}}{{\partial t}} + u \cdot \nabla u = - \nabla p + \frac{1}{{\mathit{Re}}}{\nabla ^2}u + \left( {{\alpha _s}s + {\alpha _c}c} \right){g_{\rm{e}}}. $ | (2) |
式中:▽为散度;u为流体运动速度;t为时间,p为压力;Re为雷诺数;s和c(初始时刻, 闸门封锁区浓度无量纲后为c=1)分别为无因次化之后的盐度和泥沙浓度场;ge为约化重力加速度;其中:
| $ {\alpha _s} = \frac{{{{\tilde \rho }_{\rm{L}}} - {{\tilde \rho }_{\rm{0}}}}}{{{\rho _{{\rm{in}}}} - {\rho _{{\rm{mid}}}}}},{\alpha _{\rm{c}}} = \frac{{{{\tilde \rho }_{{\rm{in}}}} - {{\tilde \rho }_{\rm{0}}}}}{{{\rho _{{\rm{in}}}} - {\rho _{{\rm{mid}}}}}}. $ | (3) |
式中:
| $ {\rho _a}\left( z \right) = {\rho _{\rm{L}}} - \left( {{\rho _{\rm{T}}} - {\rho _{\rm{L}}}} \right)\frac{z}{{{H_{\rm{d}}}}}. $ | (4) |
式中:ρL为模型底部环境水体密度;ρT为模型顶部环境水体密度;z为三维空间纵坐标任意一点高度坐标值;Hd为模型的高度.泥沙浓度场和盐度运输方程分别为
| $ \frac{{\partial c}}{{\partial t}} + \left( {u + {u_{\rm{s}}}{g_{\rm{e}}}} \right) \cdot \nabla c = \frac{1}{{S{c_c}\mathit{Re}}}{\nabla ^2}c. $ | (5) |
| $ \frac{{\partial s}}{{\partial t}} + u \cdot \nabla s = \frac{1}{{S{c_c}\mathit{Re}}}{\nabla ^2}s. $ | (6) |
式中:us为泥沙沉降速度;Scs和Scc分别为运输方程中的施密特数(Schmidt), 取Scc=Scs=1[11];浮力频率N=(-g/ρ0)dρ/dz[12], ρ0为特征参考密度,g为重力加速度.
1.2 数值方法 1.2.1 平滑初始浓度场在初始时刻, 不连续的浓度场会产生一个伪震荡, 即吉布斯现象(Gibbs effect).这是由于模型闸门内外, 泥沙浓度c值有一个从1到0的突变, 在数值模拟时会造成数值震荡.为了避免这种非物理震荡现象, 通过引入Heaviside函数来平滑这种震荡.
| $ c\left( {x,t = 0} \right) = H\left( \phi \right), $ | (7) |
| $ H\left( \phi \right) = \left\{ {\begin{array}{*{20}{c}} {0,}&{\phi < - 1.5\Delta x;}\\ {\frac{1}{2}\left[ {1 + \frac{{2\phi }}{{3\Delta x}} + \frac{1}{{\rm{ \mathsf{ π} }}}\sin \left( {\frac{{2{\rm{ \mathsf{ π} }}\phi }}{{3\Delta x}}} \right)} \right],}&{\left| \phi \right| < 1.5\Delta x;}\\ {1,}&{\phi > 1.5\Delta x.} \end{array}} \right. $ | (8) |
式中:ϕ为符号距离函数[13];Δx为网格空间步长;在环境水体和封锁区内部用函数ϕ0表示, 其中在闸门内部的封锁区ϕ0=1, 在环境水体中ϕ0=-1.
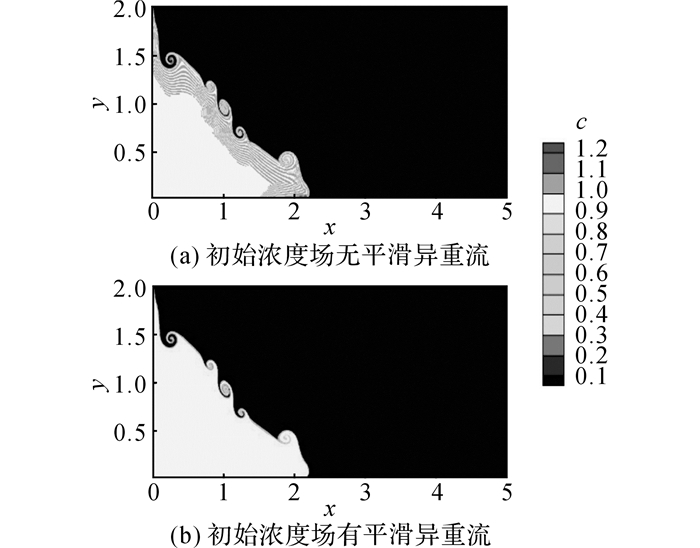
如图 1所示通过异重流泥沙运动模型验证了平滑和非平滑2种情况, 结果显示非平滑结果会导致泥沙总浓度c>1结果, 这种现象是由于在闸门区域浓度场由1到0的突变造成的, 并且随着模拟时间推移, 会造成误差累积.引入|▽ϕ|=1来使得不连续的函数ϕ0作为符号距离函数, 即可以通过方程(9)求解初始化方程.
| $ {\phi _\tau } + {\mathop{\rm sgn}} \left( {{\phi _0}} \right)\left( {\left| {\nabla \phi - 1} \right|} \right) = 0. $ | (9) |
|
图 1 不平滑与平滑的异重流运动状态及其比较 Fig. 1 Comparison of predicted history evolution of gravity current between non-slip and slip function |
式中:ϕc为虚拟时间τ时刻的ϕ值.初始化ϕ0之后, 在闸门封锁区中符号距离函数是正值, 在环境水体中是负值.通过五阶本质无震荡格式(Weighted Essentially Non-oscillatory, WENO5)[14]和三阶总变差减小Runge-Kutta格式(Total Variation Diminishing-Runge-Kutta3, TVD-RK3)[15]来近似的求解方程(9).
1.2.2 求解泥沙运输方程平滑不连续的浓度场之后, 利用UCCD求运输方程(盐度和浓度方程)的一阶空间导数项cx和二阶导数项cxx:
| $ \begin{array}{l} {\alpha _1}\frac{{\partial c}}{{\partial x}}\left| {_{i - 1}} \right. + \frac{{\partial c}}{{\partial x}}\left| {_i} \right. + {\alpha _3}\frac{{\partial c}}{{\partial x}}\left| {_{i + 1}} \right. = \\ \;\;\;\;\frac{1}{{\Delta x}}\left( {{c_1}{c_{i - 2}} + {c_2}{c_{i - 1}} + {c_3}{c_i}} \right) - \\ \;\;\;\;\Delta x\left( {{\beta _1}\frac{{{\partial ^2}c}}{{\partial {x^2}}}\left| {_{i - 1}} \right. + {\beta _2}\frac{{{\partial ^2}c}}{{\partial {x^2}}}\left| {_i} \right. + {\beta _3}\frac{{{\partial ^2}c}}{{\partial {x^2}}}\left| {_{i + 1}} \right.} \right). \end{array} $ | (10) |
| $ \begin{array}{l} - \frac{1}{8}\frac{{{\partial ^2}c}}{{\partial {x^2}}}\left| {_{i - 1}} \right. + \frac{{{\partial ^2}c}}{{\partial {x^2}}}\left| {_i} \right. - \frac{1}{8}\frac{{{\partial ^2}c}}{{\partial {x^2}}}\left| {_{i + 1}} \right. = \\ \frac{3}{{\Delta {x^2}}}\left( {{c_{i - 1}} + 2c + {c_{i + 1}}} \right) - \frac{9}{{8\Delta x}}\left( { - \frac{{\partial c}}{{\partial x}}\left| {_{i - 1}} \right. + \frac{{\partial c}}{{\partial x}}\left| {_{i + 1}} \right.} \right). \end{array} $ | (11) |
方程(10)中的系数是基于泰勒级数展开的方式推导而来, 分别为:α1=0.888 251 79, α3=0.049 229 65, c1=0.016 661 72, c2=-1.970 804 88, c3=1.954 143 16, β1=0.150 072 40, β2=-0.250 712 70, β3=-0.012 416 47, 通过修正函数减小截断误差[15].采用保色散关系来处理色散与耗散误差, 利用迎风格式在网格点i-2, i-1, i和i+1中得到的解可以达到六阶精度.最后通过TVD-RK3来求解浓度运输方程中的时间积分项.
1.2.3 求解N-S方程用三阶QUICK格式(Quadratic Upwind Interpolation for Convective Kinematics)离散对流项, 以
| $ \begin{array}{l} u\frac{{\partial u}}{{\partial x}} = \frac{u}{{2\Delta x}}\left( {{u_{i + 1,j,k}} - {u_{i - 1,j,k}}} \right) - \\ \;\;\;\;\frac{{{u^ + }{c_{\rm{f}}}}}{{\Delta x}}\left( {{u_{i + 1,j,k}} - 3{u_{i + 1,j,k}} + 3{u_{i - 1,j,k}} - {u_{i - 2,j,k}}} \right) - \\ \;\;\;\;\frac{{{u^ - }{c_{\rm{f}}}}}{{\Delta x}}\left( {{u_{i + 2,j,k}} - 3{u_{i + 1,j,k}} + {u_{i,j,k}} - {u_{i - 1,j,k}}} \right). \end{array} $ | (12) |
式中:u+=1/2(ui, j, k+|ui, j, k|), u-=1/2(ui, j, k -|ui, j, k|), cf =0.125.用二阶中心差分格式来近似求解动量方程中x方向的黏性项.通过投影法[16]求解不可压缩流体的压力场.
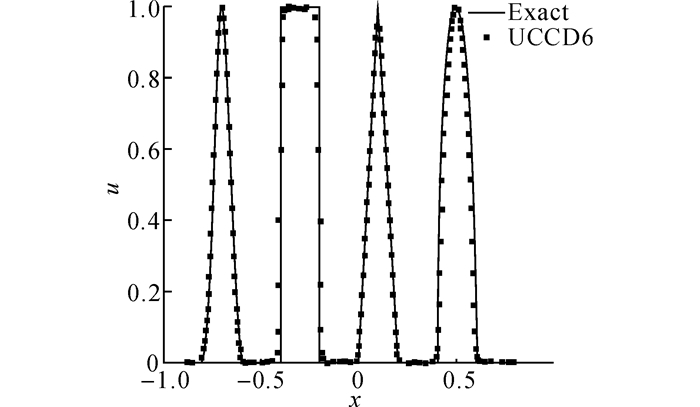
2 模型验证 2.1 数值验证采用本模型算法求解一维对流方程问题, 验证其可靠性.采用Core i5、RAM 32.0 GB的计算机基于UCCD6格式测试计算效率.网格为200×200时, CPU时间为2.406 4 s;网格为400×400时, CPU时间为8.593 8 s.初始条件[17]如方程(13), 包括不连续的矩形和不同的函数图形, 时间步长采用Δt=0.1×Δx.图 2展示了t =2.0时在计算域[-1, 1]内, 200×200的均匀网格下的数值结果.通过UCCD6数值格式的求解结果与精确解有较好的一致性.
| $ \begin{array}{l} \mathit{\Phi }\left( x \right) = \\ \;\;\;\left\{ {\begin{array}{*{20}{c}} {\exp \left( { - \log \left( 2 \right)\frac{{{{\left( {x + 7} \right)}^2}}}{{0.0009}}} \right),}&{ - 0.8 \le x \le - 0.6;}\\ {1,}&{ - 0.4 \le x \le - 0.2;}\\ {1 - \left| {10\left( {x - 0.1} \right)} \right|,}&{0 \le x \le 0.2;}\\ {\frac{{1 - 100{{\left( {x - 0.5} \right)}^2}}}{2},}&{0.4 \le x \le 0.6.}\\ {0;}&{其他.} \end{array}} \right. \end{array} $ | (13) |
|
图 2 线性对流模拟比较 Fig. 2 Predicted result for linear advection problem |
采用二维异重流从分层环境水体中间深度入侵的算例与已有文献[12]进行比较以验证模型的可靠性.该类算例可较好地体现内波运动状态, Diogo的实验是该类问题的典型算例且与当前模型属同类问题.中间入侵异重流工况:浮力频率N=1;闸门内部流体密度与模型高度的0.7倍位置处的环境流体密度相等, 即hN = 0.7;根据Diogo[12]等定义雷诺数为Re=NH2/υ, H为空间尺度,本文中H=Hd, υ为流体黏性系数,该算例中取Re=40 000;计算域为(x, y) = (150 cm, 20 cm), 网格空间在x和y方向的步长均为0.02 cm;时间步长为0.000 1 s.图 3给出了不同时刻组分异重流中间入侵问题的模拟结果, 并与文献结果做了比较.图 3(a)为Diogo[12]实验结果;图 3(b)为Diogo[12]的数值结果;图 3(c)是当前模型的数值结果.在初始时刻2种流体均为静止状态, 入侵异重流运动最快的地方是2种流体密度相等的地方, 即算例中hN = 0.7的位置.由于模型底部环境流体密度大于入侵异重流, 所以分层环境水体会反向入侵闸门封锁区.图 3展示的结果分别为t=0.25 s、t=3 s和t=5 s 3个瞬间的组分异重流中间入侵形态, 图 3(a)和图 3(b)比较结果显示, Diogo的实验与数值结果有较好的一致性, 而通过与当前模型对比, 显示当前模型可以捕捉到尺寸更小的连续的涡.在t=5 s时, 通过盐度等值线展现异重流入侵时产生的内波.

|
图 3 不同时间节点异重流运动状态及其比较[12] Fig. 3 Comparison of the predicted history evolution of the gravity current and the experimental data[12] |
在三维数学模型中分析异重流卷吸分层环境流体运动过程, 表 1给出了各工况参数, 其中各无量纲量:Vs为沉降速度,(Ld, Wd, Hd)分别为无量纲模型长、宽、高.工况设置主要有两方面, 一方面当Re=6 000时分析不同沉降速度下异重流入侵规律;另一方面是当泥沙沉降速度为0.01时, 不同的雷诺数对异重流入侵运动得影响机制.如图 4所示为当前数值模拟的初始模型.初始时刻的异重流尺寸为:Llock×Wd×Hd;Llock区域与环境水体交界面为闸门, 闸门内部为泥沙流体, 外部是分层环境水体.开启闸门后会产生溃坝式流动, 并且会观察到泥沙异重流与分层环境水体互相掺混现象.实验模型边界条件:顶部壁面和两端边壁设为滑移边界;两侧边壁和模型底部设为周期性边界[12].网格空间尺度在3个方向采用步长为0.025的均匀网格, 时间步长为0.002×0.025.
| 表 1 当前数值模型的工况参量 Table 1 Parameters of simulations |

|
图 4 当前数值模拟的初始模型 Fig. 4 Initial model of the present numerical simulation |
线性分层环境中的异重流运动中, 分层环境对异重流运动影响的实验多在斜坡运动中进行.在没有斜坡的平板实验模型中, 浮力频率对异重流运动速度、沉降、以及能量转化的影响比较小, 所以在这里仅分析相同浮力频率的算例.
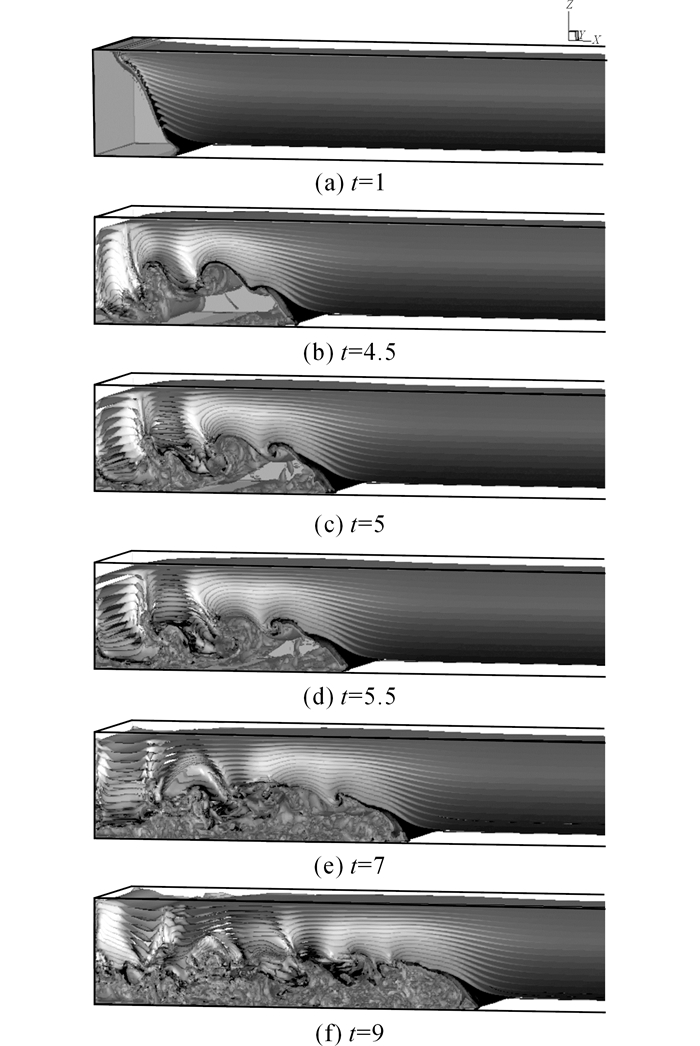
3.2.1 卷吸运动泥沙异重流在运动过程中的卷吸掺混过程对流体动量传输有重要作用.Snow and Sutherland采用盒模型来描述异重流卷吸环境水体现象[18].如图 5所示为异重流随无量纲时间的运动状态, 泥沙浓度场c=0.1形成的界面作为泥沙异重流与分层环境水体交界面, 去除交界面内部泥沙浓度值c>0.1的部分, 随着分层环境水体不断的被卷吸到阴影区内部, 异重流内部阴影区中的环境水体会不断增加直到充满整个泥沙异重流区域, 以直观的反映泥沙异重流卷吸掺混分层环境水体现象.随着时间发展, 异重流界面内部逐渐充满环境水体, 这表明分层环境水体已处于被入侵的泥沙流体卷吸掺混状态.同时通过分析卷吸过程可以看出异重流卷吸分层环境流体的动力主要依靠异重流尾部的湍动效应, 而头部对环境流体的卷吸影响很小.
|
图 5 异重流卷吸随时间的发展过程 Fig. 5 History evolution of current entrainment |
泥沙沉降率可以表示为单位时间内泥沙沉降量[11], 定义为
| $ {m_{\rm{s}}}\left( t \right) = - \frac{{\rm{d}}}{{{\rm{d}}t}}{m_{\rm{p}}}\left( t \right). $ | (14) |
其中, mp表示为
| $ {m_{\rm{p}}}\left( t \right) = \int_\mathit{\Omega } {c\left( {x,y,z,t} \right){\rm{d}}v} . $ | (15) |
式中:ms为t时刻的泥沙沉降量, mp为t时刻在计算域Ω内泥沙悬浮量.
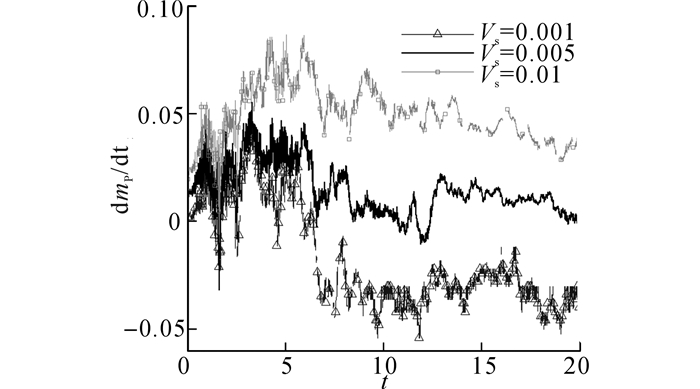
如图 6所示为工况C2至C4, Re=6 000、浮力频率N=1.825 7, 在不同沉降速度情况下的泥沙沉降率, 结果显示在运动初期, 泥沙沉降率为增长的趋势, 在无量纲时间t=5左右达到峰值, 随后开始减小.这表明在闸门开启之后, 泥沙与环境流体掺混速度在增加, 导致初始时刻的泥沙浓度降低速度较快.在运动后期, 异重流运动趋于稳定, 泥沙沉降率变化趋于稳定状态.同时可以看出沉降率随着沉降速度增加而增加.
|
图 6 不同沉降速度下的泥沙沉降率 Fig. 6 Sedimentation rates of particle in different settling velocity |
对于异重流, 其典型特征是势能转换为动能.由于动能通过流体之间的黏性耗散, 最终达到静止状态, 这种能量传输与转化过程在工程实际应用中有重要意义, 因此有必要模拟能量耗散过程.在分层环境中, 有3种机制变化影响机械能的转化, 主要包括:流体黏性耗散、泥沙沉降以及盐水分层环境.
如图 7所示为工况C9条件下, 各能量组分Ec随时间变化过程, 其中虚线表示总能量, 总能量计算误差为3.1%(在t = 20以内允许误差为5%), 体现了较好的能量守恒性.缩放图展示了比重较小的各能量组分, 可以看出, 在闸门开启后, 异重流的动能迅速增加到峰值后逐渐减小, 这说明开闸式异重流运动过程的3个不同阶段, 在本质上表现为动能的变化过程[19].在t=15, 异重流运动到模型末端撞击壁面之后有个爬升和反弹的过程, 在动能变化上表现为迅速减小后又增大, 因此在这个时刻可以看到总势能在增大.

|
图 7 各能量组分随时间变化 Fig. 7 Time history of energy components |
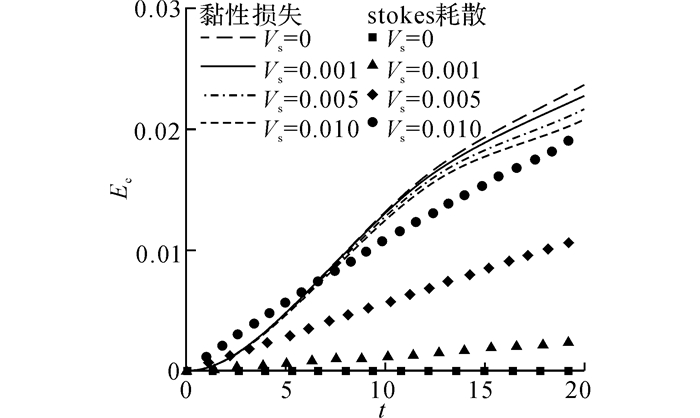
如图 8所示为不同沉降速度下流体黏性损失和stokes耗散, 其他参数分别为:Re=6 000, N=1.825 7.在运动初期, 泥沙沉降速度对流体黏性损失没有明显影响, 在t=7.5之后, 黏性损失随着沉降速度增加而减小, 这主要是由于异重流运动初期, 泥沙浓度较大, 沉降速度对流体运动影响较小, 而在运动后期, 较大的沉降速度导致泥沙浓度降低幅度较大, 泥沙对流体运动的影响相对较小, 其对应的黏性耗散相对较小;同时表明Stokes耗散是呈线性变化, 其耗散速率随着沉降速度增加而增大.
|
图 8 能量损失随时间变化 Fig. 8 Time history of energy loss |
(1) 基于六阶精度的UCCD6改进的DNS数学模型, 利用网格节点的一阶偏微分项和二阶偏微分项的数值, 直接近似求出一阶和二阶偏微分项, 最终得到高精度数值结果.通过开展二维悬浮入侵异重流算例验证了模型的可靠性, 同时在验证模型中, 通过定性的比较结果显示当前的模型结果精度更高, 捕捉中间入侵的异重流产生的内波效果更好.
(2) 同步求解三维物质输运方程和Navier-Stokes方程, 通过泥沙异重流卷吸分层环境水体, 直观的呈现了环境水体被卷吸时的演变过程.卷吸过程主要依靠异重流尾部湍动卷吸环境流体, 而异重流头部对环境水体的扰动很小.
(3) 通过不同的沉降速度分析其对泥沙沉降率, 能量损失的影响.结果显示泥沙沉降率受到异重流卷吸环境流体的影响, 初始阶段异重流卷吸速度的增加导致浓度迅速减小, 泥沙沉降率随之迅速的增加到峰值, 随后趋于平缓.同时t=7.5之前沉降速度对流体黏性损失影响较小, 当t>7.5时, 黏性损失随着沉降速度增加逐渐减小.
| [1] |
KUBO Y. Experimental and numerical study of topo-graphic effects on deposition from two-dimensional, particle-driven density currents[J]. Sedimentary Geology, 2004, 164(3/4): 311-326. |
| [2] |
VASSILIOS A, Tsihrintzis, Vahid Alavian. Spreading of three-dimensional inclined gravity plumes[J]. Journal of Hydraulic Research, 1996, 34(5): 695-711. DOI:10.1080/00221689609498466 |
| [3] |
LONGO S, UNGARISH M, FEDERICO V D, et al. Gravity currents in a linearly stratified ambient fluid created by lock release and influx in semi-circular and rectangular channels[J]. Physics of Fluids, 2016(89): 96-115. |
| [4] |
CENEDESE C, ADDUCE C. Mixing in a density-driven current flowing down a slope in a rotating fluid[J]. Journal of Fluid Mechanics, 2008, 604: 369-388. |
| [5] |
CENEDESE C, ADDUCE C. A New Parameterization for Entrainment in Overflows[J]. Journal of Physical Oceanography, 2010, 40(8): 313-322. |
| [6] |
HALLWORTH M A, HUPPERT H E, Phillips J C, et al. Entrainment into two-dimensional and axisymmetric turbulent gravity currents[J]. Journal of Fluid Mechanics, 1996, 308: 289-311. DOI:10.1017/S0022112096001486 |
| [7] |
OTTOLENGHI L, ADDUCE C, INGHILESI R, et al. Entrainment and mixing in unsteady gravity currents[J]. Journal of Hydraulic Research, 2016, 54(5): 1-17. |
| [8] |
张巍, 赵亮, 贺治国, 等. 线性层结盐水中的羽流运动特性[J]. 水科学进展, 2016, 27(4): 602-608. ZHANG Wei, ZHAO Liang, HE Zhi-guo, et al. Characteristics of plumes in linearly stratified salt-water[J]. Advances in Water Science, 2016, 27(4): 602-608. |
| [9] |
GUO Y, ZHANG Z, SHI B. Numerical simulation of gravity current descending a slope into a linearly stratified environment[J]. Journal of Hydraulic Engineering, 2014, 140(12): 1-10. |
| [10] |
PETERSON T E. Eliminating gibb's Effect from separation of variables solutions[J]. Siam Review, 1998, 40(2): 324-326. DOI:10.1137/S0036144596316224 |
| [11] |
NASR-AZADANI M M, MEIBURG E. Turbidity currents interacting with three-dimensional seafloor topo-graphy[J]. Journal of Fluid Mechanics, 2014, 74(52): 409-443. |
| [12] |
BOLSTER D, HANG A, LINDEN P F. The front speed of intrusions into a continuously stratified medium[J]. Journal of Fluid Mechanics, 2008, 594: 369-377. |
| [13] |
OSHER S, SETHIAN J A. Fronts propagating with curvature dependent speed:algorithms based on the Hamilton-Jacobi formulation[J]. Journal of Computational Physics, 1988, 79(1): 12-49. DOI:10.1016/0021-9991(88)90002-2 |
| [14] |
JIANG G S, PENG D. Weighted ENO schemes for Hamilton-Jacobi equations[J]. Siam Journal on Scientific Computing, 2000, 21(6): 2126-2143. DOI:10.1137/S106482759732455X |
| [15] |
CHU P C, FAN C. A Three-Point Combined Compact Difference Scheme[J]. Journal of Computational Physics, 1998, 140(2): 370-399. DOI:10.1006/jcph.1998.5899 |
| [16] |
CHORIN A J. Numerical solution of the Navier-Stokes equations[J]. Mathematics of Computational, 1968, 22(104): 745-762. DOI:10.1090/S0025-5718-1968-0242392-2 |
| [17] |
JIANG G S, SHU C W. Efficient Implementation of Weighted ENO Schemes[J]. Journal of Computational Physics, 1996, 126(1): 202-228. DOI:10.1006/jcph.1996.0130 |
| [18] |
SNOW K, SUTHERLAND B R. Particle-laden flow down a slope in uniform stratification[J]. Journal of Fluid Mechanics, 2014, 755: 251-273. DOI:10.1017/jfm.2014.413 |
| [19] |
NASR-AZADANI M M, MEIBURG E, KNELLER B. Mixing dynamics of turbidity currents interacting with complex seafloor topography[J]. Environmental Fluid Mechanics, 2016, 1-23. |



