2. 重庆大学 输配电装备及系统安全与新技术国家重点实验室, 重庆 400044
2. State Key Laboratory of Power Transmission Equipment and System Security and New Technology, Chongqing University, Chongqing 400044, China
近年来, 随着全球风能快速发展, 风电场与风电机组数量不断地增加, 各种运行故障也随之增多.诸多故障原因无法得到解释, 给电网安全可靠运行留下了安全隐患, 亟需对风电机组运行状态和故障进行深入研究[1-3].其中, 风力发电机组振动监测是早期发现并跟踪机组故障的一种方法[4-6].
由于风力发电机运行环境恶劣, 除了各种振动信号, 还包括噪声, 并且振动信号往往被噪声淹没, 必然要对振动信号消噪处理[7].传统的滤波器消噪方法主要针对于平稳信号, 而对于非线性、非平稳振动信号除了消噪效果不佳, 反而会影响振动信号本质.因此, 有的学者提出了小波分析和数学处理方法[8-11].向东阳等[12]采用小波硬阈值函数和软阈值函数进行降噪处理, 但结果并不是最理想的.Morlet小波变换和基于连续小波变换方法分别被用于风电设备齿轮箱和滚动轴承振动信号降噪, 都取得了不错地消噪效果.但是, 小波降噪存在基函数选择、平稳性假设和参数敏感等问题[13-14].胡爱军等[15]构建了一种基于数学形态滤波器, 可以有效地剔除旋转机械振动信号中的脉冲噪声, 而对于强噪声干扰的, 还需结合傅里叶变换.
傅里叶变换虽能对信号分解, 但同时亦将噪声分解, 且存在噪声抑制和保护信号边缘的矛盾, 难于准确识别和去除噪声.而Huang等[16]提出了一种经验模态分解(empirical mode decomposition, EMD), 能够对非平稳信号自适应分解, 可有达到有效降噪.但是, 当信号存在异常事件时, 由于分解混叠问题会使得降噪效果不佳, 且有时模态分解过多, 需较长计算时间[17-18].法国Gilles[19]结合经验模式分解的自适应性和小波分析理论提出经验小波变换(empirical wavelet transform, EWT), 这又是一种针对非平稳信号处理的一次重大突破.EWT的核心思想是对信号的傅里叶谱进行自适应划分, 构建合适的小波滤波器提取不同的AM-FM成分, 并对得到的AM-FM模态作Hilbert变换, 获得瞬时频率和幅值.EWT自适应模态分解数和计算量优于EMD, 并且具有较强的鲁棒性.国内外研究学者已将EWT作为一种新的信号处理工具, 在电能质量[20]、声音分析[21]、机械故障诊断[22]、目标加速度估计[23]、医疗信号处理[24]等领域进行研究和应用.
而风力发电机振动信号是一种典型的非平稳信号, 鉴于EWT对非平稳信号具有自适应性分解, 并且具有更高的时频分辨率.因此, 本文利用EWT对风力发电机振动信号进行数据滤波消噪, 为以振动信号进行风力发电机安全生产监测提供一种可借鉴方法.
1 经验小波变换 1.1 经验小波变换理论EMD分解的实质是将原始信号f(t)分解为N个内禀模态函数(intrinsic mode function, IMF)分量ci(t)和余项rn(t)之和, 如公式(1)所示.
| $ f\left( t \right) = \sum\limits_{i = 1}^N {{c_i}\left( t \right) + {r_n}\left( t \right)} . $ | (1) |
该分解方法存在筛分迭代终止条件、端点效应和模态混叠等问题.为了克服其缺点, Gilles在EMD分解方法基础上, 结合小波分析, 提出了经验小波变换.它将原始信号f(t)分解成N+1个模态函数fi(t)之和, 即为
| $ f\left( t \right) = \sum\limits_{i = 0}^N {{f_i}\left( t \right)} . $ | (2) |
式(2)中的fi(t)定义为调幅-调频信号(AM-FM), 如式(3).
| $ {f_i}\left( t \right) = {F_i}\left( k \right)\cos \left( {{\phi _i}\left( t \right)} \right). $ | (3) |
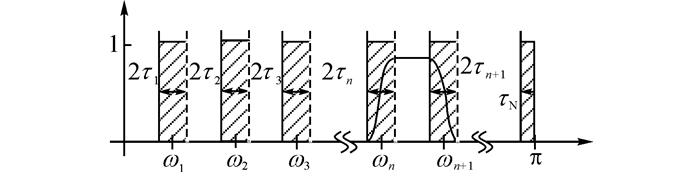
式(3)中的Fi(k)>0, ϕi(t)为时间t的相位函数,且ϕ′i(t)>0, 假设Fi和ϕ′i的变化比ϕi慢得多.该方法基于小波分析, 根据信号傅里叶谱特性进行自适应划分, 建立一个合适的小波滤波器提取不同的AM-FM成分.假设将傅里叶支撑[0, π]分割成N个连续部分Λn, 定义ωn为各连续部分的边界, 取信号傅里叶谱相邻2个极大值点之间的中点, 则可表达为
| $ \left. \begin{array}{l} {\mathit{\Lambda }_n} = \left[ {{\omega _{n - 1}},{\omega _n}} \right],n = 1,2, \cdots ,N,\left( {{\omega _0} = 0,{\omega _N} = {\rm{ \mathsf{ π} }}} \right)\\ \;\;\;\;\bigcup\nolimits_{n - 1}^N {{\mathit{\Lambda }_n} = \left[ {0,{\rm{ \mathsf{ π} }}} \right]} \end{array} \right\}. $ | (4) |
式(4)以每个ωn为中心, 取宽度Tn=2τn作为过渡段, 如图 1所示.经验小波则定义为每个Λn上的带通滤波器, 再根据Meyer小波构造经验小波, 从而确定经验尺度函数和经验小波函数, 分别如式(5)和(6)所示[19].
| $ {{\hat \phi }_n}\left( \omega \right) = \left\{ \begin{array}{l} 1,\;\;\;\;\;\left| \omega \right| \le {\omega _n} - {\tau _n};\\ \cos \left[ {\frac{{\rm{ \mathsf{ π} }}}{2}\beta \left( {\frac{1}{{2{\tau _n}}}\left( {\left| \omega \right| - {\omega _n} + {\tau _n}} \right)} \right)} \right],\\ {\omega _n} - {\tau _n} \le \left| \omega \right| \le {\omega _n} + {\tau _n};\\ 0,\;\;\;\;\;其他 \end{array} \right. $ | (5) |
| $ {{\hat \psi }_n}\left( \omega \right) = \left\{ \begin{array}{l} 1,\;\;\;\;{\omega _n} + {\tau _n} \le \left| \omega \right| \le {\omega _{n + 1}} - {\tau _{n + 1}};\\ \begin{array}{*{20}{c}} {\cos \left[ {\frac{{\rm{ \mathsf{ π} }}}{2}\beta \left( {\frac{1}{{2{\tau _{n + 1}}}}\left( {\left| \omega \right| - {\omega _{n + 1}} + {\tau _{n + 1}}} \right)} \right)} \right],}\\ {{\omega _{n + 1}} - {\tau _{n + 1}} \le \left| \omega \right| \le {\omega _{n + 1}} + {\tau _{n + 1}};} \end{array}\\ \begin{array}{*{20}{c}} {\sin \left[ {\frac{{\rm{ \mathsf{ π} }}}{2}\beta \left( {\frac{1}{{2{\tau _n}}}\left( {\left| \omega \right| - {\omega _n} + {\tau _n}} \right)} \right)} \right],}\\ {{\omega _n} - {\tau _n} \le \left| \omega \right| \le {\omega _n} + {\tau _n};} \end{array}\\ 0,\;\;\;\;\;\;\;其他. \end{array} \right. $ | (6) |
|
图 1 傅里叶轴分割 Fig. 1 Partitioning of Fourier axis |
式(5)和(6)中的τn和β(x)可表示为
| $ \left. {\begin{array}{*{20}{c}} {{\tau _n} = \gamma {\omega _n},\;\;\;\;0 < \gamma < 1\;且\;\gamma < {{\min }_n}\left( {\frac{{{\omega _{n + 1}} - {\omega _n}}}{{{\omega _{n + 1}} + {\omega _n}}}} \right);}\\ {\beta \left( x \right) = {x^4}\left( {35 - 84x + 70{x^2} - 20{x^3}} \right).} \end{array}} \right\} $ | (7) |
与传统小波变换类似, 经验小波变换定义为Wfε(n, t).用FFT (·)和IFFT-1 (·)分别表示傅里叶变换和傅里叶逆变换, 则经验小波变换细节系数可由信号与经验小波函数内积产生:
| $ \begin{array}{*{20}{c}} {W_f^\varepsilon \left( {n,t} \right) = \left\langle {f,{\psi _n}} \right\rangle = \int {f\left( \tau \right)\overline {{\psi _n}\left( {\tau - t} \right)} {\rm{d}}\tau } = }\\ {{\rm{IFF}}{{\rm{T}}^{ - 1}}\left( {f\left( \omega \right){{\hat \psi }_n}\left( \omega \right)} \right).} \end{array} $ | (8) |
用Wfε(0, t)表示近似系数, 则其可由信号与经验尺度函数内积产生:
| $ \begin{array}{*{20}{c}} {W_f^\varepsilon \left( {0,t} \right) = \left\langle {f,{\phi _1}} \right\rangle = \int {f\left( \tau \right)\overline {{\phi _1}\left( {\tau - t} \right)} {\rm{d}}\tau } = }\\ {{\rm{IFF}}{{\rm{T}}^{ - 1}}\left( {f\left( \omega \right){{\hat \phi }_1}\left( \omega \right)} \right).} \end{array} $ | (9) |
式(8)和(9)中的
| $ \begin{array}{*{20}{c}} {f\left( t \right) = W_f^\varepsilon \left( {0,t} \right) * {\phi _1}\left( t \right) + \sum\limits_{n = 1}^N {W_f^\varepsilon \left( {n,t} \right) * {\psi _n}\left( t \right)} = }\\ {{\rm{IFF}}{{\rm{T}}^{ - 1}}\left( {\hat W_f^\varepsilon \left( {0,t} \right) * {{\hat \phi }_1}\left( t \right) + \sum\limits_{n = 1}^N {\hat W_f^\varepsilon \left( {n,t} \right) * {{\hat \psi }_n}\left( t \right)} } \right).} \end{array} $ | (10) |
式(10)中的Ŵfε(n, t)和Ŵfε(0, t)分别为Wfε(n, t)和Wfε(0, t)的傅里叶变换,*表示卷积.按照公式(10), 则公式(3)中的经验模态fi可定义如下:
| $ {f_0}\left( t \right) = W_f^\varepsilon \left( {0,t} \right) * {\phi _1}\left( t \right), $ | (11) |
| $ {f_i}\left( t \right) = W_f^\varepsilon \left( {i,t} \right) * {\psi _i}\left( t \right). $ | (12) |
原信号经过EWT算法分解后, 可以获得由N+1个经验模态函数分量组成.由此, 原信号也可以看成由多个分辨率的信号分量叠加而成.即使原信号由研究对象信号和噪声组成, 基于EWT分解后, 为研究对象信号按时空滤波器分离提取提供了依据[25].时空滤波器思想是根据原信号分解后各个模态函数分量的频率设定各种滤波器, 可将是噪声的模态函数分量直接滤除掉, 从面获取研究对象信号.然而, 往往噪声信号频率覆盖整个原信号的频率范围, 这将无法使用时空滤波器获得有效的研究对象信号.
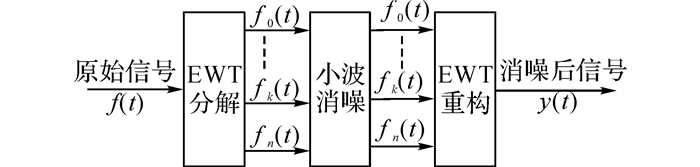
鉴于小波消噪基于对分解后的高频系数部分进行阈值消噪, 而后重新构建原始信号, 达到消噪目的.原始信号经小波消噪的效果取决于多个因素, 包括阈值规则选择、阈值模式、尺度系数、小波分解层数以及小波基函数.往往因这些因素的选择不一样, 导致消噪效果差异显著.当小波分解不同时, 噪声也并未完全呈现在高频部分.为了更好地对原信号进行消除噪声, 这就需要能够对信号进行深入多分辨率分解.为此, 提出先将原信号经过EWT算法分解得到多个分辨率的信号分量, 接着对每个分辨率的信号分量进行小波消噪, 最后再基于EWT进行信号重构, 从而达到对原始信号进行消噪, 其原理方框图如图 2所示.
|
图 2 基于EWT消噪方法原理框图 Fig. 2 Structure diagram of EWT-based de-noising method |
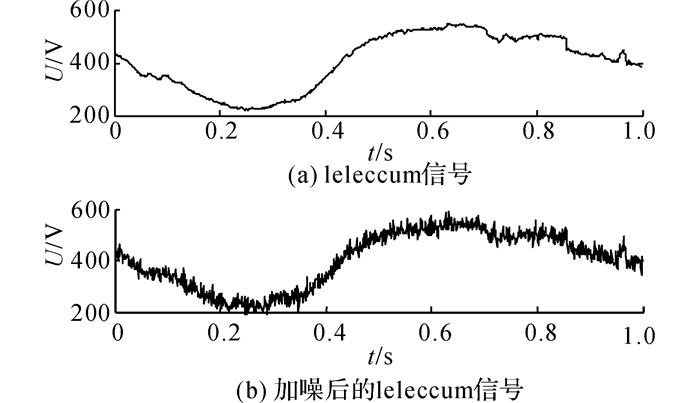
因风力发电机在野外运行, 环境比较恶劣, 振动信号检测容易遭受其他噪声干扰, 直接用实际采集到的振动信号去实现消噪, 则很难验证所提出地基于EWT消噪方法的效果.为此, 取一维非周期电压信号leleccum作为仿真信号, 选1 024个采样点数作为信号长度进行分析验证, 如图 3(a)所示, 图中, U为电压幅值,t为时间.考虑振动信号干扰影响, 叠加一随机噪声后的混合仿真信号如图 3(b)所示.
|
图 3 仿真实验信号 Fig. 3 Simulation signal |
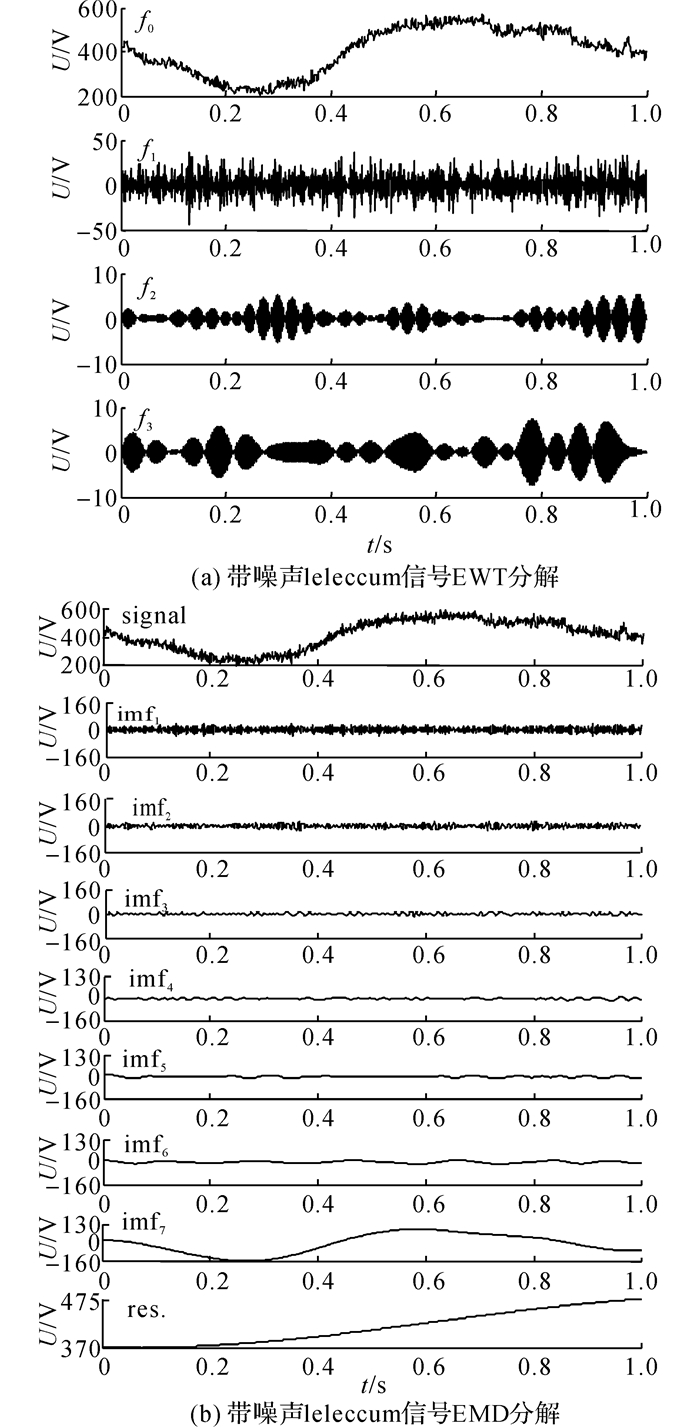
如图 4(a)所示为图 3(b)中的信号经EWT分解后的多分辨信号分量, 与EMD分解类似, 原始带有噪声的leleccum仿真信号一共被分解为4阶固有模态分量f0, f1, f2, f3, 需运算时间为0.009 s.从图 4(a)中可以看出, 带有噪声的leleccum信号分解后得到的各个经验模态函数fi(t)分量都存在噪声分量.而且噪声大部分呈现在高频率分量中.
|
图 4 带噪声leleccum信号分解 Fig. 4 Decomposition of leleccum signal with noises |
同样地, 该信号经EMD分解后, 一共被分解为7阶固有模态函数(imf)和1阶残差(res.), 需运算时间为0.013 s, 如图 4(b)所示.从图中可以看出, 同样的信号经EMD分解, 噪声大都呈现在高频率模态分量中.比较图 4(a)、(b), 以及分析各自的算法实现, 可以看出, 虽然EWT和EMD是自适应地分解, 能够真实地反映信号的分解物理构成, 具有不失原信号能量;但是它们分解的层数不一样, EWT自适应模态分解数优于EMD, 计算量远小于EMD方法, 运算时间较少, 并且具有较强的鲁棒性.
对图 4(a)经EWT分解后的每个多分辨经验模态分量采用Symlet小波函数消噪.Symlet小波函数是对db小波函数的一种改进函数, 除了与db函数在连续性、支集长度、滤波器长度等方面一致, 而且具有更好的对称性, 即一定程度上能够减少对信号进行分析和重构时的相位失真.本文采用阈值
同样地, 选用经典小波db1分别基于强制和软阈值消噪, 得到消噪后的波形如图 5(a)、(b)所示.并且采用一样地基于sym5小波基函数, 取同样地阈值规模、硬阈值模式、5层分解数, 亦根据不同的噪声估计来调整阈值对带噪声的leleccum仿真信号去噪, 并进行消噪后信号重构, 如图 5(c)所示.
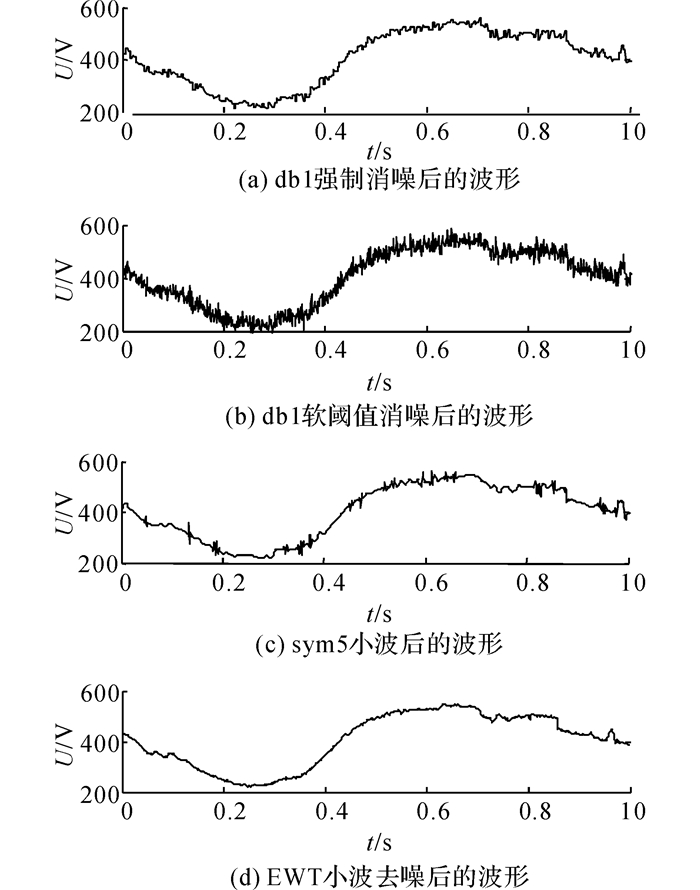
|
图 5 带噪声的leleccum仿真信号消噪后的波形 Fig. 5 Chart of leleccum signal after de-noising |
分析比较4种方法消噪后的波形与原leleccum仿真信号, 从图 5中可以看出, EWT小波消噪后波形最干净, 没有了噪声毛刺, 效果显著;基于db1强制消噪方法和sym5消噪方法比基于db1软阈值消噪的效果明显, 但还存在可见噪声.为了能定量的评价4种消噪效果, 引入信噪比(signal-noise ratio, SNR)和均方根误差(root mean square error, RMSE)作为评价指标, 进行衡量对原leleccum仿真信号的滤波消噪效果差异, 并分析比较了4种方法的运算时间tΔ.经实验, 计算得到消噪评价指标结果如表 1所示.
| 表 1 4种方法针对leleccum消噪结果及运算时间比较 Table 1 Comparisons of de-noising results and operation time of four methods for leleccum signal |
从表 1中可以看出, EWT小波消噪信噪比最大, 均方根误差值最小, 说明效果最好.基于高速计算机运算, 时间差异不大, 对应用分析影响较少.此外, 经过多次实验, 4种消噪方法对于不同的仿真数据运算分析结果会有所变化.
2.2 带噪声轴承故障仿真信号消噪为了进一步验证所提起方法针对振动信号的消噪效果, 以式(13)仿真轴承故障信号[26].
| $ y\left( t \right) = {y_0} \cdot \sin \left( {\omega \sqrt {1 - {g^2}t} } \right)\exp \left( { - g\omega t} \right). $ | (13) |
设轴承固有频率f=3 000 Hz, 位移常数y0=2, 阻尼系数g=0.1, 故障产生的重复周期为0.01, 对信号采样频率fs=20 kHz, 采样点数m=4 096, 并叠加同上述的随机噪声, 混合后仿真信号如图 6(a)所示.图中a为加速度幅值, 该信号经EWT分解为4阶固有模态分量, 需运算时间为0.013 s;经EMD分解后, 一共被分解为11阶固有模态函数和1阶残差, 需运算时间为0.018 s, 且分解的层数远大于EWT.
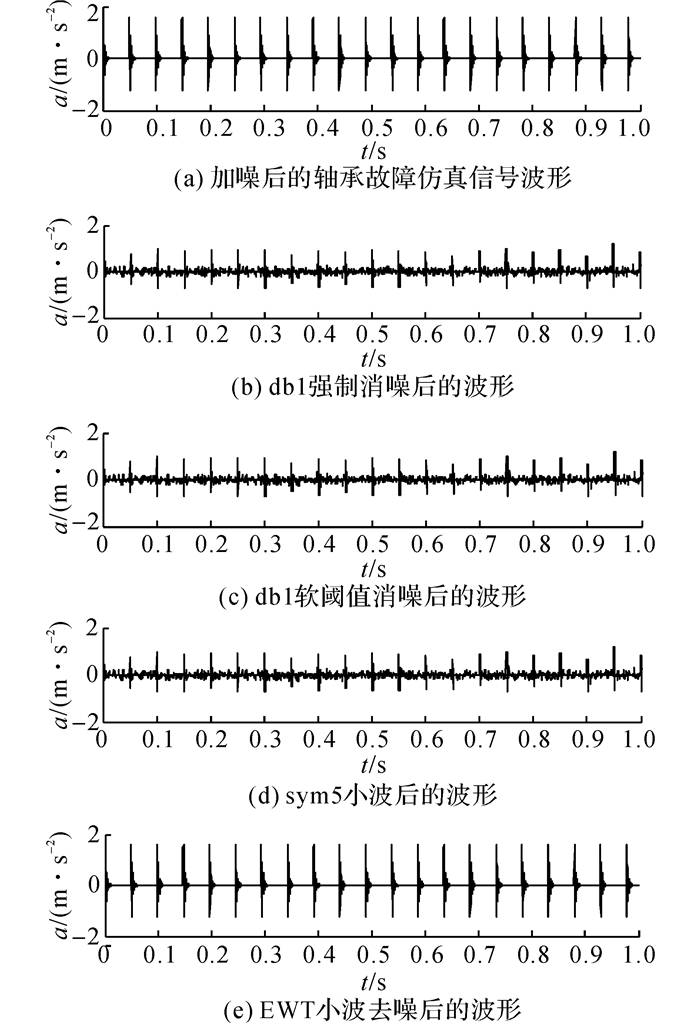
|
图 6 加噪声的轴承故障仿真信号及消噪后的波形 Fig. 6 Chart of bearing fault simulation signal and its after de-noising |
同样地, 针对该轴承故障信号, 采用基于db1强制消噪、基于db1软阈值消噪、基于sym5消噪和基于EWT小波消噪, 得到消噪后的波形如图 6(b)、(c)、(d)、(e)所示.
从图 6中可以看出, EWT小波消噪后波形还是最干净, 波形失真小, 效果显著;基于sym5消噪和db1软阈值消噪方法比基于db1强制消噪方法的效果明显, 但还存在少量失真.为了能准确定量评价4种方法针对轴承故障仿真信号消噪效果, 同样地引入信噪比SNR和均方根误差RMSE作为评价指标, 并分析比较了4种方法的运算时间tΔ.经实验综合分析计算得到消噪评价指标结果如表 2所示.
| 表 2 4种方法针对轴承故障仿真信号消噪结果及运算时间比较 Table 2 Comparisons of de-noising results and operation time of four methods for bearing fault simulation signal |
从表 2中可以看出, EWT小波消噪信噪比最大, 均方根误差值最小, 说明消噪效果还是最好.因数据量大, 对该信号的4种运算时间比leleccum时间长, 但它们之间差异不大.因此, 基于EWT小波消噪效果相对较好.
3 风力发电机振动信号消噪分析为了检验基于经验小波变换的消噪方法针对风力发电机振动信号的消噪效果, 作者到福建某风力发电厂进行数据采集.该风力发电厂现有24台单台容量为2.0 MW的双馈异步风力发电机.风力发电机振动监测系统采用SKF在线监测系统.主轴轴承载荷区的风机侧和电机侧垂直方向各安装1个低频加速度传感器WT135-1D-15, 其灵敏度为500 mV/g, 如图 7所示.
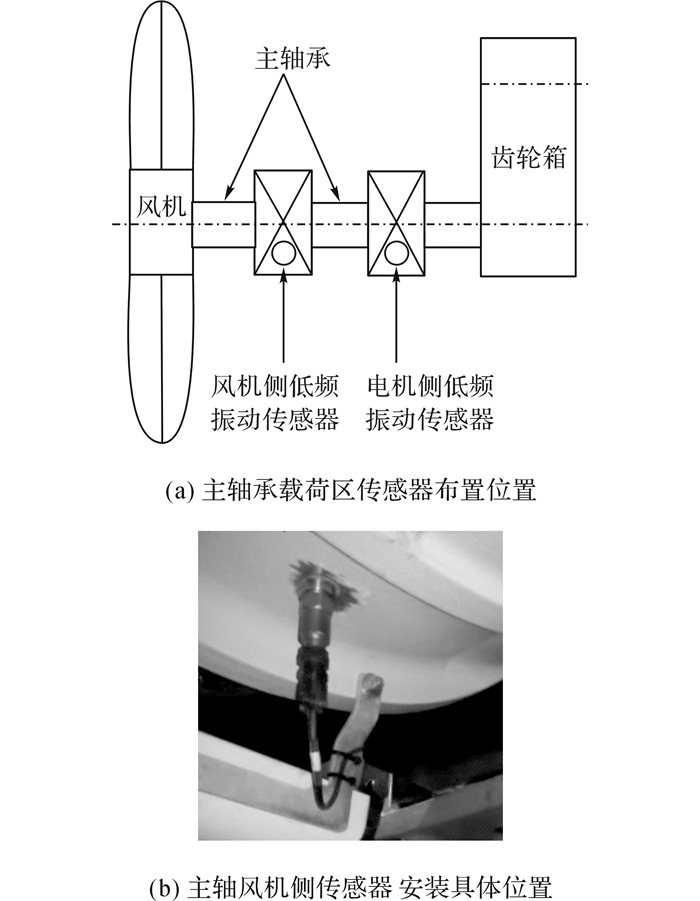
|
图 7 风力发电机主轴承传感器布置安装 Fig. 7 Arrangement and installation of sensor for main bearing of Wind Power Generator |
垂直是指传感器安装与轴的延伸方向在竖直方向上是垂直的.这2个传感器具体安装在主轴轴承底部载荷区, 近似270度的位置(即下部垂直安装, 如图 7(b)所示).数据采集单元基于SKF的IMX-W, 其具有16通道实时信号同时采集功能, 单通道采样率可高达40 kHz.
以主轴风机侧低频加速度传感器采集到的其中一段时间内的振动信号为例进行分析验证, 其信号时域图如图 8(a)所示.从图中可以看出, 振动信号中含着噪声.
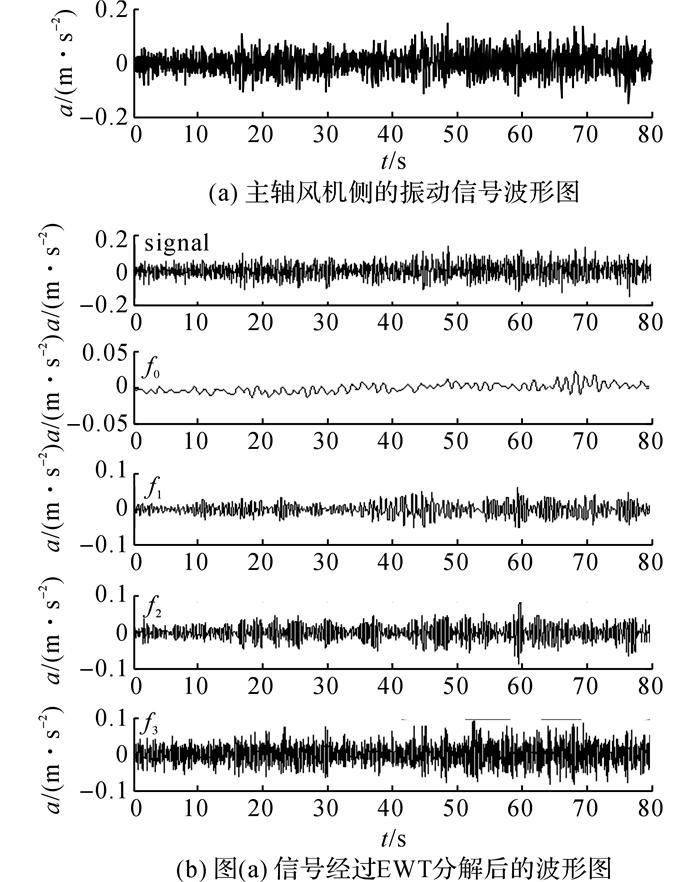
|
图 8 风力发电机主轴承风机侧信号波形图 Fig. 8 Signals chart of fan side of main bearing |
为了解振动信号组成, 对图 8(a)进行EWT分解, 得到4个经验模态分量如图 8(b)所示.从4个经验模态分量可以看出, 其中第2个经验模态分量体现了主要振动特性分量;虽然第3个和第4个分量也分解了振动信号, 但包括了振动高频噪声;而第1个分量则包含了振动低频噪声.
与分析带噪声的仿真信号一样, 对图 8(a)的振动波形信号同样基于db1强制消噪方法、db1软阈值消噪方法、sym5消噪方法和EWT小波消噪方法进行消除噪声, 其结果波形分别如图 9(a)、(b)、(c)和(d)所示.
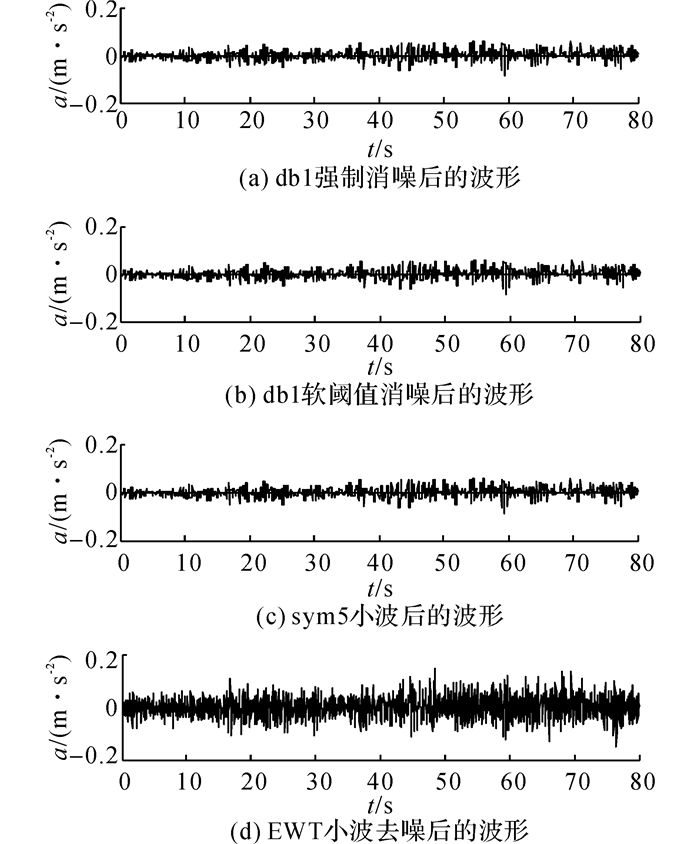
|
图 9 振动信号消噪后的波形 Fig. 9 Vibration signals after de-noising |
从图中可以看出, 图 9(a)和(b)虽然消除了噪声高频, 但同时也把部分振动信号低频消除了, 而且还存有大量的低频噪声;图 9的(d)相对于(a)、(b)在噪声分布的信号段明显没有毛刺, 消噪效果显著, 相对于图 9(c)保持了振动信号频段特征.结合仿真信号消噪后的效果波形图, 振动信号采用EWT算法消噪的效果虽有所变化, 但一样最好.由此可见, 消噪算法对不同的信号消噪的效果虽有所变化, 但消除噪声的性能还是不变的.
4 结语本文介绍了经验小波变换理论及其多分辨特性, 提出了基于经验小波变换的信号消噪方法.基于同样带噪声leleccum和轴承故障仿真信号, 分析对比采用基于db1强制消噪方法、db1软阈值消噪方法、sym5消噪方法和EWT小波消噪方法进行消除噪声的效果.此外, 为了验证基于经验小波变换消噪方法针对风力发电机振动信号的消噪效果, 采用福建某风力发电厂的2.0 MW双馈异步风力发电机振动信号进行分析, 并对其同样运用了其他3种消噪方法处理.实验结果分析表明, 对于仿真信号, 基于EWT小波消噪方法, 与基于db1强制消噪方法、db1软阈值消噪方法和sym5消噪方法能够达到同样地消噪效果和目的, 在相对误差和均方根误差方面甚至更优;4种消噪方法对风力发电机振动信号的消噪效果, 基于EWT小波消噪方法同样显得更有优势.因此, 基于EWT小波消噪方法可以为后期的课题进行风力发电机振动信号分析处理研究打下良好的基础.
| [1] |
MOON D S, KIM S K, KIM S H. A fault detection system for wind power generator based on intelligent clustering method[J]. Journal of Institute of Control, Robotics and Systems, 2013, 19(1): 27-33. DOI:10.5302/J.ICROS.2013.19.1.027 |
| [2] |
FATTAHI S J, ZABIHOLLAH A, ZAREIE S. Vibration monitoring of wind turbine blade using fiber bragg grating[J]. Wind Engineering, 2010, 34(6): 721-731. DOI:10.1260/0309-524X.34.6.721 |
| [3] |
MAY A, MCMILLAN D, TH NS S. Economic analysis of condition monitoring systems for offshore wind turbine sub-systems[J]. IET Renewable Power Generation, 2015, 9(8): 900-907. DOI:10.1049/iet-rpg.2015.0019 |
| [4] |
黄玲玲, 曹家麟, 张开华, 等. 海上风电机组运行维护现状研究与展望[J]. 中国电机工程学报, 2016, 36(3): 729-738. HUANG Ling-ling, CAO Jia-lin, ZHANG Kai-hua, et al. Status and prospects on operation and maintenance of offshore wind turbines[J]. Proceedings of the CSEE, 2016, 36(3): 729-738. |
| [5] |
李辉, 胡姚刚, 唐显虎, 等. 并网风电机组在线运行状态评价方法[J]. 中国电机工程学报, 2010, 30(33): 103-109. LI Hui, HU Yao-gang, TANG Xian-hu, et al. Method for online operating conditions assessment for a grid-connected wind turbine generator system[J]. Proceedings of the CSEE, 2010, 30(33): 103-109. |
| [6] |
盛迎新, 周继威. 风电机组在线振动监测系统及现场应用[J]. 振动、测试与诊断, 2010, 30(6): 703-705. SHENG Ying-xin, ZHOU Ji-wei. Online wind turbine vibration monitoring system and its application[J]. Journal of Vibration, Measurement and Diagnosis, 2010, 30(6): 703-705. |
| [7] |
MADSEN H A, YE M. Low frequency noise from wind turbines mechanisms of generation and its modelling[J]. Journal of Low Frequency Noise Vibration and Active Control, 2010, 29(4): 239-251. DOI:10.1260/0263-0923.29.4.239 |
| [8] |
WATSON S J, XIANG B, YANG W, et al. Condition monitoring of the power output of wind turbine generators using wavelets[J]. IEEE Transactions on Energy Conversion, 2010, 25(3): 715-721. DOI:10.1109/TEC.2010.2040083 |
| [9] |
林勇, 周晓军, 张文斌, 等. 基于形态小波理论和双谱分析的滚动轴承故障诊断[J]. 浙江大学学报:工学版, 2010, 44(3): 432-439. LIN Yong, ZHOU Xiao-jun, ZHANG Wen-bin, et al. Rolling bearing fault diagnosis based on morphological wavelet theory and bi-spectrum analysis[J]. Journal of Zhejiang University:Engineering Science, 2010, 44(3): 432-439. |
| [10] |
CHEN Q, YE M. Analysis of the fault diagnosis method for wind turbine generator bearing based on improved wavelet Packet-BP neural network[J]. Communications in Computer and Information Science, 2014, 463: 13-20. DOI:10.1007/978-3-662-45286-8 |
| [11] |
许同乐, 郎学政, 张新义, 等. 基于EMD相关方法的电动机信号降噪的研究[J]. 船舶力学, 2014, 18(5): 599-603. XU Tong-le, LANG Xue-zheng, ZHANG Xin-yi, et al. Study on the electric motor vibration signal de-noising using EMD correlation de-noising algorithm[J]. Journal of Ship Mechanics, 2014, 18(5): 599-603. |
| [12] |
向东阳, 吴正国, 侯新国, 等. 改进的多小波变换系数相关去噪算法[J]. 高电压技术, 2011, 37(7): 1728-1733. XIANG Dong-yang, WU Zheng-guo, HOU Xin-guo, et al. Improved denoising method using the correlation of multiwavelet coefficient[J]. High Voltage Engineering, 2011, 37(7): 1728-1733. |
| [13] |
TANG B, LIU W, SONG T. Wind turbine fault diagnosis based on Morlet wavelet transformation and Wigner-Ville distribution[J]. Renewable Energy, 2010, 35: 2862-2866. DOI:10.1016/j.renene.2010.05.012 |
| [14] |
ZHENG H, LI Z, CHEN X, et al. Gear fault diagnosis based on continuous wavelet transform[J]. Mechanical systems and Signal Processing, 2002, 16(2/3): 447-457. |
| [15] |
胡爱军, 唐贵基, 安连锁. 基于数学形态学的旋转机械振动信号降噪方法[J]. 机械工程学报, 2006, 42(4): 127-130. HU Ai-jun, TANG Gui-ji, AN Lian-suo. De-noising technique for vibration signals of rotating machinery based on mathematical morphology filter[J]. Chinese Journal of Mechanical Engineering, 2006, 42(4): 127-130. |
| [16] |
HUANG N E. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C]//Proceedings of the Royal Society of London A: mathematical, physical and engineering sciences. London: The Royal Society, 1998, 454(A): 903-995. http://www.jstor.org/stable/53161
|
| [17] |
HUANG N E, WU Z. A review on Hilbert-huang transform:method and its applications to geophysical studies[J]. Reviews of Geophysics, 2008, 46(2): 1-23. |
| [18] |
YAN R, GAO R. Hilbert-Huang Transform-Based vibration signal analysis for machine health monitoring[J]. IEEE Transactions on Instrumentation and Measurement, 2006, 55(6): 2320-2329. DOI:10.1109/TIM.2006.887042 |
| [19] |
Gilles J. Empirical wavelet transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 3999-4010. DOI:10.1109/TSP.2013.2265222 |
| [20] |
KARTHIK T, AMOD C U, TRAPTI J. Estimation of single-phase and three-phase power-quality indices using empirical wavelet transform[J]. IEEE Transactions on power delivery, 2015, 30(1): 445-454. DOI:10.1109/TPWRD.2014.2355296 |
| [21] |
LI Y S, XUE B, HONG H, et al. Instantaneous pitch estimation based on empirical wavelet transform[C]//Proceedings Of The 19th International Conference On Digital Signal Processing. Hong Kong: IEEE, 2014: 250-253. http://ieeexplore.ieee.org/document/6900838/
|
| [22] |
李志农, 朱明, 褚福磊, 等. 基于经验小波变换的机械故障诊断方法研究[J]. 仪器仪表学报, 2014, 35(11): 2423-2432. LI Zhi-nong, ZHU Ming, CHU Fu-lei. Mechanical fault diagnosis method based on empirical wavelet transform[J]. Chinese Journal of Scientific Instrument, 2014, 35(11): 2423-2432. |
| [23] |
陈浩, 郭军海, 齐巍. 基于经验小波变换的目标加速度估计算法[J]. 北京航空航天大学学报, 2015, 41(1): 154-159. CHEN Hao, GUO Jun-hai, QI Wei. Estimation of target's acceleration based on empirical wavelet transform[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(1): 154-159. |
| [24] |
OMKAR S, RAMESH K S. Onset detection in arterial blood pressure pulses using empirical wavelet transform[C]//2nd International Conference on Computing for Sustainable Global Development. New Delhi: IEEE, 2015: 1612-1615. http://ieeexplore.ieee.org/document/7100520/
|
| [25] |
PATRICK F, GABRRIEL R, PAULO G. Empirical mode decomposition as a filter bank[J]. IEEE Signal Processing Letters, 2004, 11(2): 112-114. DOI:10.1109/LSP.2003.821662 |
| [26] |
艾延廷, 冯研研, 周海仑. 小波变换和EEMD-马氏距离的轴承故障诊断[J]. 噪声与振动控制, 2015, 35(1): 235-239. AI Yan-ting, FENG Yan-yan, ZHOU Hai-lun. Fault diagnosis of roller bearings using wavelet transform and EEMD-Mahalanobis distance[J]. Noise and Vibration Control, 2015, 35(1): 235-239. |


