低温浆体是固液态共存的低温流体, 即在液体中含有固体小颗粒.目前受到较多关注的低温浆体有氢浆和氮浆.相较于常沸点低温液体, 浆态流体具有更低的温度、更高的密度和更大的热容量等优势.二十世纪60年代, 林德公司对氢浆的生产和储存等方面的特性进行了较为全面的理论及实验研究, 氢浆被认为是一种有应用潜力的航天推进剂, 可望有效减少航天器的尺寸及负重, 从而降低发射成本[1-2].氮浆则主要被期望应用于高温超导材料的冷却.相较于常沸点液氮, 氮浆可降低高温超导材料失超风险, 同时减少冷却剂的储存及运输等成本[3-6];此外, 氮浆在改善生物冷冻保存质量方面也有受到关注[7].
目前关于低温浆体的研究主要集中在浆体制备方法、测量技术、浆体流动传热特性[8-13]等3个方面.由于颗粒的存在, 低温浆体的液位测量有别于低温液体, 目前液位监测和测量[14-20]最常用的方法有电容法、差压法、电阻法、超声波法等.电容法由于结构简单、制作成本低、灵敏度高、适应低温环境等特点而在低温两相流的测量中得到重视.江芋叶等[20]针对电容式液位计在氮浆中的应用进行了测试, 采用双层屏蔽电缆并将内屏蔽层接地对测量电路进行优化.然而, 由于低温浆体制备的温度及物理环境都比较复杂, 这种方法尚无法做到真正的整体屏蔽, 抗干扰能力的改善程度需进一步验证.
目前, 对于电容式液位计的低温测量相关的研究还不够深入和全面, 由于低温实验环境较为复杂, 电容式传感器存在抗干扰能力较差等缺点, 需要进一步优化其结构及测量电路.本文以氮浆为例, 采用电容法进行液位测量的实验研究, 对液位计设置屏蔽层并将屏蔽层接地, 分析LCR测量频率对电容液位计稳定性的影响, 以期改善液位计的灵敏度、抗干扰能力及可靠性.此外, 将改进的电容式液位计应用到氮浆的液位及流速的测量中, 以期考察液位计对于流量估算的可靠性.
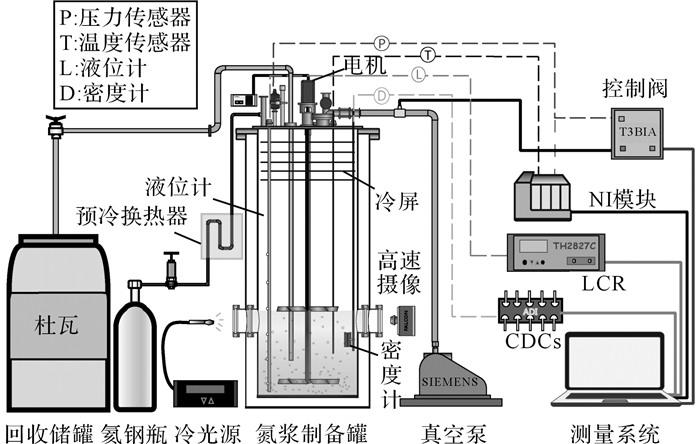
1 电容法测量原理及实验系统 1.1 氮浆制备及流速测量实验系统实验中所用氮浆由如图 1所示实验系统制备获得.氮浆的制备系统主要由制备储罐、真空系统、搅拌系统、可视化观察系统、测量系统等部分组成.制备储罐的设计静态蒸发率为1.2 L/h;真空泵采用西门子FD系列的机械泵, 最大抽速为18 L/s;用于打碎固氮层的搅拌器采用2个上下安装的四叶浆式叶轮, 可打碎固氮层, 并增强储罐内流体对流作用;氮浆颗粒组分由电容式密度计测量获得;储罐内沿竖直方向安装4个Pt100温度计, 温度计经中科院在55~300 K温度范围内标定, 精度为±0.1 K.
|
图 1 氮浆流动及测量实验系统示意图 Fig. 1 Schematic of experimental setup for flow test and measurements of slush nitrogen |
电容传感器测量的寄生电容不可忽略.寄生电容包括连接传感器与电子线路的电缆电容、电子线路的杂散电容以及传感器极板与周围导体构成的电容等, 通常会随低温环境、机械运动、环境温度而变化, 这些寄生电容是随机且不可避免的, 数值极有可能与传感器自身电容具有相同数量级, 甚至具有更高数量级, 从而导致测量结果出现偏移, 显著影响系统精度.为保证测量精度, 在每次实际使用之前需要对电容式液位计进行标定.
1.2 电容式液位计测量原理及优化电容式液位计的测量原理是将液位的变化转化为电容量的变化.由于储罐内氮的气液两相介电常数的差异[22], 电容值随液位变化而改变, 同时介电常数和电容量存在较好的线性关系, 因此探测电极间电容Ch和液位h的关系式为
| $ {C_h} = {C_{0, h}}h + {C_{d, h}}. $ | (1) |
式中:C0, h和Cd, h分别为液位计的灵敏度和无功电容.
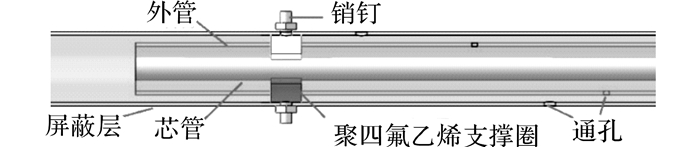
如图 2所示, 电容式液位计采用三层同轴管作为电极, 里面两层为电容极板, 芯管外径为6 mm, 外管内径为12 mm, 最外层设置屏蔽层.液位计的外管及屏蔽层上每隔一段距离设有1 mm直径小通孔, 而制备的氮浆固氮颗粒平均尺寸在1.5 mm左右.通孔在保证液氮自由地流进流出的同时, 可忽略进入电极间的极少量固体颗粒.由此, 在对氮浆进行测量时, 可认为电极间的介质均为三相点状态的液氮.同轴管采用高质量的卫生级不锈钢管, 并均匀地布置4组聚四氟支撑垫圈, 保证2根电极管的同轴度;屏蔽层外径为20 mm, 通过螺纹连接顶端安装在储罐顶盖, 并利用金属销钉将内部两根电极管定位, 壁面电极管在竖直方向的移动.屏蔽层可实现对电极的有效保护, 减少外部物理冲击的影响, 提高液位计强度, 减弱机械摆动对于液位计的测量影响;另一方面, 通过屏蔽层接地可以降低周围环境的电磁干扰, 有效改善液位计精度、稳定性及可靠性.
|
图 2 电容式液位计结构图 Fig. 2 Structure diagram of capacitance type liquid level meter |
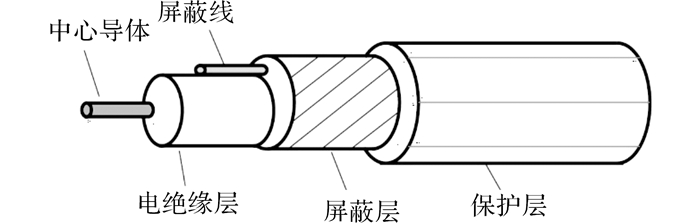
测量电路使用引线为如图 3所示Lakeshore的C型超细同轴电缆, 包括镀银纯铜中心导体, 聚四氟乙烯绝缘层, 屏蔽线和铝制屏蔽层等的多层结构, 其在低温下依然具有较好的柔性、强度及屏蔽性能, 且弯曲寿命长.
|
图 3 同轴电缆结构示意图 Fig. 3 Structure diagram of double-shielded cable |
当电极间液氮的液位高度为h时, 液位计的理论电容值为
| $ {C_h} = \frac{{2{\rm{ \mathsf{ π} }}{\varepsilon _0}}}{{{\rm{ln}}\left( {{d_2}/{d_1}} \right)}}\left[{\left( {{\varepsilon _{\rm{l}}}-{\varepsilon _{\rm{v}}}} \right)h + {\varepsilon _{\rm{v}}}H} \right]. $ | (2) |
式中:ε0为真空介电常数, 8.854×10-12 F/m.εv和εl分别为氮在常沸点下的气态和液态的相对介电常数, εv=1.002 60, εl=1.429 09.d1和d2分别为内外电极管的外径和内径, H为电极管的有效长度, 实验中H=700 mm.则可得正常沸点状态下液位计的名义灵敏度和无功电容分别为
| $ {C_{0, h}} = \frac{{2{\rm{ \mathsf{ π} }}{\varepsilon _0}\left( {{\varepsilon _{\rm{l}}}-{\varepsilon _{\rm{v}}}} \right)}}{{{\rm{ln}}\left( {{d_2}/{d_1}} \right)}}, $ | (3) |
| $ {C_{d, h}} = \frac{{2{\rm{ \mathsf{ π} }}{\varepsilon _0}{\varepsilon _{\rm{v}}}}}{{{\rm{ln}}\left( {{d_2}/{d_1}} \right)}}. $ | (4) |
计算可得正常沸点状态下液位计的C0, h= 37.59 pF/m, Cd, h=27.049 pF.
电容式液位计的电容信号使用LCR测量仪进行采集, LCR的最高测试频率为1 MHz, 分辨率为10 mHz, 基本精度为0.05%.
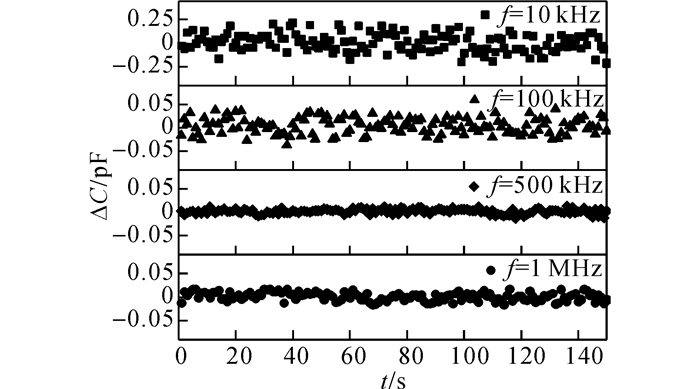
2 实验结果分析 2.1 LCR测量频率的选择LCR测量仪的测量频率对液位计读数的影响较大.电容式液位计的准确度和灵敏度都与测量频率相关.选取合适的测量频率对于实验中液位的准确测量至关重要.将液位计安装于盛有一定量常沸点液氮的储罐中.测量电压1 V, 测量频率f分别选取10、100、500和1 MHz.当测量频率改变时, LCR测得的有效电容也会发生变化.在测量频率分别为10、100、500和1 MHz时, 测得的电容平均值依次为91.54、92.72、103.90和105.81 pF.随着测量频率的升高, 有效电容增大, 分辨率也增强.图 4给出了不同测量频率对液位计稳定性能的影响, 图中t为采集时间, ΔC为电容量波动值.从图中可以发现, 测量频率不超过100 kHz时, 测量结果极不稳定, 这说明低频时液位计电路的容抗较大, 测量系统易受干扰, 故波动较大.测量频率高于500 kHz时, 测量结果稳定性明显改善, 读数较为稳定, 实验中采用1 MHz作为LCR数字电桥的测量频率.
|
图 4 LCR测量频率对液位计的影响 Fig. 4 Influence of test frequency of LCR meter on measurements of liquid level meter |
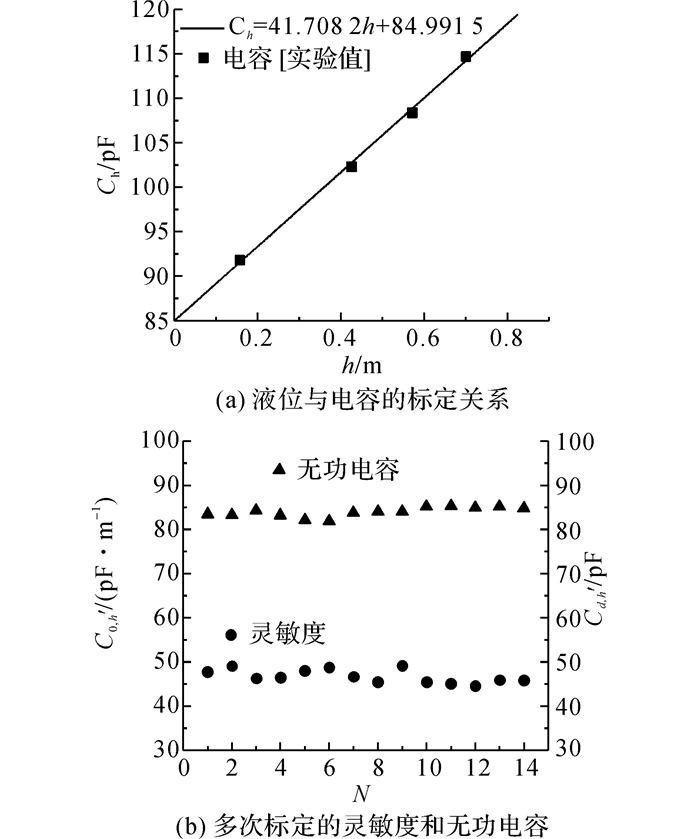
液位计的标定是在液氮充注环节进行的, 通过参考点位置来确定液氮真实的液位高度, 同时读取参考点液位时液位计相应的电容值.采用最小二乘法拟合电容值和高度值的关系, 获得液位计的灵敏度及无功电容.如图 5(a)所示给出液位计的某次标定结果.液位计在液氮中标定得到的灵敏度为41.708 2 pF/m, 无功电容为84.991 5 pF.液位计标定所得的灵敏度相较于名义灵敏度提高11%左右, 可见屏蔽层对于电极的保护效果显著.电容式液位计具有线性度良好、灵敏度高和稳定性好等优点.
|
图 5 电容式液位计的标定结果 Fig. 5 Calibration results for capacitance type liquidlevel meter |
液位在静置的常沸点液氮中标定, 而实际上, 液位计的灵敏度及无功电容均与相对介电常数相关.因此, 在测量氮浆液位时, 需根据三相点氮的介电常数对液位计的灵敏度和无功电容进行进一步修正, 修正公式为
| $ C{\prime _{0, h}} = {C_{0, h}}\frac{{{{\left( {{\varepsilon _{\rm{l}}}-{\varepsilon _{\rm{v}}}} \right)}_{{\rm{TP}}}}}}{{{{\left( {{\varepsilon _{\rm{l}}}-{\varepsilon _{\rm{v}}}} \right)}_{{\rm{NBP}}}}}}, $ | (5) |
| $ C{\prime _{d, h}} = {C_{d, h}}\frac{{{{\left( {{\varepsilon _{\rm{v}}}} \right)}_{{\rm{TP}}}}}}{{{{\left( {{\varepsilon _{\rm{v}}}} \right)}_{{\rm{NBP}}}}}}. $ | (6) |
式中:下标TP表示三相电状态参数, 下标NBP为常沸点状态参数.可查得在三相点状态下氮的相对介电常数值为:气态εv=1.000 32, 液体εl=1.468 67.修正后得到的标定公式为Ch=45.801 6h+84.796.由于在对氮浆进行测量时, 可以认为电极间的介质均为三相点状态的液氮, 因此该公式对于氮浆是适用的.
图 5(b)给出了电容式液位计多次实验的标定结果, N为实验次数.在不同实验中, 液位计标定得到的灵敏度和无功电容均会存在一定范围内的波动, 这是由寄生电容的随机性而引起.灵敏度平均值为46.76 pF/m, 平均无功电容为83.97 pF, 波动在5%以内, 总体而言, 该电容式液位计的稳定性较好, 灵敏度较高.
液位计的误差主要由系统误差与标定误差组成.根据标定公式(1), 该液位计液位测量的绝对误差可以由以下公式得到
| $ \Delta h = \pm \frac{{\left( {{C_h}-{C_{d, h}}} \right)\Delta {C_0} + {C_{0, h}}\left( {{C_h}{\delta _{\rm{C}}}-\Delta {C_d}} \right)}}{{C_{0, h}^2}}. $ | (7) |
式中:ΔC0为灵敏度的绝对误差, ΔCd为无功电容的绝对误差, δC为相对误差.表 1中给出了液位计误差分析的参数值, 其中LCR的准确度为0.05%.由表 1及式(7)可得, 该液位计的测量相对误差Δh/h=±0.23%.在同样的电极结构和尺寸下, 文献[21]中研究的电容式液位计相对误差为±1%, 灵敏度为36.965 pF/m.可见, 本研究中所研制的液位计具有较高的精度和灵敏度.
| 表 1 液位计误差分析的相关参数 Table 1 The parameters used in error analysis of liquid level meter |
对液氮抽真空可使其温度降到三相点.当液氮充注完成后, 液位计测得液氮液位为0.687 m.制备工艺开始后, 对储罐进行抽真空, 当液氮状态降到三相点时, 固氮开始生成, 此时根据修正过的液位计测得液位为0.577 m, 可计算得到液氮降温过程一共消耗约16%的液氮.
当抽真空时, 由于液氮蒸发引起的能量损耗为
| $ {Q_{{\rm{vap}}}} = {\rho _0}({V_0}-{V_t}){h_{{\rm{vap}}}}. $ | (8) |
式中:ρ0和V0分别为初始液氮的密度和体积, Vt为剩余液氮体积, hvap为液氮蒸发潜热.
剩余液氮的冷量增加为
| $ \Delta Q = {\rho _{\rm{t}}}{V_{\rm{t}}}({h_{\rm{t}}}-{h_0}). $ | (9) |
式中:ρt为三相点液氮的密度, h0和hl分别为液氮初始状态与三相点状态的焓值.
假设不考虑漏热的影响, 可以认为ΔQ=Qvap, 则可计算得到理论的液氮消耗量(V0-Vt)/V0=15.1%.与液位测得的实验结果基本吻合, 该液位计准确度较好.其余0.9%主要由于系统漏热而引起.
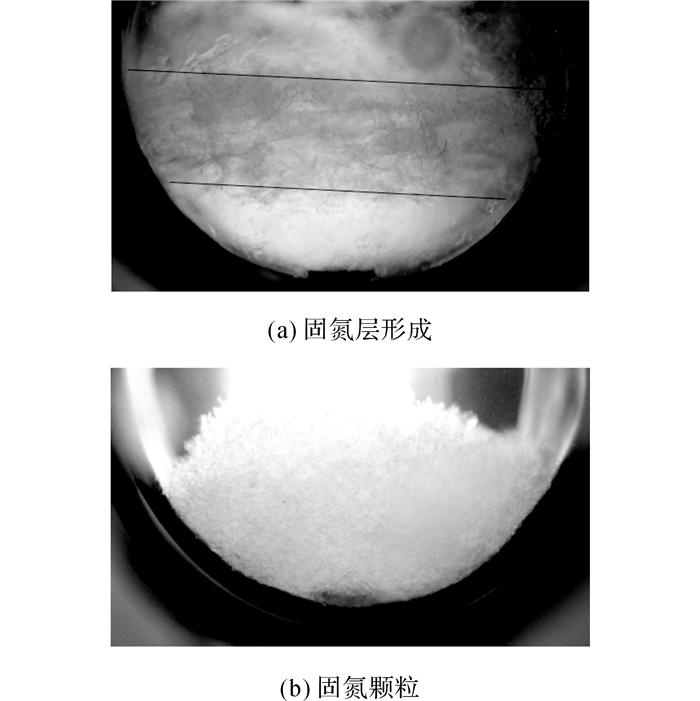
2.3 氮浆的制备实验采用冻结-融化法进行氮浆制备, 即周期性地对储罐抽真空, 在抽真空的间歇由于储罐漏热, 固氮层融化, 利用搅拌叶轮对固氮层进行打碎、搅拌.真空泵抽速、搅拌速度、冻结-融化周期等对氮浆的制备质量都有一定影响, 在氮浆制备实验中, 真空泵抽速为9 L/s, 搅拌速度115 r/min, 冻结-融化周期分别为15 s.图 6给出了制备过程氮浆实物状态图.在冻结过程中, 较为疏松的絮状固氮层在液面形成, 如图 6(a)所示;在融化过程中, 固氮层下沉, 破碎.氮浆制备初始阶段, 固氮颗粒大多呈现细小的雪花状, 由于叶轮的搅拌作用在储罐中漂浮.时间变长之后, 由于固氮之间的碰撞及固氮本身的老化, 固氮颗粒逐渐形成球体或椭球型晶状, 如图 6(b)所示.固氮颗粒均布于液氮中, 形成的固氮颗粒平均尺寸为1.5 mm左右.因此, 液位测量时, 进入液位计电极间的固体颗粒可以忽略, 从而可认为电极间均为液氮.
|
图 6 氮浆实物图 Fig. 6 Photos of prepared slush nitrogen |
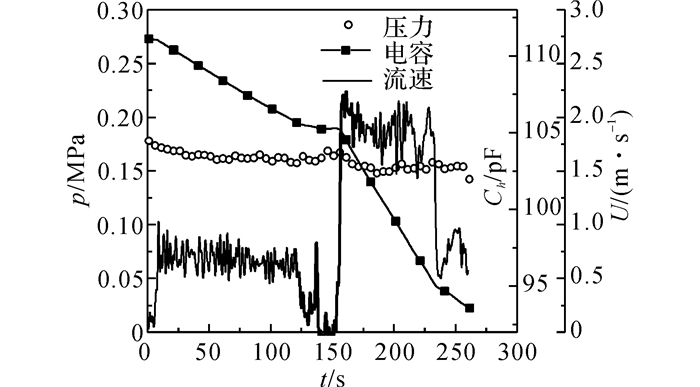
采用低温氦气对氮浆储罐增压, 将氮浆从流动管道中卸回至回收杜瓦中.利用标定和修正过的电容式液位计测量储罐内液位变化, 从而估算氮浆的卸回流速.图 7给出了液位计估算氮浆流速实验结果, p为工作压力, U为测得的流速.储罐增压0.17 MPa左右, 调节出口低温阀可改变流出速度, 速度的计算是根据每1 s内液位电容估算得到的, 因此存在一定的波动变化.从图中可以看到, 液位计灵敏度高, 稳定性好, 当用于估算一定时间段内的流速时较为可靠.
|
图 7 液位变化估算氮浆流速实验结果 Fig. 7 Slush nitrogen flow velocity calculated fromliquid level change |
电容法作为测量低温浆体液位的一种具有较好应用前景的技术手段, 目前还存在抗干扰能力及稳定性不足的缺点.本文工作对电容式液位计的结构进行优化, 并对可应用于氮浆液位及流速测量的电容式液位计进行标定及实验研究.
采用高质量的卫生级不锈钢同轴管作为液位计电极, 保证2根电极管的同轴度;电极外增设全屏蔽保护套管, 减少机械扰动对电极的冲击, 并通过屏蔽层接地降低了周围环境的电磁干扰, 有效实现对电极的保护.以标准参考点高度对液位计标定, 不同实验中, 液位计标定结果均会存在一定范围内的波动, 平均灵敏度为46.76 pF/m, 平均无功电容为83.97 pF, 波动在5%以内, 理论分析准确度在±0.23%以内.总体而言, 液位计的精度、灵敏度及稳定性都得到改善.
实验中采用的氮浆平均固相粒径为1.5 mm左右.由氮浆增压流动的实验结果可知, 在深低温、机械扰动等恶劣环境下, 优化的电容式液位计运行稳定, 灵敏度和精度较高, 用液位变化来估算一段时间内的平均流速的方法较为可靠.
| [1] |
CARNEY R R. "Slush hydrogen" production and handling as a fuel for space projects[M]. [S.l.]: Springer US, 1964, 529-536.
|
| [2] |
REYNIER P, BUGEL M, LECOîNTRE J. Review of the modelling of slush hydrogen flows[J]. Journal of Computational Multiphase Flows, 2011, 3(3): 123-146. DOI:10.1260/1757-482X.3.3.123 |
| [3] |
JIN T, LI Y J, LIANG Z B, et al. Numerical prediction of flow characteristics of slush hydrogen in a horizontal pipe[J]. International Journal of Hydrogen Energy, 2017, 42(6): 3778-3779. DOI:10.1016/j.ijhydene.2016.09.054 |
| [4] |
JIN Tao, LI Yi-jian, WU Shu-qin, et al. Numerical modeling for the flow and heat transfer of slush nitrogen in a horizontal pipe based on population balance equations[J]. Applied Thermal Engineering, 2017, 123: 301-309. DOI:10.1016/j.applthermaleng.2017.05.077 |
| [5] |
OHIRA K, ISHIMOTO J, NOZAWA M, et al. Heat transfer characteristics of slush nitrogen in turbulent pipe flows[C]//Advances in Cryogenic Engineering. Seoul, Korea: AIP Publishing, 2008, 985: 1141-1148. http://dx.doi.org/10.1063/1.2908465
|
| [6] |
PARK Y M. Literature research on the production, loading, flow, and heat transfer of slush hydrogen[J]. International Journal of Hydrogen Energy, 2010, 35(23): 12993-13003. DOI:10.1016/j.ijhydene.2010.04.074 |
| [7] |
YOON T K, LEE D R, CHA S K, et al. Survival rate of human oocytes and pregnancy outcome after vitrification using slush nitrogen in assisted reproductive technologies[J]. Fertility & Sterility, 2007, 88(4): 952-956. |
| [8] |
OHIRA K, MATSUO S, FURUMOTO H. An experimental investigation of production and density measurement of slush hydrogen[J]. Cryogenics, 1994, 34(1): 397-400. |
| [9] |
OHIRA K, NAKAGOMI K, TAKAHASHI N. Pressure-drop reduction and heat-transfer deterioration of slush nitrogen in horizontal pipe flow[J]. Cryogenics, 2011, 51(10): 563-574. DOI:10.1016/j.cryogenics.2011.07.008 |
| [10] |
BAKER M J, DENTON T T, HERR C. An explanation for why it is difficult to form slush nitrogen from liquid nitrogen used previously for this purpose[J]. Cryobiology, 2013, 66(1): 43-46. DOI:10.1016/j.cryobiol.2012.10.007 |
| [11] |
OHIRA K. Study of nucleate boiling heat transfer to slush hydrogen and slush nitrogen[J]. Heat Transfer-Asian Research, 2003, 32(1): 13-28. DOI:10.1002/(ISSN)1523-1496 |
| [12] |
ZHANG P, JIANG Y Y. Forced convective heat transfer of slush nitrogen in a horizontal pipe[J]. International Journal of Heat & Mass Transfer, 2014, 71(1): 158-171. |
| [13] |
JIANG Y Y, ZHANG P. Density determination of slush nitrogen by the improved capacitance-type densimeter[J]. Experimental Thermal & Fluid Science, 2011, 35(2): 328-337. |
| [14] |
曹建, 安刚, 马晨辉, 等. 低温液位计[J]. 导弹与航天运载技术, 2008(6): 52-54. CAO Jian, AN Gang, MA Chen-hui, et al. Low temperature liquid level indicator[J]. Missiles and Space Vehicles, 2008(6): 52-54. |
| [15] |
马登奎, 毕延芳, 冯汉升, 等. 浮力式低温液位计的设计原理及运行工况分析[J]. 低温与超导, 2009, 37(7): 16-19. MA Deng-kui, BI Yan-fang, FENG Han-sheng, et al. Design principles and operating conditions analysis of buoyancy cryogenic liquid level meter[J]. Cryogenics and Superconductivity, 2009, 37(7): 16-19. |
| [16] |
PARK H C, JEONG H J, LEE C Y, et al. Liquid nitrogen level meter for high-temperature superconductor (HTS)[J]. Journal of Central South University of Technology, 2012, 19(11): 3100-3104. DOI:10.1007/s11771-012-1384-8 |
| [17] |
KNIGHT B L, TIMMERHAUS K D, FLYNN T M. A superconducting liquid-Level sensor for slush hydrogen use[M]. [S.l]: Springer, Boston, MA, 1966, 218-222.
|
| [18] |
LERSCH D, PASCOVICI G, BIRKENBACH B, et al. The liquid nitrogen fill level meter for the AGATA triple cluster detector[J]. Nuclear Instruments & Methods in Physics Research, 2011, 640(1): 133-138. |
| [19] |
LEE C K, HWANG G W, JEONG S K. Development of cryogenic liquid-vapor separator and liquid-level meter operating under high pressure condition[J]. Progress in Superconductivity & Cryogenics, 2011, 13(1): 51-55. |
| [20] |
江芋叶, 张鹏. 氮浆电容式密度计及液位计的实验研究[J]. 低温与超导, 2010, 38(5): 19-23. JIANG Yu-ye, ZHANG Peng. Study on the capacitance-type densimeter and liquid level meter for slush nitrogen[J]. Cryogenics and Superconductivity, 2010, 38(5): 19-23. |
| [21] |
STEWART J W. Dielectric polarizability of fluid para-hydrogen[J]. Journal of Chemical Physics, 1964, 40(11): 3297-3306. DOI:10.1063/1.1724998 |



