对几何形状检测的问题是图像识别中的经典问题, 椭圆作为常见的复杂几何形状, 它的识别在许多领域有着广泛的应用.例如车轮检测[1]、路标分类[2]、人脸识别[3]、瞳孔识别[4]、细胞检测[5]以及复杂物体的几何形状表达等[6].因此, 快速、准确的检测出目标图片中的椭圆特征具有十分重要的研究价值.
常用的椭圆检测方法以霍夫变换和最小二乘法拟合为主.由于椭圆方程由5个参数组成, 因此通过霍夫变换检测椭圆的方法主要致力于克服标准霍夫变换中5维累加器计算量过大的问题. Mclaughlin等[7]提出了一种基于随机霍夫变换的椭圆检测方法, 通过随机选取3个点并根据椭圆中心的特性利用3点的切线方向计算椭圆中心, 将椭圆的参数计算从5维降至3维, 提高了计算速度. Cheng等[8]在此基础上提出了一种带约束的随机霍夫椭圆检测方法, 将图像中边缘线的连续性、拐点个数作为约束条件, 减少了随机霍夫椭圆检测的误检率.Lu等[9]提出了一种迭代随机霍夫椭圆检测的方法, 通过不断迭代寻找“感兴趣的区域”, 缩小矩形窗的大小从而减少计算量.邹荣等[10]等通过参数空间的少量投票, 依据均值漂移技术获取粗略的椭圆中心, 再由精提策略实现椭圆中心的精确像素级定位, 并采用插值方法进一步获取椭圆中心亚像素坐标.
通过最小二乘法拟合椭圆的研究致力于提高拟合的计算速度及精度. Fitzgibbon等[11]提出了直接最小二乘法拟合椭圆, 通过二次曲线的代数方程定义了一个最小值问题并通过数值约束使得所求值符合椭圆曲线的特征, 通过广义特征值的求解避免了最小二乘法的迭代求解.Liu等[12]通过直接最小二乘法的结果作为初始迭代条件, 以几何距离最小作为求解目标, 利用梯度下降法获得更加精确的椭圆拟合结果.Maini等[13]针对文献[11]中在特定情况下散布矩阵的病态性、约束矩阵的奇异性, 提出了一种矩阵归一化的方法, 解决了广义特征值难以求解的问题并提高了计算效率.
以上2类方法均从像素点的角度出发对图像中的椭圆进行识别, 故而忽略了图像中物体边缘连续性的信息.在复杂图像检测时, 由于不同物体边缘上的像素点可能满足构成同一椭圆的要求, 使得这两类方法的误检率居高不下.
近年来, 一些基于边缘连续性的复合检测方法在复杂图像椭圆检测中取得了较好的效果. Prasad等[14]首先将连续像素点转换成直线段的集合, 通过直线段的相对位置判定线段的角点并进行边缘线分割, 再利用边缘线切线斜率构建的搜索区域寻找相互匹配的边缘线, 最后通过霍夫变换方法分别计算匹配边缘线中的椭圆.吴尧锋等[15]通过边界像素连接、线段提取和圆弧聚类得到一系列候选椭圆弧对, 并采用直接最小二乘法拟合椭圆.Chen等[16]结合了边缘聚类检测方法与霍夫变换方法, 首先通过边缘连续性的方法识别出大部分椭圆, 再使用霍夫变换在候选区域识别出漏检的椭圆, 该方法在低信噪比的工业图像中取得了良好的效果.
上述基于连续性的方法虽然在复杂背景下的椭圆识别取得了较好的效果, 但是圆弧特征的提取十分繁琐, 包括像素连续性检测、线段提取、角点检测以及圆弧边缘的聚类等过程, 计算复杂, 难以达到实时性要求;另外, 利用几何特性判定椭圆中心的聚类方法存在原理性误差, 当椭圆大小相差较大时, 易出现漏检测的现象导致检测准确率降低.
因此, 本文提出了一种基于梯度分类与多边形辨识的复杂背景下椭圆快速检测算法.结合Canny算子边缘检测中的像素灰度梯度及边缘凹凸性将边缘线直接分为4类圆弧特征, 以提高圆弧特征的提取效率.根据椭圆内包多边形为凸多边形的性质, 提出了一种通过判定圆弧特征顶点间的矢量与位置关系, 快速辨识出符合约束的圆弧集合的方法.应用非迭代的几何最小二乘法对圆弧集合进行拟合, 通过拟合算子的判定及椭圆去伪处理获得最终的椭圆集合.最后通过实验对比了相关算法, 验证了本文算法的有效性与优越性.
1 基于梯度与凹凸性的边缘线分类 1.1 图像预处理图像预处理的目的是将待检测图像中的边缘信息从复杂的图像信息中提取出来, 为后续圆弧边缘的分类提供基础特征.预处理过程主要包括:
1) 色彩处理:椭圆特征是一种几何特征, 对图像颜色信息不敏感.因此为提高计算效率, 通过灰度变换将待检测图像转换为灰度图像, 并通过对比度拉伸提升图像中前景与背景之间的对比度.
2) 边缘检测:复杂场景下的椭圆边缘与其他干扰物体边缘可能产生重合与遮挡, 导致常用固定阈值的边缘检测算子检测效果良莠不济, 过高的阈值会导致椭圆边缘的丢失;较低的阈值则会降低识别效率.因此采用一种基于边缘连续性的自适应Canny检测算子[17]对图像的边缘进行检测, 以达到良好的检测效果.
3) 边缘细化:为了提高后续椭圆拟合的准确率与计算效率, 需要将边缘线尽量细化至一个像素的宽度.为此采用Chatbri等[18]提出的边缘细化算法对检测出的边缘进行细化处理.
由于在Canny检测算子中包含了高斯滤波算法对图像进行降噪处理其具有良好的降噪效果, 因此在图像预处理过程中不再使用额外的图像滤波算法.将边缘细化后得到的二值图像作为椭圆识别的基准图像, 进行边缘线的分类及聚类.
1.2 基于灰度梯度的边缘分类将预处理所得二值图像中的像素点用P(x, y, θ)表示, 其中x, y分别表示边缘点在图像中的横坐标和纵坐标, θ表示点P的整体灰度梯度与x方向灰度梯度的夹角, 取值范围为(-π/2, π/2).θ的值可以通过图像预处理阶段Canny边缘检测算子中采用的一阶差分卷积算子计算的灰度梯度求得.通过分别计算x, y方向上的梯度获得整体梯度的幅值及方向.
| $ {\mathit{\boldsymbol{s}}_x} = \left[ {\begin{array}{*{20}{c}} { - 1}&0&1\\ { - 2}&0&2\\ { - 1}&0&1 \end{array}} \right],{\mathit{\boldsymbol{s}}_y} = \left[ {\begin{array}{*{20}{c}} 1&2&1\\ 0&0&0\\ { - 1}&{ - 2}&{ - 1} \end{array}} \right]. $ | (1) |
式中:sx, sy分别为x, y方向上的梯度卷积算子.通过图像与梯度卷积算子卷积, 得到像素点在x, y方向上的灰度梯度幅值.
| $ {\varphi _x}\left( {m,n} \right) = f\left( {m,n} \right) * {\mathit{\boldsymbol{s}}_x}. $ | (2) |
| $ {\varphi _y}\left( {m,n} \right) = f\left( {m,n} \right) * {\mathit{\boldsymbol{s}}_y}. $ | (3) |
| $ \varphi \left( {m,n} \right) = \sqrt {\varphi _x^2\left( {m,n} \right) + \varphi _y^2\left( {m,n} \right)} . $ | (4) |
| $ \theta = {\tan ^{ - 1}}\frac{{{\varphi _y}\left( {m,n} \right)}}{{{\varphi _x}\left( {m,n} \right)}}. $ | (5) |
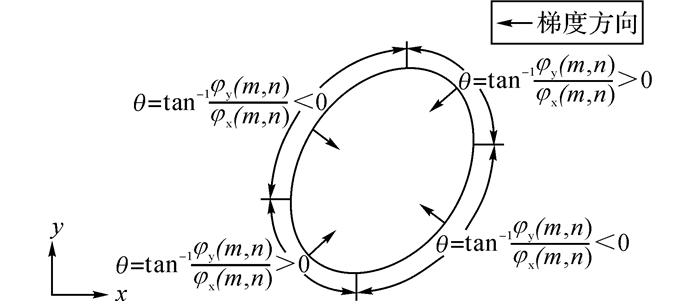
式中:*表示卷积运算, φx(m, n), φy(m, n)分别为点(m, n)在x, y方向上的灰度梯度, φ(m, n)为点(m, n)的灰度梯度值, f(m, n)为图像中像素点(m, n)的灰度值.根据式(5)可知, 椭圆边缘点对应的θ的符号存在如图 1所示的规律.
|
图 1 椭圆边缘灰度梯度特性 Fig. 1 Gray gradient property of elliptical edges |
对于椭圆边缘上的点P, 当x, y方向梯度同号时, θ大于零;当x, y方向梯度异号时, θ小于零;当x或y方向梯度为零时θ等于零或不存在(这些点不计入分类).根据θ的正负, 可以将同一椭圆特征上的圆弧粗分为2类.
1.3 基于边缘凹凸性的圆弧细分为了进一步区分边缘线相对于椭圆的位置, 引入边缘线的凹凸性判别.通过经过边缘线左右端点的直线与边缘线上像素点的位置关系判别边缘线的凹凸性.判别条件如式(6)所示.
| $ f\left( {x,y} \right) = \left\{ {\begin{array}{*{20}{c}} {y - {y_L} - \frac{{{y_L} - {y_R}}}{{{x_L} - {x_R}}}\left( {x - {x_L}} \right),}&{{x_L} \ne {x_R};}\\ {0,}&{{x_L} = {x_R}.} \end{array}} \right.. $ | (6) |
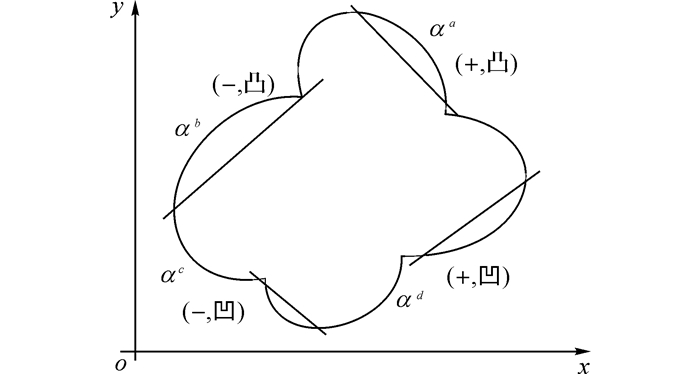
式中:下标L表示边缘线的左端点, R表示边缘线的右端点. x、y分别为边缘线上某一点的横、纵坐标. f(x, y)恒大于零时边缘线为凸;f(x, y)恒小于零时, 边缘线为凹;若f(x, y)异号, 则说明边缘线具有凹凸性变化, 不满足椭圆边缘的性质, 将此边缘线排除.在确定边缘线的梯度符号与凹凸性后, 按照逆时针顺序将边缘线分为Ⅰ、Ⅱ、Ⅲ、Ⅳ类边缘线, 分别用αa, αb, αc, αd表示.如图 2所示.
|
图 2 基于灰度梯度与凹凸性的分类判别 Fig. 2 Edge classification based on gradient and concavity |
根据上述分类方法, 将满足条件的边缘线定义为圆弧.即每一条圆弧具有相同的梯度符号, 且相邻像素点具有连续性.第k条圆弧的集合可表示为lk=(Pk1, …, PNkk):∀i, j,
一个完整的椭圆可以通过αa, αb, αc, αd共4类圆弧组成, 然而由于复杂图像中的椭圆中存在着边缘缺失的情况, 因此将具有任意3类圆弧的集合作为一个圆弧集合ψ, 表示为
| $ {\psi ^{abc}} = \left\{ {{\alpha ^a},{\alpha ^b},{\alpha ^c}} \right\}. $ | (7) |
| $ {\psi ^{acd}} = \left\{ {{\alpha ^a},{\alpha ^c},{\alpha ^d}} \right\}. $ | (8) |
| $ {\psi ^{bcd}} = \left\{ {{\alpha ^b},{\alpha ^c},{\alpha ^d}} \right\}. $ | (9) |
| $ {\psi ^{abd}} = \left\{ {{\alpha ^a},{\alpha ^b},{\alpha ^d}} \right\}. $ | (10) |
通过生成的圆弧集合将图像中离散的圆弧组合成了满足单个椭圆拟合条件的圆弧集合, 从而将复杂图像的多个椭圆拟合问题转化为多次拟合单个椭圆的问题.
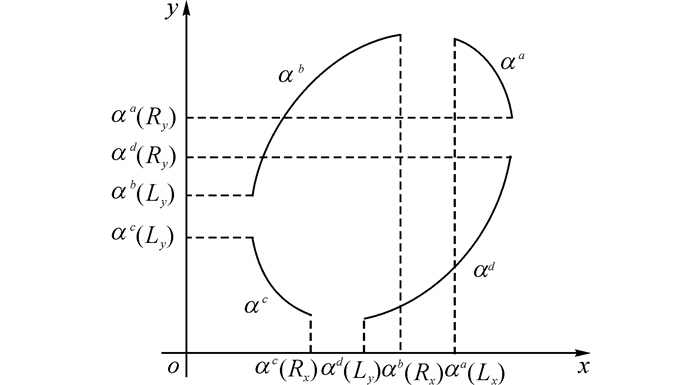
2.1 基于几何位置约束的圆弧集合筛选假设在一幅图像中4类边缘线分别有n1、n2、n3和n4条, 令表示圆弧集合的数量, 则根据排列组合原理可知圆弧集合nφ=n1n2n3+n2n3n4+n3n4n1+n4n1n2.若对全部集合进行拟合, 将消耗大量时间.因此需要通过圆弧之间几何位置约束关系排除错误的圆弧集合.从椭圆的几何特性可知, 4类边圆弧端点在图像坐标系中具有的位置关系约束如图 3所示.
|
图 3 4类圆弧端点位置关系 Fig. 3 Relationship among break points of arcs in four classes |
图 3中的圆弧间几何位置约束可以通过公式表示为
| $ \left. \begin{array}{l} {\alpha ^a}\left( {{L_x}} \right) > {\alpha ^b}\left( {{R_x}} \right)\\ {\alpha ^b}\left( {{L_y}} \right) > {\alpha ^c}\left( {{L_y}} \right)\\ {\alpha ^c}\left( {{R_x}} \right) > {\alpha ^d}\left( {{L_y}} \right)\\ {\alpha ^a}\left( {{R_y}} \right) > {\alpha ^d}\left( {{R_y}} \right) \end{array} \right\}. $ | (11) |
式中:L、R分别表示边缘线α的左、右端点, 下标x, y分别表示端点的x, y坐标, 例如,αa(Lx)>xb(Rx)表示α左端点的x坐标需要大于右端点的x坐标.对于任意的圆弧集合, 均需要满足公式(11)中的几何约束条件.因此通过圆弧的位置约束可以排除一部分不符合要求的圆弧集合.
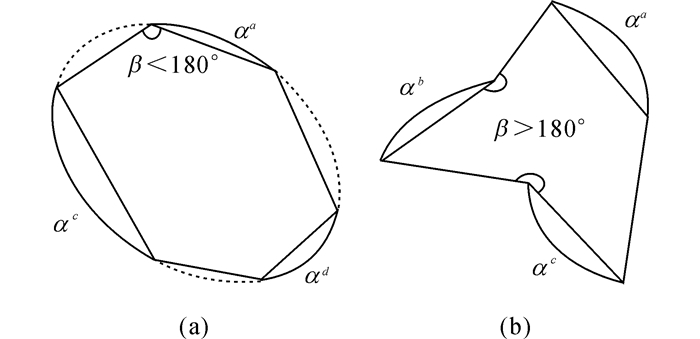
2.2 基于凸多边形特性的圆弧集合辨识在边缘线的位置约束条件下仍有一部分圆弧集合不满足椭圆的拟合条件, 如图 4(b)所示, 因此以椭圆的内包多边形为凸多边形的性质作为判别依据, 辨识出满足条件的椭圆集合, 如图 4(a)所示.
|
图 4 凸多边形判别辨识圆弧集合 Fig. 4 Arc unit classification though convex polygon |
凸多边形的判别采用向量乘积的方法, 设圆弧集合中3条圆弧的顶点分别为P1至P6, 按逆时针方向依次连接顶点构成的向量为V1至V6, 将相邻向量依次叉乘, 若存在结果小于零的情况, 则多边形为凹多边形, 不满足椭圆的性质, 将相应的椭圆集合排除.
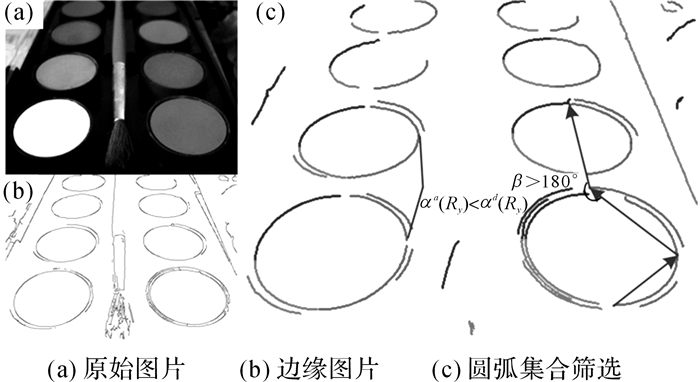
以如图 5所示为例说明圆弧集合筛选方法对排除作物圆弧集合的效果.对原始图片(如图 5(a)所示)进行预处理后获得边缘图片如图 5(b)所示, 通过边缘点的梯度方向及圆弧的凹凸性将边缘线分为4类, 数量分别为n1=11, n2=14, n3=15, n4=10.则圆弧集合总数为nψ=7 600.通过几何约束筛选后剩余圆弧集合数量为2 415, 对这些圆弧集合进行凸多边形判别后剩余圆弧集合数量为463.可见, 通过对圆弧集合的筛选, 排除了大部分错误配对的圆弧集合.
|
图 5 圆弧集合筛选示例图 Fig. 5 Illustration of arc unit selection |
筛选后的椭圆集合中的点均为椭圆特征上的点, 因此可以通过最小二乘法对椭圆进行拟合.采用文献[19]提出的一种非迭代几何最小二乘法对最终的椭圆集合ψ进行拟合.该方法相比于经典的几何最小二乘法[20]及直接最小二乘法[13]具有更高的拟合精度及计算效率.
椭圆函数方程可以表示为
| $ \begin{array}{*{20}{c}} {G\left( {x,y} \right) = \frac{{{{\left( {\left( {x - {x_c}} \right)\cos \gamma - \left( {y - {y_c}} \right)\sin \gamma } \right)}^2}}}{{{a^2}}} + }\\ {\frac{{{{\left( {\left( {x - {x_c}} \right)\sin \gamma + \left( {y - {y_c}} \right)\cos \gamma } \right)}^2}}}{{{b^2}}} - 1 = 0.} \end{array} $ | (12) |
式中:a, b分别为椭圆的长轴和短轴的长度, xc, yc分别为椭圆中心的横坐标与纵坐标, γ为椭圆长轴与坐标系x轴的夹角.通过拟合可以获得椭圆的参数g={a, b, xc, yc, γ}.定义有效像素点集合w={(xi, yi):|G(xi, yi)| < 0.1}.通过阈值ηt表示椭圆的拟合程度:
| $ \eta = \frac{{\left| w \right|}}{{\left| {{\alpha ^a}} \right| + \left| {{\alpha ^b}} \right| + \left| {{\alpha ^c}} \right|}}. $ | (13) |
式中:|·|表示集合内元素的个数, 即像素点的个数.保留η>ηt的拟合结果作为成功拟合的椭圆.导致值减小的原因分为2种: 1)圆弧集合不是椭圆, 这种情况下将存在大量外点(不在椭圆边缘上的点), 约束ηt值的目的是排除此类情况;2)由于噪声影响(反光、模糊等)导致椭圆边缘产生变形, 将椭圆的边缘点误识别为外点, 为了避免误识别需要放宽ηt的值.因此, ηt的取值主要取决于噪声对图像的影响.
由于在圆弧聚合的过程中同一条圆弧可以分配至不同的椭圆集合中, 使得在拟合过程中存在对同一条圆弧进行重复拟合的情况;另一方面, 由于复杂图像中椭圆的连续性难以保证, 在边缘线识别过程中可能被分割成多条边缘线(大于4条), 对多条圆弧拟合出的多个椭圆实际上代表的是同一个椭圆.因此为排除冗余椭圆, 需要对椭圆进行去伪.
去伪的计算分为两步:
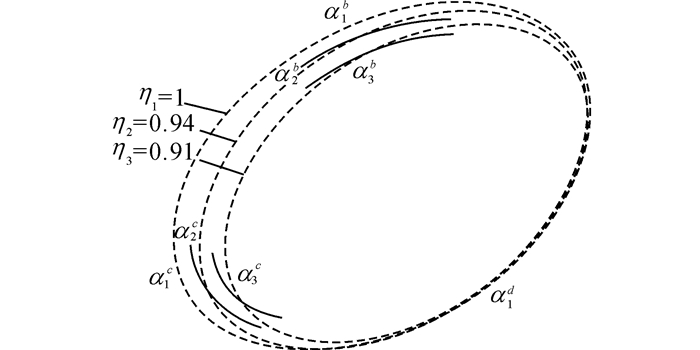
1) 局部去伪:局部去伪的对象为包含同一条边缘线的圆弧集合, 选择其中η值最大的圆弧集合作为该边缘线的唯一拟合椭圆, 并去除其他圆弧集合, 如图 6所示.
|
图 6 局部去伪示意图 Fig. 6 Illustration of the partial wrong arc unit exclusion |
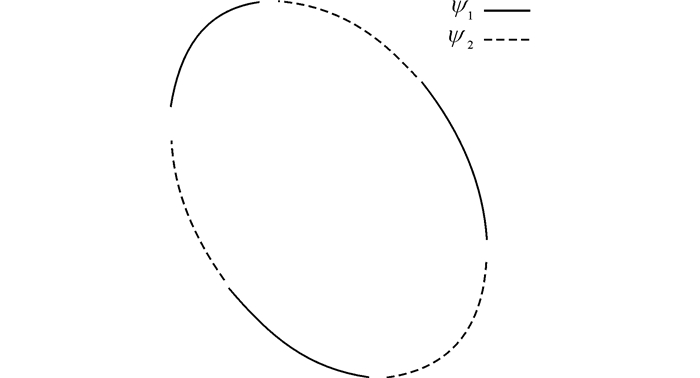
2) 全局去伪:全局去伪的对象为经过局部去伪的所有圆弧集合, 在如图 7所示情况下, 椭圆出现了过拟合现象, 为了消除这种过拟合现象, 通过对椭圆长短轴、倾角以及重心坐标进行判别(式14~17), 若这些椭圆参数相差较小, 则判定为同一椭圆, 选择其中η值最大的圆弧集合作为最终的椭圆, 并排除其他圆弧集合.
| $ {\Delta _c} = \sqrt {{{\left( {x_c^{{g_m}} - x_c^{{g_n}}} \right)}^2} + {{\left( {y_c^{{g_m}} - y_c^{{g_n}}} \right)}^2}} < 0.1. $ | (14) |
| $ {\Delta _a} = \left| {{a^{{g_m}}} - {a^{{g_n}}}} \right|/\max \left( {{a^{{g_m}}},{a^{{g_n}}}} \right) < 0.1. $ | (15) |
| $ {\Delta _b} = \left| {{b^{{g_m}}} - {b^{{g_n}}}} \right|/\max \left( {{b^{{g_m}}},{b^{{g_n}}}} \right) < 0.1. $ | (16) |
| $ {\Delta _\gamma } = \angle \left( {{\gamma ^{{g_m}}} - {\gamma ^{{g_n}}}} \right)/{\rm{ \mathsf{ π} }} < 0.1. $ | (17) |
|
图 7 全局去伪示意图 Fig. 7 Illustration of the global wrong arc unit exclusion |
式中:Δc为椭圆中心的误差, Δa, Δb分别为长短轴的误差, Δγ为旋转角误差.
4 实验验证实验验证部分首先分析了本文算法的时间复杂度(4.1节);再通过对虚拟图像的检测, 测试算法对椭圆在重叠、缺失、遮挡、嵌套等情况下的适用性(4.2节);最后在真实图片集上对算法进行了验证(4.3节).
4.1 算法时间复杂度分析算法的时间复杂度分析根据椭圆识别的流程分为3个阶段:
1) 边缘线分类阶段:通过遍历θ将边缘点粗分为2类的时间复杂度为O(n), 分别计算每条圆弧凹凸性的复杂度为O(n), 相较而言通过多条直线段表示圆弧的方法[14, 16]的时间复杂度为O(n2).
2) 圆弧集合筛选阶段:通过4类边缘线的端点几何位置约束筛选椭圆集合的时间复杂度为O(n), 基于凸多边形判定筛选椭圆集合得时间复杂度为}O(6n);而常用的利用椭圆中心点聚合边缘的方法[12, 15]的时间复杂度为O(n2).
3) 椭圆拟合与验证阶段:本文应用的非迭代几何最小二乘法[19]的时间复杂度为O(35n).
以上分析均基于n表示像素个数时, 算法的最坏情况.综合3个阶段的分析可知, 本文提出方法的总体时间复杂度为~O(n).在实际应用中, 通过圆弧集合的筛选将极大地降低n的数目, 因此本文算法在计算速度上具有一定优势.
4.2 虚拟图像检测实验选取了含5%椒盐噪声的虚拟合成图像如图 8(a)所示, 其中的椭圆具有重叠、缺失、遮挡、嵌套等特征.图像的预处理如图 8(b)所示, 自适应Canny算子完整的检测出了图像的边缘并有较好的抗噪能力.图 8(c)为对预处理图像中边缘的线分类结果.图 8(d)中的加粗边缘为拟合与去伪后的椭圆特征.可见, 本文算法能够准确的检测各种复杂状态下的椭圆.

|
图 8 虚拟图像检测过程 Fig. 8 Detection process of imaginary image |
实验采用Matlab编程, 计算机配置为Core i5 2.2GHz主频, 4GB RAM.通过模式识别问题中的经典判别条件精确率p(Precision)、召回率r(Recall)和F值(F-measure)对本文所提出的方法进行评价.精确率、召回率和F值分别为
| $ p = \frac{{检测出的正确椭圆数量}}{{检测出的椭圆数量}}. $ | (18) |
| $ r = \frac{{检测出的正确椭圆数量}}{{实际椭圆的数量}}. $ | (19) |
| $ F = \frac{{2pr}}{{p + r}}. $ | (20) |
从Caltech-256图像数据库中选取400副真实图像[14]对算法进行验证.将本文所提出的方法与现有方法包括迭代随机霍夫变换法[9](Iterative Randomized Hough transform, IRHT)、Prasad[14]和Chen[16]的方法进行了比较.
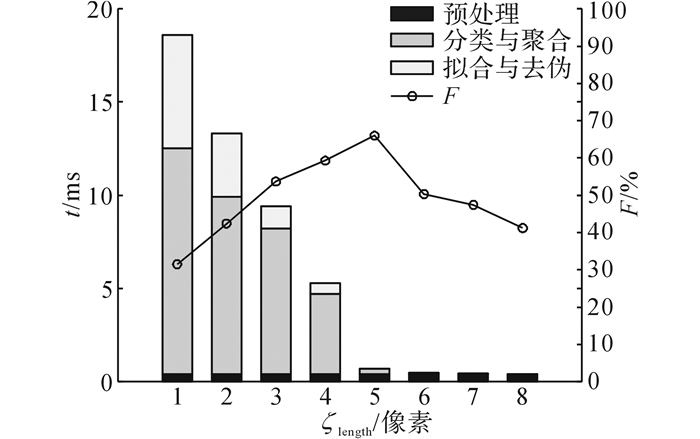
4.3.1 阈值优化选取的真实图片为一般场景下的图片, 含高噪声或模糊的情况较少, 因此拟合程度Thη取值0.9以达到良好的检测效果.如1.3节所述, 在边缘线的分组过程中, 需要通过设定阈值ζlength对过短的边缘进行筛除.然而过小的阈值无法起到筛除细小边缘的作用, 过大的阈值则会将一部分椭圆边缘筛除.因此通过实验调整阈值的大小, 如图 9所示.当阈值小于4个像素时大量的短边缘使得算法的计算时间上升, 同时由于一部分短边缘被误检测为椭圆边缘, 导致算法精确率下降.当阈值大于32个像素时, 一部分椭圆边缘被忽略, 导致算法召回率下降.因此综合考虑准确率与计算效率, 选择16个像素点作为边缘线筛除阈值.
|
图 9 边缘线筛除阈值ζlength取值分析 Fig. 9 Selection of edge filtering threshold ζlength |
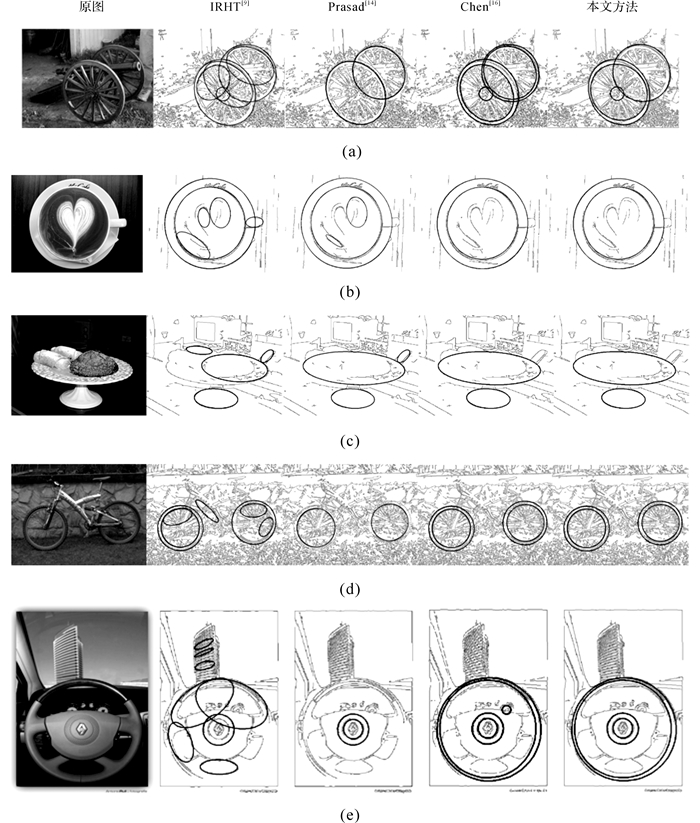
算法的比较结果如图 10所示.从图 10中可以看出, 迭代随机霍夫变换法由于以随机像素点为识别基准, 当图像内容复杂时, 常出现过检测的现象, 不适合复杂图像中的椭圆识别;Prasad提出的基于边缘连续性的方法具有较高的拟合精度, 但在边缘线分类阶段需要进行大量计算, 由于需要通过几何方法判定椭圆的中心, 所以当椭圆相差较大的数个椭圆同时出现在同一副图片中时(如图 10(e))较大的椭圆会由于中心计算时的误差溢出而被排除, 从而导致椭圆的欠检测.本文方法通过放宽边缘线聚合时的约束条件以及快速的归类算法, 在保持较高识别精度的前提下, 提高了图像的识别速度.
|
图 10 不同算法对比图例 Fig. 10 Examples of detection using different algorithms |
如表 1所示为算法对图像识别的平均精度与总体计算时间.从表中可以看出, 在图像背景复杂的情况下, 迭代随机霍夫变换法的识别精度低计算时间长;Chen等[16]提出的算法在Prasad等[14]算法的基础上通过对不确定区域的二次检测提高了检测精度,但增大了计算量.本文提出方法在保持较高识别精度的同时具有更高的计算效率.
| 表 1 不同算法的识别精度与计算时间对比 Table 1 Comparison of accuracy and runtime among different algorithms |
对图像中椭圆特征的检测问题是图像识别领域的经典问题, 具有广泛的工程应用.本文提出了一种基于梯度分类与多边形辨识的复杂背景下椭圆特征快速识别方法, 主要工作与特点如下:
(1) 提出了基于灰度梯度与凹凸性判别的边缘线分类方法, 根据图像的灰度梯度与凹凸性将边缘线分为4类圆弧, 并通过对聚类方法快速计算椭圆的待选集合, 提高了计算效率.
(2) 提出了基于几何约束与凸多边形聚合的圆弧集合筛选方法, 根据椭圆内包多边形为凸多边形的特点, 分别计算多边形边与顶点的位置关系, 从而快速确定圆弧集合的正确性.
(3) 通过局部去伪与全局去伪排除了重复检测的椭圆, 提高了椭圆拟合的准确性.
| [1] |
HUTTER M, BREWER N. Matching 2-D ellipses to 3-D circles with application to vehicle pose identification[C]//Image and Vision Computing New Zealand. Wellingtaon: IEEE, 2009: 153-158. http://dx.doi.org/10.1109/IVCNZ.2009.5378421
|
| [2] |
SOETEDJO A, YAMADA K. Fast and Robust Traffic Sign Detection[C]//IEEE International Conference on Systems, Man and Cybernetics. Waikoloa: IEEE, 2006: 1341-1346. http://yadda.icm.edu.pl/yadda/element/bwmeta1.element.ieee-000001571333
|
| [3] |
KIM H S, KANG W S, SHIN J I, et al. Face detection using template matching and ellipse fitting[J]. Ieice Transactions on Information & Systems, 2000, 83(11): 2008-2011. |
| [4] |
FENG X, FANG C, DING X, et al. Iris localization with dual coarse-to-fine Strategy[C]//International Conference on Pattern Recognition. HongKong: IEEE, 2006: 553-556. http://ieeexplore.ieee.org/xpl/abstractAuthors.jsp?tp=&arnumber=1699901
|
| [5] |
廖苗, 赵于前, 曾业战, 等. 基于支持向量机和椭圆拟合的细胞图像自动分割[J]. 浙江大学学报:工学版, 2017, 51(4): 722-728. LIAO Miao, ZHAO Yu-qian, ZENG Ye-zhan, et al. Automatic segmentation for cell images based on support vectot machine and ellipse fitting[J]. Journal of Zhejiang University:Engineering Science, 2017, 51(4): 722-728. |
| [6] |
FELZENSZWALB P F, HUTTENLOCHER D P. Pictorial structures for object recognition[J]. International Journal of Computer Vision, 2005, 61(1): 55-79. DOI:10.1023/B:VISI.0000042934.15159.49 |
| [7] |
MCLAUGHLIN R A. Randomized hough transform:improved ellipse detection with comparison[J]. Pattern Recognition Letters, 1998, 19(3/4): 299-305. |
| [8] |
CHENG Z, LIU Y. Efficient technique for ellipse detection using restricted randomized Hough transform[C]//International Conference on Information Technology: Coding and Computing. Las Vegas: IEEE, 2004(2): 714-718. http://dx.doi.org/10.1109/ITCC.2004.1286739
|
| [9] |
LU W, TAN J. Detection of incomplete ellipse in images with strong noise by iterative randomized Hough transform (IRHT)[J]. Pattern Recognition, 2008, 41(4): 1268-1279. DOI:10.1016/j.patcog.2007.09.006 |
| [10] |
邹荣, 赵稼宸, 凌俊, 等. 基于Hough投票空间的椭圆图像特征亚像素提取方法[J]. 光学技术, 2016, 42(2): 141-145. ZOU Rong, ZHAO Jia-chen, Lin Jun, et al. Sub-pixel ellipse feature extraction method based on Hough voting space[J]. Optical Technique, 2016, 42(2): 141-145. |
| [11] |
FITZGIBBON A, PILU M, FISHER R B. Direct least square fitting of ellipses[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2010, 21(5): 476-480. |
| [12] |
LIU Z Y, QIAO H. Multiple ellipses detection in noisy environments:A hierarchical approach[J]. Pattern Recognition, 2009, 42(11): 2421-2433. DOI:10.1016/j.patcog.2009.01.028 |
| [13] |
MAINI E S. Enhanced direct least square fitting of ellipses[J]. International Journal of Pattern Recognition & Artificial Intelligence, 2012, 20(6): 939-954. |
| [14] |
PRASAD D K, LEUNG M K H, CHO S Y. Edge curvature and convexity based ellipse detection method[J]. Pattern Recognition, 2012, 45(9): 3204-3221. DOI:10.1016/j.patcog.2012.02.014 |
| [15] |
吴尧锋, 王文, 卢科青, 等. 边界聚类椭圆快速检测方法[J]. 浙江大学学报:工学版, 2016, 50(3): 405-411. WU Xiao-feng, WANG Wen, LU Ke-qing, et al. Fast ellipse detection based on edge grouping[J]. Journal of Zhejiang University:Engineering Science, 2016, 50(3): 405-411. |
| [16] |
CHEN S, XIA R, ZHAO J, et al. A hybrid method for ellipse detection in industrial images[J]. Pattern Recognition, 2017, 68: 82-98. DOI:10.1016/j.patcog.2017.03.007 |
| [17] |
MEDINA-CARNICER R, OZ-SALINAS R, YEGUAS-BOLIVAR E, et al. A novel method to look for the hysteresis thresholds for the Canny edge detector[J]. Pattern Recognition, 2011, 44(6): 1201-1211. DOI:10.1016/j.patcog.2010.12.008 |
| [18] |
CHATBRI H, KAMEYAMA K. Using scale space filtering to make thinning algorithms robust against noise in sketch images[J]. Pattern Recognition Letters, 2014, 42(6): 1-10. |
| [19] |
PRASAD D K, LEUNG M K H, CHAI Q. ElliFit:An unconstrained, non-iterative, least squares based geometric Ellipse Fitting method[J]. Pattern Recognition, 2012, 46(5): 1449-1465. |
| [20] |
AHN S J, RAUH W, WARNECKE H J, et al. Least-squares orthogonal distances fitting of circle, sphere, ellipse, hyperbola, and parabola[J]. Pattern Recognition, 2001, 34(12): 2283-2303. DOI:10.1016/S0031-3203(00)00152-7 |



