2. 浙江大学 流体动力与机电系统国家重点实验室, 浙江 杭州 310027
2. State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University, Hangzhou 310027, China
近年来, 水下机器人-机械手系统(underwater vehicle-manipulator system, UVMS)被广泛的应用于海洋科学研究、资源探测开发以及海洋设备维护等水下作业任务, 是人类研究开发海洋的重要平台和手段[1].
现阶段, UVMS主要由位于母船上的操作员遥控操作进行作业.但遥控UVMS受脐带缆牵制, 需要母船跟随动力定位, 成本高、效率低.特别是针对大范围绕柱作业、长距离沿缆作业等非定点连续性作业需求, 若作业海域母船不易进入或难以沿缆运动, 则会限制其开展作业的能力.且当遥控UVMS绕柱作业时, 易引起脐带缆缠绕事故, 不利于水下作业的开展[2].而自治UVMS不受脐带缆牵制, 无需母船动力定位, 有望实现水下作业的完全自主化, 可有效降低成本、提高效率, 是目前水下机器人领域最具挑战性的研究热点[3-6], 而其高性能运动控制是实现水下自主作业的关键.
然而, 强非线性耦合、复杂参数不确定性以及未知外干扰等复杂集总干扰的存在, 导致自治UVMS的运动控制极具挑战性, 国内外学者对此展开了广泛的研究[7-9].Xu等[10]采用神经网络补偿器估算分散形式下的UVMS系统未知动态, 给出了神经网络控制算法.张奇峰[11]基于机械手运动对载体扰动的响应特性分析, 设计了一种基于输入和扰动补偿的UVMS控制算法.郭莹[12]利用滑模控制实现了UVMS的运动控制.为缩短速度响应时间并减小位置超调量, 张铭钧教授课题组提出了一种基于速度PI和位置PD的双闭环PID运动控制器[13].以上研究不论是基于模型的控制算法, 还是神经网络等智能算法, 均较繁琐、难以实际工程应用.而传统的PID控制器又难以系统满足对复杂集总干扰的强鲁棒性的需求.
工程实际应用中需要的是结构简单、对系统模型依赖较小, 且可以保证复杂集总干扰下较高控制品质的控制方法.时延估计(time delay estimation, TDE)技术可有效解决上述问题, 保证良好的控制品质和工程易用性.TDE技术的核心思想是利用闭环控制系统前段时刻的系统状态量, 实现对当前时刻系统未知集总动态的在线估算和实时补偿.而后通过设计的期望动态方程实现复杂集总干扰下系统控制效果的调节.
针对髙维度UVMS轨迹跟踪控制难题, 本文基于TDE技术, 结合UVMS自身特点, 提出一种非奇异终端滑模控制(nonsingular terminal sliding mode control, NTSMC)方法.受益于TDE无需动力学模型的特性和非奇异终端滑模控制的强鲁棒性和优异控制性能, 本文所提控制方法具有优异的控制性能、良好的鲁棒性和工程易用性.利用李雅普诺夫稳定性理论证明了闭环控制系统的稳定性, 并给出了跟踪误差的理论计算值.最终, 通过7自由度闭环控制对比试验验证了所提控制算法的有效性和优越性.
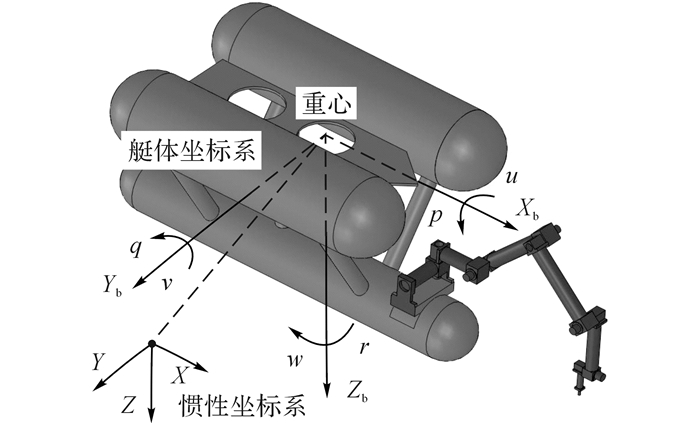
1 系统描述UVMS的坐标系分为惯性坐标系和艇体坐标系, 如图 1所示为UVMS 2种坐标系的定义.包含四自由度水下机器人和n自由度水下机械手的UVMS简化动力学和运动学模型可写为[14]
| $ \mathit{\boldsymbol{M}}\left( \varsigma \right)\dot \xi + \mathit{\boldsymbol{C}}\left( {\varsigma ,\xi } \right)\xi + \mathit{\boldsymbol{D}}\left( {\varsigma ,\xi } \right)\xi + \mathit{\boldsymbol{g}}\left( \varsigma \right) + {\mathit{\boldsymbol{\tau }}_d} = \mathit{\boldsymbol{\tau }}. $ | (1) |
| $ \dot \varsigma = {\mathit{\boldsymbol{J}}_{{\rm{joint}}}}\xi . $ | (2) |
|
图 1 UVMS惯性坐标系和艇体坐标系定义 Fig. 1 Inertial frame and body-fixed frame of UVMS |
式中:ς=[ηT, qT]T为UVMS惯性坐标系下的位姿向量, η=[x,y,z,ψ]T为水下机器人惯性坐标系下的位姿向量, q=[q1, …, qn]T为水下机械手关节角向量. ξ=[vT,
Jjoint为UVMS关节空间雅克比矩阵
| $ {\mathit{\boldsymbol{J}}_j} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{J}}\left( \eta \right)}&{{{\bf{0}}_{4 \times n}}}\\ {{{\bf{0}}_{n \times 4}}}&{{\mathit{\boldsymbol{I}}_n}} \end{array}} \right]. $ | (3) |
式中:J(η)为水下机器人的坐标转换矩阵, 可写为
| $ \mathit{\boldsymbol{J}}\left( \eta \right) = \left[ {\begin{array}{*{20}{c}} {\cos \psi }&{ - \sin \psi }&0&0\\ {\sin \psi }&{\cos \psi }&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right]. $ | (4) |
式中:ψ为水下机器人惯性坐标系下的偏航角.
2 基于时延估计的UVMS非奇异终端滑模控制器设计假设1 UVMS各方向/关节的速度是有界的, 期望轨迹qd有界连续可微, 且二阶导数存在并有界.
引理1[15] 假设V(x)为一李雅普诺夫函数, V(x0)为其初值.则对于式(5), 其收敛到V(0)所需稳定时间T可由式给出(6).
| $ \dot V\left( x \right) + aV\left( x \right) + b{V^\gamma }\left( x \right) \le 0. $ | (5) |
| $ T \le \ln \left( {1 + aV{{\left( {{x_0}} \right)}^{1 - \gamma }}/b} \right)/\left[ {a\left( {1 - \gamma } \right)} \right]. $ | (6) |
式中:a, b, γ为正系数, 且0 < γ < 1.
2.1 控制器设计为便于控制器推导, 将UVMS动力学方程在惯性坐标系下重新书写为
| $ {\mathit{\boldsymbol{M}}_\varsigma }\ddot \varsigma + {\mathit{\boldsymbol{C}}_\varsigma }\left( {\varsigma ,\xi } \right)\dot \varsigma + {\mathit{\boldsymbol{D}}_\varsigma }\left( {\varsigma ,\xi } \right)\dot \varsigma + {\mathit{\boldsymbol{\tau }}_{d\_\varsigma }} = {\mathit{\boldsymbol{\tau }}_\varsigma }. $ | (7) |
式中:Mς=J-TMJ-1, Cς=J-T(C-MJ-1
动力学方程式(7)可重写为
| $ {\mathit{\boldsymbol{M}}_\varsigma }\ddot \varsigma + \mathit{\boldsymbol{N}}\left( {\varsigma ,\xi ,{\tau _{d\_\varsigma }}} \right) = {\mathit{\boldsymbol{\tau }}_\varsigma }. $ | (8) |
式中:N(ς, ξ, τd_ς)=Cς(ς, ξ)
为便于应用TDE, 将式(8)变形为
| $ {{\mathit{\boldsymbol{\bar M}}}_\varsigma }\ddot \varsigma + \mathit{\boldsymbol{H}}\left( {\varsigma ,\xi ,{\mathit{\boldsymbol{\tau }}_{d\_\varsigma }}} \right) = {\mathit{\boldsymbol{\tau }}_\varsigma }. $ | (9) |
| $ \mathit{\boldsymbol{H}}\left( {\varsigma ,\xi ,{\mathit{\boldsymbol{\tau }}_{d\_\varsigma }}} \right) = \left( {{\mathit{\boldsymbol{M}}_\varsigma } - {{\bar M}_\varsigma }} \right)\ddot \varsigma + \mathit{\boldsymbol{N}}\left( {\varsigma ,\xi ,{\mathit{\boldsymbol{\tau }}_{d\_\varsigma }}} \right). $ | (10) |
式中:Mς为一个时变的对角系数矩阵, 下文将给出其选取方法. H(ς, ξ, τd_ς)为UVMS未知集总动态, 其组成非常复杂, 很难通过常规方法获取.为避免混淆和书写简洁, 采用x(t), x(t-L)表示当下时刻和延时L后时刻的状态量.
定义UVMS关节空间轨迹跟踪误差及其导数为
| $ \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{e}} + \mathit{\boldsymbol{K}}\;{\rm{sig}}{\left( {\mathit{\boldsymbol{\dot e}}} \right)^\alpha }. $ | (11) |
| $ \mathit{\boldsymbol{\dot s}} = - {\mathit{\boldsymbol{k}}_1}\mathit{\boldsymbol{s}} - {\mathit{\boldsymbol{k}}_2}{\rm{sig}}{\left( \mathit{\boldsymbol{s}} \right)^\beta }. $ | (12) |
式中:K, k1, k2为待设计和调节的常系数对角矩阵, 而各自由度指数系数分量满足1 < αi < 2, 0 < βi < 1, sig(x)y=|x|ysgn(x).
则基于TDE的UVMS非奇异终端滑模控制器可设计如下:
| $ {\mathit{\boldsymbol{\tau }}_\varsigma } = {{\mathit{\boldsymbol{\bar M}}}_\varsigma }\left( t \right)\mathit{\boldsymbol{u}}\left( t \right) + \mathit{\boldsymbol{\hat H}}\left( t \right). $ | (13) |
| $ \mathit{\boldsymbol{u = }}{{\ddot \varsigma }_d} + {\alpha ^{ - 1}}{\mathit{\boldsymbol{K}}^{ - 1}}{\rm{sig}}{\left( {\mathit{\boldsymbol{\dot e}}} \right)^{2 - \alpha }} + {\mathit{\boldsymbol{k}}_1}\mathit{\boldsymbol{s}} + {\mathit{\boldsymbol{k}}_2}{\rm{sig}}{\left( s \right)^\beta }. $ | (14) |
式中:
| $ \mathit{\boldsymbol{\hat H}}\left( t \right) = \mathit{\boldsymbol{H}}\left( {t - L} \right) = {\tau _\varsigma }\left( {t - L} \right) - {{\mathit{\boldsymbol{\bar M}}}_\varsigma }\left( {t - L} \right)\ddot \varsigma \left( {t - L} \right). $ | (15) |
为保证估计的精度, L一般取值较小, 比如几个采样周期, 以使H(t)≈H(t-L)成立.
结合式(13)~(15), 得到基于TDE的UVMS非奇异终端滑模控制器如下:
| $ \begin{array}{l} {\mathit{\boldsymbol{\tau }}_\varsigma }\left( t \right) = \\ \underbrace {{{\mathit{\boldsymbol{\bar M}}}_\varsigma }\left( t \right)\left( {{{\ddot \varsigma }_d} + {\alpha ^{ - 1}}{K^{ - 1}}{\rm{sig}}{{\left( {\dot e} \right)}^{2 - \alpha }} + {k_1}s + {k_2}{\rm{sig}}{{\left( s \right)}^\beta }} \right)}_{{\rm{NTSMC}}} + \\ \underbrace {{\mathit{\boldsymbol{\tau }}_\varsigma }\left( {t - L} \right) - {{\bar M}_\varsigma }\left( {t - L} \right)\ddot \varsigma \left( {t - L} \right)}_{{\rm{TDE}}}. \end{array} $ | (16) |
从式(16)可以看出, 本文所提控制器有两部分组成:NTSMC项和TDE项. TDE项用于在线估计和实时补偿复杂的系统未知集总动态;NTSMC项用于调节系统动态响应特性.由于TDE的引入, 使得期望动态项所需增益大幅降低, 可以有效提高系统鲁棒性, 保证复杂集总干扰下的控制性能.
2.2 闭环控制系统稳定性分析闭环控制系统稳定性分析可分为2步, 同时为简化分析过程, 对系统第i自由度进行分析.
第1步:系统跟踪误差及其导数的有界性证明.
将控制器式(13)-(14)代入系统动力学方程式(9)中, 可得
| $ {{\ddot e}_i} + \alpha _i^{ - 1}K_{ii}^{ - 1}{\rm{sig}}{\left( {{{\dot e}_i}} \right)^{2 - {\alpha _i}}} + {k_{1i}}{s_i} + {k_{2i}}{\rm{sig}}{\left( {{s_i}} \right)^{{\beta _i}}} = \varepsilon {\left( t \right)_i}. $ | (17) |
ε(t)为时延估计误差, 其定义可写为
| $ \varepsilon \left( t \right) = - {{\bar M}_\varsigma }{\left( t \right)^{ - 1}}\left( {\hat H\left( t \right) - H\left( t \right)} \right) = u\left( t \right) - \ddot \varsigma \left( t \right). $ | (18) |
选取李雅普诺夫函数Vi=0.5si2, 对其以时间为变量进行求导得
| $ \begin{array}{l} {{\dot V}_i} = {s_i}{{\dot s}_i} = {s_i}\left[ {{{\dot e}_i} + {K_{ii}}{\alpha _i}{{\left| {{{\dot e}_i}} \right|}^{{a_{i - 1}}}}{{\ddot e}_i}} \right] = \\ \;\;\; - {s_i}{K_{ii}}{\alpha _i}{\left| {{{\dot e}_i}} \right|^{{a_{i - 1}}}}\left[ {{k_{1i}}{s_i} + {k_{2i}}{\rm{sig}}{{\left( {{s_i}} \right)}^{{\beta _i}}} - \varepsilon {{\left( t \right)}_i}} \right]. \end{array} $ | (19) |
上式可变换为以下2种形式:
| $ \begin{array}{l} {{\dot V}_i} = - {s_i}{K_{ii}}{\alpha _i}{\left| {{{\dot e}_i}} \right|^{{a_{i - 1}}}}\left[ {\left( {{k_{1i}} - \varepsilon {{\left( t \right)}_i}s_i^{ - 1}} \right){s_i} + } \right.\\ \;\;\;\;\;\;\left. {{k_{2i}}{\mathop{\rm sig}\nolimits} {{\left( {{s_i}} \right)}^{{\beta _i}}}} \right]. \end{array} $ | (20) |
| $ \begin{array}{l} {{\dot V}_i} = - {s_i}{K_{ii}}{\alpha _i}{\left| {{{\dot e}_i}} \right|^{{a_{i - 1}}}}\left( {{k_{1i}}{s_i} + } \right.\\ \;\;\;\;\;\left. {\left. {\left( {{k_{2i}} - \frac{{\varepsilon {{\left( t \right)}_i}}}{{{\rm{sig}}{{\left( {{s_i}} \right)}^{{\beta _i}}}}}} \right)} \right){\rm{sig}}{{\left( {{s_i}} \right)}^{{\beta _i}}}} \right). \end{array} $ | (21) |
式(20)可重写为
| $ {{\dot V}_i} = - {{\tilde k}_{1i}}s_i^2 - {{\tilde k}_{2i}}{\left| {{s_i}} \right|^{{\beta _{i + 1}}}} = - 2{{\tilde k}_{1i}}{V_i} - {2^{\frac{{1 + {\beta _i}}}{2}}}{{\tilde k}_{2i}}{V^{\frac{{1 + {\beta _i}}}{2}}}. $ | (22) |
其中
当
| $ {T_{si}} \le \frac{1}{{{k_{1i}}\left( {1 - {\beta _i}} \right)}}\ln \left( {\frac{{2{k_{1i}}V_i^{\left( {1 - {\beta _i}} \right)/2}\left( {{s_{i0}}} \right)}}{{{2^{\left( {1 + {\beta _i}} \right)/2}}{k_{2i}}}} + 1} \right). $ | (23) |
式中:si0为si的初值.
因此, 当
| $ \left| {{s_i}} \right| \le \left| {\varepsilon {{\left( t \right)}_i}} \right|k_{1i}^{ - 1}. $ | (24) |
与对式(20)的分析方法相同, 由式(21)可得系统运动轨迹将在有限时间内收敛到以下球域内:
| $ \left| {{s_i}} \right| \le {\left( {\left| {\varepsilon {{\left( t \right)}_i}} \right|k_{2i}^{ - 1}} \right)^{\beta _i^{ - 1}}}. $ | (25) |
因此, 系统轨迹将在有限时间收敛到以下球域内:
| $ \begin{array}{*{20}{c}} {\left| {{s_i}} \right| \le {\Delta _i} = \min \left\{ {{\Delta _{1i}},{\Delta _{2i}}} \right\},}\\ {{\Delta _{1i}} = \left| {\varepsilon {{\left( t \right)}_i}} \right|k_{1i}^{ - 1},{\Delta _{2i}} = {{\left( {\left| {\varepsilon {{\left( t \right)}_i}} \right|k_{2i}^{ - 1}} \right)}^{\beta _i^{ - 1}}}.} \end{array} $ | (26) |
而当
| $ {{\ddot e}_i} = - {k_{1i}}{s_i} - {k_{2i}}{\rm{sig}}{\left( {{s_i}} \right)^{{\beta _i}}} + \varepsilon {\left( t \right)_i}. $ | (27) |
当si ∉Δi时, 有
| $ {{\ddot e}_i} = - \left( {{k_{1i}} - {\varepsilon _i}s_i^{ - 1}} \right){s_i} - {k_{2i}}{\rm{sig}}{\left( {{s_i}} \right)^{{\beta _i}}} \ne 0. $ | (28) |
| $ {{\ddot e}_i} = - {\left( {{k_{1i}}s + \left( {{k_{2i}} - {\varepsilon _i}{\rm{sig}}{{\left( {{s_i}} \right)}^{ - {\beta _i}}}} \right){\rm{sig}}{{\left( {{s_i}} \right)}^{{\beta _i}}}} \right)_i} \ne 0. $ | (29) |
由式(28)-(29)知, 当
将式(26)代入式(11), 得
| $ {e_i} + \left( {{K_i} - {s_i}{\rm{sig}}{{\left( {{{\dot e}_i}} \right)}^{ - {\alpha _i}}}} \right){\rm{sig}}{\left( {{{\dot e}_i}} \right)^{ - {\alpha _i}}} = 0,\left| {{s_i}} \right| \le {\Delta _i}. $ | (30) |
由式(30)知, 当(Ki-sisig(
| $ \left| {{{\dot e}_i}} \right| \le {\left( {{s_i}K_i^{ - 1}} \right)^{\alpha _i^{ - 1}}} \le {\left( {{\Delta _i}K_i^{ - 1}} \right)^{\alpha _i^{ - 1}}} = {\Delta _{{{\dot {\tilde q}}_i}}}. $ | (31) |
则由式(11)和式(31), 得
| $ \begin{array}{l} \left| {{e_i}} \right| = \left| {{s_i} - {K_i}{\rm{sig}}{{\left( {{{\dot e}_i}} \right)}^{ - {\alpha _i}}}} \right| \le \\ \;\;\;\;\;\;\;\left| {{s_i}} \right| + \left| {{K_i}{\rm{sig}}{{\left( {{{\dot e}_i}} \right)}^{{\alpha _i}}}} \right| \le 2{\Delta _i} = {\Delta _{{{\dot {\tilde q}}_i}}}. \end{array} $ | (32) |
结合式(26)、(31)和式(32)可知, 当时延估计误差ε(t)i有界时, 闭环控制系统的稳定性将得以保证.
第2步:时延估计误差ε(t)i有界性证明.
由文献[16]知, 当满足以下不等式时, ε(t)有界
| $ \left| {{\rm{Eig}}\left( {{\mathit{\boldsymbol{I}}_n} - M_\varsigma ^{ - 1}{{\mathit{\boldsymbol{\bar M}}}_\varsigma }} \right)} \right| < 1. $ | (33) |
式中:Eig (x)表示变量x的特征值.
选取Mς=J-TMJ-1, 代入式(33)有
| $ \begin{array}{*{20}{c}} {{\rm{Eig}}\left( {{\mathit{\boldsymbol{I}}_n} - \mathit{\boldsymbol{M}}_\varsigma ^{ - 1}{{\mathit{\boldsymbol{\bar M}}}_\varsigma }} \right) = }\\ {{\rm{Eig}}\left( {{\mathit{\boldsymbol{I}}_n} - {{\left( {{\mathit{\boldsymbol{J}}^{ - {\rm{T}}}}\mathit{\boldsymbol{M}}{\mathit{\boldsymbol{J}}^{ - 1}}} \right)}^{ - 1}}{\mathit{\boldsymbol{J}}^{ - {\rm{T}}}}\bar M{\mathit{\boldsymbol{J}}^{ - {\rm{1}}}}} \right) = }\\ {{\rm{Eig}}\left( {J\left( {{\mathit{\boldsymbol{I}}_n} - {\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{\bar M}}} \right){\mathit{\boldsymbol{J}}^{ - 1}}} \right) = }\\ {{\rm{Eig}}\left( {{\mathit{\boldsymbol{I}}_n} - {M^{ - 1}}\mathit{\boldsymbol{\bar M}}} \right).} \end{array} $ | (34) |
则针对UVMS第i个自由度, 式(34)可简化为
| $ \left| {1 - \mathit{\boldsymbol{M}}_{ii}^{ - 1}{{\mathit{\boldsymbol{\bar M}}}_{ii}}} \right| < 1 \Rightarrow 0 < {{\mathit{\boldsymbol{\bar M}}}_{ii}} < 2{\mathit{\boldsymbol{M}}_{ii}}. $ | (35) |
综上所述, 选取适当的参数M使式(33)~(35)成立后, 时延估计误差ε(t)有界.则根据式(26)、(31)和(32)可知, 闭环控制系统全局稳定.
2.3 控制器调整上述控制器是在固定坐标系下设计的, 不利于实际应用, 需将其转换至艇体坐标系, 有
| $ \begin{array}{l} \mathit{\boldsymbol{\tau }}\left( t \right) = \underbrace {\mathit{\boldsymbol{\tau }}\left( {t - L} \right) - \mathit{\boldsymbol{\bar M}}{\mathit{\boldsymbol{J}}^{ - 1}}\left( {t - L} \right)\varsigma \left( {t - L} \right)}_{{\rm{TDE}}} + \\ \underbrace {\mathit{\boldsymbol{\bar M}}\left( t \right){\mathit{\boldsymbol{J}}^{ - 1}}\left( t \right)\left( {{{\ddot \varsigma }_d} + {\alpha ^{ - 1}}{K^{ - 1}}{\rm{sig}}{{\left( {\dot e} \right)}^{2 - \alpha }} + {k_1}s + {k_2}{\rm{sig}}{{\left( s \right)}^\beta }} \right)}_{{\rm{NTSMC}}}. \end{array} $ | (36) |
各推进器或关节电机所需输出力/力矩为
| $ \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{B}}^ + }\mathit{\boldsymbol{\tau }}. $ | (37) |
式中:B+为UVMS推力分配矩阵的伪逆, 取决于UVMS推进器/关节电机布局.
执行器输出饱和、静摩擦等硬非线性的存在, 易导致基于TDE的闭环控制系统出现windup现象.为此, 本文采用文献[16]所提anti-windup结构实现对windup现象的抑制.同时, 设计一种补偿器实现对死区等其他非线性的补偿和抑制.最终, 系统所采用的控制器可写为
| $ \mathit{\boldsymbol{\tau }} = {\mathit{\boldsymbol{\tau }}_{{\rm{ftde}}}} + {\mathit{\boldsymbol{\tau }}_{{\rm{comp}}}}. $ | (38) |
式中:τftde为控制器经过anti-windup结构和一阶惯性滤波器1/(Ts+1)后的输控制信号.
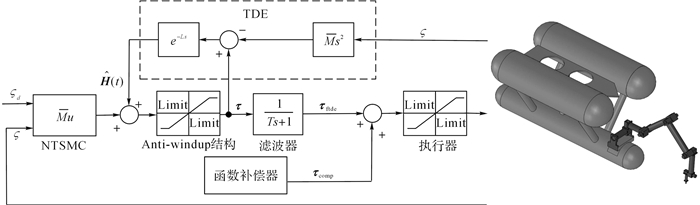
设计函数补偿器为τcomp=Kwsgn(τftde), 其中Kw为常数补偿增益, 可通过试验调节而得.最终, 系统总体框图如图 2所示.
|
图 2 闭环控制系统总体框图 Fig. 2 Overall scheme of closed-loop control system |
注1.文献[17]所提基于动力学模型的NTSMC方法采用与本文相同的非奇异终端滑模面后可写为
| $ \begin{array}{l} \mathit{\boldsymbol{\tau }} = {\mathit{\boldsymbol{\tau }}_1} + {\mathit{\boldsymbol{\tau }}_2},\\ {\mathit{\boldsymbol{\tau }}_1} = {\mathit{\boldsymbol{M}}_0}{\mathit{\boldsymbol{J}}^{ - 1}}\left( \mathit{\boldsymbol{\eta }} \right)\left[ {\left. {{{\mathit{\boldsymbol{\ddot \eta }}}_d} - \mathit{\boldsymbol{\dot J\eta }}} \right)\mathit{\boldsymbol{v}}} \right] + {\mathit{\boldsymbol{C}}_0}\left( \mathit{\boldsymbol{v}} \right)\mathit{\boldsymbol{v + }}\\ \;\;\;\;\;\;{\mathit{\boldsymbol{D}}_0}\left( \mathit{\boldsymbol{v}} \right)\mathit{\boldsymbol{v}} + {\mathit{\boldsymbol{g}}_0}\left( \mathit{\boldsymbol{\eta }} \right),\\ {\mathit{\boldsymbol{\tau }}_2} = - {\mathit{\boldsymbol{M}}_0}{\mathit{\boldsymbol{J}}^{ - 1}}\left( \mathit{\boldsymbol{\eta }} \right)\left[ {{\mathit{\boldsymbol{k}}_1}\mathit{\boldsymbol{s}} + {\mathit{\boldsymbol{k}}_2}{\rm{sig}}{{\left( \mathit{\boldsymbol{s}} \right)}^{m/n}} + } \right.\\ \;\;\;\;\;\;\left. {{\mathit{\boldsymbol{K}}^{ - 1}}{\mathit{\boldsymbol{\alpha }}^{ - 1}}{\rm{sig}}{{\left( {\mathit{\boldsymbol{\dot e}}} \right)}^{2 - p/q}}} \right]. \end{array} $ | (39) |
式中:τ1用于补偿系统动力学项, τ2用于实现复杂集总干扰下的鲁棒控制.
由式(39)可以看出, 若要实际应用该控制器, 需要得到UVMS标称动力学模型, 包括各项水动力参数.而由于作业环境的复杂性, UVMS自身的髙维度以及强耦合, 其较为准确的动力学模型很难拿到.即使通过耗时耗力的水池试验获取了较为详细的动力学参数, 一旦系统配置发生了较大变化, 所获取的参数也会跟随变化, 导致系统控制性能无法得到保证.而本文所提控制器(36)采用TDE算法对系统未知集总动态进行在线估算和实时补偿, 无需动力学模型, 可有效实现高品质运动控制和工程易用性的平衡, 有利于实际工程应用.
注2.为保证TDE算法在线估算和实时补偿的精度以及实时性, 时延值L取值较小, 一般取若干个采样周期.为此, 控制系统采样周期不宜过大.
3 仿真研究 3.1 仿真平台为验证所提算法的有效性和优越性, 本节基于研制的一型具有9自由度控制能力的UVMS展开相关对比仿真研究.同时考虑到UVMS包含水动力参数的精准动力学模型很难得到, 因此本节仿真基于Matlab/ SimMechanics展开.仿真中使用到的UVMS物理参数如表 1所示, 仿真模型如图 2-3所示.同时考虑到UVMS近似中性浮力, 故在仿真中设置g=0.
| 表 1 仿真中所用UVMS物理参数 Table 1 Physical parameters of UVMS used in simulations |
|
图 3 仿真过程中UVMS位姿变化 Fig. 3 Posture transformation of UVMS duringsimulation |
为验证所提控制算法对未知复杂集总干扰的鲁棒性, 在系统中添加时变干扰(40).控制器(36)的参数选择如下: α=1.6I9, β=0.6I9, K=0.5I9, k1=diag{0.5,0.5, 2,0.5,1,1,1,1,1}, k2=diag {0.5,0.5,2,0.5,1,1,1,2, 2},M=diag {4,4,4,4,1,0.5,0.2,0.2,0.008}, L=0.001 s.
| $ \begin{array}{l} t = 0 \sim 4\;{\rm{s}}:{T_{1 \sim 9}} = 0.\\ t = 4 \sim 20\;{\rm{s}}:{T_{1 \sim 9}} = {K_{{\rm{dis}}}}\sin \left( {\frac{{\rm{ \mathsf{ π} }}}{2}\left( {t - 4} \right)} \right). \end{array} $ | (40) |
式中:当T1~3时,单位为N;当T4~9时,单位为N·m
同时, 将所提算法与传统时延估计控制算法式(41)相对比以验证其有效性和优越性.下文用TDC表示.而为保证对比的公平性, 将所提算法参数α, β取1, 同时其余参数保持不变作为式(41)的控制参数.
| $ \begin{array}{l} \tau \left( t \right) = \underbrace {\bar M\left( t \right){J^{ - 1}}\left( t \right)\left( {{{\ddot \varsigma }_d} + {K_P}e + {K_D}\dot e} \right)}_{{\rm{Desireddynamics}}} + \\ \;\;\;\;\;\;\;\;\;\;\underbrace {\tau \left( {t - L} \right) - \bar M{J^{ - 1}}\left( {t - L} \right)\ddot \varsigma \left( {t - L} \right)}_{{\rm{TDE}}}. \end{array} $ | (41) |
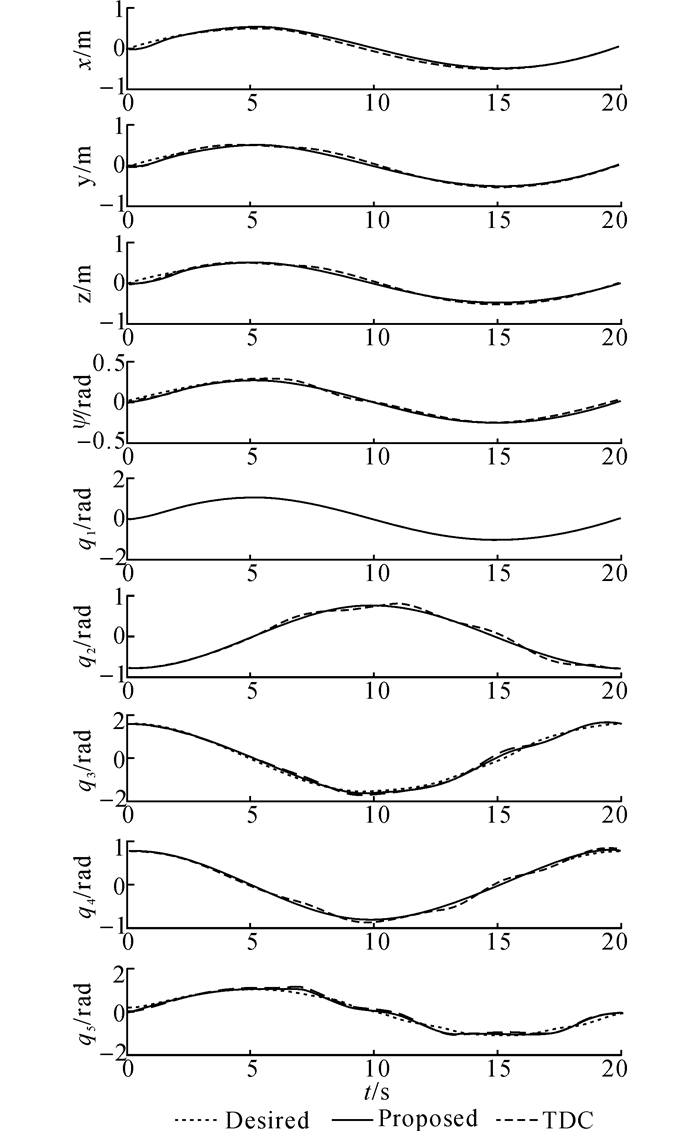
仿真结果如图 3~6所示, 其中横坐标t为时间轴, 单位:s.可以看出本文所提控制算法和TDC均可实现未知复杂集总干扰下令人满意的综合控制性能, 验证了TDE的有效性和工程易用性.同时, 从上述仿真结果也可以看出本文所提控制算法可以保证相对TDC更为优秀的控制性能, 有效证明了NTSMC的强鲁棒性和优异综合控制性能.
|
图 4 轨迹跟踪仿真结果 Fig. 4 Simulation results of trajectory tracking control |

|
图 5 轨迹跟踪误差仿真结果 Fig. 5 Simulation results of trajectory tracking errors |
|
图 6 控制信号仿真结果 Fig. 6 Simulation results of control inputs |
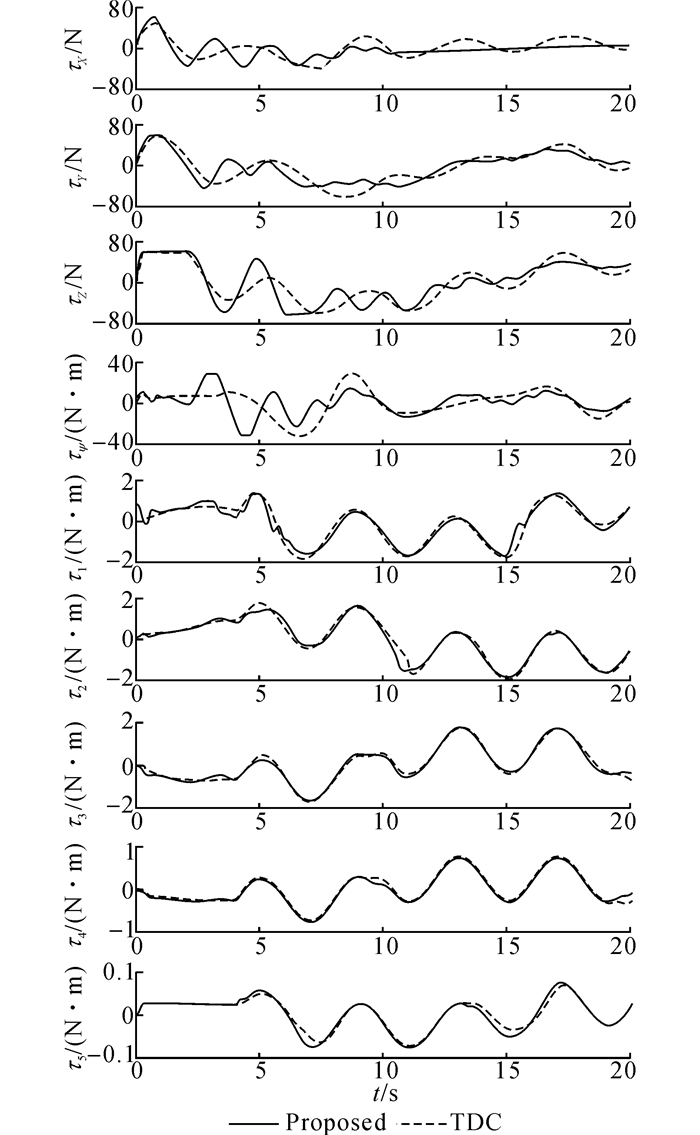
为进一步验证所提控制算法在实际工况下的控制效果, 本文展开了相应水池试验研究.试验平台如图 7所示.水下机器人配备六个200 W 12 V直流有刷电机驱动的螺旋桨推进器, 正反向最大推力分别为30和10 N, 并装备了精度为1 cm的深度传感器和0.5°的Honeywell HMR 3000罗盘.水下机械手为5自由度, 前4个关节采用Maxon Re25 118746电机和GP 32A 166174行星减速器驱动, 最后一个关节采用Maxon A-max 22 108828电机和GP22A 134168驱动.关节驱动模块安装的角度传感器精度约为0.03°.控制系统采用NI PCI-6229和Contec PCI DA12-16板卡, 采样周期为10 kHz, 控制信号限定为-5~+5 V.

|
图 7 UVMS试验平台 Fig. 7 UVMS experimental setup |
针对试验中所用水下机器人, 其推进器布局如图 8所示, 对应于式(37)中的B+可写为
| $ {\mathit{\boldsymbol{B}}^ + } = \left[ {\begin{array}{*{20}{c}} {0.5}&0&0&0\\ {0.5}&0&0&0\\ 0&{ - 0.5}&0&{0.675\;7}\\ 0&{0.5}&0&{0.675\;7}\\ 0&0&{0.5}&0\\ 0&0&{0.5}&0 \end{array}} \right]. $ | (42) |

|
图 8 水下机器人推进器布局示意图 Fig. 8 Arrangement diagram of underwater vehicle'spropellers |
由于试验所用水池较小且UVMS未装备高精度自身位置测量传感器, 故水池试验只针对其升沉、转艏及机械手关节角进行小范围7自由度轨迹跟踪控制试验.罗盘数据输出频率为10 Hz左右, 取时间长度L=0.2 s.其余方向传感器均为模拟量输出, 取L=1 ms.Kw为叠加在控制信号上的补偿器增益常量, 故下文试验结果中将只画出τftde.选取控制算法参数α=diag {1.2, 1.2, 1.6, 1.6, 1.6, 1.6, 1.6}, β=0.9I7, K=diag {2.5, 0.05, 1, 1, 1, 1, 1}, k1=diag{15, 2, 1, 1, 1, 1, 1}, k2=diag{15, 10, 1, 1, 1, 1, 1}, =0.M=0.1diag{1.5, 0.2, 3, 3, 3, 1.5, 2}.Kw=0.1diag{5, 5, 1, 1, 1, 1, 1}, T=0.1 s.
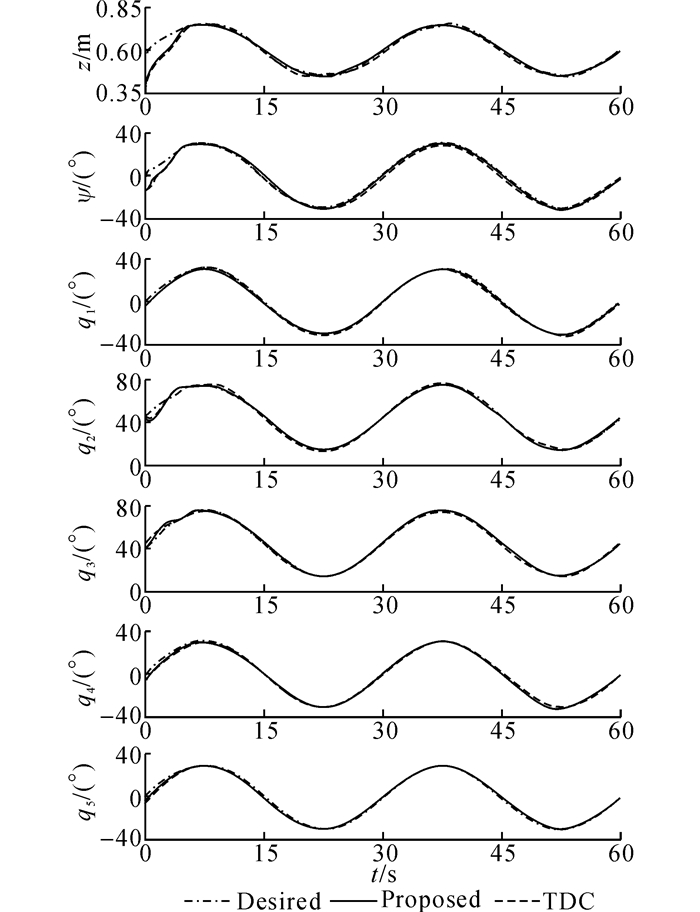
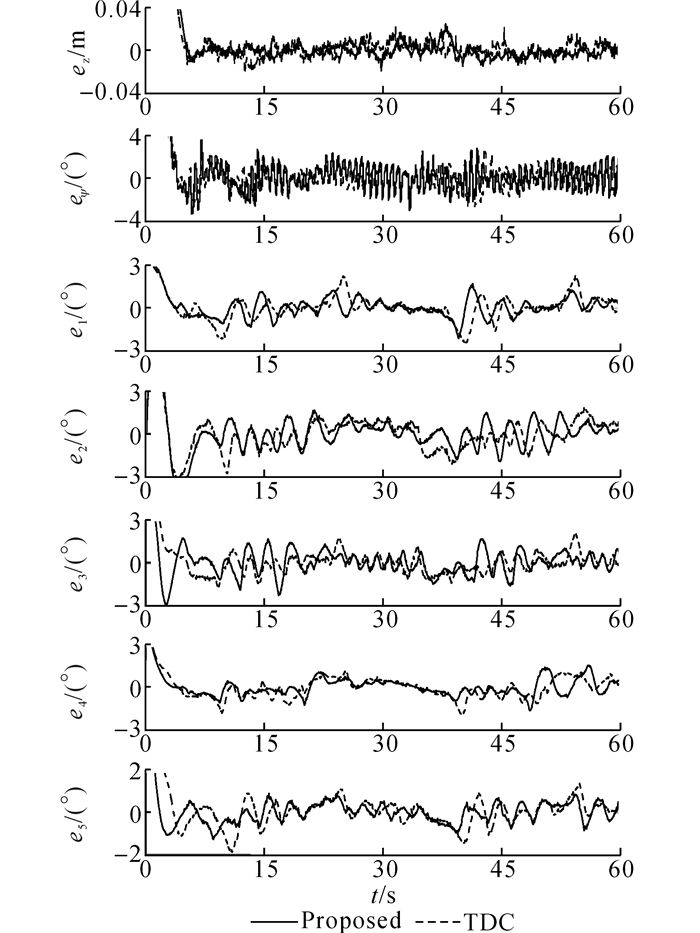
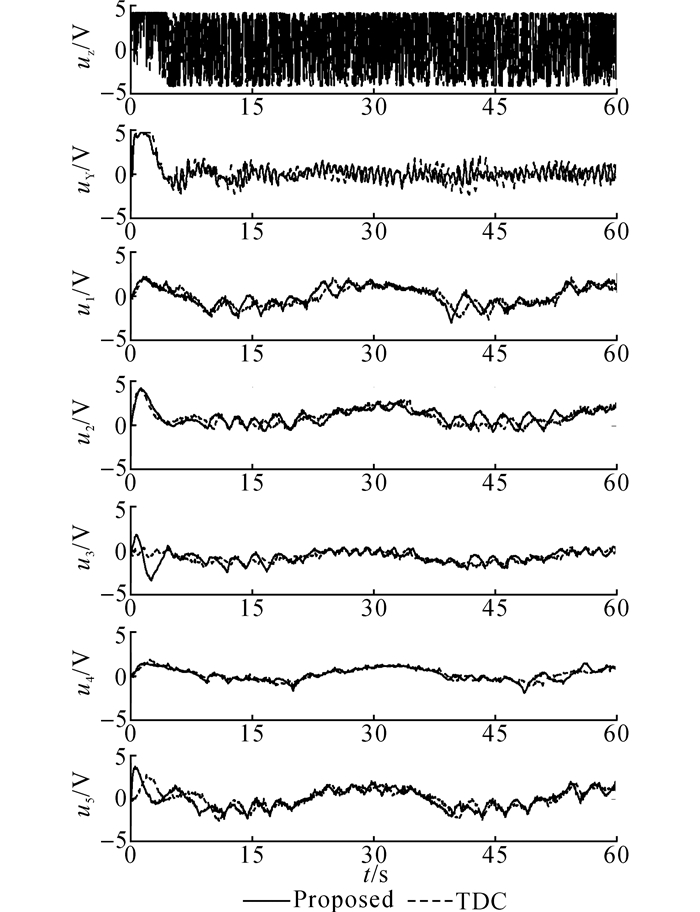
相关水池试验结果如图 9~11所示.而为显示所提算法在任务空间的控制效果, 将试验结果转换至艇体坐标系下的任务空间中, 得到如图 12~14所示的试验结果.同时采用均方根(root mean square, RMS)和最大值量化关节空间和任务空间的稳态跟踪误差, 计算数据来自第2个周期, 如表 2、3所示.
|
图 9 轨迹跟踪试验结果 Fig. 9 Experiment results of trajectory tracking control |
|
图 10 轨迹跟踪误差试验结果 Fig. 10 Experiment results of trajectory tracking errors |
|
图 11 控制信号试验结果 Fig. 11 Experiment results of control inputs |
|
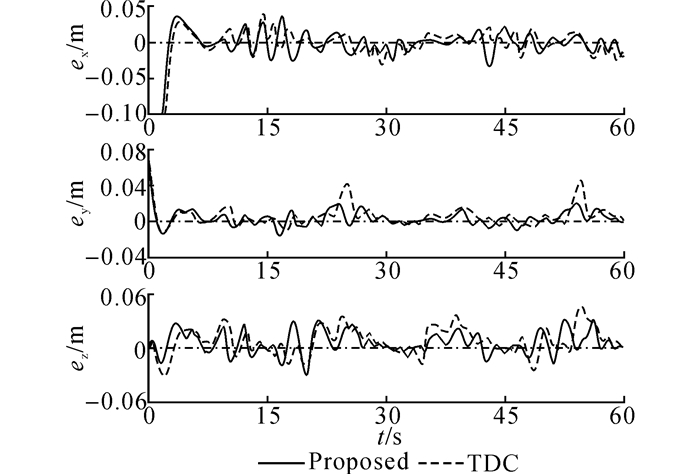
图 12 任务空间下末端手抓各方向的轨迹跟踪误差试验结果 Fig. 12 Experiment results of end effector trajectory tracking errors for each direction in task space |

|
图 13 任务空间下末端手抓轨迹跟踪误差试验结果 Fig. 13 Experiment results of end effector trajectory tracking errors in task space |
|
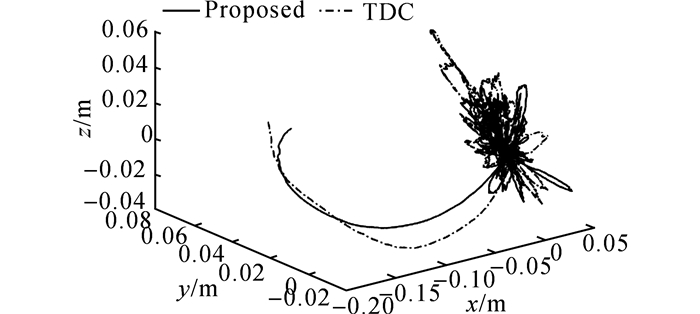
图 14 任务空间下末端手抓轨迹跟踪误差试验结果三维图 Fig. 14 Experiment results of end effector trajectory tracking errors in task space in 3-D figure |
| 表 2 稳态跟踪误差均方根及最大值 Table 2 RMS and maximum values of steady tracking errors |
| 表 3 任务空间下末端手抓稳态跟踪误差均方根及最大值 Table 3 RMS and maximum values of end effector steady tracking errors in task space |
以上试验结果与前文仿真结果高度一致, 2种控制器均可以保证令人满意的轨迹跟踪控制效果, 继而验证了TDE算法在实际工程应用中的有效性和易用性.同时, 本文所提控制算法几乎各自由度的控制效果均优于TDC, 综合控制效果更优, 从而验证了NTSMC的优越控制性能和强鲁棒性.由表 3知, 本文所提控制算法可保证系统末端控制精度为0.038 m, 而相比之下TDC仅为0.067 m, NTSMC的应用大幅提升了闭环控制系统的鲁棒性, 保证了未知复杂集总干扰下的综合控制性能.
5 结语针对复杂集总干扰下UVMS轨迹跟踪控制难题, 本文结合TDE与NTSMC, 创新提出一种高性能的非线性鲁棒控制方法.受益于TDE不基于动力学模型的特性和NTSMC的强鲁棒性和优越控制性能, 本文所提控制算法具有优异的控制性能、良好的鲁棒性和显著的工程易用性.采用李雅普诺夫稳定性理论分析了闭环控制系统的收敛性, 并给出了跟踪误差及其导数的理论收敛域.最终, 利用对比数值仿真和水池试验验证了所提控制算法相对传统时延估计控制算法的有效性和优越性, 试验结果表明前者可保证UVMS末端定位精度为0.038 m, 而后者定位精度仅为0.067 m.
未来将在本文的研究基础上, 进一步结合自适应控制、离散控制等理论, 优化算法, 并展开浪流环境下UVMS实际水下作业控制的试验研究, 以提升闭环控制系统综合控制品质.
| [1] |
OLGUÍN-DÍAZ E, ARECHAVALETA G, JARQUIN G, et al. A passivity-based model-free force-motion control of underwater vehicle-manipulator systems[J]. IEEE Transactions on Robotics, 2013, 29(6): 1469-1484. DOI:10.1109/TRO.2013.2277535 |
| [2] |
贾现军. 小型水下救援机器人位姿控制及其在水下搜救中的应用[D]. 杭州: 浙江大学, 2014. JIA Xian-jun. Position and attitude control of small rescue ROV and its applications[D]. Hangzhou: Zhejiang University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10335-1014173257.htm |
| [3] |
LYNCH B, ELLERY A. Efficient control of an AUV-manipulator system:an application for the exploration of Europa[J]. IEEE Journal of Oceanic Engineering, 2014, 39(3): 552-570. DOI:10.1109/JOE.2013.2271390 |
| [4] |
LONDHE P S, SANTHAKUMAR M, PATRE B M, et al. Task space control of an autonomous underwater vehicle manipulator system by robust single-input fuzzy logic control scheme[J]. IEEE Journal of Oceanic Engineering, 2017, 42(1): 13-28. |
| [5] |
HUANG Hai, TANG Qi-rong, LI Hong-wei, et al. Vehicle-manipulator system dynamic modeling and control for underwater autonomous manipulation[J]. Multibody System Dynamics, 2017, 41(2): 125-147. DOI:10.1007/s11044-016-9538-3 |
| [6] |
SOTIROPOULOS P, ASPRAGATHOS N. Neural networks to determine task oriented dexterity indices for an underwater vehicle-manipulator system[J]. Applied Soft Computing, 2016, 49: 352-364. DOI:10.1016/j.asoc.2016.08.033 |
| [7] |
MOHAN S, KIM J. Indirect adaptive control of an autonomous underwater vehicle-manipulator system for underwater manipulation tasks[J]. Ocean Engineering, 2012, 54(1): 233-243. |
| [8] |
MARANI G, CHOI S K, YUH J. Underwater autonomous manipulation for intervention missions AUVs[J]. Ocean Engineering, 2009, 36(1): 15-23. DOI:10.1016/j.oceaneng.2008.08.007 |
| [9] |
HAN J, PARK J, CHUNG W K. Robust coordinated motion control of an underwater vehicle-manipulator system with minimizing restoring moments[J]. Ocean Engineering, 2011, 38(10): 1197-1206. DOI:10.1016/j.oceaneng.2011.05.014 |
| [10] |
XU Bin, PANDIAN S R, SAKAGAMI N, et al. Neuro-fuzzy control of underwater vehicle-manipulator systems[J]. Journal of the Franklin Institute, 2012, 349(3): 1125-1138. DOI:10.1016/j.jfranklin.2012.01.003 |
| [11] |
张奇峰. 自治水下机器人-机械手系统运动规划与协调控制研究[D]. 沈阳: 中国科学院沈阳自动化研究所, 2007. ZHANG Qi-feng. Research on coordinated motion planning and control of autonomous underwater vehicle-manipulator system[D]. Shenyang: Shengyang Institute of Automation, Chinese Academy of Sciences, 2007. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1615191 |
| [12] |
郭莹. 水下自主作业系统协调控制技术研究[D]. 武汉: 华中科技大学, 2008. GUO Ying. Coordinated control technology of underwater vehicle-manipulator system[D]. Wuhang: Huazhong University of Science and Technology, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10487-2009141768.htm |
| [13] |
彭生全. 水下机器人-机械手系统运动规划与控制技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2012. PENG Sheng-quan. Research on the motion planning and control for underwater vehicle-manipulator system[D]. Harbin: Harbin Engineering University. http://cdmd.cnki.com.cn/Article/CDMD-10217-1013171982.htm |
| [14] |
ANTONELLI G. Underwater robots[M]. Cassino: Springer, 2014.
|
| [15] |
YU Shuang-he, YU Xing-huo, SHIRINZADEH B, et al. Continuous finite-time control for robotic manipulators with terminal sliding mode[J]. Automatica, 2005, 41(11): 1957-1964. DOI:10.1016/j.automatica.2005.07.001 |
| [16] |
CHANG P H, PARK S H. On improving time-delay control undercertain hard nonlinearities[J]. Mechatronics, 2003, 13(4): 393-412. DOI:10.1016/S0957-4158(01)00046-0 |
| [17] |
王尧尧, 顾临怡, 高明, 等. 水下运载器非奇异快速终端滑模控制[J]. 浙江大学学报:工学版, 2014, 48(9): 1541-1551. WANG Yao-yao, GU Lin-yi, GAO Ming, et al. Nonsingular fast terminal sliding mode control for underwater vehicles[J]. Journal of Zhejiang University:Engineering Science, 2014, 48(9): 1541-1551. |



