在复合材料制品压制成形过程中, 液压机需要连续完成空载快降-空载慢降-工进加压-保压-泄压-慢速回程-快速回程至停止, 完成一个循环工艺[1].工进加压过程中必须能够按照预先设定的运动轨迹进行工作.然而, 液压机电液系统在工进加压运动阶段存在参数不确定性、不确定非线性和外干扰等问题[2].因此, 如何实现精确的轨迹跟踪控制是当前的研究热点问题.
国内外学者, 为了解决上述问题所采用的PID控制器进行控制具有很好的稳态精度, 但往往动静态特性不能兼顾, 二者常常发生互相矛盾的现象.当被控对象机理复杂、具有强非线性扰动、时变不确定性和纯滞后等特点时, 很难找到一组合适的PID参数适用于整个系统的宽范围调控.另外, 在噪声、负载扰动等因素的影响下, 过程参数甚至模型结构均会随时间和工作环境的变化而变化.这就要求在PID控制中, 不仅PID参数的整定不依赖于对象数学模型, 并且PID参数能够在线调整, 以满足实时控制的要求.PID参数的自调整或自适应可通过改进或与其他先进控制策略的融合获得[3-4].因此, 吸取智能控制和自适应控制的基本思想, 将传统的PID控制加以改造成模糊PID、自适应PID等, 在一定程序上克服原先的不足, 以适应新的要求[5-8].但上述研究中的改进PID控制器均没有考虑模型的控制补偿, 因此, 开展基于模型的液压机非线性控制方法显得有所必要.
国内外一些学者开展了各类基于模型的非线性控制方法的研究, 并取得了有益的研究成果, 包括滑模变结构(鲁棒)控制[9-10]、自适应控制[11-12]、反步递推方法[13-14]以及上述方法的复合控制策略[15-16].Yao等[17-18]提出基于模型设计的自适应鲁棒控制(ARC)运动控制器, 结合了自适应控制与鲁棒控制(如滑模控制)的优点, 并采用反步递推方法, 可以同时解决系统的参数不确定性和不确定非线性等问题.目前, ARC运动控制器已成功应用于粉末成形液压机[19]、快锻液压机[20]、高频响比例阀[21]、变排量柱塞泵[22]、气动位置伺服系统[23]等领域, 表现出了广阔的应用领域和众多的研究成果.杜春燕等[24]基于反步法设计了锻造液压机速度控制器, 只在仿真层面验证了所设计的控制器比PID控制器具有更好跟随性和鲁棒性.
本文以复合材料成形液压机电液系统为研究对象, 建立了系统的非线性动力学模型, 设计一种基于非连续映射的自适应鲁棒控制器.在控制器的设计过程中, 应用Lyapunov稳定性理论证明了闭环系统是稳定的.首先, 建立了液压机的AMESim与MATLAB/Simulink联合仿真模型, 其次, 在搭建的液压机缩比样机上进行了实验研究.仿真和实验结果表明, 非线性ARC控制器克服了传统PID控制器的局限性, 具有良好的控制精度和极强的鲁棒性能.
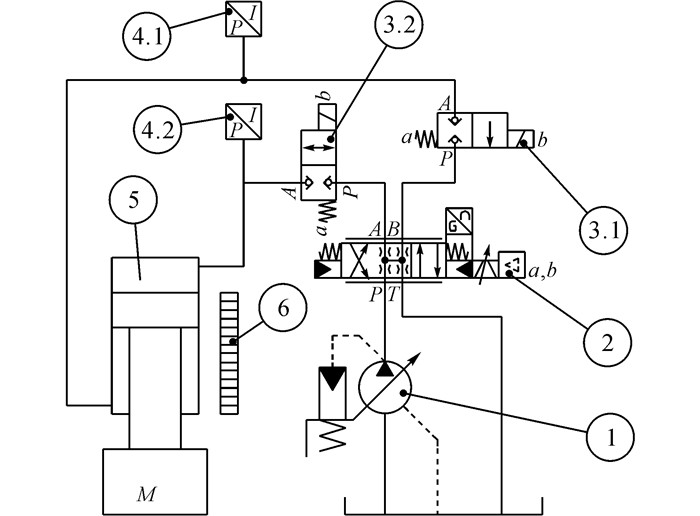
1 系统描述和数学建模以复合材料成形液压机的双作用活塞式液压缸作为具体的研究对象, 探讨基于此类非线性模型的控制方法.复合材料成形液压机的电液系统原理图如图 1所示.
|
1-恒压变量泵; 2-高频响伺服比例阀; 3-通断阀; 4-压力传感器; 5-活塞式液压缸; 6-磁栅尺 图 1 液压机电液系统原理图 Fig. 1 Principle diagram of electro-hydraulic system for hydraulic press |
液压机的液压缸力平衡方程为
| $ m{{\ddot x}_P} = {p_1}{A_1} - {p_2}{A_2} - b{{\dot x}_P} - {F_{co} }\tanh {{\dot x}_P} + G + \tilde f. $ | (1) |
式中:m为液压缸驱动的等效负载质量, xP为负载位移, p1、p2为液压缸两腔压力, A1、A2为液压缸两腔作用面积, b为活塞及负载的黏性阻尼系数, Fco为库伦摩擦力, G为等效负载重量,
液压缸两腔压力动态模型的表达式为
| $ \left. \begin{array}{l} \frac{{{V_{h1}}}}{{{\beta _e}}}{{\dot p}_1} = - {A_1}{{\dot x}_P} + {q_{V1}},\\ \frac{{{V_{h2}}}}{{{\beta _e}}}{{\dot p}_2} = {A_2}{{\dot x}_P} - {q_{V2}}. \end{array} \right\} $ | (2) |
其中
| $ \left. \begin{array}{l} {V_{h1}} = {V_{01}} + {A_1}{x_P},\\ {V_{h2}} = {V_{02}} + {A_2}\left( {L - {x_P}} \right). \end{array} \right\} $ | (3) |
式中:qV1、qV2为高频响伺服比例阀至液压缸两腔流量, Vh1、Vh2为液压缸两腔总容积, V01、V02为液压缸两腔初始容积, βe为液压油有效体积弹性模量, L为液压缸行程.
两腔流量qV1和qV2的表达式如下:
| $ \left. \begin{array}{l} {q_{V1}} = {k_{q{V_1}}}u\left[ {{s_g}\left( u \right)\sqrt {{p_{\rm{s}}} - {p_{\rm{l}}}} + {s_g}\left( { - u} \right)\sqrt {{p_{\rm{l}}} - {p_{\rm{t}}}} } \right],\\ {q_{V2}} = {k_{q{V_2}}}u\left[ {{s_g}\left( u \right)\sqrt {{p_{\rm{2}}} - {p_{\rm{t}}}} + {s_g}\left( { - u} \right)\sqrt {{p_{\rm{s}}} - {p_{\rm{2}}}} } \right]. \end{array} \right\} $ | (4) |
定义
| $ {s_g}\left( \cdot \right) = \left\{ \begin{array}{l} 1,\;\;\;\;当\; \cdot \ge 0;\\ 0,\;\;\;\;当\; \cdot < 0. \end{array} \right. $ | (5) |
式中:kqV1、kqV2为高频响伺服比例阀的流量系数, u为高频响伺服比例阀的控制电压, ps为油源供油压力, pt为回油压力.
定义u作为系统的控制输入, 并定义系统的状态变量为
| $ x = {\left[ {{x_1},{x_2},{x_3},{x_4}} \right]^{\rm{T}}} = {\left[ {{x_P},{{\dot x}_P},{p_1},{p_2}} \right]^{\rm{T}}}. $ |
则系统的状态方程表达式为
| $ \left. \begin{array}{l} {{\dot x}_1} = {x_2},\\ \begin{array}{*{20}{c}} {{{\dot x}_2} = \frac{1}{m}\left( {{A_1}{x_3} - {A_2}{x_4} - b{x_2} - } \right.}\\ {\left. {{F_{co}}\tanh {x_2} + G} \right) + d,} \end{array}\\ {{\dot x}_3} = \frac{{{\beta _e}}}{{{V_{h1}}}}\left( { - {A_1}{x_2} + {k_{q{V_1}}}{g_3}u} \right),\\ {{\dot x}_4} = \frac{{{\beta _e}}}{{{V_{h2}}}}\left( {{A_2}{x_2} - {k_{q{V_2}}}{g_4}u} \right). \end{array} \right\} $ | (6) |
其中
| $ \left. \begin{array}{l} {g_3} = {s_g}\left( u \right)\sqrt {{p_{\rm{s}}} - {x_3}} + {s_g}\left( { - u} \right)\sqrt {{x_3} - {p_{\rm{t}}}} ,\\ {g_4} = {s_g}\left( u \right)\sqrt {{x_4} - {p_{\rm{t}}}} + {s_g}\left( { - u} \right)\sqrt {{p_{\rm{s}}} - {x_4}} . \end{array} \right\} $ | (7) |
定义系统不确定参数θ1, θ2和θ3的集合为θ=[θ1, θ2, θ3]T, θ1=1/m, θ2=dn, θ3=βe.把θ代入式(6), 则系统状态方程表达式为
| $ \left. \begin{array}{l} {{\dot x}_1} = {x_2},\\ {{\dot x}_2} = {\theta _1}\left( {{A_1}{x_3} - {A_2}{x_4} - b{x_2} - } \right.\\ \;\;\;\;\;\;\;\left. {{F_{co}}\tanh {x_2} + G} \right) + {\theta _2} + \tilde d,\\ {{\dot x}_3} = {h_1}\left[ {{\theta _3}\left( { - {A_1}{x_2} + {k_{q{V_1}}}{g_3}u} \right)} \right],\\ {{\dot x}_4} = {h_2}\left[ {{\theta _3}\left( {{A_2}{x_2} - {k_{q{V_2}}}{g_4}u} \right)} \right]. \end{array} \right\} $ | (8) |
其中
| $ {h_1} = \frac{1}{{{V_{h1}}}},\;\;\;{h_2} = \frac{1}{{{V_{h2}}}},\;\;\;d = \frac{{\tilde f}}{m} = \tilde d + {d_n}. $ | (9) |
式中:
式(8)中的不确定的参数及非线性干扰是有界的且范围是确定的, 满足如下假设:
| $ \left. \begin{array}{l} \theta = {\mathit{\Omega }_\theta } \buildrel \Delta \over = \left\{ {\theta :{\theta _{\min }} < \theta < {\theta _{\max }}} \right\},\\ \left| {\tilde d\left( {t,x} \right)} \right| \le {\delta _d}\left( {x,t} \right). \end{array} \right\} $ | (10) |
式中:Ωθ为未知参数θ构成的有界集合,θmin=[θ1min, θ2min, θ3min]T, θmax=[θ1max, θ2max, θ3max]T, θ1min、θ2min、θ3min和θ1max、θ2max、θ3max分别为未知参数θ的下界和上界,且δd(x, t)是已知有界项.
分别用
| $ \left. \begin{array}{l} {{\hat {\dot x}}_2} = {{\hat \theta }_1}\left( {{A_1}{x_3} - {A_2}{x_4} - b{x_2} - } \right.\\ \;\;\;\;\;\;\;\left. {{F_{co}}\tanh {x_2} + G} \right) + {{\hat \theta }_2},\\ {{\hat {\dot x}}_3} = {h_1}\left[ {{{\hat \theta }_3}\left( { - {A_1}{x_2} + {k_{q{V_1}}}{g_3}u} \right)} \right],\\ {{\hat {\dot x}}_4} = {h_2}\left[ {{{\hat \theta }_3}\left( {{A_2}{x_2} - {k_{q{V_2}}}{g_4}u} \right)} \right]. \end{array} \right\} $ | (11) |
·i代表向量·的第i个元素, 运算 < 是针对每个向量的单个元素进行, 并假设θimin>0.上标
| $ {\rm{pro}}{{\rm{j}}_{{{\hat \theta }_i}}}\left( {{ \cdot _i}} \right) = \left\{ \begin{array}{l} 0,\;\;\;\;\;{{\hat \theta }_i} = {\theta _{i\max }}\;\;\;\;\& { \cdot _i} > 0;\\ 0,\;\;\;\;\;{{\hat \theta }_i} = {\theta _{i\min }}\;\;\;\;\& { \cdot _i} < 0;\\ { \cdot _i},\;\;\;\;\;其他. \end{array} \right. $ | (12) |
基于该非连续映射的自适应律为
| $ \dot {\hat \theta} = {\rm{pro}}{{\rm{j}}_{\hat \theta }}\left( {\mathit{\Gamma }\tau } \right), $ | (13) |
式中:Γ和τ分别为估计参数
| $ \left. {\begin{array}{*{20}{c}} {\hat \theta = {{\mathit{\bar \Omega }}_\theta } \buildrel \Delta \over = \left\{ {\hat \theta :{\theta _{\min }} \le \hat \theta \le {\theta _{\max }}} \right\},}\\ {{{\tilde \theta }^{\rm{T}}}\left( {{\mathit{\Gamma }^{ - 1}}{\rm{pro}}{{\rm{j}}_{\hat \theta }}\left( {\mathit{\Gamma }\tau } \right) - \tau } \right) \le 0,\;\;\;\;\;\forall \tau .} \end{array}} \right\} $ | (14) |
液压缸期望的运动轨迹为x1d, 运动轨迹跟踪误差定义为z1=x1-x1d, 定义一个切换面为
| $ \left. \begin{array}{l} {z_2} = {{\dot z}_1} + {k_1}{z_1} = {x_2} - {x_{2eq}},\\ {x_{2eq}} \buildrel \Delta \over = {{\dot x}_{1d}} - {k_1}{z_1}. \end{array} \right\} $ | (15) |
式中:z1=x1-x1d为轨迹跟踪误差, k1为正的反馈增益.由于z2到z1的传递函数G(s)=1/(s+k1)是稳定的, 当z2趋近于零时, z1必定也趋近于零.将式(15)对时间微分, 并与式(8)中的第2个方程结合, 可得
| $ \left. \begin{array}{l} {{\dot z}_2} = {\theta _1}\left( {{A_1}{x_3} - {A_2}{x_4} - b{x_2} - } \right.\\ \;\;\;\;\;\;\left. {{F_{co} }\tanh {x_2} + G} \right) + {\theta _2} + \tilde d - {{\dot x}_{2eq}},\\ {{\dot x}_{2eq}} \buildrel \Delta \over = {{\ddot x}_{1d}} - {k_1}{{\dot z}_1}. \end{array} \right\} $ | (16) |
将pL=A1x3-A2x4看成是式(16)的虚拟控制输入, 并令z3=pL-α2为虚拟控制输入偏差.因此, 步骤1的任务是通过设计该虚拟控制输入保证z2趋近于零, 以使轨迹跟踪误差z1趋近于零.虚拟控制函数α2包括
| $ \left. \begin{array}{l} {\alpha _2} = {\alpha _{2a}} + {\alpha _{2s}},\\ {\alpha _{2a}} = b{x_2} + {F_{co} }\tanh {x_2} - G + \frac{1}{{{{\hat \theta }_1}}}\left( {{{\dot x}_{2eq}} - {{\hat \theta }_2}} \right). \end{array} \right\} $ | (17) |
虚拟控制函数α2中的α2a为模型补偿项, α2s是鲁棒控制项, 且满足如下条件
| $ \left. \begin{array}{l} {\alpha _{2s}} = {\alpha _{2s1}} + {\alpha _{2s2}},\\ {\alpha _{2s1}} = - \frac{1}{{{\theta _{1\min }}}}{k_2}{z_2},\\ {k_2} \ge {k_{2s1}} + {w_2}{\left\| {\mathit{\Gamma }{\phi _2}} \right\|^2}. \end{array} \right\} $ | (18) |
式中:k2s1为反馈增益,ϕ2为回归向量.
定义一个半正定Lyapunov函数
| $ {V_2} = \frac{1}{2}{w_2}z_2^2. $ | (19) |
式中:w2>0为权重因子.
微分V2并将式(16)和(18)代入式(19), 可得
| $ \begin{array}{l} {{\dot V}_2} = {w_2}{z_2}\left( {{\theta _1}{\alpha _{2s2}} - {{\tilde \theta }^{\rm{T}}}{\phi _2} + \tilde d} \right) + \\ \;\;\;\;\;\;\;{w_2}{\theta _1}{z_2}{z_3} - {w_2}\frac{{{\theta _1}}}{{{\theta _{1\min }}}}{k_2}z_2^2. \end{array} $ | (20) |
其中:
| $ {\boldsymbol{\phi} _2} = \left[ \begin{array}{l} {\alpha _{2a}} - b{x_2} - {F_{co}}\tanh {x_2} + G\\ 1\\ 0 \end{array} \right]. $ | (21) |
选择鲁棒控制函数α2s2, 使其满足以下2个条件
| $ \left. {\begin{array}{*{20}{c}} {{\rm{I}}.}&{{z_2}\left( {{\theta _1}{\alpha _{2s2}} - {{\tilde \theta }^{\rm{T}}}{\phi _2} + \tilde d} \right) \le {\varepsilon _2},}\\ {{\rm{II}}.}&{{z_2}{\alpha _{2s2}} \le 0.} \end{array}} \right\} $ | (22) |
式中:ε2为设计的任意小正数.
自适应函数τ2选择为
| $ {\tau _2} = {w_2}{\phi _2}{z_2}. $ | (23) |
步骤2是使z3收敛于零. z3对时间的微分为
| $ \begin{array}{l} {{\dot z}_3} = {{\dot p}_L} - {{\dot \alpha }_2} = {\theta _3}\left[ { - \left( {A_1^2{h_1} + A_2^2{h_2}} \right){x_2} + } \right.\\ \;\;\;\;\;\;\;\left. {\left( {{A_1}{h_1}{k_{qV1}}{g_3} + {A_2}{h_2}{k_{qV2}}{g_4}} \right)u} \right] - {{\dot \alpha }_{2c}} - {{\dot \alpha }_{2u}}. \end{array} $ | (24) |
结合方程(17)和(8), 可得
| $ {{\dot \alpha }_2} = \frac{{\partial {\alpha _2}}}{{\partial {x_1}}}{{\dot x}_1} + \frac{{\partial {\alpha _2}}}{{\partial {x_2}}}{{\dot x}_2} + \frac{{\partial {\alpha _2}}}{{\partial \hat \theta }}\dot {\hat \theta} + \frac{{\partial {\alpha _2}}}{{\partial t}} = {{\dot \alpha }_{2c}} + {{\dot \alpha }_{2u}}. $ | (25) |
其中
| $ \left. \begin{gathered} {{\dot \alpha }_{2c}} = \left( {\frac{{\partial {\alpha _2}}}{{\partial {x_1}}}{x_2} + \frac{{\partial {\alpha _2}}}{{\partial {x_2}}}{{\hat {\dot x}}_2} + \frac{{\partial {\alpha _2}}}{{\partial {x_{1d}}}}{{\dot x}_{1d}} + } \right. \hfill \\ \;\;\;\;\;\;\;\left. {\frac{{\partial {\alpha _2}}}{{\partial {{\dot x}_{1d}}}}{{\ddot x}_{1d}} + \frac{{\partial {\alpha _2}}}{{\partial {{\ddot x}_{1d}}}}{{\dddot x}_{1d}} + \frac{{\partial {\alpha _2}}}{{\partial {{\dddot x}_{1d}}}}{{\ddddot x}_{1d}}} \right), \hfill \\ {{\dot \alpha }_{2u}} = \frac{{\partial {\alpha _2}}}{{\partial {x_2}}}\left\{ { - \left[ {{A_1}{x_3} - {A_2}{x_4} - b{x_2} - } \right.} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\left. {\left. {{F_{co}}\tanh \left( {{x_2}} \right) + G} \right]{{\tilde \theta }_1} - {{\tilde \theta }_2} + \tilde d} \right\} + \frac{{\partial {\alpha _2}}}{{\partial \hat \theta }}\dot {\hat \theta} . \hfill \\ \end{gathered} \right\} $ | (26) |
式(26)中
定义另一个半正定Lyapunov函数
| $ {V_3} = {V_2} + \frac{1}{2}{w_3}z_3^2. $ | (27) |
式中:w3为加权因子.
微分式(27)并结合(20), 可得
| $ \begin{array}{l} {{\dot V}_3} = {{\dot V}_2} + {w_3}{z_3}{{\dot z}_3} = \\ \;\;\;\;\;\;{{\dot V}_2}\left| {_{{\alpha _2}}} \right. + {w_2}{\theta _1}{z_2}{z_3} + {w_3}{z_3}{{\dot z}_3}. \end{array} $ | (28) |
式中:
结合方程(24)和(28),
| $ \begin{array}{l} {{\dot V}_3} = {{\dot V}_2}\left| {_{{\alpha _2}}} \right. + {w_2}{\theta _1}{z_2}{z_3} + \\ \;\;\;\;\;\;{w_3}{z_3}\left\{ {{\theta _3}\left[ { - \left( {A_1^2{h_1} + A_2^2{h_2}} \right){x_2} + } \right.} \right.\\ \;\;\;\;\;\;\left. {\left. {\left( {{A_1}{h_1}{k_{qV1}}{g_3} + {A_2}{h_2}{k_{qV2}}{g_4}} \right)u} \right] - {{\dot \alpha }_{2c}} - {{\dot \alpha }_{2u}}} \right\}. \end{array} $ | (29) |
定义
| $ \left. \begin{array}{l} {H_1} = {A_1}{h_1}{k_{qV1}}{g_3},\\ {H_2} = {A_2}{h_2}{k_{qV2}}{g_4}. \end{array} \right\} $ | (30) |
把方程(30)代入(29), 方程(29)可改写为
| $ \begin{array}{l} {{\dot V}_3} = {{\dot V}_2}\left| {_{{\alpha _2}}} \right. + {w_3}{z_3}\left\{ {\frac{{{w_2}{z_2}}}{{{w_3}}}{{\hat \theta }_1} + \left[ {{{\hat \theta }_3}\left( {{H_1} + {H_2}} \right){u_a} - } \right.} \right.\\ \;\;\left. {{{\hat \theta }_3}\left( {A_1^2{h_1} + A_2^2{h_2}} \right){x_2}} \right] + {\theta _3}\left( {{H_1} + {H_2}} \right){u_s} - {{\tilde \theta }^{\rm{T}}}{\phi _3} - \\ \;\;\left. {{{\dot \alpha }_{2c}} - \frac{{\partial {\alpha _2}}}{{\partial {x_2}}}\tilde d - \frac{{\partial {\alpha _2}}}{{\partial \hat \theta }}\dot {\hat \theta} } \right\}. \end{array} $ | (31) |
最终的控制律u设计为
| $ \left. \begin{array}{l} u = {u_a} + {u_s},\\ {u_a} = \frac{1}{{{{\hat \theta }_3}\left( {{H_1} + {H_2}} \right)}}\left[ {{{\hat \theta }_3}\left( {A_1^2{h_1} + A_2^2{h_2}} \right){x_2} + } \right.\\ \;\;\;\;\;\;\;\left. {{{\dot \alpha }_{2c}} - \frac{{{w_2}{z_2}}}{{{w_3}}}{{\hat \theta }_1} + \frac{{\partial {\alpha _2}}}{{\partial \hat \theta }}\dot {\hat \theta} } \right],\\ {u_s} = {u_{s1}} + {u_{s2}},\\ {u_{s1}} = - \frac{1}{{{\theta _{3\min }}\left( {{H_1} + {H_2}} \right)}}{k_3}{z_3},\\ {k_3} \ge {k_{3s1}} + {w_3}{\left\| {\mathit{\Gamma }{\phi _3}} \right\|^2} + \frac{1}{2}{w_3}{\left\| {\frac{{\partial {\alpha _3}}}{{\partial \hat \theta }}} \right\|^2}. \end{array} \right\} $ | (32) |
其中
| $ {\phi _3} = \left[ {\begin{array}{*{20}{c}} {\frac{{{w_2}}}{{{w_3}}}{z_2} - \frac{{\partial {\alpha _2}}}{{\partial {x_2}}}\left[ {{A_1}{x_3} - {A_2}{x_4} - b{x_2} - } \right.}\\ {\left. {{F_{co}}\tanh \left( {{x_2}} \right) + G} \right] - \frac{{\partial {\alpha _2}}}{{\partial {x_2}}}}\\ {\left( {{H_1} + {H_2}} \right){u_a} - \left( {A_1^2{h_1} + A_2^2{h_2}} \right){x_2}} \end{array}} \right]. $ | (33) |
式中:ua为模型补偿项, us为鲁棒控制项, k3为线性反馈增益且k3>0. us2用于应对模型不确定性和不确定非线性, 为光滑控制函数, 需满足条件
| $ \left. \begin{array}{l} {\rm{I}}.\;\;\;\;{z_3}\left[ {{\theta _3}\left( {{H_1} + {H_2}} \right){u_{s2}} - {{\tilde \theta }^{\rm{T}}}{\phi _3} - \frac{{\partial {\alpha _2}}}{{\partial {x_2}}}\tilde d} \right] \le {\varepsilon _3},\\ {\rm{II}}.\;\;\;{z_3}\left( {{H_1} + {H_2}} \right){u_{s2}} \le 0. \end{array} \right\} $ | (34) |
式中:ε3为控制器参数.
系统的自适应函数τ为
| $ \tau = {w_2}{\phi _2}{z_2} + {w_3}{\phi _3}{z_3}. $ | (35) |
理论1:根据方程(8)所表述的系统, 控制律满足假设(10)的条件下, 如果控制指令用式(32)和(13)综合, 得出如下结论:
Ⅰ.跟踪误差z1及其构建的状态变量为z=[z1, z2, z3]T是有界的.公式(31)中的Lyapunov函数V3(t)是指数收敛的
| $ \begin{array}{l} {V_3}\left( t \right) \le \\ \;\;\;\exp \left( { - {\lambda _V}t} \right){V_3}\left( 0 \right) + \frac{{{\varepsilon _V}}}{{{\lambda _V}}}\left[ {1 - \exp \left( { - {\lambda _V}t} \right)} \right]. \end{array} $ | (36) |
其中
| $ \left. \begin{array}{l} {\lambda _V} = 2\min \left\{ {{k_2},{k_3}} \right\},\\ {\varepsilon _V} = {\omega _2}{\varepsilon _2} + {\omega _3}{\varepsilon _3}. \end{array} \right\} $ | (37) |
Ⅱ.在有限的时间t0,
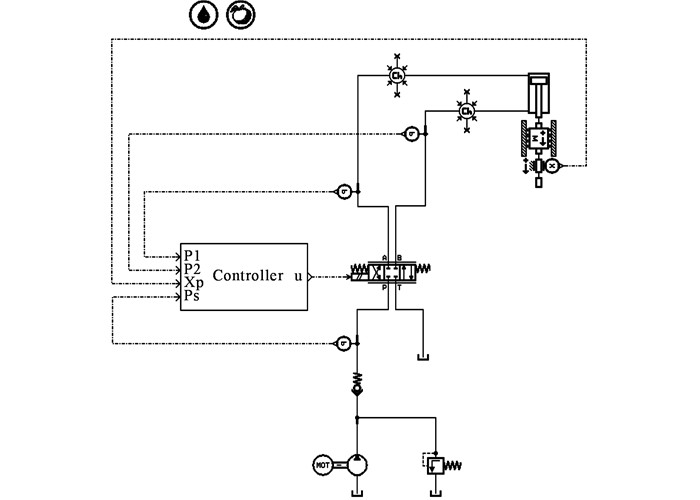
为了验证所提ARC控制器的有效性, 搭建了如图 2所示的液压机电液系统仿真模型.
|
图 2 液压机电液系统的仿真模型 Fig. 2 Simulation model of electro-hydraulic system for a hydraulic press |
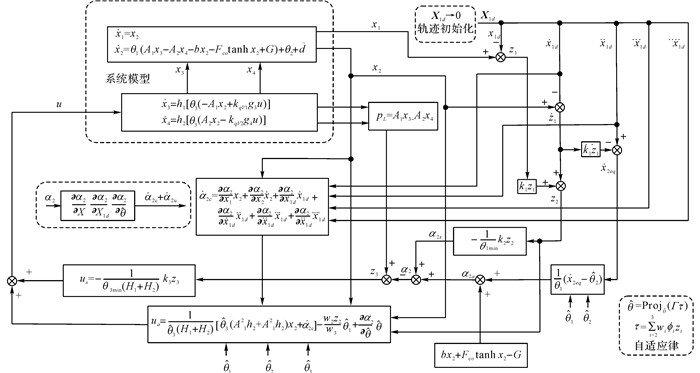
如图 3所示为ARC控制器的原理框图.如表 1所示为液压机电液系统的基本参数.
|
图 3 控制器原理框图 Fig. 3 Principle diagram of controller |
| 表 1 电液系统基本参数 Table 1 Basic parameters of electro-hydraulic system |
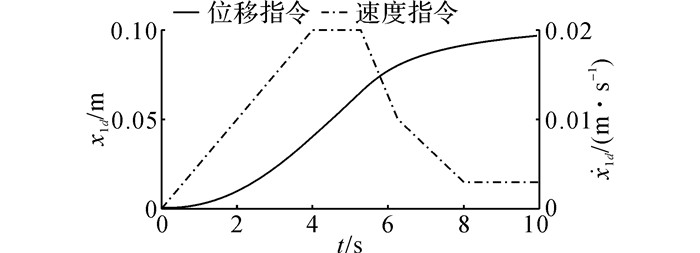
为了对比分析所提ARC控制器的性能, 采用PID控制器作为参照控制器.轨迹Ⅰ (点对点轨迹)和轨迹Ⅱ(正弦轨迹)的特性曲线分别如图 4和5所示.
|
图 4 轨迹Ⅰ的特性曲线 Fig. 4 Performance curves of trajectory Ⅰ |
|
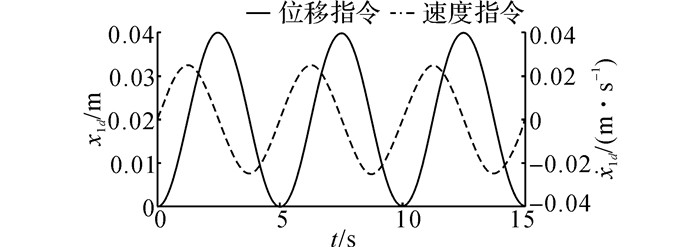
图 5 轨迹Ⅱ的特性曲线 Fig. 5 Performance curves of trajectory Ⅱ |
轨迹Ⅰ和轨迹Ⅱ的PID控制器仿真参数整定如下:
| $ \begin{array}{l} u_{{\rm{PID}}}^{\rm{I}} = 2000\left( {{x_{1d}} - {x_1}} \right) + \\ \;\;\;\;\;\;\;\;\;100\int_0^t {\left( {{x_{1d}} - {x_1}} \right){\rm{d}}t + 5\left( {{{\dot x}_{1d}} - {{\dot x}_1}} \right)} . \end{array} $ | (38) |
| $ \begin{array}{l} u_{{\rm{PID}}}^{{\rm{II}}} = 2300\left( {{x_{1d}} - {x_1}} \right) + \\ \;\;\;\;\;\;\;\;\;150\int_0^t {\left( {{x_{1d}} - {x_1}} \right){\rm{d}}t + 5\left( {{{\dot x}_{1d}} - {{\dot x}_1}} \right)} . \end{array} $ | (39) |
系统不确定参数标称值及其范围如表 2所示, 轨迹Ⅰ和轨迹Ⅱ的ARC控制器仿真参数分别如表 3和4所示.
| 表 2 不确定参数标称值及其范围 Table 2 Nominal value and extent of uncertain parameters |
| 表 3 轨迹Ⅰ的ARC控制器仿真参数 Table 3 Parameters of ARC controller for trajectory Ⅰ in simulation |
| 表 4 轨迹Ⅱ的ARC控制器仿真参数 Table 4 Parameters of ARC controller for trajectory Ⅱ in simulation |
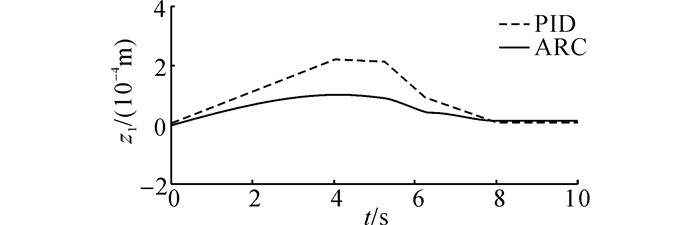
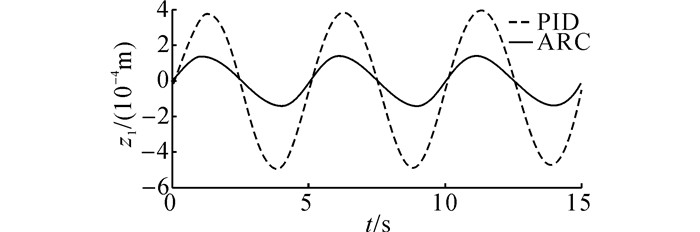
在仿真过程中, 轨迹Ⅰ的位置误差曲线如图 6所示.轨迹Ⅱ的位置误差曲线如图 7所示.由图 6仿真结果可知, 轨迹Ⅰ在PID控制器作用下, 位移跟踪偏差保持在0.22 mm范围内, 在ARC控制器作用下, 位移跟踪偏差保持在0.1 mm范围内.由图 7仿真结果可知, 轨迹Ⅱ在PID控制器作用下, 位移跟踪偏差保持在+/-0.5 mm范围内, 在ARC控制器作用下, 位移跟踪偏差保持在+/-0.2 mm范围内.
|
图 6 轨迹Ⅰ的仿真位置误差 Fig. 6 Position errors of trajectory Ⅰ in simulation |
|
图 7 轨迹Ⅱ的仿真位置误差 Fig. 7 Position errors of trajectory Ⅱ in simulation |
为了进一步验证所提ARC控制器的有效性, 搭建了复合材料成形液压机实验平台, 该实验平台只配有滑块, 但未安装有模具.控制程序在xPC目标环境中执行, 该环境由一个装有NI的PCI-6259数据采集卡的目标计算机和一个装有MATLAB/Simulink软件的主计算机构成, 2台计算机之间通过TCP/IP进行数据交互.液压机实验平台如图 8所示.液压缸的尺寸参数为80 mm/50 mm/210 mm, 并由Rexroth高频响伺服比例阀控制, 阀的型号为:4WRREH6VB40L-1X/G24K0/B5M, 该阀在±10%的控制输入信号下, 带宽为80 Hz.系统的状态变量包括液压缸的位移x1, 其值由SPM磁栅尺获得, 其型号为:MS200-30+MR200c-3.速度和加速度信号通过位移信号的微分获得.控制腔的工作压力p1和p2由Rexroth压力传感器获得, 其型号为:HM20-20/400-C-K35.控制程序为xPC目标环境中执行, 该环境由一个装有采集卡的目标计算机和一个装有MATLAB/Simulink主计算机组成.控制器的采样频率为1KS/s.轨迹Ⅰ和轨迹Ⅱ的PID控制器实验参数整定如下:

|
图 8 实验平台照片 Fig. 8 Picture of experiment set |
| $ \begin{array}{l} u_{{\rm{PID}}}^{\rm{I}} = 1500\left( {{x_{1d}} - {x_1}} \right) + \\ \;\;\;\;\;\;\;\;\;130\int_0^t {\left( {{x_{1d}} - {x_1}} \right){\rm{d}}t + 10\left( {{{\dot x}_{1d}} - {{\dot x}_1}} \right)} . \end{array} $ | (40) |
| $ \begin{array}{l} u_{{\rm{PID}}}^{{\rm{II}}} = 1800\left( {{x_{1d}} - {x_1}} \right) + \\ \;\;\;\;\;\;\;\;\;200\int_0^t {\left( {{x_{1d}} - {x_1}} \right){\rm{d}}t + 10\left( {{{\dot x}_{1d}} - {{\dot x}_1}} \right)} . \end{array} $ | (41) |
| 表 5 轨迹Ⅰ的ARC控制器实验参数 Table 5 Parameters of ARC controller for trajectory Ⅰ in experiment |
| 表 6 轨迹Ⅱ的ARC控制器实验参数 Table 6 Parameters of ARC controller for trajectory Ⅱ in experiment |
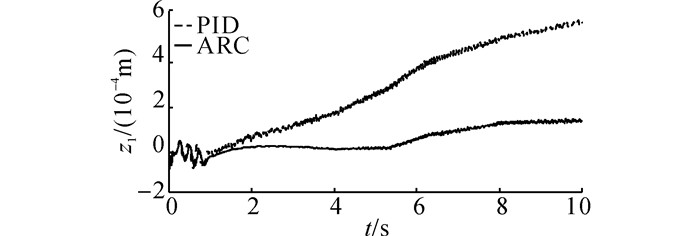
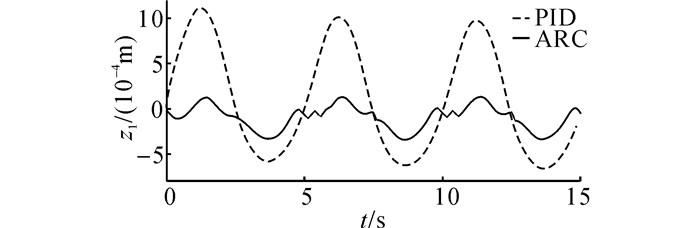
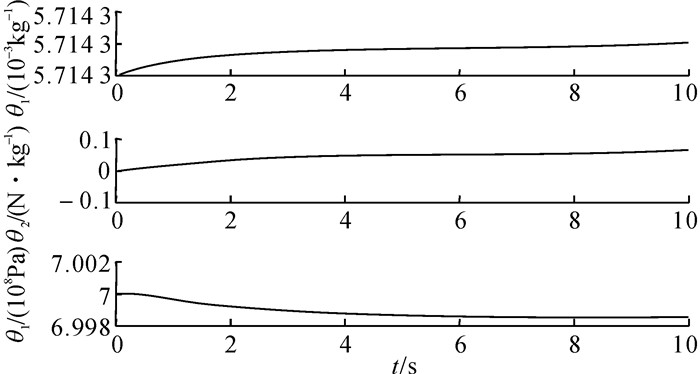
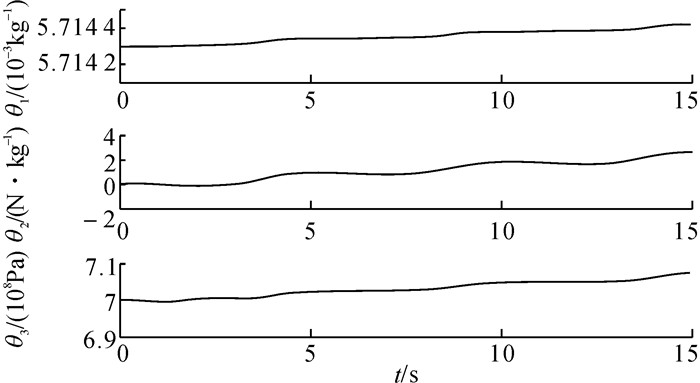
在实验过程中, 轨迹Ⅰ的位置误差曲线如图 9所示.轨迹Ⅱ的位置误差曲线如图 10所示.由图 9实验结果可知, 轨迹Ⅰ在PID控制器作用下, 位移跟踪偏差保持在0.6 mm范围内, 在ARC控制器作用下, 位移跟踪偏差保持在0.2 mm范围内.由图 10实验结果可知, 轨迹Ⅱ在PID控制器作用下, 位移跟踪偏差保持在+/-1.0 mm范围内, 在ARC控制器作用下, 位移跟踪偏差保持在+/-0.4 mm范围内.轨迹Ⅰ和轨迹Ⅱ在ARC运动控制器的作用下, 不确定参数在线估计自适应曲线分别如图 11和12所示, 由曲线可知, 参数估计值在名义值附近波动, 证明其参数是有界的.
|
图 9 轨迹Ⅰ的实验位置误差 Fig. 9 Position errors of trajectory Ⅰ in experiment |
|
图 10 轨迹Ⅱ的实验位置误差 Fig. 10 Position errors of trajectory Ⅱ in experiment |
|
图 11 轨迹Ⅰ的参数估计自适应曲线 Fig. 11 Parameter estimation curves of trajectory Ⅰ |
|
图 12 轨迹Ⅱ的参数估计自适应曲线 Fig. 12 Parameter estimation curves of trajectory Ⅱ |
论文针对复合材料成形液压机电液系统的数学模型, 设计了基于反步法的非线性ARC控制器.所设计的复合材料成形液压机非线性ARC控制器结合了自适应控制和鲁棒控制的优点, 使系统的输出在较小范围内有效地跟踪期望的运动轨迹, 并用Lyapunov函数保证系统是稳定的.轨迹Ⅰ的PID控制器和ARC控制器仿真结果表明, 在5 s之后, 液压缸在负负载的情况下, 在较低的速度条件下, 跟踪误差趋近于零.轨迹Ⅰ的PID控制器和ARC控制器实验结果表明, 在5 s之后, 液压缸在负负载的情况下, 在较低的速度条件下, 跟踪误差有增大的趋势.因此, 实际的液压回路需要设置相应的背压阀来平衡负负载.对轨迹Ⅰ和轨迹Ⅱ用PID控制器和ARC控制器进行了仿真和实验对比分析, ARC控制器的控制性能明显优于PID控制器.复合材料成形液压机电液系统采用非线性ARC控制器, 能解决参数不确定性和不确定非线性问题, 从而保证了运动轨迹跟踪性能.
| [1] |
俞新陆. 液压机的设计与应用[M]. 北京: 机械工业出版社, 2007.
|
| [2] |
MERRITT H E. Hydraulic control systems[M]. New York: John Wiley & Sons, 1967.
|
| [3] |
YAO B, JIANG C. Advanced motion control: From classical PID to nonlinear adaptive robust control[C]//IEEE International Workshop on Advanced Motion Control. Nagaoka, Niigata: IEEE, 2010: 815-829. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5464026
|
| [4] |
王伟, 张晶涛, 柴天佑. PID参数先进整定方法综述[J]. 自动化学报, 2000, 26(3): 347-355. WANG Wei, ZHANG Jing-tao, CAI Tian-you. A survey of advanced pid parameter tuning methods[J]. Acta Automatica Sinica, 2000, 26(3): 347-355. |
| [5] |
LEE Y H, KOPP R. Application of fuzzy control for a hydraulic forging machine[J]. Fuzzy Sets & Systems, 2001, 118(1): 99-108. |
| [6] |
ZHENG Jian-ming, ZHAO Sheng-dun, WEI Shu-guo. Fuzzy iterative learning control of electro-hydraulic servo system for SRM direct-drive volume control hydraulic press[J]. Journal of Central South University of Technology, 2010, 17(2): 316-322. DOI:10.1007/s11771-010-0048-9 |
| [7] |
彭雄斌, 龚国芳, 陈馈, 等. 管片拼装机提升缸模糊PID同步控制[J]. 浙江大学学报:工学版, 2014, 48(11): 2002-2008. PENG Xiong-bin, GONG Guo-fang, CHEN Kui, et al. Synchronization fuzzy PID control of lifting hydraulic cylinders for segment erector[J]. Journal of Zhejiang University:Engineering Science, 2014, 48(11): 2002-2008. |
| [8] |
吴洪波, 王记, 赵修平. 基于遗传算法和Vague集的液压位置控制系统自适应PID控制[J]. 海军航空工程学院学报, 2013(4): 372-377. WU Hong-bo, WANG Ji, ZHAO Xiu-ping. Adaptive PID control of hydraulic position control system based on genetic algorithm and vague sets[J]. Journal of Naval Aeronautical and Astronautical University, 2013(4): 372-377. DOI:10.7682/j.issn.1673-1522.2013.04.008 |
| [9] |
CHEN H M, RENN J C, SU J P. Sliding mode control with varying boundary layers for an electro-hydraulic position servo system[J]. The International Journal of Advanced Manufacturing Technology, 2005, 26(1): 117-123. |
| [10] |
FUNG R F, WANG Y C, YANG R, et al. A variable structure control with proportional and integral compensations for electrohydraulic position servo control system[J]. Mechatronics, 1997, 7(1): 67-81. DOI:10.1016/S0957-4158(96)00041-4 |
| [11] |
SUN Z, TSAO T C. Adaptive control with asymptotic tracking performance and its application to an electro-hydraulic servo system[J]. Universidad Complutense De Madrid, 2000, 122(1): 478-485. |
| [12] |
MINTSA H A, KENNE J P, VENUGOPAL R. Adaptive control of an electrohydraulic position servo system[C]//AFRICON, 2009. Nairobi, Kenya: IEEE, 2009: 1-6. http://ieeexplore.ieee.org/document/5308385/
|
| [13] |
URSU I, URSU F, POPESCU F. Backstepping design for controlling electrohydraulic servos[J]. Journal of the Franklin Institute, 2006, 343(1): 94-110. DOI:10.1016/j.jfranklin.2005.09.003 |
| [14] |
郭洪波, 李洪人. 基于Backstepping的阀控非对称缸电液伺服系统非线性控制[J]. 液压与气动, 2004(10): 38-40. GUO Hong-bo, LI Hong-ren. Backstepping-based nonlinear control for asymmetric cylinder electro-hydraulic servo system[J]. Chinese Hydraulics & Pneumatics, 2004(10): 38-40. DOI:10.3969/j.issn.1000-4858.2004.10.016 |
| [15] |
GUAN C, PAN S X. Nonlinear adaptive robust control of single-rod electro-hydraulic actuator with unknown nonlinear parameters[J]. IEEE Transactions on Control Systems Technology, 2008, 16(3): 434-445. DOI:10.1109/TCST.2007.908195 |
| [16] |
AHN K K, NAM D N C, JIN M. Adaptive Backstepping control of an electrohydraulic actuator[J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(19): 987-995. |
| [17] |
YAO B, BU F P, REEDY J, et al. Adaptive robust motion control of single-rod hydraulic actuators:theory and experiments[J]. IEEE/ASME Transactions on Mechatronics, 2000, 5(1): 79-91. |
| [18] |
YAO B, BU F, CHIU T C. Nonlinear adaptive robust control of electro-hydraulic servo systems with discontinuous projections[C]//Decision and Control, 1998. Proceedings of the 37th IEEE Conference on. Tampa, FL: IEEE, 1998: 2265-2270 vol. 2. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=758681
|
| [19] |
冯瑞琳, 魏建华. 粉末成形液压机自适应鲁棒运动控制[J]. 农业机械学报, 2015, 46(8): 352-360. FENG Rui-lin, WEI Jian-hua. Adaptive robust motion control of powder compaction press[J]. Transactions of the Chinese Society of Agricultural Machinery, 2015, 46(8): 352-360. DOI:10.6041/j.issn.1000-1298.2015.08.049 |
| [20] |
ZHANG Q, FANG J H, WEI J H, et al. Adaptive robust motion control of a fast forging hydraulic press considering the nonlinear uncertain accumulator model[J]. Proceedings of the Institution of Mechanical Engineers, Part Ⅰ:Journal of Systems and Control Engineering, 2016, 230(6): 483-497. |
| [21] |
GUO K, WEI J H. Adaptive robust control of variable displacement pumps[C]//American Control Conference. Washington, DC: IEEE, 2013, 45: 1112-1117. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6579985
|
| [22] |
XIONG Y, WEI J H, FENG R L. Adaptive robust control of a high-response dual proportional solenoid valve with flow force compensation[J]. Proceedings of the Institution of Mechanical Engineers Part Ⅰ Journal of Systems and Control Engineering, 2015, 229(1): 3-26. |
| [23] |
孟德远, 陶国良, 李艾民, 等. 高速开关阀控气动位置伺服系统的自适应鲁棒控制[J]. 机械工程学报, 2015, 51(10): 180-188. MENG Deng-yuan, TAO Guo-liang, LI Ai-min, et al. Adaptive robust control of pneumatic cylinders using fast switching on/off solenoid valves[J]. Journal of Mechanical Engineering, 2015, 51(10): 180-188. |
| [24] |
杜春燕, 吴爱国, 贾超, 等. 基于反步递推法的锻造液压机速度控制[C]//中国控制会议. 北京: 2010: 5666-5669. DU Chun-yan, WU Ai-guo, JIA Chao, et al. Speed control of hydraulic press based on backstepping method[C]//Control Conference. Beijing: IEEE, 2010: 5666-5669. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-KZLL2010070010DT.htm |



