随着隧道交通量增大、车辆行驶速度的加快和危险品的增加, 隧道发生火灾的频率随之增加.隧道衬砌混凝土是火灾过程中火焰和高温的直接作用体, 高温会导致隧道衬砌结构混凝土的开裂和力学性能的恶化, 最终导致衬砌结构产生不同程度的损伤, 大大降低了衬砌结构的承载力和安全性.因此, 亟需对混凝土衬砌结构进行高温后损伤评估, 以制定相应的修复措施.为了进行评估和修复, 首先需要对混凝土的高温损伤机制展开研究.在混凝土高温损伤研究方面, 主要通过室内试验手段, 基于大量的试验数据推演混凝土的高温损伤演化过程.Luccioni等[1-2]提出了高温混凝土热力学损伤模型;时旭东等[3-5]在试验的基础上, 通过分析和简化对混凝土高温下的力学性能展开相关研究, 分析混凝土力学性能随温度裂化的规律;但高温损伤的物理试验并不能反映混凝土因其各组分的热膨胀不同而产生热应力诱发混凝土损伤的本质.
混凝土在细观层次上由粗细骨料、水泥砂浆和二者之间的黏结界面组成, 细观各组分的力学性质直接或间接地决定了混凝土材料的宏观力学性质和损伤模式, 研究混凝土细观结构特点及其力学性能, 建立细观结构和宏观力学性能之间的关系是混凝土力学性质的重要研究内容之一.在混凝土细观损伤方面, 李朝红等[6-8]建立了细观损伤本构模型, 揭示了混凝土在轴向压力作用下单元的渐进损伤和裂缝的萌生与扩展过程;马怀发等[9]采用双折线损伤演化模型描述混凝土细观各相弹性损伤退化, 可以较好地模拟出实际试验结果.李冬等[10]对不同尺寸钢筋混凝土柱的细观模型进行了单轴受压力学特性模拟, 较细致的描述了混凝土柱裂缝的发展、破坏过程及其尺寸效应行为.现有研究大多针对常温情况下普通混凝土的细观损伤模型、损伤规律等方面进行探讨, 而对于受力及约束复杂的隧道衬砌混凝土高温损伤研究极少, 且尚未有学者在细观模型层面对高温下的衬砌混凝土裂化特征和内部损伤情况进行研究, 而衬砌混凝土各组分的热膨胀性不同使得混凝土试件产生热应力而诱发破裂, 只有准确地描述衬砌混凝土非均匀的细观结构才能更客观的反映隧道衬砌混凝土的损伤演化过程.
本文在前人的研究基础上基于细观力学理论建立了高温下的双折线损伤随机骨料模型, 分析火灾下隧道衬砌混凝土的力学行为及其损伤演化过程, 为从细观尺度研究隧道衬砌混凝土的高温损伤问题提供了一种新的方法.
1 基于细观力学的混凝土高温损伤本构模型确定Dougil[11]最早提出混凝土的非线性是由于混凝土内部的损伤发展引起结构的刚度衰减, 李灏[12]将其引入国内, 促进了混凝土损伤理论的发展.现有研究发现混凝土作为一种半脆性的建筑材料, 在受到外力作用时的本构关系的非线性状态主要是由于在细观材料部分产生和发展为细小的裂缝, 并非其塑性应变引起.本文通过弹性模量折减的方法分析各不同材料的劣化, 根据不同的裂化程度来判断该细观模型的破坏情况.根据勒梅特(Lemaitre)应变等价原理, 劣化单元的应力应变关系可以通过未劣化单元的材料属性得到, 即
| $ \varepsilon =\frac{\sigma }{{{E}_{\text{d}}}}=\frac{\sigma }{\left( 1-D \right){{E}_{0}}}. $ | (1) |
| $ \sigma ={{E}_{0}}\left( 1-D \right)\varepsilon , 0\le D\le 1. $ | (2) |
式中:σ为材料应力, ε为材料应变, E0为材料未损伤情况的弹性模量, Ed为处于损伤状态时的弹性模量, D为材料本身损伤状况的评价值, 当D取0时表示材料未损伤, 当D取1时表示材料完全损伤.
鉴于本文需考虑高温时的损伤情况, 以参数清晰表达简单的双折线损伤模型[13]为基础构建高温损伤模型, 能以损伤标度D定义材料的损伤情况, 同时能够满足高温下材料损伤参数的拟合精度.如图 1所示.
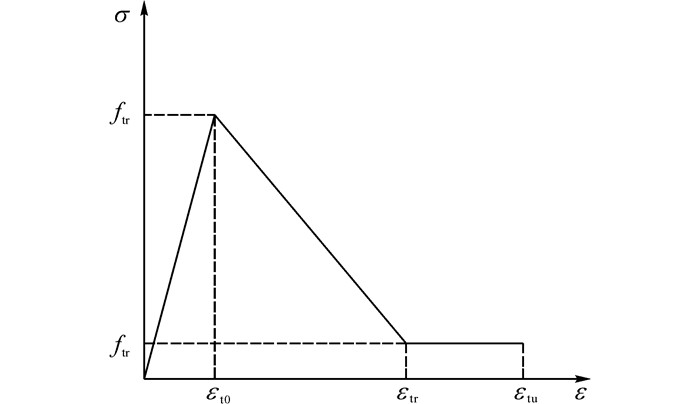
|
图 1 双折线损伤模型 Fig. 1 Bilinear damage model |
| $ D=\left\{ \begin{matrix} 0,&\varepsilon <{{\varepsilon }_{\text{t0}}}; \\ 1-\frac{\eta -\lambda }{\eta -1}\frac{{{\varepsilon }_{\text{t0}}}}{\varepsilon }+\frac{1-\lambda }{\eta -1},&{{\varepsilon }_{\text{t0}}}\le \varepsilon <{{\varepsilon }_{\text{tr}}}; \\ 1-\lambda \frac{{{\varepsilon }_{\text{t0}}}}{\varepsilon },&{{\varepsilon }_{\text{tr}}}\le \varepsilon <{{\varepsilon }_{\text{tu}}}; \\ 1,&\varepsilon \ge {{\varepsilon }_{\text{tu}}}. \\ \end{matrix} \right. $ | (3) |
式中:εt0为达到峰值应力时材料应变;εtr为混凝土到达残余强度时对应的材料应变, εtr=ηεt0;η为混凝土残余应变系数, 对于混凝土各相材料一般取值范围为1 < η≤5;ftr为残余抗拉强度;λ为残余强度系数;当应变大于εtu时, 判定混凝土处于整体破坏状态.
高温双折线模型中将高温损伤也加以考虑, 混凝土材料各组分在温度升高时, 弹性模量和抗压峰值大体呈现线性下降, 可以做相应简化, 仍以损伤力学思想对相应的弹性模量进行折减, 以温度常温为损伤度0, 以材料处于高温时损伤度为1.材料的受外力损伤和高温引起的损伤度能以叠加的形式存在, 如式4.
| $ {{D}_{Z}}=\left\{ \begin{matrix} {{D}_{F}},&当{{D}_{\theta }}=0, {{D}_{F}}>0时; \\ {{D}_{\theta }},&当{{D}_{\theta }}>0, {{D}_{F}}=0时; \\ {{D}_{\theta }}\cdot {{D}_{F}},&当{{D}_{\theta }}>0, {{D}_{F}}>0时; \\ 1,&当{{D}_{\theta }}=1, {{D}_{F}}=1时. \\ \end{matrix} \right. $ | (4) |
式中:DZ为总损伤值, DF为外力引起损伤, Dθ为温度引起损伤.
砂浆和骨料在高温下材料属性同时表现出一些特征:抗压极限峰值随着温度θ的升高逐步降低;在达到其抗压峰值之前, 应力应变曲线在各个温度基本表现为直线, 基本处于弹性状态;在较低温度时, 材料表现出典型的脆性特点, 在达到峰值应变后迅速破坏, 随着温度升高逐渐表现为塑性状态, 同时峰值应变逐步增大;弹性模量大体呈现线性下降.但骨料抗高温能力相对较强, 直到1 200 ℃仍有部分残余强度, 定义未受力时损伤度为温度损伤为0, 骨料达到1 200 ℃、砂浆达到1 000 ℃时为完全损伤, 损伤度为1, 以双折线损伤曲线为基础, 骨料、砂浆本构模型分别如图 2、3所示.
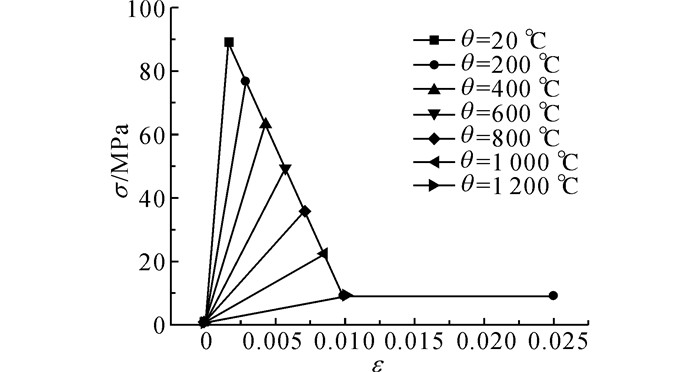
|
图 2 骨料高温本构关系 Fig. 2 Constitutive relation of aggregate at high temperature |
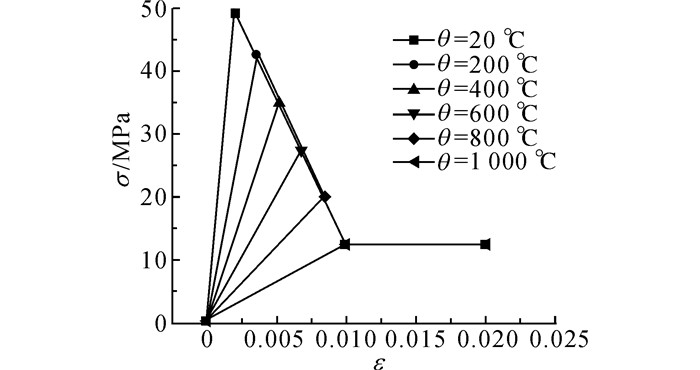
|
图 3 砂浆高温本构关系 Fig. 3 Constitutive relation of mortar at high temperature |
混凝土细观模型内的温度分析一般涉及比热容c和导热系数κ, 鉴于骨料与砂浆材料组成的不同, 其热学参数略有差别, 界面层在热学参数上认为与砂浆相同, 其热学参数如表 1所示.龚正炉[14]认为对于材料的力学参数, 砂浆部分一般通过砂浆试块的室内试验确定;不同骨料之间弹性模量E与强度等材料参数差异相对较大, 以常用的灰岩为例进行研究;现有研究对界面层属性的研究较少, 常以混凝土各材料的组合串并联模型结合试验研究宏观结构属性, 反算界面层参数.根据现有研究, 交界面材料的弹性模量根据界面厚度的不同而差异显著, 一般可取砂浆弹性模量的70%~80%[15], 本文取22 GPa, 其他具体参数(泊松比ν、密度ρ、抗压强度fcu、热膨胀系数α)如表 1所示:
| 表 1 骨料砂浆界面层力学特性参数 Table 1 Mechanical properties of interface layer of aggregate mortar |
一般混凝土由多种粒径的骨料组成, 在实际混凝土的捣固过程中, 骨料的分布基本服从随机分布.Walraven建立了混凝土级配曲线与在单个截面内骨料界面面积的关系(式5), 能够在细观分析中应用, 以进行二维平面分析.
| $ \begin{align} &{{P}_{\text{c}}}({{D}_{\text{d}}}<{{D}_{0}})={{P}_{\text{k}}}(1.065D_{_{0}}^{^{0.5}}/D_{_{\text{max}}}^{^{0.5}}-0.053D_{_{0}}^{^{4}}/D_{_{\text{max}}}^{^{4}}- \\ &\ \ \ \ \ \ 0.012D_{_{0}}^{^{6}}/D_{_{\text{max}}}^{^{6}}-0.004\text{ }5D_{_{0}}^{^{8}}/D_{_{\text{max}}}^{^{8}}+ \\ &\ \ \ \ \ \ 0.002\text{ }5D_{0}^{10}/D_{_{\text{max}}}^{^{10}}). \\ \end{align} $ | (5) |
式中:Pc为直径小于D0的概率, Pk为骨料体积占混凝土总体积百分比, Dd为骨料粒径,D0为筛孔直径;Dmax为最大骨料粒径.
在细观模拟计算模型中, 采用试验标准试块截面尺寸150 mm×150 mm进行计算分析;本模型采用二级级配, 5 mm以下骨料计入砂浆中, 最大骨料粒径40 mm, 按骨料填充率70%进行计算, 则取5~20 mm范围内随机尺寸粒径的骨料48个, 20~40 mm范围内随机尺寸粒径的骨料6个.利用蒙特卡罗方法, 随机生成骨料在截面中的位置, 最后将骨料模型投影到该平面中, 根据骨料模型所在的位置, 计算机将根据所编制的程序自动识别出各个单元的属性:骨料、界面、固化水泥砂浆各种单元, 对各类单元赋予相应的材料特性.
2.3 细观数值模型算法进行混凝土高温细观热力学性能分析步骤如下:
1) 确定骨料、交界面和砂浆物理力学特性, 及高温损伤本构;
2) 选取需要模拟混凝土结构尺寸;
3) 采用ANSYS内APDL语言的RANDOM命令在位置、骨料直径范围内随机选取参数;
4) 建立骨料几何模型, 建立交界层模型, 划分模型网络;
5) 进行高温下热学分析, 储存结构内各单元温度分布情况;
6) 导入温度分布数据, 结合高温下材料参数变化进行力学分析, 得到混凝土高温损伤的细观分析结果.
3 火灾下细观数值模拟在隧道结构中, 单面受火的混凝土处于周围结构的约束中, 与周围材料协同作用, 其两侧的混凝土限制着其向两侧膨胀.因此, 为较为真实的模拟处于整体结构中的混凝土细观模型受高温情况下的内力分布和损伤状况, 建立边界条件如图 4所示的模型进行分析, 顶部限制了Y方向位移, 两侧采用弹簧单元作为边界, 弹簧弹性系数取混凝土宏观弹性模量(3.2×1010Pa)以模拟在水平向的膨胀过程中位移限制, 两边施加1 MPa拉应力以模拟隧道顶部受火面的衬砌混凝土局部受拉状态.
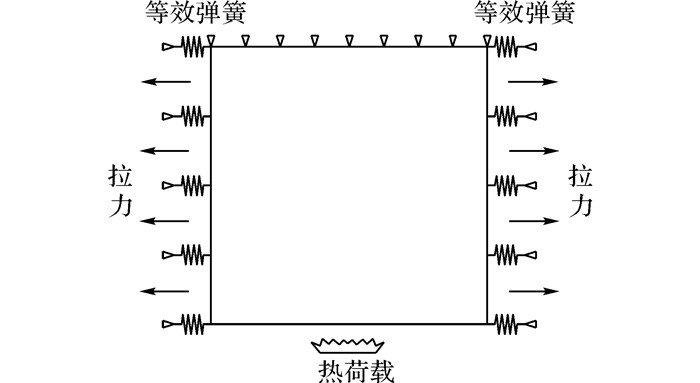
|
图 4 隧道衬砌混凝土火灾试验模型示意图 Fig. 4 Schematic diagram of tunnel lining concrete fire test |
该模型考虑热力耦合, 先采用平面单元plane55进行了高温下的热学分析, 再将热分析单元plane55的温度信息传递给对应的结构单元plane42, 同时将材料高温下的双折线损伤本构关系赋予给结构分析单元, 最后加上荷载和约束条件进行应力应变分析.
3.1 火灾下混凝土温度场分布隧道衬砌受火研究为混凝土细观模型在下侧单面受火情况下的温度分布, 受火面外温度按RABT升温曲线变化(如式6), 计算受火灾作用1 h的温度变化, 其他位置设置初始温度20 ℃, 除受热面外无热交换, 热交换系数根据已有研究选取[16].
| $ \theta =\left\{ \begin{matrix} {{\theta }_{0}}+236t,&t\le 5~\text{min}; \\ {{\theta }_{0}}+1\text{ }180,&5~\text{min}\le t\le 95\text{ }\!\!~\!\!\text{ min}; \\ 1\text{ }200-40.33\left( t-95 \right),&95~\text{min}\le t\le 125\text{ }\!\!~\!\!\text{ min}. \\ \end{matrix} \right. $ | (6) |
式中:θ为t时刻的温度(℃);t为时间(min);θ0为初始温度(℃).
热力耦合分析分为温度场分析和内力分析2部分, 当试块单面受到升温作用时, 其接受的能量一部分用于单元本身的温度升高, 一部分则通过热量传递的形式促使周围介质的温度也逐渐变化, 离受火面越远, 温度变化越慢, 该细观模型的温度分布云图如图 5所示.图中x为以模型左下角为原点,从模型左侧至右侧的距离,y为以模型左下角为原点,从模型下侧到上侧的距离.
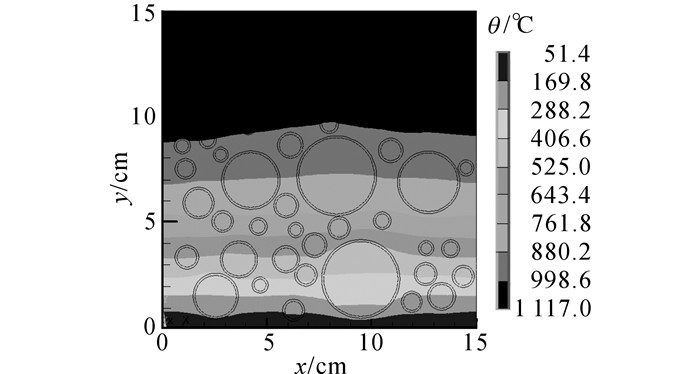
|
图 5 受火60 min时混凝土细观模型温度分布云图 Fig. 5 Temperature distribution of concrete meso model after 60 minutes of fire |
当隧道混凝土遭受火灾时, 混凝土表面温度迅速增加;由于混凝土材料的导热性能差, 导致内部温度随混凝土厚度的增加而增长缓慢.在数值模拟过程中得到的不同时刻混凝土温度分布曲线图如图 6所示, 从图中可以看出, 该温度分布图为混凝土结构中心竖向截面的温度分布, 表层(0 cm)温度初期上升极快, 15 cm处几乎不受影响, 30 min前模型内升温速率逐渐降低, 趋于平缓, 30 min后逐渐表现为线性升温.
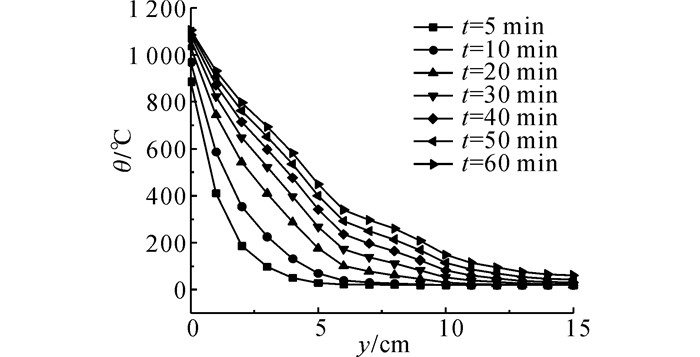
|
图 6 不同时刻混凝土温度分布图 Fig. 6 Temperature distribution of concrete at different time |
对比闫治国[4]的实验数据, 两者的变化趋势一致, 实验数据拟合曲线左边的端点需要一定的时间才能达到最大值且受火面温度最大值接近1 000 ℃, 这主要是因为实际火灾场景模拟的时候加热源与实测结构有一定距离以及试验过程中有一定的能量损失和误差.
3.2 火灾下混凝土应力变化第一主应力主要反映内部的受拉状况, 第三主应力反映内部受压状况, 由ANSYS计算分析所得应力云图如图 7所示, 当加热5 min后, 受拉损伤主要集中在模型中部约100 ℃等温线附近, 且拓展到模型中部温度20 ℃区域, 骨料两侧出现了拉应力集中现象, 当受热60 min后, 损伤范围内移, 其第一主应力较大区域呈现弧状, 并分为内外两层, 但距受火区域较近的部分拉应力较小并不意味着无损伤, 这部分材料在高温条件下应力-应变曲线的峰值出现下降, 在同应变情况下不能达到较高的应力值, 但其应变已超损伤阀值, 其损伤主要由外层的膨胀对这部分材料的拉伸引起.

|
图 7 不同时刻隧道衬砌混凝土细观模型应力分布云图 Fig. 7 Stress distribution nephogram of tunnel lining concrete meso model at different time |
在细观层次上, 高温对混凝土材料的损伤不仅局限于对材料本身强度的影响, 在其受热膨胀过程中, 不同温度下的膨胀量不同, 不同材料之间膨胀数值不同, 会对温度较低部分产生部分应力损伤.
为探求试件在细观损伤过程中的应变规律, 如图 8所示, 取同一区域内的骨料、砂浆及界面单元, 分析其在受火中的应变发展.可以看出、受火初期材料应变发展较快, 界面单元首先出现损伤, 骨料单元则保持较小的应变值.

|
图 8 应变时程曲线 Fig. 8 Strain time history curve |
混凝土受拉破坏机制与剪切破坏机制可统一为受拉破坏机制[9], 单面受火后模型以拉应变极限作为损伤准则, 以白色部分表示损伤单元.
如图 9所示为混凝土单面受火损伤数值模拟结果, 从图中分析可知:在初始5 min内, 损伤快速发展, 主要损伤区域基本以100 ℃等温线为界, 损伤范围向结构内部延伸, 边界呈弧状, 交界面单元相比砂浆更易损伤, 骨料在高温情况下相对劣化较小;当受火30 min时, 损伤以弧状向结构内部扩展, 形成一个典型的损伤分界线, 分界线以内材料出现部分损伤, 分界线外材料强度基本丧失, 部分骨料出现剥落;当受火60 min后, 在分界层内部2~3 cm范围内出现大范围损伤, 该损伤部分温度并未达到规范内混凝土宏观损伤温度标准(380 ℃), 但界面层仍劣化严重, 骨料也受到一定的损伤, 可以推断此阶段应力损伤在高温下混凝土损伤中占有重要地位.
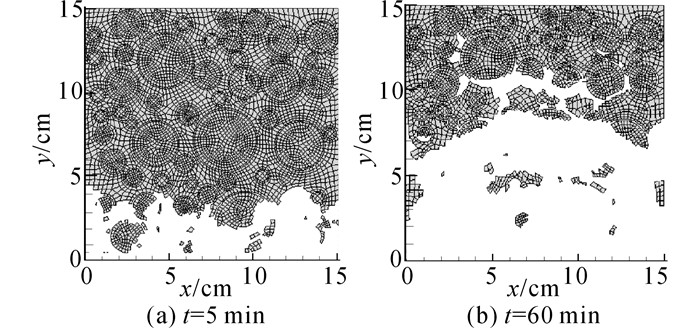
|
图 9 混凝土细观模型高温下损伤图 Fig. 9 Damage pattern of concrete meso model under high temperature |
如图 10所示为损伤比例随时间变化的曲线图,图中Bm为各材料单元损伤比.从已损伤单元与全部单元的比值来看, 在受火初期10 min以内损伤发展较为迅速, 在t=40 min以后损伤增加速率基本稳定, 损伤比例界面层最高, 当t=60 min时已达到77.1%, 初期砂浆损伤比例较高, 而在受火过程中与骨料损伤比例差距逐渐缩小.

|
图 10 损伤比例随时间变化曲线 Fig. 10 Damage ratio versus time curve |
同时, 通过数值模拟得到在t=20、40和60 min时混凝土的烧损单元累积厚度分别为5.812、7.019和7.942 cm, 而王翠娟[16]对HCM火灾下T梁进行的热力耦合分析, 得到t=20、40和60 min时梁的累积烧损深度分别为4.854、5.833和6.623 cm, 两者差异在17%以内.
3.4 火灾下隧道衬砌混凝土等效截面损失本文中衬砌混凝土的实际力学状态在一定程度上可以简化为在动态的温度应力上耦合一个静态的拉应力, 这样从宏观角度考虑, 在一定程度上将其简化为先计算高温引起的截面损失, 将原先的应力进行重分布施加在有效截面上, 据此考虑热力耦合后该混凝土的剩余承载力, 本节主要对高温引起的截面损失进行了讨论.
由于混凝土各组分的不同热膨胀率以及分布的不均匀性, 引起组分边界的热膨胀不协调, 从而造成组分间或组分内部的拉或压应力, 影响混凝土试件宏观的力学性质.根据多国试验结果, 300 ℃以下的混凝土强度与常温几乎相等, 而超过800 ℃时的混凝土强度可以忽略, 故可只考虑温度在300~800 ℃的混凝土强度.本文通过界面强度等效的方法考虑材料高温劣化所导致的截面损失, 即将温度在300 ~800 ℃的混凝土等效为厚度he的常温下的混凝土, 则累积等效烧损厚度hs=h3-he.根据强度等效[17]有
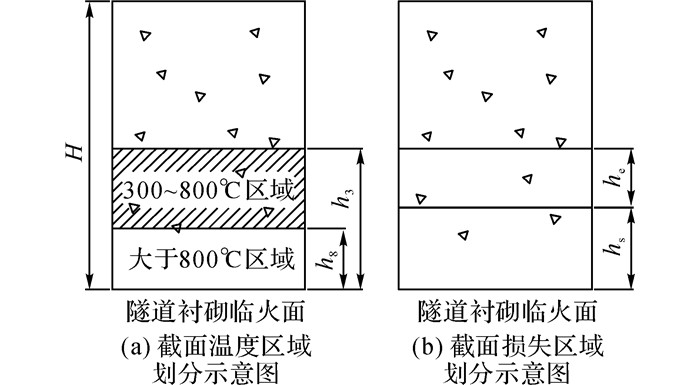
|
图 11 火灾下混凝土强度等效法示意图 Fig. 11 Schematic diagram of equivalent method of concrete strength under fire |
| $ \int _{_{{{h}_{8}}}}^{^{{{h}_{3}}}}b{{G}_{\text{c}}}\left[ \theta \left( h \right) \right]{{f}_{\text{c}}}\text{d}h=b{{h}_{\text{e}}}{{f}_{\text{c}}}. $ | (7) |
| $ {{G}_{\text{c}}}\left[ \theta \left( h \right) \right]=\frac{f_{\text{c}}^{^{\theta }}}{{{f}_{\text{c}}}}=\frac{1}{1+16{{\left[ \theta \left( h \right)/1\text{ }000 \right]}^{6.3}}}. $ | (8) |
式中:H为截面高度, h8和h3分别为800 ℃温度线和300 ℃温度线离受火面的深度;b为混凝土的宽度;fc为混凝土抗压强度;θ(h)为混凝土温度沿径向深度的变化关系函数, 由于不同竖向截面截断处的温度存在差异, 在本研究中取平均值;Gc[θ(h)]为不同温度下混凝土抗压强度折减公式[3].
则, 可得到等效厚度计算公式:
| $ {{h}_{\text{e}}}=\int _{_{{{h}_{8}}}}^{^{{{h}_{3}}}}\frac{1}{1+16{{\left[ \theta \left( h \right)/1\text{ }000 \right]}^{6.3}}}\text{d}h. $ | (9) |
如图 12所示为混凝土在RABT火灾温升模式下基于强度等效的火灾过程累积等效烧损厚度.混凝土累积等效烧损厚度随时间的延伸呈曲线变化, 由于临火面的混凝土升温较快, 其温度梯度较大, 造成内外变形差异引起较大内力, 受火前期等效烧损厚度变化明显;混凝土的热传导性较差, 截面损失主要受温度影响范围的增大而不断向结构内部扩展, 后期的损伤发展放缓, 温度影响范围后期基本线性拓展, 强度累积烧深接近3.5 cm.

|
图 12 混凝土等效烧损厚度变化 Fig. 12 Change of equivalent burn out thickness of concrete |
如图 13所示给出了宏观等效厚度相对损失Bh与损伤单元比例B的关系.以强度等效计算的宏观等效厚度相对损失与细观数值模拟的损伤单元比例存在较好的线性关系, 这为从细观角度研究隧道衬砌混凝土高温损伤演化机制提供了一定的理论基础.
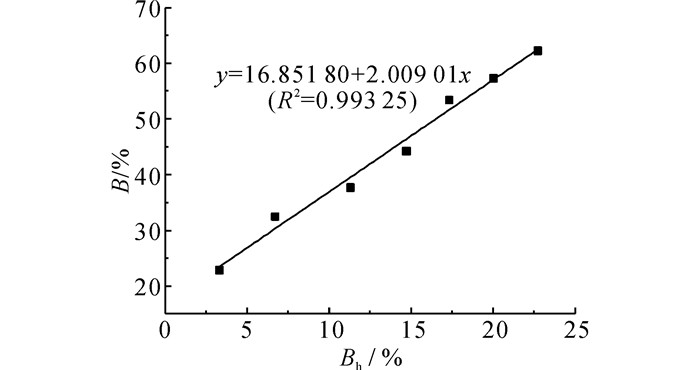
|
图 13 等效厚度相对损失与损伤单元比例相关关系 Fig. 13 Relative relation between equivalent thickness relative loss and damage element proportion |
(1) 高温下双折线损伤模型能够综合考虑材料受外荷载损伤和受高温损伤两方面因素影响, 充分考虑了随着温度升高材料强度的降低和峰值应力所对应应变的增大, 较好地体现了骨料与砂浆在高温下的本构关系.
(2) 强度较高的骨料颗粒对微裂缝扩展有阻碍作用, 混凝土细观裂缝从界面单元开始, 然后延伸到砂浆单元, 裂缝绕过骨料沿其界面扩展, 界面的力学特性决定宏观强度的差异.
(3) 以强度等效计算的宏观等效厚度相对损失与细观数值模拟的损伤单元比例存在较好的线性关系, 这为从细观角度研究隧道衬砌混凝土高温损伤演化机制提供了一定的理论基础.
| [1] |
LUCCIONI B M, FINGUEROA M I, DANNESI R E. Thermomechanic model for concrete exposed to elevated temperature[J]. Engineering Structures, 2003, 25: 729-742. DOI:10.1016/S0141-0296(02)00209-2 |
| [2] |
GAWIN D, PESAVENTO F, SCHREFLER B A. Modelling of hygrothermal behaviour of concrete at high temperature with thermochemical and mechanical material degradation[J]. Computer Methods in Applied Mechanics & Engineering, 2003, 192(13): 1731-1771. |
| [3] |
过镇海. 钢筋混凝土的高温性能及其计算[M]. 北京: 清华大学出版社, 2003, 10-65.
|
| [4] |
闫治国, 朱合华, 梁利. 火灾高温下隧道衬砌管片力学性能试验[J]. 同济大学学报:自然科学版, 2012, 40(6): 823-828. YAN Zhi-guo, ZHU He-hua, LIANG Li. Experimental study on mechanical performance of lining segment in fire accidents[J]. Journal of Tongji University:Natural Science, 2012, 40(6): 823-828. |
| [5] |
黄涛, 王珍, 张泽江. 公路隧道衬砌高性能混凝土的高温烧损试验研究[J]. 中国矿业大学学报, 2012, 41(1): 142-147. HUANG Tao, WANG Zhen, ZHANG Ze-jiang. Experimental research on the high-temperature buring of a highway tunnel lining made from high performance concrete[J]. Journal of China University of Mining & Technology, 2012, 41(1): 142-147. |
| [6] |
李朝红, 王海龙, 徐光兴. 混凝土损伤断裂的三维细观数值模拟[J]. 中南大学学报自然科学版, 2011, 42(2): 463-469. LI Chao-hong, WANG Hai-long, XU Guang-xing. 3-D mesoscopic numerical simulation of concrete damage and fracture[J]. Journal of Central South University:Science and Technology, 2011, 42(2): 463-469. |
| [7] |
白卫峰, 管俊峰, 崔莹, 等. 混凝土双轴压-压细观统计损伤本构模型[J]. 四川大学学报:工程科学版, 2013, 45(6): 74-81. BAI Wei-feng, GUAN Jun-feng, CUI Ying, et al. Staistical damage constitutive model concrete under biaxial compression[J]. Journal of Sichuan University:Engineering Science Edition, 2013, 45(6): 74-81. |
| [8] |
刘庭金, 莫海鸿, 朱合华. 非均质混凝土细观数值模型及其在双边裂纹加载中的应用[J]. 华南理工大学学报:自然科学版, 2005, 33(10): 52-56. LIU Ting-jin, MO Hai-hong, ZHU He-hua. Mesoscopic numerical model of heterogeneous concrete and its application in bilateral crack loading[J]. Journal of South China University of Technology:Natural Science Edition, 2005, 33(10): 52-56. |
| [9] |
马怀发, 陈厚群, 阳昌陆. 复杂动荷载作用下全级配混凝土损伤机理细观数值试验[J]. 土木工程学报, 2012(7): 175-182. MA Huai-fa, CHEN Hou-qun, YANG Chang-lu. Mesoscopic numerical model of heterogeneous concrete and its application in bilateral crack loading[J]. China Civil Engineering Journal, 2012(7): 175-182. |
| [10] |
李冬, 金浏, 杜修力. 钢筋混凝土柱轴心受压性能及尺寸效应的细观数值研究[J]. 水利学报, 2016, 47(2): 209-218. LI Dong, JIN Liu, DU Xiu-li. Meso numerical study on axial compression behavior and size effect of reinforced concrete columns[J]. Journal of Hydraulic Engineering, 2016, 47(2): 209-218. |
| [11] |
DOUGIL J W. On stable progressively fracturing solid[J]. Journal of Applied Mathematics and Physics, 1976, 27(4): 23-437. |
| [12] |
李灏. 损伤力学基础[M]. 济南: 山东科学技术出版社, 1992, 43-90.
|
| [13] |
唐世斌, 唐春安, 梁正召, 等. 混凝土热传导与热应力的细观特性及热开裂过程研究[J]. 土木工程学报, 2012(2): 11-19. TANG Shi-bing, TANG Chun-an, LIANG Zheng-zhao, et al. Study on the micro characteristics and thermal cracking process of heat conduction and thermal stress in concrete[J]. China Civil Engineering Journal, 2012(2): 11-19. |
| [14] |
龚正炉. 基于随机骨料模型的混凝土性能多尺度数值模拟研究[D]. 杭州: 浙江大学, 2013. GONG Zheng-lu. Multi-scale numerical simulation research of concrete based on random aggregate[D]. Hangzhou: Zhejiang University, 2013. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2269637 |
| [15] |
肖建庄, 杜江涛, 刘琼. 基于格构模型再生混凝土单轴受压数值模拟[J]. 建筑材料学报, 2009, 12(5): 511-514. XIAO Jian-zhuang, DU Jiang-tao, LIU Qiong. Numerical simulation of recycled concrete under uniaxial compression based on lattice model[J]. Journal of Building Materials, 2009, 12(5): 511-514. |
| [16] |
王翠娟. 火灾模式下多梁式混凝土T型梁桥结构性能研究[D]. 西安: 长安大学, 2013. WANG Cui-juan. Study on structure performance for multi-beam concrete T-shaped section beam girder subjected to fire[D]. Xian: Chang'an University, 2013. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D408994 |
| [17] |
廖仕超. 隧道火灾下衬砌结构承载力研究[D]. 长沙: 中南大学, 2011. LIAO Shi-chao. Study on bearing capacity of lining structure under tunnel fire[D]. Changsha: Central South University, 2011. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1917288 |


