2. 新加坡国立大学 建筑科学系, 新加坡 117566
2. Department of Building, National University of Singapore, 117566, Singapore
以简单矩形及垂直形态为特征的城市街道层峡,几乎占据2/3的城市空间,它已成为一种典型的城市形态.街道层峡的几何形态引导并决定了日照、气流、湿度、热量等微气候要素在街区空间中的变化与重新分布,继而极大地影响室外热舒适度.甚至有研究认为,与建筑材料的热工性能和表面反射率相比,街区层峡几何形态对微气候的影响更大[1].
近年来,一些相关研究通过实地测量或数值模拟的方法针对街道高宽比(H/W,H为建筑高度,W为道路宽度)及朝向与辐射热量、气温、日照入口等微气候要素在街区空间的分布特征之间关联进行分析,发现不同的街道高宽比及朝向会导致辐射热量、气温等微气候要素产生较大变化[1-4];还有一些研究则证实了街道高宽比等城市设计要素对室外热舒适度及城市热岛效应也起一定的影响作用[5-9].另外,天空视角系数(sky view factor)ΨSVF也是反映街区几何形态的一项重要参数,很多相关研究证实了ΨSVF对微气候的影响[10-11],并发现城市热岛效应的产生与街区的ΨSVF关系密切[2, 12].有研究表明,在城市区域,较低的ΨSVF往往会导致较低的昼间气温与较高的夜间气温[12-13].
因此,基于对街道层峡几何形态与微气候及热舒适度之间关联的探索研究,既可以通过改变街道形态来改善室外微气候[14-15],也可为建筑或城市设计满足气候适应性要求提供相应的设计导则与优化建议[16].
以上研究都表明了街区几何形态对微气候和室外热舒适度产生重要影响.但多数相关研究仅是针对单个街道,并没有考虑整个街区环境的影响,而实际上,某位置的气温变化受周边环境的影响极大.另外,以往研究往往针对某特定气候区域(尤其干热地区)进行实测研究或基于CFD物理模型进行模拟研究,也取得了相应成果.但一方面,相关结论并没有被证实可适用于其他不同气候区域;另一方面,基于经验模型的研究尚较缺乏;此外,基于南京地区气候条件的相关量化研究非常稀缺.
因此,本研究拟基于一个综合的视角,采用新加坡国立大学开发的基于经验模型的建筑环境气温预测工具(screening tool for estate environment evaluation, STEVE),探索南京气候条件下街区层峡形态与微气候及室外热舒适度的关联,并在以往研究的基础上,对该问题的研究范围进行了拓展.
1 场地及气候分析本研究是基于南京典型夏季气候条件,其特征为气温高,湿度大,平均最高气温达32 ℃,平均相对湿度达75%.此外,南京地区太阳辐射强度在夏季晴天时最高,日照时数比例也最高,可达57%,通过测量得到的总辐射值全年中在五、七、八月达到最高[17].
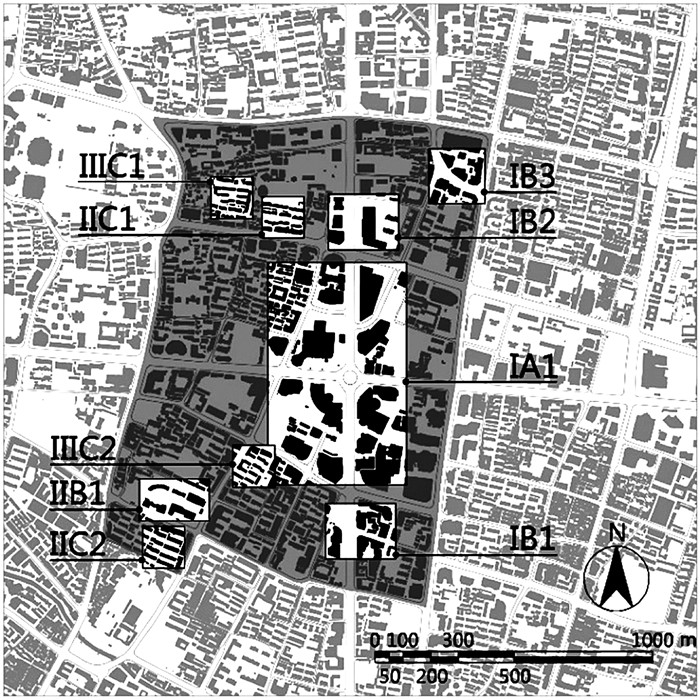
具体研究区域位于著名的新街口中心区,该区域内高楼林立,街道狭窄,绿化稀缺,地形平坦,街道朝向大多为东西向和南北向,具有高密度、紧凑型的城市形态特征.为直观地对该区域城市空间形态进行分类分析,本研究尝试从垂直和水平2个维度对三维城市形态进行解析.垂直方向主要体现为建筑高度的变化,而水平方向则表现为建筑的单体形态及组合方式.其中高度形态可归类为:超高层、高层、多层;水平形态归类为:散点式、行列式、围合式.将垂直与水平2个维度的形态限定进行组合,针对新街口中心区,选择样本地块作为重点分析的形态类型,如图 1与表 1所示,并根据各地块现状对其基本形态指标进行测算、整理如表 2所示.
|
图 1 研究区域典型空间形态单元空间分布图 Fig. 1 Distribution of typical urban morphological units in reference site |
| 表 1 新街口中心区空间形态分类 Table 1 Classification of urban spatial form in Xinjiekou CBD |
| 表 2 新街口中心区样本地块主要形态指标 Table 2 Geometrical parameters of sample plots in Xinjiekou CBD |
通过测算整理,可以发现超高层与高层建筑地块(A与B类)的高宽比大多涉及城市道路.总体来看,主道路高宽比较小,约在0.3~2.8之间,若对其间各值取整,可归纳取值为0.5、1、1.5、2、3;而次要道路高宽比较大,在0.8~8.8之间,若对其间各值取整,可归纳取值为1、1.5、2、3、4、7.5、9.其余的多层住宅地块(C类)则主要根据建筑间距计算高宽比,平均值约在1~1.3之间.
本研究所涉及的理想街区依据新街口CBD的城市形态特征而设立,也具有类似的街道高宽比及紧凑型城市设计.街区层峡在本研究中被用作城市微气候模拟分析的基本形态单元.
2 研究方法 2.1 城市街区方案的衍生设计本研究在Martin等[18]总结的城市肌理形态基本原型的基础上,如图 2所示,结合南京新街口CBD典型城市形态特征,衍生设计出一系列具有不同形态参数的城市街区方案.

|
图 2 城市肌理形态原型 Fig. 2 Urban texture typologies |
通过对新街口地区高层建筑及其地块的分析,可知该地区高层建筑单体地块边长一般在40~60 m之间,且多为矩形.因此,为便于街区模型制作与计算,本研究采用的标准地块单元尺寸设定为48 m×48 m,其尺度基本适合建造一栋独立的商业或办公建筑,每个街区由40个标准地块单元组成.同时,本研究涉及2种城市道路:城市主道路和次要道路.其中主道路为双向六车道,次要道路为双向两车道.在南京市现有的车行道中,这2种车道的最小宽度分别为22.5和7 m.为简化计算,分别将2种车道宽度设定为24和8 m.此外,将车行道两边人行道的最小宽度设定为3.5 m,路缘宽度为0.5 m.如图 3所示,包括车行道两边的路缘及人行道在内,主道路和次要道路的总宽度分别为32和16 m.

|
图 3 标准地块单元平面布局示意图 Fig. 3 Site layout of plot unit |
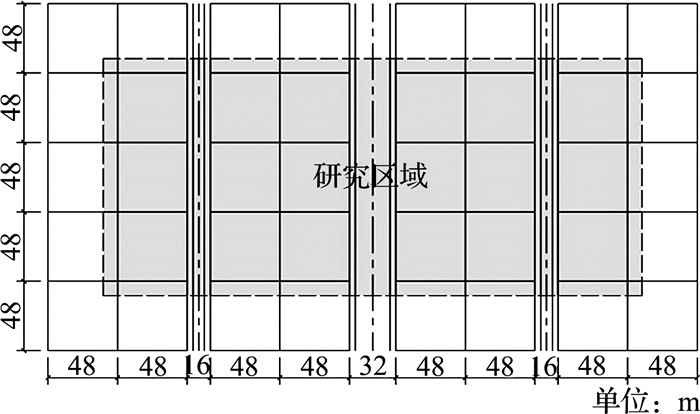
整个街区被一条主道路和与之平行的2条次要道路分为4个部分,如图 4所示.所采用的分析数据取自街区中心区域的18个标准地块单元,而周边其余22个地块单元作为中心区域的缓冲区,目的是为了尽可能减少数值模拟中边界效应对中心区域的影响.
|
图 4 进行数值模拟的街区场地示意图 Fig. 4 Layout of whole urban site for numerical simulation |
由于城市规划对新街口区域的建筑高度没有明确限制,因此,本研究将街区方案的建筑高度设定为4种,分别为16、32、64、128 m.
在4种建筑高度和2种街道宽度的基础上,通过设定2种高宽比来评估层峡形态对微气候和热舒适度的影响,包括城市道路层峡(简称街道层峡)高宽比(Street Ratio)和建筑间退让所产生的层峡(简称退让层峡)高宽比(Setback Ratio).根据前文对新街口地区9个样本地块基本形态指标的分析,为简化计算并增加可比性,在街区方案衍生设计中将主道路高宽比设定为0.5、1、2、4,次要道路高宽比设定为1、2、4、8.而退让层峡由于不涉及道路宽度,其高宽比设定以4为基数递增,分别为0、4、8、16,当退让层峡高宽比取0时,代表沿街商铺或行列式布局的住宅小区建筑侧面或后方墙贴墙的极端情况.然后,通过设置不同的层峡高宽比组合,衍生设计出16个不同形态的城市街区方案(本研究仅考虑街道朝向为南北向的情况,其他朝向的情况将在后续研究中进行),如图 5所示.为便于比较分析,根据退让层峡高宽比的4个值,将16个街区方案分为4组.所有城市街区方案的几何形态参数如表 3所示,包括街道层峡高宽比H/St、退让层峡高宽比H/Sb以及天空视角系数ΨSVF.

|
图 5 具有不同形态参数的16个城市街区方案 Fig. 5 Development of 16 urban scenarios |
| 表 3 各街区方案高宽比设置及位于层峡中心离地面1.5 m处的天空视角系数 Table 3 Aspect ratios and sky view factors at points of 1.5m above ground in middles of the canyons of all urban scenarios |
1) 区域室外最低、平均及最高气温
建筑环境气温预测工具(screening tool for estate environment evaluation, STEVE Tool)是新加坡国立大学亚洲可持续城市研究中心(center for sustainable asian cities, CSAC)开发的一个建筑环境气温预测模型.该工具是基于在新加坡国立大学Kent Ridge校区及One North地区近3年(2005.9~2008.6)的实测数据,经回归分析得到的经验模型.之后又通过针对办公、商业、住宅、城市绿地、海湾区及工业等不同用地的另9个地区的大量实测数据进行验证和补充,涉及各种不同的建筑布局方式与空间形态,使该模型对各种不同城市形态具有较好的适用性.该模型可以根据输入的气象变量和城市形态变量,准确计算出50 m半径范围内目标位置的日最低、平均及最高气温(θmin, θavg, θmax)[19-20].
其预测公式为
| $ \begin{array}{*{35}{l}} {{\theta }_{\text{min}}}=4.061+0.839{{\theta }_{\text{min}\ \text{Ref}}}+0.004{{P}_{\text{pave}}}- \\ \ \ \ \ \ \ \ \ 0.193{{R}_{\text{green}}}-0.029{{H}_{\text{building}}}+1.339\times {{10}^{-6}}{{S}_{\text{wall}}}. \\ \end{array} $ | (1) |
| $ \begin{array}{*{35}{l}} {{\theta }_{\text{avg}}}=2.347+0.904{{\theta }_{\text{avg}\ \text{Ref}}}+5.786\times {{10}^{-5}}{{G}_{\text{solar}\ \text{total}}}+ \\ \ \ \ \ \ \ \ \ 0.007{{P}_{\text{pave}}}-0.06{{R}_{\text{green}}}-0.015{{H}_{\text{building}}}+ \\ \ \ \ \ \ \ \ \ 1.311\times {{10}^{-5}}{{S}_{\text{wall}}}+0.633{{\mathit{\Psi }}_{\text{SVF}}}. \\ \end{array} $ | (2) |
| $ \begin{array}{*{35}{l}} {{\theta }_{\text{max}}}=7.542+0.684{{\theta }_{\text{max}\ \text{Ref}}}+0.003{{G}_{\text{solar}\ \text{max}}}+ \\ \ \ \ \ \ \ \ \ 0.005{{P}_{\text{pave}}}-0.016{{H}_{\text{building}}}+6.777\times {{10}^{-6}}{{S}_{\text{wall}}}+ \\ \ \ \ \ \ \ \ \ 1.467{{\mathit{\Psi }}_{\text{SVF}}}+1.466{{\omega }_{\text{albedo}}}. \\ \end{array} $ | (3) |
式中:θmin、θavg、θmax分别为预测的日最低、平均、最高气温,单位为℃,是该气温预测模型的因变量;θmin Ref、θavg Ref、θmax Ref分别为典型气象年中某月参考日最低、平均、最高气温(℃),Gsolar total为参考日平均太阳辐射总量(W/m2),Gsolar max为参考日平均太阳辐射最大值(W/m2),这些是主要的气象自变量;Ppave为铺地面积比(%),Rgreen为绿积率,Hbuilding为平均建筑高度与占地面积比(1/m),Swall为外墙总面积(m2),ωalbedo为表面平均反射率,这些是主要的城市形态变量.目前的STEVE是基于Google SketchUp的插件程序,可根据SketchUp三维建模自动计算公式中所需的形态变量,并直接进行气温预测计算,较简单方便.需要指出的是,该模型并没有考虑风速和人体排热的影响,因此,只适用于晴朗无风的夏季情况.但针对南京夏季闷热潮湿、风速较低或无风的情况进行热舒适评价,将风速设为0,一定程度上能揭示静风或微风时城市形态对热环境的影响规律,因此具有一定的现实意义.而STEVE工具,虽然由于其局限性,还未被广泛应用,但作为经验模型,其准确性值得肯定.
STEVE是基于新加坡气候条件开发,初期没有相关研究证明可用于其他地区.王频等[21]以广州地区为例对其普适性进行了检验,结论证实STEVE可对与新加坡气候特征相似的中国湿热地区(建筑气候区划Ⅲ和Ⅳ区)夏季时段的日气温值进行相对有效的预测,也可以应用于湿热地区夏季城市微气候研究.
南京位于气候区划Ⅲ区,夏季气温高,湿度大,气候特征与新加坡、广州均较相似,如表 4所示.表中RH为相对湿度.因此,本研究尝试将STEVE预测模型应用于南京夏季晴朗无风情况的城市微气候研究,具一定的探索意义.
| 表 4 新加坡, 广州, 南京夏季典型气象日气候参数对比 Table 4 Comparison of weather data of summer typical meteorological day in Singapore, Guangzhou and Nanjing |
本研究的形态变量采用由街道层峡及退让层峡不同高宽比组合形成的参数值组合(表 3),气象变量采用南京典型气象年中8月29日的气象数据,具体如下:
θmin Ref:25.9 ℃,θavg Ref:29.3 ℃,θmax Ref:33.3 ℃;
Gsolar total:5 348.37 W/m2
Gsolar max:818.19 W/m2
2) 24小时温度曲线
STEVE的直接输出结果只包括目标位置的日最低、平均、最高气温θmin, θavg和θmax,因此,需要利用与STEVE配套的经验模型(公式4~6)来获取预测日的24小时温度曲线[22].但该方法得到的温度曲线代表一般正常天气下的数据.
若θt rec < θavg rec,
| $ {{\theta }_{t}}={{\theta }_{\text{min}}}+({{\theta }_{t~\text{rec}}}-{{\theta }_{\text{min rec}}})\frac{({{\theta }_{\text{max rec}}}-{{\theta }_{\text{min rec}}}){{({{\theta }_{\text{avg}}}-{{\theta }_{\text{min}}})}^{2}}}{{{({{\theta }_{\text{avg rec}}}-{{\theta }_{\text{min rec}}})}^{2}}({{\theta }_{\text{max}}}-{{\theta }_{\text{min}}})}. $ | (4) |
若θt rec>θavg rec,
| $ {{\theta }_{t}}={{\theta }_{\text{max}}}-({{\theta }_{\text{max rec}}}-{{\theta }_{t~\text{rec}}})\frac{({{\theta }_{\text{max rec}}}-{{\theta }_{\text{min rec}}}){{({{\theta }_{\text{max}}}-{{\theta }_{\text{avg}}})}^{2}}}{{{({{\theta }_{\text{max rec}}}-{{\theta }_{\text{avg rec}}})}^{2}}({{\theta }_{\text{max}}}-{{\theta }_{\text{min}}})}. $ | (5) |
| $ {\theta _{t\;{\rm{rec}}}} = {({\theta _{d,t\;{\rm{rec}}}})_m} = \left( {\frac{1}{n}} \right)\mathop {\mathop \sum \limits^N }\limits_{{\rm{Day}}\;d = 1,{\rm{month}} = m} {\mkern 1mu} {\theta _{d,t\;{\rm{rec}}}}. $ | (6) |
式中:N为第m月的天数,θd, t rec为气象站记录的第d天第t小时的气温,θt rec由(θd, t rec)m得到,定义为第m月中所有天数中各天第t小时温度变量θd, t rec的平均值,最后得到的24小时温度曲线即由若干个平均值θt rec组成.θmin rec, θavg rec, θmax rec分别为气象站记录的第m月的平均最低、平均和最高气温.
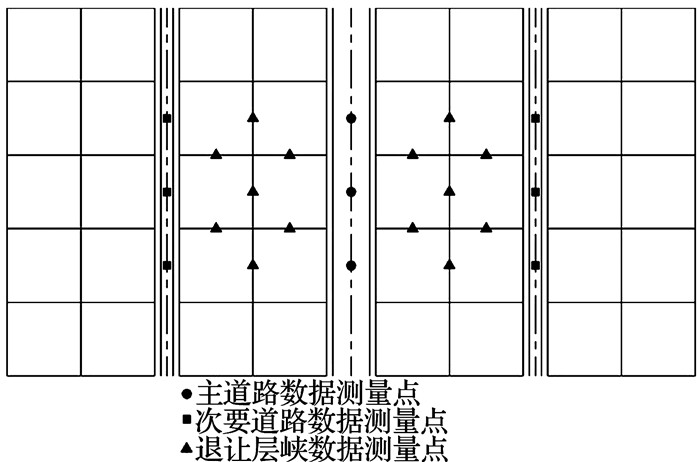
另外,在研究范围内选择均匀分布的23个点作为数据采集点,并分为3组,如图 6所示.本研究将这3组测量点最低、平均、最高气温的平均值分别作为θmin, θavg, θmax,分别代表各街区方案主道路、次要道路及退让层峡的实际气温,并用这3个平均值来获取相应位置的24小时温度曲线.
|
图 6 数据测量点位置分布 Fig. 6 Locations of measure points |
研究表明,室外热舒适度同时受微气候条件等外界因素和心理、生理以及身体热平衡等人自身因素影响[23-24].外界环境因素,主要包括空气温度(θa)、平均辐射温度(θmrt)、风速(v)、辐射通量等.其中,θmrt是一种能反映与复杂辐射环境进行净辐射能量交换的均匀温度,能对生理等效温度(physiological equivalent temperature, PET)和预测平均感知度(predicted mean vote, PMV)等热舒适评价指标产生明显影响[25].因此,热舒适度指标多数是基于概括多种因素对人体感知与生理反应的影响而开发.目前,有效的热舒适度指标主要分为2类:一类是经验模型指标,偏重于评估θa、RH及v对轻微活动的人的综合影响,不涉及人体的生理、衣物热阻、活动率以及其他如身高、体重等个体差异,例如ET[26]、WBGT[27]及WCI[28]等;另一类是机理模型指标,例如PMV[29]、ET*[30]、SET*[31]、PET[32]等,更侧重评估基于人体能量平衡的人体热工状况,因此相对更客观.目前由于人们对室外热舒适度的研究兴趣持续增加,出现一些新的评价指标,例如ETU[33]、UTCI[34]、COMFA[35]以及ETF [36]等.总的来看,由于PET的单位(℃)较容易表达和理解,对不同地区也具有普适性、可比性,另外,也能较准确、真实地反映人体对气候环境的感知度[27],因此,本研究采用PET作为热舒适度评价指标.
本研究中,PET的计算是基于STEVE的预测结果,采用RayMan模型进行.RayMan是用来计算复杂城市形态结构中的短波和长波辐射通量密度、日照时数、阴影空间以及热生理相关的评价指标[13].其计算结果包括表面温度θs, θmrt, PMV和PET等指标.
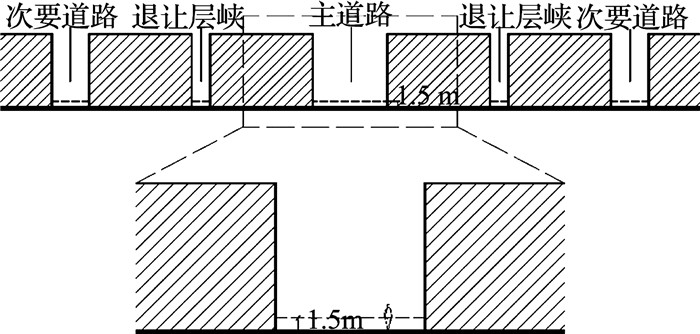
RayMan所需环境变量,包括θa、RH、v、ΨSVF.由于STEVE只适用于晴朗无风条件,因此,利用RayMan计算PET时将风速v设为0.需要指出的是,这些环境变量的测量点均位于街道层峡和退让层峡中心离地面1.5 m高的位置,如图 7所示.另外,本研究中PET指标计算所设定的人体热环境感知参数是基于一个35岁的男性,体重70 kg,身高1.7 m,衣服热阻0.7 clo,人体代谢率85 W/m2.
|
图 7 用于计算热舒适度(PET)的模拟数据采集点位置 Fig. 7 Location of simulation results used to calculate PET |
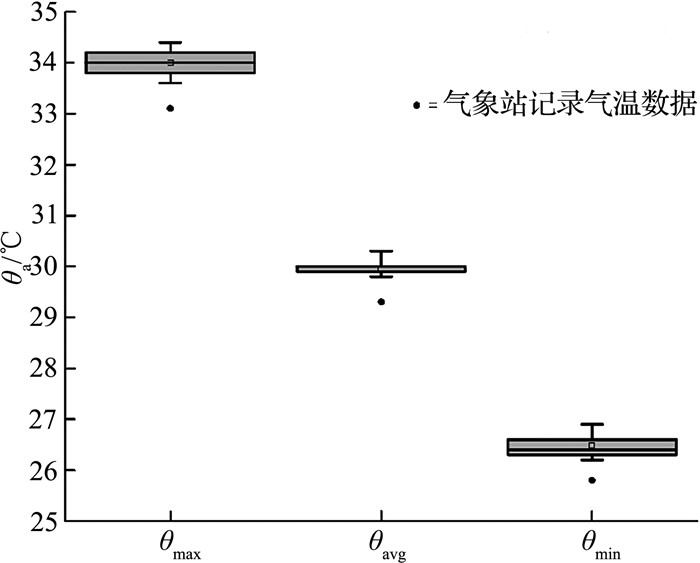
由于STEVE模型考虑了预测点周边环境因素的影响,其计算结果能够较准确地反映预测点的实际温度及热岛效应的影响.本研究基于气象变量参考值,采用STEVE工具对上述16个街区方案分别进行预测计算,得到16组θmin, θavg, θmax值,其中位于主道路的区域室外气温分布情况如图 8所示.从图中可以看到,由于不同街道层峡的几何形态不同,其室外实际气温在一定范围内也不同.另外,由STEVE得到的θmin, θavg, θmax均明显高于气象站记录的气温值(0.7 ℃≤Δθ≤1.2 ℃),这是由于气象站大多位于空间形态较开敞的郊区,所记录空气温度不能准确反映城市中心区实际情况,而城市中心区建筑密集,热岛效应显著,因此实际区域室外气温较高.
|
图 8 街区主道路中最低、平均、最高气温分布箱线图 Fig. 8 Box plot of θmin, θavg, θmax in main street |
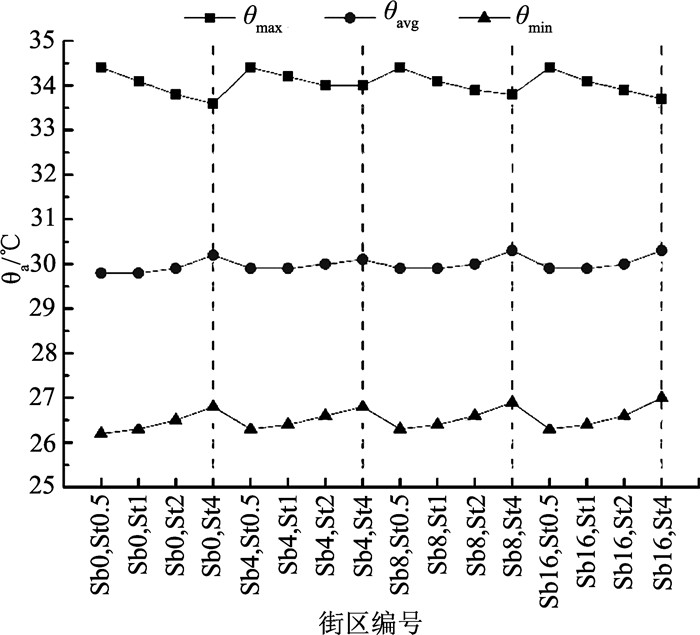
根据由STEVE得到的16组θmin, θavg, θmax分布情况,分析各街区形态参数,发现区域室外气温分布与街区空间的开敞或封闭程度密切相关,也就是说天空视角系数ΨSVF对区域室外气温有较大影响,如图 9所示.在白天,街区形态越开敞,ΨSVF越高,室外最高气温θmax越高,街区形态越封闭,建筑越密集,ΨSVF越低,θmax越低.这是由于越封闭的街区,周边建筑对直射阳光的遮挡作用越明显,因此θmax越低,反之亦然.而夜晚,ΨSVF越高的街区,θmin越低,这是由于开敞的空间形态使得街区建筑、地表等蓄热体白天吸收的热量较顺利地释放到上层空气中,而ΨSVF较低的街区,蓄热体白天吸收的热量不易散发.
|
图 9 位于各街区主道路的最低、平均、最高气温分布 Fig. 9 Temperature prediction results for θmin, θavg, θmax from main street of all scenarios |
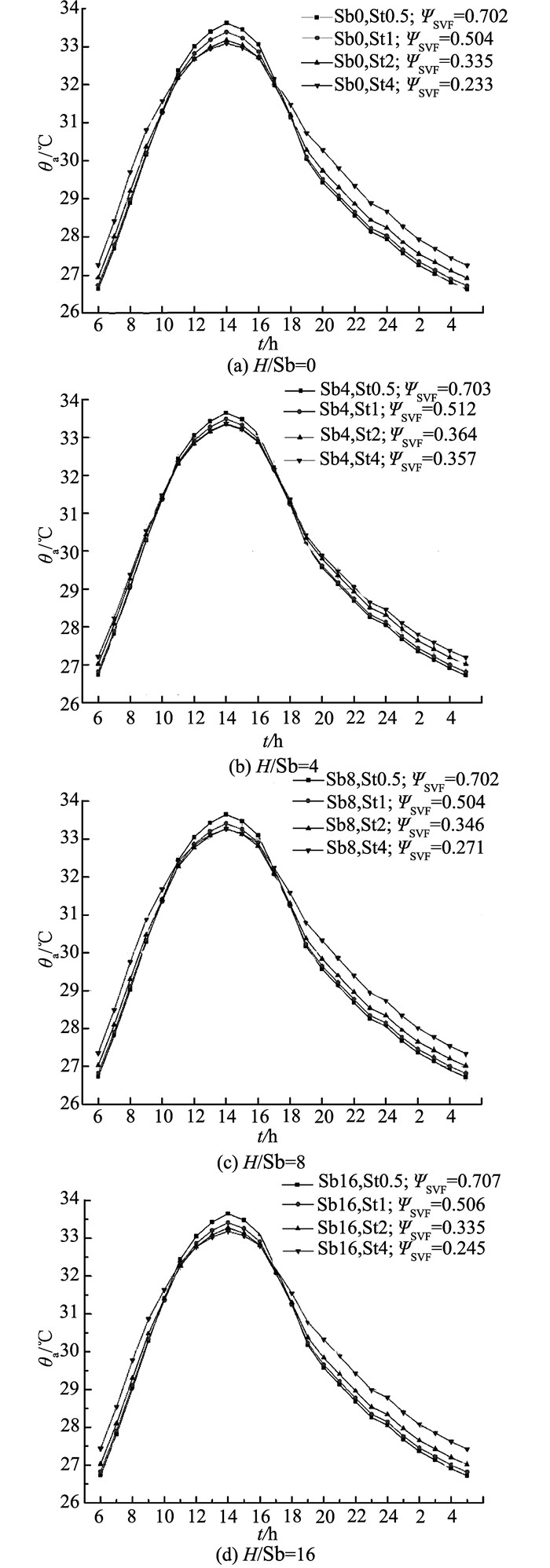
根据STEVE计算的16组θmin, θavg, θmax值,采用式(4)~(6),分别计算获取各街区不同位置的24 h温度曲线.同时,根据退让层峡高宽比不同,将这16组曲线分为4组,如图 10~12所示.
|
图 10 各街区主道路24 h区域室外气温曲线 Fig. 10 24-hour local temperature profiles in main street |

|
图 11 各街区次要道路24 h区域室外气温曲线 Fig. 11 24-hour local temperature profiles in secondary street |
|
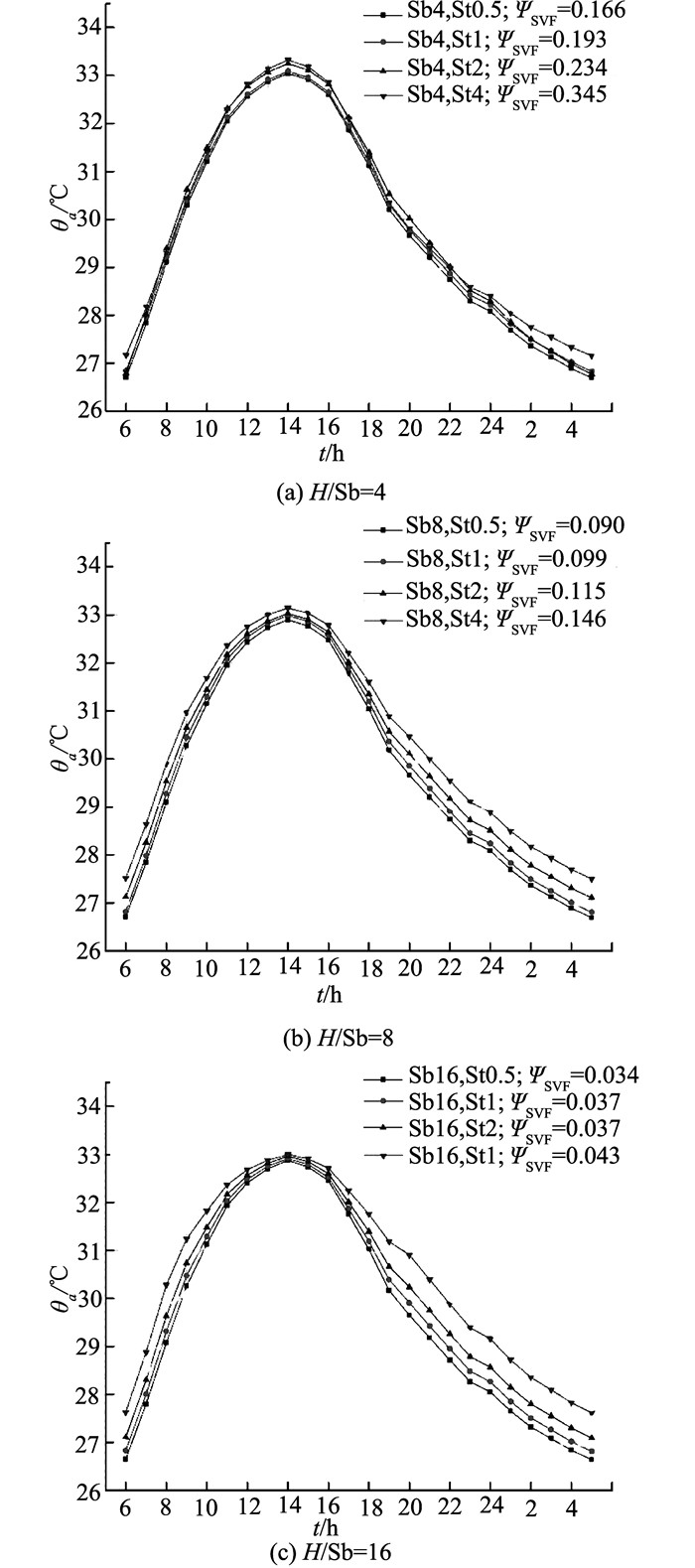
图 12 各街区退让层峡24小时区域室外气温曲线 Fig. 12 24-hour local temperature profiles in setback canyon |
图 10为街区主道路24 h气温曲线分布情况.从图中可以看到,4组曲线的高温时间都在11:00~17:00间,θa在32~34 ℃间变化,14:00时达到峰值.高温期间,ΨSVF越高的街区,θa越高,反之亦然.另外,6:00~11:00及17:00~5:00分别为气温上升期与下降期,期间ΨSVF越高的街区,θa越低,反之亦然.不同的是气温升速比气温降速明显偏高,这是由于夜间城市热岛效应对环境气温下降起到一定的延缓作用导致.值得注意的是第2组退让层峡高宽比为4的情况,该组不同曲线的分布情况较接近,气温峰值相差也较小.对比4组街区方案中主道路ΨSVF的最大差值,ΔΨSVF max从1~4组分别为0.469, 0.346, 0.431, 0.462,其中第2组最小为0.346,说明该组各街区主道路的开敞程度差异最小,反映在对主道路气温的影响上,表现为:与其他3组相比,第2组各街区主道路的24 h气温曲线分布情况较为接近,气温峰值差异也较小.由此可见,ΨSVF值对区域室外气温具有直接影响.
图 11为次要道路24 h气温曲线分布情况.其基本趋势与图 10相似,但高温期间,不同街区气温差异较小,而气温下降期,不同街区气温差异比主道路中气温差异较大,这是由于次要道路ΨSVF值比主道路较小,其夜间热岛效应更显著.
图 12为退让层峡24 h气温曲线分布情况.与图 10和11不同,在全天24 h周期内,ΨSVF越低,θa越低,ΨSVF越高,θa越高.需注意的是,高温期间不同退让层峡的θa差异较小,而气温下降期的θa差异较大.在白天晴朗无风条件下,街区层峡内气温主要受直射阳光的影响,其制约因素主要包括层峡高宽比与ΨSVF.由于同组街区退让层峡高宽比相同,其ΨSVF差值不大,且从2~4组逐渐变小(ΔΨSVF max=0.176, 0.056, 0.009),因此θa在高温期差异较小;而在夜晚,层峡中气温受街区散热能力影响极大,同组街区退让层峡深度差异较大,由此而产生的散热路径差异较大,因此,越浅的街区散热越快,气温越低,而越深的街区散热越慢,气温越高,同组街区散热能力的较大差异导致θa在气温下降期差异较大.
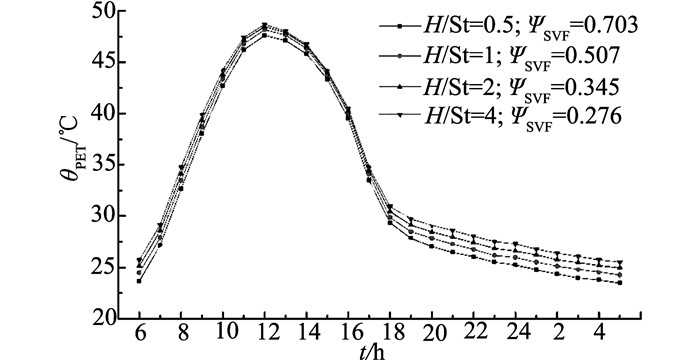
3.2 热舒适度评价(PET)基于STEVE计算的各街区不同位置的区域室外气温,采用RayMan V1.2计算获取相应的24 h室外热舒适度(PET)曲线.同样,将16个街区不同位置的PET曲线按退让层峡高宽比分组,但对比发现无论在主道路还是次要道路,各组的24 h PET曲线分布情况极为相似,这说明退让层峡高宽比变化对2种道路热舒适度的影响不大,而在退让层峡高宽比相同时,与街道ΨSVF相关的街道层峡高宽比对2种道路PET的影响更为显著.因此主道路和次要道路中的PET曲线分别取所有4组的平均值进行分析,如图 13~14所示.
|
图 13 各街区主道路的24小时PET曲线 Fig. 13 24-hour PET profiles in main street |
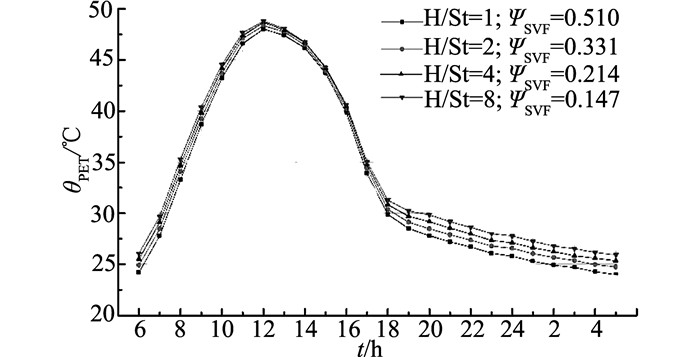
|
图 14 各街区次要道路的24 h PET曲线 Fig. 14 24 h PET profiles in secondary street |
如图 13所示为主道路24 h PET曲线分布情况.总体来看,位于主道路的PET曲线在白天(6:00~18:00)波动范围较大,在23~49 ℃间;夜晚(18:00~5:00)变化较平缓,在23~30 ℃间.与θa曲线不同,对所有街区,感觉较热的时间都在9:00~16:00,在40~49 ℃间变化,且都在12:00时感觉最热,达到峰值,这很可能由于正午的太阳辐射强度最高.另外,与θa曲线不同,在24 h周期内,主道路ΨSVF越低,感觉越热,在夜晚,这种趋势更明显.这是由于越密集的街区所产生的昼间热岛效应越明显,而夜间热岛效应则更显著.
如图 14所示,为次要道路24 h PET曲线分布情况.其总体分布情况与主道路类似,不同的是,同组内,改变道路层峡高宽比时,PET曲线间差异变小,也就是说,退让层峡高宽比相同时,与次要道路ΨSVF相关的次要道路高宽比对其PET的影响较小,这是由于次要道路ΨSVF值的差异较小导致.
退让层峡24 h PET曲线分布情况如图 15所示.与图 13、14不同,退让层峡的3组PET曲线在白天时接近重合,这是由于各组退让层峡的ΨSVF较接近导致;而在夜间各组PET随退让层峡高宽比的增加,差异越明显,也即退让层峡的ΨSVF越小,其夜间热舒适度受街道层峡高宽比的影响越大.例如当退让层峡高宽比为16时,街道层峡高宽比越小,夜间感觉越凉爽,这是由于街道层峡高宽比越小,街区夜间散热越容易.
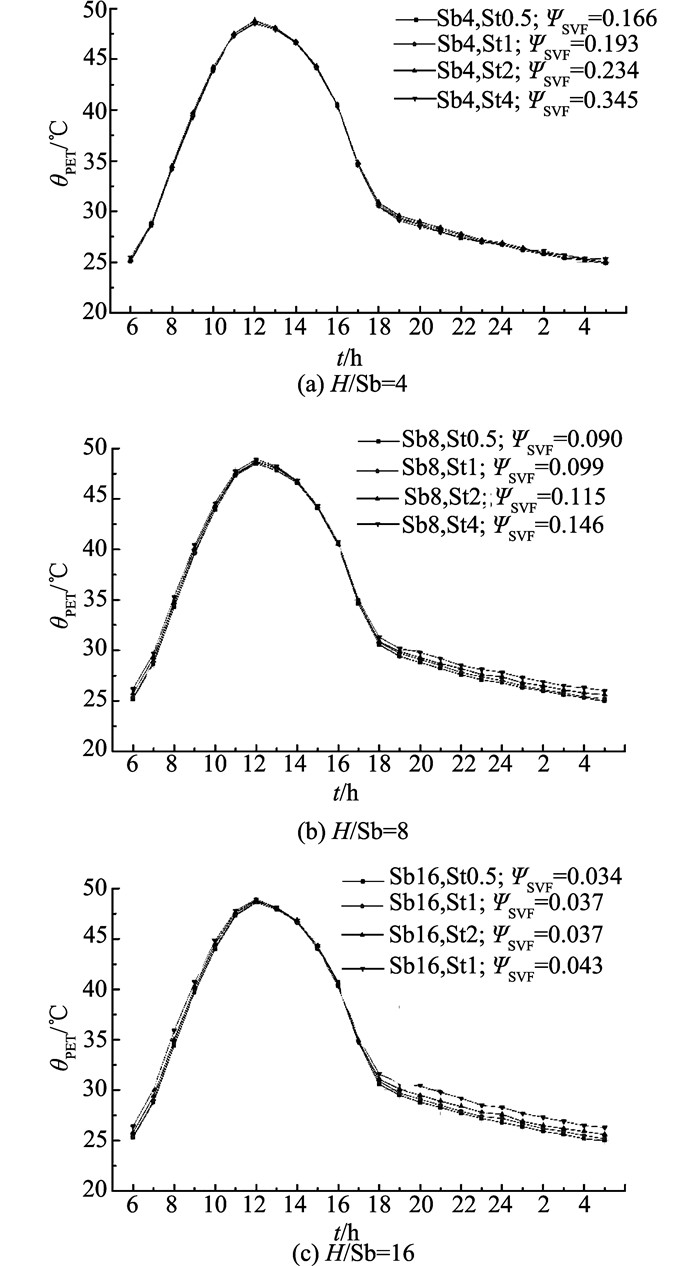
|
图 15 各街区退让层峡的24小时PET曲线 Fig. 15 24 h PET profiles in setback canyon |
另外,对比图 13~15,可看出14:00~17:00间,每组PET曲线均较其他时间段更趋于重合,这是由于在这段时间内,θa、RH等各微气候条件较其他时间来说变化较小,因此人的热感知较稳定.
3.3 ΨSVF与区域室外气温及热舒适度关联性分析根据对16个街区室外气温及热舒适度分布情况的分析,可以看到除空气温度、太阳辐射等相关气候参数外,街区几何形态,包括层峡高宽比与天空视角系数等对室外热环境起着重要的影响作用.分析ΨSVF与θa和PET之间的关系,如图 16所示.
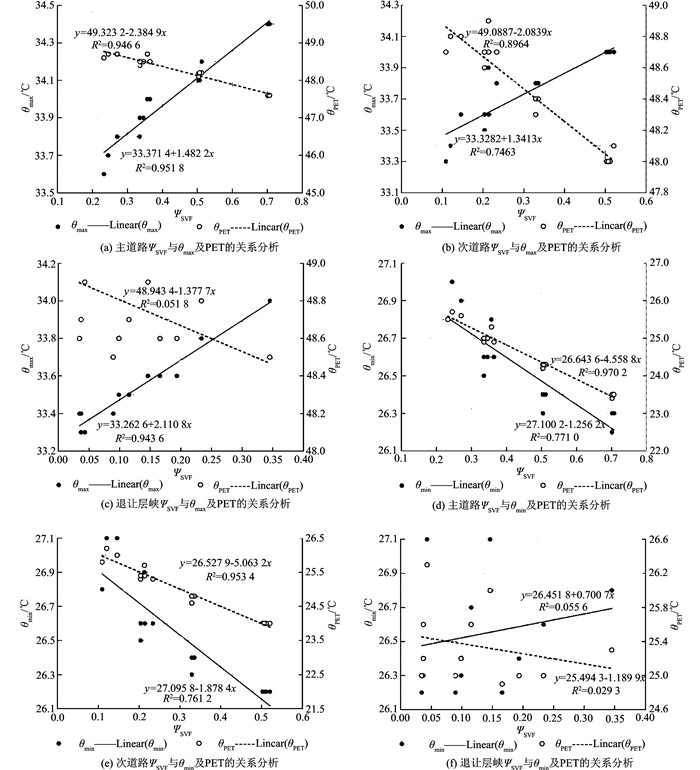
|
图 16 街区不同位置ΨSVF与θa和PET之间的关系 Fig. 16 Relationship between SVF obtained from different locations and θa and PET in outdoor spaces at pedestrian level |
图 16(a)(b)(c)分别为主道路、次要道路及退让层峡中白天最高气温θmax及对应PET与ΨSVF的关系,从(a)(b)可看到θmax和PET都与ΨSVF间存在较强的线性关系(R2≥0.746),从斜率看,在白天,ΨSVF越高的街区,θmax越高,而PET呈相反的趋势.与街道层峡不同,退让层峡中虽然ΨSVF与θmax间存在较强的线性关系(R2=0.944),但PET与ΨSVF之间的线性关系较弱(R2=0.052),离散点大多分布在高宽比为16的退让层峡中(图 16(c)).这是由于该组街区退让层峡ΨSVF较小(ΨSVF < 0.1),相互间差异也较小,从而导致室外热环境差异较小.但从斜率看,与街道层峡相同,ΨSVF与θmax间关系是正向,与PET间呈相反趋势.
至于夜晚时,主道路和次道路中ΨSVF与θmin和PET间都存在较强的反向线性关系(R2≥0.761),也即ΨSVF越高的街区,θmin越低,PET也越低,感觉越凉爽(图 16(d)(e)).而退让层峡中ΨSVF与θmin和PET间的线性关系较弱(R2 < 0.1)(图 16(f)).这也是由于退让层峡高宽比较大时,其ΨSVF值不仅较小,之间差异也较小,从而导致室外热环境差异较小.
总的来看,以上分析说明代表街区层峡几何形态特征的ΨSVF与θa及PET间存在明确线性关系.由于城市热岛效应的影响,无论白天还是夜晚,越深的街道层峡感觉越热.但白天时不同形态层峡中舒适度差异不大,而由于夜间热岛效应更明显,不同形态层峡中舒适度差异较大.
4 结论(1) 街区层峡高宽比与开敞度对区域室外气温产生重要影响.白天,高宽比越大,空间越封闭,建筑间遮阳效果越好,θa越低,反之亦然;而夜晚,高宽比越小,空间越开敞,城市蓄热体散热越容易,θa越低,反之亦然.
(2) 由街区几何形态决定的ΨSVF对实际区域室外气温起主要的影响作用.白天,ΨSVF越高的街区,θmax越高,反之亦然;而夜晚,ΨSVF越高的街区,θmin越低,反之亦然.
(3) 街区层峡高宽比与ΨSVF对热舒适度也起主要的影响作用.但与区域室外气温不同,对全天24 h周期来说,高宽比越小,ΨSVF越高的街区,感觉越凉爽,高宽比越大,ΨSVF越低的街区,感觉越热,夜晚时,这种趋势更明显.
综上,对夏热冬冷地区而言,城市形态越紧凑,白天建筑间遮阳效果越好,但也需综合考虑紧凑的城市形态对夜间热岛效应的加剧作用.首先,从层峡高宽比的角度看,一方面高宽比较大的退让层峡能够形成较好的遮阳条件,另一方面高宽比较小的街道层峡使街区较容易散热.因此,城市设计应综合两方面要求,设计合理的层峡高宽比,寻找既能够有效利用白天建筑间遮阳效果,又能减缓夜间热岛效应的平衡点.对本研究而言,退让层峡高宽比不宜小于8,而主道路和次要道路高宽比分别不宜大于2和4.考虑城市CBD土地资源的稀缺性,本研究中最佳方案是sb8st2街区.其次,由于具有较好的遮阳条件,退让层峡也可以通过恰当设计使其不只作停车用途,也更适合作为人行通道.另外,由于当前版本STEVE的局限性,本研究暂不考虑风环境的影响,但实际上,风对室外热环境影响极为显著.随着STEVE模型的逐步完善,该因素的影响将在后续研究中进行分析.
| [1] |
TODHUNTER P E. Microclimatic variation attributable to urban canyon asymmetry and orientation[J]. Physics and Geography, 1990, 11(2): 131-141. |
| [2] |
OKE T R. Canyon geometry and the nocturnal urban heat island:comparison of scale model and field observations[J]. Journal of Climatology, 1981, 1(3): 237-254. DOI:10.1002/joc.3370010304 |
| [3] |
EMMANUEL R, JOHANSSON E. Influence of urban morphology and sea breeze on hot humid microclimate:the case of Colombo, Sri Lanka[J]. Climate Research, 2006, 30(3): 189-200. |
| [4] |
ARNFIELD A J. Street design and urban canyon solar access[J]. Energy and Buildings, 1990, 14(2): 117-131. DOI:10.1016/0378-7788(90)90031-D |
| [5] |
LIN T P, MATZARAKIS A, HWANG R L. Shading effect on long-term outdoor thermal comfort[J]. Building and Environment, 2010, 45(1): 213-221. DOI:10.1016/j.buildenv.2009.06.002 |
| [6] |
BOURBIA F, AWBI H B. Building cluster and shading in urban canyon for hot dry climate part 1:air and surface temperature measurements[J]. Renewable Energy, 2004, 29(2): 249-262. DOI:10.1016/S0960-1481(03)00170-8 |
| [7] |
ALI-TOUDERT F, MAYER H. Numerical study on the effects of aspect ratio and orientation of an urban street canyon on outdoor thermal comfort in hot and dry climate[J]. Building and Environment, 2006, 41(2): 94-108. DOI:10.1016/j.buildenv.2005.01.013 |
| [8] |
ALI-TOUDERT F, MAYER H. Effects of asymmetry, galleries, overhanging façades and vegetation on thermal comfort in urban street canyons[J]. Solar Energy, 2007, 81(6): 742-54. DOI:10.1016/j.solener.2006.10.007 |
| [9] |
MATZARAKIS A, RUTZ F, MAYER H. Modelling radiation fluxes in simple and complex environments-application of the RayMan model[J]. International Journal of Biometeorology, 2007, 51(4): 323-334. DOI:10.1007/s00484-006-0061-8 |
| [10] |
CHEN L, NG E, AN X, et al. Sky view factor analysis of street canyons and its implications for daytime intra-urban air temperature differentials in high-rise, high-density urban areas of Hong Kong:a GIS-based simulation approach[J]. International Journal of Climatology, 2012, 32(1): 121-136. DOI:10.1002/joc.v32.1 |
| [11] |
KRVGER E L, MINELLA F O, RASIA F. Impact of urban geometry on outdoor thermal comfort and air quality from field measurements in Curitiba, Brazi l[J]. Building and Environment, 2011, 46(3): 621-634. DOI:10.1016/j.buildenv.2010.09.006 |
| [12] |
YAMASHITA S, SEKINE K, SHODA M, et al. On relationships between heat island and sky view factor in the cities of Tama River basin, Japan[J]. Atmospheric Environment (1967), 1986, 20(4): 681-686. DOI:10.1016/0004-6981(86)90182-4 |
| [13] |
SVENSSON M K. Sky view factor analysis-implications for urban air temperature differences[J]. Meteorological applications, 2004, 11(3): 201-211. DOI:10.1017/S1350482704001288 |
| [14] |
OKE T R. Street design and urban canopy layer climate[J]. Energy and Buildings, 1988, 11(1): 103-113. |
| [15] |
PEARLMUTTER D, BITAN A, BERLINER P. Microclimatic analysis of "compact" urban canyons in an arid zone[J]. Atmospheric Environment, 1999, 33(24): 4143-4150. |
| [16] |
王振, 李保峰. 微气候视角下的城市街区环境定量分析技术[C]//第六届国际绿色建筑与建筑节能大会论文集. 北京: 中国城市科学研究会, 2010: 118-122. WANG Zhen, LI Bao-feng. Quantitative analysis methods of environment on urban blocks based on micro-climate[C]//Paper Collection for the 6th International Conference on Green and Energy-Efficient Building. Beijing: Chinese Society for Urban Studies, 2010: 118-122. http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=7298601 |
| [17] |
ZHANG Y, QIN B, CHEN W. Analysis of solar radiation variations over Nanjing region in recent 40 years[J]. Journal of Geographical Sciences, 2003, 13(1): 97-104. DOI:10.1007/BF02873152 |
| [18] |
MARTIN L, MARCH L. Urban space and structures[M]. Cambridge: Cambridge University Press, 1972, 55-96.
|
| [19] |
JUSUF S K, WONG N H. Development of empirical models for an estate level air temperature prediction in Singapore[C]//Proceedings of the Second International Conference on Countermeasures to Urban Heat Island. Berkeley: [s. n. ], 2009: 21-23. https://www.researchgate.net/publication/228582040_Development_of_empirical_models_for_an_estate_level_air_temperature_prediction_in_Singapore
|
| [20] |
JUSUF S K, WONG N H, TAN C L, et al. STEVE Tool: bridging the gap between urban climatology research and urban planning process[C]//International Conference on Sustainable Design and Construction 2011: Integrating Sustainability Practices in the Construction Industry. Kansas: ASCE, 2012: 25-33. https://www.researchgate.net/publication/268484250_STEVE_Tool_Bridging_the_Gap_between_Urban_Climatology_Research_and_Urban_Planning_Process
|
| [21] |
王频, 孟庆林. STEVE气温预测模型的普适性检验——以广州地区为例[J]. 土木建筑与环境工程, 2013, 35(4): 151-160. WANG Pin, MENG Qing-lin. Validation tests for air temperature prediction model steve:an example of Guangzhou[J]. Journal of Civil, Architectural & Environmental Engineering, 2013, 35(4): 151-160. |
| [22] |
CHONG Z M A, WONG N H, IGNATIUS M, et al. Predicting the envelope performance of commercial office buildings in Singapore[J]. Energy and Buildings, 2013, 66: 66-76. DOI:10.1016/j.enbuild.2013.07.008 |
| [23] |
NIKOLOPOULOU M, STEEMERS Κ. Thermal comfort and psychological adaptation as a guide for designing urban spaces[J]. Energy and Buildings, 2003, 35(1): 95-101. DOI:10.1016/S0378-7788(02)00084-1 |
| [24] |
丁沃沃, 胡友培, 窦平平. 城市形态与城市微气候的关联性研究[J]. 建筑学报, 2012(7): 16-21. DING Wo-wo, HU You-pei, DOU Ping-ping. Study of the interrelationship between urban pattern and urban microclimate[J]. Architectural Journal, 2012(7): 16-21. |
| [25] |
MATZARAKIS A, MAYER H, IZIOMON M G. Applications of a universal thermal index:physiological equivalent temperature[J]. International Journal of Biometeorology, 1999, 43(2): 76-84. DOI:10.1007/s004840050119 |
| [26] |
HOUGHTON F C, YAGLOU C P. Determining equal comfort lines[J]. Journal of the American Society of Heating and Ventilating Engineers, 1923, 29: 165-176. |
| [27] |
YAGLOU C P, MINAED D. Control of heat casualties at military training centers[J]. Archives of Industrial Health, 1957, 16(4): 302-316. |
| [28] |
SIPLE P, PASSEL C F. Measurements of dry atmospheric cooling in subfreezing temperatures[J]. Proceedings of the American Philosophical Society, 1945, 89(1): 177-199. |
| [29] |
FANGER P O. Assessment of man's thermal comfort in practice[J]. Occupational and Environmental Medicine, 1973, 30(4): 313-324. DOI:10.1136/oem.30.4.313 |
| [30] |
GAGGE A P, STOLWIJK J A J, NISHI Y. An effective temperature scale based on a simple model of human physiological regulatory response[J]. ASHRAE Transactions, 1971, 77: 247-272. |
| [31] |
GONZALEZ R R, NISHI Y, GAGGE A P. Experimental evaluation of standard effective temperature:a new biometeorological index of man's thermal discomfort[J]. International Journal of Biometeorology, 1974, 18(1): 1-15. DOI:10.1007/BF01450660 |
| [32] |
HÖPPE P. The physiological equivalent temperature-a universal index for the biometeorological assessment of the thermal environment[J]. International Journal of Biometeorology, 1999, 43(2): 71-75. DOI:10.1007/s004840050118 |
| [33] |
NAGANO K, HORIKOSHI T. New index indicating the universal and separate effects on human comfort under outdoor and non-uniform thermal conditions[J]. Energy and Buildings, 2011, 43(7): 1694-1701. DOI:10.1016/j.enbuild.2011.03.012 |
| [34] |
JENDRITZKY G, DE DEAR R, HAVENITH G. UTCI-why another thermal index?[J]. International Journal of Biometeorology, 2012, 56(3): 421-428. DOI:10.1007/s00484-011-0513-7 |
| [35] |
KENNY N A, WARLAND J S, BROWN R D, et al. Part A:Assessing the performance of the COMFA outdoor thermal comfort model on subjects performing physical activity[J]. International Journal of Biometeorology, 2009, 53(5): 415-428. DOI:10.1007/s00484-009-0226-3 |
| [36] |
KURAZUMI Y, TSUCHIKAWA T, KONDO E, et al. Conduction-corrected modified effective temperature as the indices of combined and separate effect of environmental factors on sensational temperature[J]. Energy and Buildings, 2010, 42(4): 441-448. DOI:10.1016/j.enbuild.2009.10.012 |



