2. 上海同恩土木工程科技咨询有限公司, 上海 200092
2. Tongen Civil Engineering Technology Consulting Co. Shanghai 200092, China
几何缺陷是影响网壳结构力学性态的主要因素之一.大量试验和理论研究表明[1-8], 初始几何缺陷的存在将改变网壳结构的稳定性态, 显著降低结构的稳定承载能力.由于受施工过程、安装误差及使用环境因素的影响, 网壳结构几何缺陷的形成与发展变化难以预测.因此, 在既有网壳结构的鉴定分析中, 建立一种等效的几何缺陷分布模式进行网壳结构承载力评估是目前有效且实用的方法.
网壳结构节点几何坐标偏差形成的缺陷是影响结构整体稳定性的重要因素之一[9-10].Peek[11]提出临界失稳缺陷模态法, 将临界平衡位移模态作为结构最不利的初始缺陷分布模式.Chen等[12]提出采用一致缺陷模态法和随机缺陷模态法引入网壳结构初始几何缺陷.Bruno等[9]采用最低阶屈曲模态作为结构初始几何缺陷的模态, 认为结构按此模态变形后将处于势能最小状态.蔡建等[13]认为一致缺陷模态法求得的稳定承载力并非最不利, 网壳结构稳定承载力的下限值可能出现在高阶缺陷模态.刘慧娟等[14]提出了缺陷模态随机叠加法, 假定缺陷模式为若干屈曲模态的耦合, 作为影响网壳结构稳定性的最不利缺陷模态.随机缺陷模态法认为结构的初始几何缺陷是一个多维随机变量, 样本空间每一个样本都对应结构一种初始几何缺陷模态.Borri等[1]和Kiyohiro等[15]假定节点几何偏差符合独立正态分布, 采用随机缺陷模态法对单层网壳结构进行稳定承载力分析.Chen等[10]考虑了实际结构各节点的相关关系, 提出了基于协相关矩阵的随机缺陷模型, 但该模型的标定参数只针对单层球面网壳, 应用范围具有局限性.
所有上述网壳结构缺陷模态引入方法均只适用于结构的设计阶段.既有网壳结构的初始缺陷模态是确定的, 分析时采用的计算模型应符合结构的实际工作状态[16], 采用假定缺陷模态计算稳定承载力的方法显然是不合理的.由于既有结构本身的视觉障碍、现场检测的时间成本以及其他环境限制因素影响, 通常无法通过测量所有节点坐标的方法确定结构初始几何缺陷.因此, 常采用抽样检测部分节点坐标的方法近似拟合整体结构缺陷分布.然而, 目前针对如何利用已知测点几何信息推断整体结构缺陷模态的研究成果很少, 不能满足建立既有结构计算模型的需要[17].
本文在现有研究成果的基础上, 结合网壳节点位形的空间相关性, 引入概率图模型理论, 提出既有网壳结构的马尔可夫随机场模型[18-19];基于双节点团和三节点团的几何状态函数, 构建既有网壳结构几何缺陷分布的反演方程, 计算节点的几何偏差.通过设计制作K6单层球面网壳实验模型, 分析网壳节点坐标的实测值和反演迭代方程计算结果, 验证了理论的可行性和适用性.
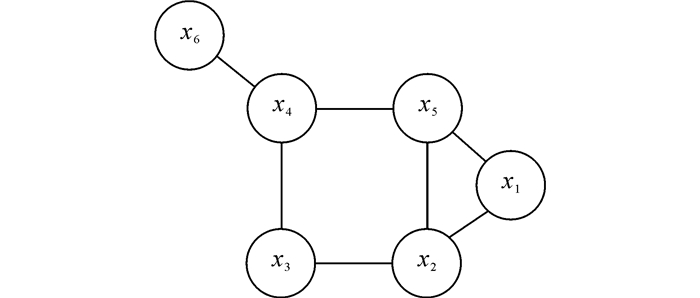
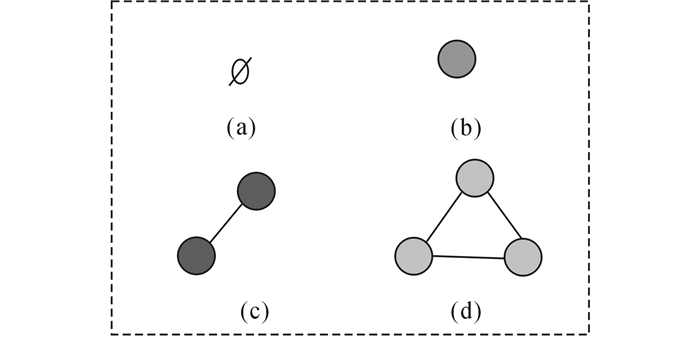
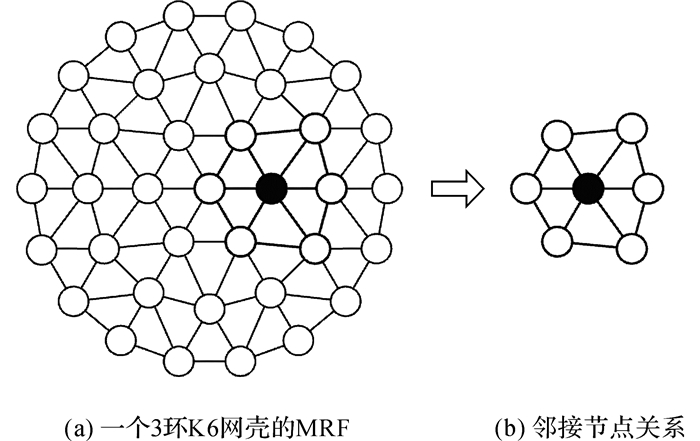
1 马尔可夫随机场马尔可夫随机场(MRF)是一种使用无向图建立随机变量之间相关关系的概率图模型, 其理论能够较为准确地描述相邻节点间的相互影响.如图 1所示表达了一个简单的马尔可夫随机场.图中每个节点表示一个随机变量, 节点间的连线表示2个变量之间的依赖关系.图中任意若干节点均可构成子集, 若子集中任意两节点间都有边连接, 则称该节点子集为一个“团”(clique), 如图 2所示.若在一个团中加入另外任何一个节点都不再形成团, 则称该团为一个“极大团”(maximal clique), 因此, 极大团被定义为不能被其他任何团所包含的团.图 1中的极大团有{x1, x2, x5}, {x4, x5}, {x3, x4}, {x4, x6}, {x2, x3}.
|
图 1 马尔可夫随机场模型示意图 Fig. 1 Sketch map of MRF model |
|
图 2 MRF系统的团类型 Fig. 2 Clique type of MRF model system |
根据Hammersley-Clifford定理[20], 马尔可夫随机场的联合概率分布P(X)可定义为基于团分解的多因子乘积, 每一个因子仅与一个团Q相关, 即
| $ P\left( X \right) = \frac{1}{T}\prod\limits_{Q \in C} {{\mathit{\Psi }_Q}\left( {{X_Q}} \right)} . $ | (1) |
式中:C为所有团构成的集合;XQ为与团Q∈C对应的随机变量集合;ΨQ(XQ)是一个关于XQ的势函数(非负实数函数), 亦被称为团的偏好函数, 以表征团Q中随机变量取值的偏好程度;T是归一化函数(partition function), 取值为
显然所有相互连接的2个变量都会构成团, 若变量个数较多, 则会给式(1)的计算带来负担.若团Q不是极大团, 则它一定被一个极大团Q*所包含, 即XQ⊆XQ*, 意味着XQ同时体现在势函数ΨQ(XQ)和ΨQ*(XQ*)中.因此, 为简化计算, 联合概率分布P(X)可等效为基于极大团分解的多因子乘积.
例如图 1中, X={x1, x2, …, x6}的联合概率分布函数可简化为
| $ \begin{array}{l} P\left( X \right) = \frac{1}{T}{\mathit{\Psi }_{125}}\left( {{x_1},{x_2},{x_5}} \right){\mathit{\Psi }_{45}}\left( {{x_4},{x_5}} \right) \times \\ \;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\Psi }_{34}}\left( {{x_3},{x_4}} \right){\mathit{\Psi }_{46}}\left( {{x_4},{x_6}} \right){\mathit{\Psi }_{23}}\left( {{x_2},{x_3}} \right). \end{array} $ | (2) |
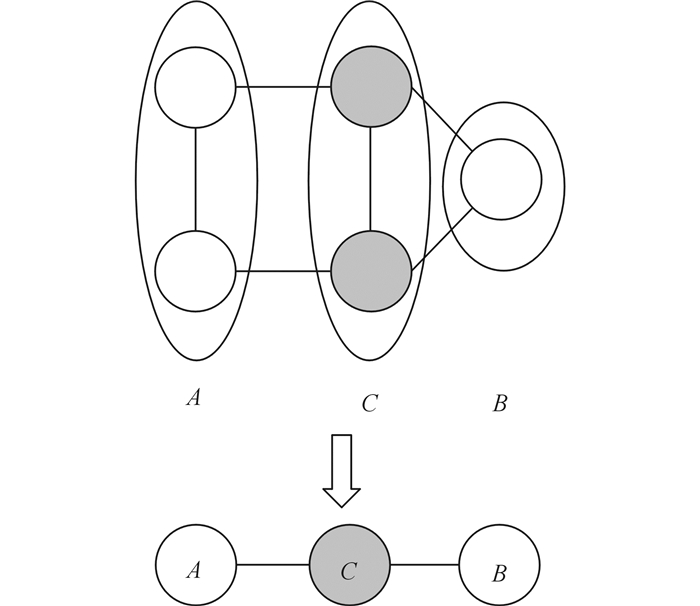
根据马尔可夫随机场的定义式, 容易推导条件独立性的结论, 即给定2个变量子集的分离集, 则这2个变量子集条件独立.如图 3所示, 令A、B和C对应的变量集为XA、XB和XC, 则XA和XB在给定XC条件下独立, 记XA⊥XB|XC, 即从节点集A到节点集B都必须经过节点集C, C称为“分离集”.
|
图 3 节点集A和B的条件独立 Fig. 3 Conditional independence of node A and B |
由马尔可夫随机场的条件独立性可以得到一个重要的局部马尔可夫性推论:即给定变量的邻接变量, 则该变量条件独立于其他变量.
本文将利用马尔可夫随机场的联合概率分布及其局部马尔可夫性的推论, 推导网壳结构的几何状态函数表达式, 构建既有网壳结构初始几何缺陷的反演方程.
2 结构位形反演算法 2.1 缺陷模型假定假定一:影响网壳结构整体稳定承载力的初始几何缺陷主要包括杆件初弯曲和节点坐标偏差.由于杆件初弯曲在构件设计时已考虑, 因此, 本文研究只考虑网壳结构节点几何坐标偏差的影响.
假定二:网壳结构节点i的几何坐标偏差通常采用三维向量ui表达, 基于节点所在曲面位置的切平面, 可以将该向量分解为平面内(平行于切平面)向量ui1和平面外(沿曲率半径方向)向量ui2, 即ui=ui1+ui2.一方面, 网壳结构由于其独特的曲面形式使得其面内薄膜刚度远远大于面外刚度, 节点的径向几何偏差对网壳曲面的形状有较大影响;另一方面, 如图 4所示提取了网壳结构一阶屈曲模态的几何偏差成分uij/ui(j=1, 2), 可以看出网壳结构屈曲模态中径向几何偏差ui2占绝对主要成分, 由于屈曲模态代表了结构的势能最小方向, 可以说明径向偏差对网壳结构整体稳定性的影响远大于切向偏差.因此, 为了简化分析方法, 本文只考虑节点沿曲率半径方向的几何偏差.

|
图 4 网壳结构屈曲模态的几何偏差成分分析 Fig. 4 Component analysis of Geometric imperfections of reticulated shells |
在该假定下, 节点i的几何偏差可简化为随机变量xi, 其值等于沿曲率半径向量ui2的模, 即xi=|ui2|.如图 5所示为节点沿平面外的几何偏差, 规定几何偏差以向结构外侧为正, 向结构内侧为负.为便于描述, 本文的几何缺陷均指节点几何坐标偏差, 且均表示偏差沿径向的分量.
|
图 5 网壳结构沿曲率半径方向的几何偏差 Fig. 5 Geometric imperfections along radius of curvature |
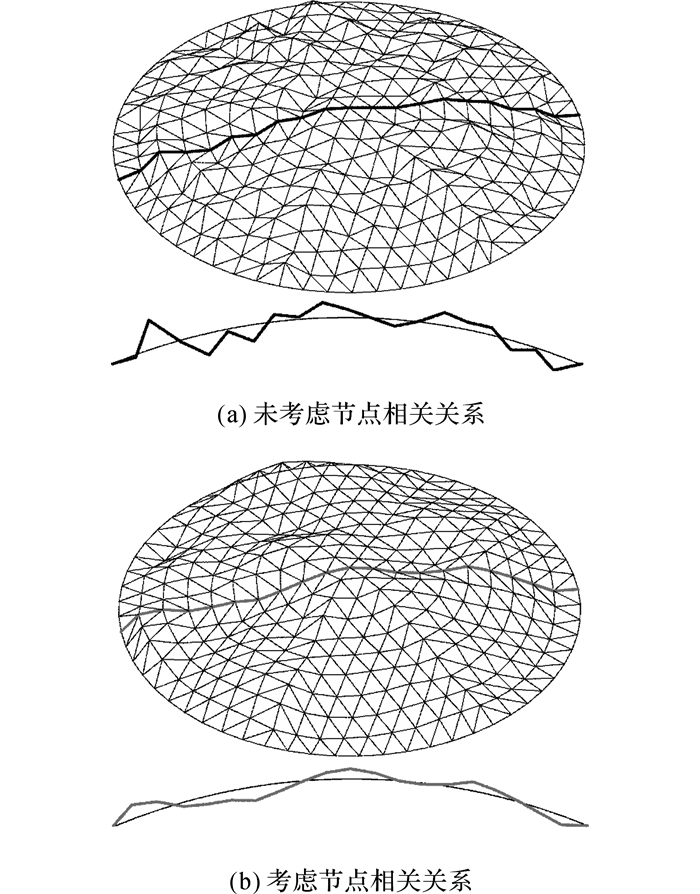
假定三:传统的随机缺陷模态法假定各节点的几何缺陷相互独立且满足正态分布, 其结果可能出现如图 6(a)所示的锯齿状模型.而实际工程中, 结构几何缺陷分布模式往往如图 6(b)所示, 说明节点几何偏差具有相关关系, 且缺陷值过渡较为平缓, 无尖锐的锯齿状变化.同时任意两节点的相关系数满足ρij=ρji, 即结构几何缺陷模态相关关系矩阵满足对称正定性, 变量相关关系无方向性.因此, 本文引入马尔可夫随机场模型, 以网壳节点的几何坐标偏差作为随机场的节点随机变量, 节点之间连接的杆件作为随机场的边以表达节点几何坐标偏差的相关关系, 如图 7(a)所示.在此基础上, 本文假定结构中某一节点的几何坐标偏差只与其邻接节点相关, 而与其他节点无关, 即节点几何坐标偏差具有马尔可夫性, 符合马尔可夫随机场的局部马尔可夫性条件, 如图 7(b)所示.可见, 网壳结构的几何特性造就了其本身就能作为一个天然的马尔可夫随机场.
|
图 6 节点几何缺陷分布模式 Fig. 6 Nodal geometric imperfection distribution mode |
|
图 7 网壳结构的马尔可夫随机场(MRF)模型 Fig. 7 MRF model of reticulated structure |
公式(1)给出了马尔可夫随机场中随机变量联合概率分布的一般表达式, 其中归一化函数
| $ G\left( {Y,Z} \right) = T \cdot P\left( X \right) = \prod\limits_{Q \in C} {{\mathit{\Psi }_Q}\left( {{X_Q}} \right)} . $ | (3) |
式中:Y为观测节点的几何缺陷集, Z为待计算的节点几何缺陷集, X为所有节点的几何缺陷集, 即满足X=Y∪Z, 且Y∩Z=∅;G(Y, Z)被定义为几何缺陷分布的反演方程, 其含义为所有团的势函数乘积.反演方程的核心内容即为根据已知缺陷集Y求解最可能存在的未知缺陷集Z.
公式(3)中团集合C的构成成员有若干种形式, 根据网壳结构的类型, 本文将考虑最常用的2种团类型:1)双节点团, 即网壳曲面内一根杆件所连的2个节点构成的团, 如图 2(c)所示;2)3节点团, 即由网壳曲面内3根杆件组成的最小三角形中所含的3个节点构成的团, 如图 2(d)所示.
势函数ΨQ(XQ)的作用是定量描述变量集XQ中变量之间的相关关系, 应是非负函数.为满足非负性, 势函数可利用指数函数来表达, 即
| $ {\mathit{\Psi }_Q}\left( {{X_Q}} \right) = \exp \left( { - {\mathit{H}_Q}\left( {{\mathit{\boldsymbol{X}}_Q}} \right)} \right). $ | (4) |
式中:HQ(XQ)是一个定义在变量XQ上的几何状态函数, 其取值越大, 势函数ΨQ(XQ)越小, 表征对变量取值xQ的偏好程度越低.
若采用双节点团进行计算, 节点几何偏差将导致杆件产生倾斜角.杆件倾斜角越大, 对周围其他节点的影响越大, 导致其所蓄的“能量”越高, 变量取值的偏好程度越低.因此, HQ(XQ)可由节点偏移引起的杆件空间夹角变化量表达, 考虑到节点相关关系的无向性(即去符号化), 可令
| $ {\mathit{H}_Q}\left( {{X_Q}} \right) = \frac{{{{\left( {{x_i} - {x_j}} \right)}^2}}}{{l_Q^2}}. $ | (5) |
式中:XQ={xi, xj};lQ为团Q中杆件的长度.
联立式(3)、(4)、(5), 可得
| $ G\left( {Y,Z} \right) = \prod\limits_{Q \in C} {\exp \left( { - \frac{{{{\left( {{x_i} - {x_j}} \right)}^2}}}{{l_Q^2}}} \right)} . $ | (6) |
式中:xi以及xj可以属于Y、Z中的任意一个集合.
若将缺陷集Y作为系统的样本集, 将缺陷集Z作为待计算的参数集, 可利用极大似然估计法确定参数集Z的最佳估计值.对于一个既有网壳结构, 一旦确定观测对象, 则样本集Y是唯一确定的, 似然函数L即为反演方程本身, 令
| $ L\left( {y;Z} \right) = \prod\limits_{Q \in C} {\exp \left( { - \frac{{{{\left( {{x_i} - {x_j}} \right)}^2}}}{{l_Q^2}}} \right)} . $ | (7) |
式中:{y}为已知的样本集观测值, L为参数集Z的函数.
若L在
| $ \frac{{\partial \ln L}}{{\partial {x_k}}} = 0,{x_k} \in Z. $ | (8) |
对于某一待估计的节点k, 将式(8)代入式(7), 得一维反演迭代方程
| $ - 2\sum\limits_{Q \in {C^ * }} {\frac{{\left( {{x_k} - {x_j}} \right)}}{{l_Q^2}}} = 0. $ | (9) |
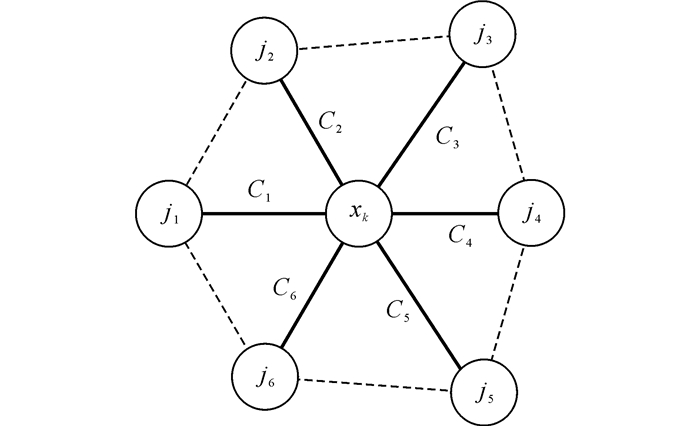
式中:C*为包含节点k的所有双节点团集合, 如图 8实线所示.从图 7中可以看出, 只要已知与节点k直接相邻节点的缺陷值, 可利用团C1~C6, 按式(9)计算节点k的缺陷值, 符合马尔可夫性的特点.
|
图 8 一维迭代方程的团集合 Fig. 8 Clique list of 1-D iterative equation |
若采用三节点团进行计算, 节点几何偏差导致三角形面发生偏移和倾斜.与双节点团同理, HQ(XQ)可用平面偏移后的法线与理论位置法线的夹角余弦cos θ表达.
三角形偏移前, 以其中任意一个顶点作为原点, 以其法线作为z的基向量, 构建该三角形平面的局部仿射向量空间.三节点均处于局部放射空间的XY平面内, 法向量记为n=0, 0, 1.则三角形三节点的几何偏移均为局部空间沿z向的偏移, 偏移值记为(z1, z2, z3).偏移后的三角形平面方程为
| $ Ax + By + Cz + D = 0. $ | (10) |
三角形平面一般方程的法向量m=[A, B, C];将m归一化, 令A2+B2+C2=1;偏移前后的法向量夹角余弦为
| $ \cos \theta = \frac{{\left| {\mathit{\boldsymbol{m}} \cdot \mathit{\boldsymbol{n}}} \right|}}{{\left| \mathit{\boldsymbol{m}} \right| \cdot \left| \mathit{\boldsymbol{n}} \right|}} = \frac{C}{{\sqrt {{A^2} + {B^2} + {C^2}} }} = C. $ | (11) |
为求出该偏角, 可将节点偏移简化为原点不偏移, 其余两点偏移量分别记为(z2-z1)和(z3-z1), 代入式(10), 得
| $ \left. {\begin{array}{*{20}{c}} {D = 0}\\ {A{x_2} + B{y_2} + C\left( {{z_2} - {z_1}} \right) = 0,}\\ {A{x_3} + B{y_3} + C\left( {{z_3} - {z_1}} \right) = 0.} \end{array}} \right\}. $ | (12) |
由于节点偏移量与结构尺度相比是很小值, 容易判断出A、B相对于C的值很小, 故当(x2, y2)和(x3, y3)确定时, 可近似认为C∝1/(z2-z1), C∝1/(z3-z1);考虑到选取原点的一般性, 变量(z1, z2, z3)在表达式中具有轮换对称性, 则有
| $ C \propto \frac{1}{{{{\left( {{z_1} - {z_2}} \right)}^2}{{\left( {{z_2} - {z_3}} \right)}^2}{{\left( {{z_3} - {z_1}} \right)}^2}}}. $ | (13) |
类比式(5), 结合式(11)、(13), 并考虑当θ在零值附近时C与θ的单调性相反, 用(xi1, xi2, xi3)替换(z1, z2, z3), 可令
| $ {\mathit{H}_Q}\left( {{X_Q}} \right) = \frac{{{{\left( {{x_{i1}} - {x_{i2}}} \right)}^2}{{\left( {{x_{i2}} - {x_{i3}}} \right)}^2}{{\left( {{x_{i3}} - {x_{i1}}} \right)}^2}}}{{S_Q^3}}. $ | (14) |
式中:SQ表示团Q所在三角形的面积;当(xi1-xi2)、(xi2-xi3)或(xi3-xi1)的绝对值小于10-1mm时, 取10-1mm.
联立式(3)、(4)、(14), 得反演方程为
| $ \begin{array}{l} G\left( {Y,Z} \right) = \\ \;\;\;\prod\limits_{Q \in C} {\exp \left( { - \frac{{{{\left( {{x_{i1}} - {x_{i2}}} \right)}^2}{{\left( {{x_{i2}} - {x_{i3}}} \right)}^2}{{\left( {{x_{i3}} - {x_{i1}}} \right)}^2}}}{{S_Q^3}}} \right)} . \end{array} $ | (15) |
与双节点团的反演方程求解方法相同, 以xk作为待计算节点, 将式(8)代入式(15), 得二维反演迭代方程
| $ \sum\limits_{Q \in C_1^ * } {\frac{{ - {{\left( {{x_{i2}} - {x_{i3}}} \right)}^2}}}{{S_Q^3}}\left[ {2x_k^3 + {\zeta _b}x_k^3 + {\zeta _c}{x_k} + {\zeta _d}} \right]} = 0. $ | (16) |
式中:
| $ {\xi _b} = - 3\left( {{x_{i2}} + {x_{i3}}} \right). $ | (17) |
| $ {\zeta _c} = \left( {x_{i2}^2 + x_{i3}^2 + 4{x_{i2}}{x_{i3}}} \right). $ | (18) |
| $ {\zeta _d} = - \left( {{x_{i2}}x_{i3}^2 + x_{i2}^2{x_{i3}}} \right). $ | (19) |
C1*为包含节点k的所有三节点团集合, 如图 9中三角形面所示.

|
图 9 二维迭代方程的团集合 Fig. 9 Clique list of 2-D iterative equation |
当三节点团不能遍历整个结构时, 需要采用双节点团补全剩余位置, 因而节点周围可能同时出现双节点团和三节点团.根据公式(3), 反演方程定义为双节点团和三节点团的势函数乘积, 即
| $ \begin{array}{l} G\left( {Y,Z} \right) = \prod\limits_{Q \in C} {\exp \left( { - \frac{{{{\left( {{x_i} - {x_j}} \right)}^2}}}{{l_Q^2}}} \right)} \times \\ \;\;\;\prod\limits_{Q \in C} {\exp \left( { - \frac{{{{\left( {{x_{i1}} - {x_{i2}}} \right)}^2}{{\left( {{x_{i2}} - {x_{i3}}} \right)}^2}{{\left( {{x_{i3}} - {x_{i1}}} \right)}^2}}}{{S_Q^3}}} \right)} . \end{array} $ | (20) |
从而得到混合迭代方程为
| $ \begin{array}{l} \sum\limits_{Q \in {C^ * }} {\frac{{ - {{\left( {{x_{i2}} - {x_{i3}}} \right)}^2}}}{{S_Q^3}}\left[ {2x_k^3 + {\zeta _b}x_k^3 + {\zeta _c}{x_k} + {\zeta _d}} \right]} - \\ \;\;\;\;2\sum\limits_{Q' \in {C^ * }} {\frac{{\left( {{x_k} - {x_j}} \right)}}{{l_{Q'}^3}}} = 0. \end{array} $ | (21) |
式中:ζb、ζc、ζd见公式(17~19).
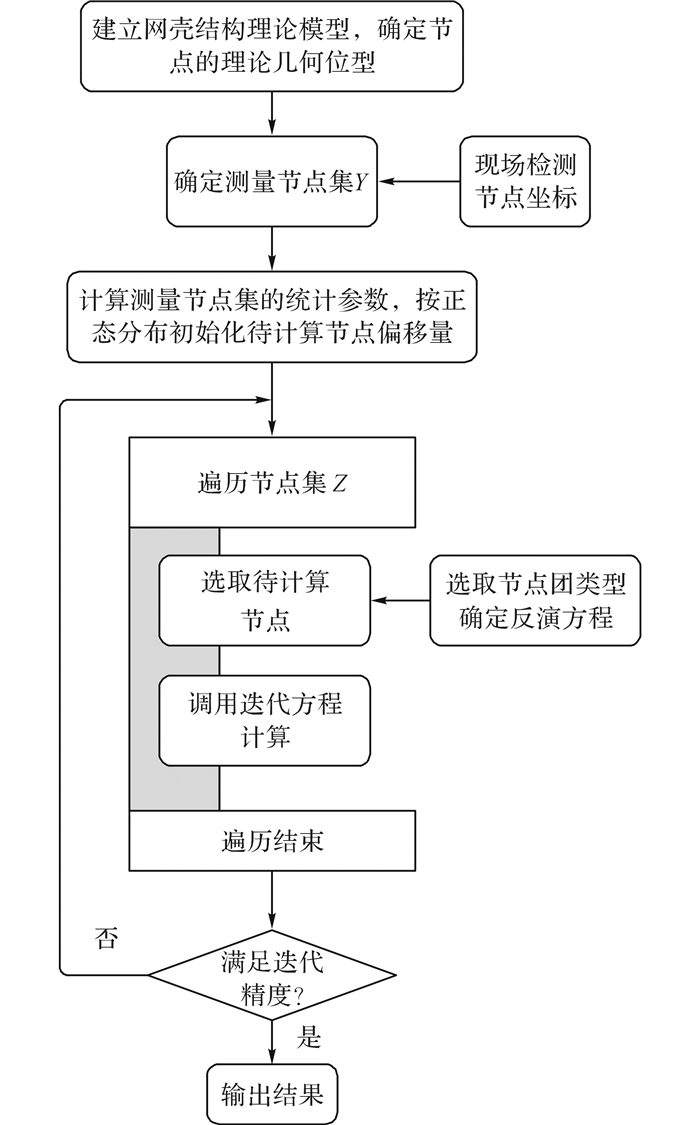
如图 10所示为一个既有网壳结构的节点几何缺陷计算流程.
|
图 10 既有网壳结构几何缺陷反演计算流程图 Fig. 10 Geometric imperfection inversion calculation flow chart of reticulated structures |
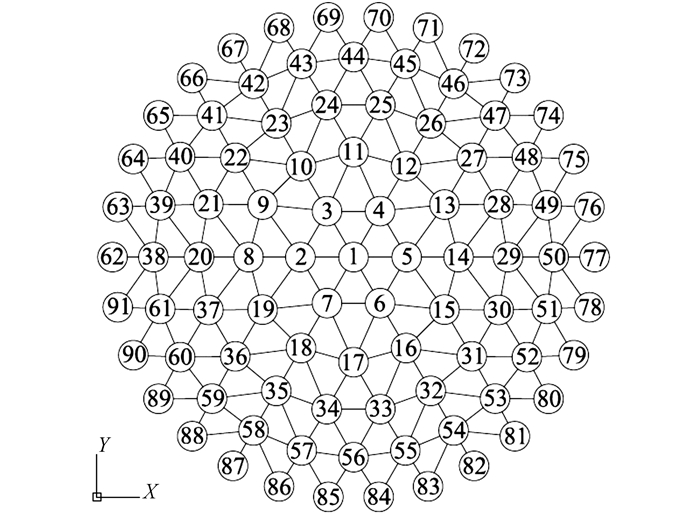
试验设计了一个5环K6型单层球面网壳结构模型(如图 11所示), 节点数量为91(含网壳周边布置的30个固定支座), 编号如图 12所示.模型跨度为3.6 m, 矢跨比为1/4;杆件采用ϕ6×1热轧无缝钢管;节点采用半径70 mm焊接球, 球节点平均质量11 kg;材料均为Q235钢.

|
图 11 试验单层球面网壳模型 Fig. 11 Experimental single layer reticulated shell model |
|
图 12 网壳节点编号图 Fig. 12 Node numbering of reticulated shell model |
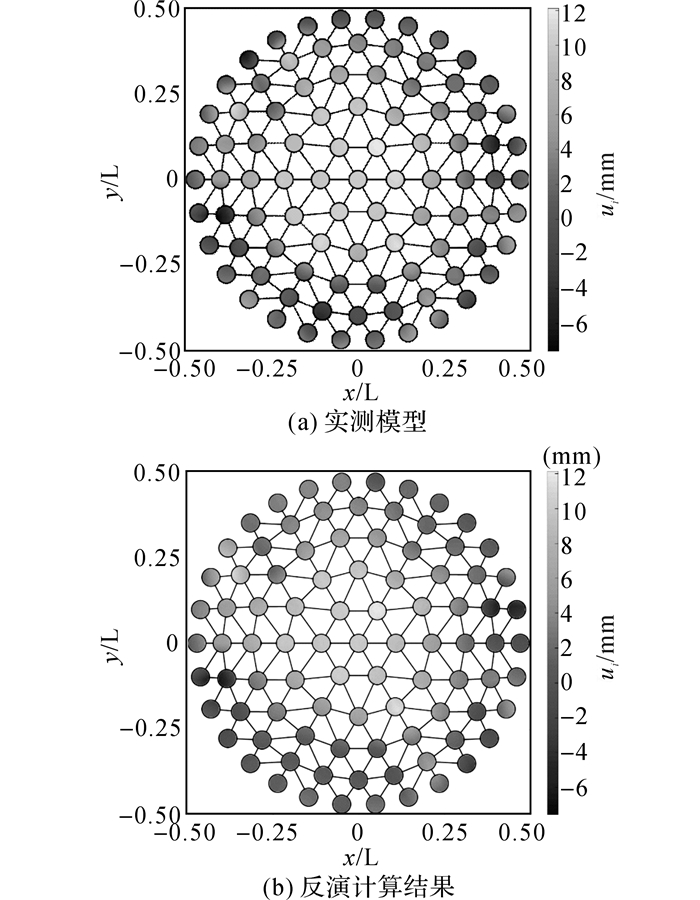
试验对该网壳结构成型后的全部节点几何位形进行测量, 并根据理论模型的几何位形计算节点偏移值.由于球节点体积较大, 试验分别测量了各球节点表面4个随机点的坐标, 通过最小二乘法拟合球心坐标, 以提高节点偏移量测量的准确度.测量结果按上述2.2节假定二换算成几何缺陷的径向偏移值, 其分布如图 13(a)所示.
|
图 13 网壳几何缺陷分布云图 Fig. 13 Nephogram of geometric imperfection of experimental mode |
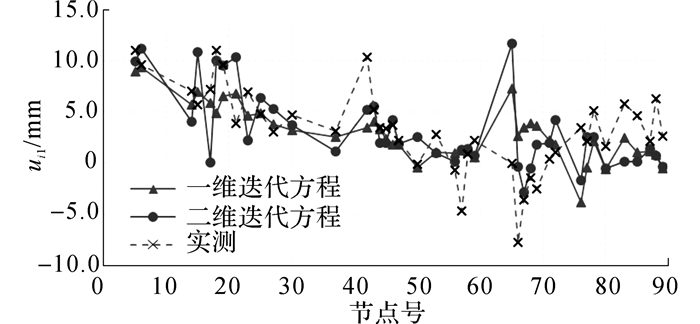
随机选取50个节点(占总比约55%)的径向偏移值ui1作为实测样本集Y(见表 1), 其余节点偏移值作为计算节点集Z;根据已知样本集的均值和方差, 利用Box-Muller算法[22]初始化节点集Z的几何缺陷值;采用C#编制自动化分析计算程序, 分别利用式(9)和式(21)计算节点集Z的几何缺陷值, 结果如图 14中所示.需注意当采用三节点团时, 对图 12中的62、67、72、77、82、87号等孤立节点仍采用双节点团.
|
图 14 节点集Z的几何缺陷计算值(标记点均为计算节点) Fig. 14 Computational geometric imperfection curves of node set Z |
| 表 1 测量样本集Y的节点几何缺陷值 Table 1 Nodal geometric imperfection values of sample set Y |
从图 14中可以看出, 节点几何缺陷的迭代计算结果与实测值在趋势上总体较为接近.网壳跨中位置(节点号1~61)的计算结果与实测值基本保持一致, 支座位置(节点号62~91)的计算值略有偏差, 其原因是支座节点处于结构边缘, 与其他节点的联系较少, 因此, 对支座节点进行反演计算时的信息量不足, 降低了计算结果的精度.结构中65号节点处(图 12左上角支座附近)的计算值出现了异常.根据马儿可夫随机场的条件独立性推论, 65号节点仅与40、41号节点相关联, 与其余节点均相互独立.而由表 1可知40号节点处的测量值为11 mm, 与周围偏差较大, 可能为单点漂移值.因此, 65号节点受其影响而产生较大偏差, 计算结果可识别节点偏移实测值的可能异常区域.
将反演结果绘制成缺陷分布云图, 如图 13(b)所示.通过对比图 13(a)和13(b)的缺陷分布模式, 可以得出两者的缺陷分布差异、缺陷值过渡差异均很小.由于反演方法是建立在假定三的条件下, 即节点几何缺陷具有相关性, 且满足局部马尔可夫性的条件.因此, 对比的结果间接的验证了假定三的合理性.
为衡量几何缺陷计算曲线与实测曲线的相似度, 引入Pearson相关系数(PCC), 即
| $ {\rm{PCC}} = \frac{{N\sum {XY} - \sum X \sum Y }}{{\sqrt {N\sum {{X^2}} - {{\left( {\sum X } \right)}^2}} \sqrt {N\sum {{Y^2}} - {{\left( {\sum Y } \right)}^2}} }}. $ | (22) |
式中:N为节点总数,X为几何缺陷的计算值集合,Y为几何缺陷的实测值集合.
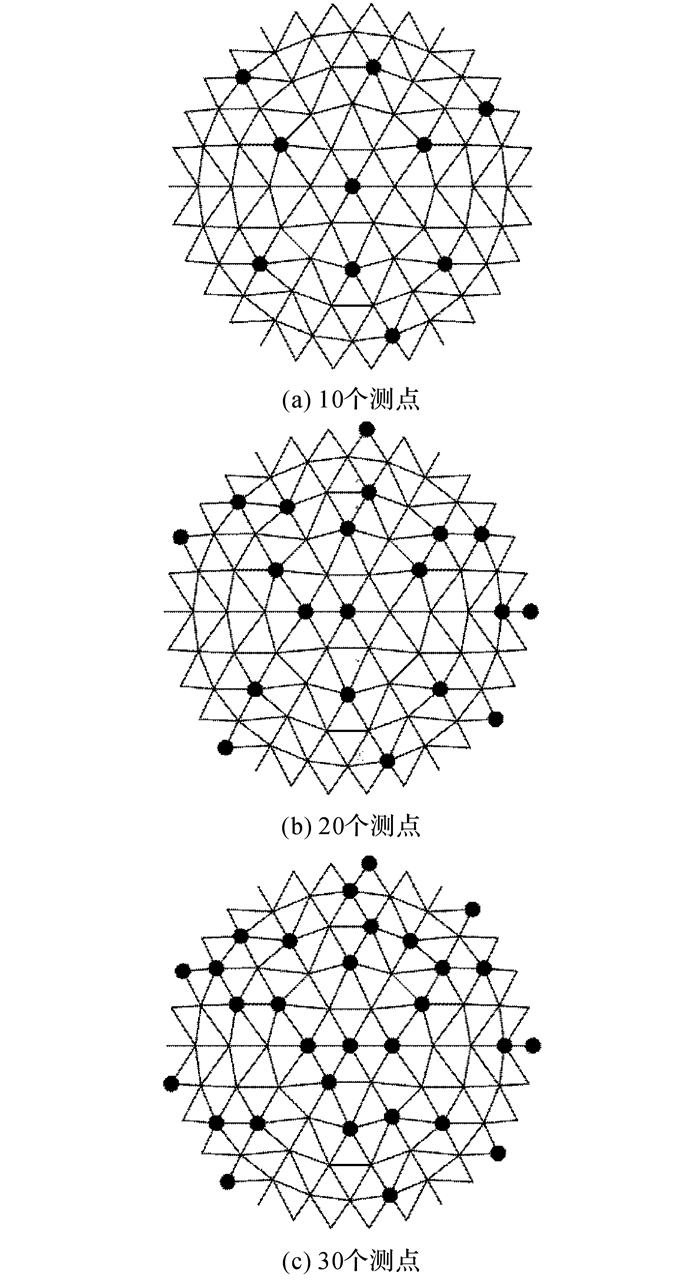
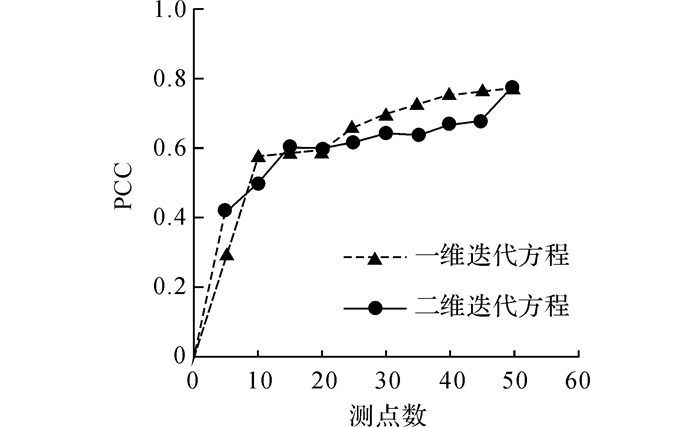
当测点数为50时, 将计算值和实测值代入公式(22), 分析得一维迭代方程计算结果的PCC值为0.769, 二维迭代方程计算结果的PCC值为0.772, 说明此时2种计算结果与实测值曲线相似度相近.为了考虑测点数量变化时计算与实测相似度的变化情况, 将测点数从5逐级递增至50, 节选测点布置图如图 15所示.
|
图 15 测点分布图(节选) Fig. 15 Distribution of measuring points (excerpt) |
当测点数变化时, 计算结果的PCC值如图 16所示.从图 16中可以看出, 当测点数小于15时, PCC值随测点数增加迅速增至0.6, 当测点数大于15时, PCC值增大较为缓慢.因此, 对于该网壳结构, 当测点数量达到15/91×100%=16.5%时, 可由最小的测点数量得到满意的计算相似度.
|
图 16 计算几何缺陷的PCC趋势 Fig. 16 PCC trends of computational geometric imperfection |
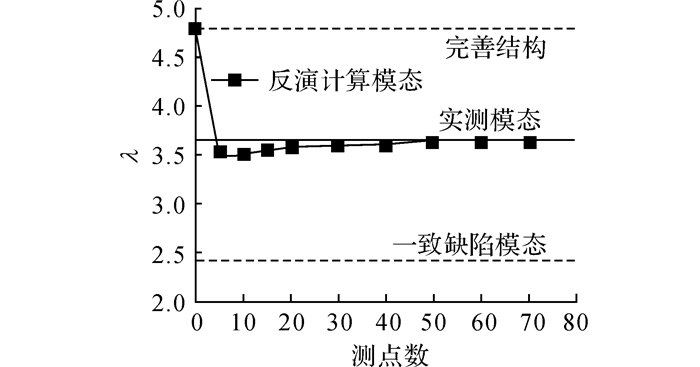
为进一步分析反演方法计算的几何偏差对网壳结构的整体稳定承载力的影响, 本文对试验模型进行了完善结构模态、实测模态、传统一致缺陷模态及不同测点数对应的反演计算模态下的整体稳定承载力分析, 其结果如图 17所示.其中反演计算模态的极限荷载因子λ取相同测点数中多组随机测点下的最小值.
|
图 17 网壳试验模型的极限荷载 Fig. 17 Ultimate loads of sample shell |
从图 17中可以得出, 当测点数较少时, 网壳的稳定承载力略低于实测结构, 当测点数大于20后, 其稳定承载力与实测结构基本相当.该计算结果说明反演方法所得出的网壳稳定承载力与真实值接近, 且略有保守, 这对网壳结构的承载力评估是略偏于安全的.
4 结论本文将马尔可夫随机场及其节点团理论引入既有网壳结构几何缺陷分布推算中, 提出在已知部分抽样节点几何缺陷情况下推演既有网壳结构几何缺陷分布模态的算法.不同于过去单纯利用既有网壳几何缺陷数字特征而随机生成缺陷的方法, 本文通过研究网壳节点在局部马尔可夫性假定下的几何拓扑关系, 提出双节点团和三节点团的拓扑概念及其几何势函数, 从而推导了节点几何缺陷的反演迭代方程.为验证反演迭代方程的可行性及适用性, 建立了K6单层球面网壳试验模型, 通过对比分析节点几何位形的反演计算结果与实测值, 得到以下研究结论:
(1) 通过试验分析表明, 当测点数量占总比约55%时, 反演迭代方程的计算结果与实测值的Pearson相关系数(PCC)为0.77, 计算值与实测值具有很高的相似度.
(2) 当实测值出现漂移异常时, 反演迭代方程的计算结果可识别节点偏移实测值的异常区域.
(3) 通过将测点数量逐级递增并计算对应的PCC值, 得出当测点数量递增至16.5%的过程中, PCC值迅速达到0.6;而后当测点数量继续增加时, PCC值增加缓慢, 说明测点数量占总比16.5%时, 可由最小的测点数量得到满意的计算相似度.
(4) 依据反演结果计算的网壳稳定承载力与真实结构相当, 略偏安全.
算例分析表明, 本文提出的缺陷分布反演算法能较好地拟合既有网壳结构的节点几何缺陷模态.从节点团的拓扑关系可以得出, 本文提出的节点几何缺陷反演算法可以适用于缺陷敏感型的具有任意曲率的单层网壳结构.而对于具有双层或多层节点的网壳或拱架, 还需要在后续研究中对算法做出一些修正和拓展, 从而应对更为复杂的网壳结构形式.
| [1] |
BORRI C, SPINELLI P. Buckling and post-buckling behaviour of single layer reticulated shells affected by random imperfections[J]. Computers & Structures, 1988, 30(4): 937-943. |
| [2] |
罗永峰. 建筑钢结构稳定理论与应用[M]. 北京: 人民交通出版社, 2010, 48-54.
|
| [3] |
GIONCU V. Buckling of reticulated shells:State-of-the-art[J]. International Journal of Space Structures, 1995, 10(1): 1-46. DOI:10.1177/026635119501000101 |
| [4] |
YAMADA S, TAKEUCHI A, TADA Y, et al. Imperfection-sensitive overall buckling of single-layer lattice domes[J]. Journal of Engineering Mechanics, 2001, 127(4): 382-386. DOI:10.1061/(ASCE)0733-9399(2001)127:4(382) |
| [5] |
ELISHAKOFF I. Uncertain buckling:its past, present and future[J]. International Journal of Solids & Structures, 2000, 37(46): 6869-6889. |
| [6] |
FAN F, CAO Z, SHEN S. Elasto-plastic stability of single-layer reticulated shells[J]. Thin-Walled Structures, 2010, 48(10): 827-836. |
| [7] |
FAN F, YAN J, CAO Z. Stability of reticulated shells considering member buckling[J]. Journal of Constructional Steel Research, 2012, 77(10): 32-42. |
| [8] |
FAN F, YAN J, CAO Z. Elasto-plastic stability of single-layer reticulated domes with initial curvature of members[J]. Thin-Walled Structures, 2012, 48(10/11): 827-836. |
| [9] |
BRUNO L, SASSONE M, VENUTI F. Effects of the Equivalent geometric nodal Imperfections on the stability of single layer grid shells[J]. Engineering Structures, 2016, 112: 184-199. DOI:10.1016/j.engstruct.2016.01.017 |
| [10] |
CHEN G, ZHANG H, RASMUSSEN K J R, et al. Modeling geometric imperfections for reticulated shell structures using random field theory[J]. Engineering Structures, 2016, 126: 481-489. DOI:10.1016/j.engstruct.2016.08.008 |
| [11] |
PEEK R. Worst shapes of imperfections for space trusses with multiple global and local buckling modes[J]. International Journal of Solids & Structures, 1993, 30(16): 2243-2260. |
| [12] |
CHEN X, SHEN S Z. Complete load-deflection response and initial imperfection analysis of single-layer lattice dome[J]. International Journal of Space Structures, 1993, 8(4): 271-278. DOI:10.1177/026635119300800405 |
| [13] |
蔡健, 贺盛, 姜正荣, 等. 单层网壳结构稳定性分析方法研究[J]. 工程力学, 2015, 32(7): 103-110. CAI Jian, HE Sheng, JIANG Zheng-Rong, et al. Investigation on stability analysis method of single layer latticed shells[J]. Engineering Mechanics, 2015, 32(7): 103-110. DOI:10.6052/j.issn.1000-4750.2013.12.1191 |
| [14] |
刘慧娟, 罗永峰, 杨绿峰, 等. 单层网壳结构稳定性分析的随机缺陷模态迭加法[J]. 同济大学学报:自然科学版, 2012, 40(9): 1294-1299. LIU Hui-juan, LUO Yong-feng, YANG Lv-feng, et al. Stochastic imperfection mode superposition method for stability analysis of single-layer lattice domes[J]. Journal of Tongji University:Natural Science, 2012, 40(9): 1294-1299. |
| [15] |
KIYOHIRO I, KAZUO M. Statistics of normally distributed initial imperfections[J]. International Journal of Solids & Structures, 1993, 30(18): 2445-2467. |
| [16] |
罗永峰. 国家标准《高耸与复杂钢结构检测与鉴定技术标准》编制简介[J]. 钢结构, 2014, 29(4): 44-49. LUO Yong-feng. Brief introduction of composition of technical standard for inspection and appraisal of high-rising and complex steel structures[J]. Steel Construction, 2014, 29(4): 44-49. |
| [17] |
罗立胜, 罗永峰, 郭小农. 考虑节点几何位置偏差的既有网壳结构稳定计算方法[J]. 湖南大学学报:自科版, 2013, 40(3): 26-30. LUO Li-Sheng, LUO Yong-Feng, GUO Xiao-Nong. Overall stability of existing reticulated shells considering the effect of geometric position deviation of joints[J]. Journal of Hunan University:Natural Sciences, 2013, 40(3): 26-30. |
| [18] |
KOLLER D, Friedman N. Probabilistic graphical models:principles and techniques[M]. Massachusetts: MIT press, 2009, 3-5.
|
| [19] |
GEMAN S, GEMAN D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images[J]. IEEE Transactions on Pattern Analysis and Machine intelligence, 1984(6): 721-741. |
| [20] |
FRANK O, STRAUSS D, Markow graphs. Markow graphs[J]. Journal of the American Statistical Association, 1986, 81(395): 832-842. DOI:10.1080/01621459.1986.10478342 |
| [21] |
JGJ 7-2010. 空间网格结构技术规程[S]. 北京: 中国建筑工业出版社, 2011.
|
| [22] |
BOX G E P, MULLER M E. A note on the generation of random normal deviates[J]. Annals of Mathematical Statistics, 1958, 29(2): 610-611. DOI:10.1214/aoms/1177706645 |
| [27] |
BOX G E P, MULLER M E. A note on the generation of random normal deviates[J]. Annals of Mathematical Statistics, 1958, 29(2): 610-611. https://www.informs.org/Explore/History-of-O.R.-Excellence/Biographical-Profiles/Box-George-E.-P
|



