2. 浙江水利水电学院 建筑工程学院, 浙江 杭州 310058
2. College of Civil Engineering and Architecture, Zhejiang University of Water Resources and Electric Power, Hangzhou 310058, China
考虑风向相关性的多风向极值风速估计是合理计算结构风荷载的重要基础[1].目前工程界对于风向的处理, 是把所有风向最大风速加到结构各个方向进行最不利荷载组合验算[2].全涌等[3-4]系统地总结了美、英、澳、日等国相关规范对风向效应的规定和已有的实用极值风速计算方法, 包括Davenport方法、Holmes方法、Cook方法以及Simiu方法, 并针对Cook方法提出改进.联合概率分布函数能够用于定量描述多风向相关性, 但构造过程一般较为复杂且需要大量的样本数据.通过Copula函数可以较为方便地建立多变量联合分布概率模型, Copula函数已在金融等领域获得了大量的应用[5-6], 已经在风工程中得到了初步的应用[7-10].Huang等[7-8]提出基于Copula函数的高层建筑动力风荷载相关性组合方法.Luo等[9]采用多元极值理论、Copula理论和Nataf变换理论, 研究建立屋盖表面极值风压的空间相关结构, 并且考察了极值风压相关性对屋盖结构抗风易损性分析的影响.Zhang等[10-11]应用Gaussian Copula和Gumbel Copula函数来建立多风向极值风速的联合分布并进行概率风荷载效应评估.在实际应用中, 为保证联合分布模型的准确性, 应选择最优Copula函数来构造变量的联合分布模型.在备选Copula函数中, 同时满足以下2个条件的Copula函数可称为最优Copula函数[12]:1)能够准确描述各变量的边缘分布特性;2)能够准确描述变量间的相关关系.
本文采用核密度-广义帕累托混合模型(kernel density-generalized pareto model, KP模型)描述风速母体样本的分布, 通过提高极值风速边缘分布模型的准确性获得更为可靠的多风向极值风速联合分布.讨论不同Copula函数在多风向极值风速的联合分布模型构造中的适用性, 并用赤池信息量(akaike information criterion, AIC)准则进行拟合优度评价.以杭州地区的日最大风速数据和相应的风向记录为风速风向样本, 采用最优的联合分布模型估计得到不同重现期下各风向角的极值风速, 并与对应的不考虑风向相关性的全风向极值风速进行了对比.
1 极值风速边缘分布模拟:Up-crossings法设NV+(v)表示风速随机过程V(t)穿越某给定风速阈值v的年均穿越次数, 其表达式可以根据Rice方程[13-14]给出, 即
| $ N_V^ + \left( v \right) = \int_0^\infty {\dot v{f_{V\dot V}}\left( {v,\dot v} \right){\rm{d}}\dot v} . $ | (1) |
式中:
当风速阈值v足够高, 则V(t)穿越v的相邻事件可以认为相互独立.基于泊松假设, 年最大风速的概率分布函数FAM(v)可表示为
| $ {F_{{\rm{AM}}}}\left( v \right) = \exp \left[ { - N_V^ + \left( v \right)} \right]. $ | (2) |
值得一提的是, Up-crossings法估计极值风速的准确性主要受风速母体分布模型(如Weibull分布)的尾部拟合效果影响.但是, 采用单Weibull分布模拟风速母体分布的尾部往往效果欠佳.Wen[15]、Isyumov等[16]通过比较不同的估计方法得出, 采用单Weibull分布作为风速母体分布来估计极值风速难以取得令人信服的结果.
根据乘法定理, 可以将NV+(v)改写为
| $ N_V^ + \left( v \right) = N_{{V_0}}^ + P\left( {V > v\left| {V > {v_0}} \right.} \right). $ | (3) |
式中:P为概率,N+V0为风速随机过程V(t)穿越尾部阈值v0的年均穿越次数.这样风速母体分布可以采用KP混合模型, 即:当v≤v0时, 采用核密度法估计风速母体分布;而当v>v0时, 则采用广义Pareto分布(GPD)来模拟风速母体的尾部分布, 具体表达式为
| $ \begin{array}{*{20}{c}} {{F_{{\rm{GPD}}}}\left( v \right) = P\left( {V \le v\left| {V > {v_0}} \right.} \right) = \frac{{{F_V}\left( v \right) - {F_V}\left( {{v_0}} \right)}}{{1 - {F_V}\left( {{v_0}} \right)}} = }\\ {\left. \begin{array}{l} 1 - {\left[ {1 + a\left( {\frac{{v - {v_0}}}{b}} \right)} \right]^{ - 1/a}},\;\;\;a \ne 0;\\ 1 - \exp \left[ {\left( {\frac{{v - {v_0}}}{b}} \right)} \right],\;\;\;\;\;\;\;\;\;a = 0. \end{array} \right\}} \end{array} $ | (4) |
式中:FV(·)为风速V(t)的母体分布, a和b分别为形状和比例参数, 可以采用极大似然法来估计得到.
将式(4)、(3)代入式(2), 年最大风速的概率分布函数FAM(v)可表示为
| $ {F_{{\rm{AM}}}}\left( v \right) = \exp \left[ { - N_{{V_0}}^ + \left( {1 - {F_{{\rm{GPD}}}}\left( v \right)} \right)} \right]. $ | (5) |
此外, Naess等[17-18]提出了ACER法估计极值风速, 年最大风速概率分布可表达如下:
| $ {F_M}\left( v \right) \approx \exp \left[ { - \left( {n - k + 1} \right){{\hat \varepsilon }_k}\left( v \right)} \right]. $ | (6) |
式中:n为风速观测样本年均总量, k为条件穿越参数.
构造多风向极值风速的联合概率分布函数是考虑风向相关性的有效方法.本文出现的风向相关性均是指不同风向的极值风速相关性.大部分传统的多维联合分布函数是一维分布函数的简单延伸, 要求变量服从同样的边缘分布, 而通过Copula函数则可以将任意形式的边缘分布连接起来, 生成一个有效的多维分布.设N维极值风速变量Vd1, Vd2, …, VdN分别表示第1, 2, …, N个方向的极值风速, 则考虑风向相关性的联合分布函数可表示为
| $ F\left( {{v_{{d_1}}}, \cdots ,{v_{{d_N}}}} \right) = P\left( {{V_{{d_1}}} < {v_{{d_1}}}, \cdots ,{V_{{d_N}}} < {v_{{d_N}}}} \right). $ | (7) |
式中:F(vd1, …, vdN)为Vd1, Vd2, …, VdN的联合分布函数.Sklar[6]指出, 一个多维随机变量的联合分布可分解为N个边缘分布和一个Copula函数, 这个Copula函数描述了变量之间的相关性.根据Sklar定理, 设FVd1(vd1), …, FVdN(vdN)为N维极值风速变量Vd1, Vd2, …, VdN的边缘分布函数, 那么存在一个多维Copula函数C(u1, u2, …, uN), ui=FVdi(vdi), i=1, 2, …, N, 满足
| $ F\left( {{v_{{d_1}}}, \cdots ,{v_{{d_N}}}} \right) = C\left( {{u_1},{u_2}, \cdots ,{u_N}} \right). $ | (8) |
假设N维极值风速变量两两之间的相关结构均服从同一类Copula函数, 本文直接采用多维Copula函数来考虑风向相关性.常用的多维Copula函数表达式和参数取值范围如表 1所示, 其中Gumbel Copula既属于阿基米德Copula族又属于极值Copula族;Frank Copula和Clayton Copula属于阿基米德Copula族;Gaussian Copula和Student t Copula的函数结构类似, 属于椭圆Copula族[5].表 1中, Φθ为相关系数矩阵为θ的N维标准正态分布函数, Φ-1为标准正态分布函数Φ的逆函数;Tθ, λ表示相关系数矩阵为θ、自由度为λ的N维标准t分布函数, T-1为标准t分布函数T的逆函数.对于Gumbel Copula、Frank Copula和Clayton Copula, 变量间的相关性由单一参数θ表达.对于Gaussian Copula和Student t Copula, 变量间的相关性由N×N阶对称正定矩阵θ表达.由于相关矩阵θ的维数与变量的维数一致, 能够同时表达任意两变量间的相关关系, 本文中采用Gaussian Copula和Student t Copula直接应用到三维及以上随机变量相关性分析中[5].Aas等[19]在二维Copula函数基础上引入了Pair-Copula分解法来构造多维随机变量相关结构.相比直接应用多维Copula函数, 它能够更为合理地考虑变量间的局部相关结构, 如可以采用Pair-Copula建立高维的阿基米德型Copula模型.
| 表 1 常用的多维Copula函数 Table 1 Common multi-dimensional Copula functions |
为保证多风向极值风速联合分布构造的准确性, 应选择最优Copula函数来构造极值风速的联合分布模型.本文采用的最优Copula评价准则为AIC准则[12], 表达式为
| $ {\rm{AIC}} = - 2 \times \ln \hat L + 2q. $ | (9) |
式中:
Cook[4, 20]通过分析英国地区的极值风速数据, 认为各风向极值风速随超越概率的变化基本遵循同一比例, 即极值风速玫瑰图随超越概率的变化或放大或缩小, 但基本形状不变.基于这一假设, 将多元极值问题简化为一元极值问题来求解.假设各个风向角上的超越概率p相等, 则考虑风向相关性的R年重现期下各风向极值风速vd1, …, vdN可通过下式计算得到唯一的解.
| $ \left. \begin{array}{l} F\left( {{v_{{d_1}}}, \cdots ,{v_{{d_N}}}} \right) = C\left( {{u_1},{u_2}, \cdots ,{u_N}} \right) = 1 - 1/R;\\ {u_1} = {F_{{V_{{d_1}}}}}\left( {{v_{{d_1}}}} \right) = 1 - p;\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {u_N} = {F_{{V_{{d_N}}}}}\left( {{v_{{d_N}}}} \right) = 1 - p. \end{array} \right\} $ | (10) |
如果假设各风向极值风速一致, 则可通过下式计算得到考虑风向相关性的全风向极值风速vd.
| $ \begin{array}{l} F\left( {{v_d}, \cdots ,{v_d}} \right) = C\left( {{F_{{V_{{d_1}}}}}\left( {{v_d}} \right), \cdots ,{F_{{V_{{d_N}}}}}\left( {{v_d}} \right)} \right) = \\ \;\;\;\;\;\;1 - 1/R. \end{array} $ | (11) |
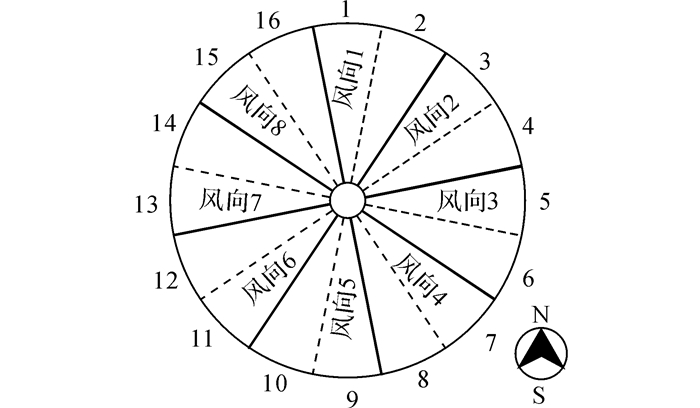
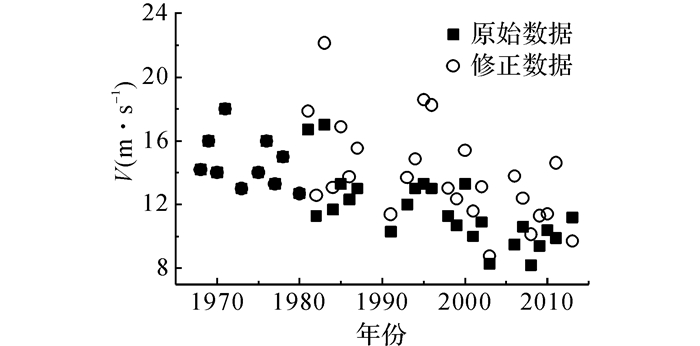
本文以杭州地区1968年1月1日至2014年12月31日的日最大风速数据(10 min平均时距)和相应的风向记录(共16个方位)为风速风向样本, 数据来源于中国气象数据网(http://data.cma.cn/).16个风向方位如图 1所示.利用气象台站获得的日极大风速记录(即3 s平均阵风风速)修正了1980年之后受城市化影响的非标准地貌风速样本[21], 经过地貌修正后的年最大风速序列和原始风速序列如图 2所示.为了进一步提高每个风向下的风速样本数量, 本文将16个风向方位重新归类为8个风向进行极值风速概率分布模拟, 归类后的8个风向如图 1所示.
|
图 1 风向示意图 Fig. 1 Diagram of incident wind directions |
|
图 2 年最大风速序列 Fig. 2 Annual maximum wind speed series |
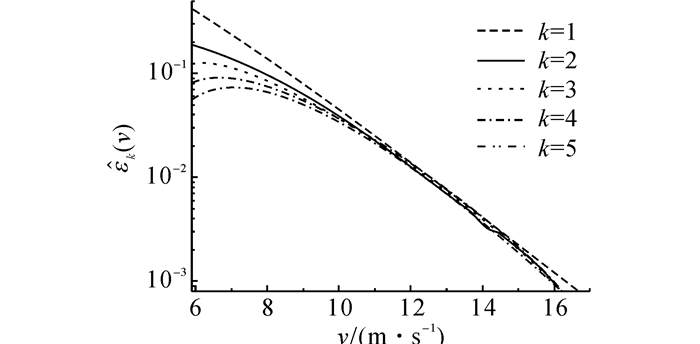
在采用Up-crossings法估计极值风速之前, 需要检验日最大风速序列穿越风速阈值v的相邻穿越事件的独立性.如图 3所示为不同条件参数下平均条件穿越率
|
图 3
不同条件参数下平均条件穿越率 |
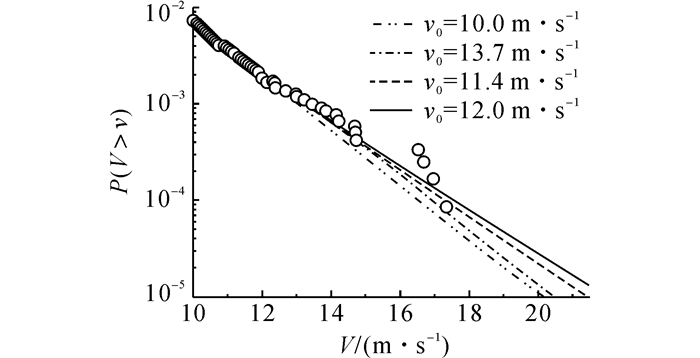
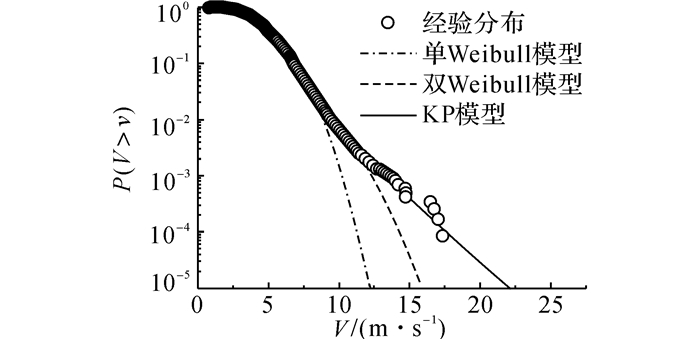
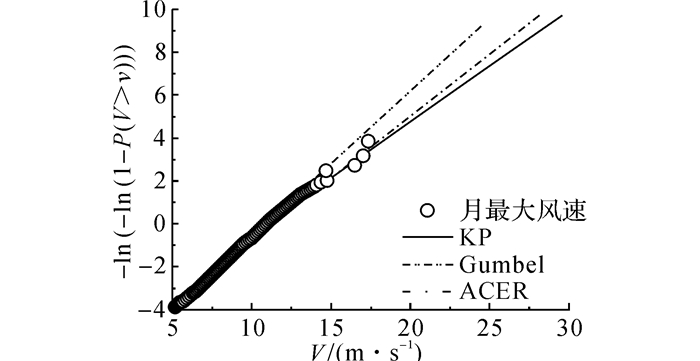
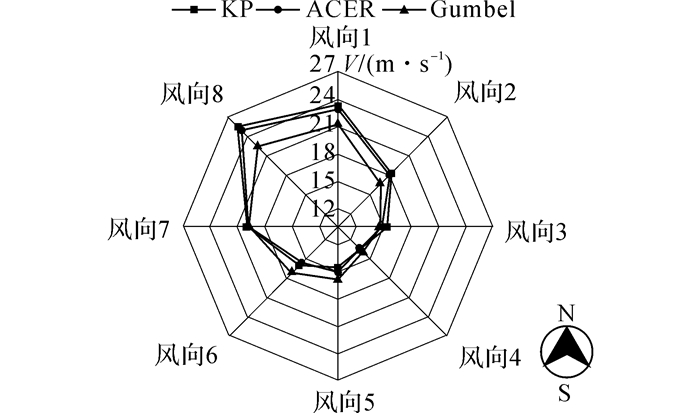
分别采用单Weibull、双Weibull以及形状参数a=0时的KP模型来模拟8个风向角以及不区分风向的全风向风速母体分布的尾部.其中, 阈值的选取影响KP模型的尾部拟合效果.如图 4所示为采用不同备选阈值的KP模型拟合得到的风向2下风速母体尾部分布曲线.从图中可以看出, 当v0=12.0 m/s时, 采用KP模型拟合得到的尾部分布曲线最接近经验分布.其余风向下的KP模型参数如表 2所示.如图 5所示为采用不同模型拟合得到的风向2下风速母体尾部分布曲线.由图可知, 相比于单Weibull、双Weibull模型, KP模型可以较准确地模拟风速母体的尾部分布.如图 6所示给出了风向2下采用KP模型作为风速母体分布的Up-crossings法估计得到的年最大风速分布曲线, 同时给出了采用ACER方法以及以月极值风速作为极值样本并采用Gumbel分布模拟得到的年最大风速分布曲线作为比较.可以发现, 风向2下风速样本的极值分布与Gumbel模型存在一定的偏差.若继续采用Gumbel分布模型估计长重现期下的极值风速容易产生较大的误差.而采用KP模型作为风速母体分布的Up-crossings法与ACER法则可准确地基于风速实测样本来模拟风速的极值概率分布.如表 3所示分别给出了采用上述3种方法估计得到的50/100年重现期下8个风向以及全风向的极值风速估计值.通过比较表 3中不同风向下的极值风速可以发现, 杭州地区的最大风速主要集中于风向8.如图 7所示为采用3种方法估计得到的50年一遇8个风向的极值风速对比.由图 7可知, 采用KP模型的Up-crossings方法与采用ACER方法计算得到的极值风速估计值较为接近.在除风向4~6外的其余风向下, 采用Gumbel分布均给出了偏于风险的风速估计值.
|
图 4 风向2下风速母体尾部分布(KP模型) Fig. 4 Parent tail distributions of wind speed in Direction 2 (KP model) |
|
图 5 风向2下风速母体尾部分布 Fig. 5 Parent tail distributions of wind speed in Direction 2 |
|
图 6 风向2下年最大风速分布 Fig. 6 Distributions of annual maximum wind speed in Direction 2 |
|
图 7 50年一遇各风向极值风速对比(不考虑风向相关性) Fig. 7 Comparison between directional wind speed estimates with MRI of 50 years (take no account of correlation of wind direction) |
| 表 2 多风向及全风向风速母体KP模型参数估计 Table 2 Parameters of KP model for parent distribution of directional and non-directional wind speeds |
| 表 3 50/100年重现期下多风向及全风向极值风速(不考虑风向相关性) Table 3 Extreme wind speeds with MRI of 50/100 years for directional and non-directional wind speeds |
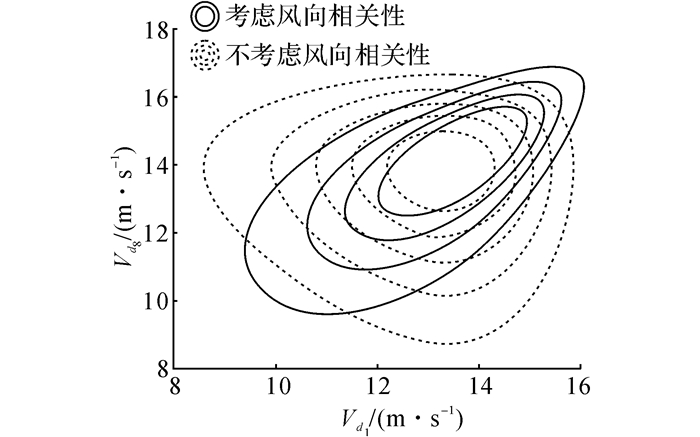
以采用KP模型的Up-crossings法估计得到的年最大风速分布作为边缘分布, 在表 1中选择最优Copula函数来构造多风向极值风速的联合分布.采用极大似然法估计多维Copula函数的参数, 并采用AIC准则选择最优Copula, 结果如表 4所示.由于年极值风速样本量不足, 表中相关系数和相关矩阵是基于各个风向下的月极值风速样本估计得到.由表可知, t Copula为最优Copula函数.表 5分别列出了Gaussian Copula和t Copula的相关矩阵θG, θt中相邻风向的相关系数.Grigoriu[22]通过研究指出, 当2个方向风速的相关系数不超过0.7时, 即可忽略这2个方向风速间的相关性.由表 5可知杭州地区极值风速在相邻风向5-6和8-1下存在显著的相关性.其中风向8-1下的极值风速联合概率密度等值线如图 8所示, 将等值线近似看作一簇椭圆, 考虑风向相关性的等值线椭圆长轴与水平轴的夹角约为45°, 表明风向8和风向1下极值风速呈正相关关系.而不考虑风向相关性的等值线椭圆长轴与水平轴近乎平行.因此, 考虑和不考虑风向相关性, 联合概率密度函数呈现出明显的差异.
|
图 8 联合概率密度等值线 Fig. 8 Contours of JPDF |
| 表 4 多维Copula函数的拟合参数及AIC Table 4 Parameters and AIC of multi-dimensional Copulas |
| 表 5 相关矩阵中相邻风向的相关系数 Table 5 Correlation coefficient for adjacent directions incorrelation martix |
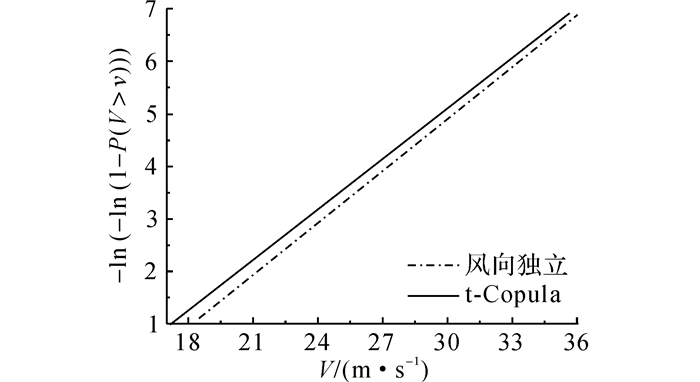
如图 9所示给出了通过式(11)采用t Copula函数计算得到的全风向年最大风速分布曲线, 同时给出了假设各风向相互独立的年最大风速分布曲线作为比较.随着重现期增大, 考虑风向相关性的年最大分布曲线与假设风向之间相互独立的分布曲线逐渐重合, 表明随着风速重现期增大, 不同风向之间极值风速的相关性在逐渐减弱.
|
图 9 全风向年最大风速分布(考虑风向相关性) Fig. 9 Distribution of non-directional annual maximum wind speed (take account of correlation of wind direction) |
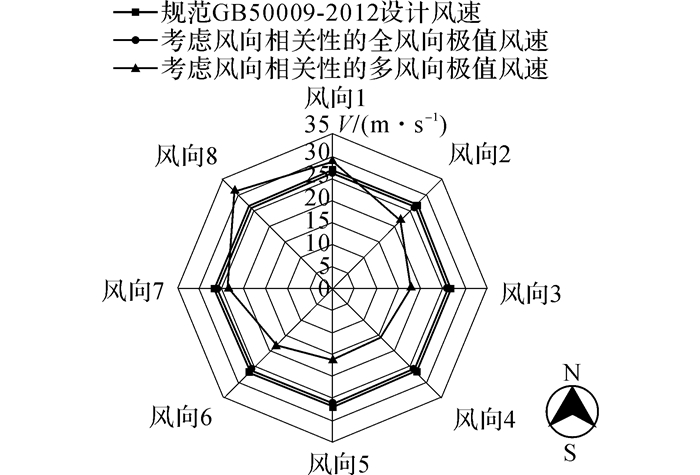
通过式(10)计算得到了不同重现期下8个风向的极值风速.对应50和100年的重现期, 8个风向极值风速的超越概率p分别为0.316%和0.158%.表 6列出了考虑风向相关性的50/100年重现期下8个风向极值风速以及不区分风向的全风向极值风速估计值, 同时给出了现行荷载规范[20]对应重现期下的设计风速作为比较.对比表 3和6的极值风速估计值可以发现, 不考虑风向相关性的极值风速估计结果偏于风险.其中, 考虑风向相关性, 风向8下50年一遇极值风速估计值为31.4 m/s(如表 6所示), 而不考虑风向相关性, 风向8下采用KP模型估计得到的对应极值风速估计值为25.6 m/s(如表 3所示).如图 10所示为考虑风向相关性的50年一遇8个风向及全风向极值风速估计值与规范设计风速的对比.从图中可以发现, 考虑风向相关性的全风向极值风速估计结果与现行荷载规范给出的设计风速较为接近.全风向极值风速估计值和规范对应的设计风速都明显小于杭州地区风向1和风向8下的极值风速估计值.由于风向8是杭州地区最大风速出现的方向, 全风向极值风速估计结果偏于风险.
|
图 10 考虑风向相关性的50年一遇极值风速与规范设计风速的对比 Fig. 10 Comparison between extreme wind speed with MRI of 50 years taking account of correlation of wind direction and design wind speed in load code |
| 表 6 50/100年重现期下多风向及全风向极值风速(考虑风向相关性) Table 6 Extreme wind speeds with MRI of 50/100 years for directional and non-directional wind speeds (take account of correlation of wind direction) |
本文采用了KP模型模拟风速母体的尾部分布, 提高了Up-crossings法估计极值风速的准确性.基于优选得到的t Copula函数, 建立了多风向极值风速的联合概率分布模型并计算得到了不同重现期下各风向的极值风速.利用本文方法完成了杭州地区多风向极值风速的估计, 其中考虑了风向相关性的影响.主要结论如下:
(1) 采用KP模型可有效拟合风速母体的尾部分布, 从而获得更为可靠的多风向极值风速联合分布.
(2) 多风向极值风速的联合概率分布可通过多维Copula函数构造, 不同Copula函数的拟合优度可采用AIC准则来检验.
(3) 具有给定重现期的设计风速估计应考虑风向相关性的影响.在不考虑风向相关性的情况下容易给出偏于风险的极值风速估计值.采用本文方法, 可以有效估计考虑风向相关性的多风向极值风速, 为结构抗风性能设计提供更为合理的依据.
| [1] |
李宏男, 王杨, 伊廷华. 极值风速概率方法研究进展[J]. 自然灾害学报, 2009, 18(2): 15-26. LI Hong-nan, WANG Yang, YI Ting-hua. Advance in research onextreme wind speed models[J]. Journal of Natural Disasters, 2009, 18(2): 15-26. |
| [2] |
陈朝晖, VanMarcke, 孙毅, 等. 常规风与飓风的极值风速预测模型评述[J]. 自然灾害学报, 2008, 17(5): 158-163. CHEN Zhao-hui, VANMARCKE Erik, SUN Yi, et al. A review of model predicting extreme wind speed of normal wind and hurricane[J]. Journal of Natural Disasters, 2008, 17(5): 158-163. |
| [3] |
全涌, 姚博, 顾明. 高层建筑结构抗风可靠性研究进展[J]. 同济大学学报:自然科学版, 2015, 43(6): 807-815. QUAN Yong, YAO Bo, GU Ming. Research progress of wind reliability of high-rise buildings[J]. Journal of Tongji University:Natural science, 2015, 43(6): 807-815. |
| [4] |
全涌, 刘磊, 顾明. 考虑风向的极值风速估计的Cook方法改进[J]. 同济大学学报:自然科学版, 2015, 43(2): 189-192. QUAN Yong, LIU Lei, GU Ming. Improvement of Cook method considering directional extreme wind speed[J]. Journal of Tongji University:Natural Science, 2015, 43(2): 189-192. |
| [5] |
韦艳华, 张世英. Copula理论及其在金融分析上的应用[M]. 北京: 清华大学出版社, 2008, 1-40.
|
| [6] |
NELSON R B. An Introduction to Copulas[M]. New York: Springer Series in Statistics, 2006.
|
| [7] |
HUANG M F, TU Z, LI Q, et al. Dynamic wind load combination for a tall building based on copula functions[J]. International Journal of Structural Stability & Dynamics, 2017, 17(8): 1750092. |
| [8] |
涂志斌, 黄铭枫, 楼文娟. 基于Copula函数的建筑动力风荷载相关性组合[J]. 浙江大学学报:工学版, 2014, 48(8): 1370-1375. TU Zhi-bin, HUANG Ming-feng, LOU Wen-juan. Dynamic wind load combination of tall buildings based on Copula functions[J]. Journal of Zhejiang university:Engineering Science, 2014, 48(8): 1370-1375. |
| [9] |
LUO Y, HUANG G. Characterizing dependence of extreme wind pressures[J]. Journal of Structural Engineering (ASCE), 2017, 143(4): 04016208. DOI:10.1061/(ASCE)ST.1943-541X.0001699 |
| [10] |
ZHANG X, CHEN X. Assessing probabilistic wind load effects via a multivariate extreme wind speed model:A unified framework to consider directionality and uncertainty[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2015, 147: 30-42. |
| [11] |
ZHANG X, CHEN X. Influence of dependence of directional extreme wind speeds on wind load effects with various mean recurrence intervals[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2016, 148: 45-56. |
| [12] |
TRIVEDI P K, ZIMMER D M. Copula modeling: an introduction for practitioners. Foundations and Trends in Econometrics[M]. Boston: Now Publishers, 2007: 53-70.
|
| [13] |
GOMES L, VICKERY B J. On the prediction of extreme wind speeds from the parent distribution[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1977, 2(77): 21-36. |
| [14] |
MILFORD R V. Annual maximum wind speeds from parent distribution functions[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1987, 25(2): 163-178. |
| [15] |
WEN Y K. Wind direction and structural reliability[J]. Journal of Structural Engineering, 1983, 109(4): 1028-1041. DOI:10.1061/(ASCE)0733-9445(1983)109:4(1028) |
| [16] |
ISYUMOV N, HO E, CASE P. Influence of wind directionality on wind loads and responses[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2014, 133: 169-180. |
| [17] |
NAESS A, GAIDAI O. Estimation of extreme values from sampled time series[J]. Structural Safety, 2009, 31(4): 325-334. DOI:10.1016/j.strusafe.2008.06.021 |
| [18] |
KARPA O, NAESS A. Extreme value statistics of wind speed data by the ACER method[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2013, 112(1): 1-10. |
| [19] |
AAS K, CZADO C, FRIGESSI A, et al. Pair-copula constructions of multiple dependence[J]. Insurance Mathematics & Economics, 2009, 44(2): 182-198. |
| [20] |
COOK N J. Note on directional and seasonal assessment of extreme winds for design[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1983, 12(3): 365-372. |
| [21] |
陈凯, 金新阳, 钱基宏. 考虑地貌修正的基本风压计算方法研究[J]. 北京大学学报:自然科学版, 2012, 48(1): 13-19. CHEN Kai, JIN Xin-yang, QIAN Ji-hong. Calculation method on the reference wind pressure accounting for the terrain variations[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2012, 48(1): 13-19. |
| [22] |
GRIGORIU M. Algorithms for generating large sets of synthetic directional wind speed data for hurricane, thunderstorm, and synoptic winds[R]. : NIST Technical Note, 2009.
|


